Координаты и векторы

1.

B1
A1
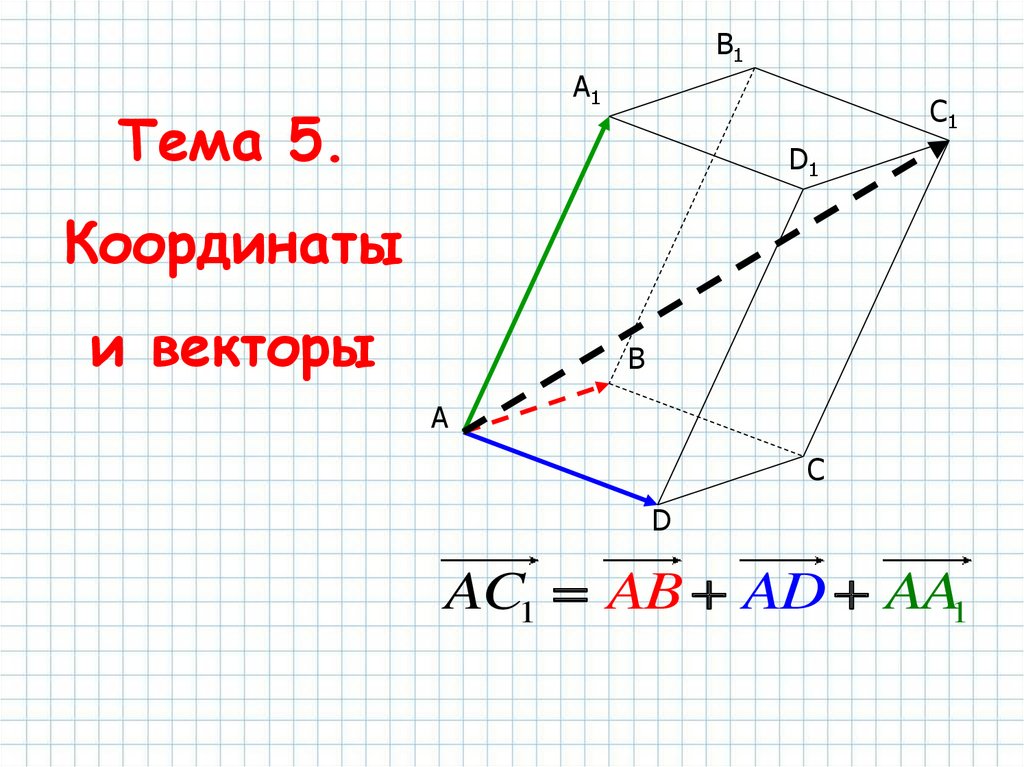
Тема 5.
C1
D1
Координаты
и векторы
B
A
C
D
AC1 AB AD AA1

2. Тема 5. Координаты и векторы

I. Определение вектора.
Основные понятия, связанные с векторами.

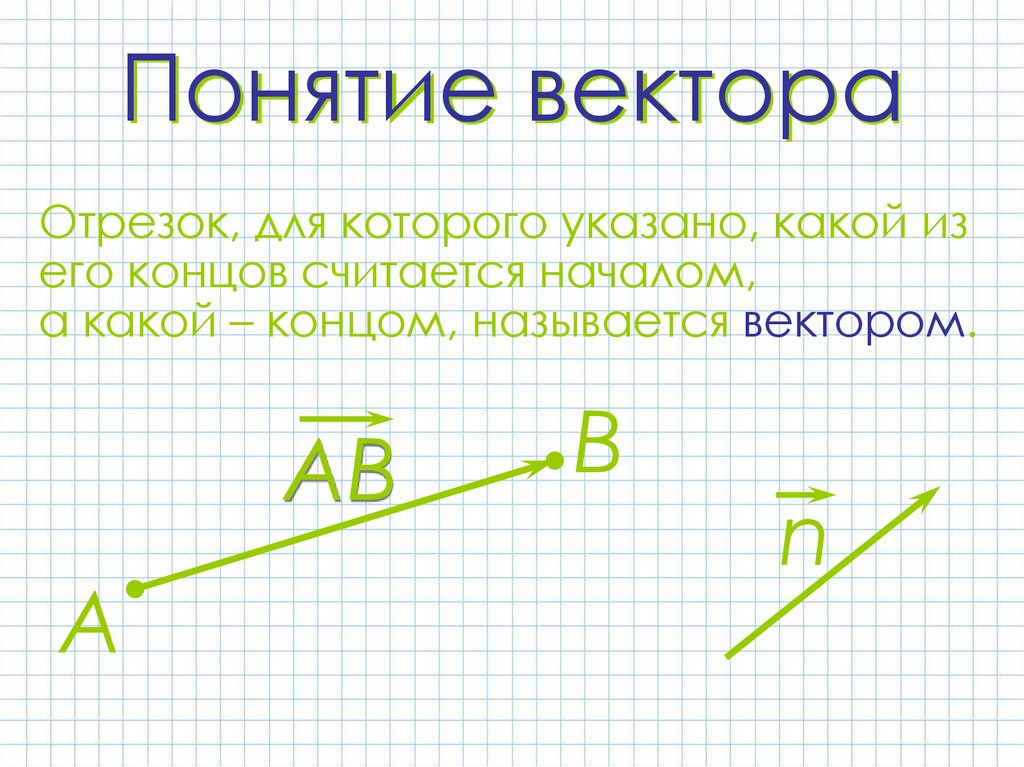
3. Понятие вектора

Отрезок, для которого указано, какой из
его концов считается началом,
а какой – концом, называется вектором.
АВ
А
В
n

4. Нулевой вектор

Любая точка на плоскости может
рассматриваться как вектор.
Такой вектор называется нулевым.
М
ММ = 0

5. Длина вектора

Длиной ненулевого вектора АВ
называется длина отрезка АВ.
В
а
А
АВ = а
0
0 = 0

6.

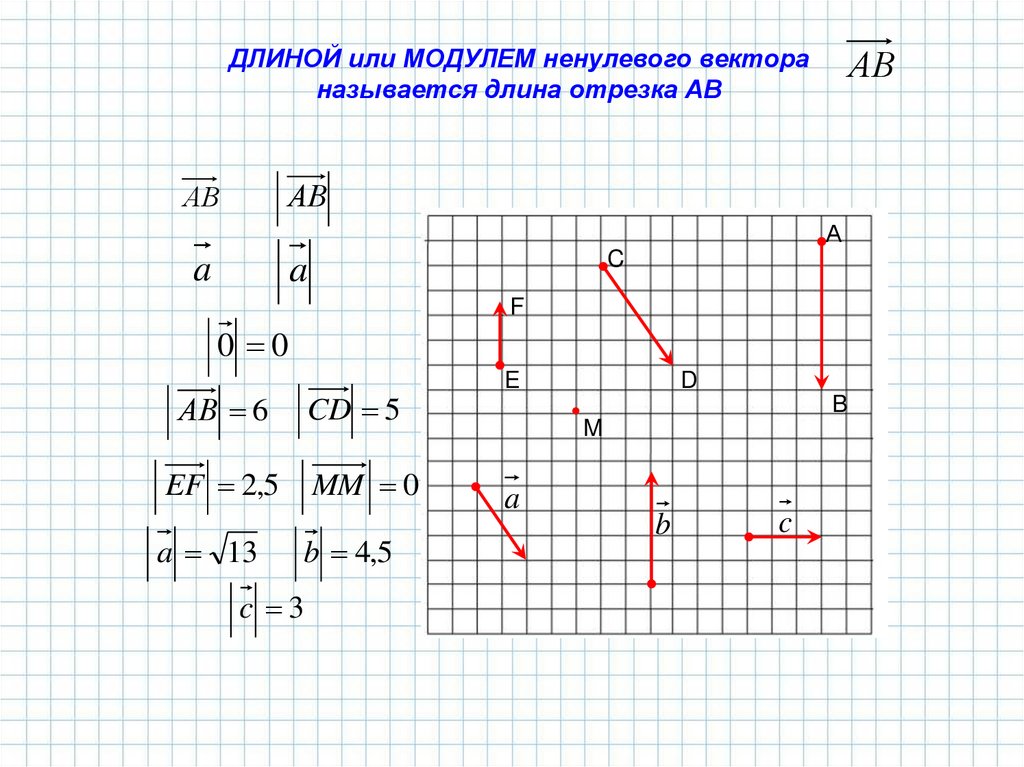
ДЛИНОЙ или МОДУЛЕМ ненулевого вектора
называется длина отрезка АВ
АВ
АВ
АВ
А
a
C
a
F
0 0
CD 5
АВ 6
EF 2,5
a 13
MM 0
b 4,5
c 3
E
D
B
M
a
b
c

7.

Как и в плоскости, в пространстве ВЕКТОР определяется как
B
направленный отрезок:
A
Точка А – начало вектора, В – конец вектора. Записывают:
AB
или
a.
Обычную точку в пространстве мы также можем считать вектором, у которого
начало совпадает с конечной точкой. Такой вектор называется нулевым и
обозначается: 0 или AA .
0
A
Длина отрезка, изображающего вектор, называется модулем (или абсолютной
величиной) вектора, т.е.
AB AB åä.î ò ð. .
Естественно, что
B
AA 0.
Векторы AB и BA являются
противоположными. Очевидно, что:
AB BA .
A

8.

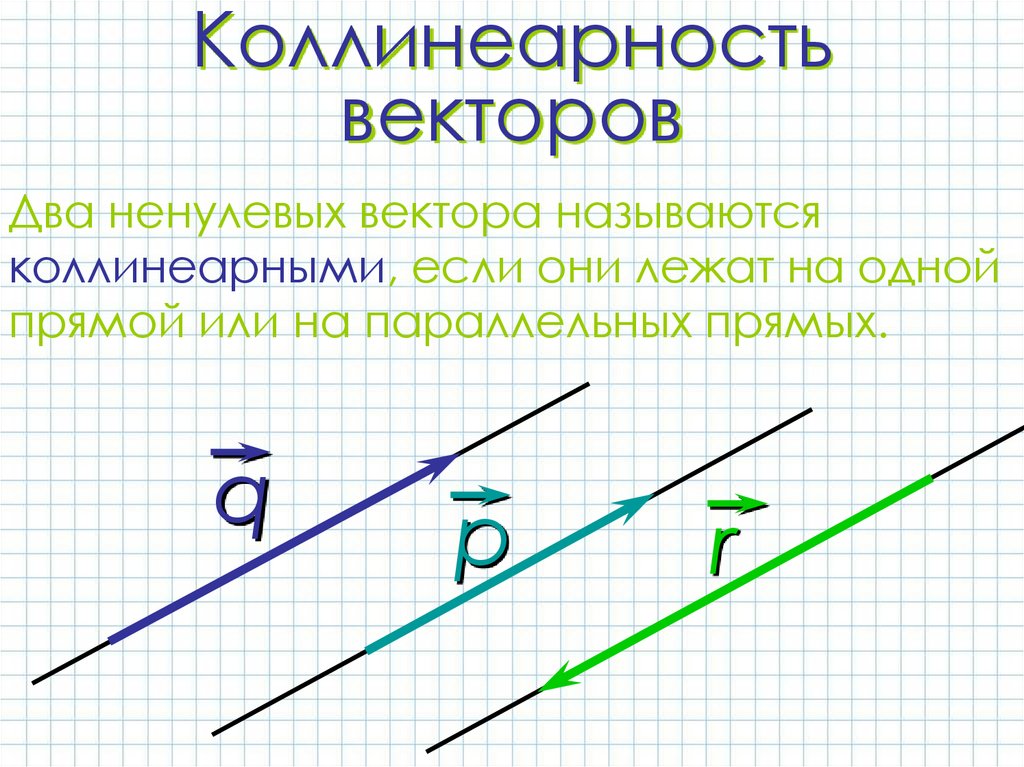
9. Коллинеарность векторов

Два ненулевых вектора называются
коллинеарными, если они лежат на одной
прямой или на параллельных прямых.
q
р
r

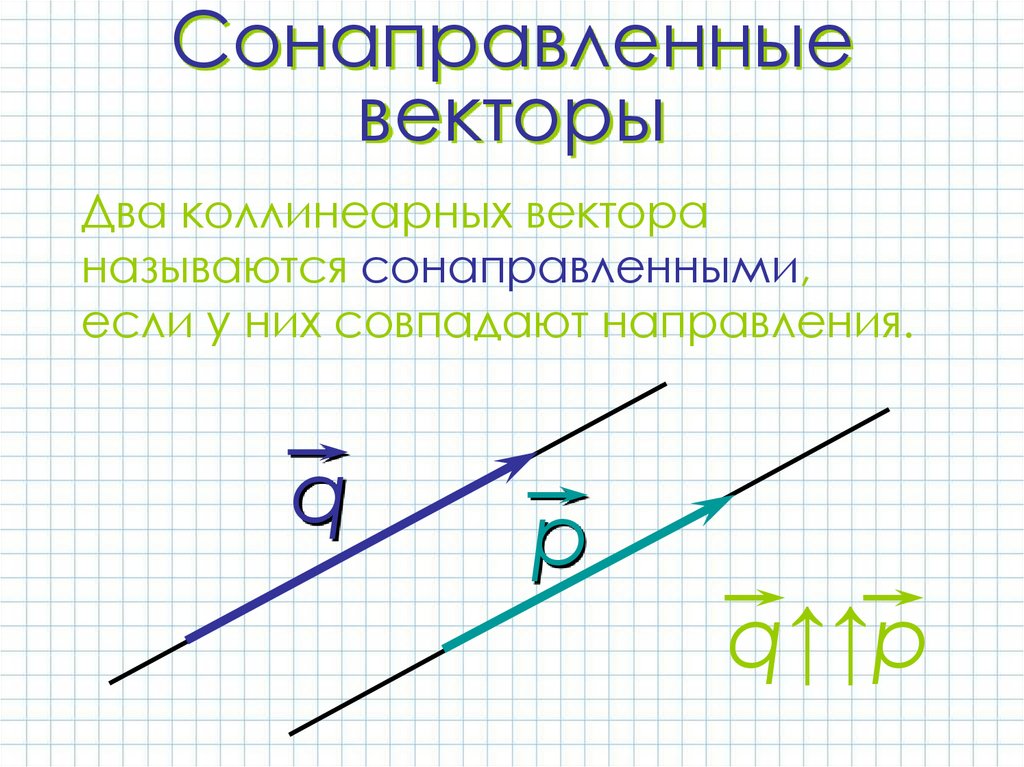
10. Сонаправленные векторы

Два коллинеарных вектора
называются сонаправленными,
если у них совпадают направления.
q
р
q↑↑р

11. Противоположно направленные векторы

Два коллинеарных вектора называются
противоположно направленными, если
они не сонаправлены.
а
b
a↑↓b

12.

Два вектора называются коллинеарными, если они лежат на одной прямой или на
параллельных прямых:
m n
Обозначение коллинеарных векторов:
a b, a c, c b.
Коллинеарные векторы, в свою очередь, бывают одинаково направленными (или
соноправленными) и противоположно направленными. В нашем случае:
a ↑↑ c
– соноправленные векторы,
a ↑↓ b , c ↑↓ b
– противоположно
направленные векторы.
Два вектора называются равными, если: 1) они соноправлены; и 2) их модули
равны, т.е.
a b a ↑↑ b è a b
a
b

13.

14.

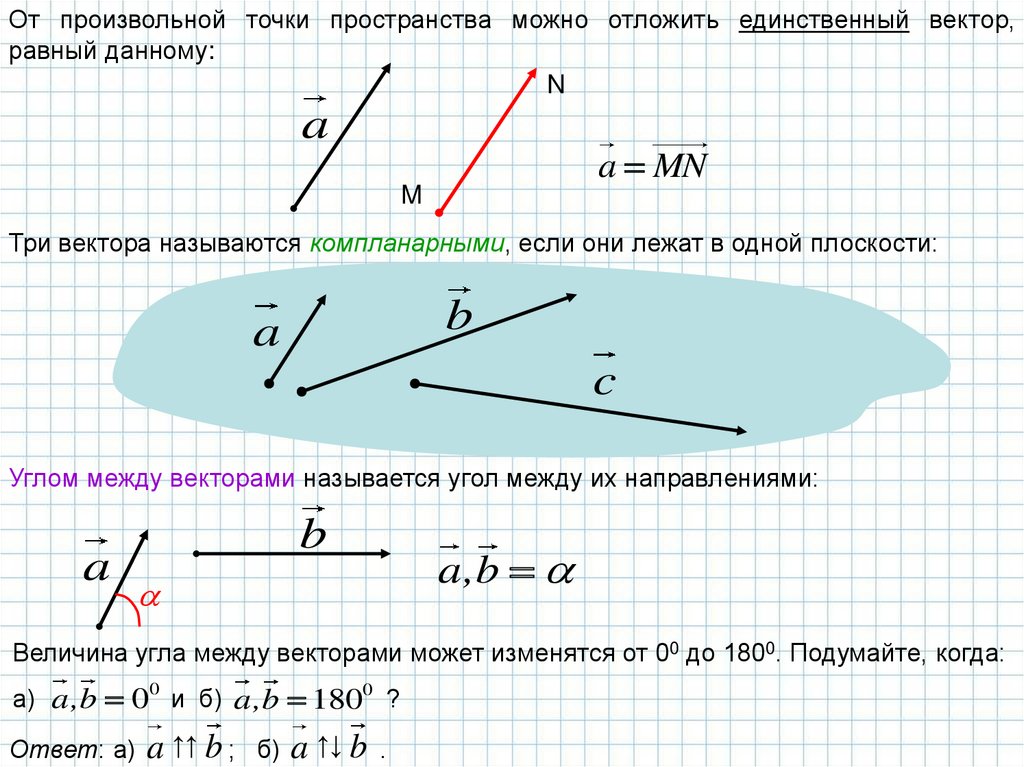
От произвольной точки пространства можно отложить единственный вектор,
равный данному:
N
a
a MN
M
Три вектора называются компланарными, если они лежат в одной плоскости:
b
a
c
Углом между векторами называется угол между их направлениями:
a
b
a,b
Величина угла между векторами может изменятся от 00 до 1800. Подумайте, когда:
а) a,b 0 и б) a,b 1800 ?
0
Ответ: а)
a ↑↑ b ;
б)
a ↑↓ b
.

15. Тема 5. Координаты и векторы

II. Действия с векторами

16.

ОТКЛАДЫВАЕНИЕ ВЕКТОРА
ОТ ДАННОЙ ТОЧКИ
a
А
вектор
a отложен
от точки А
https://youtu.be/DlLM97OvqsA

17.

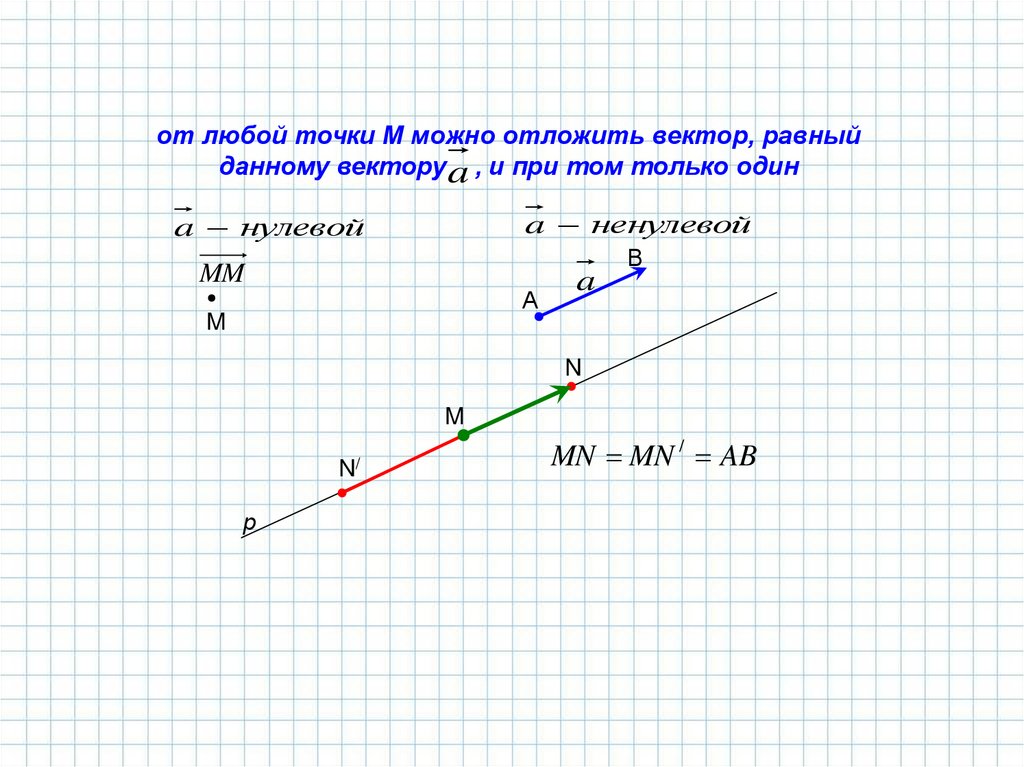
от любой точки М можно отложить вектор, равный
данному вектору a , и при том только один
a ненулевой
a нулевой
MM
А
M
a
В
N
M
N/
р
MN MN / AB

18.

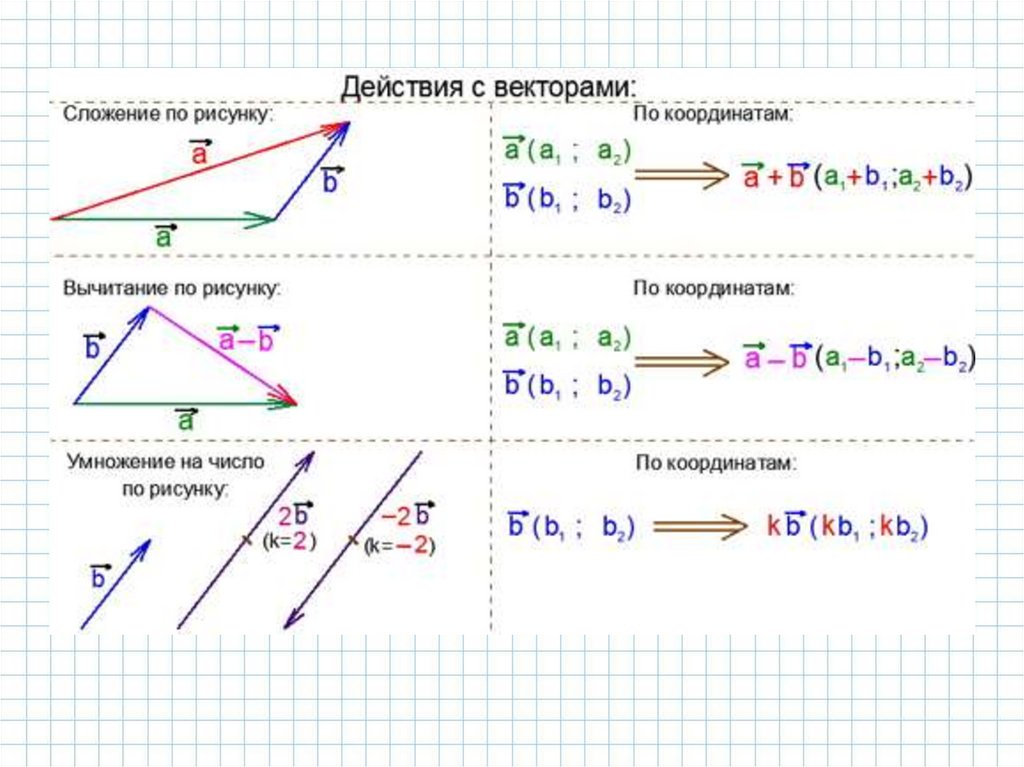
Векторы можно складывать – в результате получается вектор. При сложении двух
векторов применяются
Правило треугольника:
a b
a
b
a b
O
a
F
b

19.

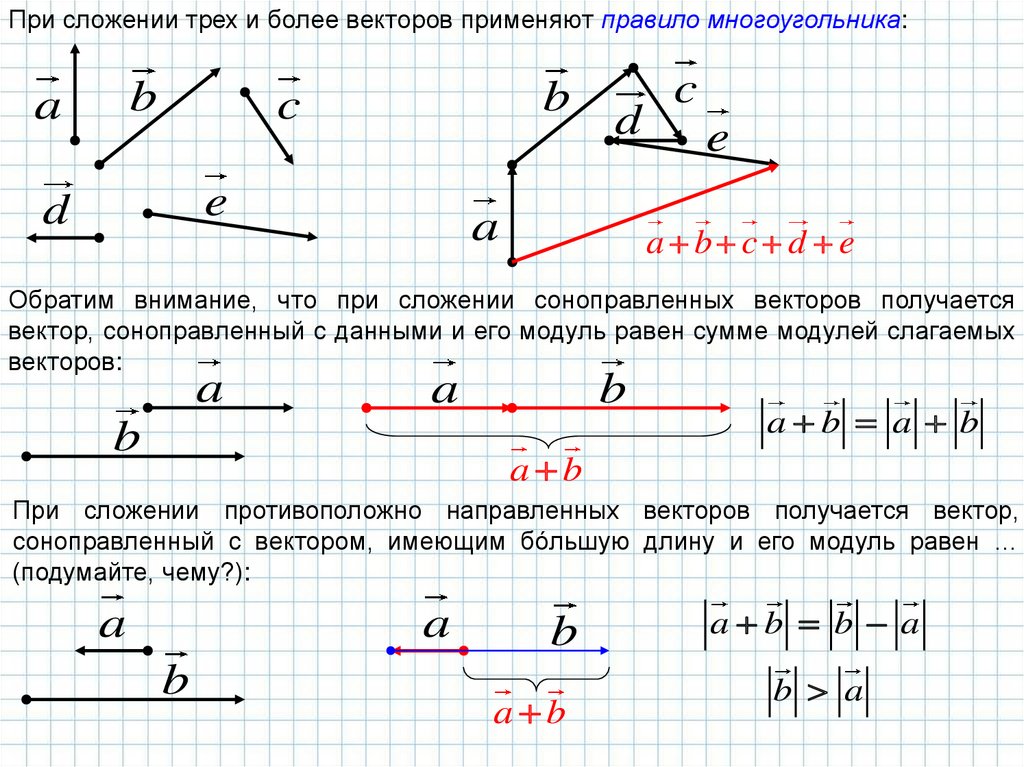
При сложении трех и более векторов применяют правило многоугольника:
b
a
b
c
e
d
d
a
c
e
a b c d e
Обратим внимание, что при сложении соноправленных векторов получается
вектор, соноправленный с данными и его модуль равен сумме модулей слагаемых
векторов:
a
a
b
b
a b a b
a b
При сложении противоположно направленных векторов получается вектор,
соноправленный с вектором, имеющим бóльшую длину и его модуль равен …
(подумайте, чему?):
a
a
b
b
a b
a b b a
b a

20.

Также можно найти разность двух векторов – в результате получается вектор. При
вычитании двух векторов применяется видоизмененное правило треугольника –
вначале оба вектора строятся с общей начальной точкой, затем соединяются
концы этих векторов с выбором направления к «уменьшаемому» вектору:
b
a
a b
Или: т.к. a b a b
, то можно вначале построить вектор, противоположный
вектору b , а затем оба вектора сложить по правилу треугольника.
a
–
b
a b

21. Задача 1.

22.

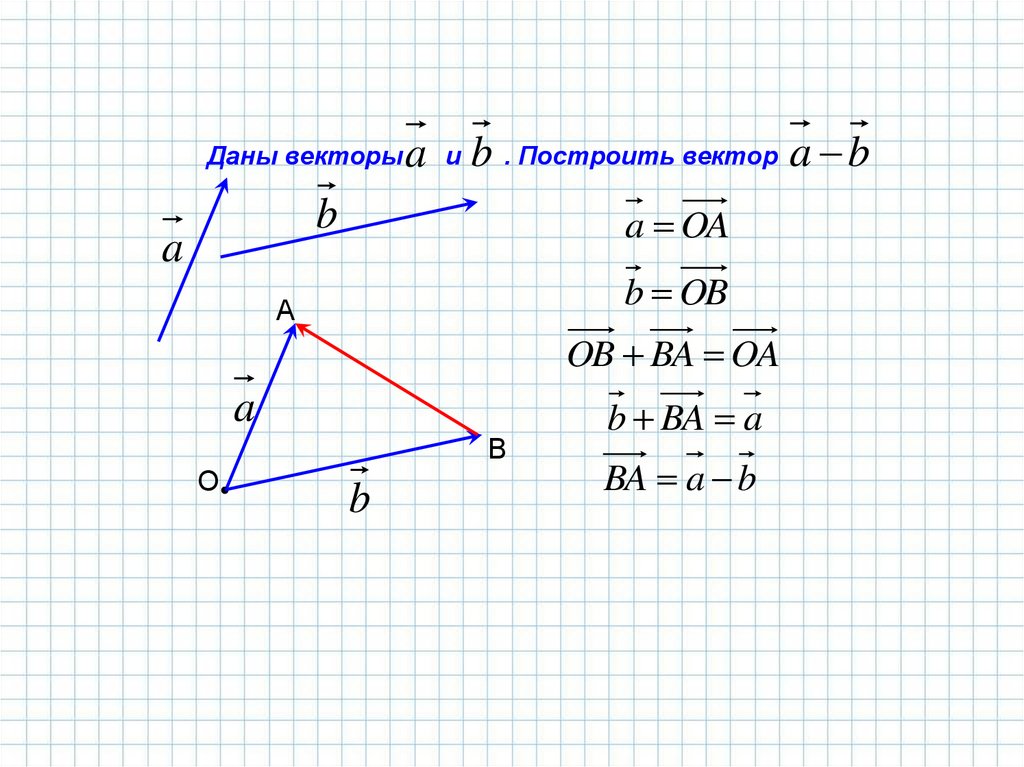
Даны векторы
a и b . Построить вектор a b
b
a
a OA
b OB
А
OB BA OA
a
В
О
b
b BA a
BA a b

23.

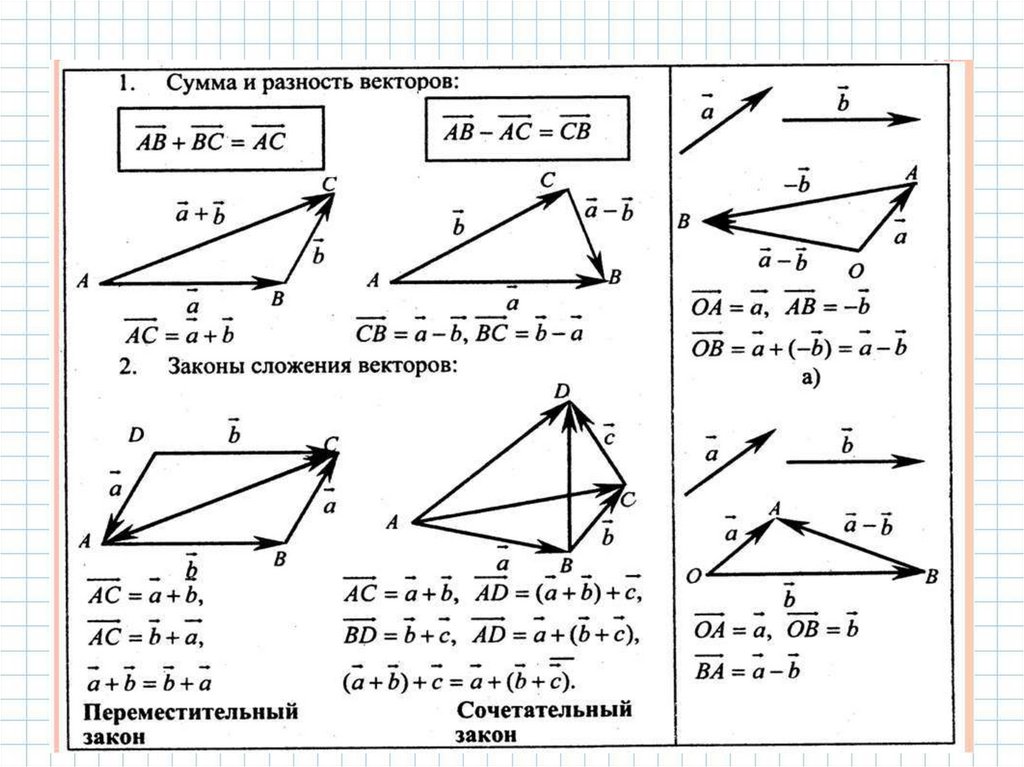
Сложение векторов, как и сложение чисел подчиняется законам:
1)
a b b a
2)
a b c a b c – сочетательный закон сложения;
– переместительный закон сложения;
a 0 a ;
4) a a 0 .
3)
Следующее действие с векторами – умножение вектора на число k. В результате
этого действия получается вектор, причем:
1) если k>0, то
2) если k<0, то
k a ↑↑ a
k a ↑↓ a
ka k · a ;
и ka k · a ;
и
3) если k=0, то 0 ·a 0 .
a
8
a
3
0·a
3a
2a
4
a
3

24.

И еще одно действие с векторами – умножение двух векторов. В школьном курсе
геометрии изучается скалярное произведение векторов. В результате этого
действия (в отличии от предыдущих действий с векторами) получается число,
равное произведению модулей двух данных векторов на косинус угла между этими
векторами, т.е.
a·b a · b ·cos a,b.
Геометрически скалярное произведение векторов можно понимать как площадь
параллелограмма (или противоположная ей величина), стороны которого
образуются одним из данных векторов и вектором, перпендикулярным второму с
таким же модулем:
S a ·b' ·sin 900 a ·b ·cos a·b;
S a ·b' ·sin 900 a ·b ·cos a·b.
ò .å. a·b S
a
900
b'
b b'
b'
– острый угол
a
b
900
– тупой угол
b

25.

26.

Задача 2.
Упростить выражение:
Решение:
Первый распределительный закон позволяет нам раскрыть скобки.
А переместительное свойство сложения векторов – привести подобные.

27.

28.

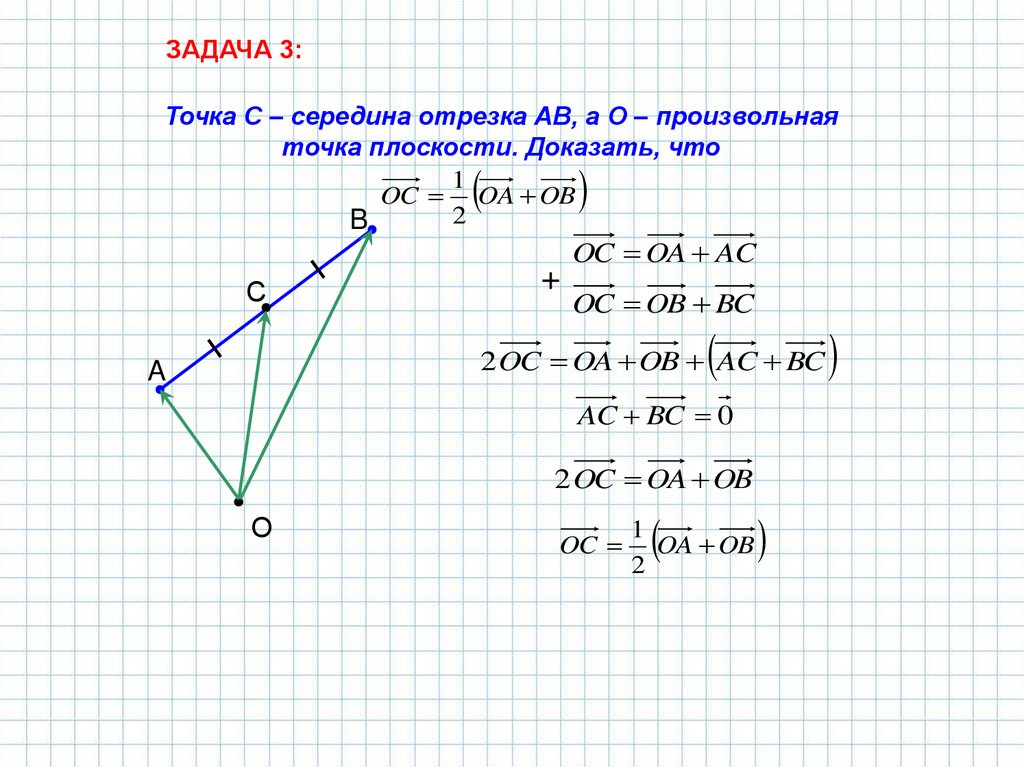
ЗАДАЧА 3:
Точка С – середина отрезка АВ, а О – произвольная
точка плоскости. Доказать, что
1
OC OA OB
2
B
С
+
OC OA AC
OC OB BC
2 OC OA OB AC BC
A
AC BC 0
2 OC OA OB
О
OC
1
OA OB
2

29.

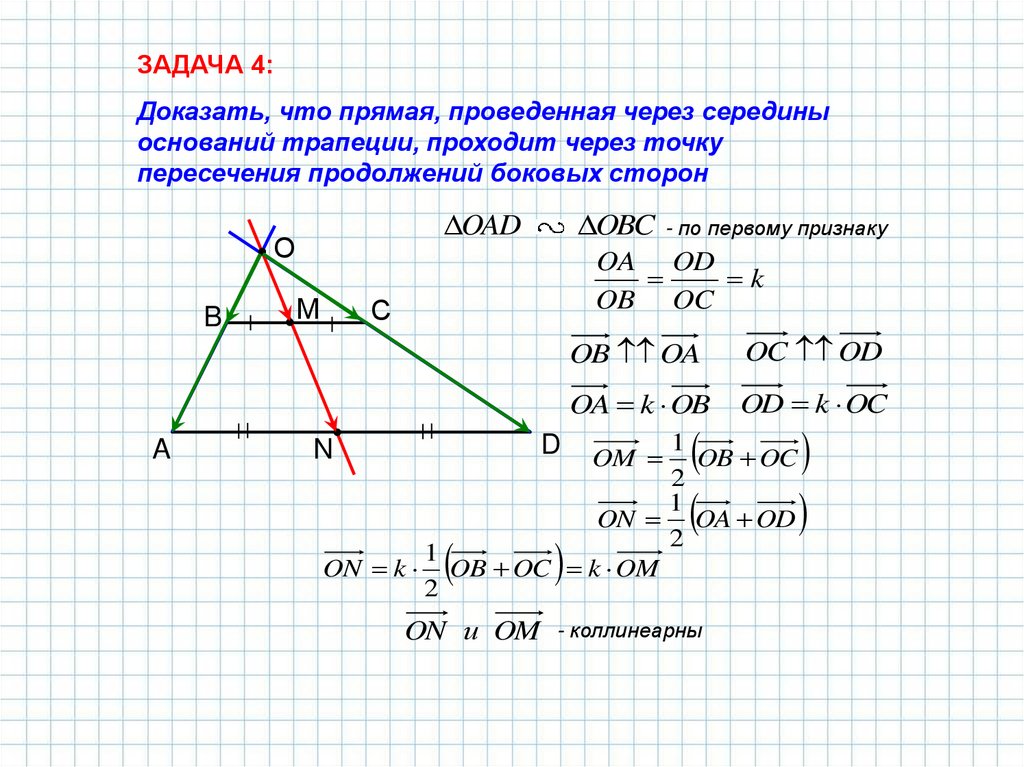
ЗАДАЧА 4:
Доказать, что прямая, проведенная через середины
оснований трапеции, проходит через точку
пересечения продолжений боковых сторон
О
B
A
OBC
OAD
М
- по первому признаку
OA OD
k
OB OC
С
OB OA
OC OD
OA k OB
OD k OC
1
OB OC
2
1
ON OA OD
2
1
ON k OB OC k OM
2
D
N
ON и OM
OM
- коллинеарны

30.

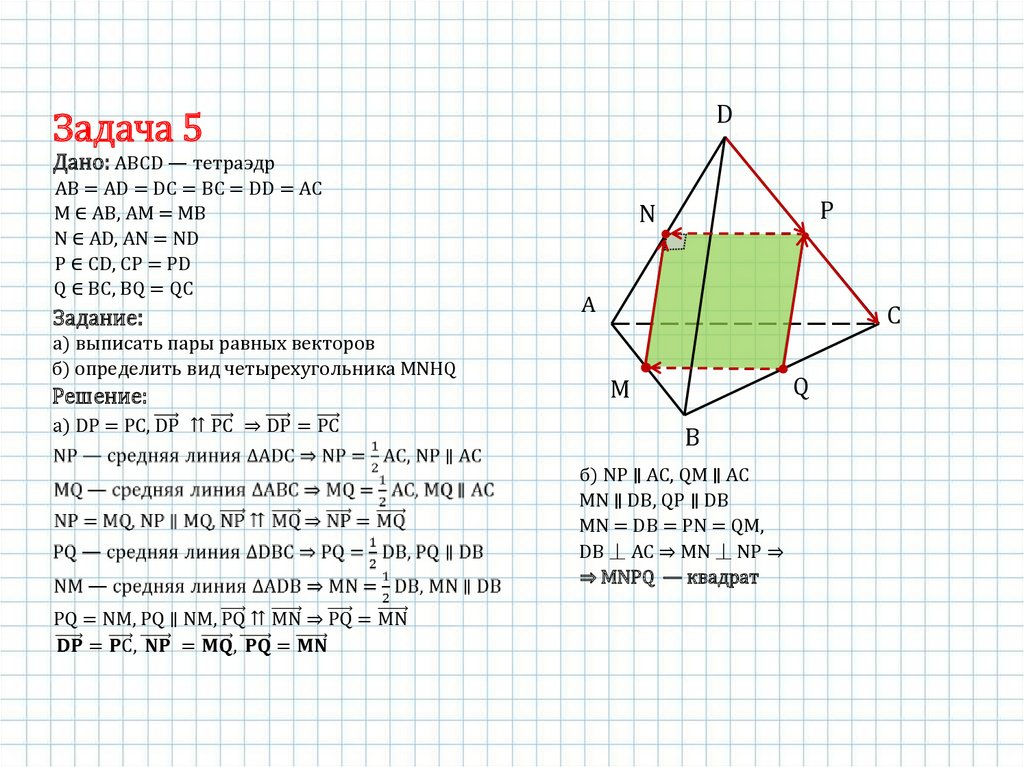
D
Задача 5
Дано: АВСD — тетраэдр
AB = AD = DC = BC = DD = AC
M ∈ АB, AM = MB
N ∈ AD, AN = ND
P ∈ СD, CP = PD
Q ∈ BС, BQ = QC
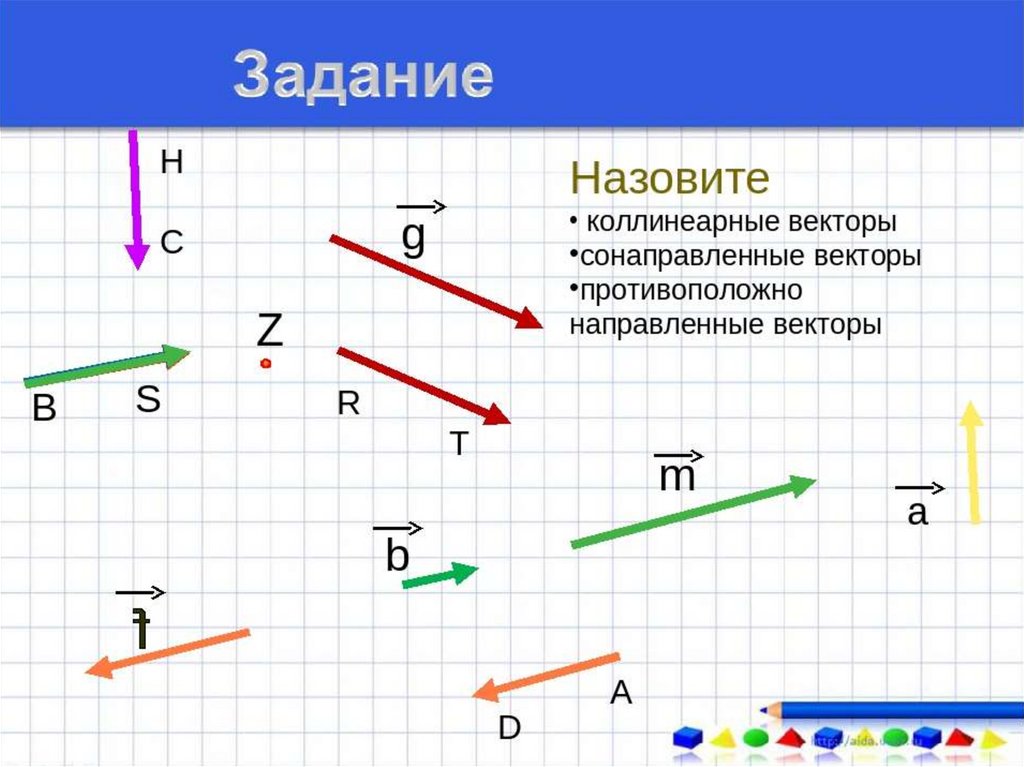
Задание:
а) выписать пары равных векторов
б) определить вид четырехугольника MNHQ
Решение:
P
N
A
C
Q
M
B
б) NP ∥ АС, QM ∥ АС
MN ∥ DB, QP ∥ DB
MN = DB = PN = QM,
DB ⏊ AC ⇒ MN ⏊ NP ⇒
⇒ MNPQ — квадрат

31.

Задача 6
Упростить выражение:
Решение:
- Заменим в выражении
на сумму.
- Для этого заменим
отрицательные векторы
на противоположные.
Вектор – ВС = вектор СВ,
вектор – РМ = вектор МР.
Вектор – АР = вектор РА.
Вектор АС + вектором СВ =
вектор АВ.
Векторы МР + РА = вектор
МА.
Затем, складывая векторы АВ и ВМ,
получаем вектор АМ.
В итоге сумма векторов АМ и МА дают нулевой
вектор. Выражение упрощено.