Стереометрия (многогранники)

1.

СТЕРЕОМЕТРИЯ
(МНОГОГРАННИКИ)

2.

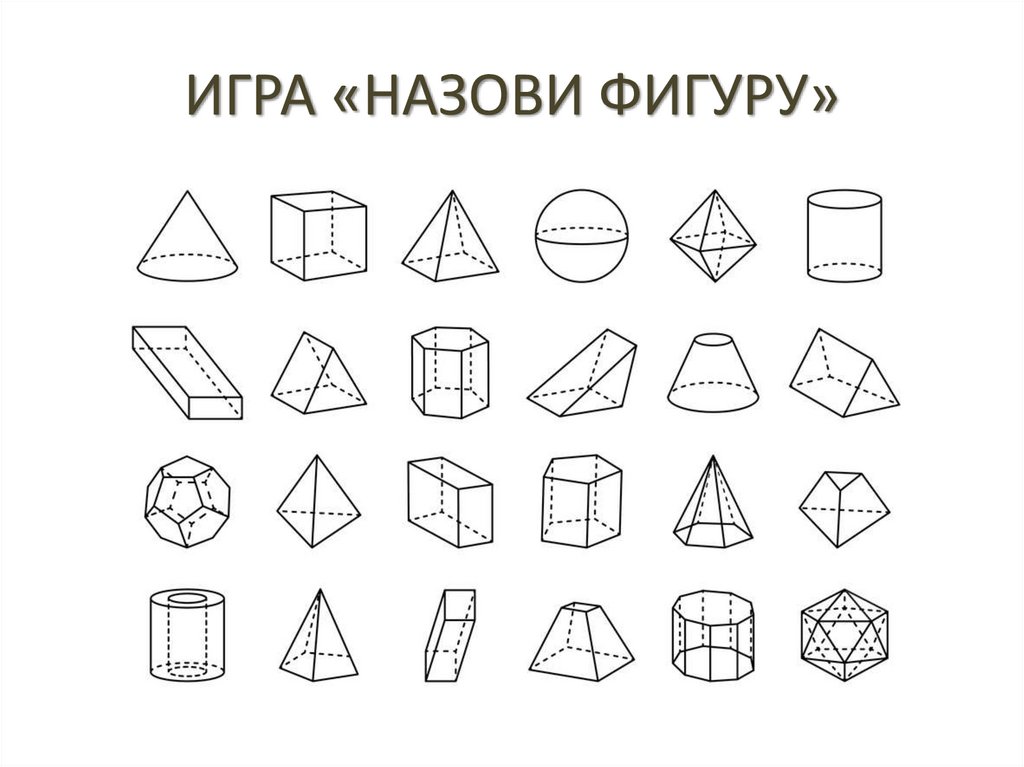
ИГРА «НАЗОВИ ФИГУРУ»

3.

4.

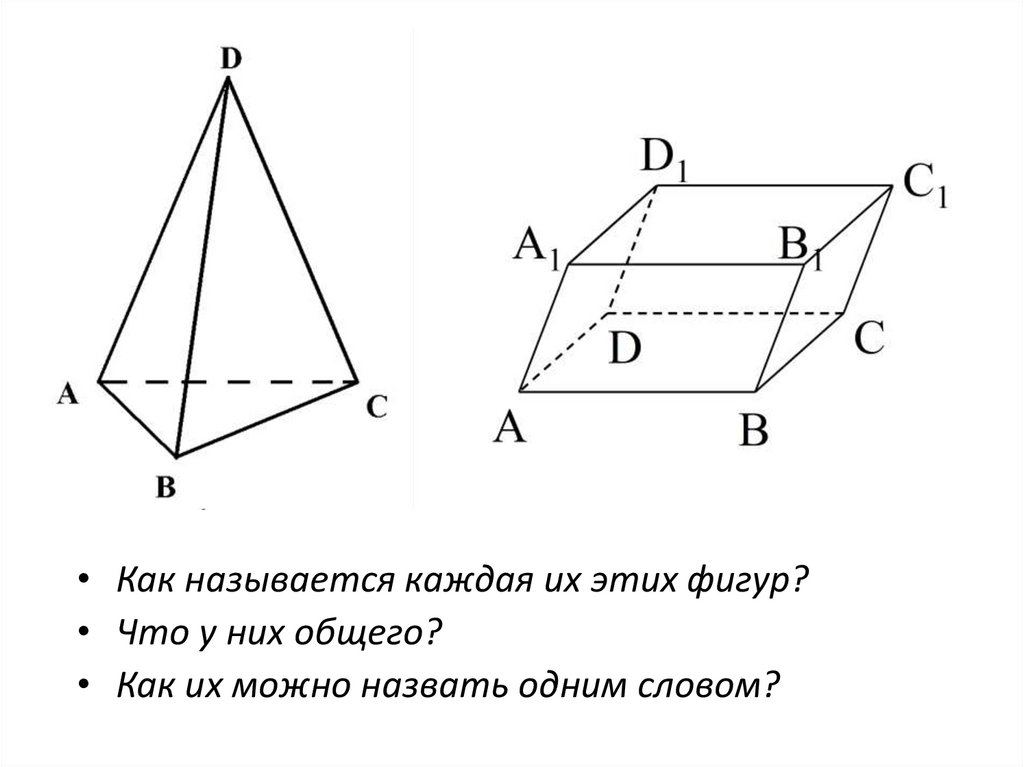
• Как называется каждая их этих фигур?
• Что у них общего?
• Как их можно назвать одним словом?

5.

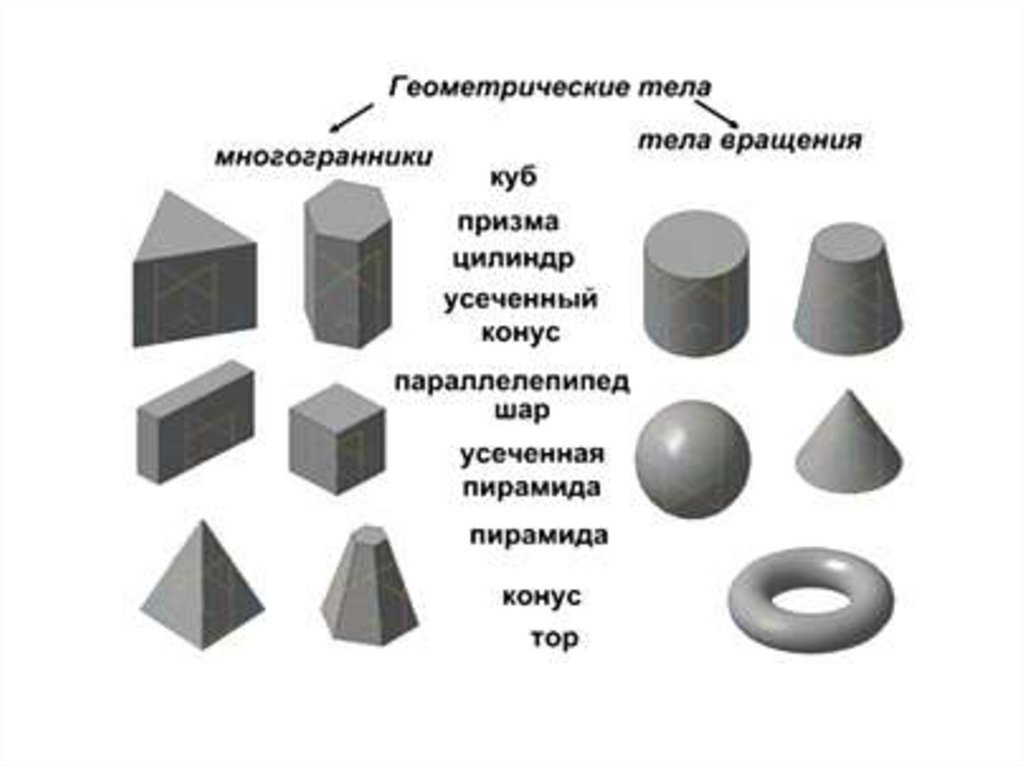
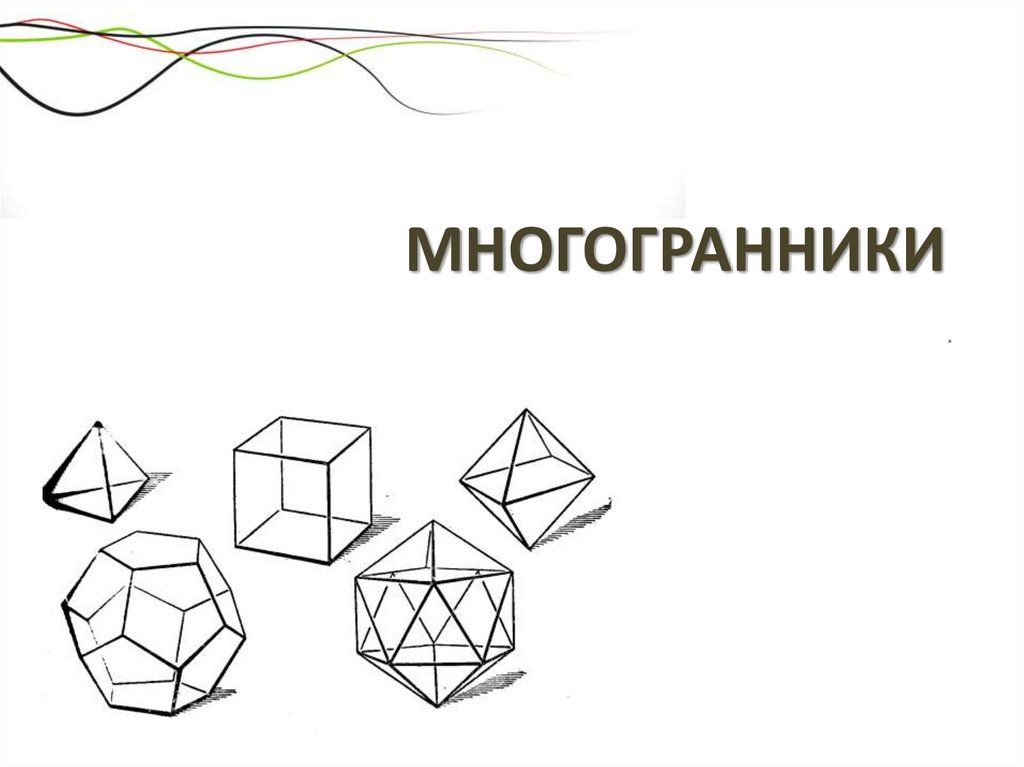
МНОГОГРАННИКИ
.

6.

Понятие многогранника
Попробуем сами сформулировать определение…
Опр.: МНОГОГРАННИК – поверхность, составленная
из многоугольников и ограничивающая некоторое
геометрическое тело.
*(само тело тоже называется многогранником)

7.

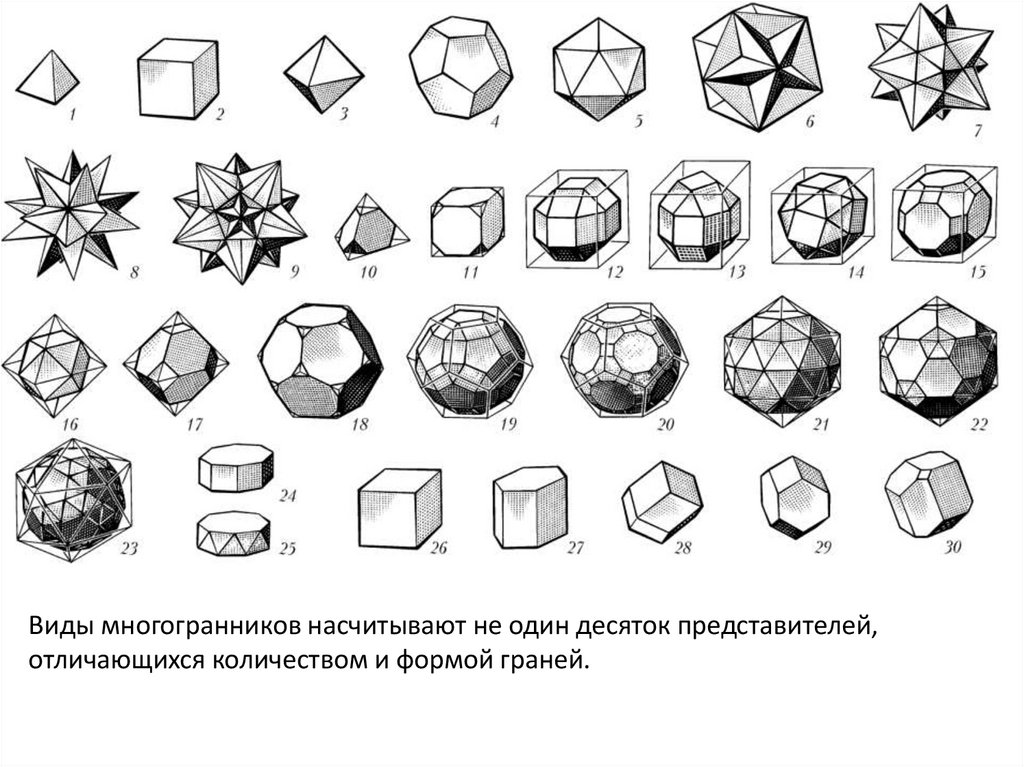
Виды многогранников насчитывают не один десяток представителей,
отличающихся количеством и формой граней.

8.

9.

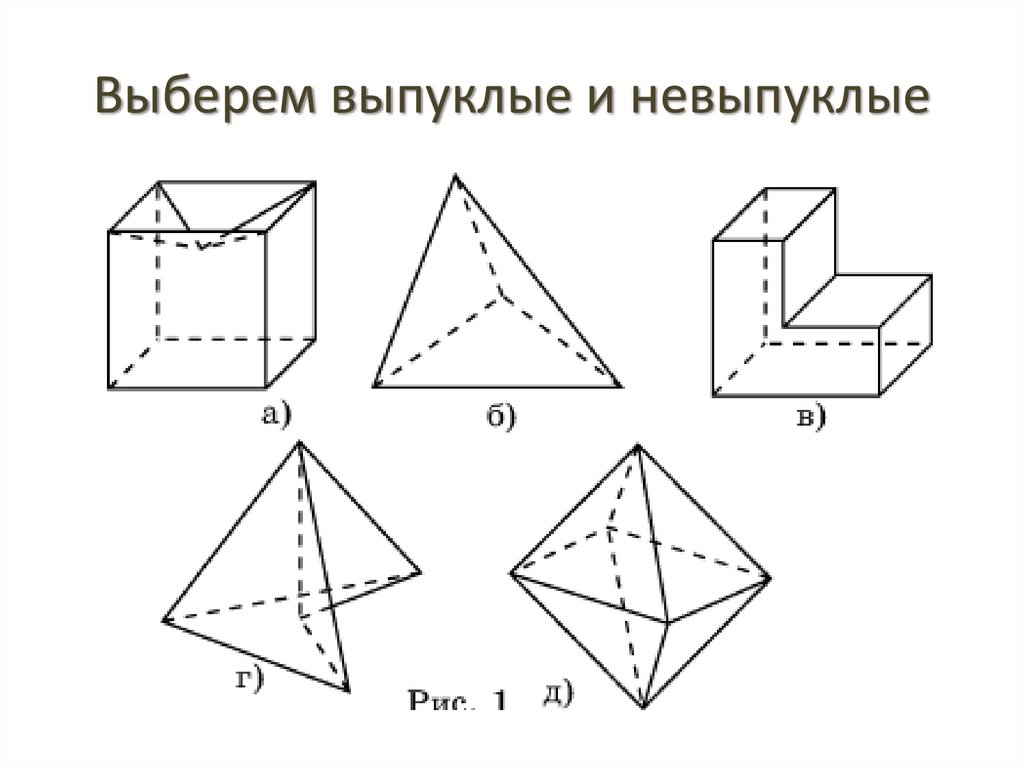
Многогранники делятся на:
• Выпуклые
Многогранник называется выпуклым, если он расположен
по одну сторону от плоскости каждой его грани.
*Грани выпуклого многогранника являются выпуклыми
многоугольниками;
** В выпуклом многограннике сумма всех плоских углом
при каждой его вершине меньше 3600 .
• Невыпуклые

10.

Выберем выпуклые и невыпуклые

11.

Общие свойства многогранников:
Все они имеют 3 неотъемлемых компонента:
грани – многоугольники, из которых составлен
многогранник;
ребра – стороны граней многогранника;
вершины – концы ребер.
Каждое ребро многоугольника соединяет две, и только две
грани, которые по отношению друг к другу являются
смежными.

12.

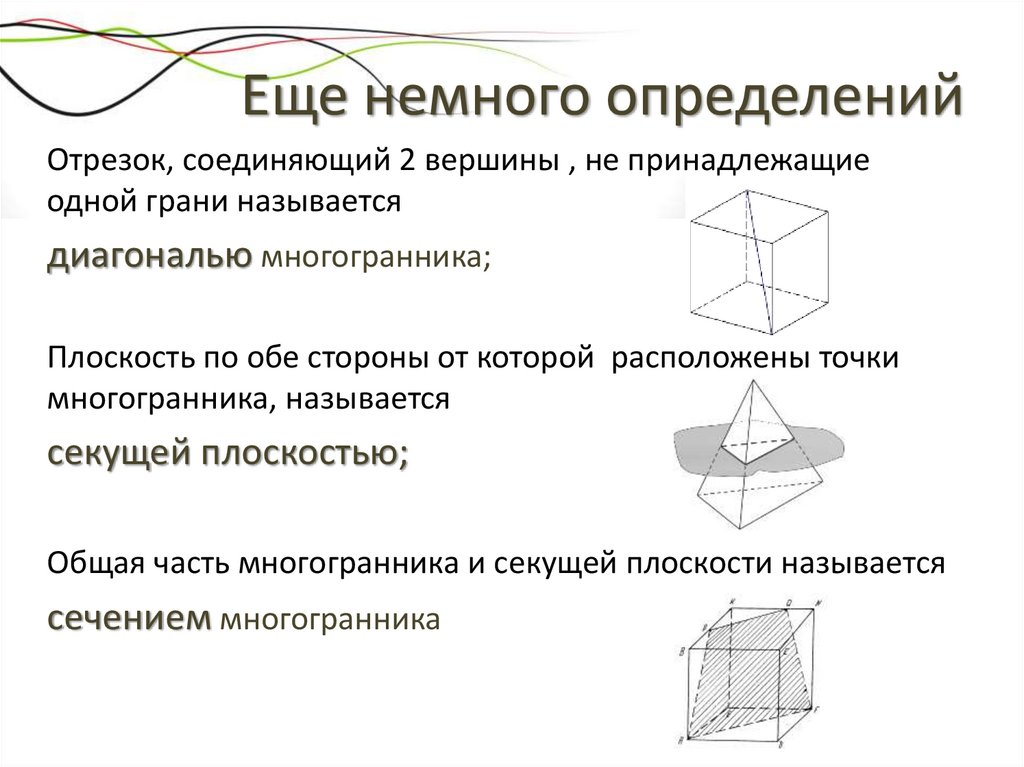
Еще немного определений
Отрезок, соединяющий 2 вершины , не принадлежащие
одной грани называется
диагональю многогранника;
Плоскость по обе стороны от которой расположены точки
многогранника, называется
секущей плоскостью;
Общая часть многогранника и секущей плоскости называется
сечением многогранника

13.

Теорема Эйлера
Леонард Эйлер (1707 - 1783)
Th: В любом выпуклом многограннике сумма
числа граней и числа вершин больше числа
ребер на 2.
Г+В–Р=2

14.

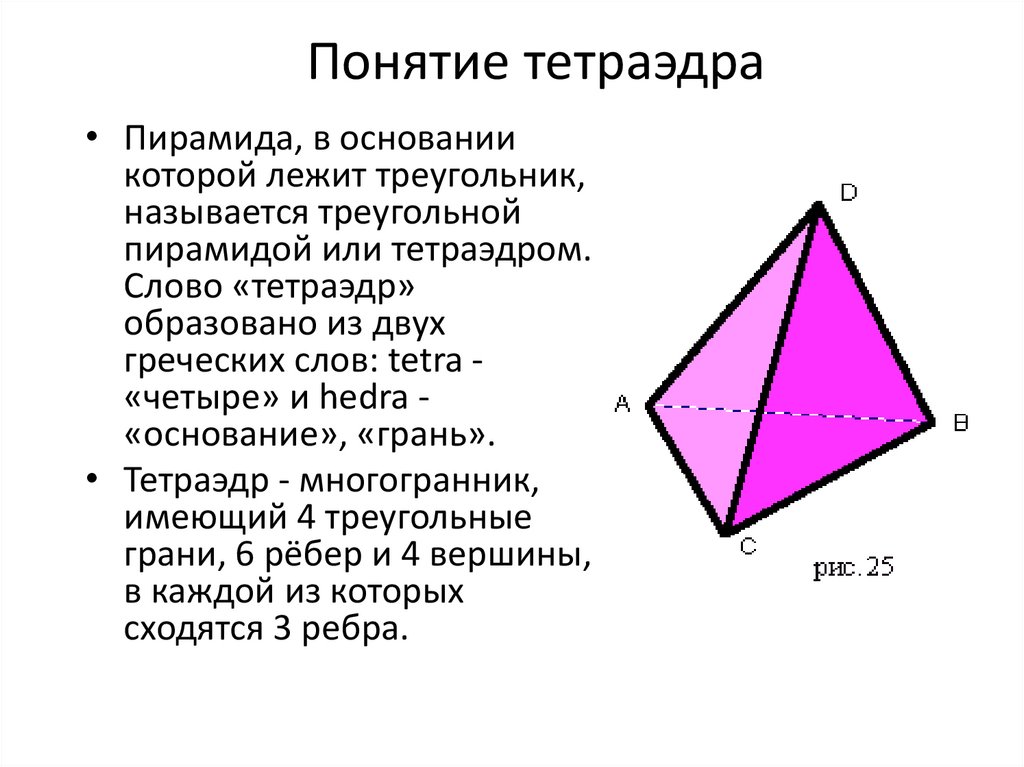
Понятие тетраэдра
• Пирамида, в основании
которой лежит треугольник,
называется треугольной
пирамидой или тетраэдром.
Слово «тетраэдр»
образовано из двух
греческих слов: tetra «четыре» и hedra «основание», «грань».
• Тетраэдр - многогранник,
имеющий 4 треугольные
грани, 6 рёбер и 4 вершины,
в каждой из которых
сходятся 3 ребра.

15.

Построение тетраэдра
• Изображают обычно тетраэдр как
четырехугольник с диагоналями, одну из
которых (соответствующую невидимому
ребру) изображают пунктирно.
D
С
А
В

16.

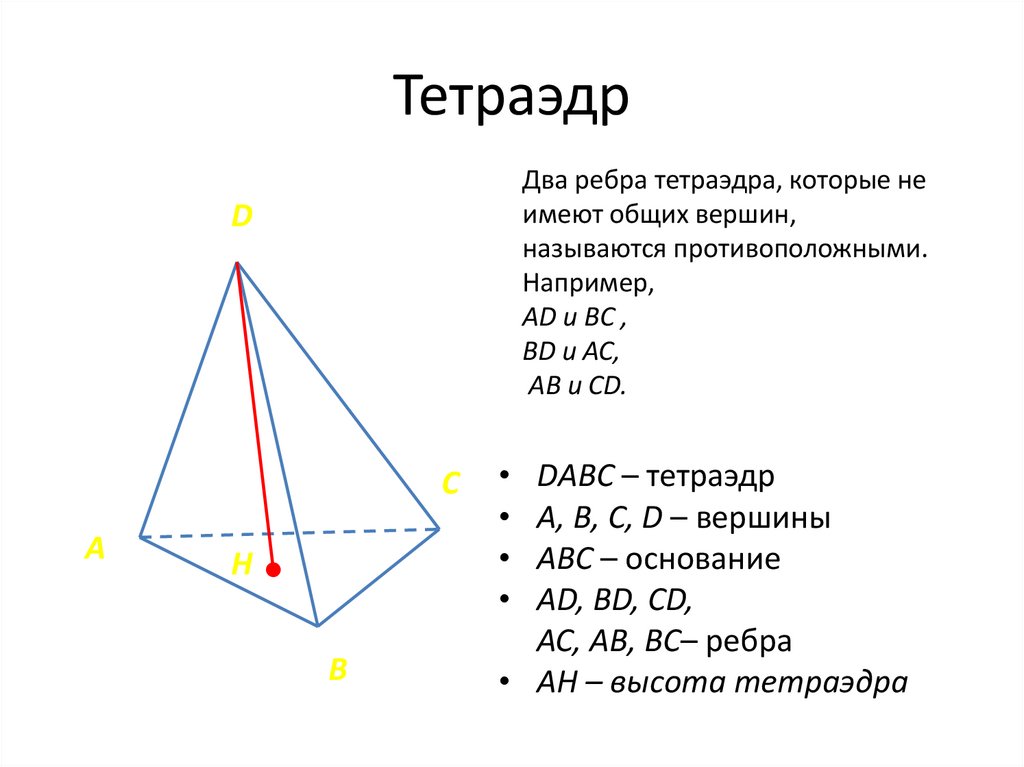
Тетраэдр
Два ребра тетраэдра, которые не
имеют общих вершин,
называются противоположными.
Например,
АD и ВС ,
ВD и АС,
АВ и СD.
D
C
A
H
B
DАВС – тетраэдр
А, В, С, D – вершины
АВС – основание
АD, ВD, СD,
АС, АВ, ВС– ребра
• АH – высота тетраэдра

17.

ПРИЗМА

18.

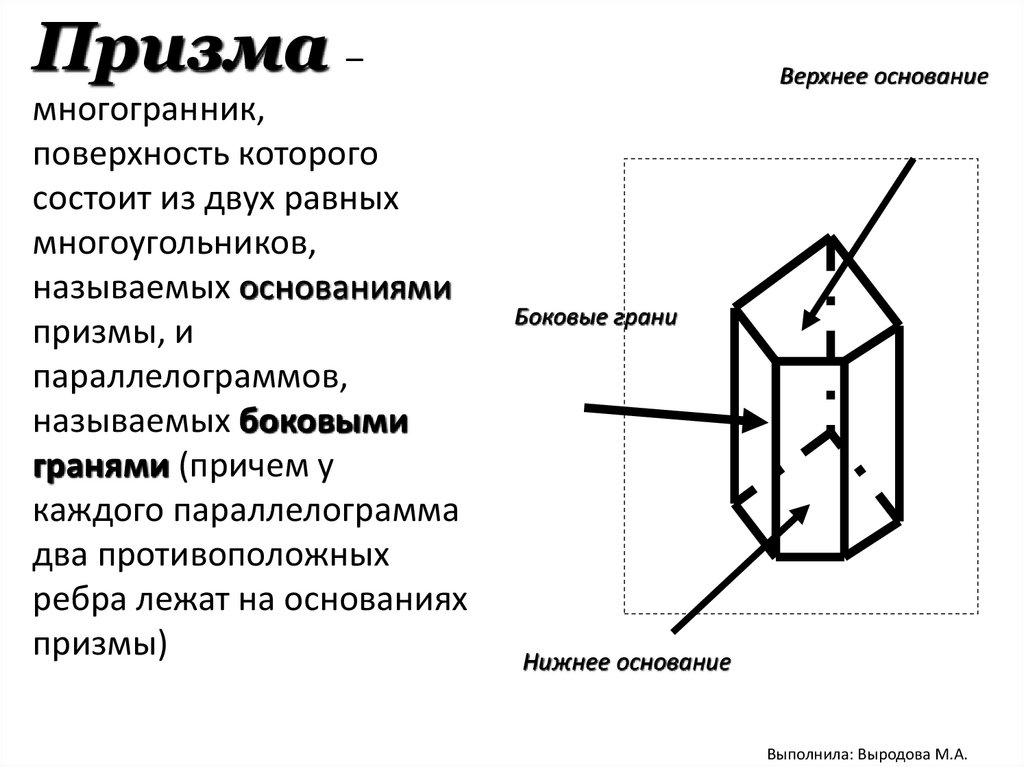
Определение
Опр.: ПРИЗМА - многогранник, составленный из
двух равных n- угольников, расположенных в
параллельных плоскостях, и n параллелограммов

19.

Призма –
многогранник,
поверхность которого
состоит из двух равных
многоугольников,
называемых основаниями
призмы, и
параллелограммов,
называемых боковыми
гранями (причем у
каждого параллелограмма
два противоположных
ребра лежат на основаниях
призмы)
Верхнее основание
Боковые грани
Нижнее основание
Выполнила: Выродова М.А.

20.

Нарисуем призму

21.

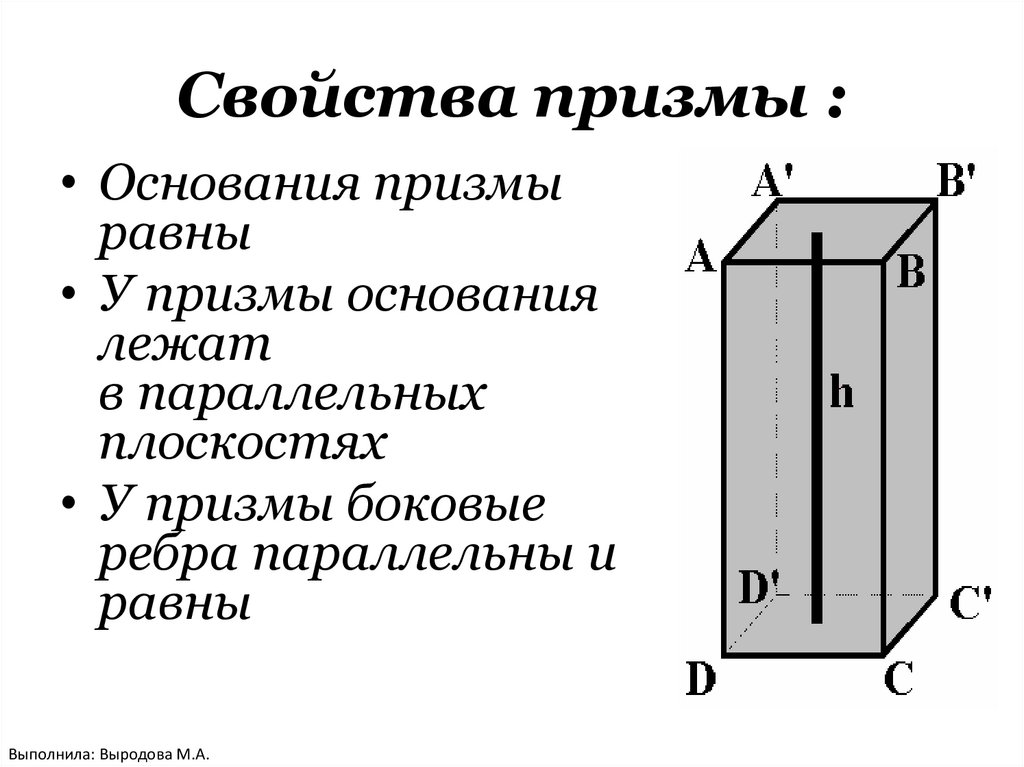
Свойства призмы :
• Основания призмы
равны
• У призмы основания
лежат
в параллельных
плоскостях
• У призмы боковые
ребра параллельны и
равны
Выполнила: Выродова М.А.

22.

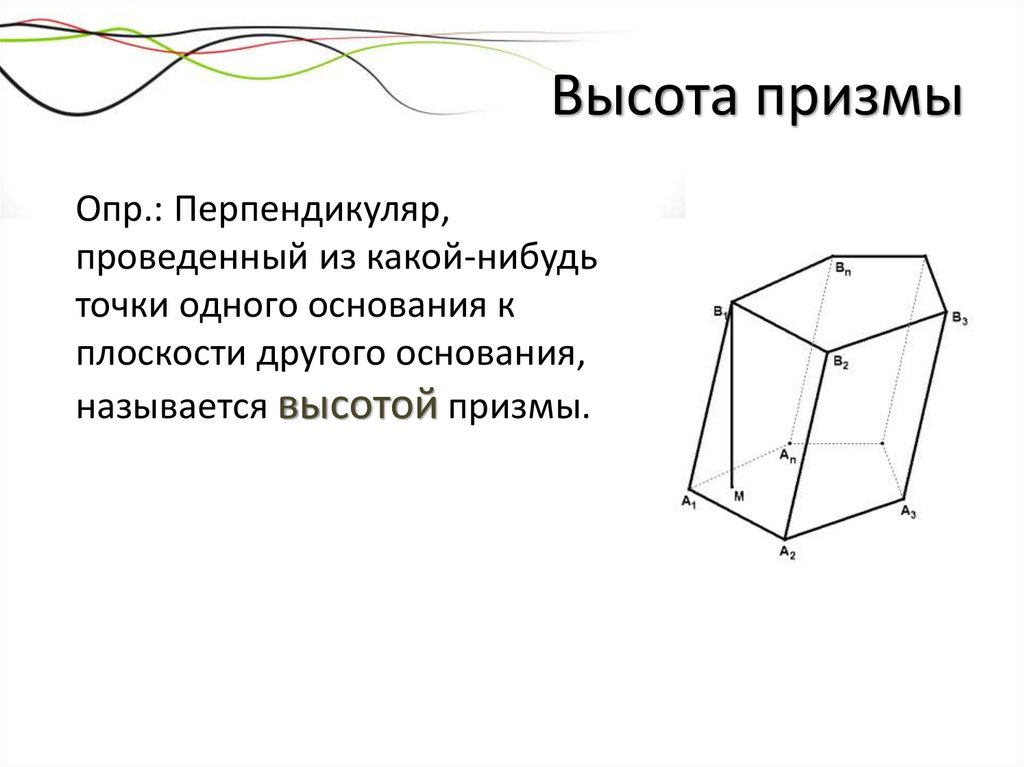
Высота призмы
Опр.: Перпендикуляр,
проведенный из какой-нибудь
точки одного основания к
плоскости другого основания,
называется высотой призмы.

23.

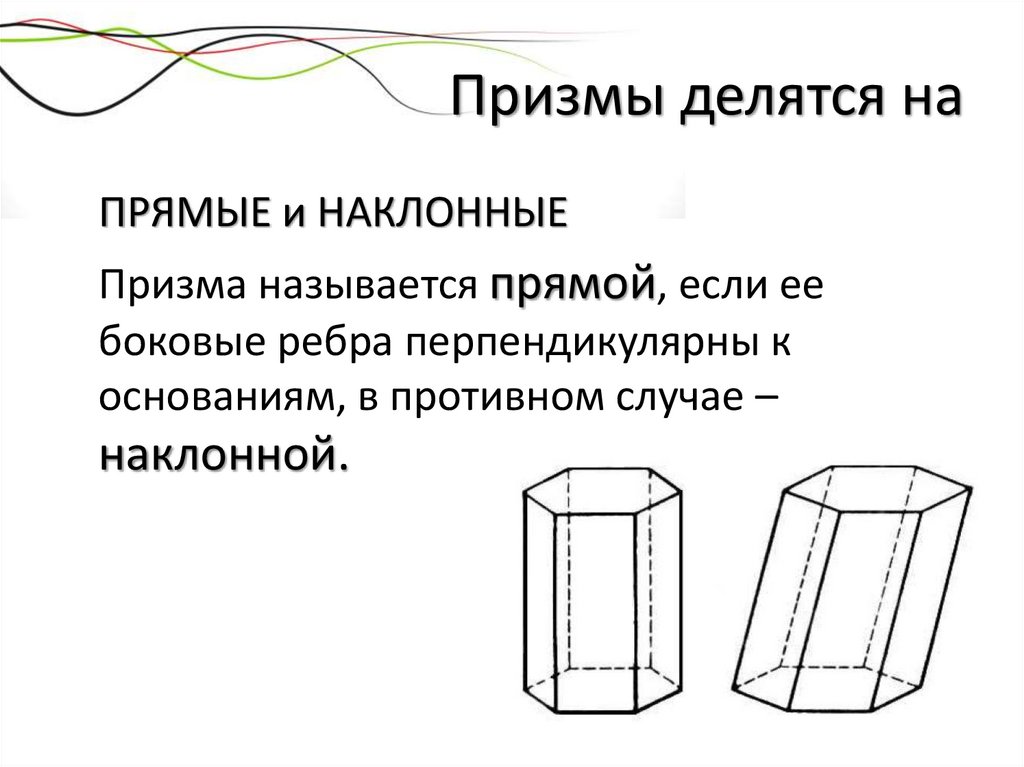
Призмы делятся на
ПРЯМЫЕ и НАКЛОННЫЕ
Призма называется прямой, если ее
боковые ребра перпендикулярны к
основаниям, в противном случае –
наклонной.

24.

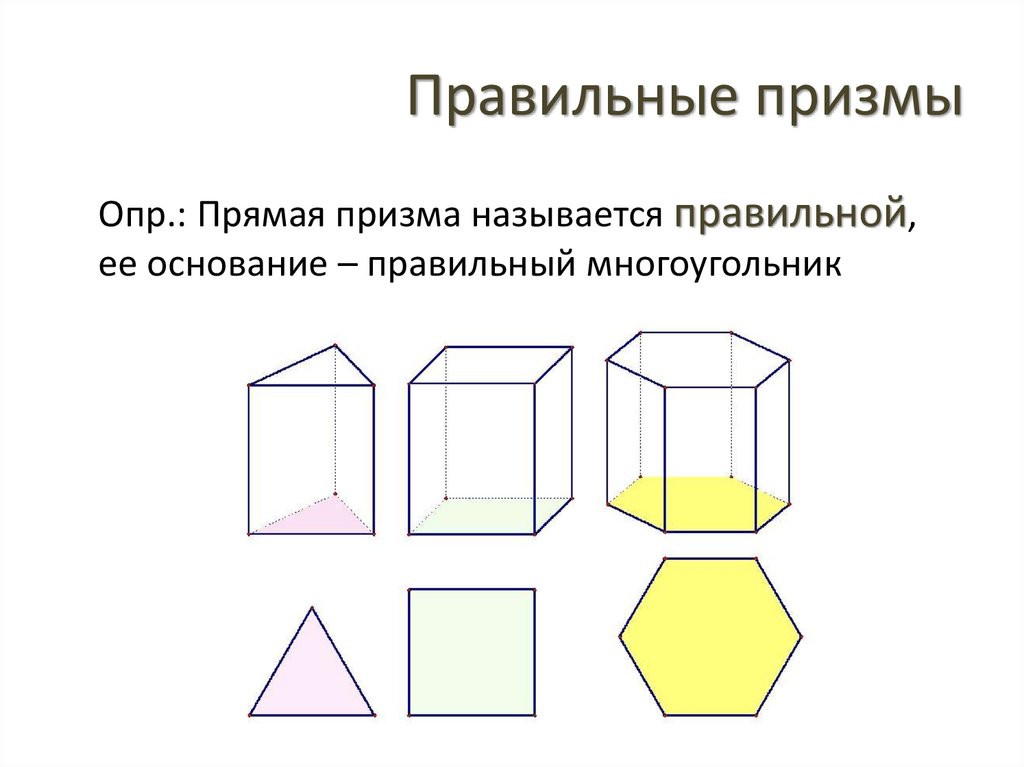
Правильные призмы
Опр.: Прямая призма называется правильной,
ее основание – правильный многоугольник

25.

Параллелепипед
Параллелепипед - призма,
основанием которой служит
параллелограмм. Наклонный
параллелепипед — это
параллелепипед, у которого
боковые грани расположены, по
отношению к основаниям, под
углом, не равным 90 градусов.
Sполн Sбок 2Sосн
V Sосн h

26.

Прямоугольный параллелепипед
Прямоугольный параллелепипед – это такой прямой
параллелепипед, у которого все грани являются
прямоугольниками.
Sполн Sбок 2Sосн
Sполн 2 ab bc ac
V Sосн h
V abc
d a 2 b2 c2

27.

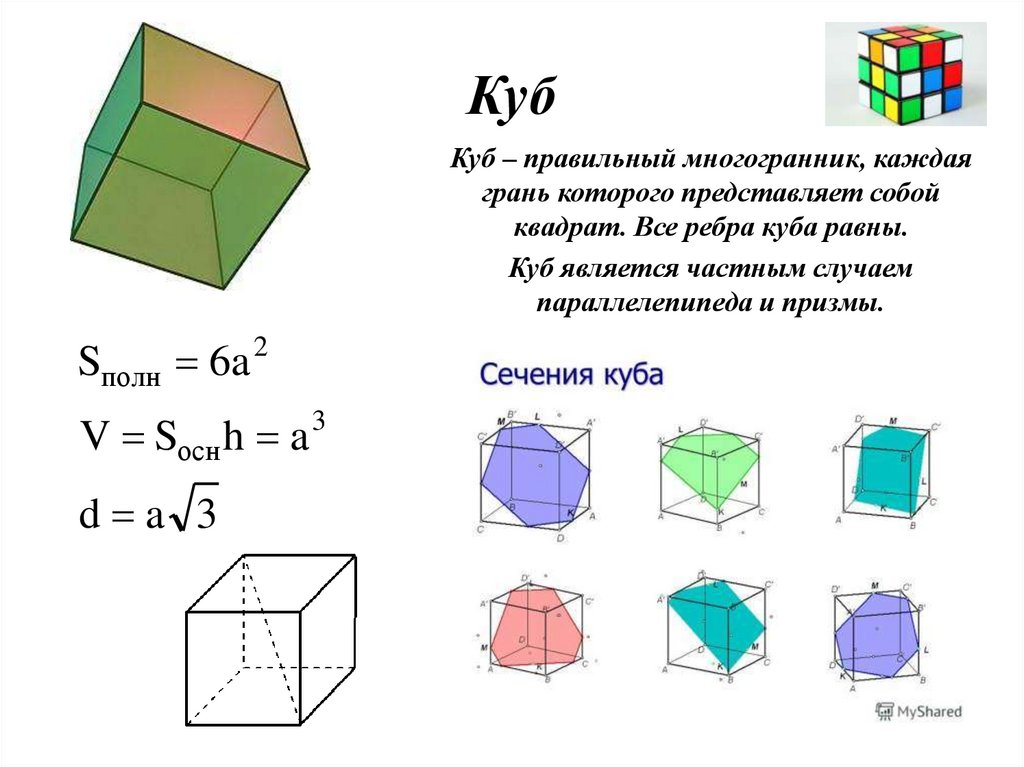
Куб
Куб – правильный многогранник, каждая
грань которого представляет собой
квадрат. Все ребра куба равны.
Куб является частным случаем
параллелепипеда и призмы.
Sполн 6a 2
V Sосн h a
d a 3
3

28.

Площадь поверхности

29.

30.

Это интересно!
Многие художники, искажая законы перспективы,
рисуют необычные картины. Кстати, эти рисунки очень
популярны среди математиков. В сети Internet можно
найти множество сайтов, где публикуются эти
невозможные объекты.
Популярные художники Морис Эшер, Оскар
Реутерсвард, Жос де Мей и другие, удивляли своими
картинами математиков.
http://www.im-possible.info/english/art/mey/mey2.html
http://alone.sammit.kiev.ua/moremind/illusion/index.html
http://lib.world-mobile.net/culture/special/imp/imp-world-r.narod.ru/art/index.html

31.

"Такое может нарисовать только тот, кто делает
дизайн, не зная перспективы..."
Жос де Мей

32.

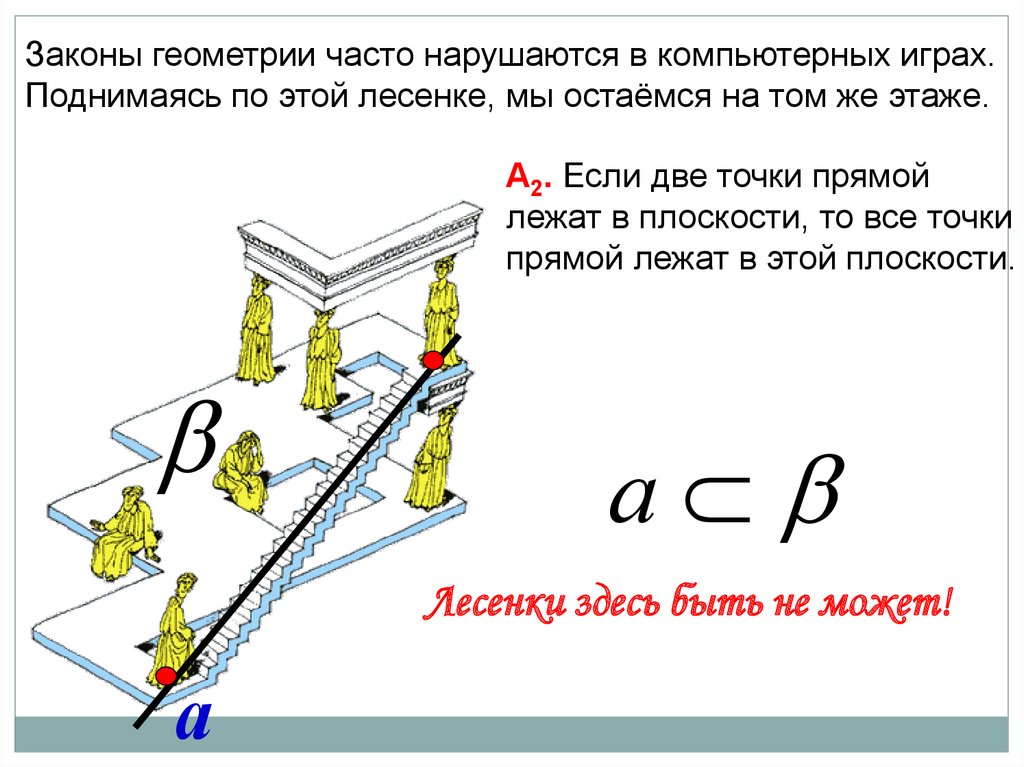
Законы геометрии часто нарушаются в компьютерных играх.
Поднимаясь по этой лесенке, мы остаёмся на том же этаже.
А2. Если две точки прямой
лежат в плоскости, то все точки
прямой лежат в этой плоскости.
а
Лесенки здесь быть не может!
а

33.

"Те, кто влюбляются в практику без
теории,
уподобляются
мореплавателю,
садящемуся
на
корабль без руля и компаса и потому
никогда не знающему, куда он
плывет".
http://blogs.nnm.ru/page6/
Леонардо да Винчи

34.

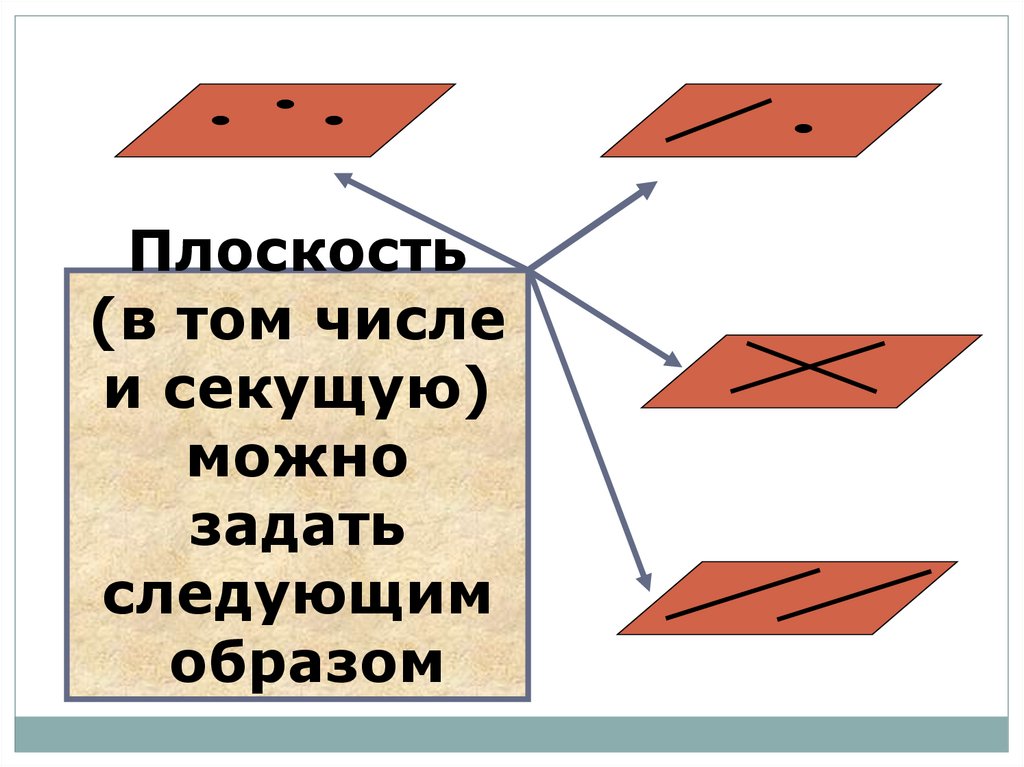
Плоскость
(в том числе
и секущую)
можно
задать
следующим
образом

35.

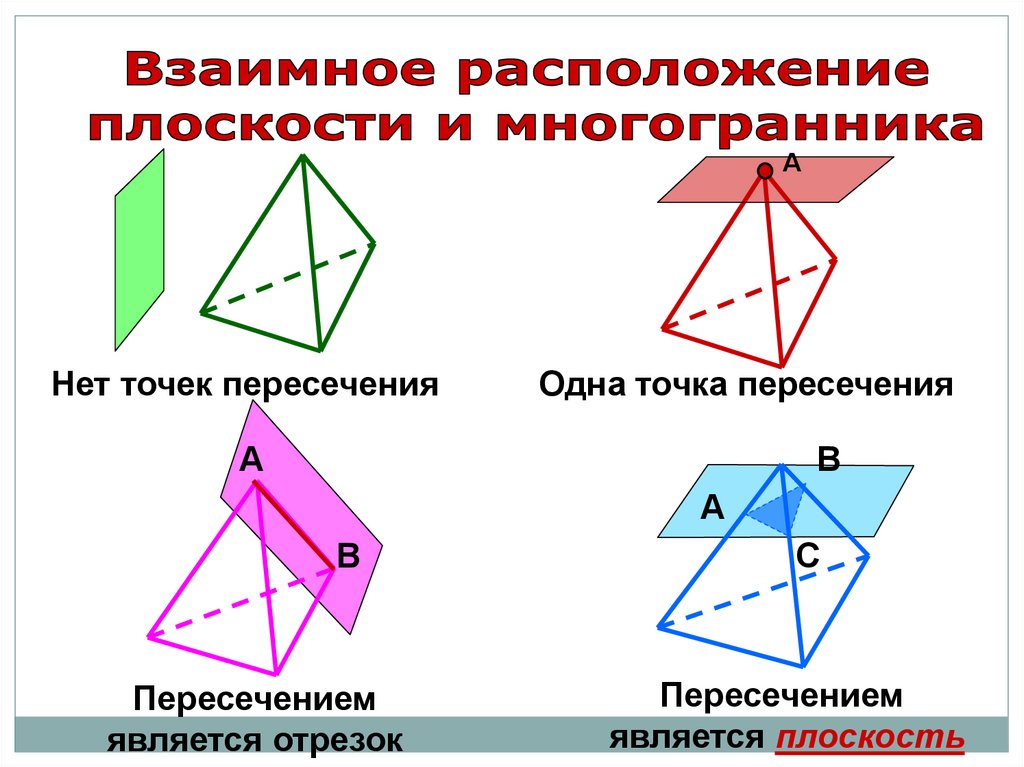
А
Нет точек пересечения
Одна точка пересечения
А
В
А
В
Пересечением
является отрезок
С
Пересечением
является плоскость

36.

1.Секущая плоскость тетраэдра(параллепипеда)-это
любая плоскость, по обе стороны от которой имеются точки
данного тетраэдра (параллепипеда).
2.Многоугольник, сторонами которого являются отрезки,
пересекающие грани тетраэдра (параллепипеда)
называется сечением тетраэдра (параллепипеда).

37.

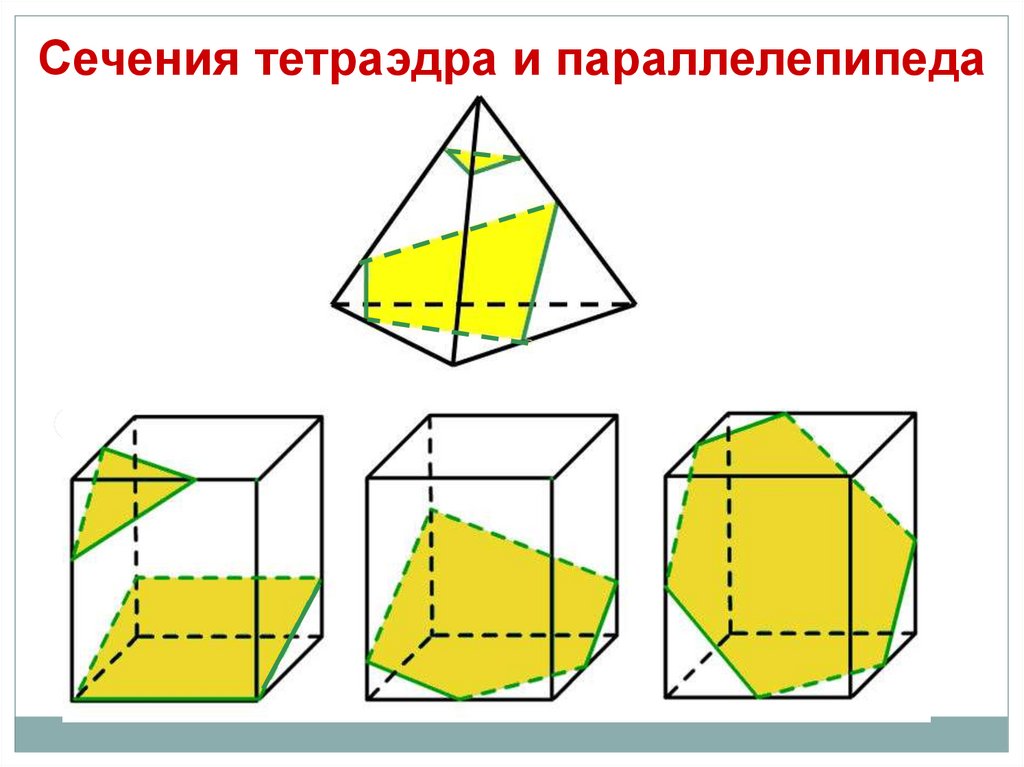
Сечения тетраэдра и параллелепипеда

38.

Построить сечение многогранника
плоскостью – это значит указать
точки пересечения секущей плоскости с
ребрами многогранника и соединить эти
точки отрезками, принадлежащими граням
многогранника.
Для построения сечения многогранника
плоскостью нужно в плоскости каждой
грани указать 2 точки, принадлежащие
сечению, соединить их прямой и найти
точки пересечения этой прямой с ребрами
многогранника.

39.

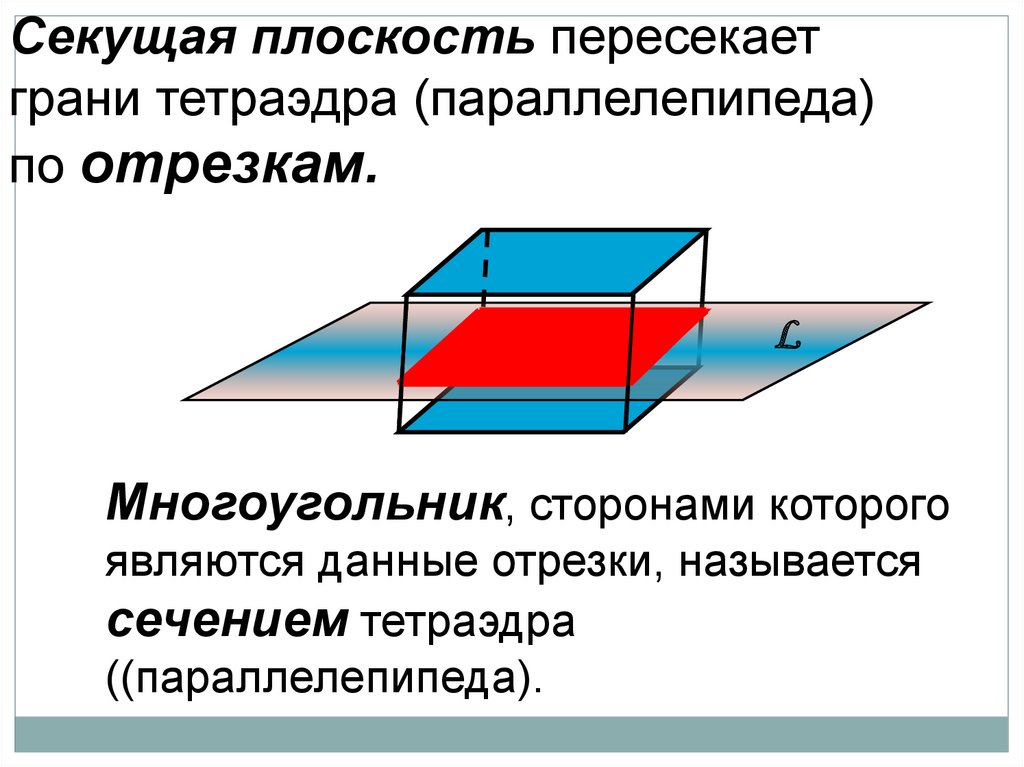
Секущая плоскость пересекает
грани тетраэдра (параллелепипеда)
по отрезкам.
L
Многоугольник, сторонами которого
являются данные отрезки, называется
сечением тетраэдра
((параллелепипеда).

40.

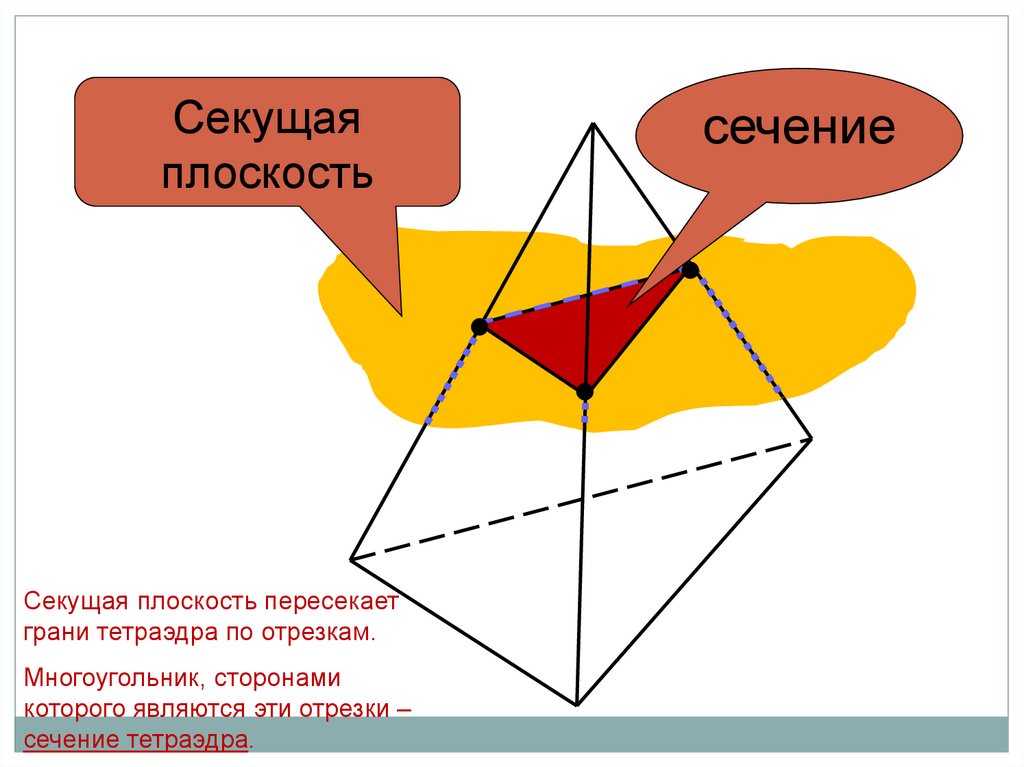
Секущая
плоскость
Секущая плоскость пересекает
грани тетраэдра по отрезкам.
Многоугольник, сторонами
которого являются эти отрезки –
сечение тетраэдра.
сечение

41.

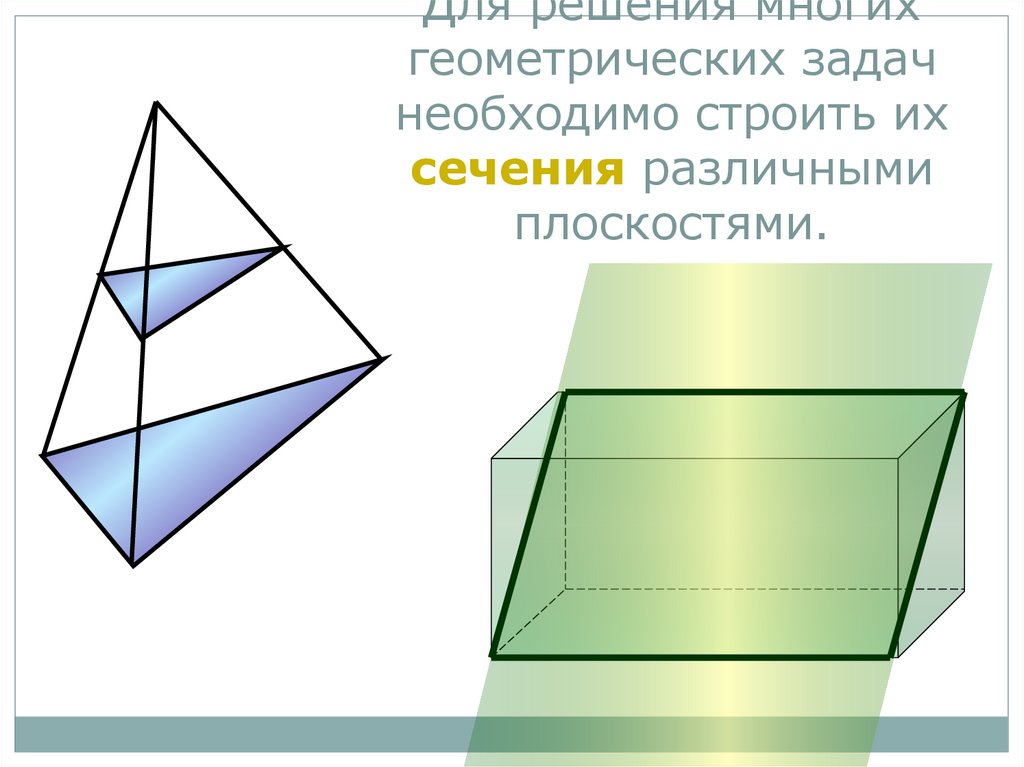
Для решения многих
геометрических задач
необходимо строить их
сечения различными
плоскостями.

42.

АКСИОМЫ
планиметрия
Характеризуют взаимное
расположение точек и прямых
1. Каждой прямой
принадлежат по крайней
мере две точки
стереометрия
А1. Через любые три точки, не
лежащие на одной прямой,
проходит плоскость, и притом
только одна
2. Имеются по крайней мере
три точки, не лежащие на
одной прямой
А2. Если две точки прямой
лежат в плоскости, то все
точки прямой лежат в этой
плоскости
3. Через любые две точки
проходит прямая, и притом
только одна.
Основное понятие геометрии
«лежать между»
4. Из трех точек прямой одна и
только одна лежит между двумя
другими.
А3. Если две плоскости
имеют общую точку, то они
имеют общую прямую, на
которой лежат все общие
точки этих плоскостей.

43.

Для построения сечения нужно построить
точки пересечения секущей плоскости с
ребрами и соединить их отрезками.
При этом необходимо учитывать
следующее:
1. Соединять можно только две точки,
лежащие
в
одной грани.
2. плоскости
Секущая плоскость
пересекает
параллельные грани по параллельным
отрезкам.
3.
Если в плоскости грани отмечена только одна
точка, принадлежащая плоскости сечения, то
надо построить дополнительную точку. Для этого
необходимо найти точки пересечения уже
построенных прямых с другими прямыми,
лежащими в тех же гранях.

44.

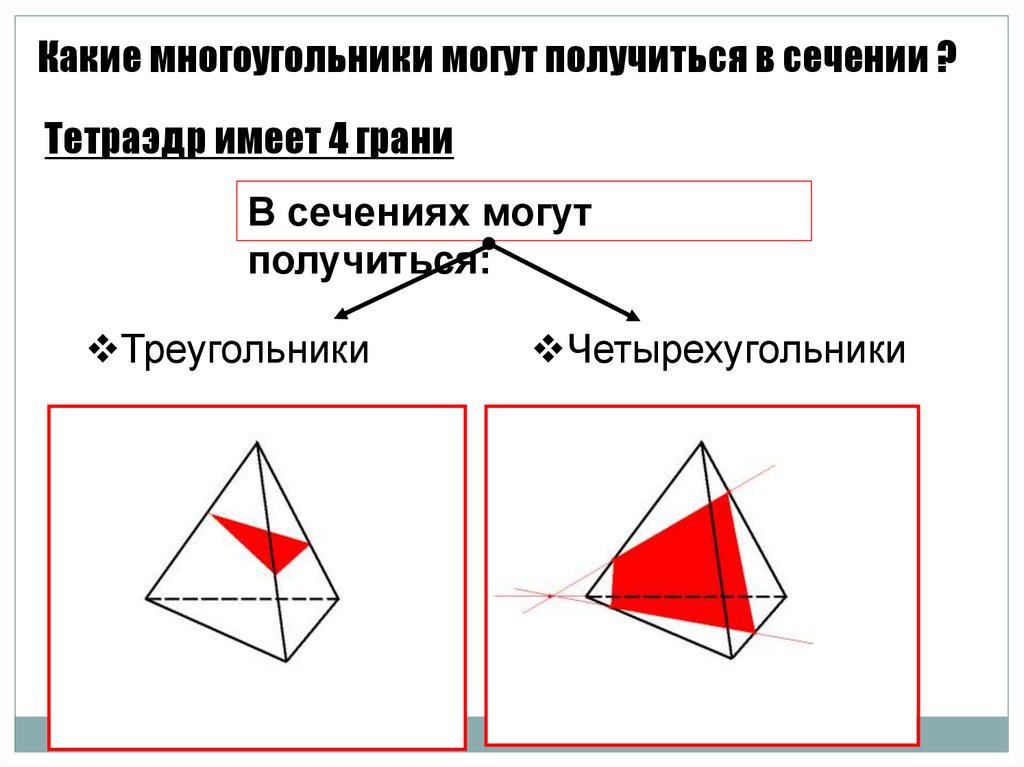
Какие многоугольники могут получиться в сечении ?
Тетраэдр имеет 4 грани
В сечениях могут
получиться:
Треугольники
Четырехугольники

45.

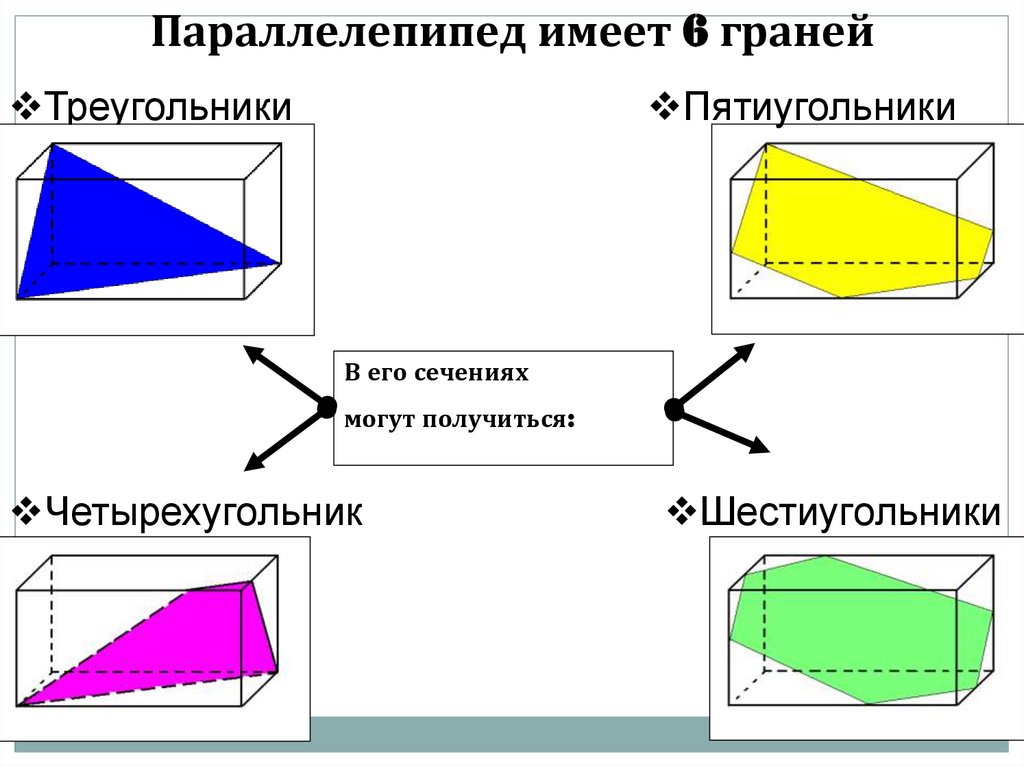
Параллелепипед имеет 6 граней
Треугольники
Пятиугольники
В его сечениях
могут получиться:
Четырехугольник
и
Шестиугольники

46.

Блиц - опрос
Задача блиц – опроса: ответить
на вопросы и обосновать ответ с
помощью аксиом, теорем и
свойств параллельных
плоскостей.

47.

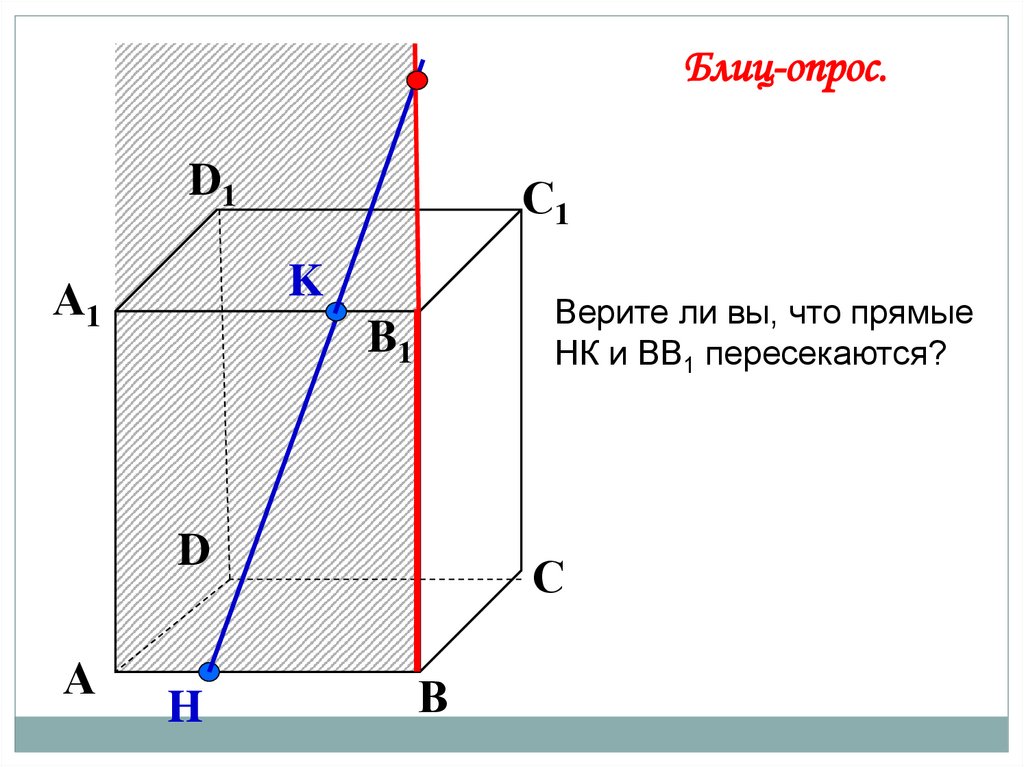
Блиц-опрос.
D1
С1
K
А1
Верите ли вы, что прямые
НК и ВВ1 пересекаются?
B1
D
А
H
С
В

48.

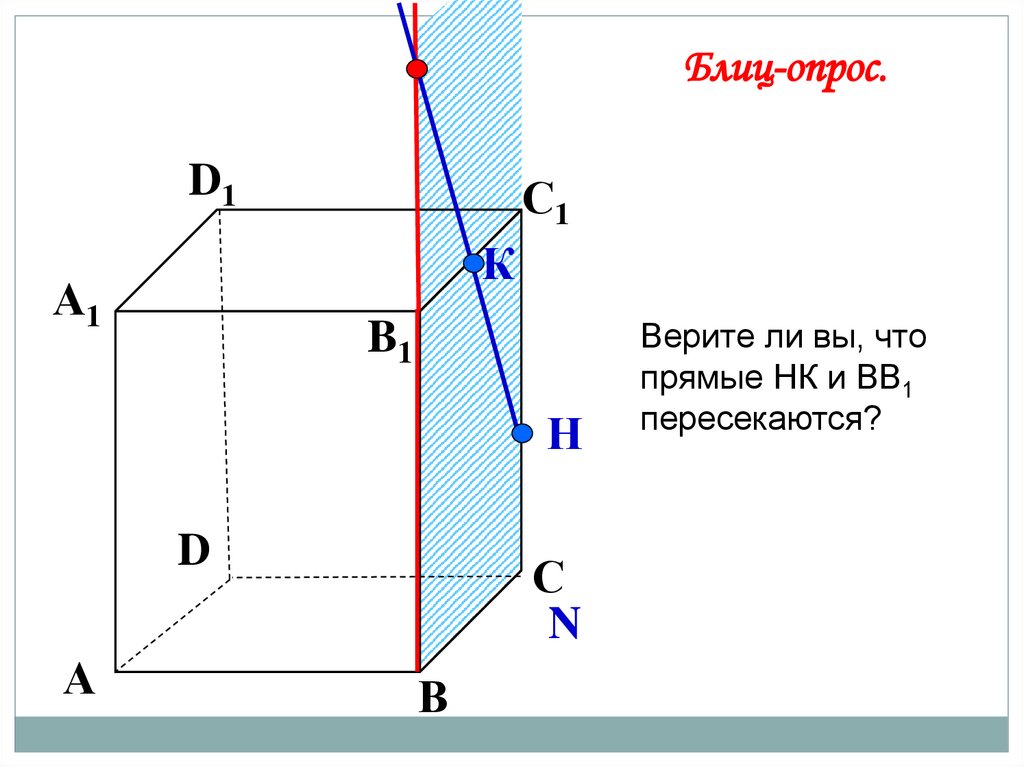
Блиц-опрос.
D1
С1
К
А1
B1
Н
D
А
С
N
В
Верите ли вы, что
прямые НК и ВВ1
пересекаются?

49.

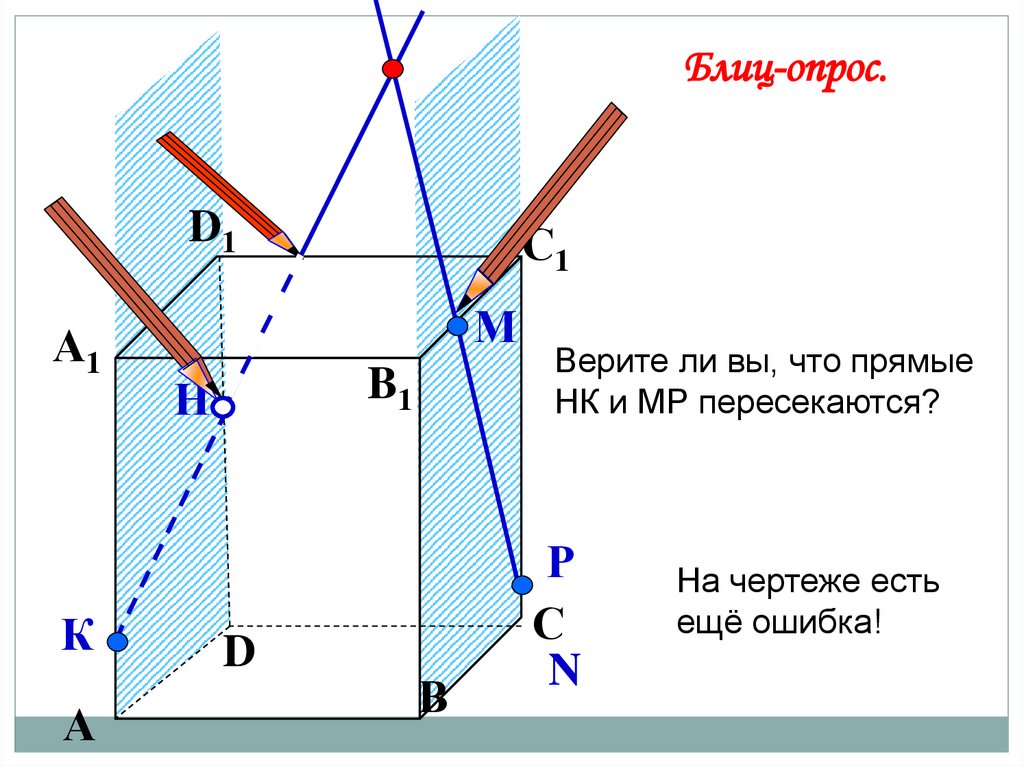
Блиц-опрос.
D1
А1
К
А
С1
М
B1
Н
D
В
Верите ли вы, что прямые
НК и МР пересекаются?
Р
С
N
На чертеже есть
ещё ошибка!

50.

Верите ли вы, что прямые НR и NK
пересекаются?
D1
С1
Н
А1
R
B1
С
D
На чертеже есть
ещё ошибка!
N
А
Блиц-опрос.
К
В

51.

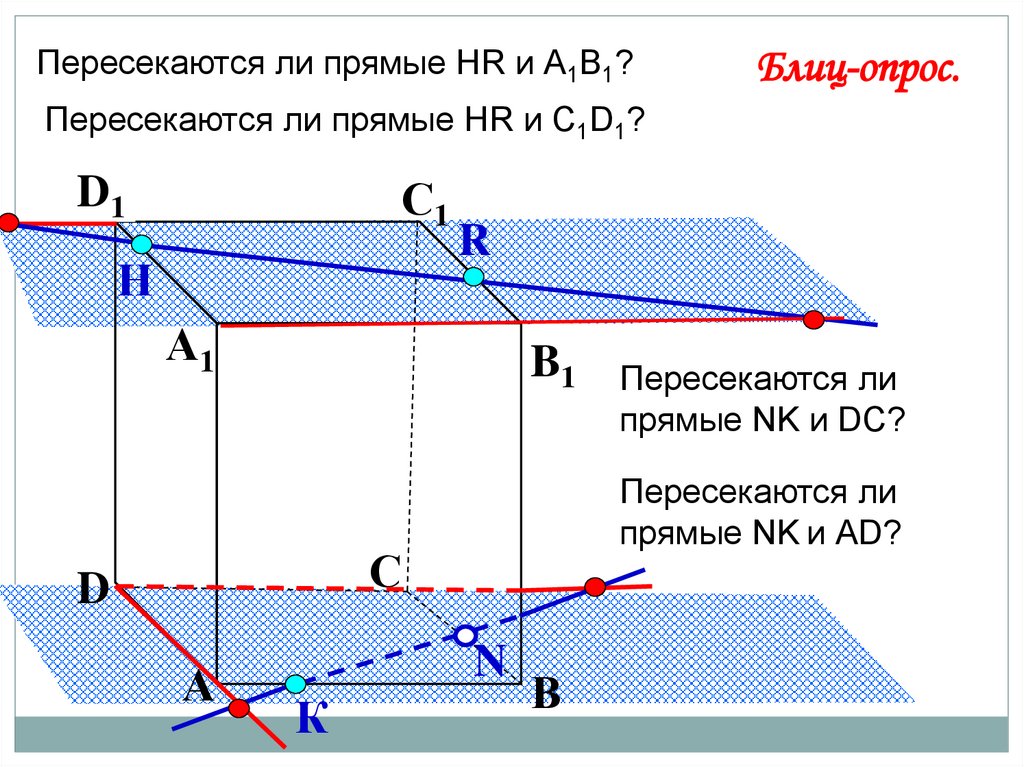
Пересекаются ли прямые НR и А1В1?
Блиц-опрос.
Пересекаются ли прямые НR и С1D1?
С1
D1
Н
R
А1
B1
Пересекаются ли
прямые NK и АD?
С
D
А
N
К
Пересекаются ли
прямые NK и DC?
В

52.

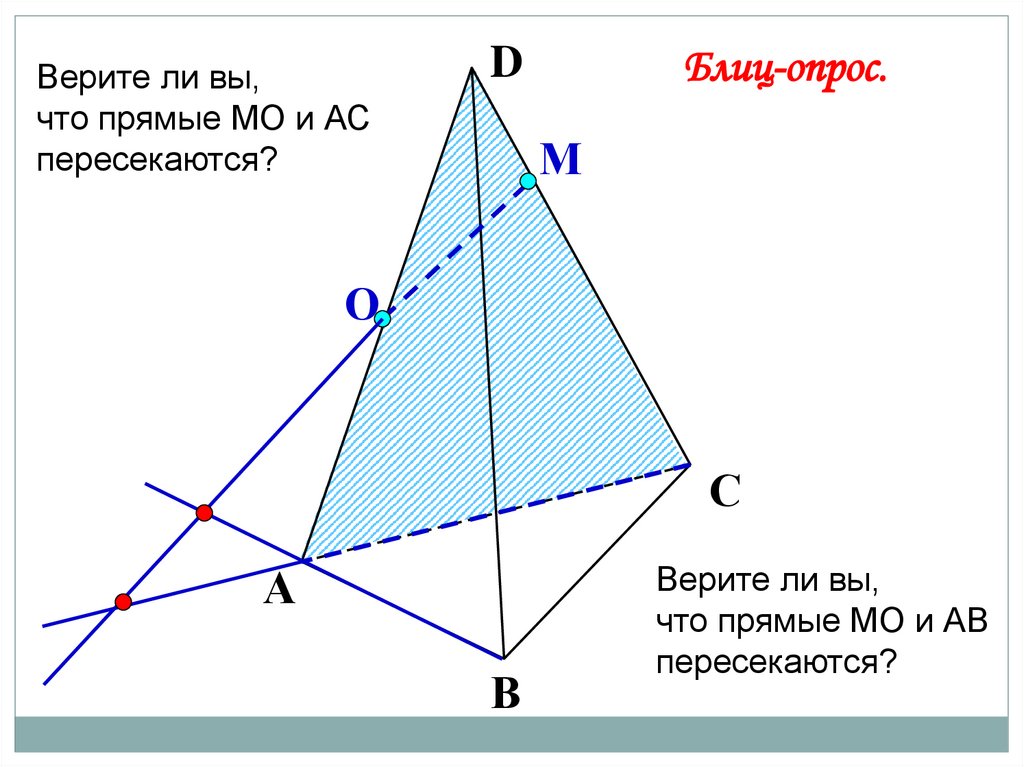
Верите ли вы,
что прямые МО и АС
пересекаются?
Блиц-опрос.
D
М
О
С
А
В
Верите ли вы,
что прямые МО и АВ
пересекаются?

53.

Умение решать задачи – практическое
искусство, подобное плаванию, или
катанию на лыжах … : научиться этому
можно лишь подражая избранным образцам
и постоянно тренируясь..
Д. Пойа

54.

Свойство
параллельных плоскостей.
а
Если две параллельные плоскости
пересечены третьей,
то линии их пересечения
параллельны.
b
Это свойство нам поможет
при построении сечений.

55.

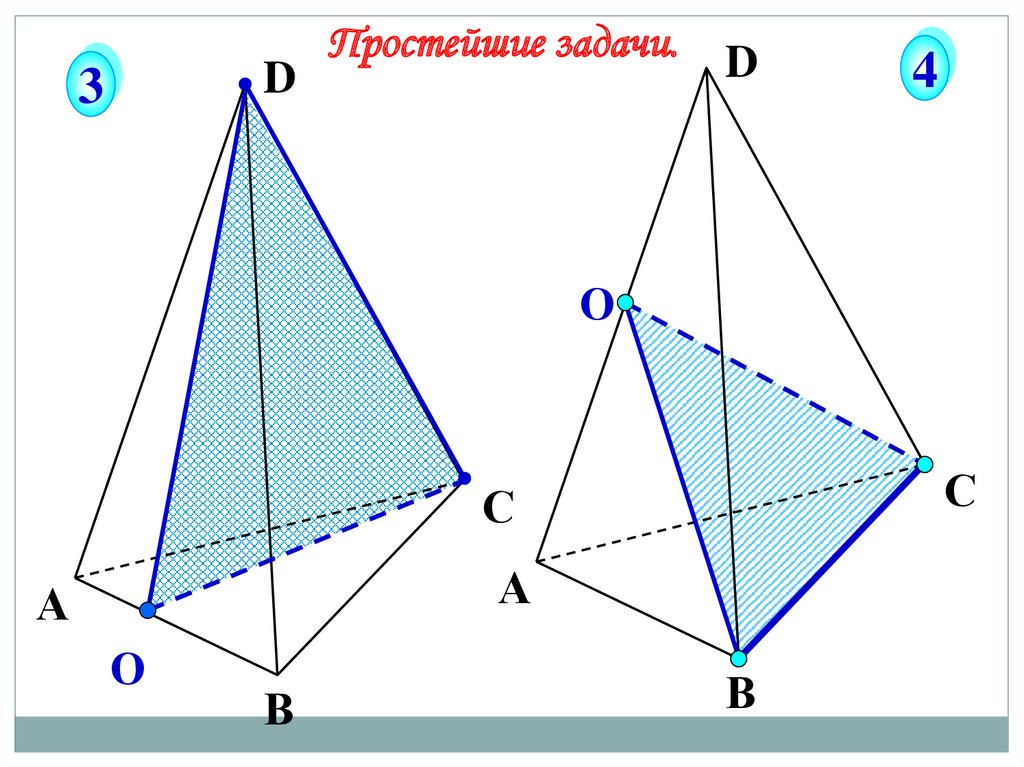
1
Простейшие задачи.
D1
С1
D
B1
А1
K
М
О
D
А
2
H
С
N
В
Р
С
А
В

56.

D
3
Простейшие задачи.
D
4
О
С
С
А
А
О
В
В

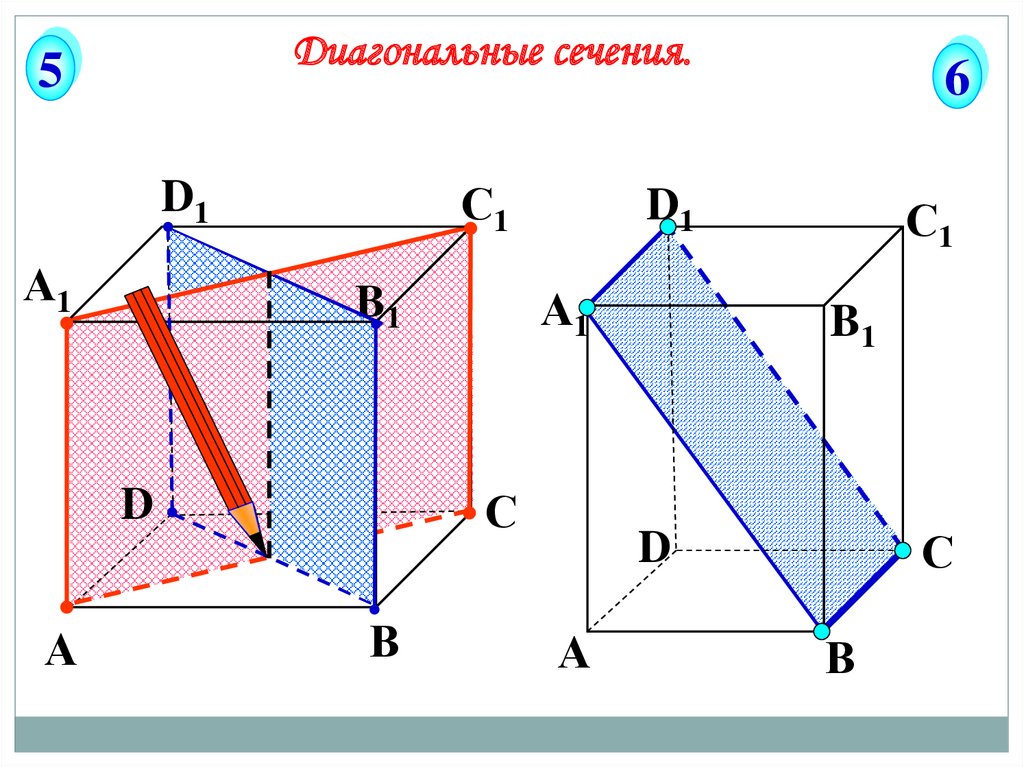
57.

Диагональные сечения.
5
С1
D1
А1
С
D
А
D1
А1
B1
В
6
С1
B1
С
D
А
В

58.

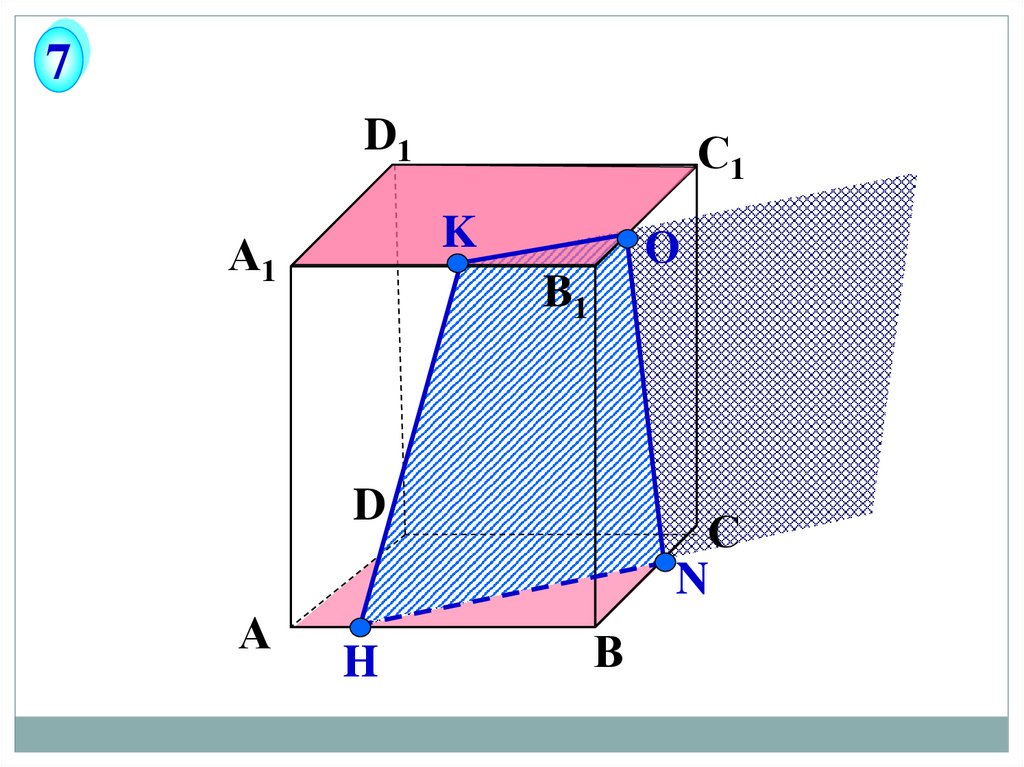
7
D1
С1
K
А1
О
B1
D
А
H
С
N
В

59.

Аксиоматический метод
Метод следов
Суть метода заключается в построении
вспомогательной прямой, являющейся изображением
линии пересечения секущей плоскости с плоскостью
какой-либо грани фигуры . Удобнее всего строить
изображение линии пересечения секущей плоскости с
плоскостью нижнего основания. Эту линию называют
следом секущей плоскости. Используя след, легко
построить изображения точек секущей плоскости,
находящихся на боковых ребрах или гранях фигуры .

60.

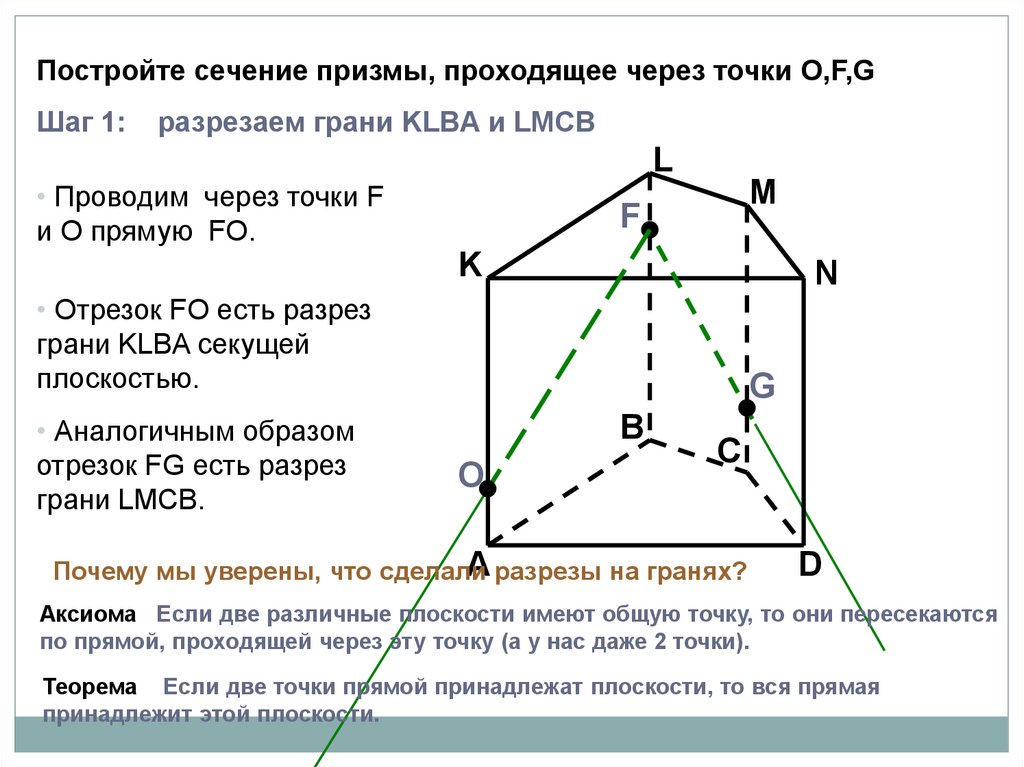
Постройте сечение призмы, проходящее через точки O,F,G
Шаг 1:
разрезаем грани KLBA и LMCB
L
• Проводим через точки F
и O прямую FO.
M
F
K
N
• Отрезок FO есть разрез
грани KLBA секущей
плоскостью.
• Аналогичным образом
отрезок FG есть разрез
грани LMCB.
G
B
O
C
A разрезы на гранях?
Почему мы уверены, что сделали
D
Аксиома Если две различные плоскости имеют общую точку, то они пересекаются
по прямой, проходящей через эту точку (а у нас даже 2 точки).
Теорема Если две точки прямой принадлежат плоскости, то вся прямая
принадлежит этой плоскости.

61.

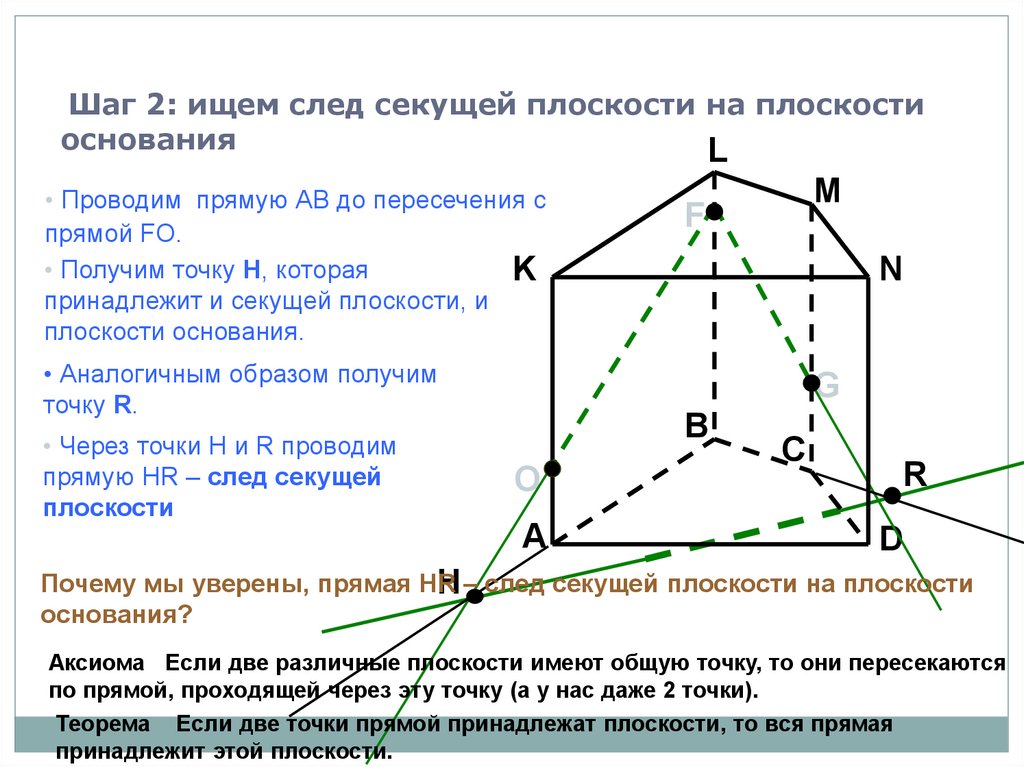
Шаг 2: ищем след секущей плоскости на плоскости
основания
L
• Проводим прямую АВ до пересечения с
прямой FO.
• Получим точку H, которая
K
принадлежит и секущей плоскости, и
плоскости основания.
• Аналогичным образом получим
точку R.
• Через точки H и R проводим
прямую HR – след секущей
плоскости
M
F
N
G
B
O
A
C
R
D
Почему мы уверены, прямая HR
H – след секущей плоскости на плоскости
основания?
Аксиома Если две различные плоскости имеют общую точку, то они пересекаются
по прямой, проходящей через эту точку (а у нас даже 2 точки).
Теорема Если две точки прямой принадлежат плоскости, то вся прямая
принадлежит этой плоскости.

62.

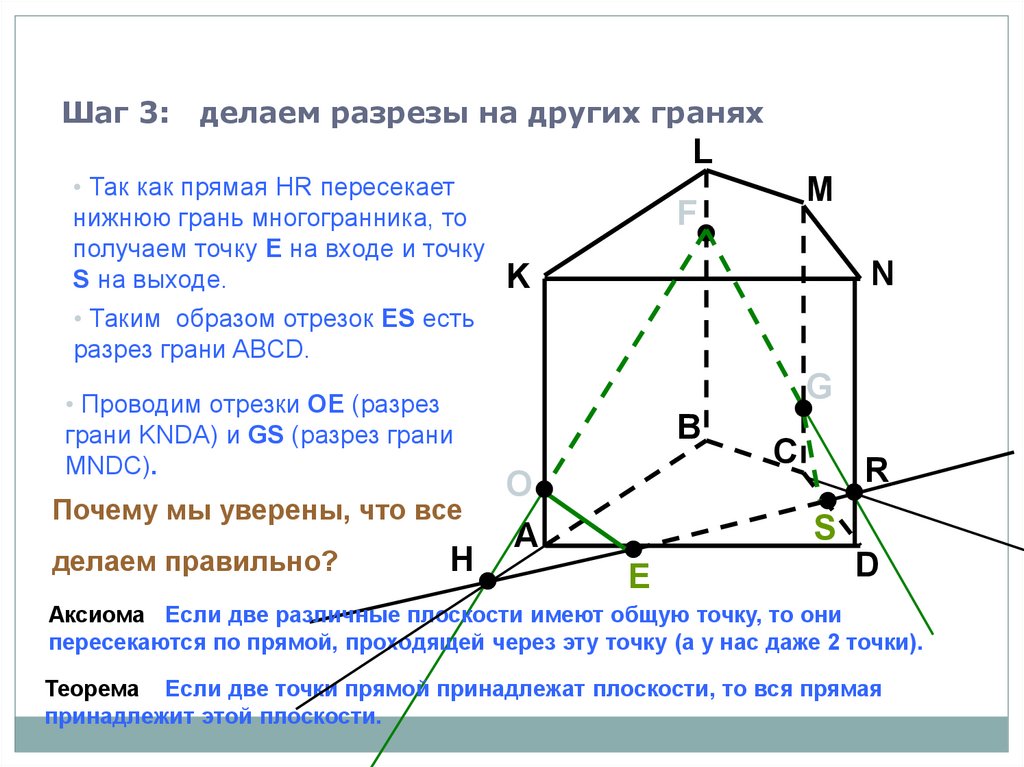
Шаг 3:
делаем разрезы на других гранях
L
• Так как прямая HR пересекает
нижнюю грань многогранника, то
получаем точку E на входе и точку
S на выходе.
M
F
N
K
• Таким образом отрезок ES есть
разрез грани ABCD.
• Проводим отрезки ОЕ (разрез
грани KNDA) и GS (разрез грани
MNDC).
Почему мы уверены, что все
делаем правильно?
H
G
B
O
A
C
R
S
E
D
Аксиома Если две различные плоскости имеют общую точку, то они
пересекаются по прямой, проходящей через эту точку (а у нас даже 2 точки).
Теорема Если две точки прямой принадлежат плоскости, то вся прямая
принадлежит этой плоскости.

63.

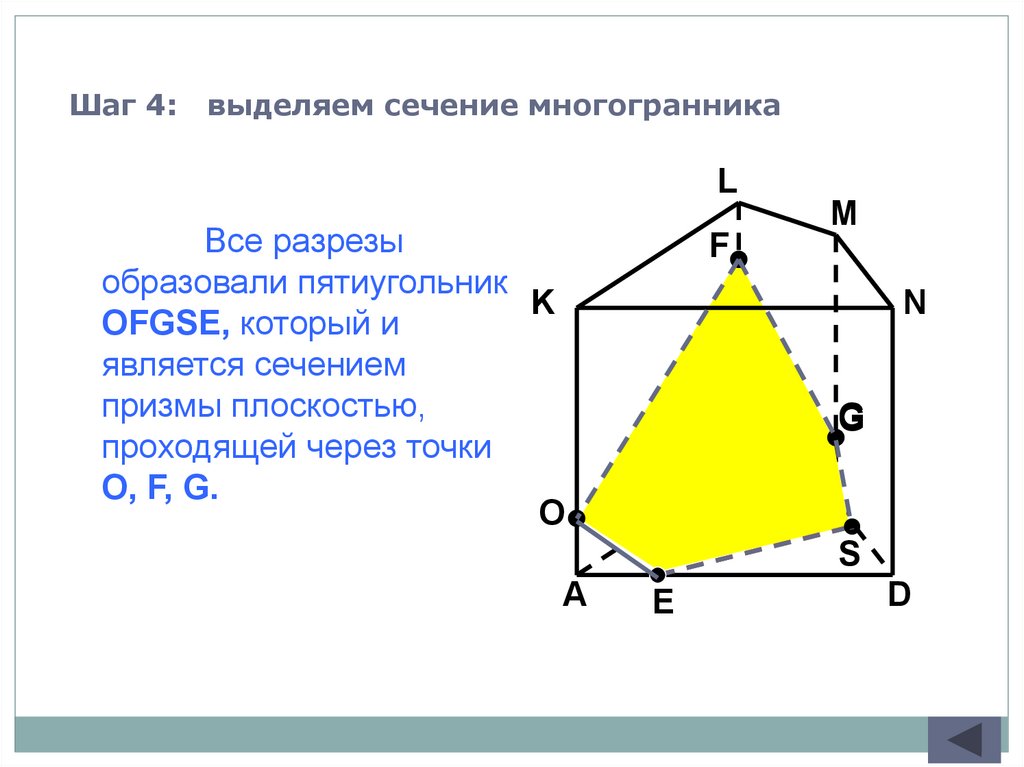
Шаг 4:
выделяем сечение многогранника
L
M
Все разрезы
образовали пятиугольник
K
OFGSE, который и
является сечением
призмы плоскостью,
проходящей через точки
O, F, G.
O
F
N
G
B
C
S
A
E
D

64.

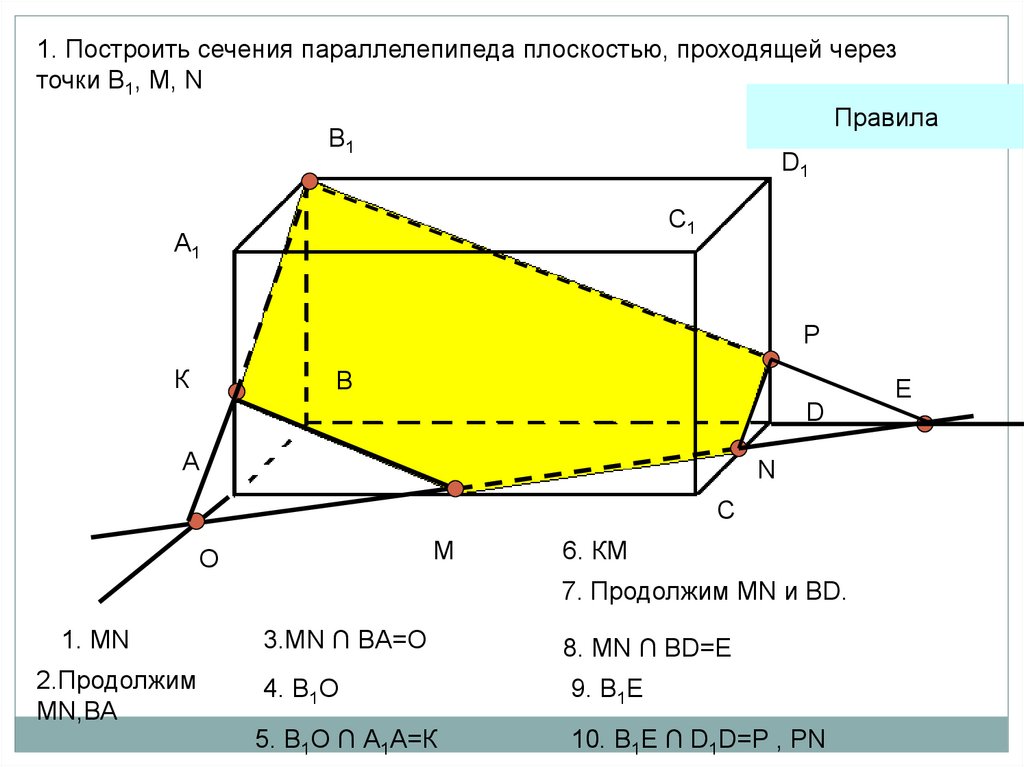
1. Построить сечения параллелепипеда плоскостью, проходящей через
точки В1, М, N
Правила
В1
D1
С1
A1
P
К
В
D
А
N
С
M
O
6. КМ
7. Продолжим MN и BD.
1. MN
2.Продолжим
MN,ВА
3.MN ∩ BA=O
4. В1О
5. В1О ∩ А1А=К
8. MN ∩ BD=E
9. В1E
10. B1Е ∩ D1D=P , PN
Е

65.

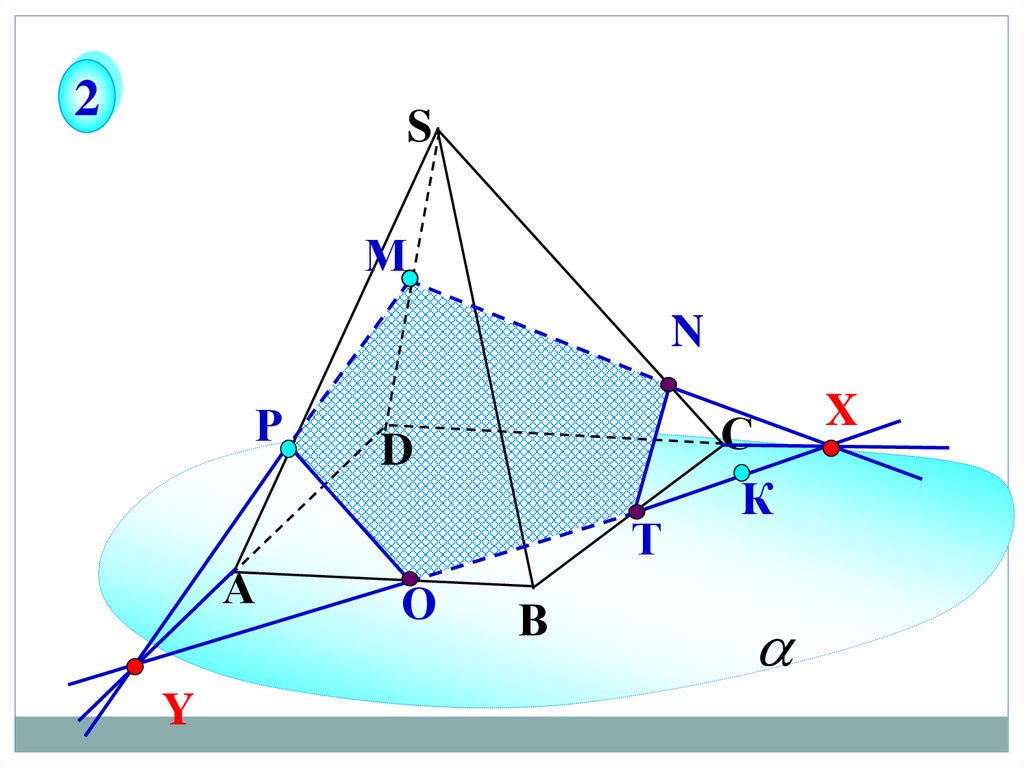
2
S
М
N
Р
А
Y
D
Т
О
В
С
К
X

66.

M
M
P
N
P
M
N
N
P
N
M
N
M
P
P
N
P
M

67.

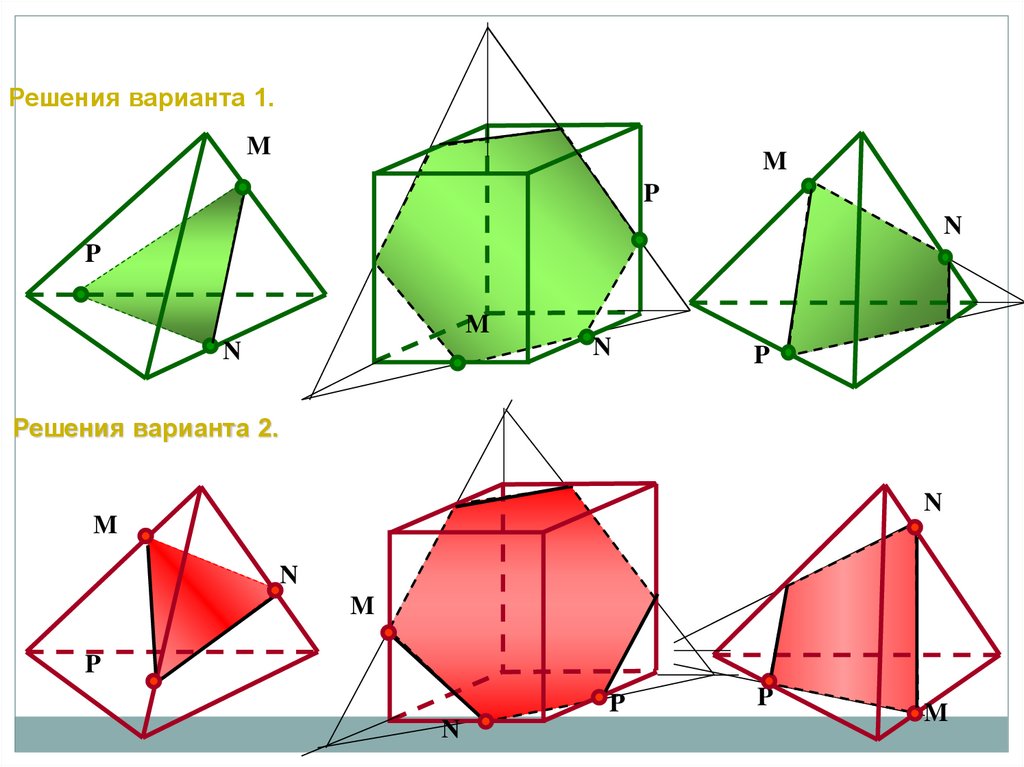
Решения варианта 1.
M
M
P
N
P
M
N
N
P
Решения варианта 2.
N
M
N
M
P
P
N
P
M

68.

Правила для самоконтроля:
Вершины сечения находятся
только на ребрах.
Стороны сечения находятся
только на грани многогранника.
Секущая плоскость пересекает
грань или плоскость грани, то
только один раз.

69.

Составить две
задачи на
построение сечений
многогранников с
использованием
полученных знаний.

70.

Если вы хотите научиться плавать, то
смело входите в воду, а если хотите
научиться решать задачи, то решайте
их
(Д. Пойа)

71.

Задача 1. Построить сечение плоскостью, проходящей
через данные точки D, Е, K.
Построение:
S
1. DE
2. ЕК
3. ЕК ∩ АС = F
4. FD
5. FD ∩ BС = M
6. KM
DЕKМ – искомое сечение
E
K
А
С
M
D
В
F

72.

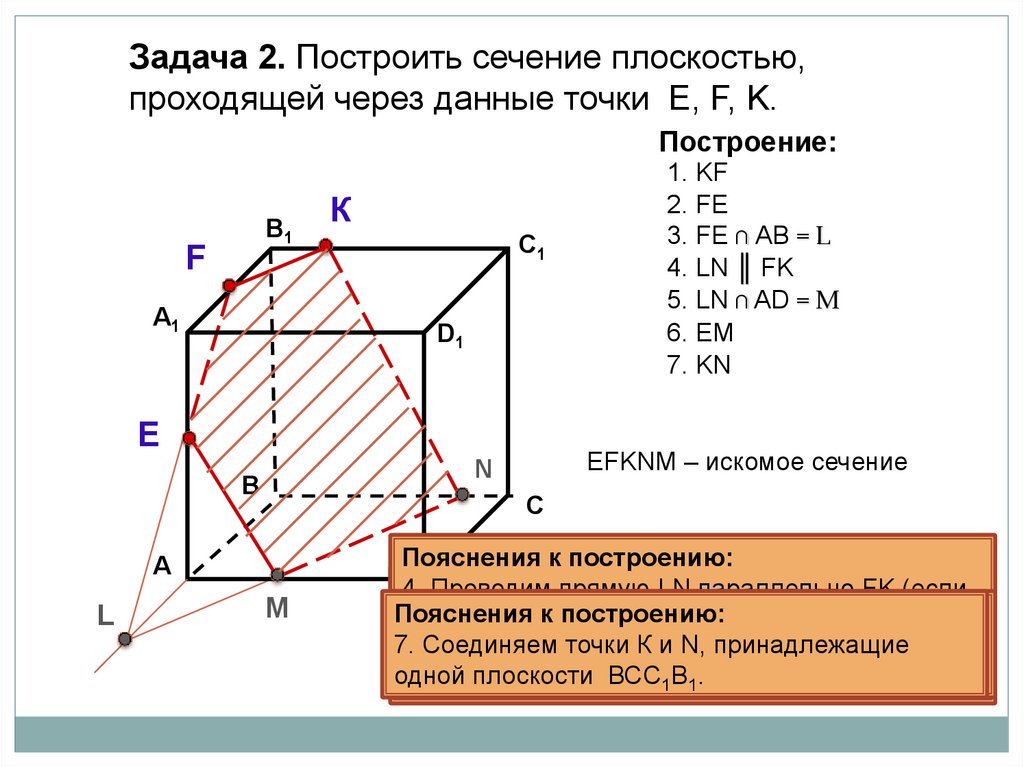
Задача 2. Построить сечение плоскостью,
проходящей через данные точки Е, F, K.
Построение:
В1
F
А1
К
C1
D1
E
С
А
L
EFKNM – искомое сечение
N
В
1. KF
2. FE
3. FE ∩ АB = L
4. LN ║ FK
5. LN ∩ AD = M
6. EM
7. KN
М
Пояснения к построению:
4.
Проводим
LN параллельно FK (если
Пояснения
кпрямую
построению:
Пояснения
к построению:
Пояснения
Пояснения
кккпостроению:
построению:
секущая
плоскость
3.DПрямые
FE
и АВ,пересекает
лежащие
в принадлежащие
одной
плоскости
Пояснения
построению:
1. Соединяем
2.
точки
K и E,
F
F,
принадлежащие
7.
6.
Соединяем
точки
точкиграни,
КЕииN,
М,ребро
принадлежащие
принадлежащие
противоположные
она
пересекает
их
АА1В1одной
В,LN
пересекаются
вАА
L .в точке M.
5.Соединяем
Прямая
пересекает
AD
плоскости то
А1точке
В1В
1С
1В.
1D1.
одной
одной
плоскости
плоскости ВСС
АА
по параллельным
отрезкам).
1D
1В
1D.
1.

73.

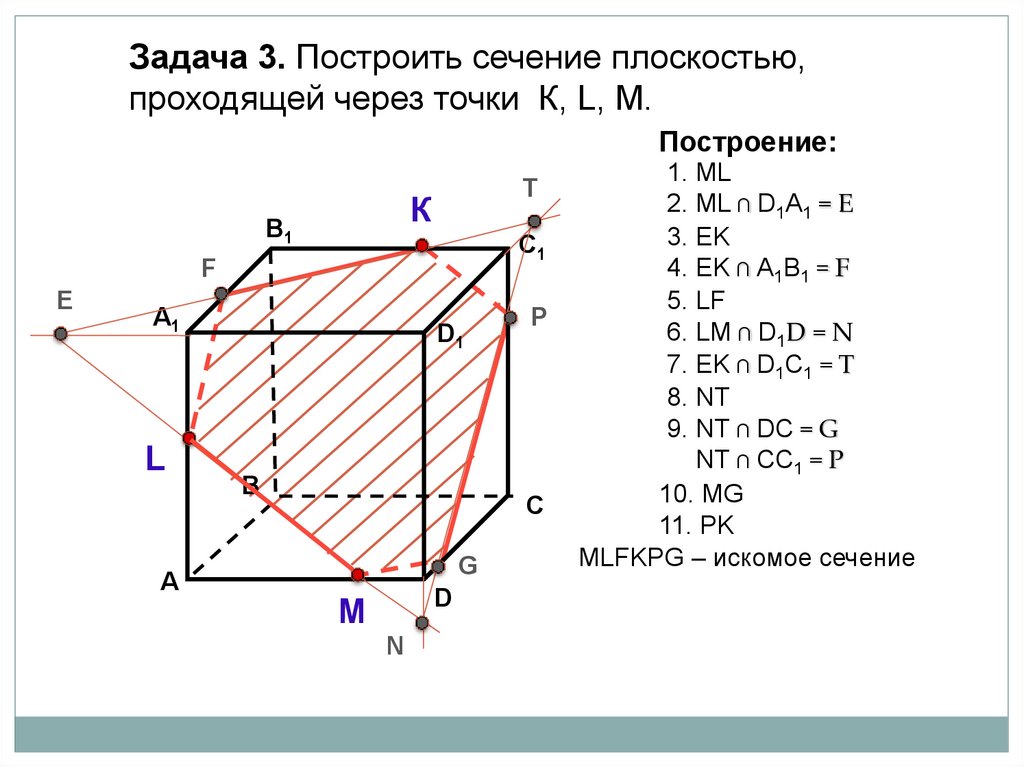
Задача 3. Построить сечение плоскостью,
проходящей через точки К, L, М.
Построение:
T
К
В1
C1
F
E
А1
L
А
D1
В
P
С
G
D
М
N
1. ML
2. ML ∩ D1А1 = E
3. EK
4. EK ∩ А1B1 = F
5. LF
6. LM ∩ D1D = N
7. ЕK ∩ D1C1 = T
8. NT
9. NT ∩ DC = G
NT ∩ CC1 = P
10. MG
11. PK
МLFKPG – искомое сечение

74.

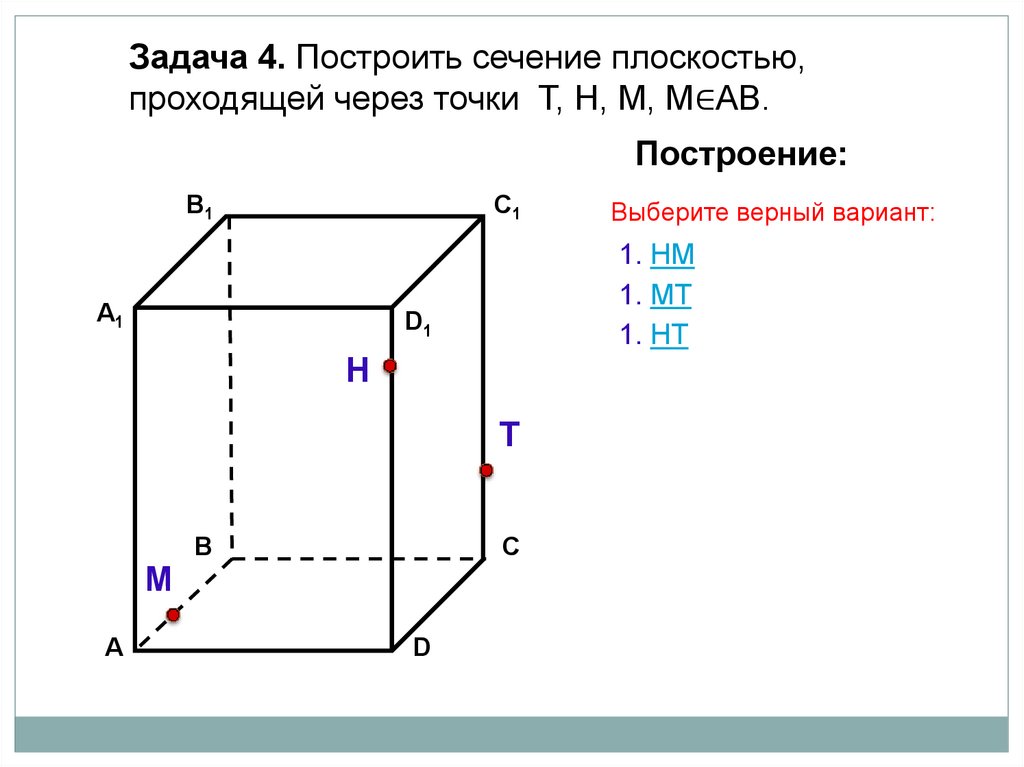
Задача 4. Построить сечение плоскостью,
проходящей через точки Т, Н, М, М∈АВ.
Построение:
В1
C1
А1
1. НМ
1. МТ
1. НT
D1
Н
Т
М
А
В
С
D
Выберите верный вариант:

75.

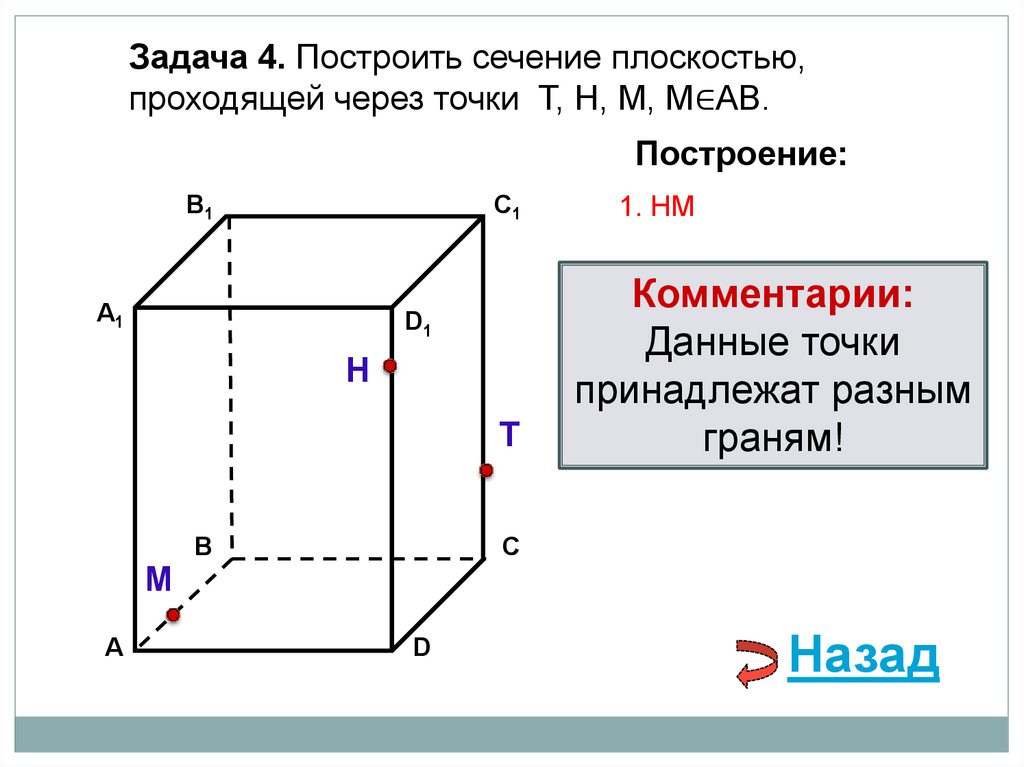
Задача 4. Построить сечение плоскостью,
проходящей через точки Т, Н, М, М∈АВ.
Построение:
В1
C1
А1
D1
Н
Т
М
А
В
1. НМ
Комментарии:
Данные точки
принадлежат разным
граням!
С
D
Назад

76.

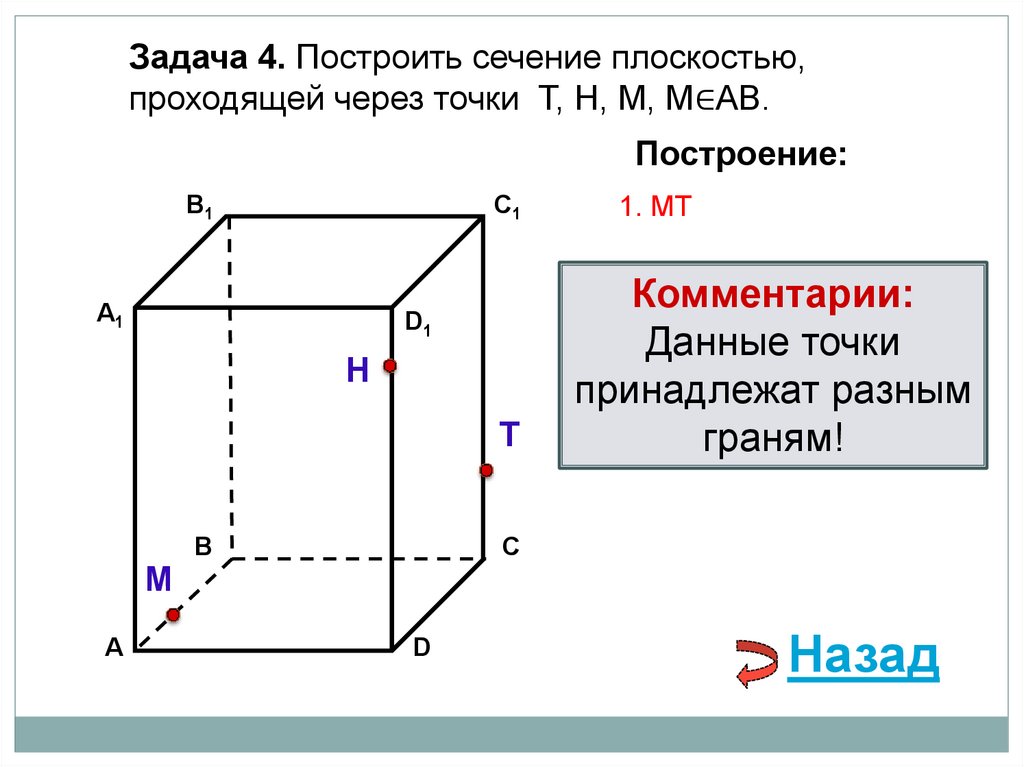
Задача 4. Построить сечение плоскостью,
проходящей через точки Т, Н, М, М∈АВ.
Построение:
В1
C1
А1
D1
Н
Т
М
А
В
1. МT
Комментарии:
Данные точки
принадлежат разным
граням!
С
D
Назад

77.

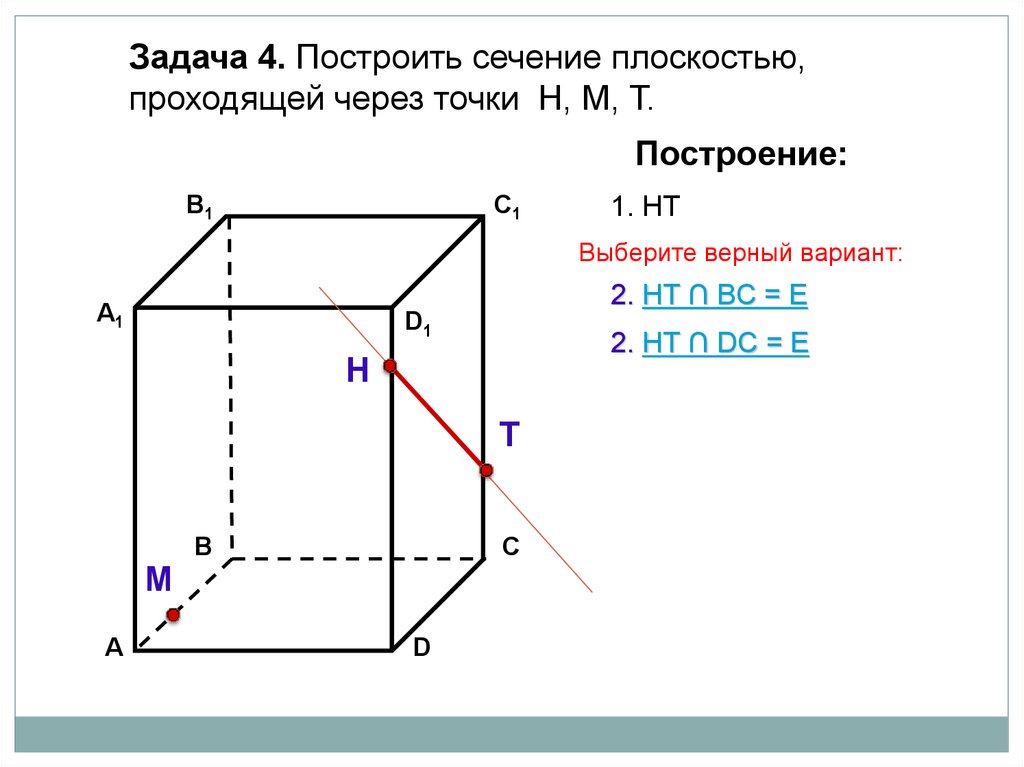
Задача 4. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
C1
1. НТ
Выберите верный вариант:
2. НТ ∩ BС = Е
А1
D1
2. НТ ∩ DС = Е
Н
Т
М
А
В
С
D

78.

Задача 4. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
C1
А1
D1
Н
Т
М
А
В
С
D
1. НТ
2. НТ ∩ ВС = Е
Комментарии:
Данные прямые скрещивающиеся!
Пересекаться не
могут!
Назад

79.

Задача 4. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
2. НТ ∩ DС = Е
C1
Выберите верный вариант:
А1
D1
3. ME ∩ AA1 = F
3. ME ∩ CC1 = F
3. ME ∩ BС = F
Н
Т
М
А
В
С
D
Е

80.

Задача 4. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
2. НТ ∩ DС = E
3. ME ∩ AA1 = F
C1
А1
D1
Н
Т
М
А
В
С
D
E
Комментарии:
Данные прямые скрещивающиеся!
Пересекаться не
могут!
Назад

81.

Задача 4. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
2. НТ ∩ DС = E
3. ME ∩ CC1 = F
C1
А1
D1
Н
Т
М
А
В
С
D
E
Комментарии:
Данные прямые скрещивающиеся!
Пересекаться не
могут!
Назад

82.

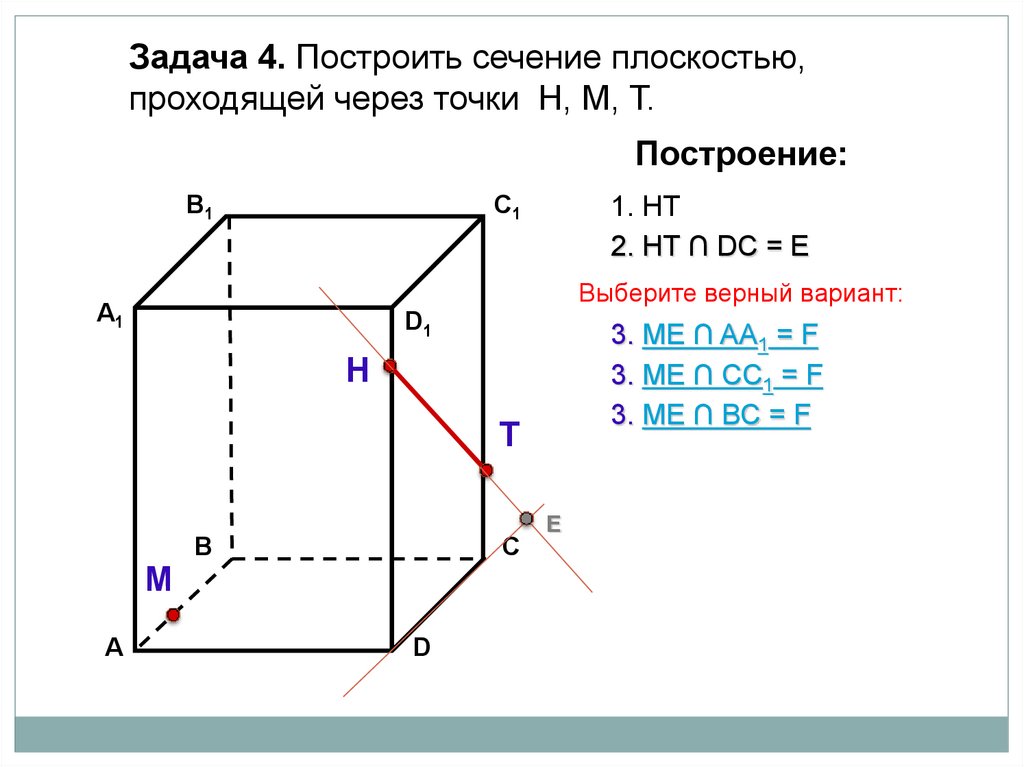
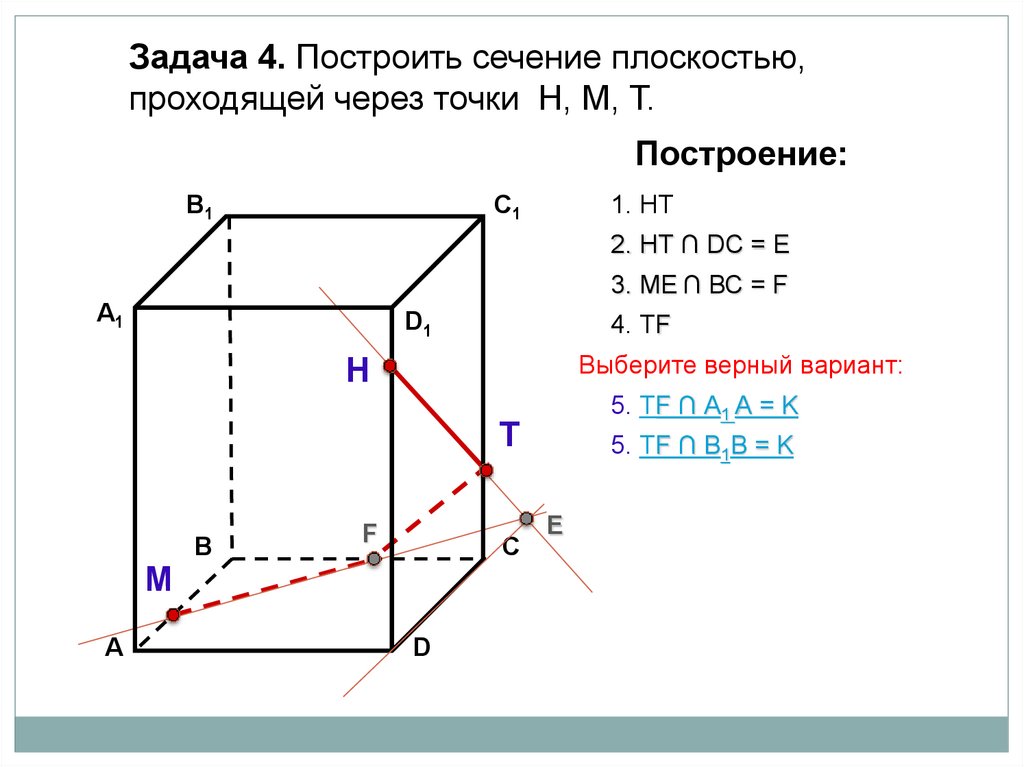
Задача 4. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
Выберите верный вариант:
D1
4. НF
Н
4. МТ
Т
М
А
В
F
С
D
4. ТF
E

83.

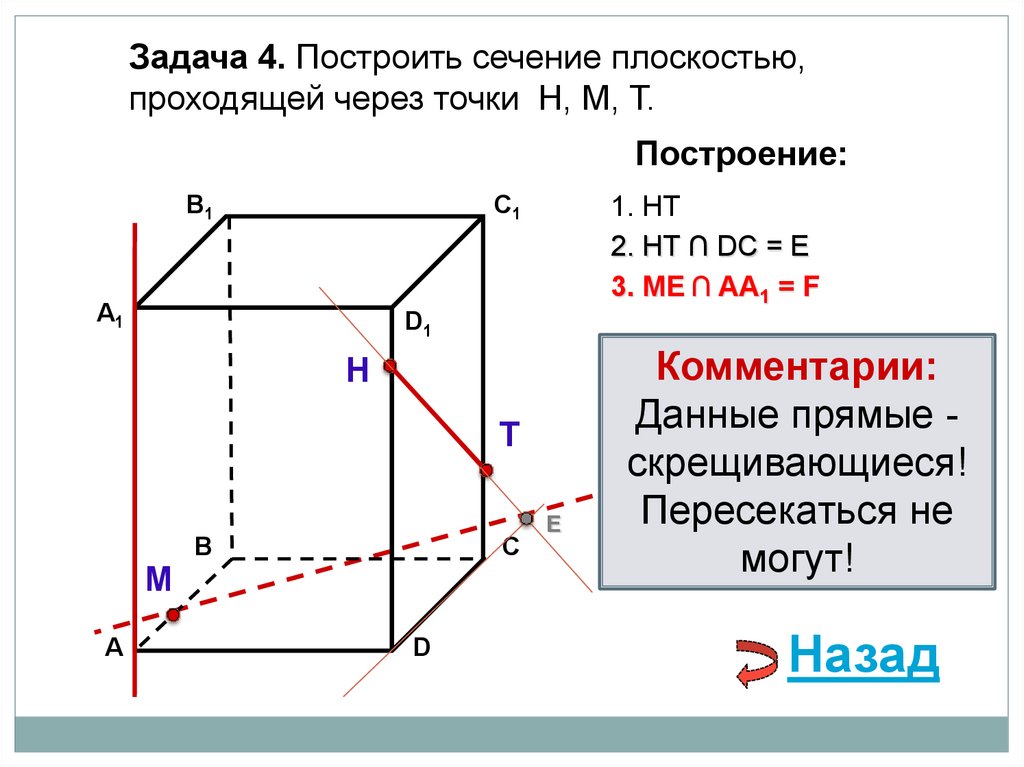
Задача 4. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
4. НF
D1
Н
Т
М
А
В
F
С
D
E
Комментарии:
Данные точки
принадлежат
разным граням!
Назад

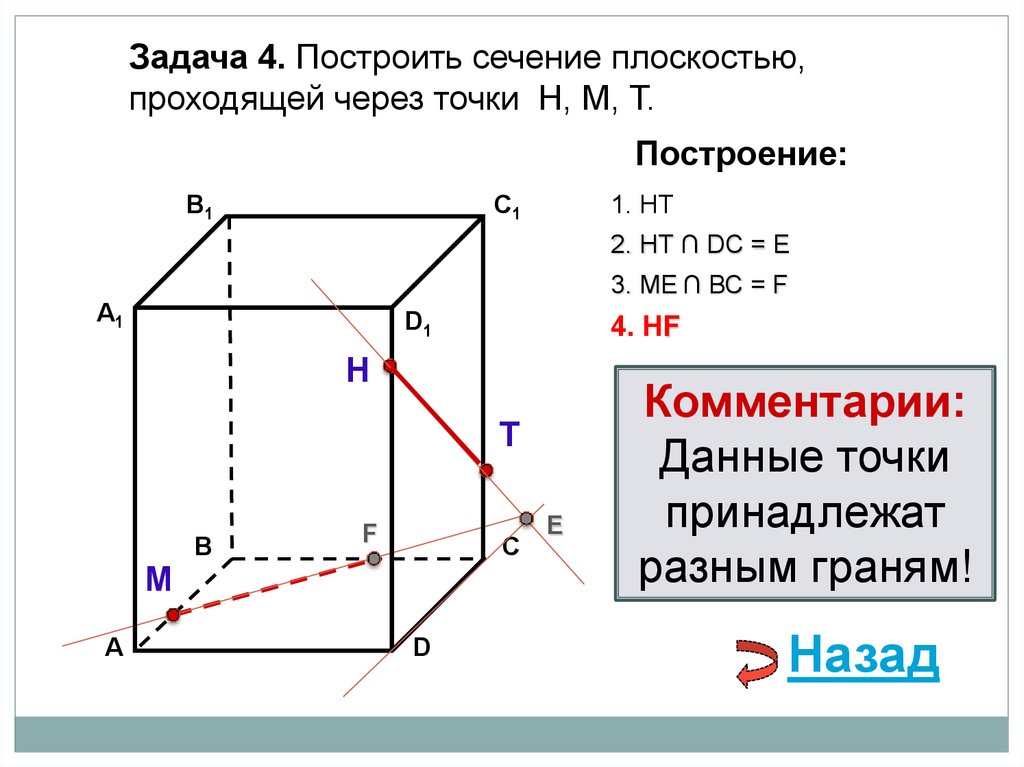
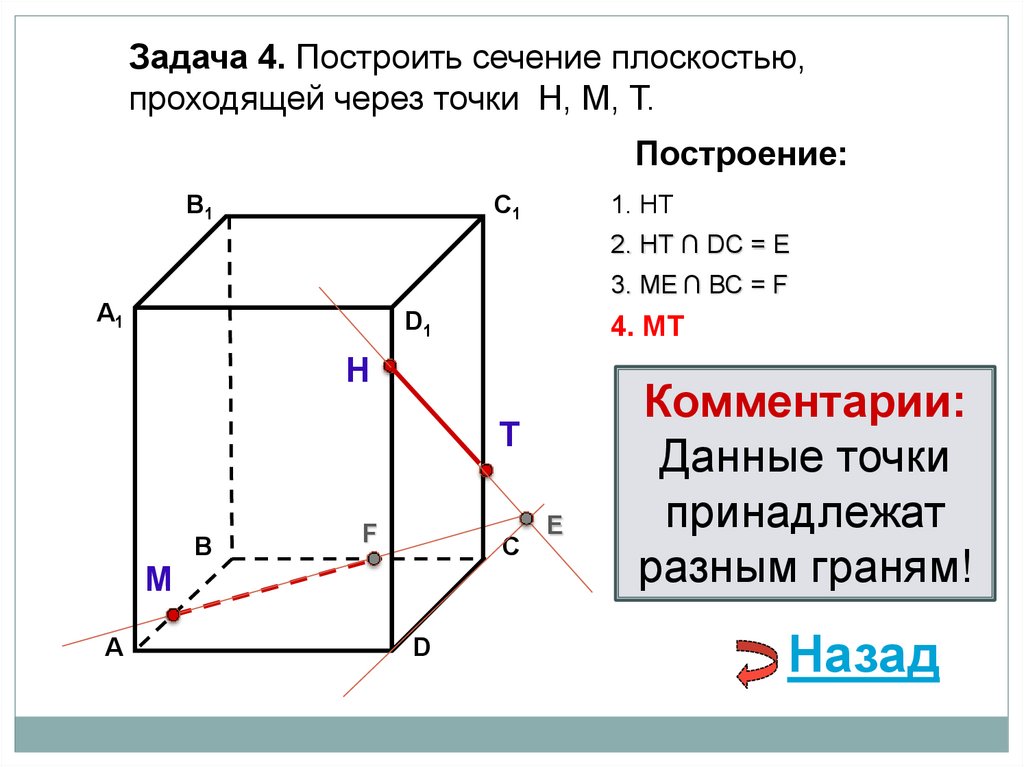
84.

Задача 4. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
D1
4. MT
Н
Т
М
А
В
F
С
D
E
Комментарии:
Данные точки
принадлежат
разным граням!
Назад

85.

Задача 4. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
4. ТF
D1
Выберите верный вариант:
Н
5. ТF ∩ А1 А = K
Т
М
А
В
F
С
D
5. ТF ∩ В1В = K
E

86.

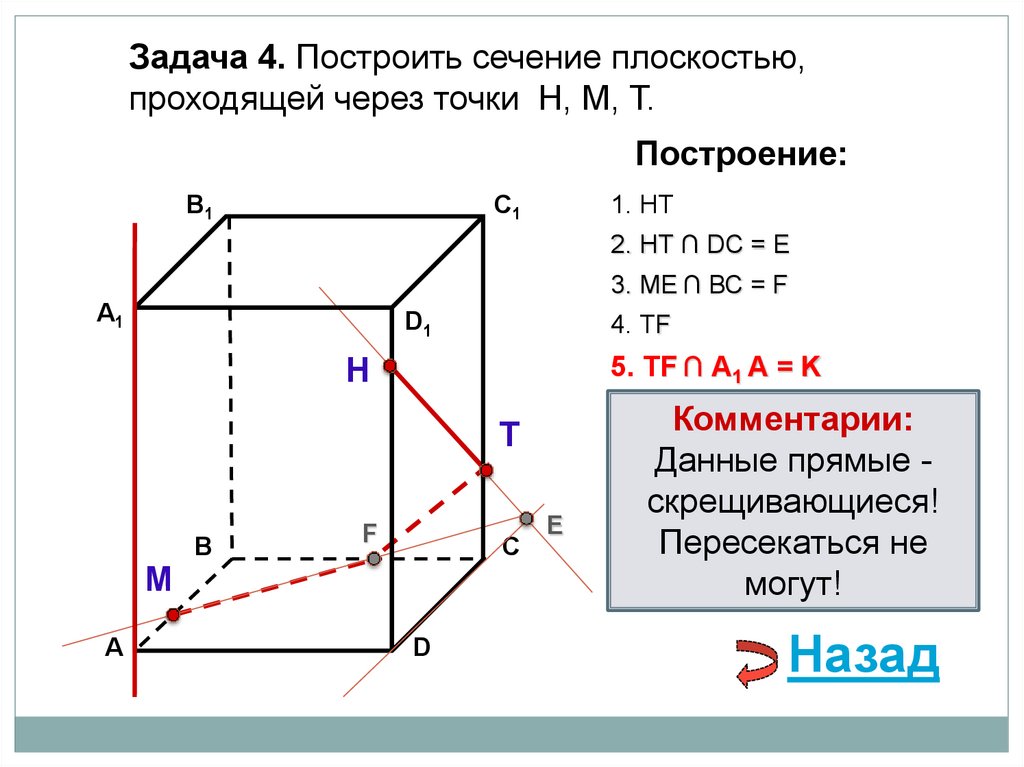
Задача 4. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
4. ТF
D1
5. ТF ∩ А1 А = K
Н
Т
М
А
В
F
С
D
E
Комментарии:
Данные прямые скрещивающиеся!
Пересекаться не
могут!
Назад

87.

Задача 4. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
4. ТF
D1
5. ТF ∩ В1В = K
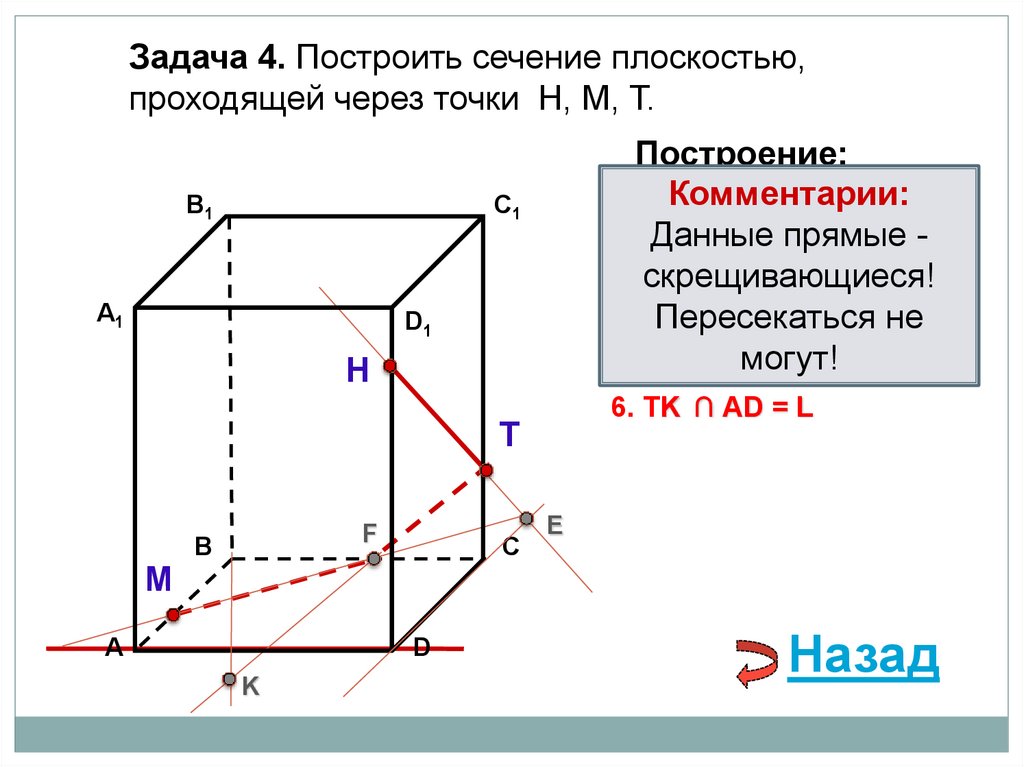
Н
Выберите верный вариант:
Т
6. НK ∩ АD = L
6. ТK ∩ АD = L
М
F
В
А
С
D
K
E
6. МK ∩ АА1= L

88.

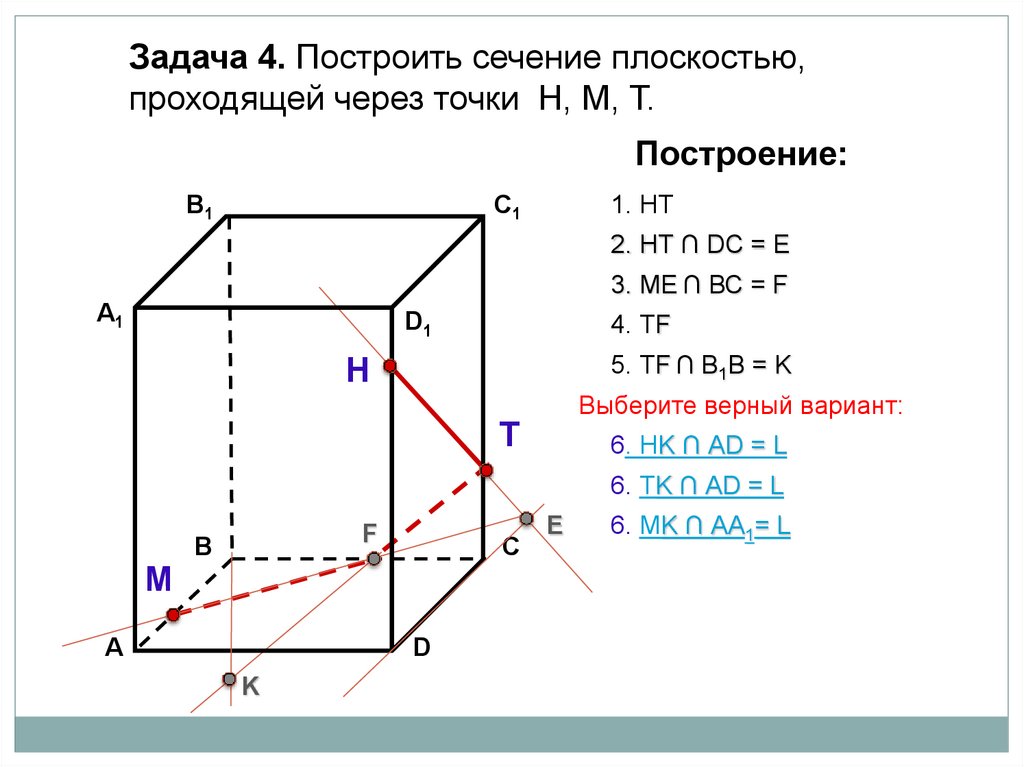
Задача 4. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
В1
Построение:
1. НТКомментарии:
Данные
2. НТ
∩ DС = Eпрямые скрещивающиеся!
3. ME
∩ ВС = F
Пересекаться не
4. ТF
5. ТF ∩ В1Вмогут!
=K
C1
А1
D1
Н
6. НK ∩ АD = L
Т
М
F
В
А
С
D
K
E
Назад

89.

Задача 4. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
В1
Построение:
1. НТКомментарии:
Данные
2. НТ
∩ DС = Eпрямые скрещивающиеся!
3. ME
∩ ВС = F
Пересекаться не
4. ТF
5. ТF ∩ В1Вмогут!
=K
C1
А1
D1
Н
6. TK ∩ АD = L
Т
М
F
В
А
С
D
K
E
Назад

90.

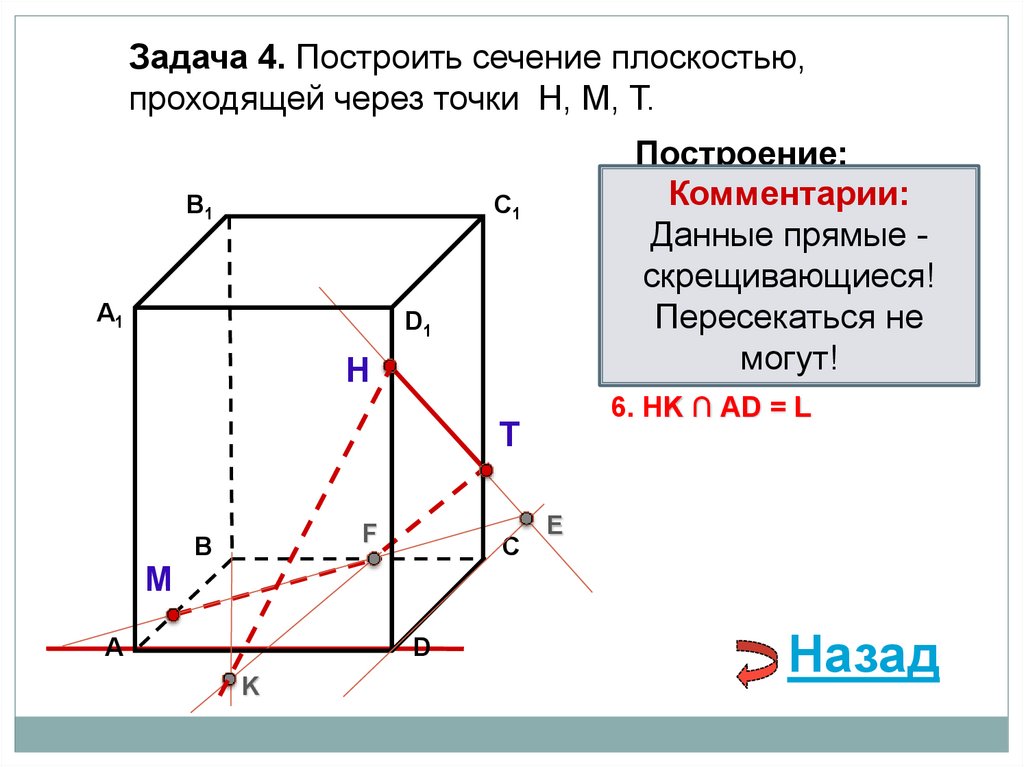
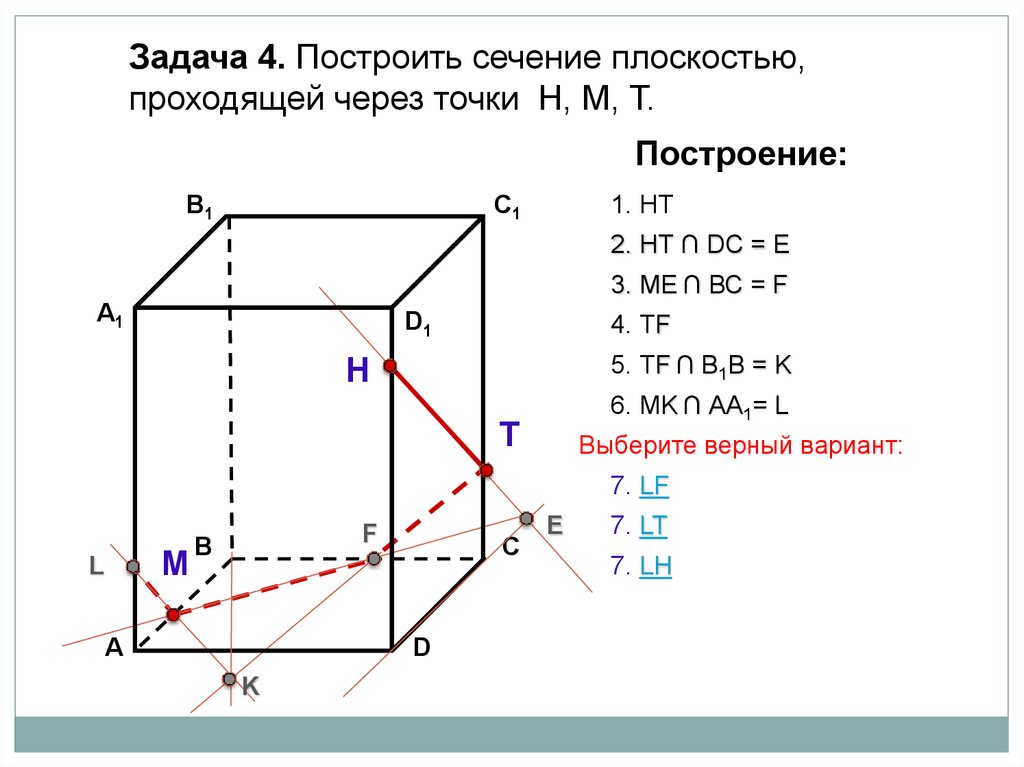
Задача 4. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
4. ТF
D1
5. ТF ∩ В1В = K
Н
6. МK ∩ АА1= L
Т
Выберите верный вариант:
7. LF
М
L
F
В
А
С
D
K
E
7. LT
7. LH

91.

Задача 4. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
А1
Комментарии:
3. ME ∩ ВС = F
Данные точки
4. ТF
5. ТFпринадлежат
∩ В1В = K
6. разным
МK ∩ АА1= Lграням!
D1
Н
Т
F
В
L
С
7. LТ
E
М
А
D
K
Назад

92.

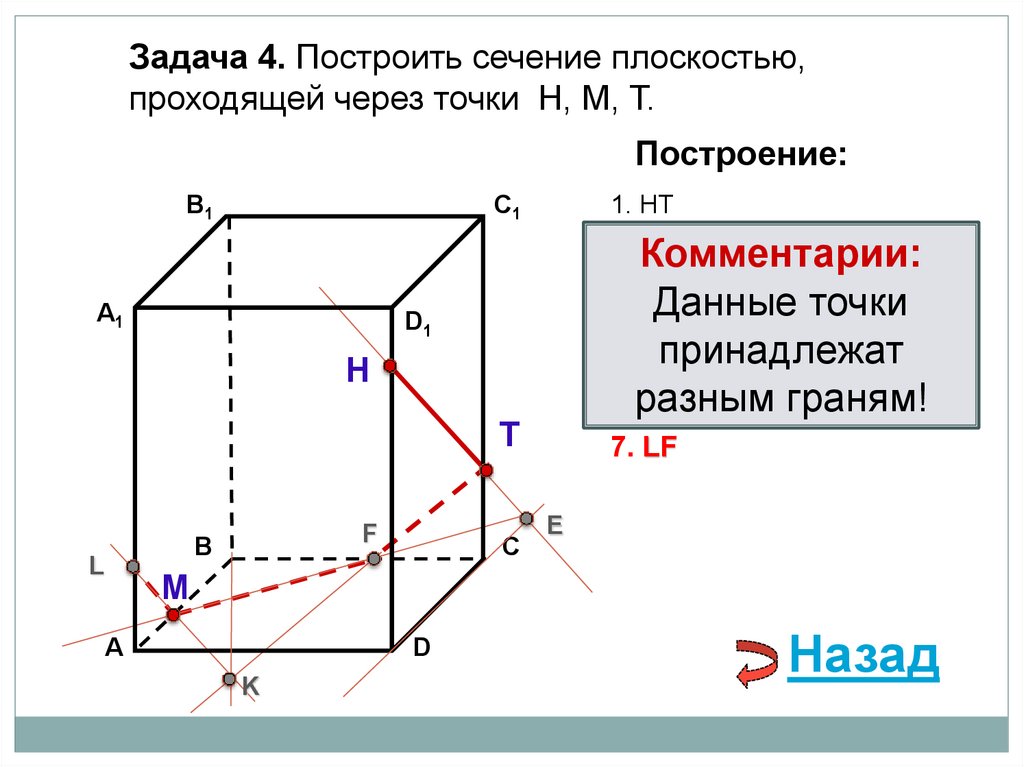
Задача 4. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
А1
Комментарии:
3. ME ∩ ВС = F
Данные точки
4. ТF
5. ТFпринадлежат
∩ В1В = K
6. разным
МK ∩ АА1= Lграням!
D1
Н
Т
F
В
L
С
7. LF
E
М
А
D
K
Назад

93.

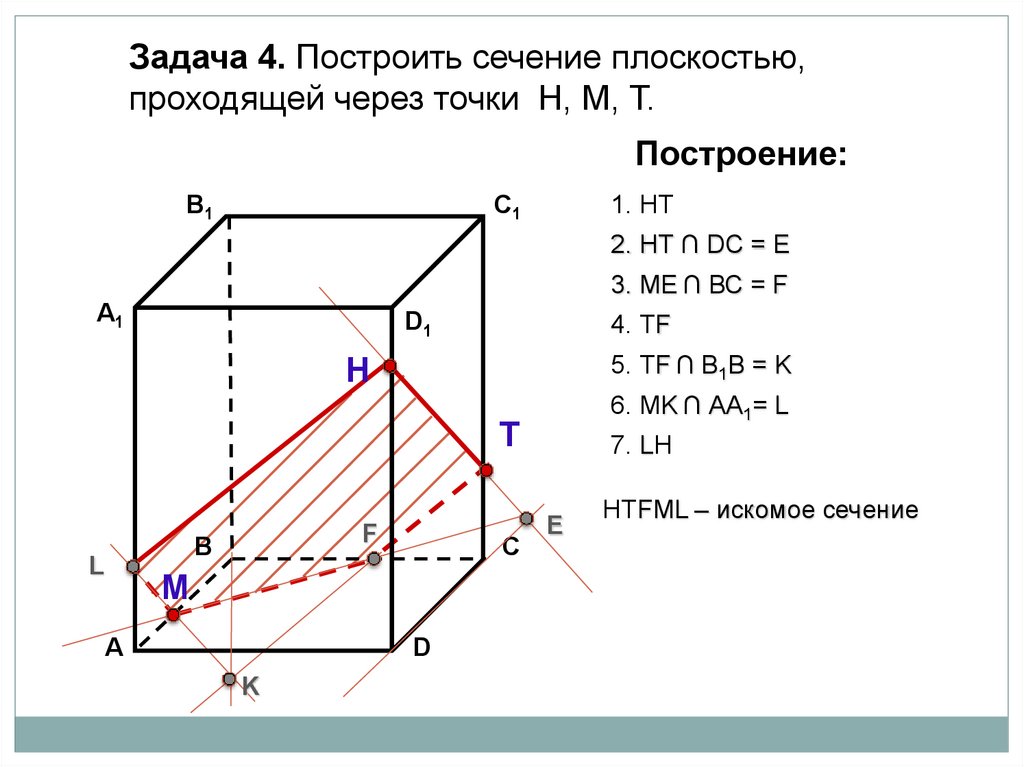
Задача 4. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
4. ТF
D1
5. ТF ∩ В1В = K
Н
6. МK ∩ АА1= L
Т
F
В
L
С
М
А
D
K
7. LН
E
НТFМL – искомое сечение

94.

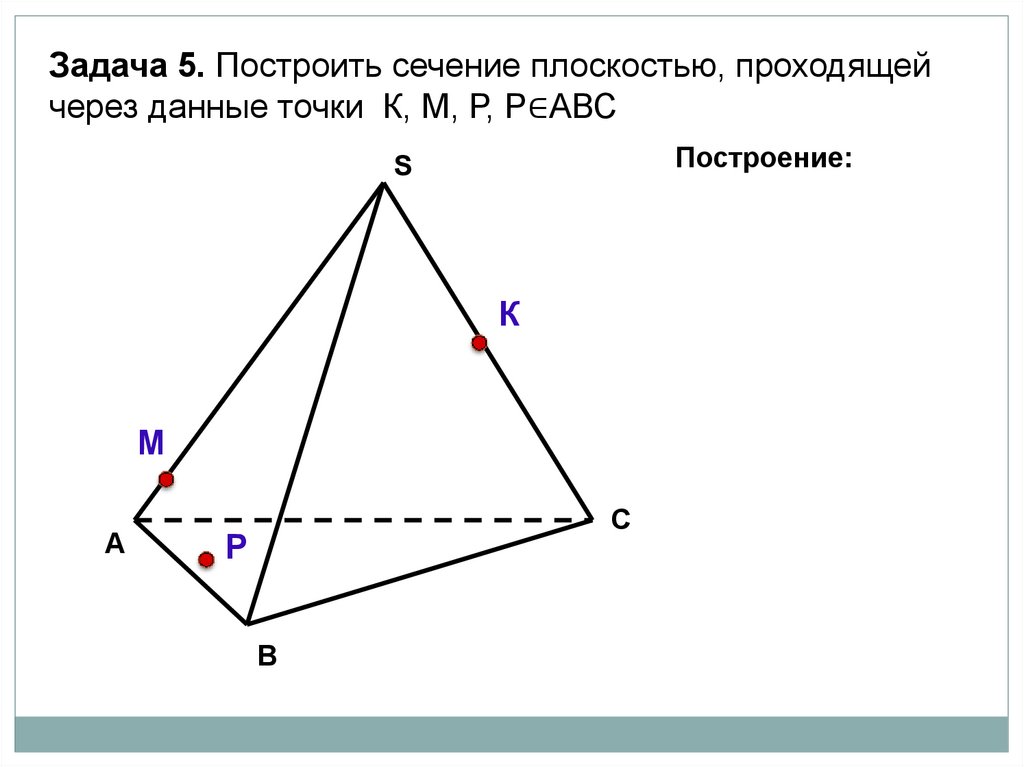
Задача 5. Построить сечение плоскостью, проходящей
через данные точки К, М, Р, Р∈АВС
Построение:
S
К
М
А
С
Р
В

95.

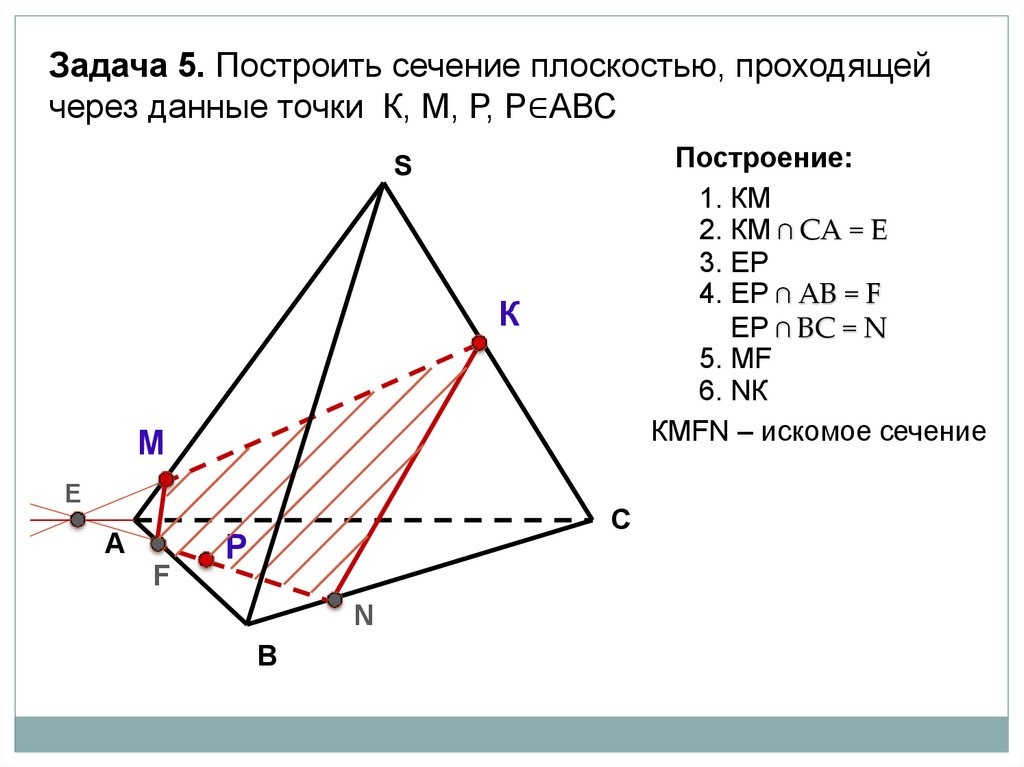
Задача 5. Построить сечение плоскостью, проходящей
через данные точки К, М, Р, Р∈АВС
Построение:
1. КМ
2. КМ ∩ СА = Е
3. EР
4. ЕР ∩ АВ = F
ЕР ∩ ВC = N
5. МF
6. NК
КМFN – искомое сечение
S
К
М
Е
А
F
С
Р
N
В