Свойства преобразования Лапласа. Лекция 19

1. Здравствуйте!

Лекция №19

2.

Свойства преобразования Лапласа
Прежде
всего
рассмотрим
два
примера
нахождения
преобразования Лапласа.
Пример 1. Пусть f ( x ) x n . Тогда
1
n!
px
n px
n y
f
(
x
)
e
dx
x
e
dx
y
e
dy
,
0
0
n 1
n 1
p 0
p
где сделана замена переменных y px .
Пример 2. Пусть f ( x ) e ax . Тогда
1
px
ax px
( p a ) x
f
(
x
)
e
dx
e
e
dx
e
dx
.
0
0
0
p a
А теперь перейдем к изучению свойств преобразования Лапласа,
обеспечивших ему популярность. В дальнейшем F ( p ) и G ( p ) будут
преобразованиями Лапласа от функций f ( x ) и g ( x ) соответственно.

3.

1. Линейность.
f ( x ) g ( x ) F ( p ) G ( p ) .
Действительно
( f ( x) g ( x))e
0
px
dx f ( x)e
0
px
dx g ( x)e px dx F ( p ) G ( p ) .
0
Пример 3.
1 i x i x
e e 1 1 1 2 2 ,
2i
2i p i p i p
1
1 1
1
p
cos x e i x e i x
.
2
2
2
2 p i p i p
sin x

4.

2. Теорема подобия.
f ( x )
Имеем
1 p
F .
p
y
1
1 p
f ( x ) f ( x )e dx f ( y )e dy F ,
0
0
где в интеграле сделана замена переменных х = у.
px

5.

3. Дифференцирование оригинала.
f ( n ) ( x ) p n F ( p ) p n 1 f ( 0 ) p n 2 f ( 0 ) ... f
Доказательство.
0
0
( n 1 )
( 0).
f ( x ) f ( x )e px dx e px df ( x )
f ( x)e
px
0
p f ( x )e px dx pF ( p ) f ( 0 ) ;
0
Аналогично
0
0
f ( x ) f ( x )e px dx e px df ( x )
f ( x ) e
px
0
p f ( x )e px dx p 2 F ( p ) pf ( 0 ) f ( 0 ) ,
0
где учтено выражение для изображения f ( x ) . Общую формулу
можно вывести по индукции.

6.

4. Дифференцирование изображения.
F ( n ) ( p ) ( 1) n x n f ( x ) .
Действительно, дифференцируя по р выражение
F ( p ) f ( x )e px dx
0
получим:
F ( p ) xf ( x )e px dx ( 1) xf ( x ) ,
0
F ( p ) x 2 f ( x )e px dx ( 1) 2 x 2 f ( x )
0
и так далее.

7.

5. Интегрирование оригинала.
x
f ( t )dt
0
F ( p)
.
p
Действительно, пусть
x
f ( t )dt G ( p ) .
0
Используя свойство 3, получим
f ( x ) f ( t )dt pG ( p ) 0 F ( p ) ,
0
откуда и следует, что G ( p ) F ( p ) p .
x

8.

6. Интегрирование изображения.
f ( x)
F(~
p ) d~
p,
x
p
где интегрирование идет по пути, изображенному на рис., где
Re p a s 0 .
~
Im p
p
~
Re p
s0
a

9.

Имеем
~
~
~
F
(
p
)
d
p
d
p f ( x)e
p
p
0
0
~
px
dx f ( x )dx e
0
f ( x ) px
f ( x)
e dx
.
x
x
p
~
px
d~
p

10.

7. Теорема запаздывания.
f ( x ) e p F ( p ) .
Заметим, что, так как f ( x ) 0 при х 0, то f ( x ) 0 при х .
А теперь имеем
0
f ( x ) f ( x )e px dx f ( x )e px dx
f ( y )e py p dy e p f ( y )e py dy e p F ( p ) ,
0
0
где сделана замена переменных х = у.

11.

8. Теорема смещения.
e p x f ( x ) F ( p p0 ).
0
Имеем
e p x f ( x ) e p x f ( x )e px dx f ( x )e ( p p
0
0
0
Пример 4.
0
)x
0
,
2
2
( p )
p
x
e cos x
.
2
2
( p )
e x sin x
dx F ( p p 0 ) .

12.

9. Теорема умножения.
x
F ( p ) G ( p ) f ( y )g ( x y ) dy .
0
Заметим, что написанный выше интеграл называется сверткой
функций f ( x ) и g ( x ) и часто обозначается f ( x ) g ( x ) . Эта
операция очень часто встречается в теории вероятностей, где
показывается, что плотность вероятностей суммы двух независимых
случайных величин есть свертка плотностей вероятностей слагаемых.
Доказательство.
Имеем
x
0
x
0
0
f ( y )g ( x y ) dy e px dx f ( y )g ( x y ) dy

13.

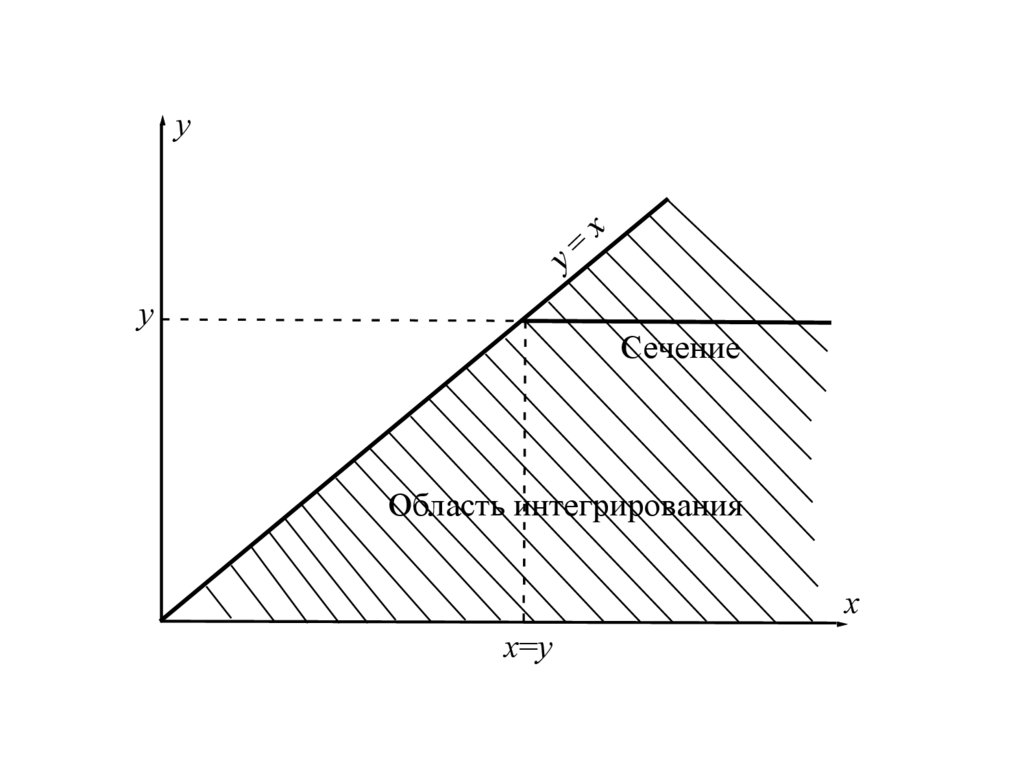
y=
x
y
y
Сечение
Область интегрирования
x
x=y

14.

Переставим местами интегралы в двойном интеграле используя
методику, изложению в части 2. Во внутреннем интеграле стоят
пределы интегрирования от 0 до х. Поэтому область
интегрирования ограничена прямыми у = 0 и у = х (см. рис.). Проектируя эту область на ось OY получаем, что у меняется в пределах от
0 до . Беря какое-то значение у и проводя прямую, параллельную
оси ОХ, получим, что при фиксированном у переменная х меняется в
пределах от у до . Поэтому
e
0
px
x
0
0
y
0
0
dx f ( y )g ( x y )dy f ( y )dy g ( x y )e px dx
f ( y )e py dy g ( z )e pz dz F ( p ) G ( p ) ,
где во внутреннем интеграле сделана замена переменных x y z ,
так что x y z .

15.

10. Предельные соотношения.
lim pF ( p ) f ( 0 ) ; lim pF ( p ) f ( ) .
p
p 0
А) Так как f ( x ) pF ( p ) f ( 0 ) , то
f ( x ) e px dx pF ( p ) f ( 0 ) .
(7)
0
Пусть существуют числа М и s1 такие, что для любых х
| f ( x ) | Me s x . Тогда, если взять р у которого Re p = s, то
M
( s s ) x
px
f
(
x
)
e
dx
M
e
dx
s
0 .
0
0
s s1
Поэтому, переходя в (7) к пределу р , получим
0 lim pF ( p ) f ( 0 ) ,
1
1
p
откуда и следует, что lim pF ( p ) f ( 0 ) .
p

16.

Б) Аналогично, переходя в (7) к пределу р 0, получим
f ( x ) dx f ( ) f ( 0 ) lim pF ( p ) f ( 0 ) .
p 0
0
Сокращая f ( 0 ) получим, что lim pF ( p ) f ( ) .
p 0