Теоретические основы электротехники. Теория электромагнитного поля. Лекция 2

1.

Теоретические основы электротехники
Теория электромагнитного поля
ВШВЭ, проф. Л. И. Сахно 2020
1

2.

Теоремы Остроградского – Гаусса и Стокса
Теорема Остроградского – Гаусса позволяет преобразовать объемный интеграл в
поверхностный, а теорема Стокса – поверхностный интеграл в линейный для
произвольных функций, непрерывных вместе со своими первыми производными
в исследуемых областях.
Запишем выражение для электрического заряда в некоторой области V, ограниченной
замкнутой поверхностью S, и применим постулат Максвелла к левой и правой части
этого уравнения:
q dV
D ds div DdV
V
S
V
Теорема Остроградского – Гаусса: Интеграл от дивергенции
вектора D по некоторому объему равен интегралу от вектора D по
замкнутой поверхности, ограничивающей этот объем.
16

3.

Используя выражение для электрического тока через некоторую поверхность S ,
ограниченную контуром l , и применив закон полного тока к обеим частям этого
уравнения, получим:
i J ds
S
H dl rot H ds
l
S
Теорема Стокса: Интеграл от ротора вектора H по некоторой поверхности
равен интегралу от вектора H по замкнутому контуру, ограничивающему
эту поверхность
3

4.

Электростатическое поле

5.

Определение электростатического поля
Электростатическое поле создается неподвижными (по отношению к наблюдателю)
электрическими зарядами. В таком поле отсутствуют электрические токи (J=0), а,
следовательно, (при отсутствии намагниченных тел) и магнитное поле (H=0; B=0).
Из полной системы уравнений электромагнитного поля для электростатического
поля получаем:
.
B
rot E
0
t
div D
D E
В реальных устройствах объемные заряды в диэлектрике не могут находиться в
покое, т.е. появляются электрические токи, что нарушат статичность поля. Поэтому
во многих случаях второе уравнение имеет нулевую правую часть:
div D 0

6.

Потенциальность электростатического поля
Векторное поле , ротор которого равен нулю , называется безвихревым или
потенциальным
rot E ds E dl 0 - из теоремы Стокса
S
l
Это соотношение определяет независимость интеграла между фиксированными
точками от пути интегрирования
p
U а E dl - электрический потенциал
а
P - точка нулевого потенциала
U a U b E dl
b
a

7.

Связь между потенциалом и напряженностью
электрического поля
P
E
la
a
lp
dl
lp
lp
U E dl E cos dl
l
l
U
E cos
l
O
Скорость изменения потенциала вдоль некоторого направления равна
проекции вектора напряженности электрического поля на это направление со
знаком минус.

8.

Проводя кривую « l » по разным направлениям, получим:
1. Проходя через точку «a» в направлении осей координат:
U
U
U
E y
Ex
E z
y
z
x
2. Проходя через точку «a» по линии l1 перпендикулярно вектору напряженности
электрического поля и вдоль него по линии l2 , получим:
U
E cos 90 0 0
l1
l1
E
a
l2
U
E cos 0 0 E
l2
Поверхности, перпендикулярные силовым линиям,
называются равнопотенциальными
(эквипотенциальными). Это направление
обозначают через «a»
U U
0
l1 a

9.

Направление вдоль линии напряженности перпендикулярно поверхности равного
потенциала. Часто это направление обозначают через «n», имея в виду нормаль к
равнопотенциальной поверхности, тогда последнее соотношение можно записать
иначе:
U U
E
l2 n
U
n
Производная
ведет себя как вектор, имеет составляющие, определяемые
направляющими косинусами, и называется градиентом потенциала.
U
n
gradU E
U
U
U
E gradU U
i
j
k
x
y
z

10.

Уравнения Пуассона и Лапласа
Преобразуем уравнения электростатического поля, выразив векторные величины
через потенциал:
div D
div( E )
Если const
div gradU
div gradU
2
2U 2U 2U
U
x 2 y 2
z 2
div ( grad U )
- уравнение Пуассона в инвариантной форме
- уравнение Пуассона в декартовой системе
координат
div grad U 2U U 0 - уравнение Лапласа
- оператор Лапласа

11.

Основная задача электростатики
Общей задачей расчета электрического поля является определение напряженности во всех его
точках по заданным зарядам или потенциалам тел.
Распределение потенциала в пространстве позволяет определить напряженность электрического поля ,
вектор смещения и поляризации в любой точке пространства
Определение потенциала обычно является более простой задачей, чем расчет напряженности,
поскольку:
1. Он является скалярной, а не векторной величиной
2. Граничные условия проще;
3. Потенциал может быть определен как решение одного дифференциального уравнения, в то
время, как напряженность определяется решением системы трех уравнений;
4. Потенциал – функция непрерывная, напряженность электрического поля на границах раздела
сред с разными диэлектрическими проницаемостями может изменяться скачком.
Поэтому определение пространственного распределения потенциала часто называют
основной задачей электростатики

12.

Определение потенциала по заданному
распределению заряда
Для уединенного точечного заряда:
q
U
4 r
Для совокупности точечных зарядов, распределенных в
ограниченной по размерам области пространства:
1 n qk
U
4 k 1 rk
Если задана система тел с зарядами, причем известно распределение зарядов в пространстве, то можно все
распределенные заряды разбить на элементарные заряды dq , каждый из которых можно рассматривать как
точечный. Составляющая потенциала от каждого элементарного точечного заряда равна:
dq
dU
4 r
Потенциал от совокупности элементарных зарядов получаем интегрированием:
U
dq
1 dq
4 r 4 r

13.

Определение потенциала по заданному
распределению зарядов
Объемное распределение заряда: dq = dV.
U
1 dV
4 r
Распределение зарядов на поверхности проводников dq = ds
U
1 ds
4 r
Линейное распределение зарядов вдоль тонких проводников dq = dl
U
1 dl
4 r

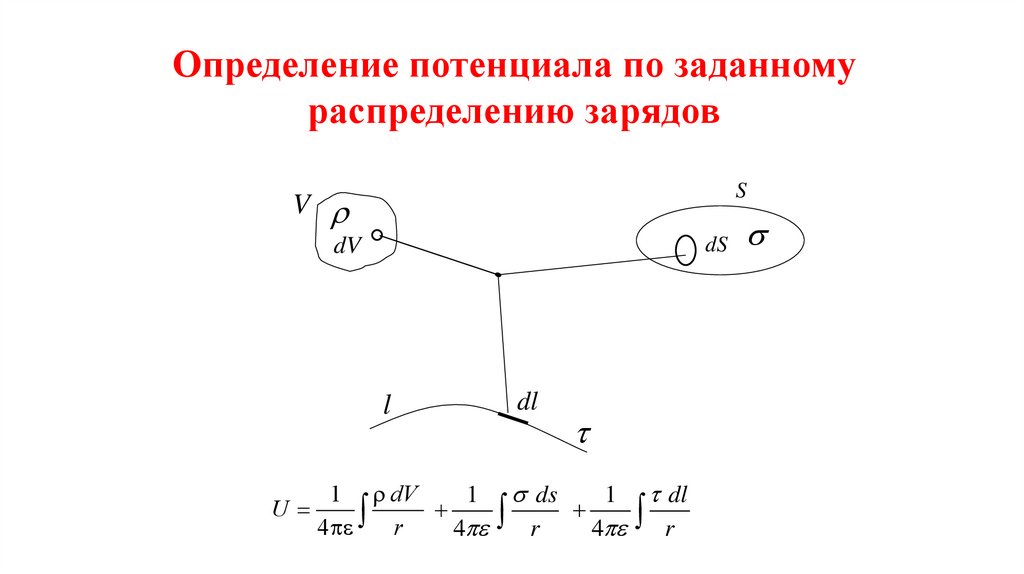
14.

Определение потенциала по заданному
распределению зарядов
S
V
dS
dV
l
dl
1 dV
1 ds
1 dl
U
4
r
4
r
4 r

15.

Способы задания граничных условий в
электростатических задачах
Граничные условия первого рода или условия Дирихле: заданы значения
потенциала
Для определения неизвестных потенциалов тел следует использовать дополнительные условия,
связывающие полные заряды с рассчитываемыми характеристиками поля – напряженностью и смещением
U
qi i ds Di ds E i ds
ds
n
Si
Si
Si
Si
При решении задачи расчета поля в кусочно-однородных диэлектриках получаем общее
решение уравнения Пуассона в каждой области и сопрягаем их на границах областей с различными
диэлектрическими проницаемостями, используя известные соотношения:
E ( k ) E ( k 1)
D n( k 1) D n( k )
k 1 E n( k 1) k E n( k )
или
Uk = Uk+1.
U k
U k 1
k
k 1
n
n
K- номер среды