Логическая символика. Числовая ось. Бином Ньютона. Абсолютная величина действительного числа. Сложные функции и неявные функции

1.

1. Логическая символика. Числовая ось. Бином Ньютона. Абсолютная величина действительного числа. Определение функции и последовательности. Обратная
функция. Классификация функций. Сложные функции и неявные функции. Параметрическое задание функций.
2. Определение предела функции и последовательности. Ограниченные и неограниченные функции и последовательности. Бесконечно малые величины и их
свойства, сравнение бесконечно малых величин.
3. Основные теоремы о пределах – пределах суммы, произведения, частного и сложной функции. О неопределенностях при отыскании пределов и их раскрытии.
Замечательные пределы и следствия. Признаки существования пределов.
4. Непрерывность функций. Классификация точек разрыва.
5. Производная Определение. Физический и геометрический смысл. Уравнение касательной к функции. Правила дифференцирования. Производная сложной
функции и обратной функции. Таблица производных.
6. Гиперболические функции и их производные. Производные неявных и параметрически заданных функций. Логарифмическое дифференцирование.
Дифференциал функции и его свойства.
7. Свойство инвариантности дифференциала. Геометрический смысл. Применение дифференциала для приближенных вычислений. Производные высших
порядков, формула Лейбница.
8. Правила дифференцирования. Производная сложной функции и обратной функции.
9. Производные неявных и параметрически заданных функций. Логарифмическое дифференцирование.
10. Дифференциал функции. Применение дифференциала для приближенных вычислений. Производные и дифференциалы высших порядков, формула
Лейбница.
11. Теоремы о среднем значении. Теоремы Ферма, Ролля, Лагранжа и Коши. Правило Лопиталя. Раскрытие неопределенностей различных видов.
12. Формула Тейлора для многочлена и для дифференцируемой функции. Остаточный член формулы Тейлора в форме Лагранжа и Пеано.
13. Разложение по формуле Тейлора некоторых элементарных функций. Формула Маклорена. Приложение формулы Тейлора к приближенным вычислениям и к
вычислению пределов.
14. Возрастание и убывание функций. Необходимое и достаточное условие возрастания и убывания дифференцируемой функции. Определение экстремумов.
15. Выпуклость и вогнутость графика функции. Точки перегиба. Асимптоты плоской кривой. Построение графиков функций.
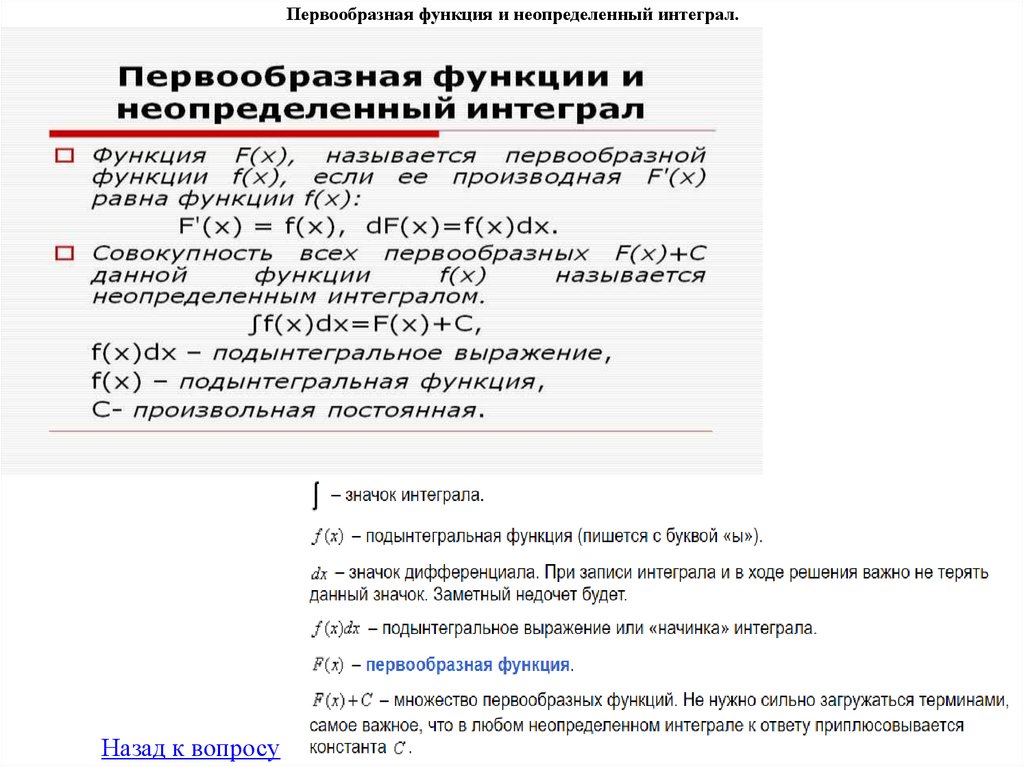
16. Первообразная функция и неопределенный интеграл. Свойства неопределенного интеграла. Таблица интегралов. Интегрирование подстановкой.
17. Интегрирование по частям. Интегрирование дробно-рациональных рациональных функций. Интегрирование элементарных рациональных дробей.
18. Интегрирование иррациональных функций. Тригонометрические подстановки.
19. Интегрирование тригонометрических функций.
20. Интегральная сумма, определенный интеграл. Свойства определенного интеграла. Теорема о среднем значении для определенного интеграла. Производная
интеграла по верхнему пределу. Формула НьютонаЛейбница.
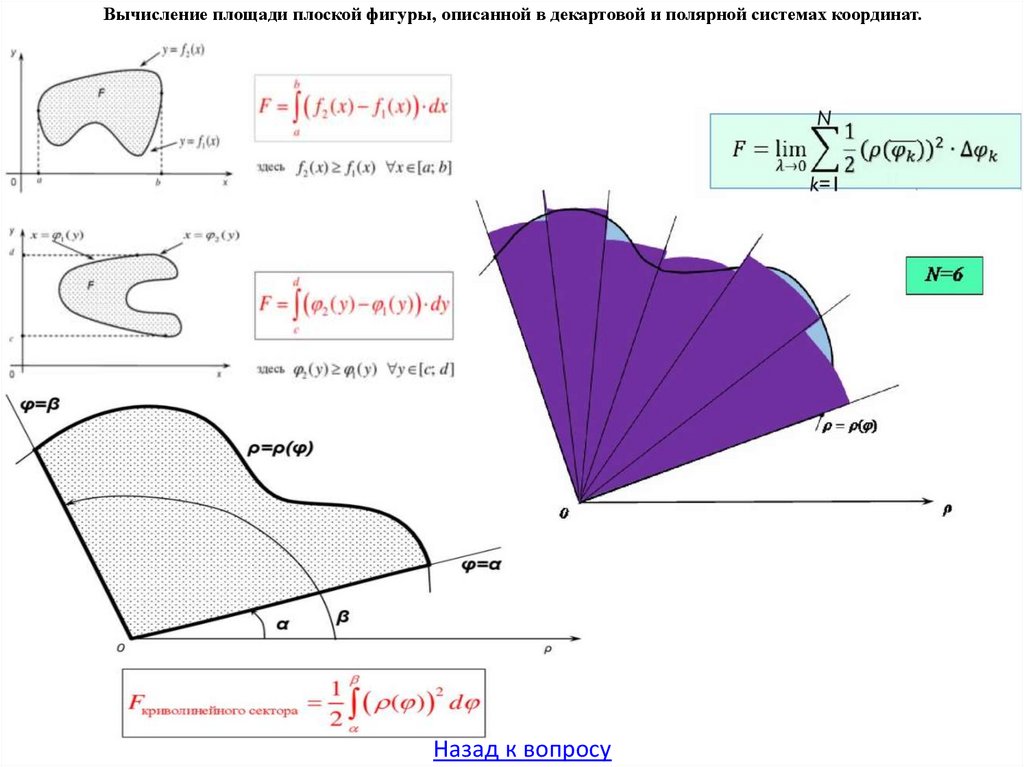
21. Замена переменных в определенном интеграле. Формула интегрирования по частям для определенного интеграла. Вычисление площади плоской фигуры,
описанной в декартовой и полярной системах координат. Длина дуги плоской кривой и ее вычисление в декартовой и полярной системах координат и кривой,
заданной в параметрической форме. Вычисление объем тела по площади поперечных сечений, объем тела вращения.
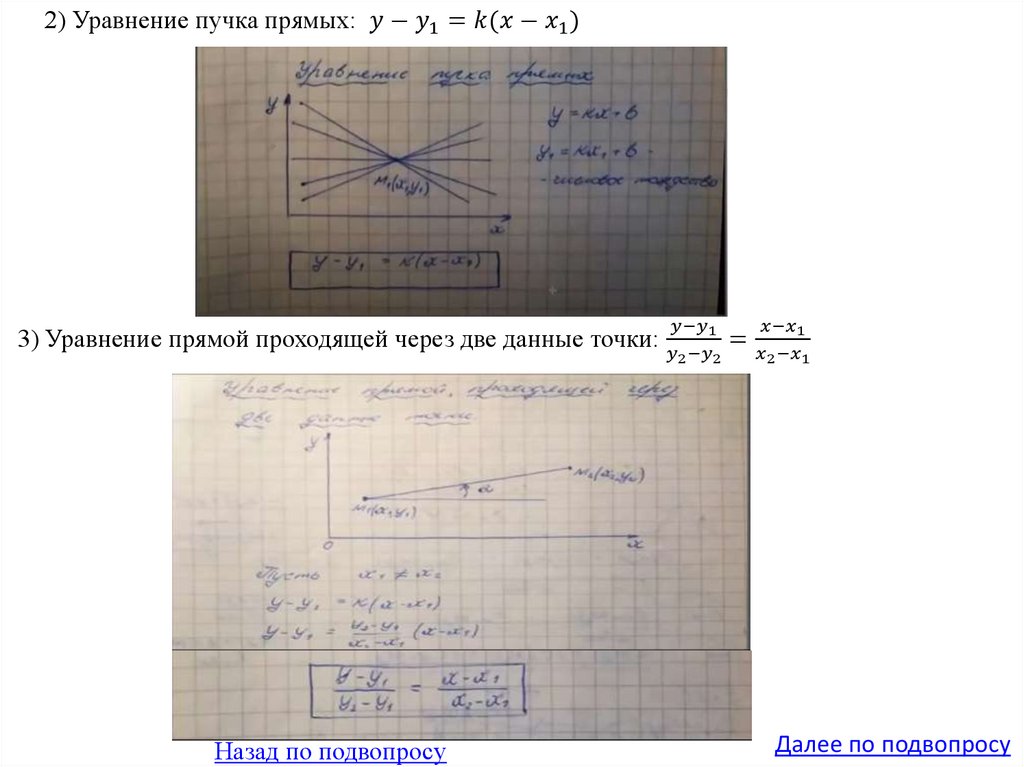
22. Декартова и полярная системы координат. Прямая на плоскости, виды уравнений. Расстояние от точки до прямой. Деление отрезка в данном отношении.
Кривые второго порядка.
23. Определители. Векторы. Координаты вектора. Линейная зависимость. Разложение вектора по координатам. Базисные векторы. Направляющие косинусы.
Линейные операции над векторами.
24. Скалярное, векторное и смешанное произведения векторов и их свойства.
25. Векторное и смешанное произведения векторов.
26. Прямая и плоскость в пространстве. Общее и каноническое уравнение прямой. Взаимное расположение прямой и плоскости.

2.

Вопрос 1
Логическая символика.
Числовая ось.
Бином Ньютона.
Абсолютная величина действительного числа.
Определение функции и последовательности.
Обратная функция.
Классификация функций.
Сложные функции и неявные функции.
Параметрическое задание функций.
Назад к билетам

3.

Логическая символика.
Наряду с математической символикой в математике
широко используется логическая символика, применяемая
к высказываниям и предикатам. Под высказыванием
понимается предложение, которое либо только истинно,
либо только ложно. Например, высказывание «–3 > 0»
ложно, а высказывание «2+2 = 4» истинное.
Назад к вопросу

4.

Числовая ось.
Числовая прямая (или координатная ось) — это прямая, на
которой задана начальная точка, положительное направление и
единичный отрезок. Начальную точку принято обозначать
точкой O. Луч, выходящий из точки O в положительном
направлении, называют положительной полуосью. Луч,
выходящий из точки O в противоположном, отрицательном,
направлении, называют отрицательной полуосью.
Каждой точке числовой прямой соответствует некоторое
действительное число.
Начальной точке O соответствует число 0. Точке на
положительной полуоси соответствует число, равное
расстоянию от этой точки до точки O. Точке на отрицательной
полуоси соответствует число, равное расстоянию от этой точки
до точки O, взятое со знаком минус.
Число, соответствующее точке на числовой прямой,
называют координатой этой точки.
Если отметить на прямой точки a и b и все точки, которые лежат
между ними. Получим отрезок, который обозначают [a;b].
Если отметить все точки, которые лежат между точками a и b,
получим интервал (a;b).
Если один "конец" промежутка включен, а другой нет, такой
промежуток называется полуинтервалом и
обозначается [a;b) или (a;b]. Квадратная скобка говорит о том,
что данный "конец" включён в промежуток, круглая − что не
включён.
Отметим точку a и все точки правее неё. Это множество точек
называется лучом и обозначается [a;+∞). Знак ∞ означает
бесконечность, это не число, поэтому квадратной скобки около
этого знака быть не может. Аналогично определяется
луч (−∞;a] − все числа, меньшие или равные числу a.
Если из луча удалить одну точку − его "конец", то
получится открытый луч. Он обозначается (a;+∞) или (−∞;a).
Всю числовую прямую можно обозначить (−∞;+∞).
Назад к вопросу

5.

Бином Ньютона.
Бино́м Нью́ то́на — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы
двух переменных, имеющая вид. где. — биномиальные коэффициенты, — неотрицательное целое число.
Назад к вопросу

6.

Абсолютная величина действительного числа
Абсолютной величиной (модулем) действительного числа x называется само это число, если x>=0 или число -x если x<0.
Абсолютная величина действительного числа x обозначается символом |x| . Таким образом:
Так, например,|2|=2, |0|=0, |-3|=-(-3)=3. Модуль любого действительного числа либо положителен (если число не равно нулю),
либо равен нулю (если само число равно нулю). Отсюда следует, что любое действительное число не больше своего модуля, т. е.
x<=|x|
Равенство будет иметь место при x>=0 , а неравенство при x<0 (так как в последнем случае число х отрицательно, а его модуль
положителен).
Назад к вопросу

7.

Определение функции и последовательности.
Определение функции:
Пусть каждому вещественному числу x из некоторого числового множества D поставлено в
соответствие однозначно определенное вещественное число y. Тогда говорят, что на
множестве D задана функция f, такая, что f (x) = y.
• Множество D называется областью определения функции f, число x — ее аргументом, а число y —
значением функции f в точке x.
• Множество E состоящее из всех значений, которые принимает функция называется областью
значений функции f.
Основными элементарными функциями называются известные из школьного курса математики
функции: степенная y = x a (с целым или дробным показателем), показательная y = a x,
логарифмическая y = loga x, все тригонометрические и обратные тригонометрические функции.
Функции, полученные из основных элементарных функций с помощью арифметических действий
Последовательность – это набор элементов множества, который удовлетворяет следующим условиям:
• для каждого натурального числа существует элемент данного множества;
• это число является номером элемента и обозначает позицию данного элемента в
последовательности;
• для любого элемента последовательности можно указать следующий за ним элемент.
Числовая последовательность – это функция переменной n, которая принадлежит множеству
натуральных чисел N.
Существованием функции, по которой можно вычислить любой член последовательности, она и
отличается от случайного набора чисел.
Отличие последовательности от функции
• Последовательность - это факт, а функция - это закон по которому строится последовательность.
Назад к вопросу

8.

Обратная функция.
Допустим, что у нас есть некая функция y=f(x), которая является строго
монотонной (убывающей или возрастающей) и непрерывной на
области определения x∈(a; b); область ее значений y∈(c; d), а на
интервале (c; d) при этом у нас будет определена функция x=g(y) с
областью значений (a; b). Вторая функция также будет непрерывной и
строго монотонной. По отношению к y=f(x) она будет обратной
функцией. То есть мы можем говорить об обратной
функции x=g(y) тогда, когда y=f(x) на заданном интервале будет либо
убывать, либо возрастать.
Две этих функции, f и g, будут взаимно обратными.
Основные свойства взаимно обратных функций
1. Первое свойство мы уже вывели ранее: y=f(g(y) и x=g(f(x)).
2. Второе свойство вытекает из первого: область
определения y=f(x) будет совпадать с областью значений обратной
функции x=g(y), и наоборот.
3. Графики функций, являющихся обратными, будут симметричными
относительно y=x.
4. Если y=f(x) является возрастающей, то и x=g(y) будет возрастать, а
если y=f(x) убывает, то убывает и x=g(y).
Назад к вопросу

9.

Классификация функций.
1. Основные элементарные функции:
- степенная у=ха, а ∈ R;
- показательная у=ах, a>0, a ≠1;
- логарифмическая у=logax, a>0, a ≠ 1;
- тригонометрические sin (x), cos (x), tg (x), ctg (x);
- аркфункции arcsin (x), arccos (x), arctg (x), аrcctg (x).
Полино́м - матем. алгебраическое выражение,
2. Алгебраические функции:
представляющее собой конечную сумму одночленов, то
- целая рациональная (полином) y=a0xn + a1xn-1 + ...+ an (n∈N; a∈R) есть каких-либо переменных, возведенных в
- рациональные - отношение полиномов.
неотрицательную степень и умноженных на постоянные
- иррациональные - наличие радикалов (дробных степеней).
коэффициенты
3. Неалгебраические (трансцендентные) функции.
К ним относятся тригонометрические, логарифмические, показательные и смешанные функции.
4. Неявные функции.
Если значение y определяется из уравнения F(x,y)=0, то функция называется неявной. Примеры: x2 + y2 =
25; sqrt(xy)+ sin2y = 5.
5. Сложные функции.
Это функции составного типа y=f1[f2(x)] или более громоздкие y=f1[f2[f3(x)]] и т. п. Для анализа удобно представлять
их системами:
и
Например, функция y=sin23x => .
Назад к вопросу

10.

Сложные функции и неявные функции.
Сложная функция — это функция от функции. Если u — функция от x, то есть u=u(x), а f —
функция от u: f=f(u), то функция y=f(u) — сложная.
y=sin x — эта функция «простая». Синус зависит от x. Как только вместо x под знаком синуса
появится выражение, зависящее от x, даже самое простое — такая функция называется сложной.
То есть y=sin (u) — сложная функция, если u — некоторая функция от x.
• Примеры сложных функций с синусом:
• y=sin (x+1). Эта функция — сложная. Внутренняя функция u здесь равна x+1, а внешняя
функция f — это синус. То есть u=x+1, f=sin (u).
Термин «неявная функция» относится к способу задания функциональной зависимости
между x и y и означает, что вместо явной формулы y=f(x) эта зависимость представлена
уравнением F(x,y)=0.
Если значение y определяется из уравнения F(x,y)=0, то функция называется неявной.
Примеры: x2 + y2 = 25; sqrt(xy)+ sin2y = 5.
Назад к вопросу

11.

Параметрическое задание функций.
• Параметрическое представление —
используемая в математическом
анализе разновидность
представления переменных, когда их зависимость
выражается через дополнительную величину —
параметр.
• Предположим, что функциональная
зависимость y от x не задана непосредственно y =
f(x), а через промежуточную величину — t. Тогда
формулы
• x=ϕ((фи))(t) y=τ((тау))(t) задают параметрическое
представление функции одной переменной.
Назад к вопросу

12.

Вопрос 2
• Определение предела функции и
последовательности.
• Ограниченные и неограниченные функции
и последовательности.
• Бесконечно малые величины и их свойства,
сравнение бесконечно малых величин.
Назад к билетам

13.

Определение предела функции и последовательности.
Постоянное число а называется пределом последовательности {xn}, если для любого сколь угодно
малого положительного числа ε > 0 существует номер N, что все значения xn, у которых n>N,
удовлетворяют неравенству
• |xn - a| < ε.
(6.1)
• Записывают это следующим образом:
или xn→ a.
• Неравенство (6.1) равносильно двойному неравенству
a - ε < xn < a + ε которое означает, что точки x n, начиная с некоторого номера n>N, лежат внутри
интервала (a-ε , a+ε), т.е. попадают в какую угодно малую ε-окрестность точки а.
• Последовательность, имеющая предел, называется сходящейся, в противном случае - расходящейся.
• Понятие предел функции является обобщением понятия предел последовательности, так как предел
последовательности можно рассматривать как предел функции xn = f(n) целочисленного аргумента n.
• Пусть дана функция f(x) и пусть a - предельная точка области определения этой функции D(f), т.е.
такая точка, любая окрестность которой содержит точки множества D(f), отличные от a.
Точка a может принадлежать множеству D(f), а может и не принадлежать ему.
Определения 1 и 2 равносильны. (Говорите что-то одно, а если дед спросит, то и второе)
• Определение 1. Постоянное число А называется предел функции f(x) при x→ a, если для всякой
последовательности {xn} значений аргумента, стремящейся к а, соответствующие им
последовательности {f(xn)} имеют один и тот же предел А.
• Это определение называют определением предела функции по Гейне, или “на языке
последовательностей”.
• Определение 2. Постоянное число А называется предел функции f(x) при x→a, если, задав
произвольное, как угодно малое положительное число ε, можно найти такое δ >0 (зависящее от ε), что
для всех x, лежащих в ε-окрестности числа а, т.е. для x, удовлетворяющих неравенству
0 < x-a < ε , значения функции f(x) будут лежать в ε-окрестности числа А, т.е. |f(x)-A| < ε
• Это определение называют определением предел функции по Коши, или “на языке ε - δ«
Если функция f(x) при x → a имеет предел, равный А, это записывается в виде
• В том случае, если последовательность {f(xn)} неограниченно возрастает (или убывает) при любом
способе приближения x к своему пределу а, то будем говорить, что функция f(x) имеет бесконечный
предел, и записывать это в виде:
Далее по подвопросу

14.

• Eсли x → a и при этом x > a, то пишут x →a
+ 0. Если, в частности, a = 0, то вместо 0+0
пишут +0. Аналогично если x→a и при
этом x<a, то пишут x→ -0. Это называется
соответственно предел справа и предел
слева функции f(x) в точке а. Чтобы
существовал предел функции f(x) при x→ a
необходимо и достаточно, чтобы предел
справа был равен пределу слева.
Назад по подвопросу
Назад к вопросу

15.

Ограниченные и неограниченные функции и последовательности
Числовая последовательность {хn} называется ограниченной, если существуют числа m и M, такие, что любой
элемент xn этой последовательности удовлетворяет неравенствам m ≤ xn ≤ M.
Определение. Последовательность
{ xn}называется ограниченной сверху, если для любого n существует такое число М, что xn ≤ M
Определение. Последовательность {xn}называется ограниченной снизу, если для любого n существует такое число
m, что m ≤ xn
Постоянное число а называется пределом последовательности {xn}, если для любого сколь угодно малого
положительного числа ε > 0 существует номер N, что все значения xn, у которых n>N, удовлетворяют неравенству
|xn - a| < ε. Это записывается: lim xn = a.
В этом случае говорят, что последовательность {xn} сходится к а Свойство: Если отбросить какое-либо число
членов последовательности, то получаются новые последовательности, при этом если сходится одна из них, то
сходится и другая.
Ограниченные и неограниченные функции
Обозначим буквой X некоторое множество чисел, входящих в область
определения D ( f ) функции y = f (x).
Определение 1. Функцию y = f (x) называют ограниченной сверху на множестве X , если существует
такое число a , что для любого x из множества X выполнено неравенство
Определение 2. Функцию y = f (x) называют ограниченной снизу на множестве X , если существует такое
число b , что для любого x из множества X выполнено неравенство
Определение 3. Функцию y = f (x) называют ограниченной на множестве X , если существуют такие
числа a и b , что для любого x из множества X выполнено неравенство
Определение 4. Функцию y = f (x) называют неограниченной сверху на множестве X , если для любого
числа a существует такой x из множества X , для которого выполнено неравенство
Определение 5. Функцию y = f (x) называют неограниченной снизу на множестве X , если для любого
числа b существует такой x из множества X , для которого выполнено неравенство
Определение 6. Функцию y = f (x) называют неограниченной на множестве X , если эта функция или
неограничена сверху, или неограничена снизу, или неограничена и сверху, и снизу.
Назад к вопросу

16.

Бесконечно малые величины и их свойства, сравнение бесконечно малых величин.
Переменная величина (т.е. последовательность или функция), предел которой равен или стремится к нулю,
называется бесконечно малой величиной.
Переменная величина, предел которой равен бесконечности или стремится к ней, называется бесконечно
большой величиной.
Свойства бесконечно малых
Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.
Произведение бесконечно малых - бесконечно малая.
Произведение бесконечно малой последовательности на ограниченную (или константу) - бесконечно малая.
1
Если an - бесконечно малая последовательность, сохраняющая знак, то