Похожие презентации:
Системы принятия решений. Алгоритмы оптимизации
1.
НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМ. Н.И.ЛОБАЧЕВСКОГОНАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ
ИНСТИТУТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ, МАТЕМАТИКИ И МЕХАНИКИ
Системы принятия решений
VLADIMIR GRISHAGIN
2.
Характеристические алгоритмыоптимизации
( x) min, x Q [a, b]
(2.1)
Определение. Алгоритм решения задачи (*) называется характеристическим,
k 1
если, начиная с некоторого шага поиска k0 1 , выбор координаты x
очередного испытания (k k0 ) заключается в выполнении следующих
действий.
1. Задать множество
k {x0 , x1 ,..., x }
конечного числа 1 (k ) 1 точек области Q [a, b] , полагая, что
i
a k , b k , все координаты предшествующих испытаний x k , 1 i k ,
множество k упорядочено (нижним индексом) по возрастанию координаты,
т.е.
a x0 x1 ... x 1 x b.
и сопоставить точкам множества значения zi ( xi ), 0 i .
3.
Характеристические алгоритмыоптимизации
2. Каждому интервалу ( xi 1 , xi ) , 1 i , поставить в соответствие число R (i ) ,
называемое характеристикой этого интервала.
3. Определить интервал ( xt 1 , xt ) , которому соответствует максимальная
характеристика R (t ) , т.е.
R(t ) max{ R(i ) : 1 i }
4. Провести очередное испытание в точке
x k 1 d (t ) ( xt 1 , xt )
и вычислить значение z
k 1
( x k 1 ).
4.
Двусторонняя сходимость.(2.1)
( x ) min, x Q [a, b]
*
Теорема 2.1. Пусть точка x является предельной точкой (точкой накопления)
k
последовательности испытаний{x }, генерируемой характеристическим алгоритмом
*
при решении задачи (2.1), причем x* a, x b . Если характеристики R(i ) и
правило d (t ) выбора координаты x k 1 очередного испытания обеспечивают
выполнение условий:
i) если точка x [ xi ( k ) 1 , xi ( k ) ] и xi ( k ) 1 x , xi ( k ) x , когда k , тогда
(2.2)
R(i (k )) ( x ) c
ii) если, начиная с некоторого шага поиска , интервал ( xi 1 , xi ), i i (k ) , не будет
содержать точек испытаний, т.е. существует номер k s 1 такой, что для всех k k s
(2.3)
( xi 1 , xi ) {x k }
тогда для характеристики этого интервала выполняется строгое неравенство
(2.4)
lim R (i ) min{ ( xi 1 ), ( xi )} c
k
k 1
iii) для точки нового испытания x имеет место неравенство
max{x k 1 xt 1 , xt x k 1} ( xt xt 1 )
где в (2.2), (2.4), (2.5) величины , c, и некоторые константы, причем
0, 0 1
k
(2.5)
(2.6)
тогда последовательность {x } содержит две подпоследовательности, одна из
которых сходится к x * слева, другая справа.
5.
Двусторонняя сходимость.Следствие. В вычислительную схему алгоритма, удовлетворяющего условиям
Теоремы 2.1, может быть введено условие остановки вида
(2.7)
xt xt 1
где t - это номер интервала с максимальной характеристикой, а 0 заданная точность поиска.
6.
Двусторонняя сходимость (перебор)i) Если точка x [ xi 1 , xi ] и xi 1 x , xi x , когда k , тогда
R(i) xi xi 1 0, т.е. 0, c 0
ii) Если ( xi 1 , xi ) {x k } , то требуется
lim R (i ) min{zi 1 , zi } c 0
k
iii) для точек новых испытаний
max{ x k 1 xt 1 , xt x k 1} ( xt xt 1 )
x k 1 0.5( xt 1 xt ).
x k 1 xt 1 xt x k 1 0.5( xt xt 1 )
0.5
7.
Двусторонняя сходимость (метод Пиявского)R(i) 0.5m( xi xi 1 ) ( zi zi 1 ) / 2,
x k 1 0.5( xt xt 1 ) ( zt zt 1 ) /( 2m),
Условие Липшица
( x ) ( x ) L x x , x , x [a, b]
i) если точка x [ xi 1 , xi ]
тогда
R (i ) (x )
1, c 0
и xi 1 x , xi x , когда n
8.
Двусторонняя сходимость (метод Пиявского)ii) если
тогда
( xi 1 , xi ) {x k }
lim R (i ) min{zi 1 , zi }
n
1
min{ zi 1 , zi } ( zi 1 zi zi 1 zi )
2
Возьмем m L. Вследствие условия Липшица
L( xi xi 1 ) zi 1 zi
xi xi 1 zi zi 1
xi xi 1 zi zi 1 zi 1 zi ( zi 1 zi )
m
L
min{ zi 1 , zi }
2
2
2
2
2
9.
Двусторонняя сходимость (метод Пиявского)iii) для точек новых испытаний
max{ x k 1 xt 1 , xt x k 1} ( xt xt 1 )
xt x k 1
xt xt 1 zt zt 1 xt xt 1
x xt 1
L x xt 1
L t
1 t
2
2m
2
2m
m 2
0,5(1 L / m)
10.
Двусторонняя сходимость (метод Стронгина)( zi zi 1 ) 2
R(i) m( xi xi 1 )
2( zi zi 1 ),
m( xi xi 1 )
x k 1 0.5( xt xt 1 ) ( zt zt 1 ) /( 2m),
Условие Липшица
( x ) ( x ) L x x , x , x [a, b]
i) если точка x [ xi 1 , xi ]
тогда
R (i ) 4 ( x )
4, c 0
и xi 1 x , xi x
, когда n
11.
Двусторонняя сходимость (метод Стронгина)ii) если ( xi 1 , xi ) {x }
R(i ) i 4 min{ zi 1 , zi }
тогда lim
n
k
min{ zi 1 , zi }
1
( zi 1 zi zi 1 zi )
2
Возьмем m L.
Случай 1. zi 1 zi
R(i) m( xi xi 1 ) 2( zi zi 1 ) 2( zi zi 1 ) 4 min{zi 1 , zi }
Случай 2.
zi 1 zi
R(i) zi zi 1 (
1
) 2( zi zi 1 )
m( xi xi 1 ) m
1
zi zi 1
L
1
2
R(i) 2 zi zi 1 2( zi zi 1 ) 4 min{ zi , zi 1}
12.
Двусторонняя сходимость (метод Стронгина)iii) для точек новых испытаний
max{ x k 1 xt 1 , xt x k 1} ( xt xt 1 )
xt x k 1
xt xt 1 zt zt 1 xt xt 1
x xt 1
L x xt 1
L t
1 t
2
2m
2
2m
m 2
0,5(1 L / m)
rM , M 0
m
1, M 0
M max
1 i
r 1
zi zi 1
xi xi 1
- параметр метода
xt x k 1
xt xt 1 zt zt 1 xt xt 1
x xt 1 1 xt xt 1
M t
1
2
2m
2
2rM
r 2
0.5(1 1 / r )
13.
Двусторонняя сходимость (метод Кушнера)4( k* k zi )( k* k zi 1 )
R(i)
,1 i ,
xi xi 1
( xt xt 1 )( k* k zt )
k 1
x xt 1
2( k* k ) zt zt 1
где k 0 - параметр метода, а k* min zi .
0 i
Потребуем непрерывность целевой функции
i) Пусть точка x [ xi 1 , xi ] и xi 1 x , xi x , когда k ,
и, начиная с некоторого шага поиска, параметр метода k 0 , тогда
*
k* zi 1 k 0 , k zi k 0 и характеристика
4( k* k zi )( k* k zi 1 )
R (i (k ))
xi xi 1
т.к. длина интервала ( xi 1 , xi ) стремится к нулю. Следовательно, (2.2)
выполняется при 0 и c (доказательство теоремы 2.1 не меняется,
если предел в правой части (2.2) будет равен ).
14.
Двусторонняя сходимость (метод Кушнера)ii) Если ( xi 1 , xi ) {x k } , то требуется
lim R (i ) min{zi 1 , zi } c
k
При 0, c это неравенство имеет вид
lim R (i )
k
Но любой интервал, в который испытания больше не попадают, имеет
положительную длину, что доказывает требуемое неравенство.
15.
Двусторонняя сходимость (метод Кушнера)iii) для точек новых испытаний
max{ x k 1 xt 1 , xt x k 1} ( xt xt 1 )
Рассмотрим разности
x k 1 xt 1 1 ( xt xt 1 ), xt x k 1 2 ( xt xt 1 )
где
zt 1 k* k
zt k* k
1
, 2
zt 1 zt 2( k* k )
zt 1 zt 2( k* k )
Введем вспомогательную функцию ( w, )
имеем
1 ( zt 1 k* , k ), 2 ( zt k* , k.)
w
.Так как min{ zt 1 , zt } k* ,
w 2
Для любого положительного w функция ( w, ) убывает по , потому что
производная ( w, )
w
0, откуда для k 0
( w 2 )2
1 ( zt 1 k* , ), 2 ( zt k* , )
16.
Двусторонняя сходимость (метод Кушнера)Кроме того, функция ( w, ) возрастает по w для любого положительного , т.к.
0, поэтому
производная w ( w, )
( w 2 ) 2
max{ ( zt 1 k* , ), ( zt k* , )} ( max min , )
Последнее неравенство означает, что
max{ 1 , 2 } ( max min , )
max min
max min 2
следовательно,
x k 1 xt 1
max min
min
( xt xt 1 ), xt x k 1 max
( xt xt 1 )
max min 2
max min 2
Таким образом, в качестве константы в (2.6) можно взять величину
которая, очевидно, положительна и меньше единицы.
max min
max min 2
17.
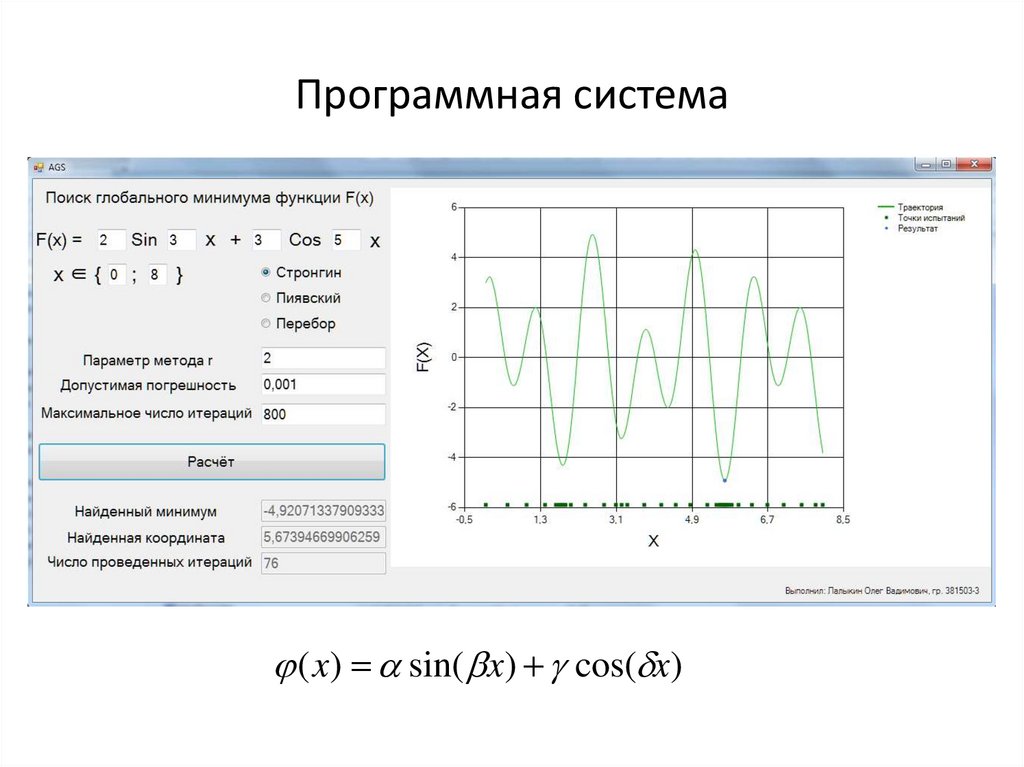
Программная система18.
Программная система( x) sin( x) cos( x)

















 Математика
Математика








