Полиномы от одной переменной. Нохождение НОД. (Лекция 5.2)

1. Полиномы от одной переменной

Нахождение НОД

2. «Наивный» метод

Пример: Вычислить НОД полиномов
f = x8 + x 6 - 3 x 4 - 3 x 3 + x 2 + 2 x - 5
g = 3x 6 + 5 x 4 - 4 x 2 - 9 x + 21
x8 + x 6 - 3x 4 - 3x3 + x 2 + 2 x - 5 3x 6 + 5 x 4 - 4 x 2 - 9 x + 21
x8 + 5 3 x 6 - 4 3 x 4 - 3x 3 + 7 x 2
x2
3
- 29
- 2 3 x6 - 2 3 x4 + x2 + 2x - 5
æ x2 2 ö
f -ç - ÷× g
è 3 9ø
т.е.
5 4 1 2 1
x + x 9
9
3

3. Пример:

p5=НОД(f5,g5):
w=х-3, v=х+2, НОД=1,
но w5=v5=х+2 и, таким образом,
НОД(w5,v5)=х+2.

4. Граница для коэффициентов НОД двух полиномов.

Теорема (неравенство Ландау-Миньотта).
b = bi x
i
a=
i=0
a
bi 2
b
i=0
i
a
x
i
i=0
2
a
i
i=0

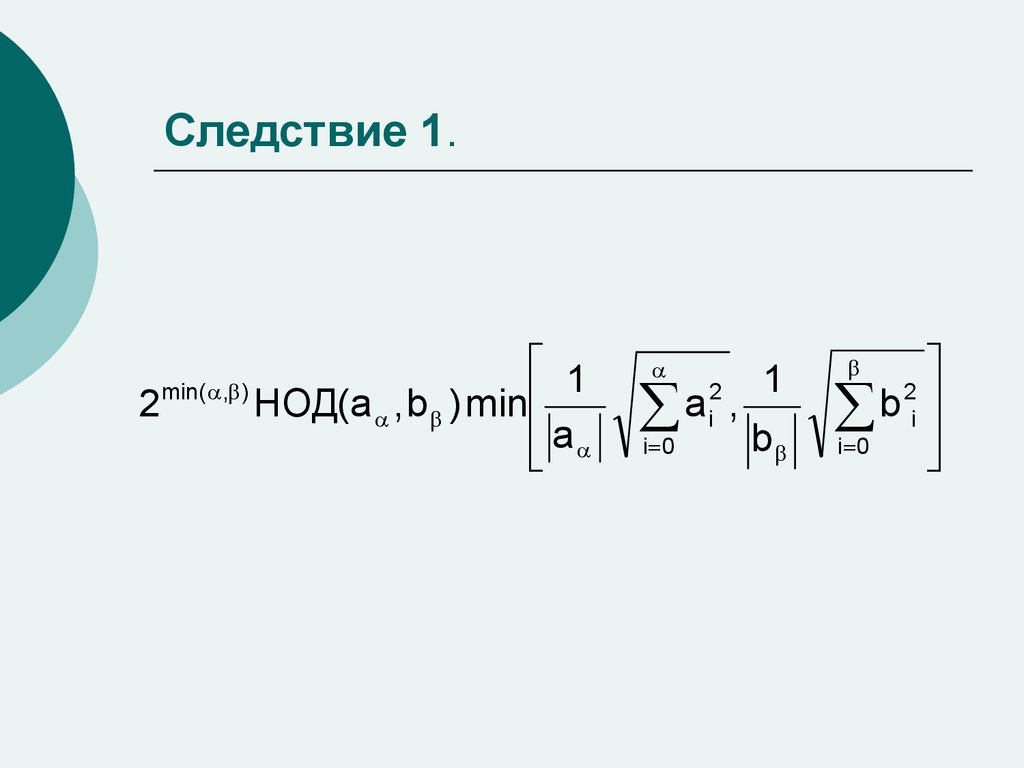
5. Следствие 1.

1
2 min( , ) НОД(a , b ) min
a
1
i=0
b
2
a
i,
2
b
i
i=0

6. Лемма 1.

Если число p не делит старший
коэффициент НОД(a,b) полиномов
a и b, то степень НОД(aр,bр)
больше или равна степени
НОД(f,g).

7. Следствие.

Если число р не делит старшие
коэффициенты полиномов a и b (в
частности, может делить один из
них, но не оба одновременно), то
степень НОД (aр,bр) больше или
равна степени НОД(a,b).

8.

Лемма 2. Пусть с=НОД(а,b). Если число р
удовлетворяет условию следствия и
если р не делит Resx(a/c,b/c), то
НОД(ap,bp)=cp.
Отсюда следует, что существует только конечное
число значений р, таких, что степень НОД(ap,bp)
отличается от степени НОД(а,b):
1)это те р, которые делят НОД
старших коэффициентов;
2)это те р, которые делят
результант, упоминающийся в лемме
(почему у него конечное число
делителей !!??).

9. Вычисление НОД

М:= граница_Ландау_Миньотта (А,В);
цикл до бесконечности
Р:= найти_большое_простое (2М)
если степень_остатка (р,А) или
степень_остатка (р,В)
то С:=модулярный_НОД (А,В,р);
если делит (С,А) и делит (С,В)
то выход С;

10.

алгоритм граница_Ландау_Миньотта
применяет следствие их неравенства;
алгоритм найти_большое_простое
возвращает простое число, большее чем
его аргумент (каждый раз новое число);
алгоритм степень_остатка проверяет, что
редукция по модулю р не меняет степень,
т.е. р не делит старший коэффициент;
алгоритм модулярный_НОД применяет
алгоритм Евклида по модулю р;
алгоритм делит проверяет, что многочлены
делятся над кольцом целых чисел

11.

М:= граница_Ландау_Миньотта (А,В);
Кроме:= НОД(lc(A), lc(B));
E0: р:=найти_простое (Кроме);
С:= модулярный_НОД (А,В,р);
E1: если степень (С)=0 то выход 1;
Дано:=р;
Результат:=С;
Цикл пока Дано 2М
р:=найти_простое (Кроме);
С:= модулярный_НОД (А,В,р);
если степень (С)< степень (Результат) то идти на Е1;
если степень (С)= степень (Результат)
то Результат:=CRT(Результат, Дано, С, р);
Дано:= Дано·р;
если делит (Результат, А) и делит (Результат, В)
то выход Результат;
идти на ЕО;

12.

lc – старший коэффициент полинома;
найти_простое – выдает простое число, не
делящее его аргумент (каждый раз новое
число);
CRT – применяет китайскую теорему об
остатках к каждому коэффициенту двух
полиномов – Результат (по модулю Дано)
и С (по модулю р), представляя целые
числа по модулю М между –М/2 и М

13. Оценка стоимости алгоритма

Время вычисления ограничивается
величиной О(n3·log23·H), где n - такое, что
степени полиномов a, b не больше этого
числа;
H - величина, удовлетворяющая
неравенству
a
i =0
2
i
2
b
i H
i=0