Похожие презентации:
Моделирование линейных звеньев. Лекция 9
1.
Кафедра Радиотехнических систем (РТС)Математическое моделирование
РТУ и С
Лекция 9.
Моделирование линейных звеньев
yk
k
n
xn hk n
Преподаватель:
к.т.н. старший преподаватель
кафедры РТС Захарова Елена Владимировна
2.
ЛитератураМонаков А.А. Основы
математического
моделирования
радиотехнических систем.
Учебное пособие. – СПб.: ГУАП,
2005. – 100с.
Глава 2, Раздел 2.1:
Моделирование линейных
звеньев
2
3.
ЛитератураА.Б.Сергиенко. Цифровая
обработка сигналов. СПб,
Питер, 2002. — 608 с.: ил.
А.Б.Сергиенко.
Signal Processing Toolbox –
обзор:
http://matlab.exponenta.ru/sign
alprocess/book2/index.php
3
4.
ЛитератураРичард Лайонс - Цифровая
обработка сигналов /
Understanding Digital Signal
Processing, 2006
Глава 5. Фильтры с импульсной
характеристикой конечной
длины
Глава 6. Фильтры с импульсной
характеристикой бесконечной
длины
Глава 7. Специальные КИХфильтры нижних частот
4
5.
Преобразование сигналовЛюбое обрабатывающее радиосигнал устройство может быть представлено как
совокупность линейных и нелинейных звеньев
Формально отличие в дифференциальных уравнениях
(м.б. линейные / нелинейные):
t
1
u t i t rC i t dt
C
i I s exp u
nV
1
0
Но важно следствие:
при действии суммы сигналов отклик звена есть суперпозиция откликов на
каждое воздействие в отдельности:
K p i S i i K p S i
5
6.
Коэффициент передачиЛинейное звено описывается дифференциальным уравнением:
aM y
M
t ... a1 y
1
t a0 y t bN x
N
t ... b1 x
1
t b0 x t
x t e
Нам достаточно научиться его решать для воздействия
а потом воспользоваться преобразованием Фурье и линейностью
j t
,
& j t :
Решение лежит на поверхности - y t Ue
j
M
& j t ... j a Ue
& j t , a Ue
& j t
aM Ue
1
0
j bN e j t ... j b1 e j t , b0 e j t
N
откуда
N
j bN ... j b1 , b0
U& U& j
j M aM ... j a1 a0
6
7.
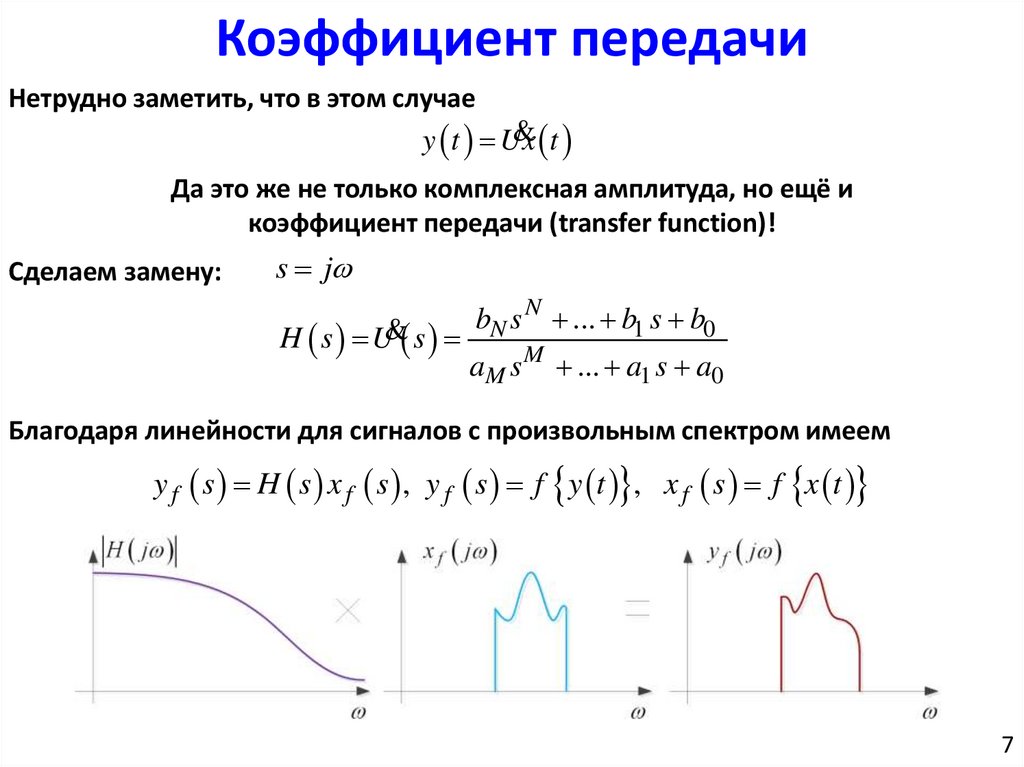
Коэффициент передачиНетрудно заметить, что в этом случае
& t
y t Ux
Да это же не только комплексная амплитуда, но ещё и
коэффициент передачи (transfer function)!
Сделаем замену:
s j
H s U& s
bN s N ... b1 s b0
aM s M ... a1 s a0
Благодаря линейности для сигналов с произвольным спектром имеем
y f s H s x f s , y f s f y t , x f s f x t
7
8.
Коэффициент передачиx(t ) i (t ) R y (t ), i t C
RC
dy t
dt
dy t
dt
y (t ) x(t )
a1 RC ; a0 1; b0 1;
H s
1
RC s 1
В MATLAB есть функции
для работы с линейными
звеньями
clear all; clc; close all;
RC = 1e-6;
a = [RC 1];
b = [1];
freqs(b, a);
8
9.
Коэффициент передачиclear all; clc; close all;
RC = 1e-6;
a = [RC 1]; b = [1];
Fs = 100; Fmax = 4e5; f = 0:Fs:Fmax;
H = freqs(b, a, 2*pi*f);
figure(1); subplot(2,1,1);
plot(f/1e6, 20*log10(abs(H)));
subplot(2,1,2);
plot(f/1e6, rad2deg(unwrap(angle(H))));
9
10.
Функция unwrap10
11.
Импульсная характеристика (ИХ)Умножению в частотной области соответствует свертка во временной
y t
h x t d
Для нашей RC-цепи и П-импульса:
1
h t
2
H j e j t d
А можно и через преобразование Лапласа:
h t
1
2 j
j
H s e st ds
j
Это интегрирование по линии, параллельной мнимой оси.
Выбором сигмы все особенности подынтегральной функции
оставляют слева от контура интегрирования.
Обратно:
H j
0
h t e
j t
dt H s
h t e st dt
0
11
12.
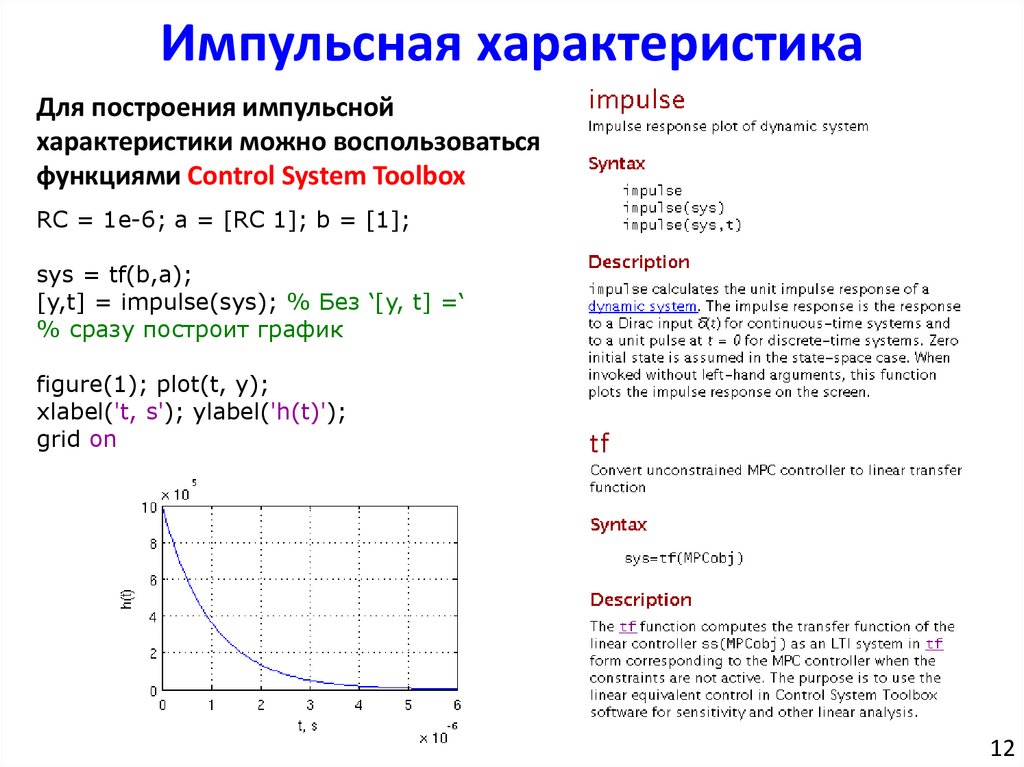
Импульсная характеристикаДля построения импульсной
характеристики можно воспользоваться
функциями Сontrol System Toolbox
RC = 1e-6; a = [RC 1]; b = [1];
sys = tf(b,a);
[y,t] = impulse(sys); % Без ‘[y, t] =‘
% сразу построит график
figure(1); plot(t, y);
xlabel('t, s'); ylabel('h(t)');
grid on
12
13.
Нулии
полюсы
Функцию передачи можно представить в виде
s z N s z N 1 ... s z1
H s k
s pM s pM 1 ... s p1
здесь
k
zi – нули,
bN
aM
– коэффициент усиления,
pi – полюсы
Re pi 0 устойчивость
ZPLANE – отображение нулей и полюсов дискретной
системы на комплексной плоскости
zplane(z,p)
zplane(b,a)
zplane(Hd)
[hz,hp,ht] = zplane(z,p) 13
14.
Цифровые фильтрыВсё это здорово, наглядно и удобно описывает аналоговые системы, но нам же
нужно уметь их моделировать – получать отклик на сигнал
И входные, и выходные сигналы в машине мы представляем в виде
дискретных последовательностей:
Нужна модель, для которой это приближенное равенство выполняется как
можно точнее
Да это же задача синтеза цифрового фильтра по аналоговому прототипу!
14
15.
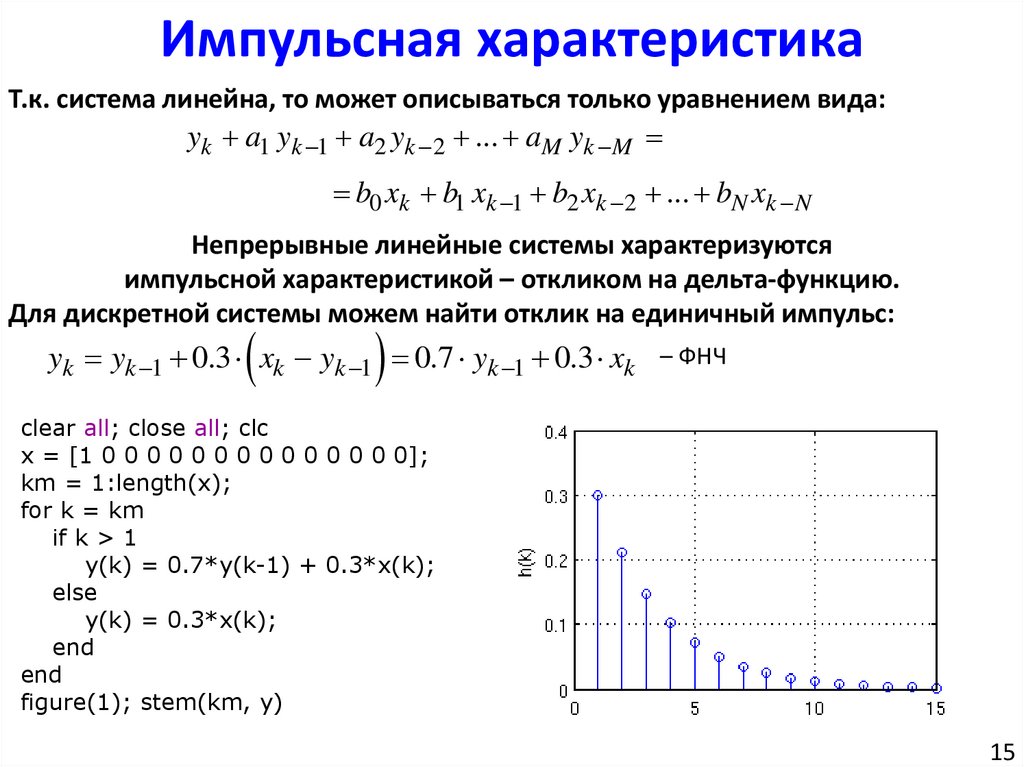
Импульсная характеристикаТ.к. система линейна, то может описываться только уравнением вида:
yk a1 yk 1 a2 yk 2 ... aM yk M
b0 xk b1 xk 1 b2 xk 2 ... bN xk N
Непрерывные линейные системы характеризуются
импульсной характеристикой – откликом на дельта-функцию.
Для дискретной системы можем найти отклик на единичный импульс:
yk yk 1 0.3 xk yk 1 0.7 yk 1 0.3 xk – ФНЧ
clear all; close all; clc
x = [1 0 0 0 0 0 0 0 0 0 0 0 0 0 0];
km = 1:length(x);
for k = km
if k > 1
y(k) = 0.7*y(k-1) + 0.3*x(k);
else
y(k) = 0.3*x(k);
end
end
figure(1); stem(km, y)
15
16.
impz(…)yk 0.7 yk 1 0.3 xk
a0 1, a1 0.7, b0 0.3
clear all; close all; clc
a = [1 -0.7]; b = [0.3];
h = impz(b, a, 15);
figure(1); stem(h);
xlabel('k'); ylabel('h_k'); grid on
16
17.
Свертка: conv(…), deconv(…)Т.к. система линейная, то
нынешний выход есть сумма
реакций:
yk
k
n
xn hk n
Можем воспользоваться
функциями conv и deconv
clear all; close all; clc
a = [-0.7]; b = [0.3];
xh = [1 0 0 0 0 0 0 0 0 0 0 0 0 0 0];
km = 2:length(xh); h(1) = b(1)*xh(1);
for k = km
h(k) = -a(1)*h(k-1) + b(1)*xh(k);
end
x = [0 0 0 0 0 1 1 1 1 1 1 1 1 1 1];
y = conv(x, h);
xdec = deconv(y, h);
figure(1)
stem(1:length(y), y); hold on
stem(1:length(xdec), xdec, 'r'); hold off
grid on; legend('y', 'x'); xlabel('k')
17
18.
Transfer functionВспоминаем РЦС, z-преобразование и его свойства:
yk
n
xn hk n
k
n
xn hk n
Y z H z X z , H z
k
h
z
k
k 0
Или из уравнения:
yk a1 yk z 1 ... aM yk z M b0 xk b1 xk z 1 ... bN xk z N
H z
b0 b1 z 1 ... bN z N
1 a1 z 1 ... aM z M
Связь с преобразованием Фурье:
H j H z
z e
j T
hk e j T
k 0
H z
0.3
1 0.7 z 1
18
19.
clear all; close all; clca = [-0.7]; b = [0.3];
Transfer function
xр = [1 0 0 0 0 0 0 0 0 0 0 0 0 0 0];
km = 1:length(x);
for k = km
if k > 1
h(k) = -a(1)*h(k-1) + b(1)*xh(k);
else
h(k) = b(1)*xh(k);
end
end
H j H z
z e
j T
j T
h
e
k
k 0
yk 0.7 yk 1 0.3 xk
H z
0.3
1 0.7 z 1
T = 0.001; f = 0:(1/T/100):(1/T);
z = exp(1i*2*pi*f*T);
H2 = 0;
for k = km
H2 = H2 + h(k) * z.^-k;
end
H1 = 0.3 ./ (1 - 0.7 * z.^-1);
figure(1); plot(f, abs(H1), f, abs(H2), '*')
xlabel('f, Hz'); ylabel('|H|'); grid('on');
19
20.
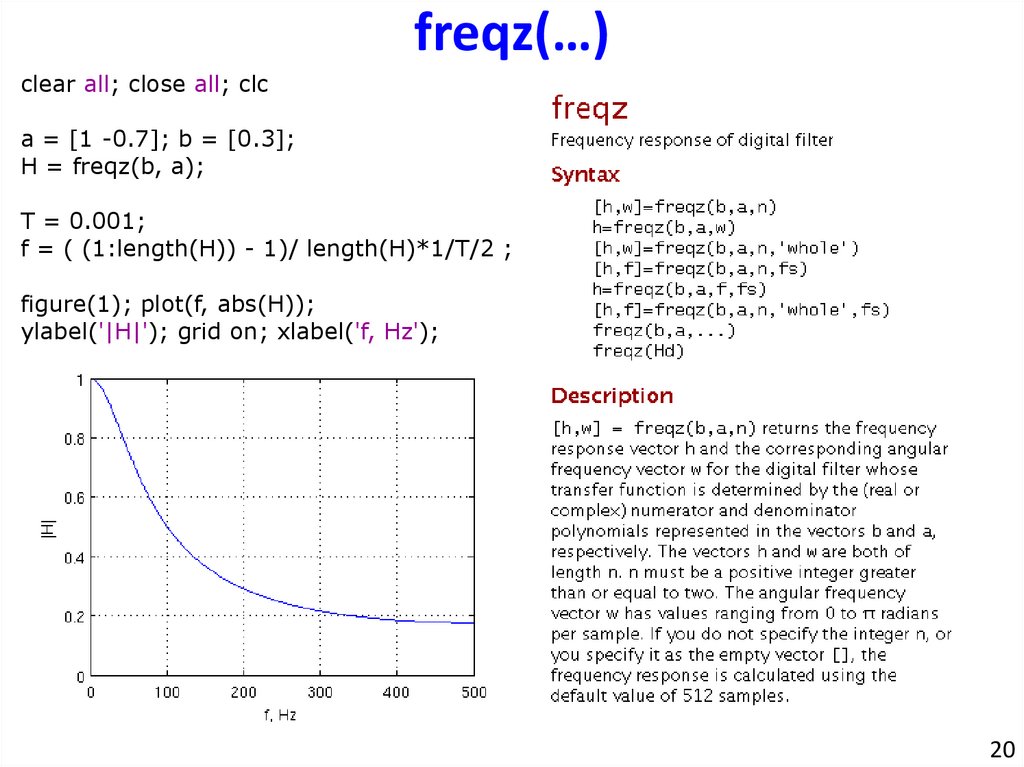
freqz(…)clear all; close all; clc
a = [1 -0.7]; b = [0.3];
H = freqz(b, a);
T = 0.001;
f = ( (1:length(H)) - 1)/ length(H)*1/T/2 ;
figure(1); plot(f, abs(H));
ylabel('|H|'); grid on; xlabel('f, Hz');
20
21.
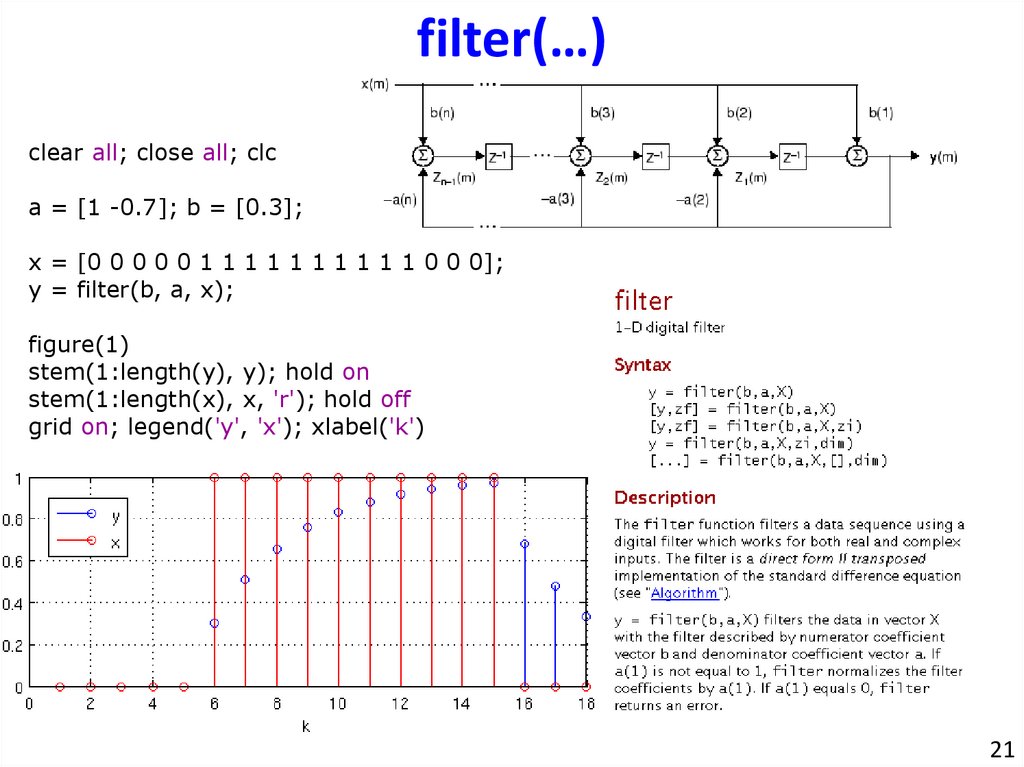
filter(…)clear all; close all; clc
a = [1 -0.7]; b = [0.3];
x = [0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 0 0 0];
y = filter(b, a, x);
figure(1)
stem(1:length(y), y); hold on
stem(1:length(x), x, 'r'); hold off
grid on; legend('y', 'x'); xlabel('k')
21
22.
Нули и полюсыКоэффициенты ПФ – строки,
нули/полюсы - столбцы
clear all; close all; clc
a = [1 -0.7]; b = [0.3];
[z, p, k] = tf2zp(b, a);
1 z1 z 1 1 z2 z 1 ... 1 z N z 1
H z k
1 p1 z 1 1 p2 z 1 ... 1 pM z 1
TF2ZP
% zplane(b, a);
zplane(z, p);
pi 1
устойчивость
22
23.
Метод инвариантности h(t)Реализовывать цифровые фильтры в MATLAB научились, вернемся к задаче
синтеза цифрового фильтра по аналоговому прототипу
xk x tk yk y tk ; a sj , b sj a zj , b zj ???
hk h tk
Метод инвариантности импульсной характеристики:
N
h t An e
n 1
pns t
N
hk An e
n 1
pns kT
, An H s s zns
H z hk z
k 1
а)
k
s z
N
s
n
An e
n 1 k 1
pns kT k
z
N
An
p s kT
n 11 e n z k
б)
23
24.
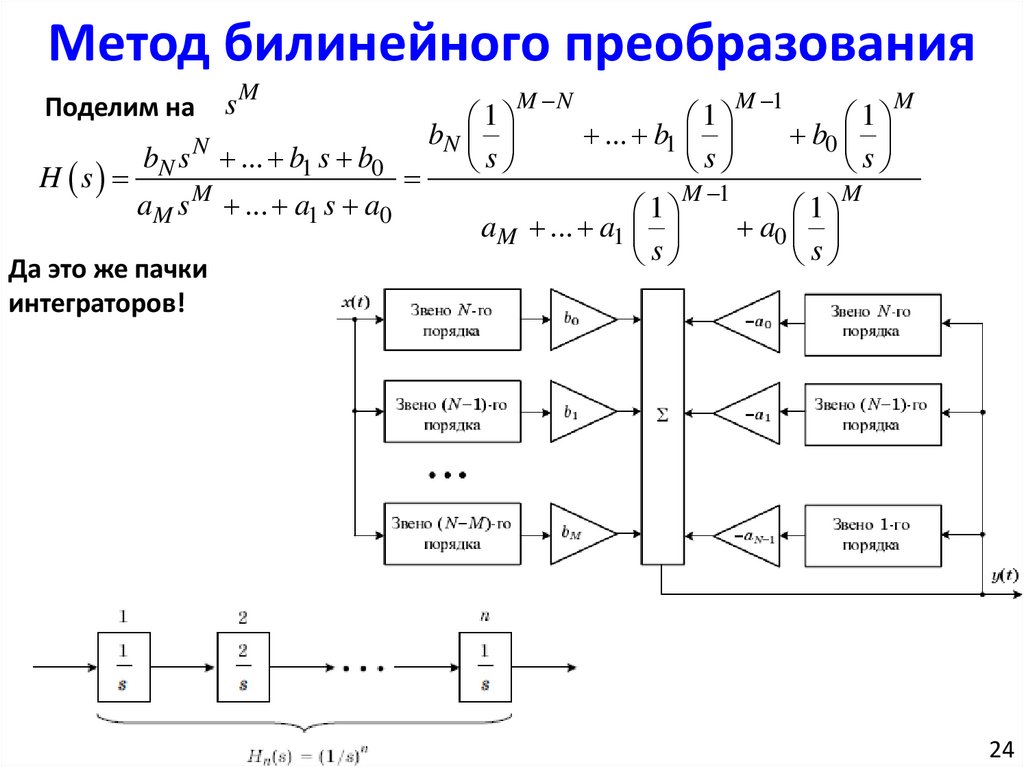
Метод билинейного преобразованияПоделим на
H s
sM
bN s N ... b1 s b0
aM s
M
Да это же пачки
интеграторов!
... a1 s a0
1
bN
s
M N
aM
1
... b1
s
1
... a1
s
M 1
M 1
1
b0
s
1
a0
s
M
M
24
25.
Метод билинейного преобразованияА давайте аналоговый интегратор заменим цифровым!
Интегрировать будем методом трапеций:
g k g k 1
f k 1 f k T
2
Итого, в качестве s должны использовать:
2 1 z 1
s
T 1 z 1
Это преобразование и
называется билинейным
25
26.
Метод билинейного преобразованияПолуплоскость переменной s отображается в окружность единичного радиуса в
плоскости переменной z
Есть явление деформации оси частот
s j s , z e j e j z T
2 z T
s tg
T
2
Можно заранее скомпенсировать
в аналоговом прототипе
s
2 s T
tg
T
2
26
27.
Метод билинейного преобразованияПример. Смоделируем RC цепь, что использовали ранее.
1
H s
H z
RC s 1
clear all; clc; close all;
1 z 1
1
2
2 1
2 1 z
1
RC
1
RC
RC
1
z
1
T
T
T 1 z
RC = 1e-6;
T = RC/3;
1
b0z 1, b1z 1, a0z 1
2 RC z
2 RC
, a1 1
T
T
as = [RC 1]; bs = [1];
[Hs, w] = freqs(bs, as);
az = [1+2*RC/T, 1-2*RC/T]; bz = [1, 1];
Hz = freqz(bz, az);
figure(1)
plot(w/2/pi/1000, abs(Hs), ...
((1:length(Hz)) - 1)/ length(Hz) *
1/T/2/1000, abs(Hz))
xlabel('f, kHz'); ylabel('|H|')
legend('|H(s)|', '|H(z)|'); grid on
27
28.
Метод замены дифференциаловЕсли 1/s – интегратор, то s – дифференциатор!
Итого, в качестве s должны использовать:
1 z 1
s
T
Не стоит использовать когда:
- нули передаточной функции аналогового прототипа имеют вещественную
часть больше удвоенной частоты дискретизации
- нулей у передаточной функции аналогового прототипа нет
28
29.
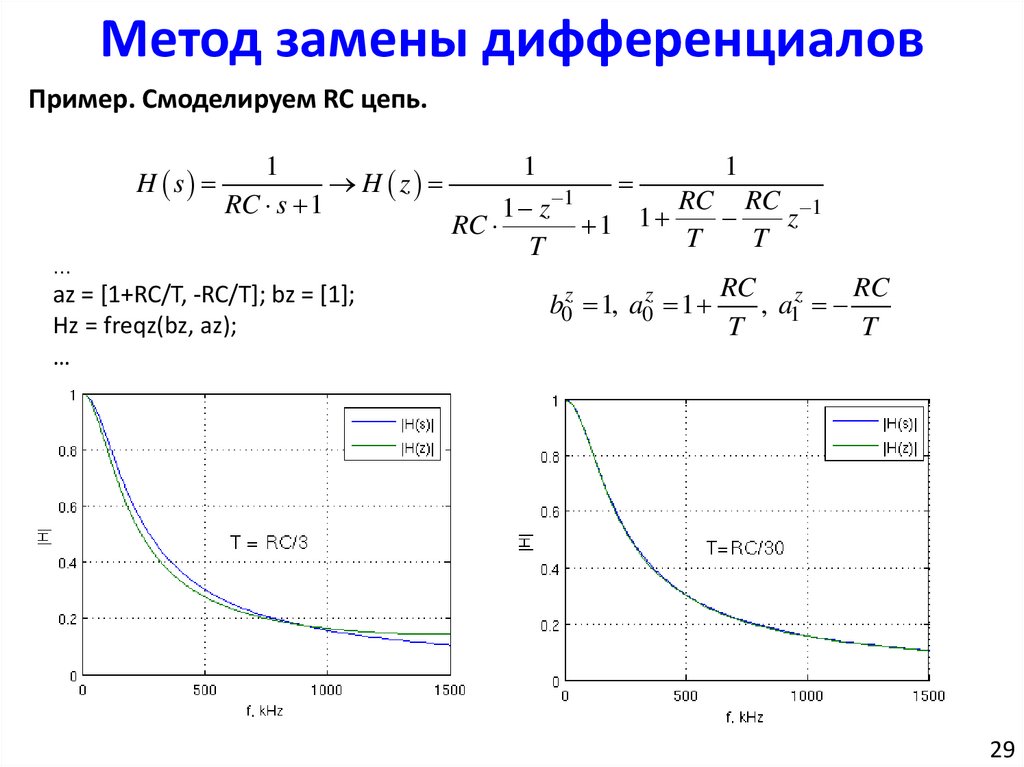
Метод замены дифференциаловПример. Смоделируем RC цепь.
H s
1
H z
RC s 1
…
az = [1+RC/T, -RC/T]; bz = [1];
Hz = freqz(bz, az);
…
1
1
RC RC 1
1 z 1
1
z
RC
1
T
T
T
b0z 1, a0z 1
RC z
RC
, a1
T
T
29
30.
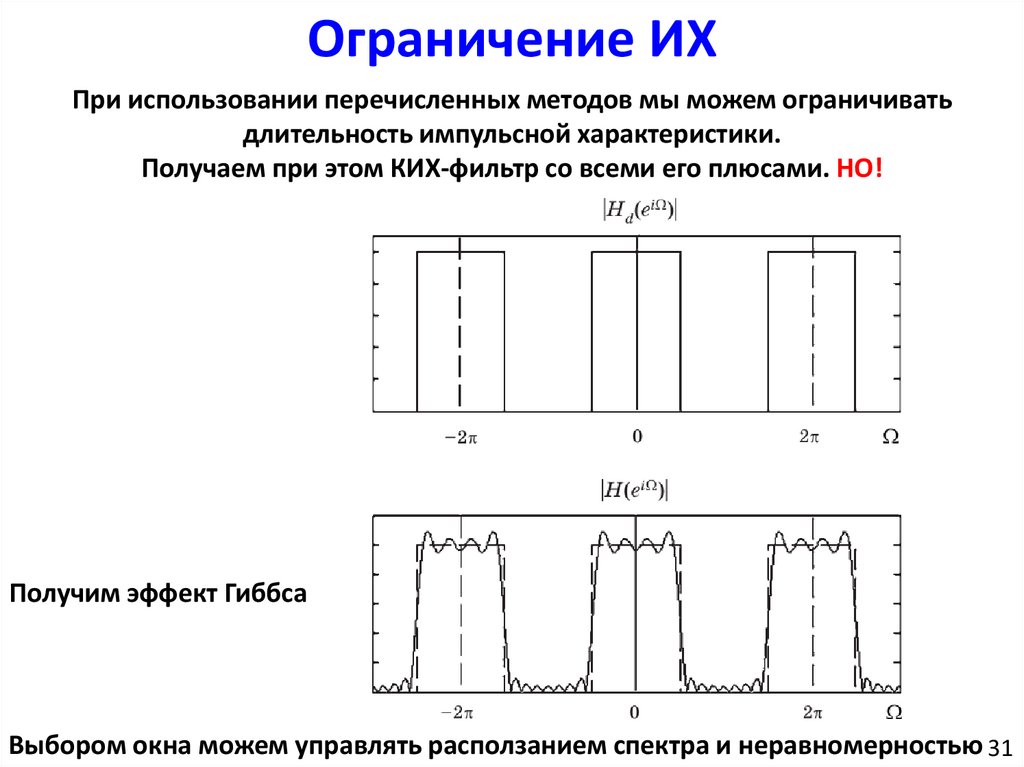
Ограничение ИХПри использовании перечисленных методов мы можем ограничивать
длительность импульсной характеристики.
Получаем при этом КИХ-фильтр со всеми его плюсами. НО!
Но это же применение
прямоугольного окна!
А значит и
коэффициент передачи
свернется со спектром окна!
yk
n
xnhk n wk n
Y z X z H z *W z
Свертка АЧХ БИХ фильтра и АЧХ
окна:
30
31.
Ограничение ИХПри использовании перечисленных методов мы можем ограничивать
длительность импульсной характеристики.
Получаем при этом КИХ-фильтр со всеми его плюсами. НО!
Получим эффект Гиббса
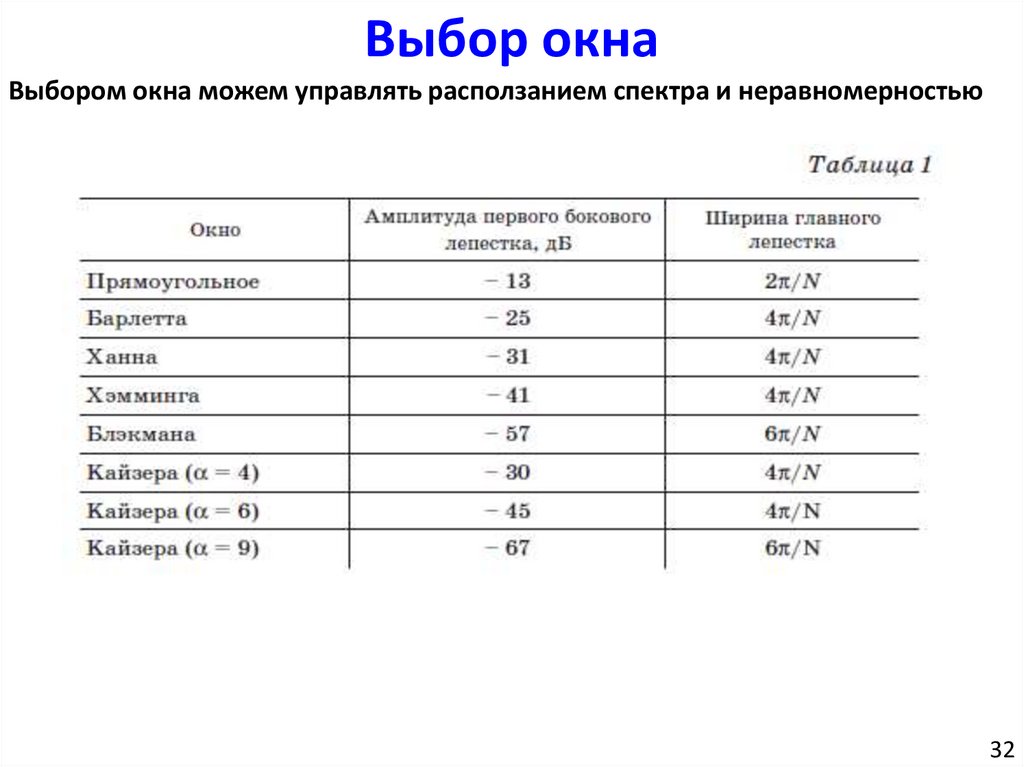
Выбором окна можем управлять расползанием спектра и неравномерностью 31
32.
Выбор окнаВыбором окна можем управлять расползанием спектра и неравномерностью
32
33.
Кафедра Радиотехнических систем (РТС)Математическое моделирование
РТУ и С
e-mail: [email protected]
33
























 Математика
Математика Информатика
Информатика








