Похожие презентации:
Применение интеграла к решению физических задач
1.
Тема урока:«Применение интеграла к
решению физических задач»
2.
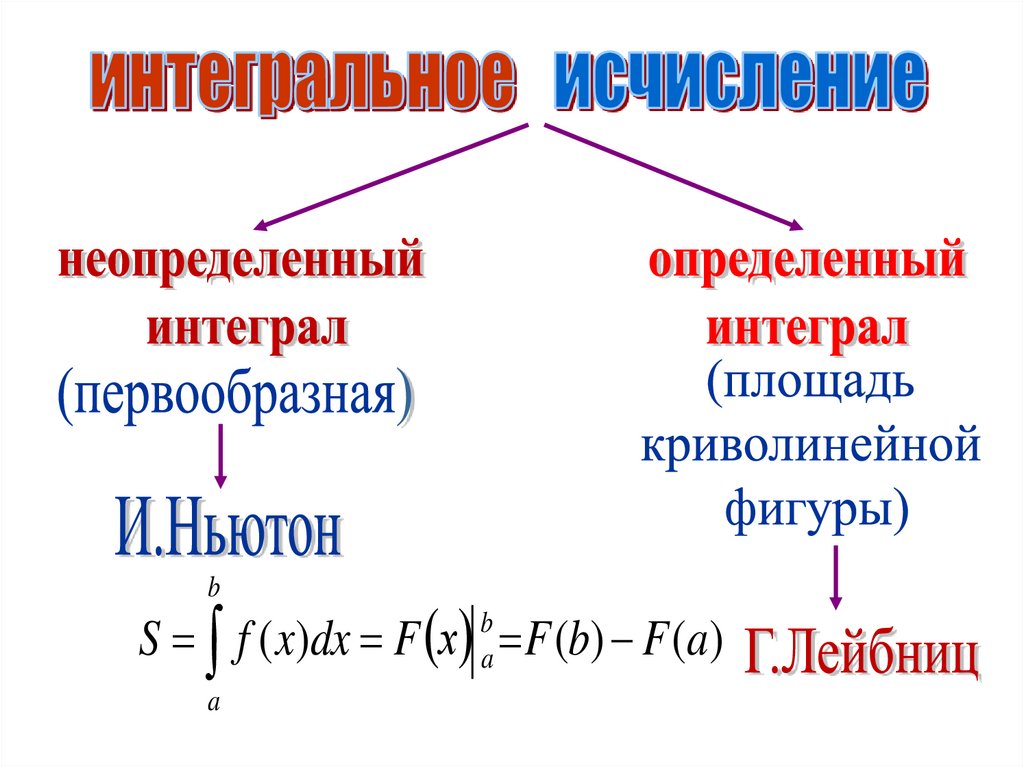
Практическая работа«Применение
определенного
интеграла при решении
прикладных задач»
Тема:
3.
• Цели урока:1. обобщить и закрепить ключевые задачи по теме
2. научиться работать с теоретическими вопросами
темы
3. научиться применять интеграл к решению
физических задач
4.
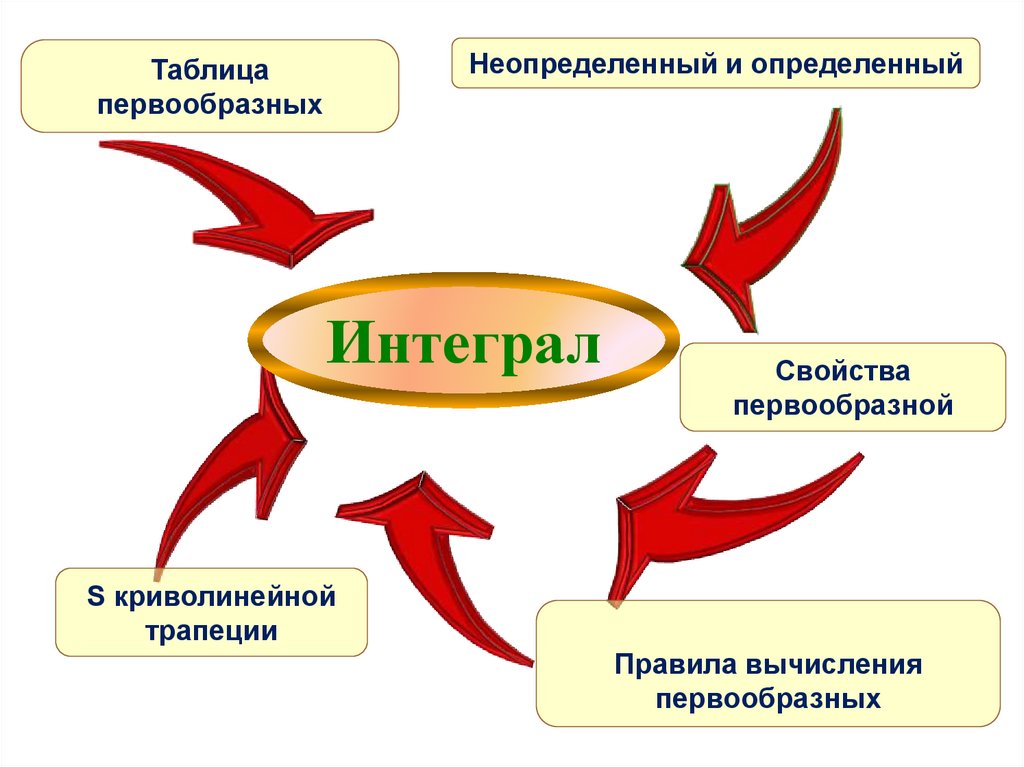
Неопределенный и определенныйТаблица
первообразных
Интеграл
Свойства
первообразной
S криволинейной
трапеции
Правила вычисления
первообразных
5.
bS f ( x)dx F х ba F (b) F (a)
a
6.
Верны ли равенства:а)
1
1
0 x dx 4
да
б)
3
1
0 x dx 2 3
2
нет
3
5
x
г) 5dx
0
2
д)
5
1
2 3
0
4
в) x 2 dx 2 x
2
нет
5 2
45
2
(3 0 )
2
2
нет
3 1
x
x
dx
0
3
2
0
1
1
(1 0)
3
3
да
7.
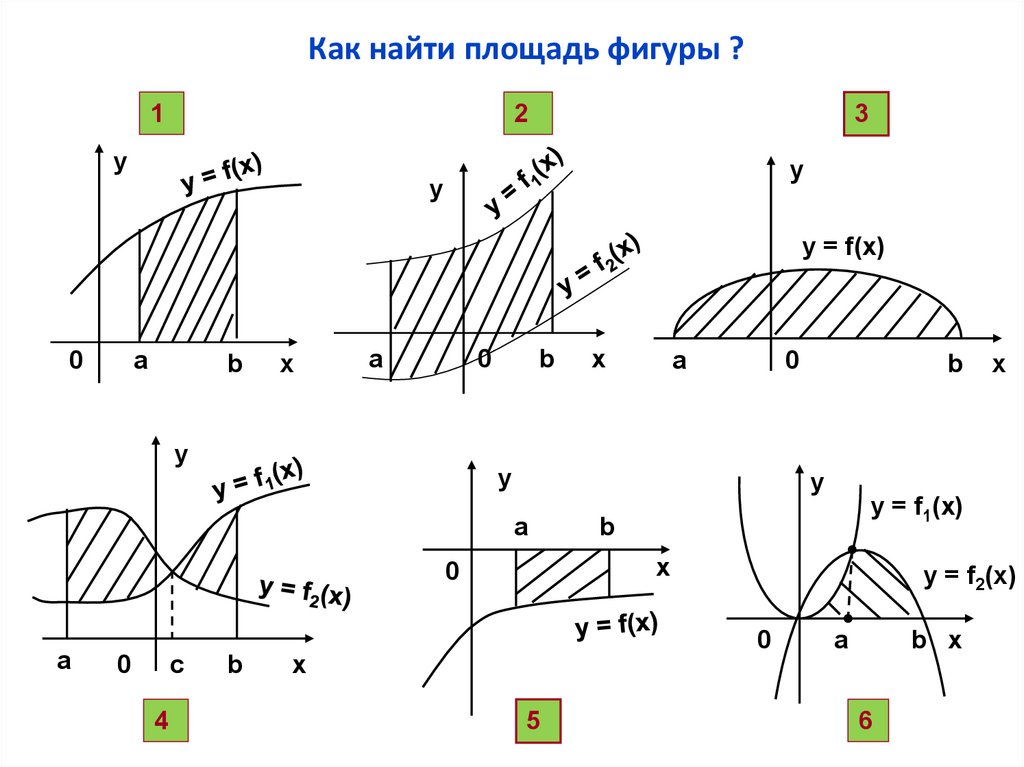
Как найти площадь фигуры ?1
2
3
у
y
y
y = f(x)
0
a
b
х
a
0
b
x
a
0
b
x
y
y
y
a
b
x
0
a
y = f1(x)
y = f2(x)
0
0
c
4
b
a
b x
x
5
6
8.
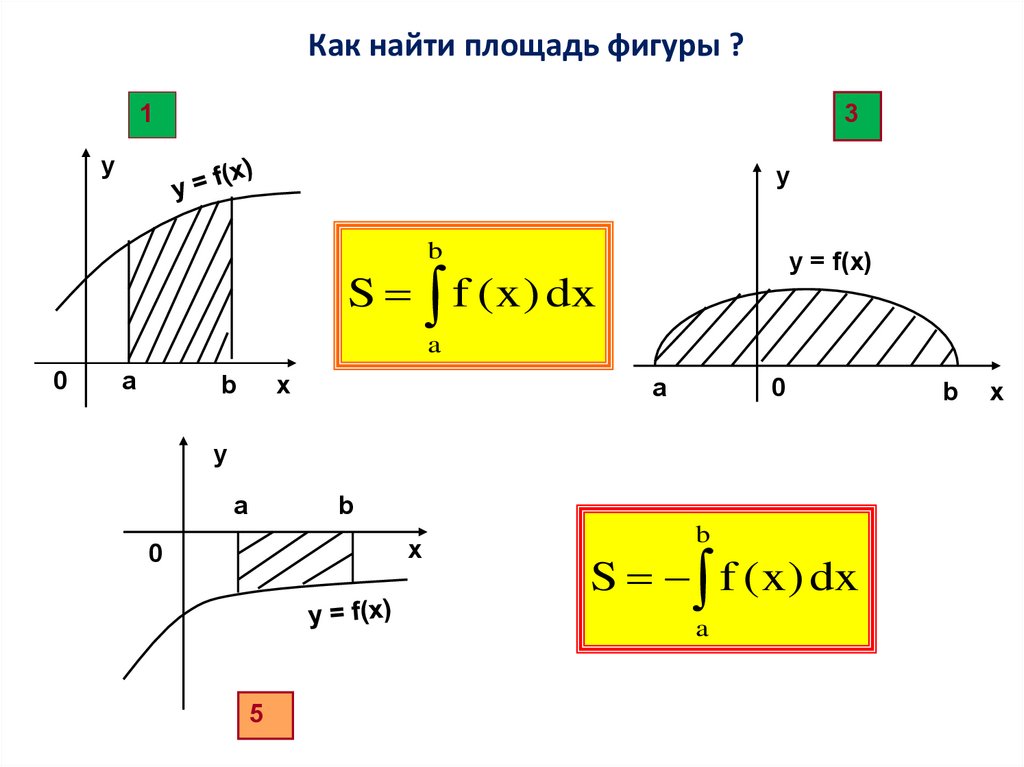
Как найти площадь фигуры ?1
3
у
y
b
y = f(x)
S f ( x ) dx
a
0
a
х
b
a
0
y
a
b
x
0
b
S f ( x ) dx
a
5
b
x
9.
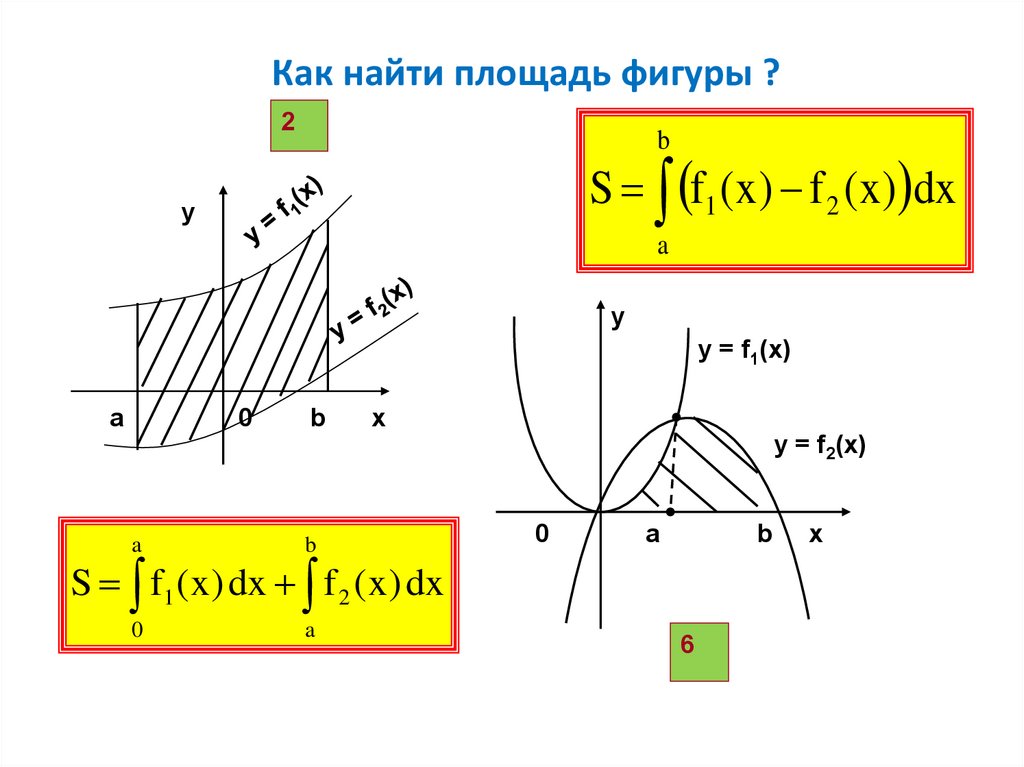
Как найти площадь фигуры ?2
b
S f1 (x) f 2 ( x) dx
y
a
y
y = f1(x)
a
0
b
x
y = f2(x)
a
b
0
a
0
a
b
S f1 ( x ) dx f 2 ( x ) dx
6
x
10.
ГипотезаВозможно ли развитие
современной
науки без
использования интеграла?
11.
Вычисление площадиплоской фигуры в
полярных
координатах
Вычисление площади плоской
фигуры в прямоугольных
координатах
Математика
Вычисление площади
поверхности тела
вращения
Вычисление
интеграла
Вычисление длины дуги
кривой
12.
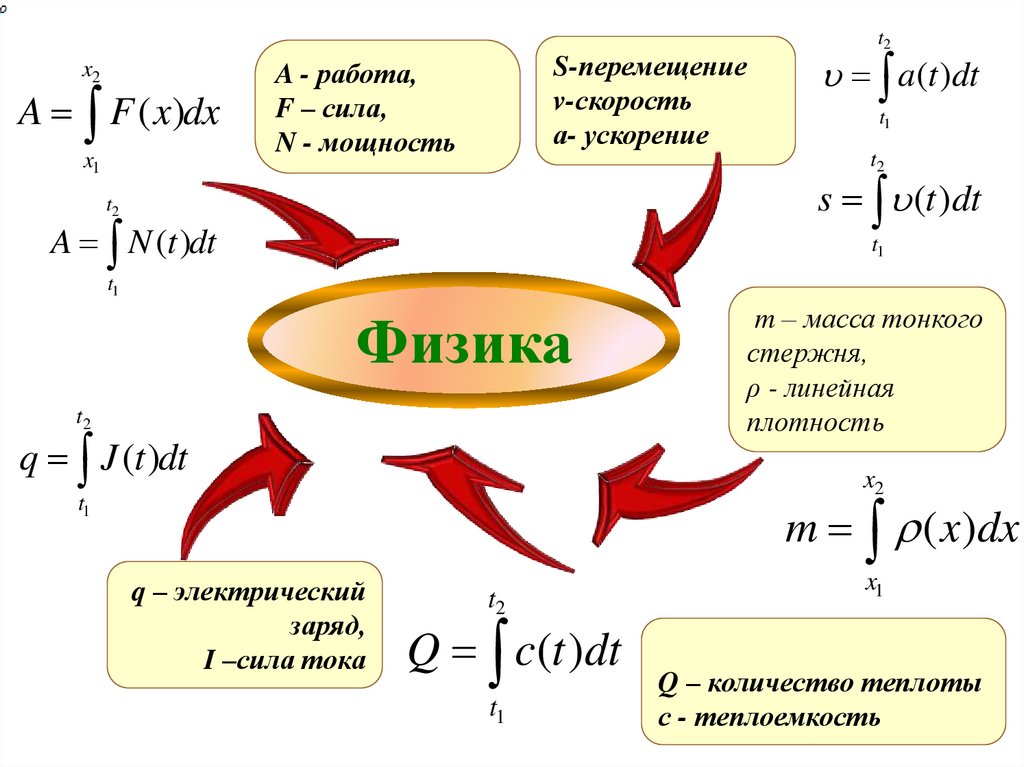
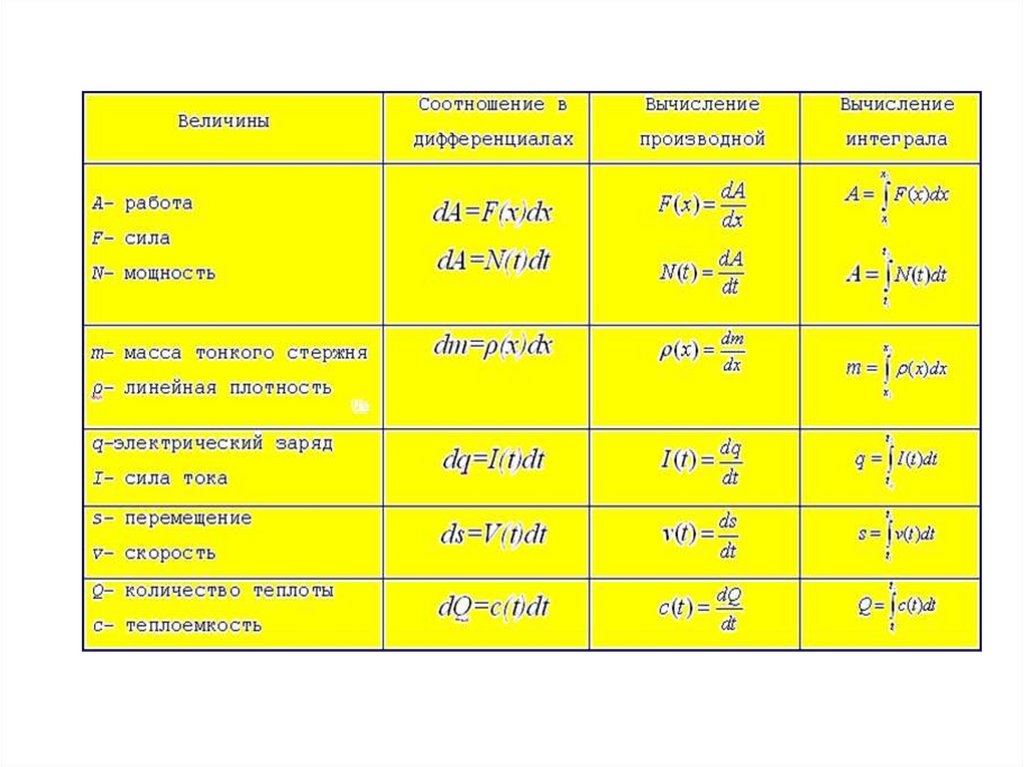
t2x2
A F ( x)dx
x1
S-перемещение
v-скорость
а- ускорение
A - работа,
F – сила,
N - мощность
a(t )dt
t1
t2
s (t )dt
t2
A N (t )dt
t1
t1
Физика
t2
q J (t )dt
x2
m ( x)dx
t1
q – электрический
заряд,
I –сила тока
m – масса тонкого
стержня,
ρ - линейная
плотность
t2
Q c(t )dt
t1
x1
Q – количество теплоты
с - теплоемкость
13.
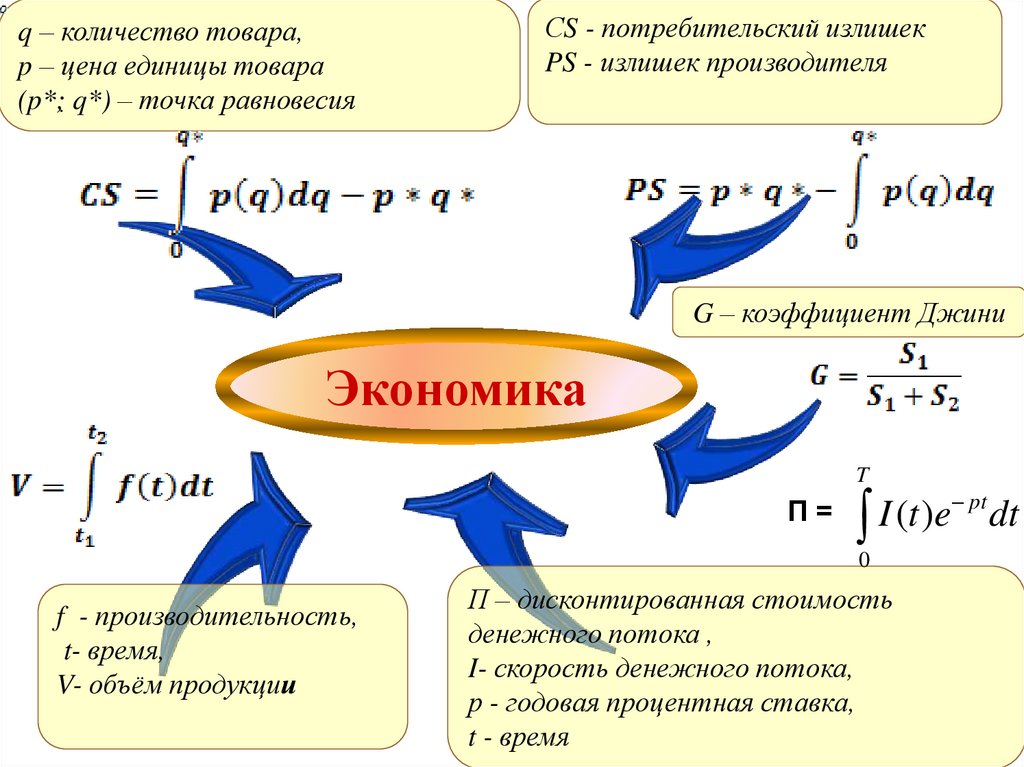
q – количество товара,p – цена единицы товара
(p*;. q*) – точка равновесия
СS - потребительский излишек
PS - излишек производителя
G – коэффициент Джини
Экономика
T
П=
pt
I
(
t
)
e
dt
0
f - производительность,
t- время,
V- объём продукции
П – дисконтированная стоимость
денежного потока ,
I- скорость денежного потока,
р - годовая процентная ставка,
t - время
14.
Физические приложенияопределенного интеграла
А) Вычисление работы движущегося тела
Б) Вычисление перемещения движущегося тела
В) Вычисление массы тела
Г)
Вычисление
электрического
заряда
в
проводнике с током
15.
Схема решения физических задач сиспользованием определенного
интеграла
А)
Б)
В)
Г)
сделать чертеж, соответствующий условию задачи,
выбрать систему координат,
выбрать независимую переменную,
выбрать формулу классической физики,
соответствующую условию задачи,
Д) найти дифференциал искомой величины на основании
этой формулы,
Е) установить промежуток интегрирования,
Ж) вычислить интеграл, т.е. найти искомую величину.
16.
17.
Повторение основных понятий:1. Скажите основное определение
интеграла?
2. Что вы знаете о интеграле
(свойства, теоремы)?
3. Знаете ли вы какие-нибудь примеры
задач с применением интеграла?
18.
План урока:1. Схема решения задач на приложения определенного
интеграла
2. Нахождение пути, пройденного телом при
прямолинейном движении
3. Вычисление работы силы, произведенной при
прямолинейном движении тела
4. Вычисление работы, затраченной на растяжение или
сжатие пружины
5. Определение силы давления жидкости на
вертикально расположенную пластинку
19.
Рассмотрим теориюпо данной теме
20.
1. Схема решения задач наприложения определенного
интеграла
С помощью определенного интеграла можно решать
различные задачи физики, механики и т. д., которые
трудно или невозможно решить методами
элементарной математики.
Так, понятие определенного интеграла применяется
при решении задач на вычисление работы переменной
силы, давления жидкости на вертикальную
поверхность, пути, пройденного телом, имеющим
переменную скорость, и ряд других.
Несмотря на разнообразие этих задач, они
объединяются одной и той же схемой рассуждений при
их решении. Искомая величина (путь, работа, давление
и т. д.) соответствует некоторому промежутку
изменения переменной величины, которая является
переменной интегрирования. Эту переменную
величину обозначают через Х, а промежуток ее
изменения — через [а, b].
Отрезок [a, b] разбивают на n равных частей, в каждой
из которых можно пренебречь изменением переменной
величины. Этого можно добиться при увеличении
числа разбиений отрезка.
На каждой такой части задачу решают
по формулам для постоянных величин.
Далее составляют сумму (интегральную
сумму), выражающую приближенное
значение искомой величины. Переходя к
пределу при n→∞, находят искомую
величину I в виде интеграла
21.
2. Нахождение пути, пройденноготелом при прямолинейном движении
Как известно, путь, пройденный телом при равномерном движении за время t,
вычисляется по формуле S=vt.
Если тело движется неравномерно в одном направлении и скорость его
меняется в зависимости от времени t, т. е. v=f(t), то для нахождения пути,
пройденного телом за время от t1 до t2, разделим этот промежуток времени
на n равных частей Δt. В каждой из таких частей скорость можно считать
постоянной и равной значению скорости в конце этого промежутка. Тогда
пройденный телом путь будет приблизительно равен сумме:
22.
3. Вычисление работы силы, произведеннойпри прямолинейном движении тела
23.
4.Вычисление работы, затраченной нарастяжение или сжатие пружины
24.
5.Определение силы давления жидкости на вертикальнорасположенную пластинку
25.
26.
Пример 1. Нахождение пути позаданной скорости.
Пусть точка движется со скоростью V(t). Нужно найти путь s, пройденный точкой от момента t=a до
момента t=b. Обозначим s(t) путь, пройденный точкой за время t от момента a. Тогда s’(t)=V(t),
т.е. s(t) – первообразная для функции V(t). Поэтому по формуле Ньютона - Лейбница найдём:
s= V(t)dt.
Например, если точка движется со скоростью V(t)=2t+1(м/с), то путь, пройденный точкой
за первые 10 с, по формуле равен
10
2
10
S= ∫ (2t+1)dt = (t + t)| = 110(м)
27.
Рассмотрим примерызадач по данной теме
№1
28.
РЕШЕНИЕ:29.
№230.
Решение:Ответ: 5 м
31.
№332.
Решение:Ответ: 32 м
33.
№434.
Решение:Ответ: 44,1 м
35.
№5Какую работу совершает сила в
10Н при растяжении пружины
на 2 см?
36.
Решение:37.
№6Сила в 60Н растягивает пружину на
2 см. Первоначальная длина
пружины равна 14 см. Какую работу
нужно совершить, чтобы растянуть
ее до 20 см?
38.
Решение:39.
№7Определить силу давления воды на
стенку шлюза, длина которого 20 м, а
высота 5 м (считая шлюз доверху
заполненным водой).
40.
Решение:41.
№8В воду опущена прямоугольная
пластинка, расположенная
вертикально. Ее горизонтальная
сторона равна 1 м, вертикальная 2 м.
Верхняя сторона находится на
глубине 0,5 м. Определить силу
давления воды на пластинку.
42.
РЕШЕНИЕ:43.
№944.
РЕШЕНИЕ:45.
№ 1046.
РЕШЕНИЕ:47.
№ 1148.
РЕШЕНИЕ:49.
№ 12Вычислить силу давления воды на
плотину, имеющую форму трапеции,
у которой верхнее основание,
совпадающее с поверхностью воды,
имеет длину 10 м, нижнее основание
20 м, а высота 3 м.
50.
РЕШЕНИЕ:51.
№ 1352.
РЕШЕНИЕ:53.
Эталон решения:y=f(x) - функция, график которой есть
кривая(прямая), вращающаяся вокруг оси Ох и
образующая поверхность искомого тела вращения;
а и b пределы интегрирования
y=f(x)
y
x=a
0
x=b
x
b
V y dx
2
a
54.
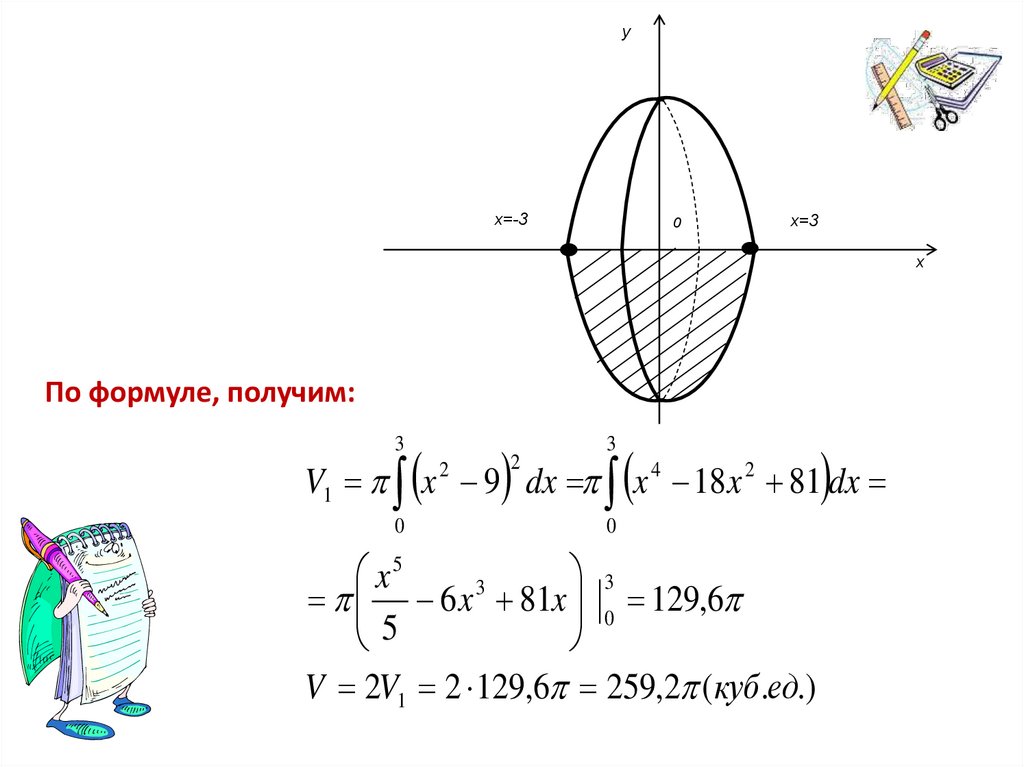
• Вычислить объем тела образованноговращением вокруг оси Ох, ограниченного
указанными линиями у = х2-9 и у = 0.
Решение. Выполним построение.
Пределы
интегрирования
в
силу
симметричности
фигуры
относительно
оси Оу возьмем от 0 до 3, а затем
полученный результата удвоим.
55.
yx=-3
0
x=3
x
По формуле, получим:
3
3
V1 x 2 9 dx x 4 18 x 2 81 dx
0
2
0
x5
3
3
6 x 81x 0 129,6
5
V 2V1 2 129,6 259,2 (куб .ед.)
56.
Задача о нахождении объёма телаНайдём объём тела, ограниченного поверхностью вращения линии
(при
).
Для вычисления объёма тела вращения применим формулу:
Имеем:
вокруг оси

















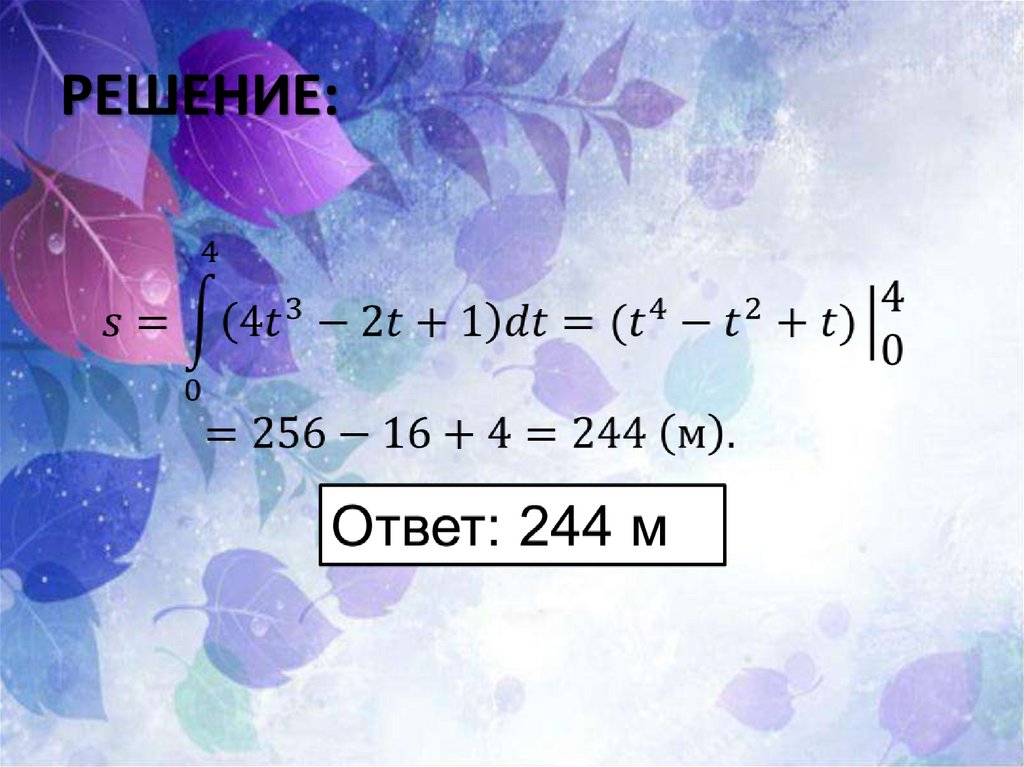

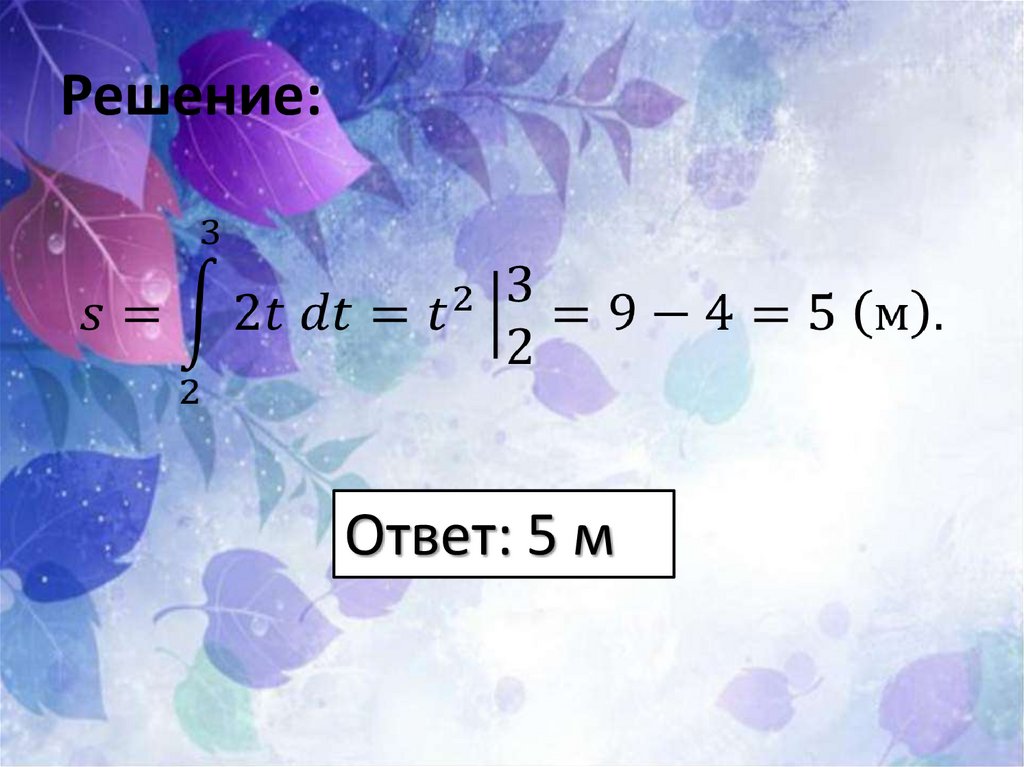









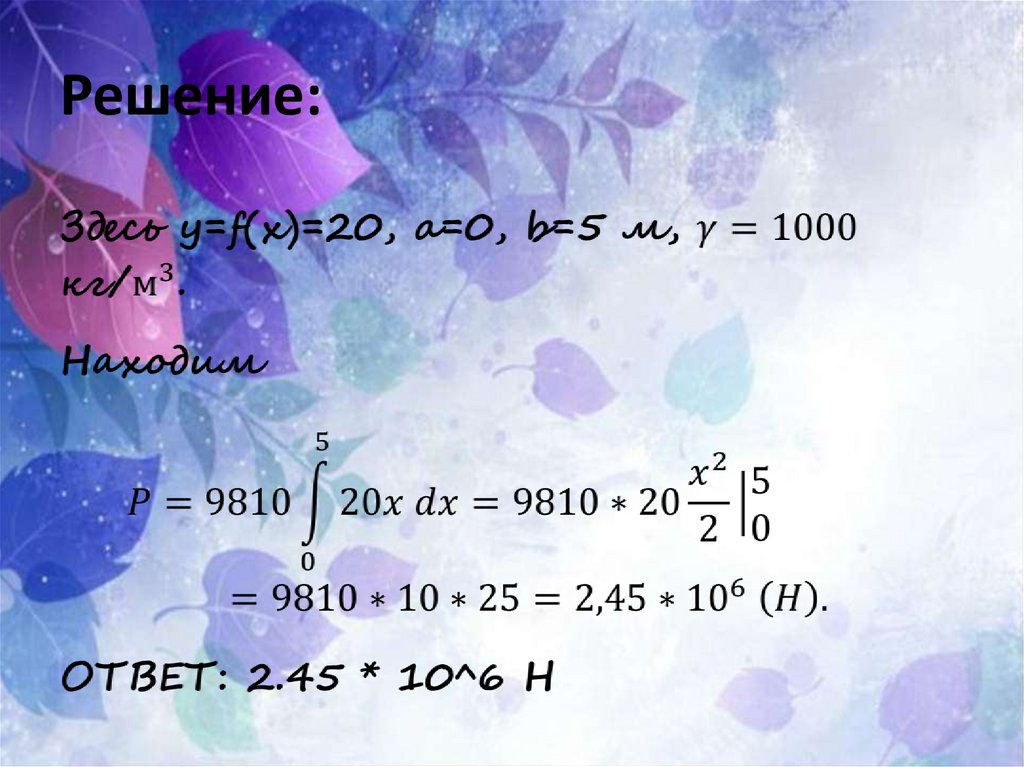

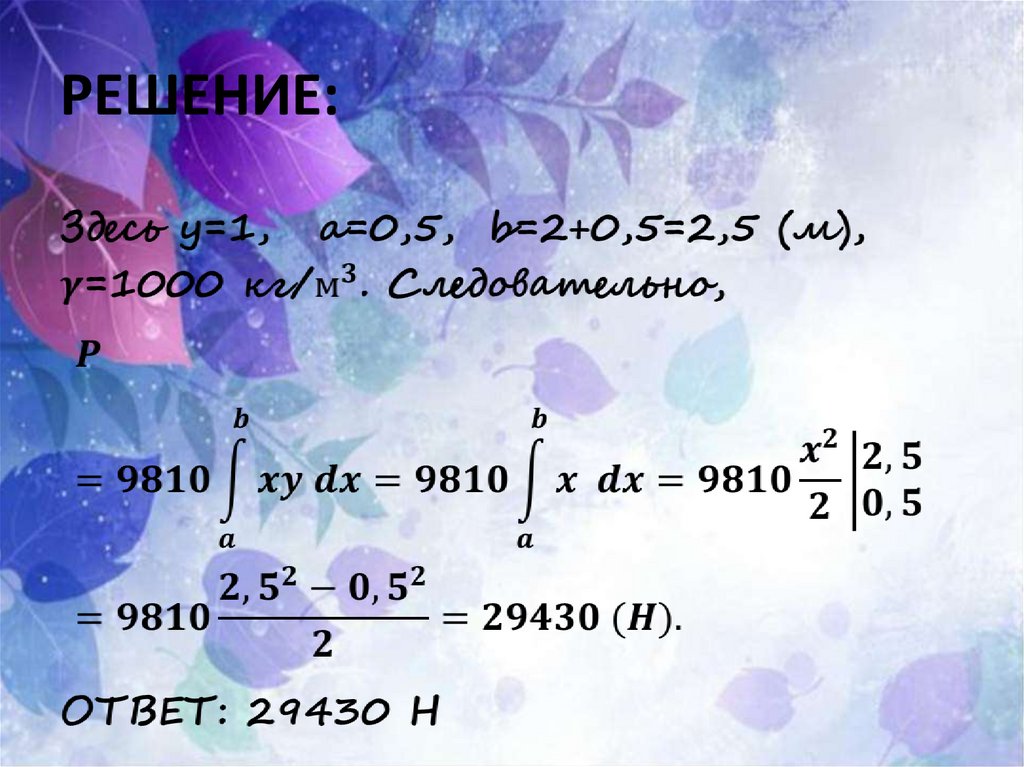













 Математика
Математика Физика
Физика








