Похожие презентации:
Двойственные задачи линейного программирования. Лекция 3
1.
Липецкий государственный технический университетКафедра прикладной математики
Прикладная математика
Лекция 3
Двойственные задачи линейного программирования
2.
Постановка двойственной задачи линейногопрограммирования
Рассмотрим задачу линейного программирования в виде
L c0 c1 x1 ... cn xn max;
a11 x1 ... a1n xn b1 ;
...
a x ... a x b ;
m1 1
mn n
m
x1 0, ..., xn 0.
Назовем эту задачу исходной.
Тогда двойственной к ней будет называться задача вида
F c0 b1 z1 ... bm zm min;
a11 z1 ... am1 zm c1;
...
a z ... a z c ;
1n 1
mn m
n
z1 0, ..., zm 0.
2
3.
Постановка двойственной задачи линейногопрограммирования
Двойственная задача
следующим образом.
линейного
программирования
ставится
1. В исходной задаче L max, в двойственной F min .
2. Коэффициенты при переменных в целевой функции исходной
задачи являются коэффициентами в правой части при ограничениях
двойственной задачи.
3. Коэффициенты при переменных в целевой функции
двойственной задачи равны свободным коэффициентам ограничений
исходной задачи.
3
4.
Постановка двойственной задачи линейногопрограммирования
4. Свободный коэффициент
коэффициенту функции L.
функции
F
равен
свободному
5. Матрица коэффициентов ограничений двойственной задачи
является транспонированной к соответствующей матрице исходной
задачи.
6. Ограничения в исходной задаче имеют вид " " ,
а в двойственной – " ".
Между решениями исходной задачи и двойственной имеется
тесная связь.
4
5.
Лемма (основное неравенство)Лемма (основное неравенство)
Пусть ( x1 , x2 , ..., xn ) и ( z1 , z2 , ..., zm )
–
(то есть опорные планы) исходной и
соответственно.
Тогда L( x1 , ..., xn ) F ( z1 , ..., zm ).
допустимые наборы
двойственной задач
Доказательство.
n
Обозначим yi bi aij x j 0 для любого i 1, ..., m
m
j 1
дополнительные переменные исходной задачи и w j aij zi c j 0
i 1
для любого j 1, ..., n дополнительные переменные двойственной
задачи.
5
6.
Лемма (основное неравенство)Рассмотрим
m
m
n
m
m n
yi zi (bi aij x j ) zi bi zi aij zi x j 0, поскольку yi 0, zi 0
i 1
i 1
j 1
i 1
i 1 j 1
m
m
n
для любого i. Отсюда bi zi aij zi x j .
i 1
i 1 j 1
Теперь рассмотрим
n
n
m
m n
n
x j w j x j ( aij zi c j ) aij zi x j c j x j 0, поскольку x j 0, w j 0
j 1
j 1
i 1
i 1 j 1
j 1
m
n
n
для любого j. Отсюда aij zi x j c j x j .
i 1 j 1
j 1
m
n
Сравниваем полученные неравенства и замечаем, что bi zi c j x j .
i 1
j 1
n
m
Тогда
L( x1 , ..., xn ) c0 c j x j c0 bi zi F ( z1 , ..., zm ).
j 1
i 1
Лемма доказана.
6
7.
Теорема о двойственных задачахТеорема (о двойственных задачах)
Пусть ( x1 , x2 , ..., xn ) и ( z1 , z2 , ..., zm ) – допустимые наборы исходной
и двойственной задач соответственно. Равенство L( x1 , ..., xn ) F ( z1 , ..., zm )
имеет место тогда и только тогда, когда ( x1 , ..., xn ) и ( z1 , ..., zm ) являются
решениями соответствующих задач.
Если L не ограничена сверху ( L ), то область допустимых
решений двойственной задачи пуста.
7
8.
Теорема о двойственных задачахДоказательство.
Если
для допустимых наборов, то для
L( x1 , ..., xn ) F ( z1 , ..., zm )
`
`
любого допустимого набора ( x1 , ..., xn ) из основного неравенства
L( x1` , ..., xn` ) F ( z1 , ..., zm ) L( x1 , ..., xn ).
Следовательно, ( x1 , ..., xn ) является решением исходной задачи.
Для набора ( z1 , ..., zm ) – аналогично (доказать самостоятельно).
Достаточность
данного
утверждения
принимаем
без
доказательства.
Докажем второе утверждение теоремы.
Предположим, что область допустимых решений не пуста и
существует набор ( z1 , ..., zm ) в двойственной задаче. Тогда для любого
допустимого набора ( x1 , ..., xn ) выполняется неравенство
L( x1 , ..., xn ) F ( z1 , ..., zm ) M .
Следовательно, функция L ограничена сверху, что противоречит
условию.
Теорема доказана.
8
9.
Теорема о двойственных задачахЗамечание.
Обратное ко второму утверждению неверно. Если область
допустимых решений двойственной задачи пуста, то из этого не
следует, что L .
Область допустимых решений исходной задачи также может
быть пуста.
9
10.
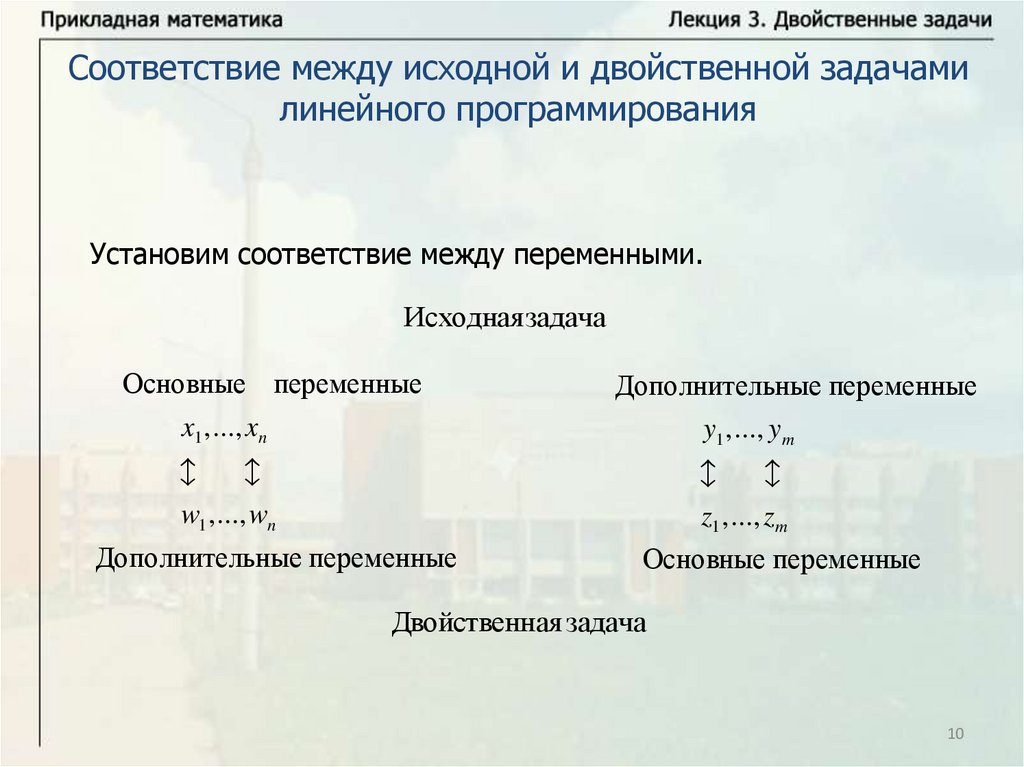
Соответствие между исходной и двойственной задачамилинейного программирования
Установим соответствие между переменными.
Исходная задача
Основные переменные
Дополнительные переменные
x1 , ..., xn
y1 , ..., ym
w1 , ..., wn
z1 , ..., zm
Дополнительные переменные
Основные переменные
Двойственная задача
10
11.
Лемма о дополняющей нежёсткостиЛемма (о дополняющей нежесткости)
0
0
0
0
Пусть ( x1 , ..., xn ) и ( z1 , ..., zm ) – решения исходной и двойственной
задачи соответственно. Выполнены следующие соотношения.
1). Если x 0j 0, то w 0j 0.
2). Если w 0j 0, то x 0j 0.
3). Если y 0j 0, то z 0j 0.
4). Если z 0j 0, то y 0j 0.
11
12.
Лемма о дополняющей нежёсткостиДоказательство.
n
n
m
m n
n
Рассмотрим x w x ( a z c j ) aij x z c j x 0j .
j 1
0
j
0
j
m
j 1
0
j
i 1
0
ij i
0 0
j i
i 1 j 1
m
n
i 1
j 1
m
j 1
m n
С другой стороны, y z (bi aij x ) z b z aij x 0j zi0 .
i 1
0 0
i i
0
j
0
i
i 1
0
i i
i 1 j 1
Заметим, что так
( x10 , ..., xn0 ) и ( z10 , ..., zm0 ) – решения, то
n
m
0
0
0
0
0
0
L( x1 , ..., xn ) F ( z1 , ..., zm ), а, следовательно, c0 c j x j c0 bi zi ,
j 1
n
i 1
m
0
Отсюда, c j x bi zi .
j 1
0
j
i 1
n
n
0 0
Тогда получаем, что x w yi zi .
j 1
0
j
0
j
i 1
12
13.
Лемма о дополняющей нежёсткостиНо поскольку x 0j 0, w 0j 0, y 0j 0, z 0j 0,
n
n
0 0
0 0
x j w j yi zi 0.
j 1
получаем
i 1
Так как x 0j 0, w 0j 0, y 0j 0, z 0j 0, то x 0j w 0j 0
для любого j 1, ..., n и yi0 zi0 0 для любого i 1, ..., m.
Отсюда и следует утверждение леммы. Лемма доказана.
13
14.
Следствие из второй теоремы двойственностиЗамечание.
Из второй теоремы двойственности для рассматриваемых
симплекс-таблиц следует, что переменные, соответствующие
базисным переменным исходной задачи, равны 0. Переменные,
соответствующие свободным переменным исходной задачи,
будут равны соответствующим числам первой строки (строки L )
с противоположным знаком.
14
15.
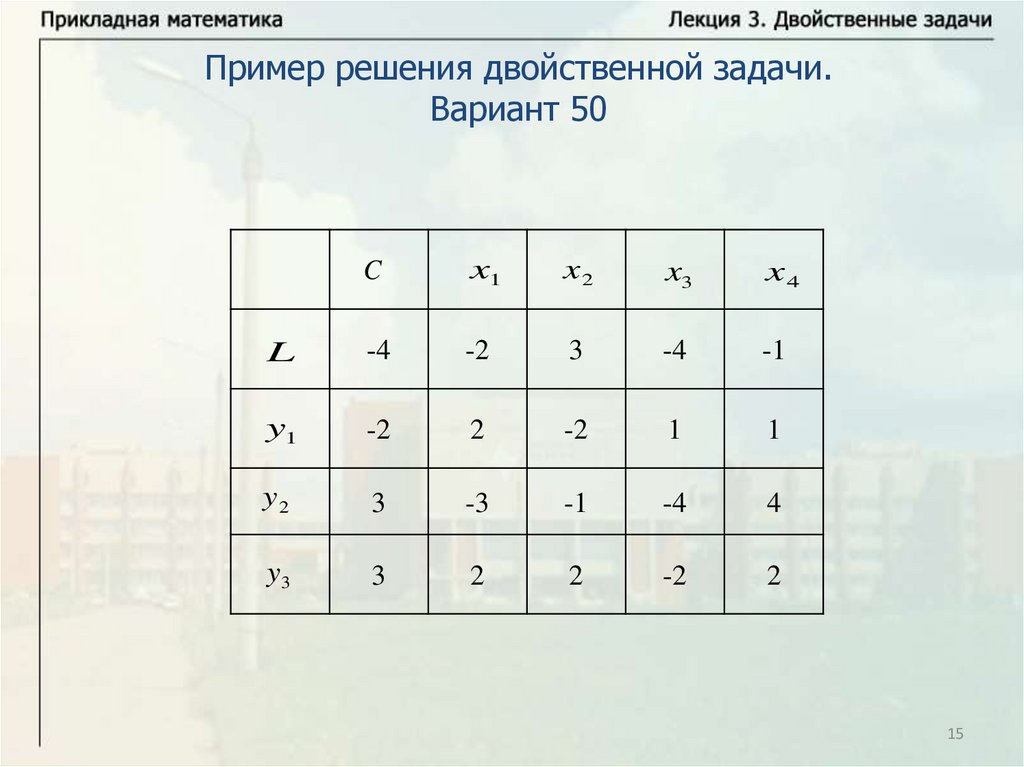
Пример решения двойственной задачи.Вариант 50
C
x1
x2
x3
x4
L
-4
-2
3
-4
-1
y1
-2
2
-2
1
1
y2
3
-3
-1
-4
4
y3
3
2
2
-2
2
15
16.
Пример решения двойственной задачиЗадача, соответствующая этой симплекс-таблице имеет вид
L 4 2 x1 3x2 4 x3 x4 max,
y1 2 (2 x1 2 x2 x3 x4 ) 0;
y2 3 ( 3 x1 x2 4 x3 4 x4 ) 0;
y 3 (2 x 2 x 2 x 2 x ) 0.
3
1
2
3
4
x1 0, x2 0, x3 0, x4 0.
Ограничения можно записать в виде
2 x1 2 x2 x3 x4 2;
3 x1 x2 4 x3 4 x4 3;
2 x 2 x 2 x 2 x 3.
1
2
3
4
16
17.
Пример решения двойственной задачиДвойственная задача ставится следующим образом
F 4 2 z1 3z2 3z3 min
2 z1 3 z 2 2 z3 2;
2 z z 2 z 3;
1
2
3
z1 4 z 2 2 z3 4;
z1 4 z 2 2 z3 1.
z1 0, z2 0, z3 0.
Дополнительные
переменные
удовлетворяют неравенствам
двойственной
задачи
w1 2 z1 3 z 2 2 z3 2 0;
w 2 z z 2 z 3 0;
2
1
2
3
w3 z1 4 z 2 2 z3 4 0;
w4 z1 4 z 2 2 z3 1 0.
17
18.
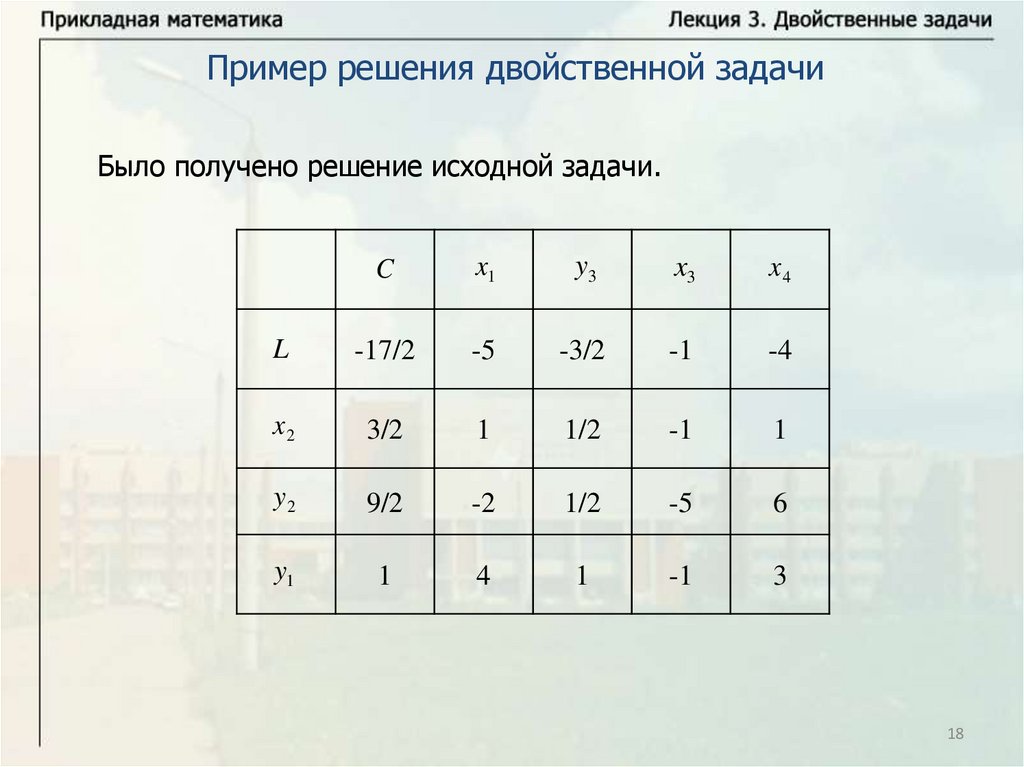
Пример решения двойственной задачиБыло получено решение исходной задачи.
C
x1
y3
x3
x4
L
-17/2
-5
-3/2
-1
-4
x2
3/2
1
1/2
-1
1
y2
9/2
-2
1/2
-5
6
y1
1
4
1
-1
3
18
19.
Пример решения двойственной задачиИз второй теоремы двойственности
Fmax Lmin ( L) max
17
;
2
w2 0, z2 0, z1 0;
3
w1 5, z3 , w3 1, w4 4.
2
По лемме о дополняющей нежесткости
w2 z 2 z1 0;
w2 2 z1 z2 2 z3 3,
3
2
следовательно, z3 .
3
3
w1 0 0 2 2 5; w3 0 0 2 4 1;
2
2
3
w4 0 0 2 1 4.
2
Это совпадает с полученными результатами.
19
20.
Задания для самоконтроля1.
В двойственной задаче линейного программирования целевая
функция F …
1) исследуется на минимум;
2) исследуется на максимум;
3) неотрицательна;
4) равна нулю.
20
21.
Задания для самоконтроля2. Ограничения в двойственной задаче задаются при
помощи знаков…
1)
" ";
2)
" ";
3)
" ";
4)
" ".
21
22.
Задания для самоконтроля3. Свободные коэффициенты целевых функций в прямой и
двойственной задаче линейного программирования…
1) положительны;
2) равны;
3) взаимно обратны;
4) отличаются знаком.
22
23.
Задания для самоконтроля4.
Матрица
коэффициентов
ограничений
двойственной
задачи по отношению к соответствующей матрице исходной
задачи является…
1) обратной;
2) вырожденной;
3) транспонированной;
4) противоположной.
23





















 Математика
Математика








