Логарифмические уравнения. Основные методы их решения

1.

Логарифмические
уравнения.
Основные методы их решения.

2.

«Ничему тому, что важно
знать, научить нельзя, всё, что может сделать
учитель, это указать
дорожки»
Ричард
Олдингтон
(1892 – 1962гг..) английский поэт,
прозаик, критик
«Кто говорит – тот сеет, кто
слушает – тот собирает».
Русская народная пословица

3.

Уравнение, содержащее неизвестное под знаком логарифма или (и) в
его основании, называется логарифмическим уравнением.
log a f ( x) b
log f ( x ) b a
1. Решение логарифмических уравнений на основании определения
логарифма.
Определение логарифма:
log a b c : a c b, a 0, b 0, a 1.
log a f ( x ) c f ( x ) a c ,
Пример 1:
f ( x ) 0, a 0, a 1.
log 4 x 2,
ОДЗ : х 0,
x 42 ,
x 16.
Ответ: 16.

4.

Пример 2:
Пример 3:
log 3 (2 x 1) 2,
4x 3 5,
2 x 1 32 ,
2 x 1 9,
x 4.
x 3 log 4 5,
Ответ: 4.
х 3 log 4 5.
Ответ:
3 log 4 5.
В таких уравнениях нет посторонних корней, поэтому
проверка не требуется.

5.

Способы решения логарифмических
уравнений
1.
2.
3.
4.
5.
6.
Решение уравнений на основании
определения логарифма, например,
уравнение
loga х = б (а > 0, а≠ 1, б>0 ) имеет решение
b
х=а .
Метод потенцирования. Под потенцированием
понимается переход от равенства,
содержащего логарифмы, к равенству, не
содержащему их:
если , loga f(х) = loga g(х), то f(х) = g(х), f(х)>0, g(х)>0 , а
> 0, а≠ 1.
Метод введение новой переменной.
Метод логарифмирования обеих частей
уравнения.
Метод приведения логарифмов к одному и
тому же основанию.
Функционально – графический метод.

6.

2. Метод потенцирования.
Под потенцированием понимается переход от равенства, содержащего
логарифмы, к равенству, не содержащему их.
log a f ( x ) log a g ( x )
Пример :
f ( x ) g ( x ), где a 0, a 1, f ( x ) 0, g ( x ) 0.
log 2 ( x 2 7 x 5) log 2 (4 x 1),
x 2 7 x 5 4 x 1,
x 2 3x 4 0,
x1 1, x2 4.
Проверка:
x 1
x 4
log 2 (12 7 1 5) log 2 (4 1 1)
log 2 3 log 2 3 - верно
log 2 (( 4) 2 7 ( 4) 5) log 2 (4 ( 4) 1)
log 2 ( 17) log 2 ( 17)
- не верно
Ответ: 1.
В таких уравнениях обязательна проверка или нахождение ОДЗ.

7.

Метод потенцирования
(с нахождением ОДЗ)
log3 (x²-3x-5)=log3 (7-2x)
Записать условия, определяющие область допустимых
значений (О.Д.З.): f (x)>0, g (x)>0
• Перейти от уравнения logа f (x)=logа g (x)
к уравнению f (x)=g (x)
• Решить полученное уравнение
• Проверить полученные корни по условиям, определяющим
область допустимых значений переменной (О.Д.З.).
Те корни уравнения, которые удовлетворяют этим условиям,
являются корнями логарифмического уравнения. Те корни
уравнения, которые не удовлетворяют хотя бы одному из этих
условий, объявляются посторонними корнями логарифмического
уравнения.
Записать ответ

8.

Решение уравнения методом
потенцирования
Освободимся
от знаков
логарифмов
Найдём
О.Д.З.
log3 (x²-3x-5)=log3 (7-2x)
Проверим
корни по
условиям
x²-3х-5>0,
7-2x>0
х² -3х-5=7-2х
Решим
квадратное
уравнение
Х=4
Х= - 3
х² –х-12=0
х=4, х=-3
Не
удовлетворяет
второму
неравенству
системы
Удовлетворяет
обоим
неравенствам
Ответ
х = -3

9.

3.Метод введения новой
переменной(алгоритм)
2log25x+5log5x+2=0
• Ввести новую переменную, найти О.Д.З.
• Решить получившееся уравнение и найти
значение новой переменной
• Сделать подстановку найденного
значения новой переменной и вычислить
неизвестную переменную
• Записать ответ

10.

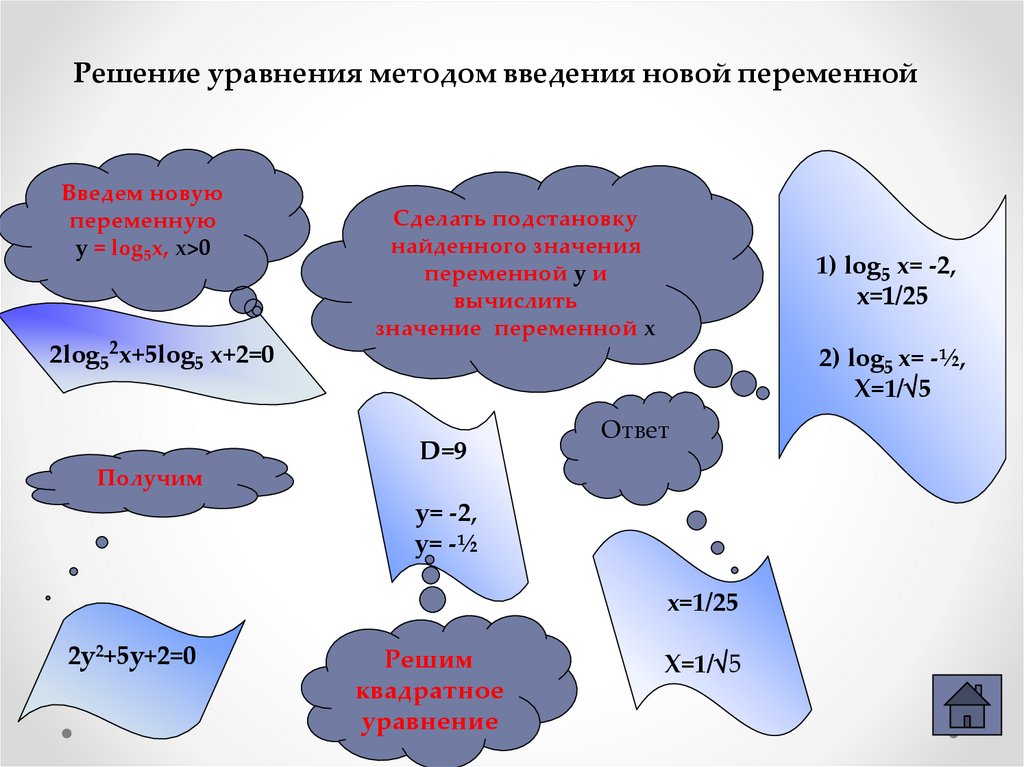
Решение уравнения методом введения новой переменной
Введем новую
переменную
y = log5x, х>0
2log52x+5log5 x+2=0
Сделать подстановку
найденного значения
переменной у и
вычислить
значение переменной х
1) log5 x= -2,
x=1/25
2) log5 x= -½,
X=1/√5
D=9
Ответ
Получим
y= -2,
y= -½
x=1/25
2у2+5у+2=0
Решим
квадратное
уравнение
X=1/√5

11.

Введение новой переменной.
.
Решить уравнение:
Решение: ОДЗ: х > 0.
Пусть log 3 x y , тогда уравнение примет вид:
Дискриминант D > 0. Корни по теореме Виета:
Вернемся к замене:
или
Решив простейшие логарифмические уравнения,
получим:
Ответ: 27;

12.

Пример
log 32 x log 3 x 2
ОДЗ:
Пусть
log 3 x t ,
x 0.
тогда
t 2 t 2, t 2 t 2 0.
t1 1, t2 2.
Значит,
log 3 x 1
или
log 3 x 2
x 3 1
x 32
1
x .
3
x 9.
1
Ответ:
, 9.
3

13.

1.
4. Метод логарифмирования обеих частей
уравнения.
Если в показатели степени содержится логарифм, то обе части
уравнения логарифмируют по тому основанию, которое содержится
в основании логарифма, находящегося в показателе степени.

14.

Решите уравнение
= ЗХ , возьмем от обеих частей уравнения логарифм
по основанию 3
Вопрос :
1.Это – равносильное преобразования ?
2.Если да то почему ?
Получим
log3
= log3 (3х)
.
Учитывая теорему 3 , получаем :
log3 х2 log3 х = log3 3х,
2log3 х log3 х = log3 3+ log3 х,
2 log32 х = log3 х +1,
2 log32 х - log3 х -1=0,
х >0 2 t 2 - t -1 =0 ; Д = 9 ; t1 =1 , t2 = -1/2
заменим log3 х = t ,
log3 х = 1 , х=3,
log3 х = -1/ 2 , х= 1/√3.
Ответ: 3 ; 1/√3.

15.

Метод логарифмирования.
f ( x ) g ( x ) log h ( x ) f ( x ) log h ( x ) g ( x )
f ( x ) 0, g ( x ) 0, h( x ) 0, h( x ) 1.
Пример :
x
log3 x 4
log 3 ( x log3 x 4 ) log 3
Пусть
Значит,
x 0,
ОДЗ: x 1.
1
,
27
1
27,
(log 3 x 4) log 3 x 3.
log 3 x t ,
тогда
log 3 x 1
x 3,
x 3.
1
log c a p p log c a
(t 4)t 3,
t 2 4t 3 0,
t1 1, t2 3.
log 3 x 3,
или
x 33 ,
x 27.
Ответ: 3; 27.

16.

5. Метод приведения логарифмов к одному и тому
основанию.

17.

Решение уравнений с разными основаниями
log a x log
a
2 log 1 3
одз : x 0
a
log a x log
1
a2
2 log a 1 3
1
1
log a x log a 2 log a 3
1
1
2
log a x 2 log a 2 log a 3
22
log a x log a
3
4 4
x ; одз
3 3
Опираясь на свойство:
1
log a q b log a b
q
4
Ответ :
3

18.

Пример :
log 7 x log x 7 2,5
x 0,
ОДЗ:
x 1.
log a b
1
log b a
1
5
.
log 7 x 2
1 5
Подстановка: t log 7 x. Уравнение примет вид: t ,
t 2
2t 2 5t 2 0,
Приведём логарифмы к одному основанию – 7:
log 7 x
t1 2, t 2
Значит,
log 7 x 2
x 72 ,
x 49.
или
log 7 x
1
2
1
.
2
1
2
x 7 ,
x 7.
Ответ:
7 , 49.

19.

Функционально-графический метод(алгоритм)
log2x = -x+1
• Ввести функцию f(x),равную левой части и
g(x),равную правой части
• Построить на одной координатной
плоскости графики функций y=f(x) и
y=g(x)
• Определить точки пересечения графиков
• Найти абсциссы точек пересечения – это
и есть корни уравнения
• Записать ответ

20.

Решение уравнения функциональнографическим методом
Решим уравнение
графически
у
log2 x= -х+1
Построим
график уравнения
у = -х+1
y = log 2 x
у = log2 x
х 2 1
у 1 0
Построим
график уравнения
х
у = -х+1
х 2 0
у -1 1
Ответ: х=1

21.

Решите самостоятельно:
x
log 3 5 0
2
log 2 3 x 0
log 3 5x 3 log 3 7 x 5
log 1 3x 1 log 1 6 x 8
2
2
log 52 x log 5 x 2

22.

Спасибо за внимание!
Удачи !
Успехов!