Похожие презентации:
Теорема Пифагора
1. 25.11.16. Классная работа. Теорема Пифагора.
“…Геометрия владеет двумя сокровищами– теоремой Пифагора и
золотым сечением…”
2. Цели урока
• Сформулировать и доказать теоремуПифагора;
• Отработать навыки применения теоремы
при решении задач.
25.11.2021
http://aida.ucoz.ru
2
3.
ВопросыЧто изображено?
Как называются стороны АС и ВС?
Чему равна площадь этого треугольника?
Чему равна сумма острых углов в прямоугольном
треугольнике?
A
с
B
b
a
C
1
S ab
2
А + В = 90°
4.
Докажите, что треугольники равны.B
A1
C
A
B1
C1
5.
CB
D
A
E
SABCDE = SABC + SADC + SADE
6.
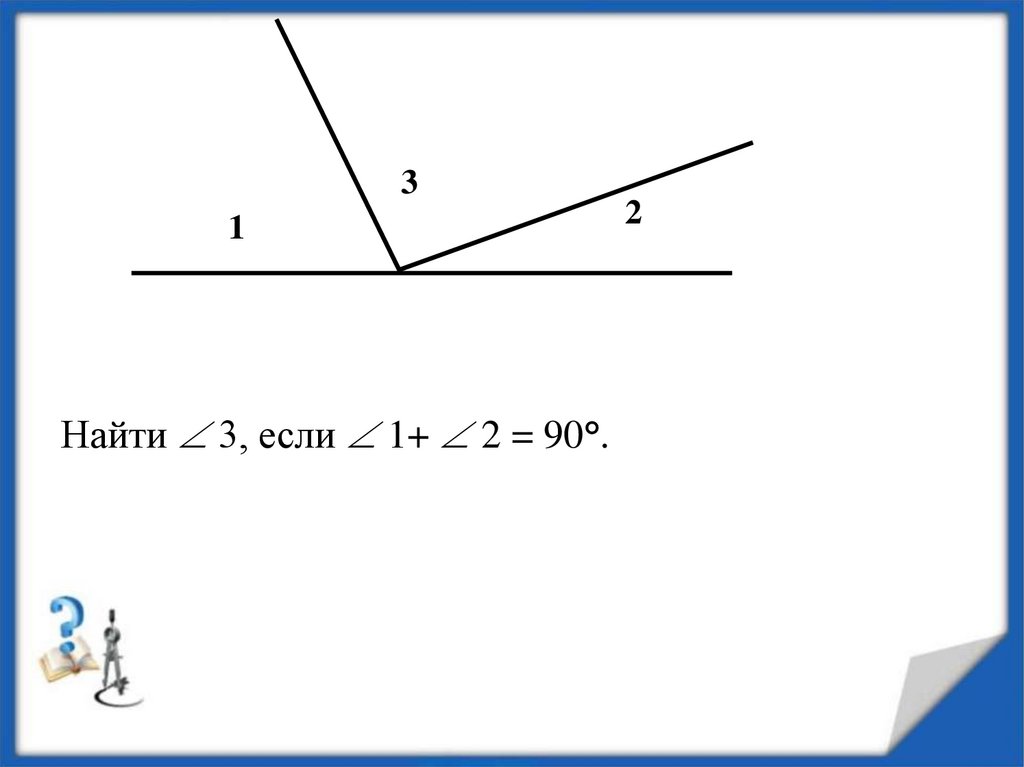
31
Найти 3, если 1+ 2 = 90°.
2
7.
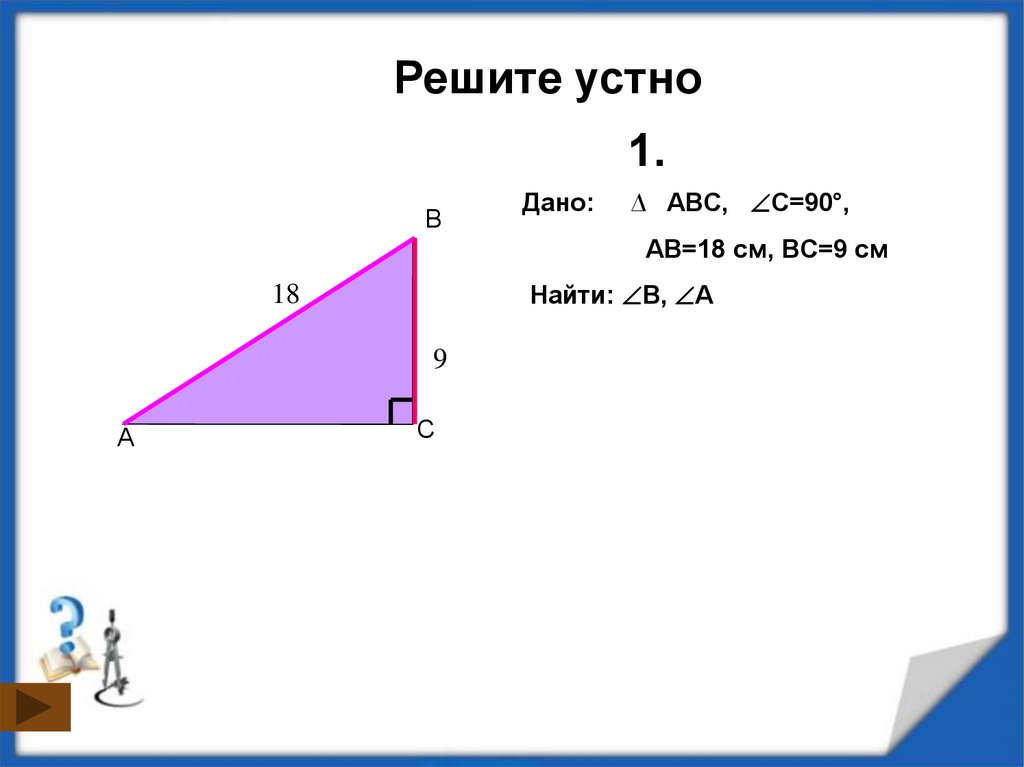
Решите устно1.
B
Дано:
∆ ABC, C=90°,
AB=18 см, ВC=9 см
Найти: B, А
18
9
A
C
8. Нужно знать зависимость между катетами и гипотенузой в прямоугольном треугольнике.
Эту зависимость подметили еще в глубокойдревности и доказали теорему, которую знают
теперь почти все школьники. Эта теорема носит
имя Пифагора.
8
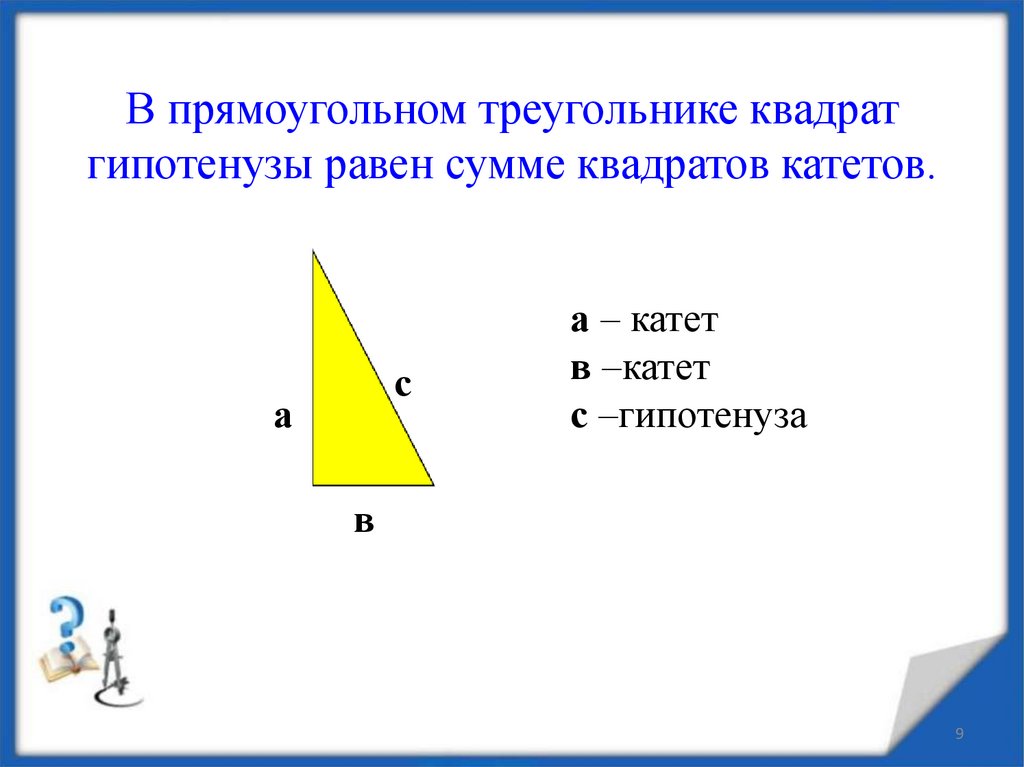
9. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
са
а – катет
в –катет
с –гипотенуза
в
9
10.
В прямоугольном треугольнике квадрат гипотенузыравен сумме квадратов катетов
в
а
с
в
а
с
а
с
а
вв
с
с
в
а
в
11. Доказательство теоремы
В прямоугольном треугольнике квадрат гипотенузыравен сумме квадратов катетов
Дано: прямоугольный треугольник
а
в
а, в – катеты, с – гипотенуза
с
в
с
2= а2 + в2
Доказать:
с
а
Доказательство:
1. Достроим треугольник до
а
с
квадрата со стороной а+в;
в
с
2. S=(а+в)2 - площадь квадрата
в
а
3. Четыре прямоугольных
треугольника, S = ½ ав
4. S= 4*1/2ав+с2 =2ав+с2
5. (а+в)2 = 2ав+с2
6. с2= а2 + в2
12. Формулировка теоремы
Во времена Пифагора теорема звучала так:« Доказать, что квадрат,
построенный на гипотенузе
прямоугольного треугольника,
равновелик сумме квадратов,
построенных на катетах»
« Площадь квадрата,
построенного на гипотенузе
прямоугольного
треугольника, равна сумме
площадей квадратов,
построенных на его катетах».
13. Немного истории
Для нас Пифагор – математик. В древности былоиначе. Геродот называет его "выдающимся
софистом", то есть учителем мудрости. Для своих
современников Пифагор прежде всего был
религиозным пророком, воплощением высшей
божественной мудрости. Пифагор был
разносторонней личностью. Он занимался и
медициной, и музыкой, и астрономией, а так же
был четыре раза подряд олимпийским чемпионом.
13
14. Немного истории
Пифагор Самосский это древнегреческийматематик, философ и
мистик, родоначальник
школы пифагорейцев.
Годы его жизни - 570490 гг. до н. э.
14
15. Значение теоремы Пифагора
Теорема Пифагора- это одна из самыхважных теорем геометрии. Значение её
состоит в том, что из неё или с её
помощью можно вывести большинство
теорем геометрии.
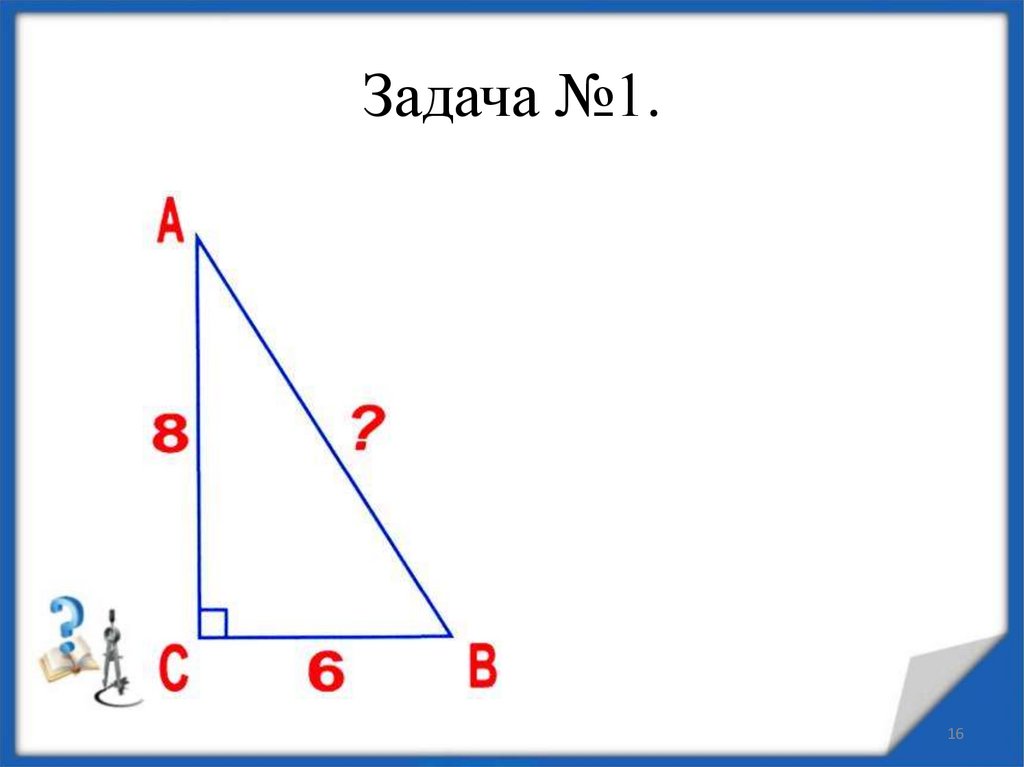
16. Задача №1.
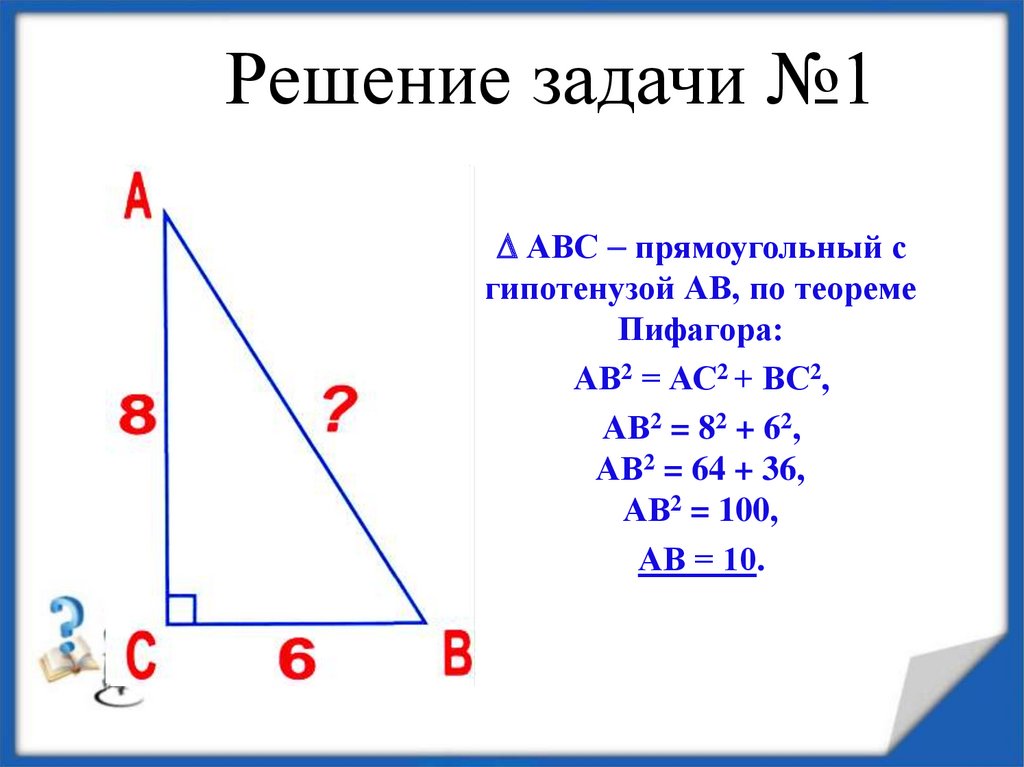
1617. Решение задачи №1
АВС прямоугольный сгипотенузой АВ, по теореме
Пифагора:
АВ2 = АС2 + ВС2,
АВ2 = 82 + 62,
АВ2 = 64 + 36,
АВ2 = 100,
АВ = 10.
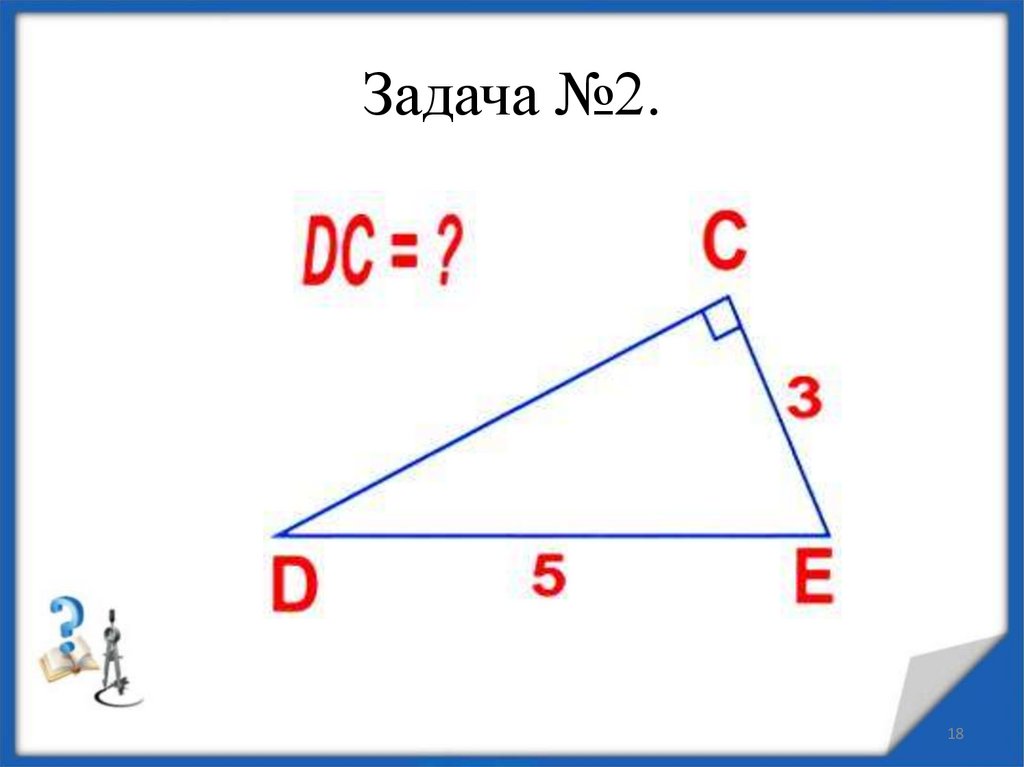
18. Задача №2.
1819. Решение задачи №2
DCE прямоугольныйс гипотенузой DE
По теореме Пифагора:
DE2 = DС2 + CE2,
DC2 = DE2 CE2,
DC2 = 52 32,
DC2 = 25 9,
DC2 = 16,
DC = 4.
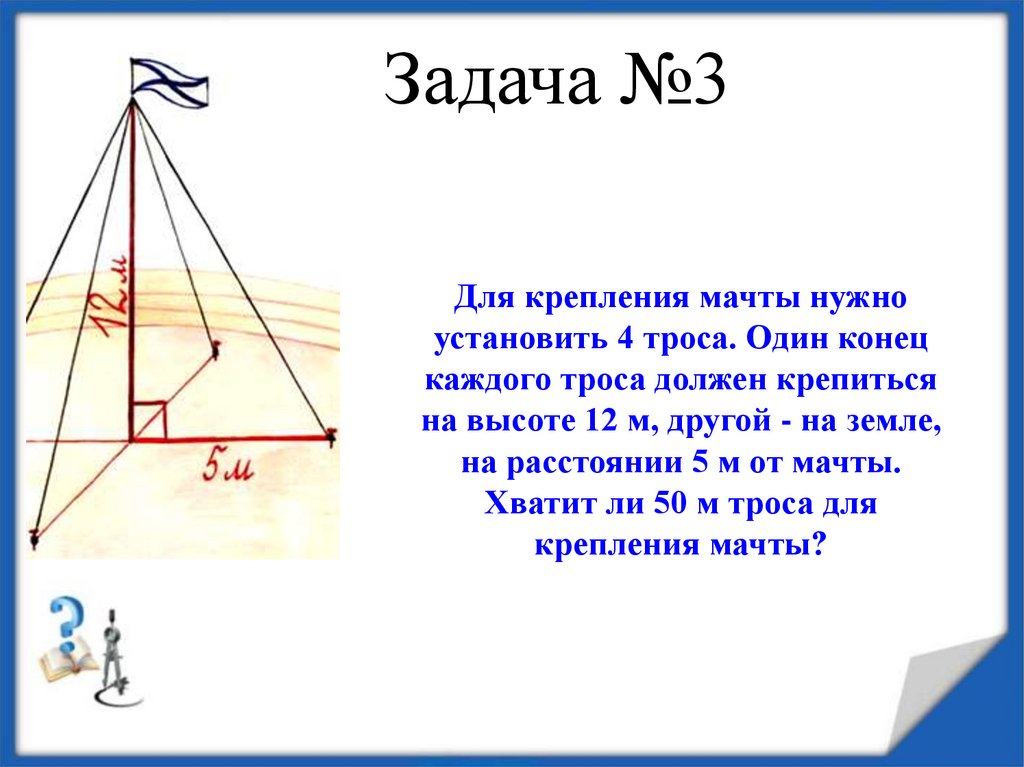
20. Задача №3
Для крепления мачты нужноустановить 4 троса. Один конец
каждого троса должен крепиться
на высоте 12 м, другой - на земле,
на расстоянии 5 м от мачты.
Хватит ли 50 м троса для
крепления мачты?
21. Итог урока
1. Возможно было решение задач данного типа беззнания теоремы Пифагора? Почему?
2. В чем суть теоремы Пифагора?
3. О чем надо помнить, применяя теорему
Пифагора?
21
22. Стих о теореме Пифагора
Если дан нам треугольникИ притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдём:
Катеты в квадрат возводим,
Сумму степеней находим
И таким простым путём
К результату мы придём.
22
23.
25.11.2021http://aida.ucoz.ru
23
















 Математика
Математика