Похожие презентации:
Лекция 2. Сортировки
1.
Сортировки2.
Задача сортировкиАлгоритм сортировки — это алгоритм для упорядочивания элементов в
списке. В случае, когда элемент списка имеет несколько полей, поле,
служащее критерием порядка, называется ключом сортировки. На практике в
качестве ключа часто выступает число, а в остальных полях хранятся какиелибо данные, никак не влияющие на работу алгоритма.
3.
Характеристики сортировкиУстойчивость -- элементы с равными ключами не меняются местами
Локальная -- не требует дополнительной памяти
Внутренняя/внешняя -- работает с данными в оперативной памяти/с
физическими данными
Основанные на операциях сравнения
Адаптивная/неадаптивная -- требуют результатов предыдущих шагов для
проведения следующего
4.
Квадратичные сортировки● Сортировка пузырьком
● Сортировка выбором
● Сортировка вставками
5.
Сортировка слиянием6.
Сортировка с помощью кучи7.
Слияние К отсортированных массивов спомощью кучи
8.
TimSort● Массив делится на подмассивы разной длины
● Каждый массив сортируется вставками (или другой устойчивой
сортировкой)
● Отсортированные подмассивы объединяются с помощью слияния
9.
TimSort1. Выберем значение minrun -- минимального размера подмассива, на
которые будет делиться массив (желательно, чтобы n/minrun было
степенью двойки)
2. Начинаем набирать отсортированные подмассивы:
a. Если первый элемент не меньше нулевого -- идём, пока элементы неубывают. Иначе -пока убывают.
b. Если прошли меньше элементов, чем minrun -- докидываем до minrun и фиксируем
c. Если элементы в подмассиве упорядочены по убыванию -- инвертируем его
10.
TimSort1. Начинаем процедуру слияния:
Заведём стек пар {Индекс начала подмассива, Размер}
Добавляем очередной подмассив
Пусть X,Y,Z -- длины последних трёх интервалов.
Пока Z<=X+Y ИЛИ Х>=Y:
i. Если X>=Y -- сливаем их
ii. Если Z<=X+Y -- сливаем Y с min(X,Z)
e. Возвращаемся к шагу b
Оптимизация -- галоп:
a.
b.
c.
d.
2.
Если несколько элементов подряд взяли из одного подмассива -- предполагается, что и
дальше будем брать из него. Тогда найдём следующий элемент из второго подмассива
бинпоиском по первому и скопируем весь первый до него.
11.
Быстрая сортировка● Массив a[i;j] разбивается на два подмассива a[i;k], a[k+1;j] так, что для
любого x из a[i;k] и для любого y из a[k+1;j] x<=y
● Подмассивы сортируются рекурсивно
● Объединять не надо, так как между собой подмассивы уже
упорядоченны
12.
Быстрая сортировкаОпорный элемент -- значение ключа, относительно которого разбивается
массив на каждом шаге. Выбор опорного элемента -- первая оптимизация
быстрой сортировки:
1. Случайный элемент из подмассива
2. Центральный элемент из подмассива
3. Медиана трёх
При малом размере подмассива его можно отсортировать вставками
13.
Среднее время работыЛемма: время работы быстрой сортировки равно O(nlogn)
Пусть X -- количество сравнений за всё время сортировки
Z -- массив, Zij = {z[i], z[j]} -- подмассив
Каждый элемент сравнивается только с опорным, опорный дальше не
участвует в сравнении -- то есть максимум любая пара элементов
сравнивается один раз
14.
Среднее время работыВероятность того, что zi сравнивается с zj равна вероятности того, что в множестве Zij
опорным элементом выбран либо zi, либо zj
Pr{zi<>zj} = 2/(j-i+1)
15.
Интроспективная сортировкаIntroSort -- быстрая сортировка, которая переключается на пирамидальную
по достижении некоторой глубины рекурсии
16.
Поиск к-й порядковой статистики за линейноевремя
17.
Нижняя оценка времени работы для сортировоксравнением
Теорема: В худшем случае любой алгоритм сортировки сравнениями
выполняет Ω(nlogn) сравнений, где n — число сортируемых элементов.
18.
Сортировка подсчётом19.
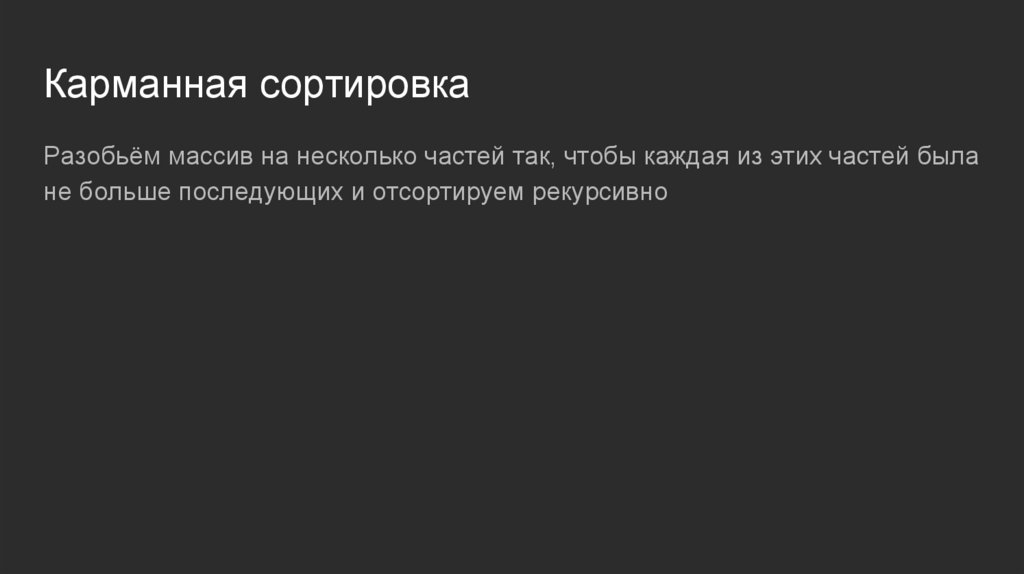
Карманная сортировкаРазобьём массив на несколько частей так, чтобы каждая из этих частей была
не больше последующих и отсортируем рекурсивно
20.
MSD, LSD, Сортировка строк21.
Binary QuickSort22.
Интерполяционный поискОптимизация бинпоиска, опирающаяся на то, что ключи распределены
равномерно
m = l + (r - l) * (x-a[l]) / (a[r] - a[l])
m -- опорный элемент
l, r -- границы подмассива
x -- искомый элемент
23.
Интерполяционная сортировка24.
Интерполяционная сортировкаhttp://www.ijcte.org/papers/575-A280.pdf
25.
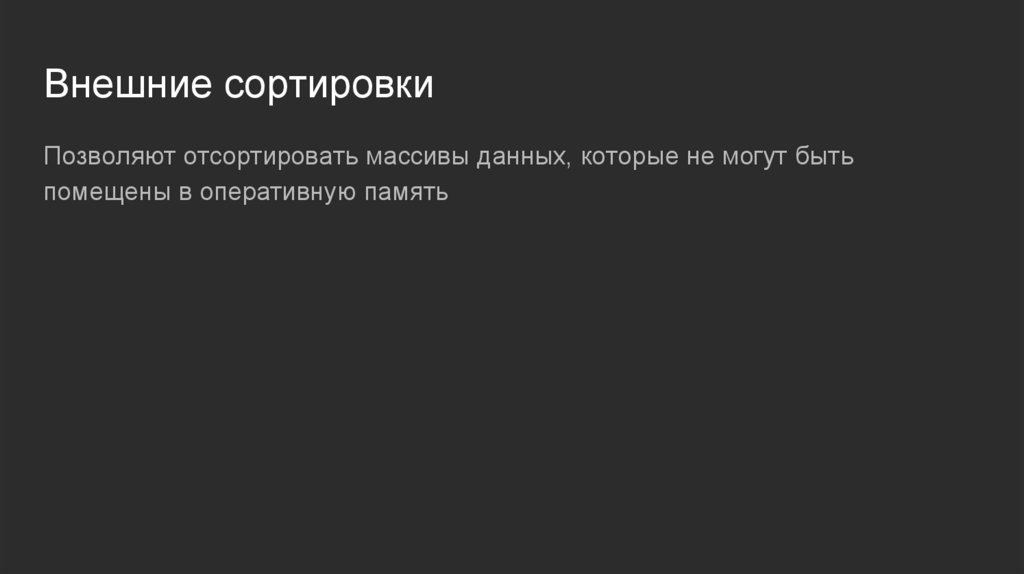
Внешние сортировкиПозволяют отсортировать массивы данных, которые не могут быть
помещены в оперативную память
26.
Сортировка многопутевым слияниемПусть имеем 2Р устройств (внешних файлов)
M -- количество данных, которые можем отсортировать
Изначально все данные в устройстве 0
Считываем первые M данных, сортируем и записываем на устройство P
Так далее, пока не заполним устройства P..2P-1
Если ещё остались данные -- снова сортируем кусок размера M и
помещаем в P, P+1 и так далее
27.
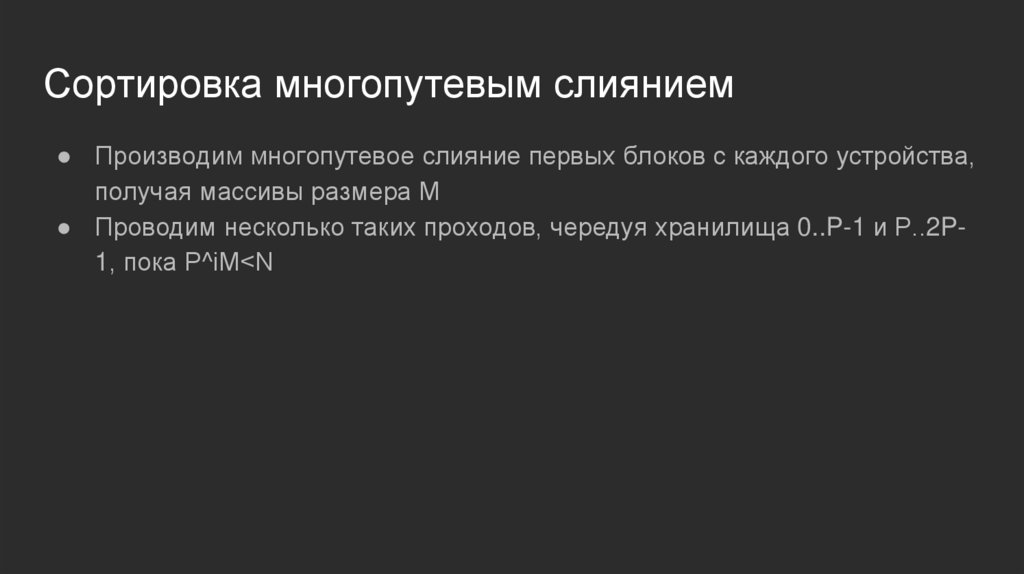
Сортировка многопутевым слиянием● Производим многопутевое слияние первых блоков с каждого устройства,
получая массивы размера M
● Проводим несколько таких проходов, чередуя хранилища 0..P-1 и P..2P1, пока P^iM<N
28.
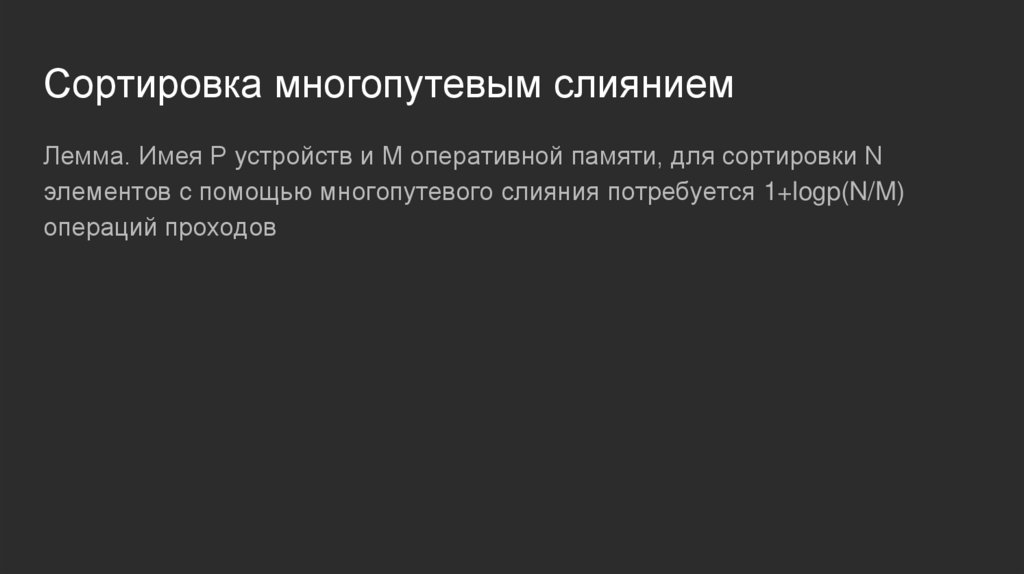
Сортировка многопутевым слияниемЛемма. Имея P устройств и M оперативной памяти, для сортировки N
элементов с помощью многопутевого слияния потребуется 1+logp(N/M)
операций проходов
29.
Сортировка естественным слиянием● Исходный файл разбивается на P-1 файлов по принципу “пока значения
элементов возрастают -- записываем их в первый файл, если нет -меняем файл”
● Сливаем файлы в один с помощью кучи
● Повторяем, пока из всех файлов не получится одна серия
30.
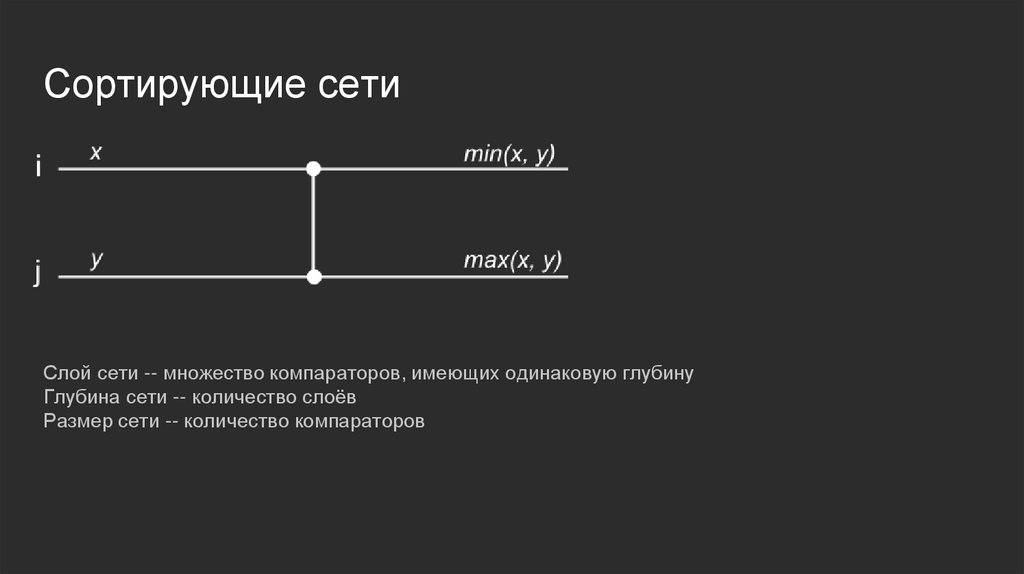
Сортирующие сетиСлой сети -- множество компараторов, имеющих одинаковую глубину
Глубина сети -- количество слоёв
Размер сети -- количество компараторов
31.
0-1 принципЕсли сортирующая сеть сортирует любую последовательность из 0 и 1 -- она
сортирует все числовые последовательности.
1. Монотонная функция сохраняет минимум, т.е. f(min(a,b)) = min(f(a), f(b))
2. Сортировка и монотонная функция коммутируют, то есть неважно,
сначала отсортировать массив, а потом применить к каждому элементу
монотонную функцию или наоборот.
32.
0-1 принципДоказательство:
Пусть сортирующая сеть сортирует все последовательности 0 и 1, но не
сортирует массив чисел a[0..n-1]. Тогда существует a[i] т.ч. a[i]<a[i-1]
Построим на массиве a монотонную функцию f т.ч. f(a[j]) = 0, если a[j]<=a[i] и
f(a[j]) = 1 иначе
Тогда f(N(a)) == {0000….101….1111}, значит N(f(a)) == {0000….101….1111}
Значит, сортирующая сеть N не сортирует все массивы из 0 и 1
33.
Сортирующая сеть Бэтчера● Рассмотрим 0-1 битонические последовательности (имеющие вид
0^i1^j0^k или 1^i0^j1^k)
● Рассмотрим полуфильтр. Если ему на вход подать битоническую
последовательность -- получим две последовательности -- одну
битоническую и одну однородную.
● Если применять полуфильтры рекурсивно к получившимся
подпоследовательностям -- отсортируем битоническую
последовательность
34.
Сортирующая сеть Бэтчера● Построим объединяющую сеть, которая будет преобразовывать две
отсортированные последовательности в две битонические
● К получившимя битоническим последовательностям применим
битонический сортировщик
● Последовательно применяя такую сеть к подмассивам размера 2,4,8 и
так далее, получим сортирующую сеть для N=2^k элементов
35.
Сортирующая сеть БэтчераГлубина сортирующей сети -- O(log^2(n))
Размер сортирующей сети -- O(nlog^2(n))
36.
Мастер-теоремаОсновная теорема об асимптотических оценках устанавливает метод
решения рекуррентных соотношений вида
T(n) = aT(n/b) + f(n)

































 Программирование
Программирование








