Похожие презентации:
Правильные многогранники
1.
2. Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины
различных наук.Л. Кэрролл
3. Содержание
1. Основные понятия о многогранниках2. Виды и элементы правильных
многогранников
3. Правильные многогранники в
философской картине мира
4. Ученые, внесшие вклад в изучение
правильных многогранников
5. Теорема Эйлера
6. Многогранники в природе
7. Многогранники в искусстве
4. Основные понятия о многогранниках
Многогранник – это геометрическое тело, ограниченноесо всех сторон плоскими многоугольниками, называемыми
гранями.
Стороны граней – рёбра многогранника, а концы рёбер –
вершины многогранника.
Многогранник называется выпуклым, если он весь
расположен по одну сторону от плоскости, каждой из его
граней.
Выпуклый многогранник называется правильным, если
все его грани – равные правильные многоугольники, в
каждой вершине сходится одно и то же число рёбер, а
соседние грани образуют равные углы.
Надо отметить, что Платоновых тел ровно пять – ни
больше, ни меньше. О них и их свойствах пойдет речь
ниже…
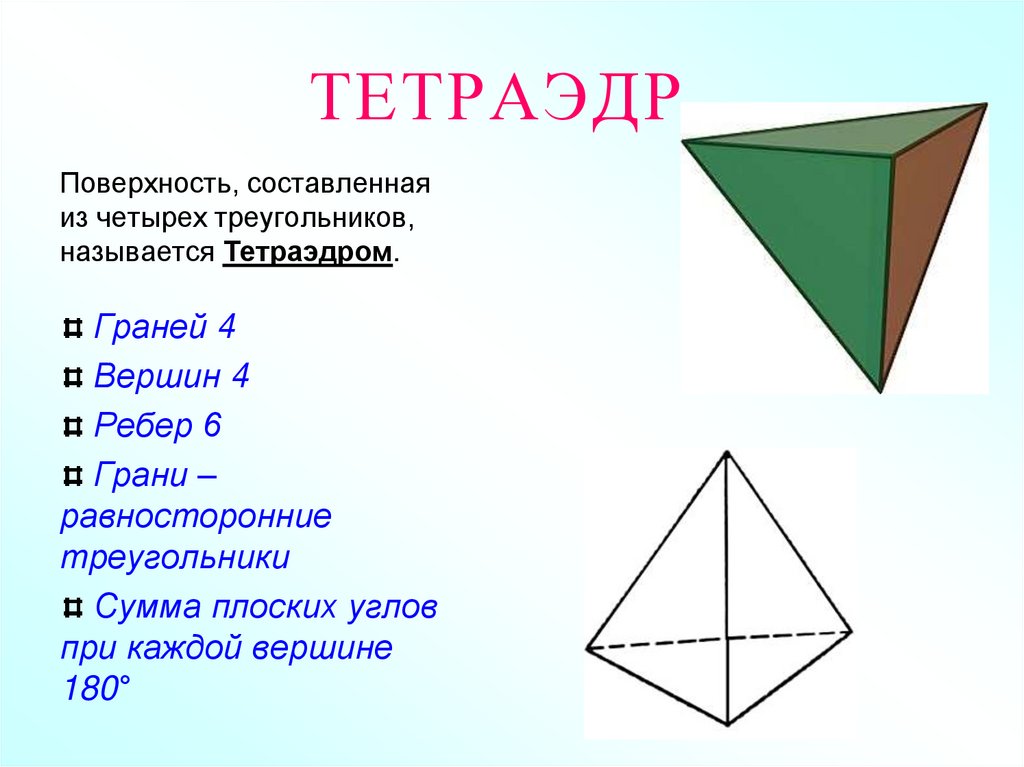
5. ТЕТРАЭДР
Поверхность, составленнаяиз четырех треугольников,
называется Тетраэдром.
Граней 4
Вершин 4
Ребер 6
Грани –
равносторонние
треугольники
Сумма плоских углов
при каждой вершине
180°
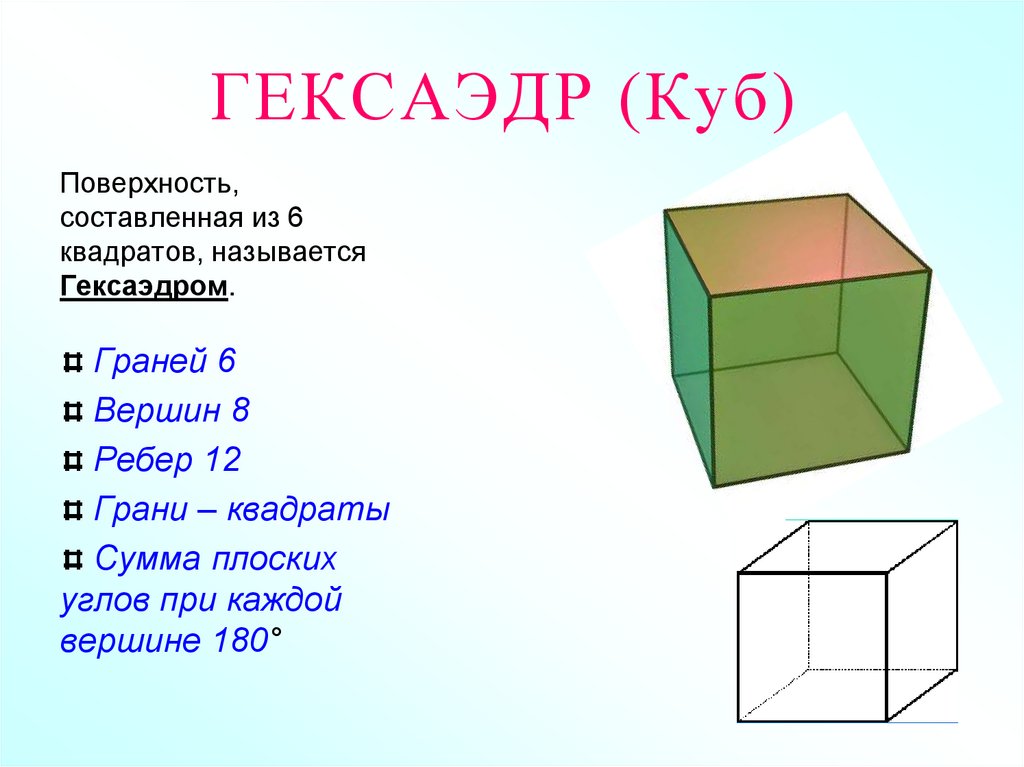
6. ГЕКСАЭДР (Куб)
Поверхность,составленная из 6
квадратов, называется
Гексаэдром.
Граней 6
Вершин 8
Ребер 12
Грани – квадраты
Сумма плоских
углов при каждой
вершине 180°
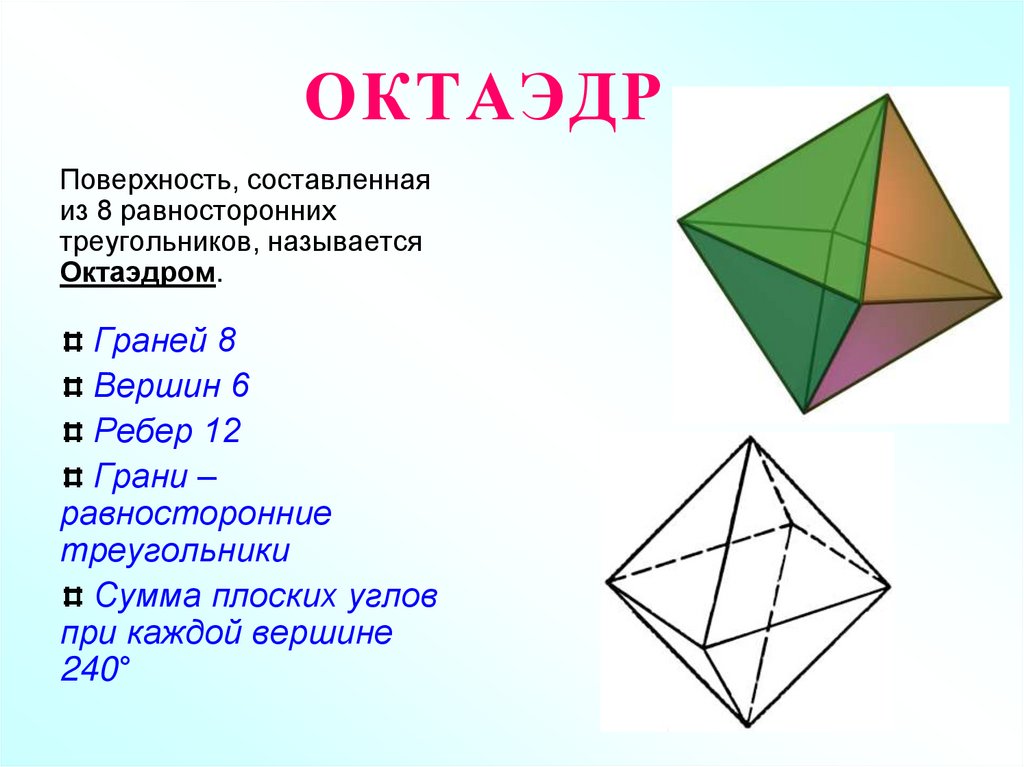
7. ОКТАЭДР
Поверхность, составленнаяиз 8 равносторонних
треугольников, называется
Октаэдром.
Граней 8
Вершин 6
Ребер 12
Грани –
равносторонние
треугольники
Сумма плоских углов
при каждой вершине
240°
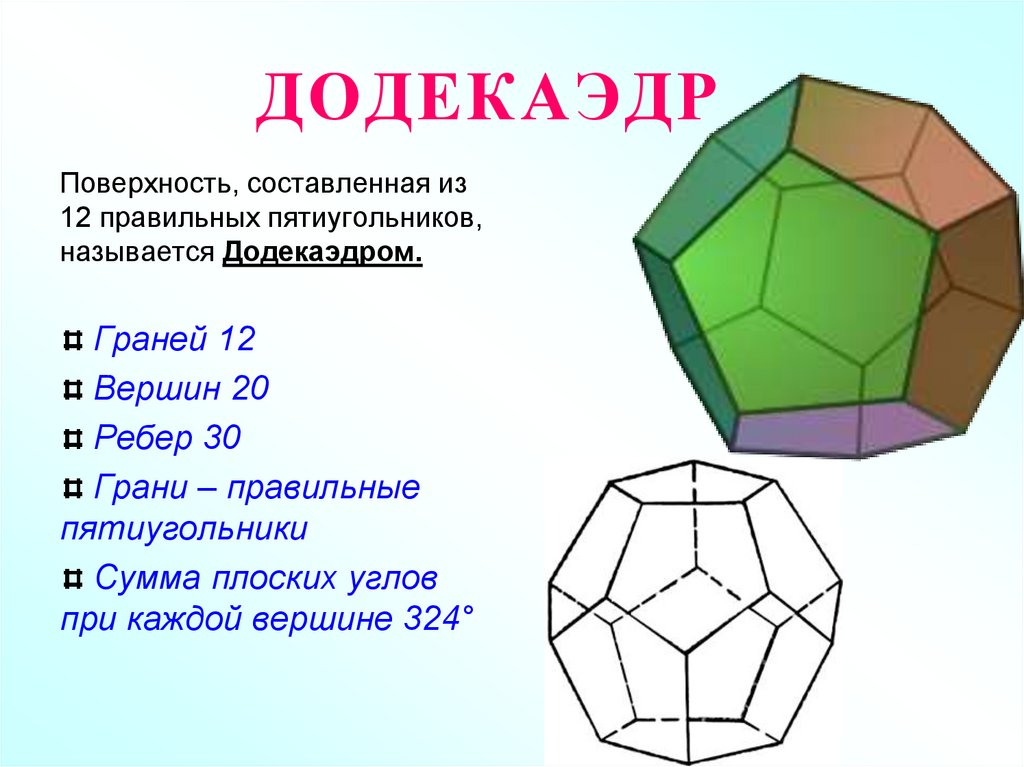
8. ДОДЕКАЭДР
Поверхность, составленная из12 правильных пятиугольников,
называется Додекаэдром.
Граней 12
Вершин 20
Ребер 30
Грани – правильные
пятиугольники
Сумма плоских углов
при каждой вершине 324°
9. ИКОСАЭДР
Поверхность, составленная из20 равносторонних
треугольников, называется
Икосаэдром.
Граней 20
Вершин 12
Ребер 30
Грани –
равносторонние
треугольники
Сумма плоских углов
при каждой вершине 300°
10.
Первым свойства правильных многогранников описалдревнегреческий ученый Платон. Именно поэтому
правильные многогранники называют также телами Платона.
Платон считал, что мир
строится из четырёх
«стихий» - огня, земли,
воздуха и воды, а атомы этих
«стихий» имеют форму
четырёх правильных
многогранников.
Платон
428 – 348 г. до н.э.
11.
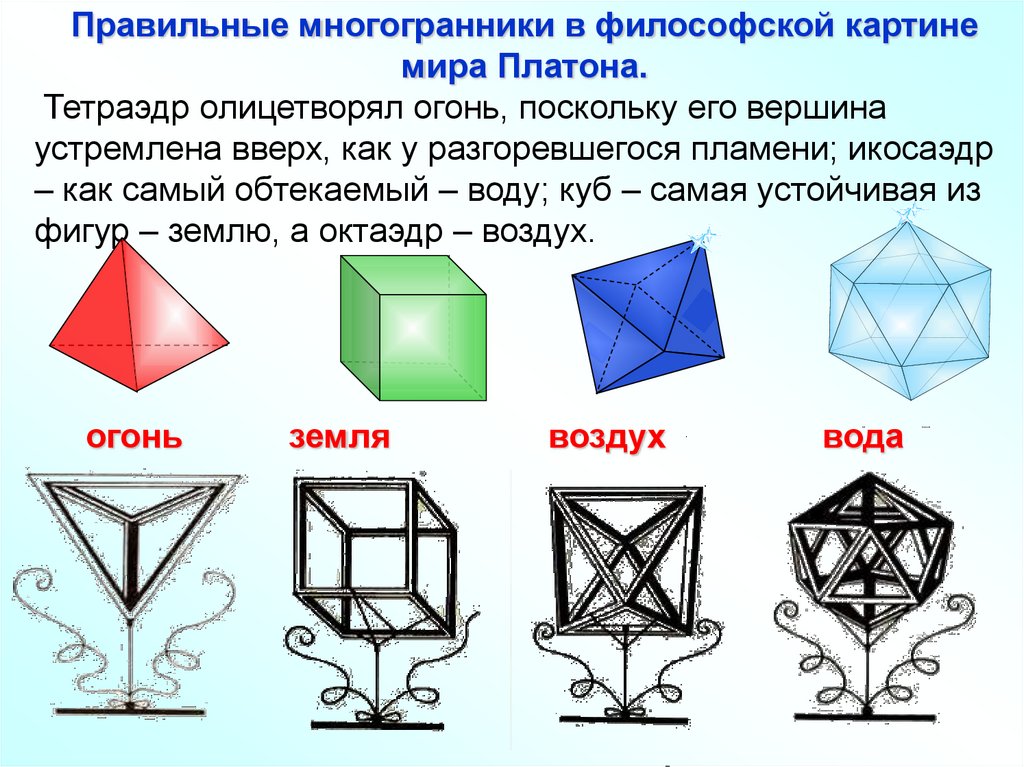
Правильные многогранники в философской картинемира Платона.
Тетраэдр олицетворял огонь, поскольку его вершина
устремлена вверх, как у разгоревшегося пламени; икосаэдр
– как самый обтекаемый – воду; куб – самая устойчивая из
фигур – землю, а октаэдр – воздух.
огонь
земля
воздух
вода
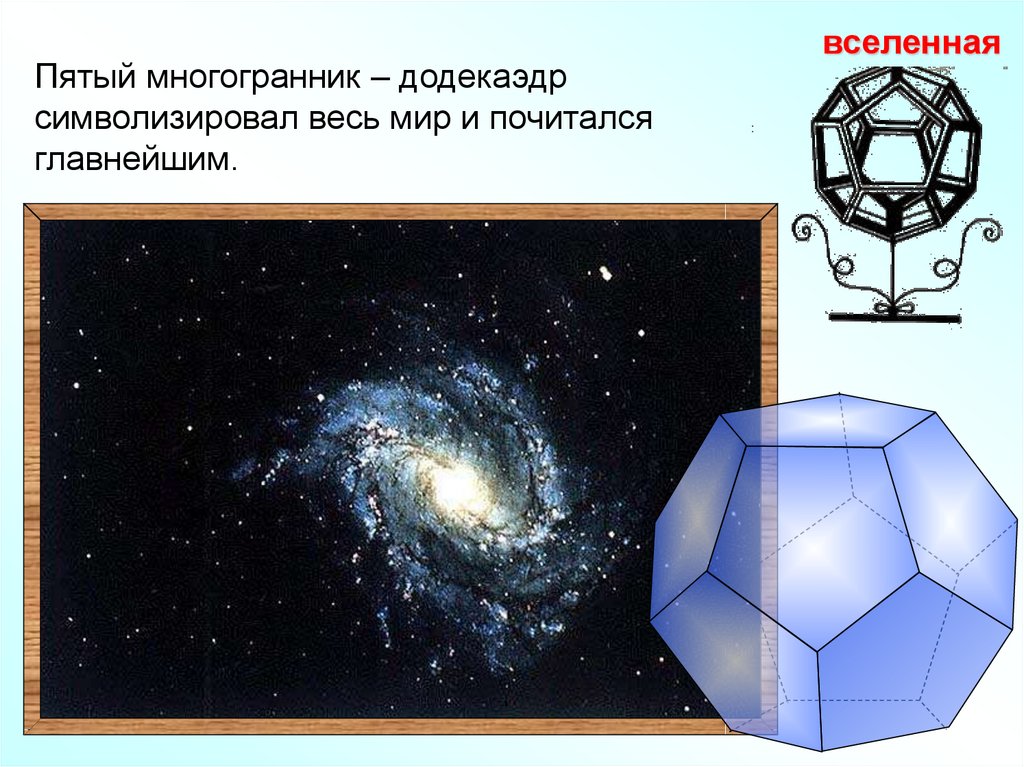
12.
Пятый многогранник – додекаэдрсимволизировал весь мир и почитался
главнейшим.
вселенная
13.
Большой интерес к формам правильных многогранниковпроявляли скульпторы, архитекторы, художники. Их поражало
совершенство, гармония многогранников. Леонардо да Винчи
(1452 – 1519) увлекался теорией многогранников и часто
изображал их на своих полотнах. Сальвадор Дали на картине
«Тайная вечеря» изобразил И. Христа со своими учениками на
фоне огромного прозрачного додекаэдра.
14.
Архимед описалполуправильные многогранники
Это многогранники, которые
получаются из платоновых
тел в результате их усечения.
усечённый тетраэдр,
усечённый гексаэдр (куб),
усечённый октаэдр,
усечённый додекаэдр,
усечённый икосаэдр.
Архимед
287 – 212 гг. до н.э.
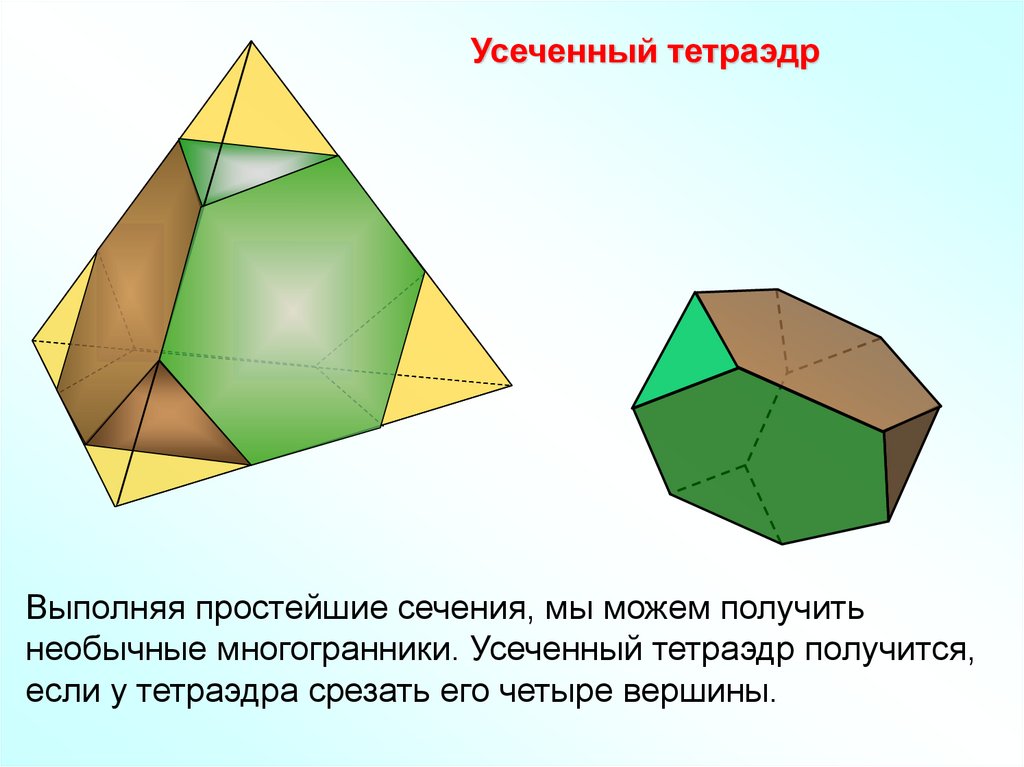
15.
Усеченный тетраэдрВыполняя простейшие сечения, мы можем получить
необычные многогранники. Усеченный тетраэдр получится,
если у тетраэдра срезать его четыре вершины.
16.
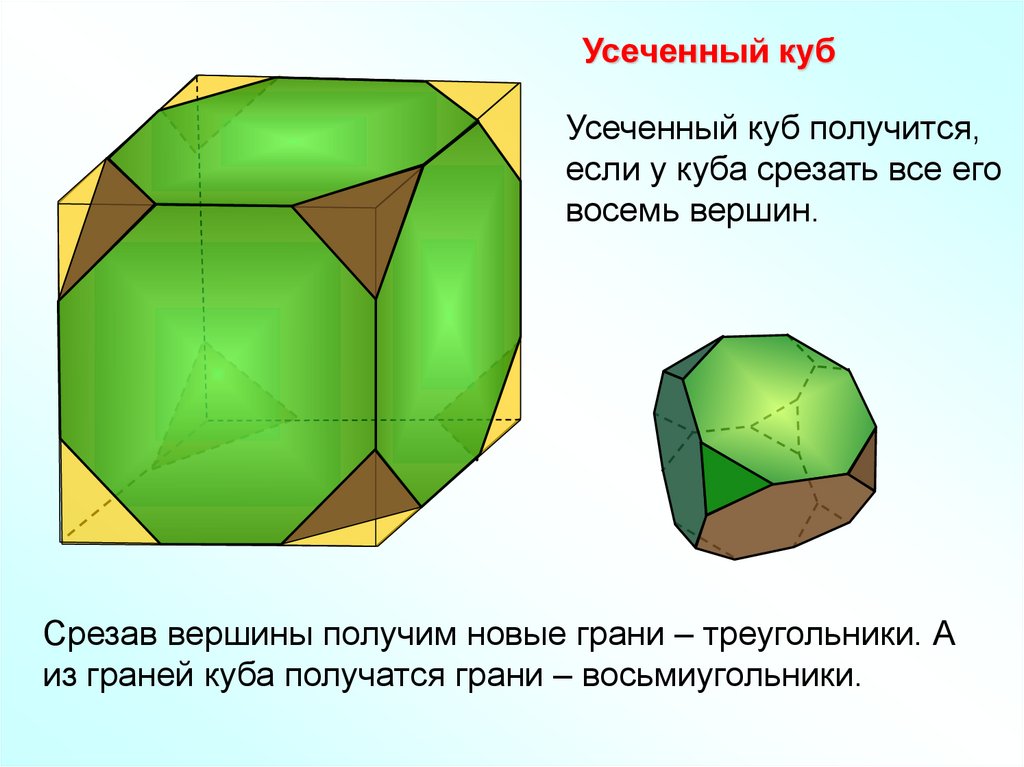
Усеченный кубУсеченный куб получится,
если у куба срезать все его
восемь вершин.
Срезав вершины получим новые грани – треугольники. А
из граней куба получатся грани – восьмиугольники.
17.
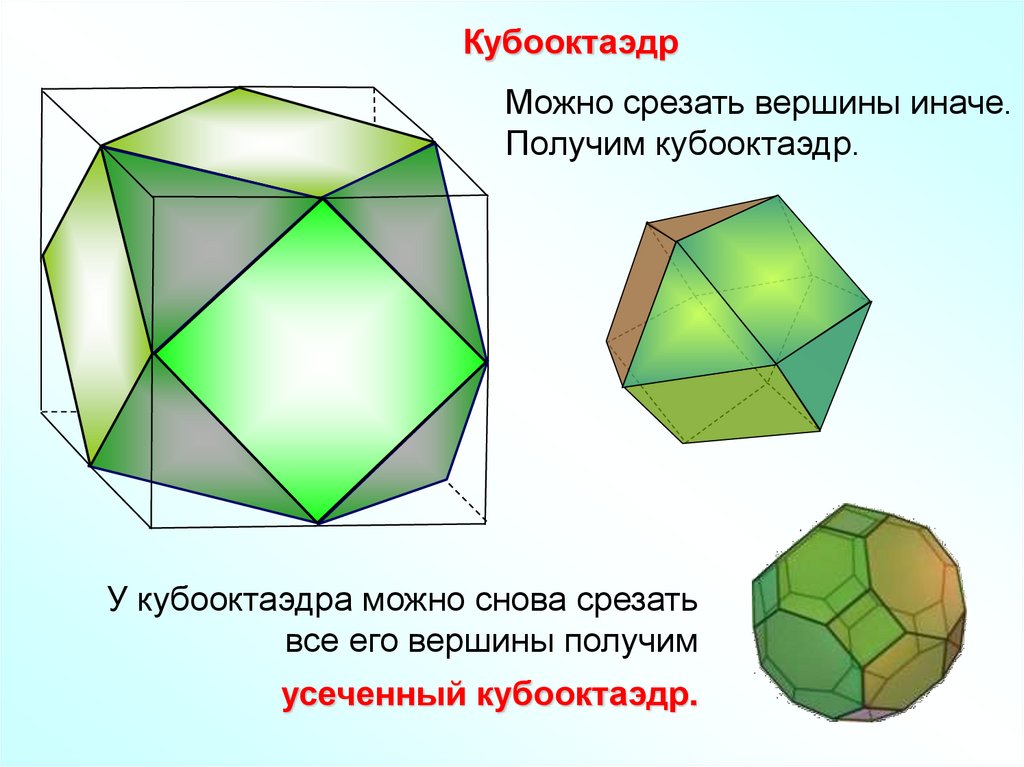
КубооктаэдрМожно срезать вершины иначе.
Получим кубооктаэдр.
У кубооктаэдра можно снова срезать
все его вершины получим
усеченный кубооктаэдр.
18.
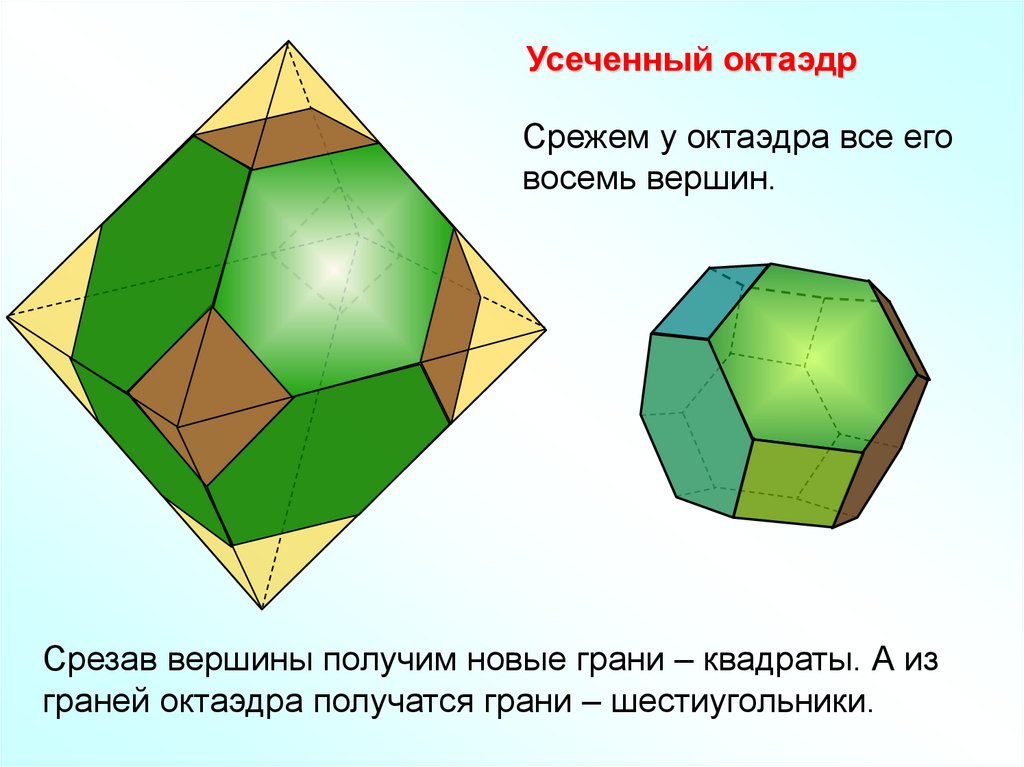
Усеченный октаэдрСрежем у октаэдра все его
восемь вершин.
Срезав вершины получим новые грани – квадраты. А из
граней октаэдра получатся грани – шестиугольники.
19.
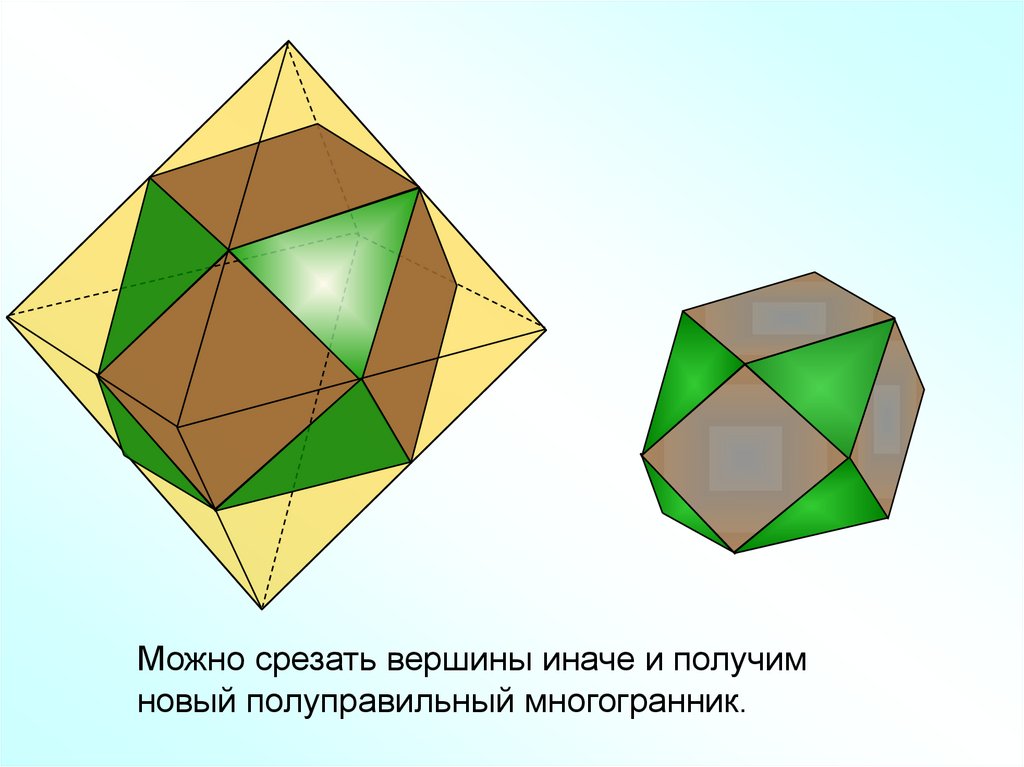
Можно срезать вершины иначе и получимновый полуправильный многогранник.
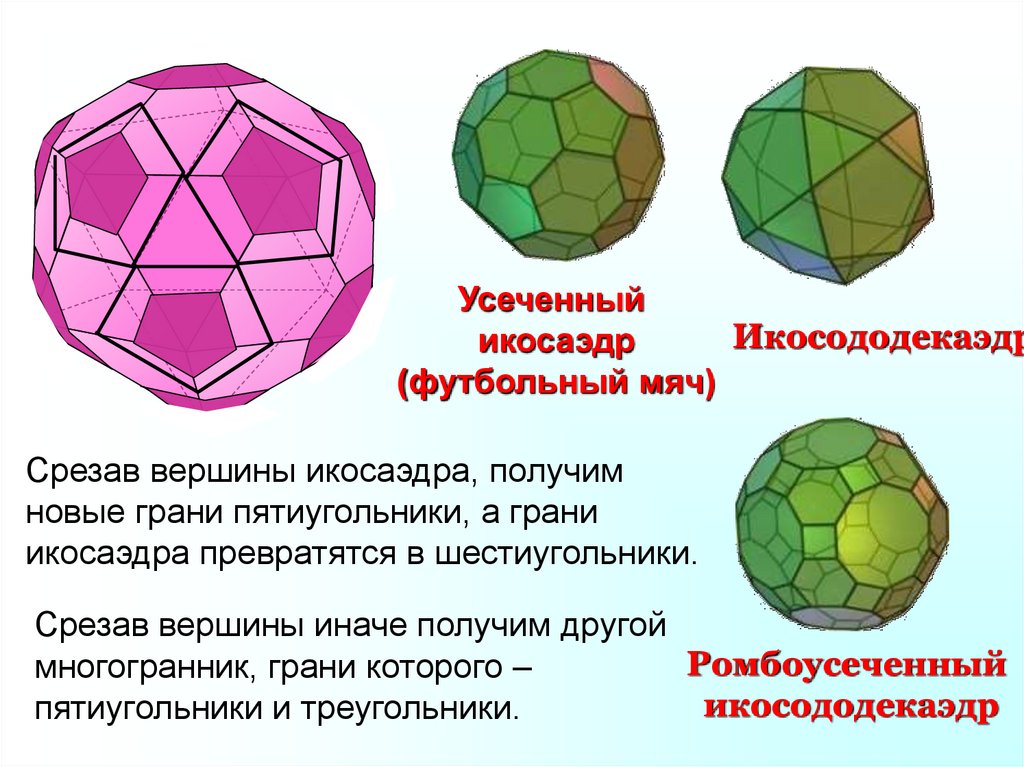
20.
УсеченныйИкосододекаэдр
икосаэдр
(футбольный мяч)
Срезав вершины икосаэдра, получим
новые грани пятиугольники, а грани
икосаэдра превратятся в шестиугольники.
Срезав вершины иначе получим другой
Ромбоусеченный
многогранник, грани которого –
икосододекаэдр
пятиугольники и треугольники.
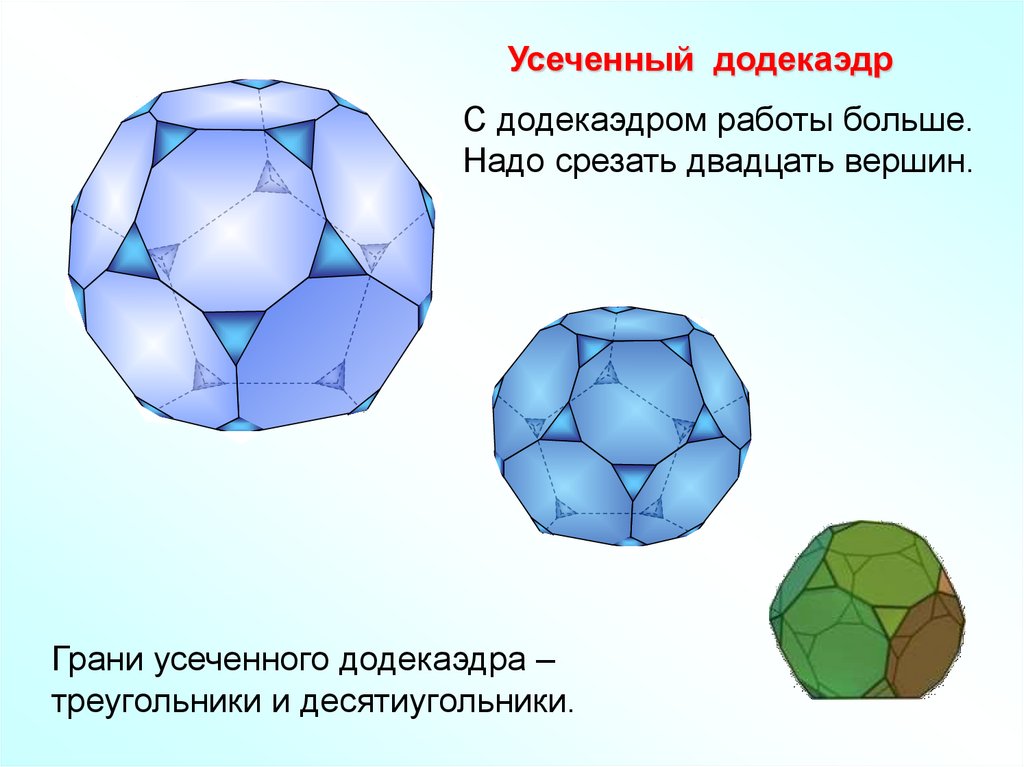
21.
Усеченный додекаэдрС додекаэдром работы больше.
Надо срезать двадцать вершин.
Грани усеченного додекаэдра –
треугольники и десятиугольники.
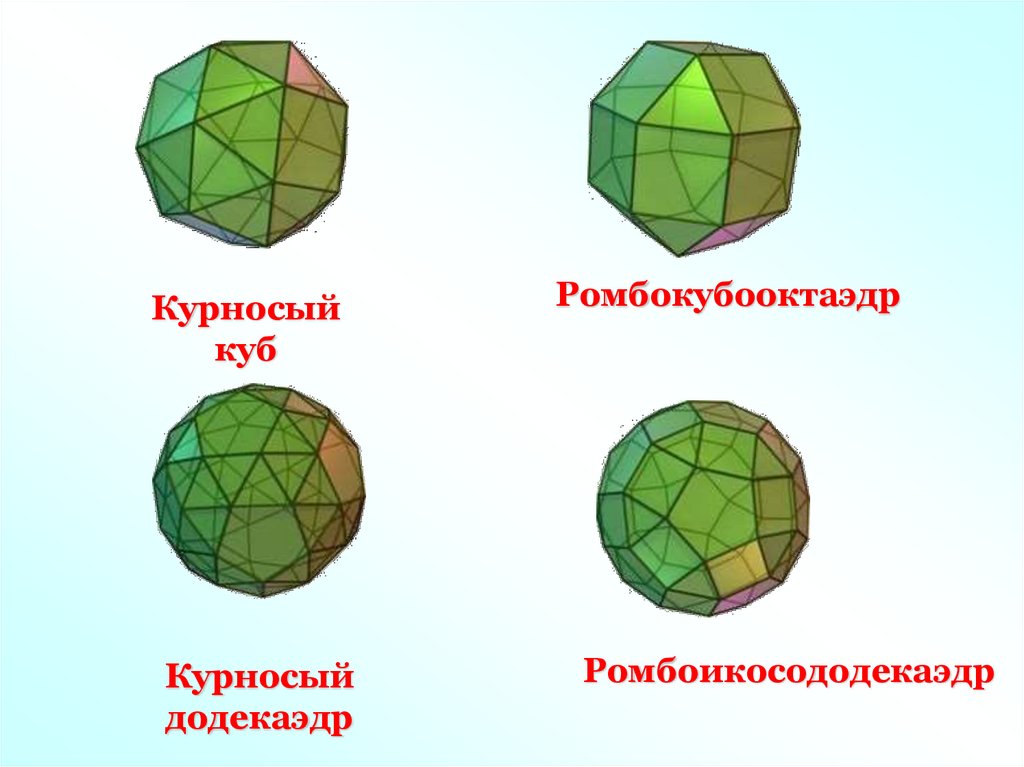
22.
Курносыйкуб
Курносый
додекаэдр
Ромбокубооктаэдр
Ромбоикосододекаэдр
23. Ученые, внесшие вклад в изучение правильных многогранников.
24.
В своих философскихтеориях
правильные многогранники
использовали:
Кеплер
Архимед
Евклид
Пифагор
Платон
25. Теорема Эйлера
Леонард Эйлер(1707 – 1783 гг.)
немецкий математик , физик и
астроном
Теорема:
Для любого выпуклого многогранника число вершин (В),
число рёбер (Р) и граней (Г), связаны формулой:
В-Р+Г=2
26.
«Сумма числа граней ивершин равна числу рёбер,
увеличенному на 2», т.е.
Г + В = Р + 2. Эту формулу
называют
Эйлерова
характеристика.
1640 г. формула
подмечена Р. Декартом.
1752 г. вновь открыта
Эйлером, с тех пор и
носит его имя.
27. МНОГОГРАННИКИ В ПРИРОДЕ
28. Александрийский Маяк
В 285 году до н.э. на острове Фаросархитектор Сострат Книдский
приступил к строительству маяка. Маяк
строился пять лет и получился в виде
трехэтажной башни высотой 120
метров. В основании он был квадратом
со стороной тридцать метров, первый
60-метровый этаж башни был сложен из
каменных плит и поддерживал 40метровую восьмигранную башню,
облицованную белым мрамором. На
третьем этаже, в круглой, обнесенной
колоннами башне, вечно горел
громадный костер, отражавшийся
сложной системой зеркал.
29. Висячие сады Семирамиды
Дворец Навуходоносора былпостроен для его жены
Семирамиды на обширной
кирпичной площадке, высоко
поднимавшейся над
окружающей местностью. Пять
дворов следовали один за
другим с востока на запад, во
дворы выходили двери
многочисленных комнат. Фасад
украшали стройные желтые
колонны с голубыми завитками.
Окон не было, и свет проникал
через три широкие двери.
Висячие сады украшали северозападную часть дворца. На
сводчатых арках из кирпича
были расположены террасы,
напоминающие уступы гор.
Поверх кирпичей залит
асфальт, на нем – свинцовые
плиты, а на них насыпан слой
плодородной земли и посажены
деревья, кусты и цветы. Издали
кажется, что эти сады как бы
висят в воздухе.
30. Египетские Пирамиды
Они словно вырастают изпесков пустыни колоссальные,
величественные,
подавляющие человека
необычайными размерами и
строгостью очертаний. Стоя у
подножия пирамиды, трудно
себе представить, что эти
огромные каменные горы
созданы руками людей. А
между тем они были
действительно сложены из
отдельных каменных глыб,
как в наше время дети
складывают пирамиды из
кубиков.
31. Галикарнасский мавзолей
Лучшие архитекторы того временипостроили мавзолей в виде почти
квадратного здания, первый этаж
которого был собственно
усыпальницей. Снаружи эта
громадная погребальная камера,
площадью 5000 кв. метров и
высотой около 20 метров, была
обложена отесанными и
отполированными плитами белого
мрамора. Во втором этаже,
окруженном колоннадой,
хранились жертвоприношения,
крышей же мавзолея служила
пирамида.
32.
Скелет одноклеточного организмафеодарии по форме
напоминает икосаэдр . Из всех
многогранников с тем же
числом граней именно
икосаэдр имеет наибольший
объём при наименьшей
площади поверхности. Это
свойство помогает морскому
организму преодолевать
давление водной толщи.
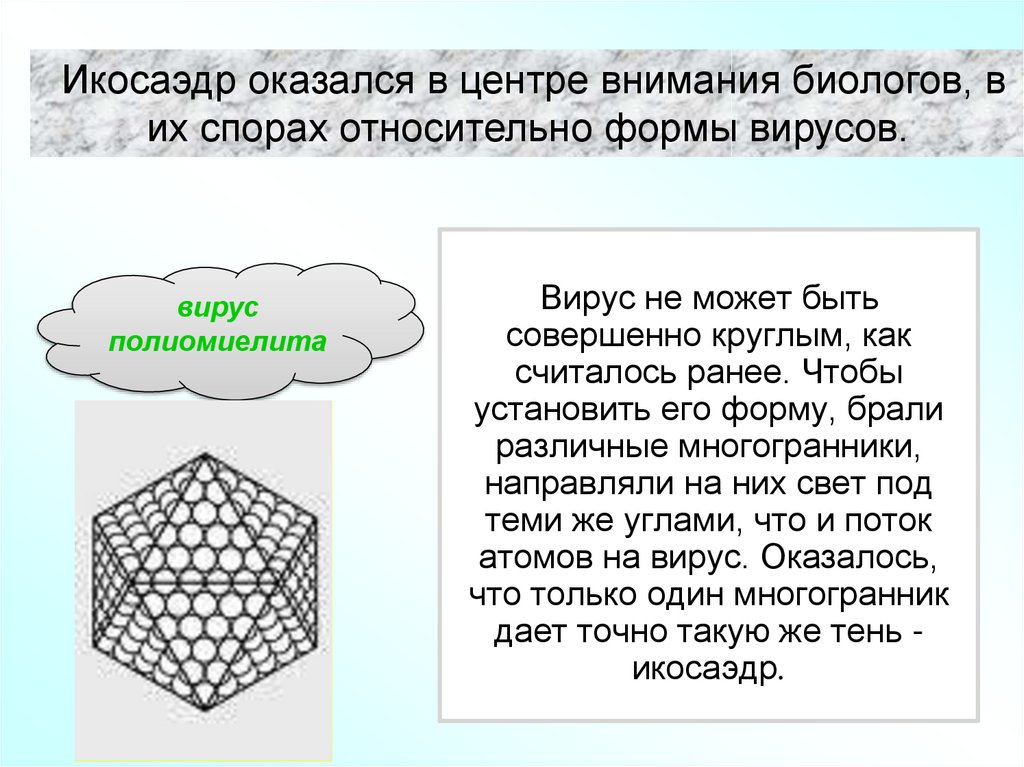
33.
Икосаэдр оказался в центре внимания биологов, вих спорах относительно формы вирусов.
вирус
полиомиелита
Вирус не может быть
совершенно круглым, как
считалось ранее. Чтобы
установить его форму, брали
различные многогранники,
направляли на них свет под
теми же углами, что и поток
атомов на вирус. Оказалось,
что только один многогранник
дает точно такую же тень икосаэдр.
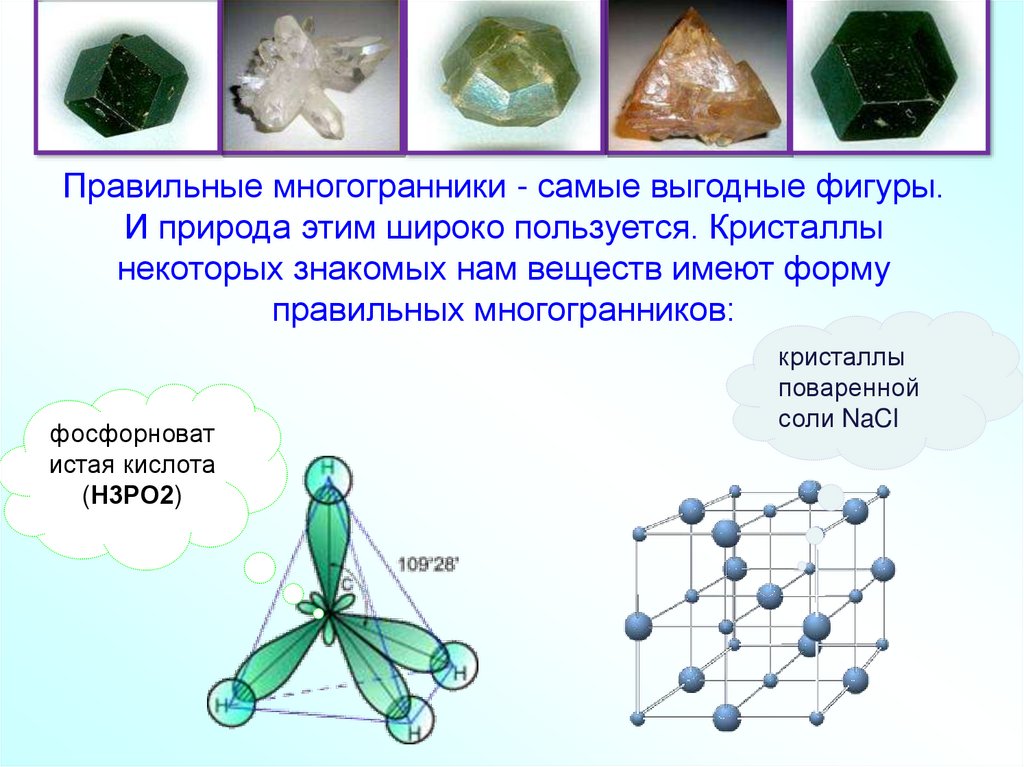
34. Чудо природы – кристаллы
Правильные многогранники - самые выгодные фигуры.И природа этим широко пользуется. Кристаллы
некоторых знакомых нам веществ имеют форму
правильных многогранников:
фосфорноват
истая кислота
(Н3РО2)
кристаллы
поваренной
соли NaCl
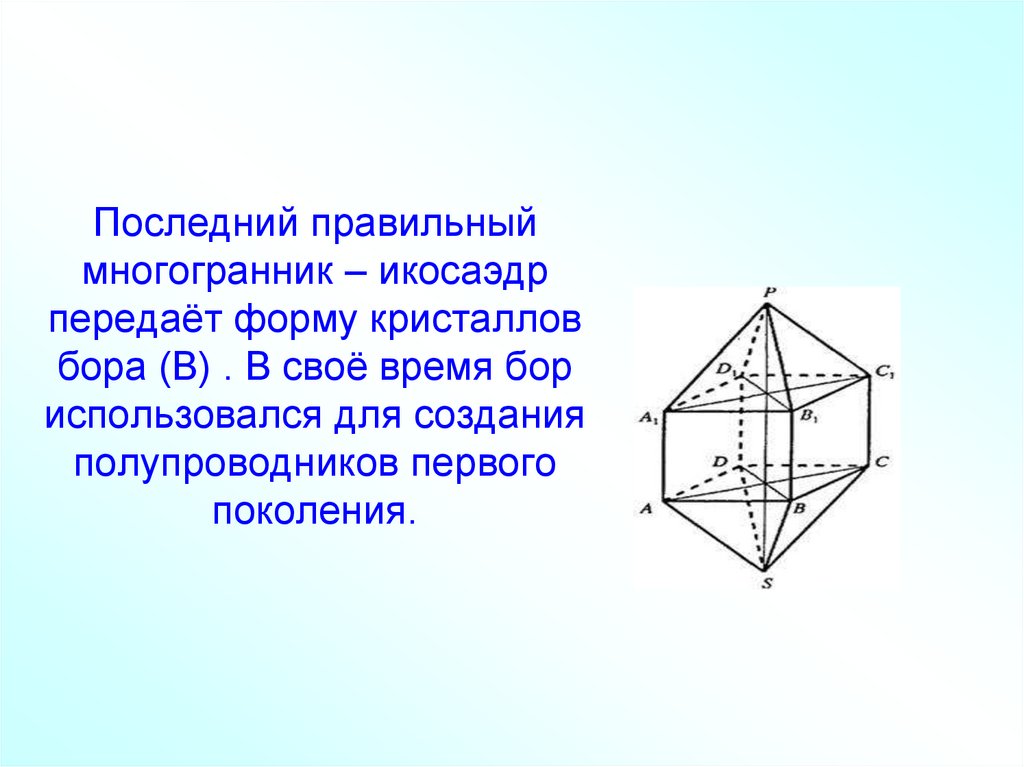
35. Последний правильный многогранник – икосаэдр передаёт форму кристаллов бора (В) . В своё время бор использовался для создания
полупроводников первогопоколения.
36. Многогранники в искусстве
В эпоху Возрождениябольшой интерес к
формам правильных
многогранников проявили
скульпторы. Знаменитый
художник, увлекавшийся
геометрией Альбрехт
Дюрер (1471- 1528) , в
известной гравюре
''Меланхолия '‘ на
переднем плане изобразил
додекаэдр.
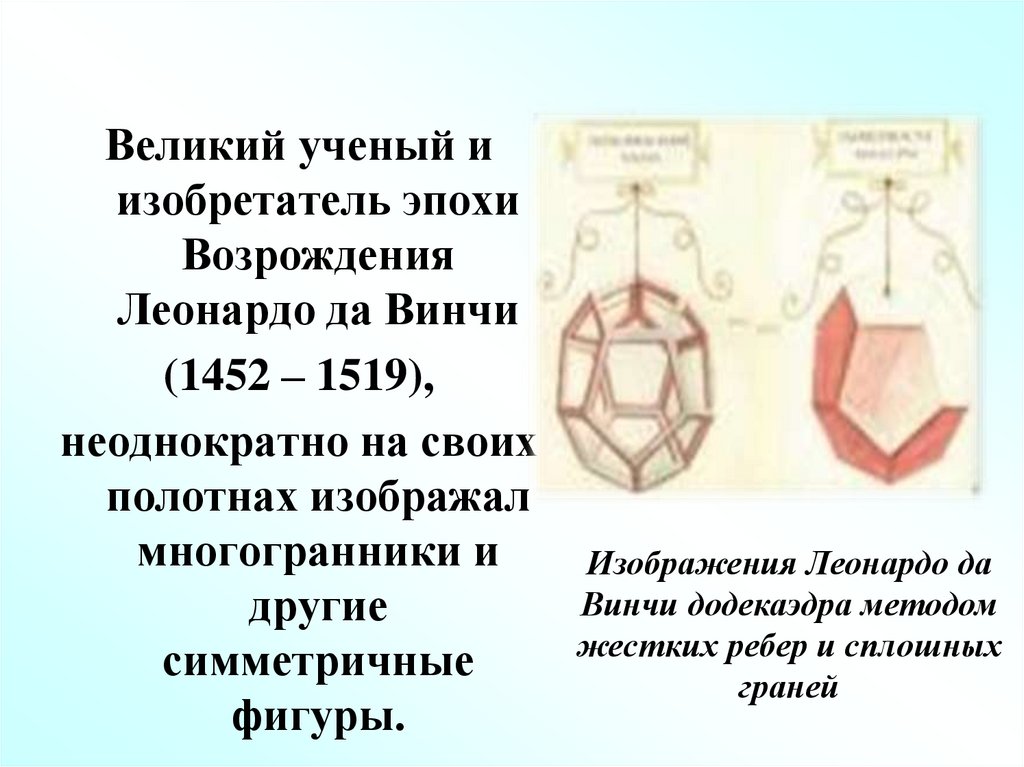
37.
Великий ученый иизобретатель эпохи
Возрождения
Леонардо да Винчи
(1452 – 1519),
неоднократно на своих
полотнах изображал
многогранники и
другие
симметричные
фигуры.
Изображения Леонардо да
Винчи додекаэдра методом
жестких ребер и сплошных
граней
38.
В список крупнейшихмастеров эпохи
Возрождения, часто
изображавших и
глубоко изучивших
геометрию
многогранников
кроме Леонардо да
Винчи можно по праву
внести:
Альбрехта Дюрера
(1471 – 1528)
Пьеро де ла Франческа
(около 1420 – 1492)
39.
МногогранникАльбрехта Дюрера
(1471 – 1528)
Картина Сальвадора Дали
(1904 – 1989)
«Тайная вечеря». XX век.
40.
• Интереснымипредставители
правильных
многогранников
являются механические
головоломки, созданные
венгерским
преподавателем
архитектуры Эрнё
Рубиком «Кубик
Рубика»(гексаэдр),
составленный из 26
кубов, и «Пирамидка
Мефферта»(тетраэдр),
созданная русским
инженером А. А.
Ордынцовым.
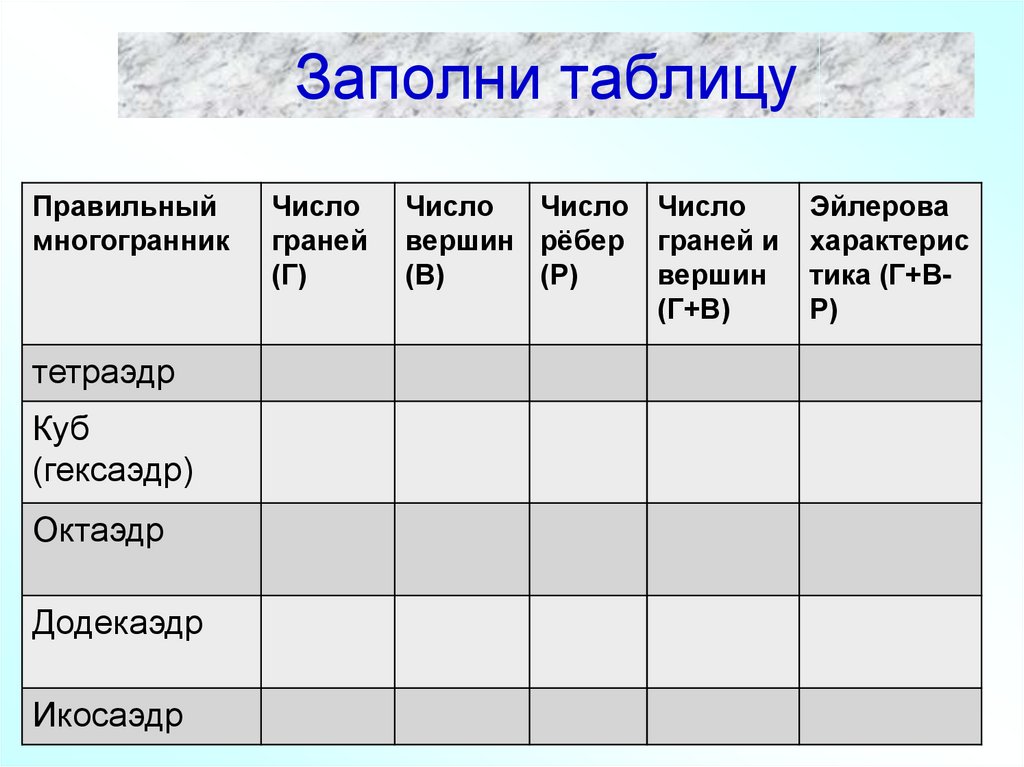
41. Заполни таблицу
Правильныймногогранник
тетраэдр
Куб
(гексаэдр)
Октаэдр
Додекаэдр
Икосаэдр
Число
граней
(Г)
Число
Число Число
вершин рёбер граней и
(В)
(Р)
вершин
(Г+В)
Эйлерова
характерис
тика (Г+ВР)






















 Математика
Математика