Логические основы компьютерной техники. Булева алгебра

1. Логические основы компьютерной техники

ЛОГИЧЕСКИЕ ОСНОВЫ
КОМПЬЮТЕРНОЙ ТЕХНИКИ
2016
Парамонов А.И.

2. Что такое Булева алгебра !?

2
АЛГЕБРА – …раздел
???
БУЛЕВА АЛГЕБРА – …мат.???аппарат,
математики,
посвященный
изучению операций над элементами
множеств, которые могут так или иначе
обобщать множества чисел, а операции
— обобщать сложение и умножение.
в котором
операции выполняются не
над
числами,
а
над
высказываниями,
представленными двоичными
переменными.

3.

3
В обычной алгебре (арифметической)
над переменными (чаще это числа)
выполняются операции сложения /
вычитания, умножения / деления и т. д.
В булевой алгебре основными являются
только три операции:
дизъюнкция, конъюнкция, инверсия.

4. Операция дизъюнкции

4
Аксиомы:
0+0 = 0;
0+1 = 1;
1+0 = 1;
1+1 = 1.

5. Операция конъюнкции

5
Аксиомы:
0•0 = 0;
0•1 = 0;
1•0 = 0;
1•1 = 1.

6. Инверсия

6
Аксиомы:

7. Полный список аксиом :

7

8. Формы представления булевых функций

8
Булевы формулы могут быть записаны
либо в виде дизъюнкции, либо в виде
конъюнкции каких-либо выражений.
В первом случае говорят о
ДИЗЪЮНКТИВНОЙ ФОРМЕ,
во втором— о КОНЪЮНКТИВНОЙ ФОРМЕ.

9. Формы представления булевых функций

9
ЭЛЕМЕНТАРНАЯ КОНЪЮНКЦИЯ (ЭК) –
логическое произведение любого конечного
числа различных между собой булевых
переменных, взятых со знаком инверсии или
без него.
ЭЛЕМЕНТАРНАЯ ДИЗЪЮНКЦИЯ (ЭД) –
логическая сумма любого конечного числа
различных между собой булевых переменных,
взятых со знаком инверсии или без него.

10. Нормальные формы

10
ДИЗЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА
(ДНФ)
– булева формула, которая записана в виде
дизъюнкции выражений, каждое из которых
представляет
собой
либо
отдельный
аргумент (с инверсией или без инверсии),
либо конъюнкцию некоторых аргументов.
– дизъюнкция конечного числа ЭК.

11. Нормальные формы

11
КОНЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА
(КНФ)
– булева формула, которая записана в виде
конъюнкции выражений, каждое из которых
представляет собой либо отдельный
аргумент (с инверсией или без инверсии),
либо дизъюнкцию некоторых аргументов.
– конъюнкция конечного числа ЭД.

12. Инвертирование сложных выражений

12
Правило:
Чтобы найти инверсию, необходимо
знаки умножения заменить знаками
сложения, а знаки сложения — знаками
умножения и поставить инверсии над
каждой переменной.
(независимо от того, есть над
переменными знаки отрицания или нет)

13. МИНТЕРМЫ

13
Функции, которые принимают единичное
значение только на одном наборе
называются
минимальными термами,
или — МИНТЕРМАМИ
(иногда конституентами единицы).

14. МИНТЕРМЫ

14
Минтермом n переменных называется
такая их конъюнкция, в которую каждая
переменная входит только один раз в
прямой или инверсной форме.
Обозначаются минтермы буквой m с
десятичным индексом, являющимся номером
минтерма.
mi

15.

15
Свойство:
конъюнкция
любых
двух
различных
минтермов, зависящих от одних и тех же
аргументов, тождественно равна нулю.

16. МАКСТЕРМЫ

16
Макстермом n переменных называется
такая их дизъюнкция, в которую каждая
переменная входит только один раз в
прямой или инверсной форме.
Макстерм (конституента нуля) — это булева
функция, которая принимает единичное
значение на всех наборах, за исключением
одного.

17. МАКСТЕРМЫ

17
Макстермы
обозначают
большой
буквой M с десятичными индексами (по
аналогии с обозначением минтермов).
Mi
СВОЙСТВО:
дизъюнкция
любых
двух
различных
макстермов, зависящих от одних и тех же
аргументов, равна единице.

18. Связь между индексами минтермов и макстермов :

18

19. Совершенные нормальные формы

19
СОВЕРШЕННАЯ КОНЪЮНКТИВНАЯ
НОРМАЛЬНАЯ ФОРМА (СКНФ)
СОВЕРШЕННАЯ ДИЗЪЮНКТИВНАЯ
НОРМАЛЬНАЯ ФОРМА (СДНФ)

20. СОВЕРШЕННАЯ ДИЗЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА – это

20
ДНФ, в которой все конъюнкции
имеют ранг n
дизъюнкция минтермов n аргументов
дизъюнкцию простых конъюнкций
простые конъюнкции содержат все переменные в
своей прямой или инверсной форме

21.

21
y = х1δ1 х2δ2 х3δ3... х(n–1)δ(n–1) хnδn ,
xi
δi
xi , если δi 1,
x i , если δi 0.

22.

22
Всякая булева функция для заданного
числа аргументов представима в виде
суммы минтермов единственным образом.
Поэтому СДНФ называют
стандартной формой, или канонической.

23. СОВЕРШЕННАЯ КОНЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА – это

23
КНФ, в которой все дизъюнкции имеют
ранг n
конъюнкция макстермов n аргументов
конъюнкция простых дизъюнкций.
простая дизъюнкция – дизъюнкция переменных
или их отрицаний

24.

24
y = (х1δ1 + х2δ2 +х3δ3 + ... + х(n–1)δ(n–1) + хnδn),
xi
δi
xi , если δi 1,
x i , если δi 0.

25. Карта Вейча

25
её модификацию называют диаграммой Карно
На рис.1 приведены минтермы функции от двух
переменных А и В.
На рис.2 указаны десятичные номера минтермов.

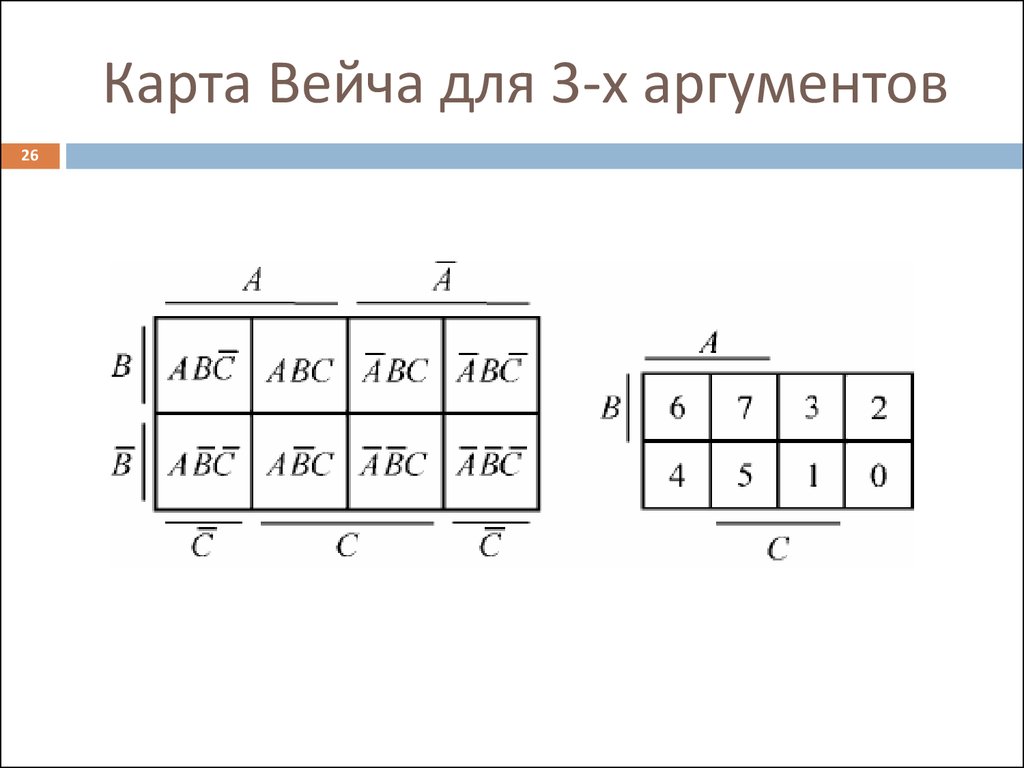
26. Карта Вейча для 3-х аргументов

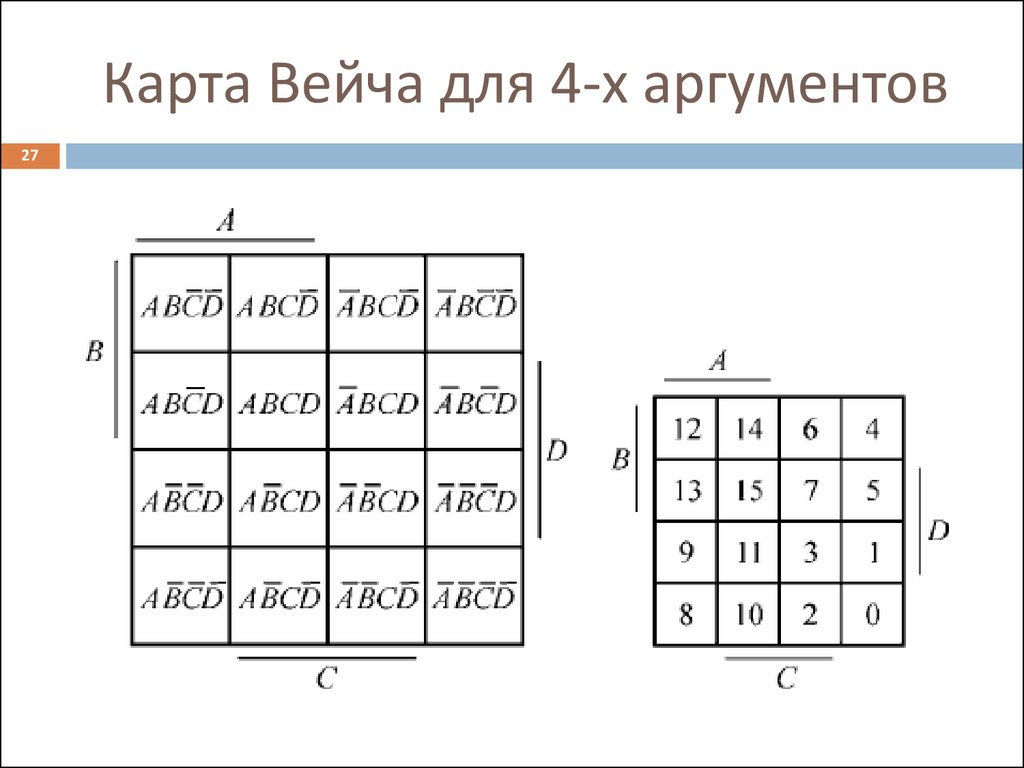
26

27. Карта Вейча для 4-х аргументов

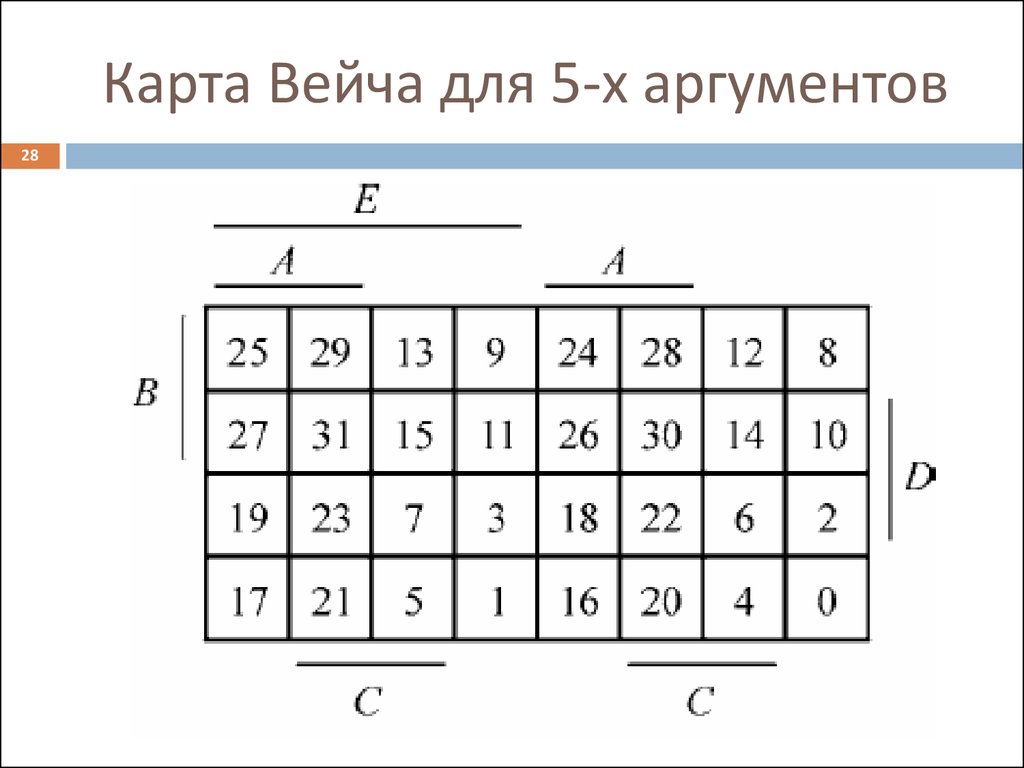
27

28. Карта Вейча для 5-х аргументов

28

29. Нанесение функций на карту Вейча

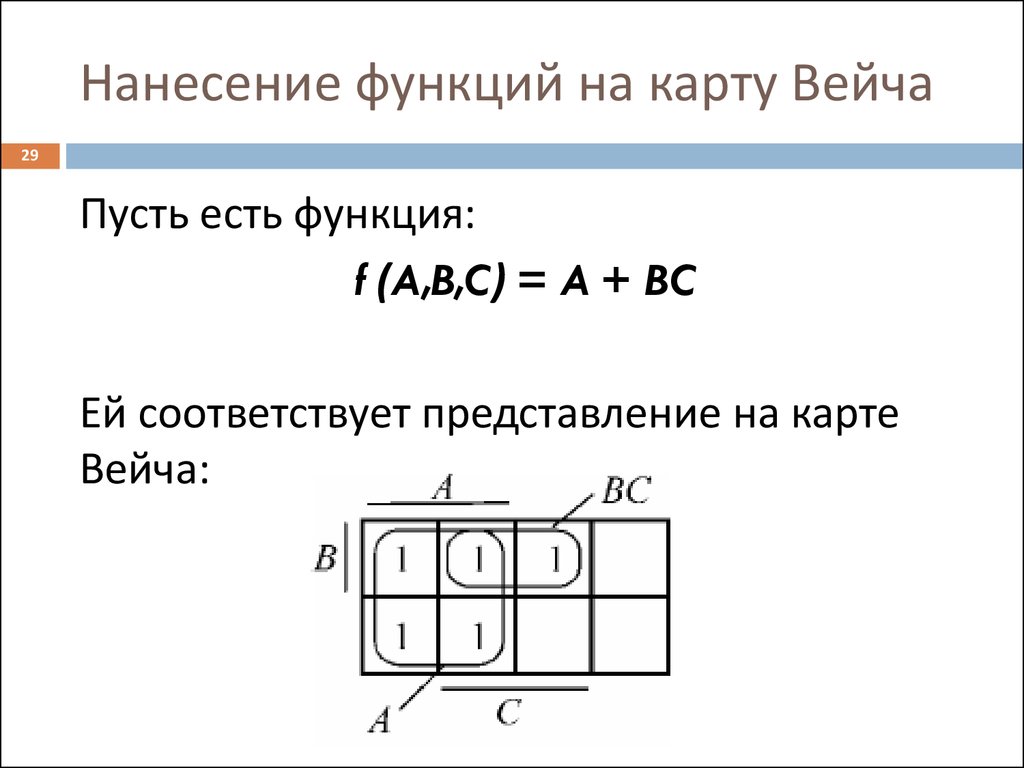
29
Пусть есть функция:
f (A,B,C) = A + BC
Ей соответствует представление на карте
Вейча:

30. Минимальная ДНФ (МДНФ)

30
МДНФ
булевой функции называется
ДНФ, которая содержит наименьшее
число букв в записи (по отношению ко
всем другим ДНФ этой функции).

31. Импликанта булевой функции

31
Функция g(x 1 , …, x n ) называется
импликантой функции f(x 1 , …, x n ),
если для любого набора аргументов, на
котором g=1, справедливо что f=1.

32.

32
Импликанта булевой функции, которая
представлена
элементарной
конъюнкцией,
называется простой, если никакая ее часть
больше не является импликантой этой функции.
Т.Е. простая импликанта – это такая, к которой
нельзя применить операцию склеивания.

33. Пример импликант:

33
Пусть дана функция:
f = AB + BC.
Представим её в СДНФ:
f = (3,6,7) .
Эта функция содержит три минтерма.
Из них можно образовать семь различных
функций, каждая из которых является
импликантой функции f.

34. Импликанты ф-ции f = AB + BC

34

35. Методы минимизации функций алгебры логики

35
минимизация методом Квайна;
минимизация с использованием карт Карно;
минимизация не полностью определенных (частичных)
функций;
минимизация КНФ;
минимизация методом кубического задания функций
алгебры логики;
минимизация методом Квайна–Мак–Класски;
минимизация с использованием алгоритма извлечения
(Рота);
минимизация ФАЛ методом преобразования логических
выражений.

36. минимизация методом Квайна

36
Основу метода составляет теорема
склеивания, которая применяется к каждой
паре минтермов заданной функции.
Например:
f (A,B,C,D) = (0, 1, 3, 6, 7, 8, 12, 13, 14, 15)

37.

37

38.

38
Выражение, полученное методом Квайна,
называется сокращённой дизъюнктивной
нормальной формой заданной функции,
а каждая его конъюнкция называется
простой импликантой.

39.

39
Для всякой булевой функции
существует единственная
сокращённая ДНФ

40. Найти методом Квайна минимальное выражение для функции y

40
y x1 x 2 x3 x4 x1 x2 x 3 x 4 x1 x2 x 3 x4 x1 x2 x3 x 4 x1 x2 x 3 x 4 x1 x2 x 3 x4
x1 x 2 x3 x 4 x1 x2 x3 x 4 x1 x 2 x3 x4 x1 x 2 x3 x 4 .

41. 1–й этап

41
1
2
3
4
5
6
y x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4
7
8
9
10
1
2
3
1 9
1 10
2 5
x1 x 2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x2 x3 x4 x1 x2 x3 x2 x3 x4
4
5
6
7
8
9
10
11
12
2 8
3 5
3 6
4 5
4 8
4 10
7 8
7 9
7 10
x1 x2 x4 x1 x2 x3 x2 x3 x4 x1 x2 x4 x2 x3 x 4 x1 x3 x4 x1 x3 x4 x1 x2 x3 x2 x3 x4
1
2
3
4
5
6
7
8
1 12
2 11
3 6
3 8
4 7
8 12
9 10
5
1
2
3
x2 x3 x2 x3 x2 x3 x2 x4 x2 x4 x3 x4 x3 x4 x1 x2 x3 x2 x3 x2 x3 x2 x4
4
5
x3 x4 x1 x2 x3 y тупиковая форма.

42. 2–й этап - Импликантная таблица

1
_
х2х3
_
х2х3
_
х2х4
_
х3х4
_ _
х1х2х3
2
*
3
*
*
4
*
*
5
*
*
*
6
*
7
*
*
*
*
__ _
х1х2х3х4
8
_
х1х2х3х4
_ _
х1х2х3х4
_
_
х1х2х3х4
_ _ _
х1х2х3х4
_
х1х2х3х4
_ _
х1х2х3х4
_
х1х2х3х4
__
х1х2х3х4
_ _
х1х2х3х4
2–й этап - Импликантная таблица
42
9
10
*
*
*
*
*

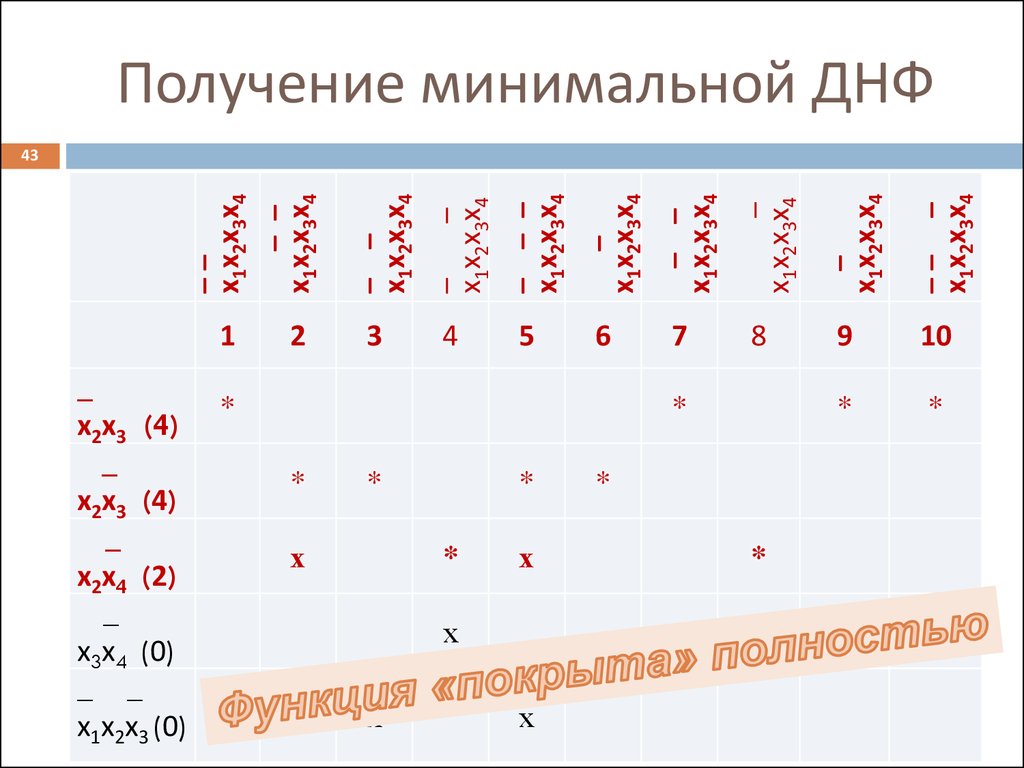
43. Получение минимальной ДНФ

1
_
х 2х 3 (4)
_
(4)
х2х33 (4)
_
(2)
х2 х44 (4)
(2)
_
(0)
х3х4 (2)
(4)
_ _
(0)
х1х2х3 (2)
2
*
3
*х
*х
4
*
*
5
*
*
х
*х
6
*
7
*х
*х
*
*
х
__ _
хх11хх222хх333хх444
8
_
хх11хх222хх333хх444
_ _
хх11хх22хх33хх44
_
_
х11х22х33х44
_ _ _
хх11хх22хх33хх44
_
хх11хх22хх33хх44
_ _
хх11хх222хх333хх444
_
х11х22х33х44
__
хх11хх222хх333хх444
_ _
хх11хх22хх33хх44
Получение минимальной ДНФ
43
9
10
*
*
*
*
*х

44. Минимальная ДНФ из 3-х импликант

44
1
2
3
y min x 2 x3 x 2 x3 x 2 x 4

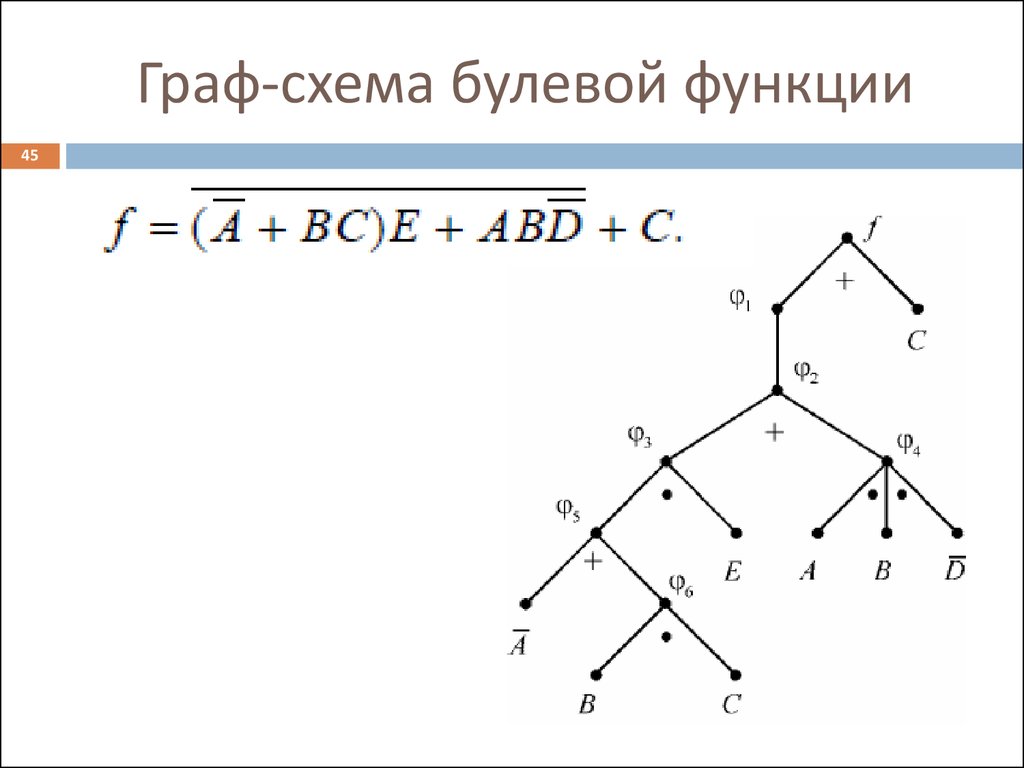
45. Граф-схема булевой функции

45

46. Формы булевых функций

46
Совершенные
Сокращенные
ДНФ
Нормальные
Тупиковые
формы
КНФ
Минимальные

47. Литература по теме:

47
Лысиков Б. Г. Арифметические и логические основы
цифровых автоматов // Минск: Высшая школа, 1980. –
268 с.
Савельев А. Я. Прикладная теория цифровых
автоматов: учебник для вузов по специальности ЭВМ //
М.: Высшая школа, 1987. – 462 с.
Шевелев Ю. П. Дискретная математика. Ч. 1: Теория
множеств. Булева алгебра Автоматизированная
технология обучения «Символ»): Учебное пособие //
Томск. гос. ун-т систем управления и
радиоэлектроники, 2003. — 118 с.