Восьмеричная и шестнадцатеричная системы счисления. «Компьютерные» системы счисления

1.

Классная работа
16.12.2021
Восьмеричная и
шестнадцатеричная системы
счисления.
«Компьютерные» системы
счисления.
МАТЕМАТИЧЕСКИЕ ОСНОВЫ
ИНФОРМАТИКИ
Урок 4
По данной теме урок 3

2.

Ключевые слова
система счисления
цифра
алфавит
позиционная система счисления
основание
развёрнутая форма записи числа
свёрнутая форма записи числа
двоичная система счисления
восьмеричная система счисления
шестнадцатеричная система счисления

3.

Вопросы и задания
Какими преимуществами и недостатками обладает
двоичная система счисления по сравнению с
десятичной?
Правило перевода натуральных двоичных чисел в
десятичную систему счисления.
Правило перевода целых десятичных чисел в двоичную
систему счисления.

4. Проверка домашнего задания

№ 11 с. 15
89
44
22
11
5
2
1
0
0
1
1
0
600 300 150 75
0
0
0
1
37
1
18
0
1
8910 10110012
9
1
4
0
2
0
1
60010 10010110002
2010 1005 501 250 125 62 31 15 7
0
1
1
0
1
201010 110110101102
0
1
1 0
3
1
1

5. Проверка домашнего задания

№ 15 с. 16
101010 2
а)
+
б)
+
11012
1101112
1010 2
в)
+
101012
1112
111002
1010 2
101002
№ 16 с. 16
а)
Х
1010 2
112
1010
1010
111102
+
б)
Х
1112
1012
111
+
111
1000112
в)
Х
1010 2
1112
1010
+ 1010
1010
10001102

6.

Восьмеричная система
счисления
Восьмеричной
системой
счисления
называется
позиционная система счисления с основанием 8.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7.
an–1an–2…a1a0 = an–1 8n–1+an–2 8n–2+…+a0 80
Пример: 10638 =1 83 +0 82+6 81+3 80=56310.
Для перевода целого восьмеричного числа в десятичную
систему счисления следует перейти к его развёрнутой
записи и вычислить значение получившегося выражения.
Для перевода целого десятичного числа в восьмеричную
систему счисления следует последовательно выполнять
деление данного числа и получаемых целых частных на 8 до
тех пор, пока не получим частное, равное нулю.

7.

Шестнадцатеричная
система счисления
Основание: q = 16.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
3АF16 =3 162+10 161+15 160 =768+160+15=94310.
Переведём десятичное число 154 в шестнадцатеричную
систему счисления
154 16
-144
9
16
10
(А)
9
0
15410 = 9А16

8.

Таблица соответствия 10-х, 2-х, 8-х и 16-х чисел от 1 до 16
Десятичная
система
Двоичная
система
Восьмеричная
система
Шестнадцатеричная
система
1
1
1
1
2
10
2
2
3
11
3
3
4
100
4
4
5
101
5
5
6
110
6
6
7
111
7
7
8
1000
10
8
9
1001
11
9
10
1010
12
A
11
1011
13
B
12
1100
14
C
13
1101
15
D
14
1110
16
E
15
1111
17
F
16
10000
20
10
17
10001
21
11
18
10010
22
12

9.

«Компьютерные» системы счисления
Двоичная система используется в компьютерной технике,
так как:
двоичные числа представляются в компьютере с
помощью простых технических элементов с двумя
устойчивыми состояниями;
представление информации посредством только двух
состояний надёжно и помехоустойчиво;
двоичная арифметика наиболее проста;
существует математический аппарат, обеспечивающий
логические преобразования двоичных данных.
Двоичный код удобен для компьютера.
Человеку неудобно пользоваться длинными и
однородными кодами.
Специалисты заменяют двоичные коды на
величины в восьмеричной или шестнадцатеричной
системах счисления.

10.

Самое главное
Система счисления — это знаковая система, в которой приняты
определённые правила записи чисел.
Система
счисления
называется
позиционной,
если
количественный эквивалент цифры в числе зависит от её положения
в записи числа.
В позиционной системе счисления с основанием q любое число
может быть представлено в виде:
Aq =±(an–1 qn–1 + an–2 qn–2 +…+ a0 q0 + a–1 q–1 +…+ a–m q–m)
Здесь:
А — число;
q — основание системы счисления;
ai — цифры, принадлежащие алфавиту данной системы счисления;
n — количество целых разрядов числа;
m — количество дробных разрядов числа;
qi — «вес» i-го разряда.

11. Задания

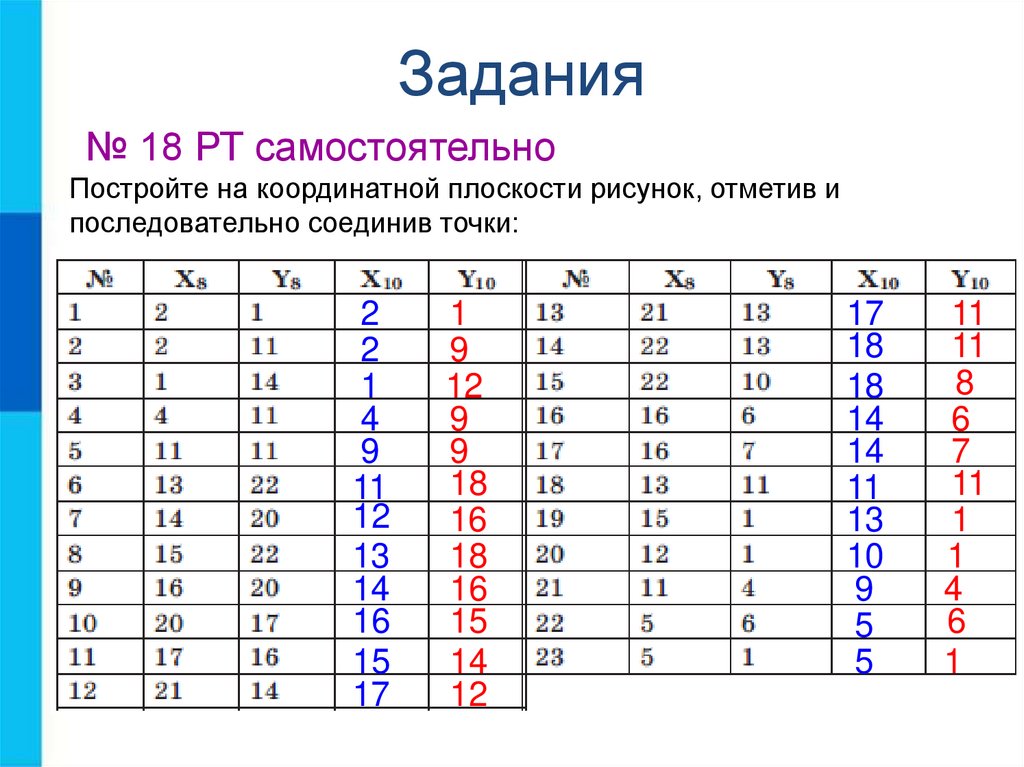
№ 18 РТ самостоятельно
Постройте на координатной плоскости рисунок, отметив и
последовательно соединив точки:
2
2
1
4
9
11
12
13
14
16
15
17
1
9
12
9
9
18
16
18
16
15
14
12
17
18
18
14
14
11
13
10
9
5
5
11
11
8
6
7
11
1
1
4
6
1

12. Задания

№ 18 РТ самостоятельно

13. Задания

№ 26 РТ
Задания
Переведите целые числа из десятичной системы счисления в
восьмеричную:

14. Задания

№ 26 РТ
Задания
Переведите целые числа из десятичной системы счисления в
восьмеричную:

15. Задания

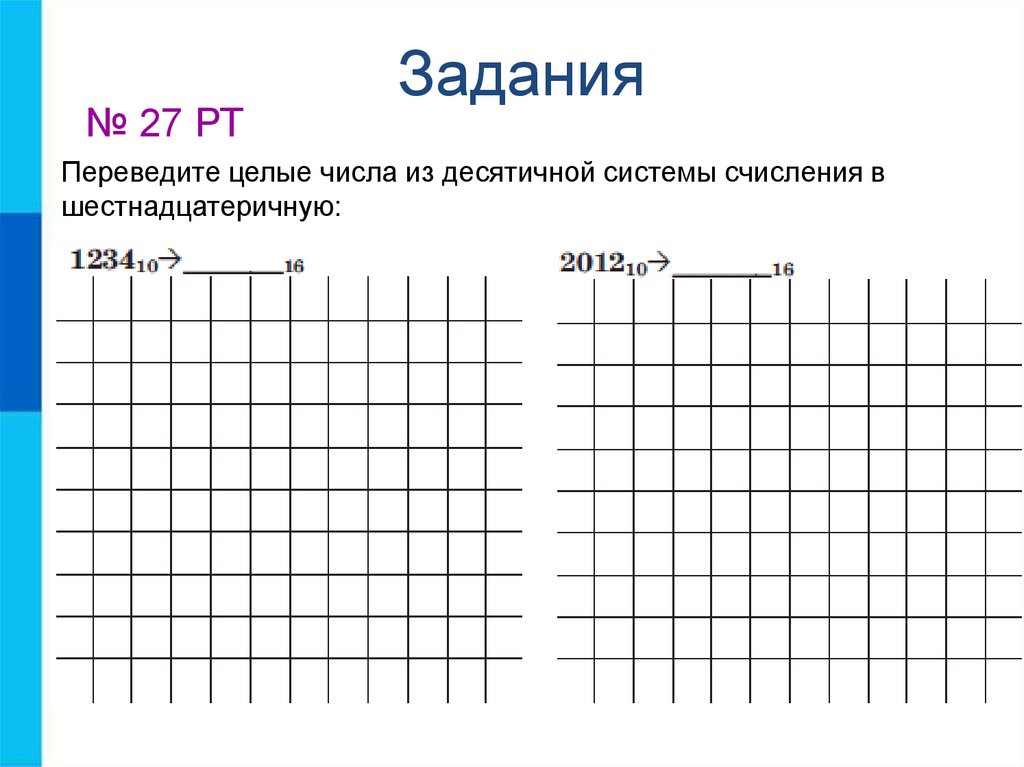
№ 27 РТ
Задания
Переведите целые числа из десятичной системы счисления в
шестнадцатеричную:

16. Задания

№ 27 РТ
Задания
Переведите целые числа из десятичной системы счисления в
шестнадцатеричную:

17. Задания

№ 31 РТ; № 20 УЧ с. 16
Разработайте таблицы сложения и умножения для
восьмеричной системы счисления.

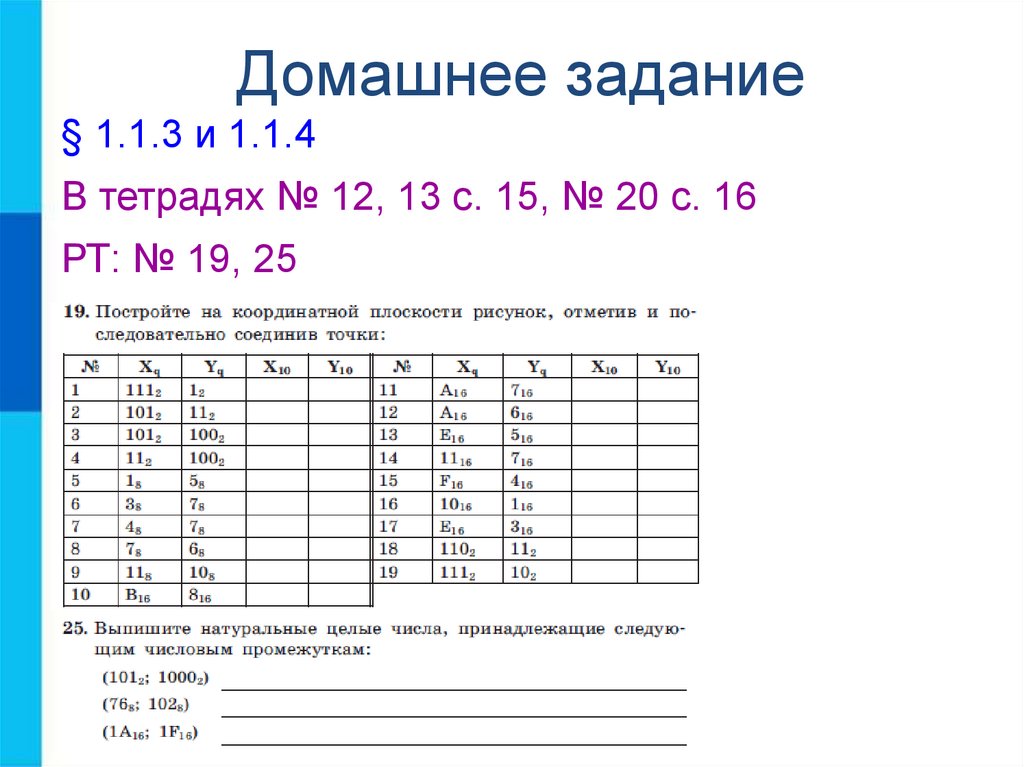
18. Домашнее задание

§ 1.1.3 и 1.1.4
В тетрадях № 12, 13 с. 15, № 20 с. 16
РТ: № 19, 25

19.

Опорный конспект
Система счисления — это знаковая система, в которой приняты
определённые правила записи чисел.
Цифры - знаки, при помощи которых записываются числа.
Алфавит - совокупность цифр системы счисления.
Система счисления
Позиционная
Двоичная
Восьмеричная
Десятичная
Непозиционная
Римская
Шестнадцатеричная
В позиционной системе счисления с основанием q любое число
может быть представлено в виде:
Aq =±(an–1* qn–1 + an–2* qn–2 +…+ a0*q0 + a–1* q–1 +…+ a–m * q–m).