Декодирование циклического кода

1. Декодирование циклического кода

Синдромы

2. Синдромные полиномы

• Синдром – это вектор длиной n – k,
равный произведению принятой
последовательности на проверочную
матрицу.
- вектор
• s = yHT
Полином
v
s( x) sv x sv 1x
s = (sv, sv – 1 , …, s0)
v 1
... s1x s0

3. Синдром

• 1
Синдром можно определить как многочлен s(x)
степени (n – k), являющийся остатком от деления
принятой последовательности
на порождающий
многочлен
s( x) rem{ y( x) / g ( x)} mod g ( x)
• Поскольку все кодовые слова делятся на g(x), то s(x),
не зависит от переданного слова, а зависит лишь от
комбинации ошибок.

4. Синдром

• 2.
Второй вид синдрома может быть введен в случае,
если порождающий многочлен является
произведением двух или большего числа
неприводимых сомножителей. Предположим, что
g ( x) g1 ( x) g 2 ( x)...g j ( x)
Тогда
s1 ( x) y ( x) mod g1 ( x),
s2 ( x) y ( x) mod g 2 ( x),
..................................
s j ( x) y ( x) mod g j ( x).
Связаны с
синдромом
s(x) через
китайскую
теорему об
остатках

5. Синдром

• 3. Третья форма синдрома состоит в том, чтобы
определить векторы форм синдромов s1, s2 ,… в виде
s1 y ( 1 ), s 2 y ( 2 ),
• где 1 – корень g1(x); 2 – корень g2(x) и т. д.
• Эта форма синдрома соответствует проверочной
матрице, задаваемой корнями (коды БЧХ, РС)

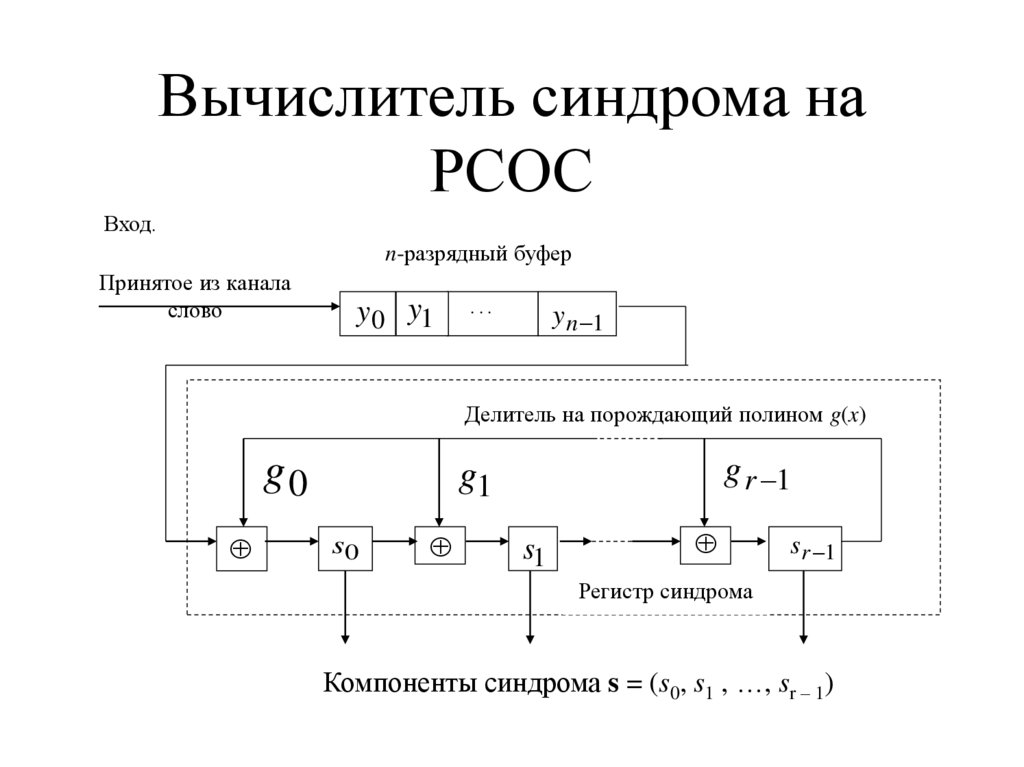
6. Вычислитель синдрома на РСОС

Вход.
n-разрядный буфер
Принятое из канала
слово
y 0 y1
...
y n 1
Делитель на порождающий полином g(x)
g0
g r 1
g1
s0
s1
sr 1
Регистр синдрома
Компоненты синдрома s = (s0, s1 , …, sr – 1)

7. Пример код Хэмминга (7,4) g(x) = x3+x2+1

Список информационных
и кодовых слов 16.20
a
Таблица соответствия
s( x) mod e( x) / g ( x)

8. Декодирование

y = 1 1 0 1 1 0 1 y(x) = x6 + x5 + x3 + x2 + 1
Вычисление синдрома
s(x) = rem{y(x) / g(x)} =
= rem{ (x6 + x5 + x3 + x2 + 1)/ g(x) = x3+x2+1)} = x2 + 1
s(x) = x2 + 1 s = 1 0 1
• Из таблицы соответствия находим
• s es = 0 0 0 1 0 0 0
• Коррекция ys = y – es mod 2 = 1 1 0 1 1 0 1 - 1 1 0 1 1 0 1 =
• = 1 1 0 0 1 0 1;
a=1100

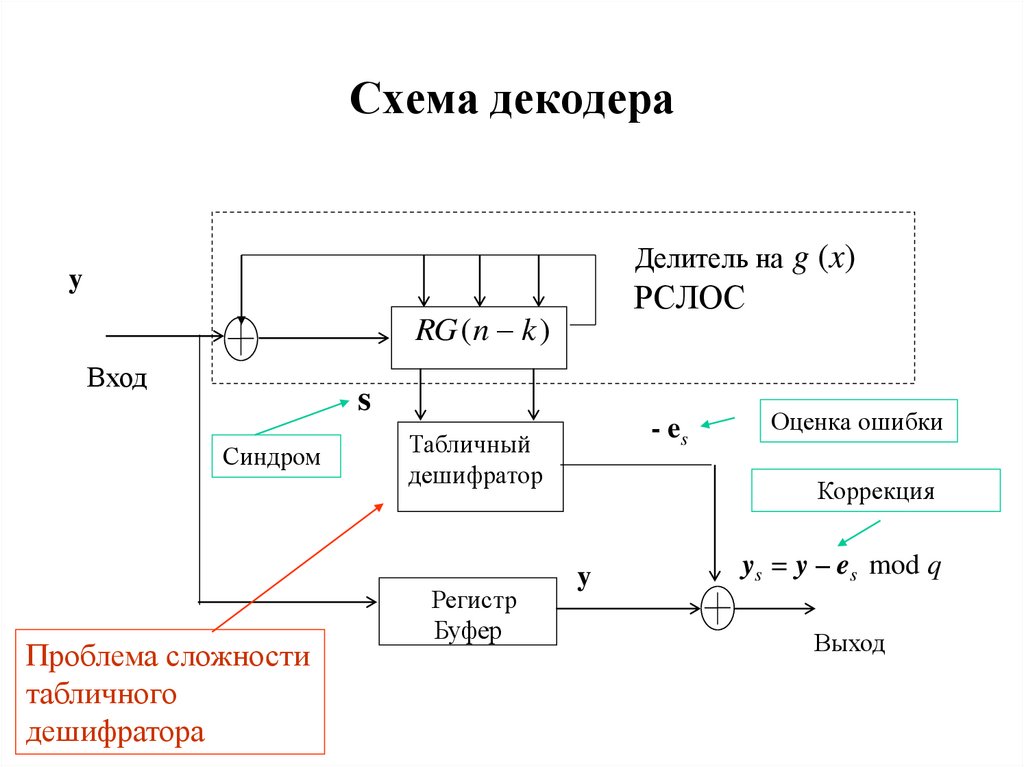
9. Схема декодера

Делитель на g (x)
y
РСЛОС
RG ( n k )
Вход
s
Синдром
Проблема сложности
табличного
дешифратора
- es
Табличный
дешифратор
Регистр
Буфер
Оценка ошибки
Коррекция
y
ys = y – es mod q
Выход

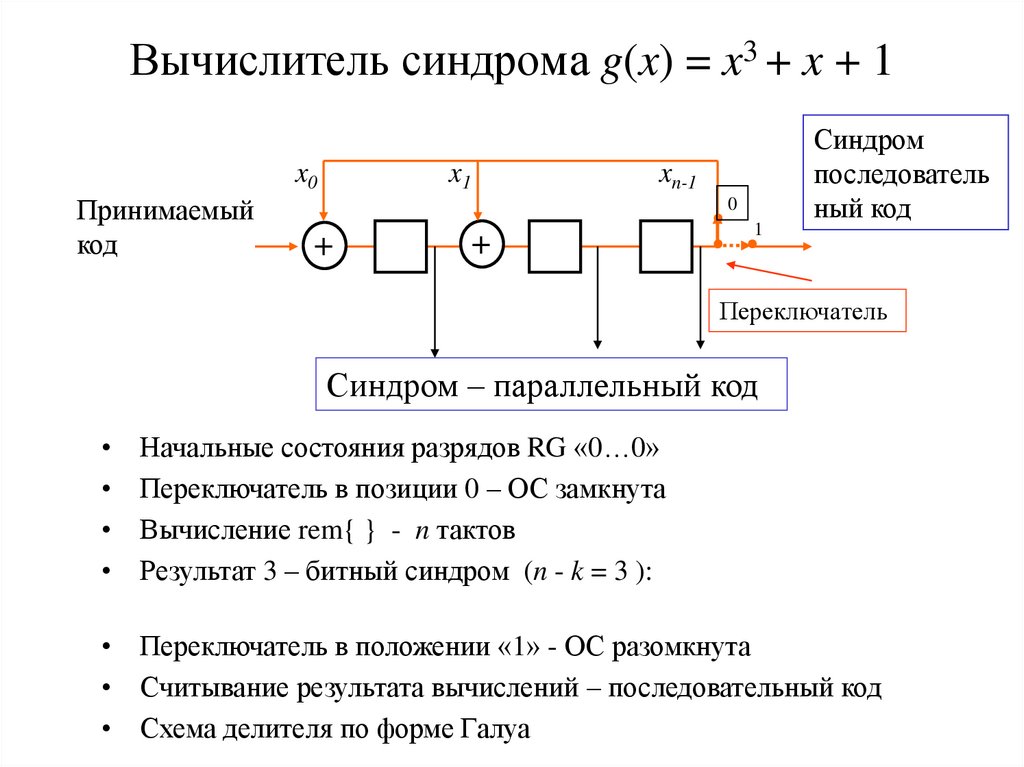
10. Вычислитель синдрома g(x) = x3 + x + 1

x0
x1
xn-1
Принимаемый
код
0
1
Синдром
последователь
ный код
Переключатель
Синдром – параллельный код
Начальные состояния разрядов RG «0…0»
Переключатель в позиции 0 – ОС замкнута
Вычисление rem{ } - n тактов
Результат 3 – битный синдром (n - k = 3 ):
• Переключатель в положении «1» - ОС разомкнута
• Считывание результата вычислений – последовательный код
• Схема делителя по форме Галуа

11. Теорема

12. Пример

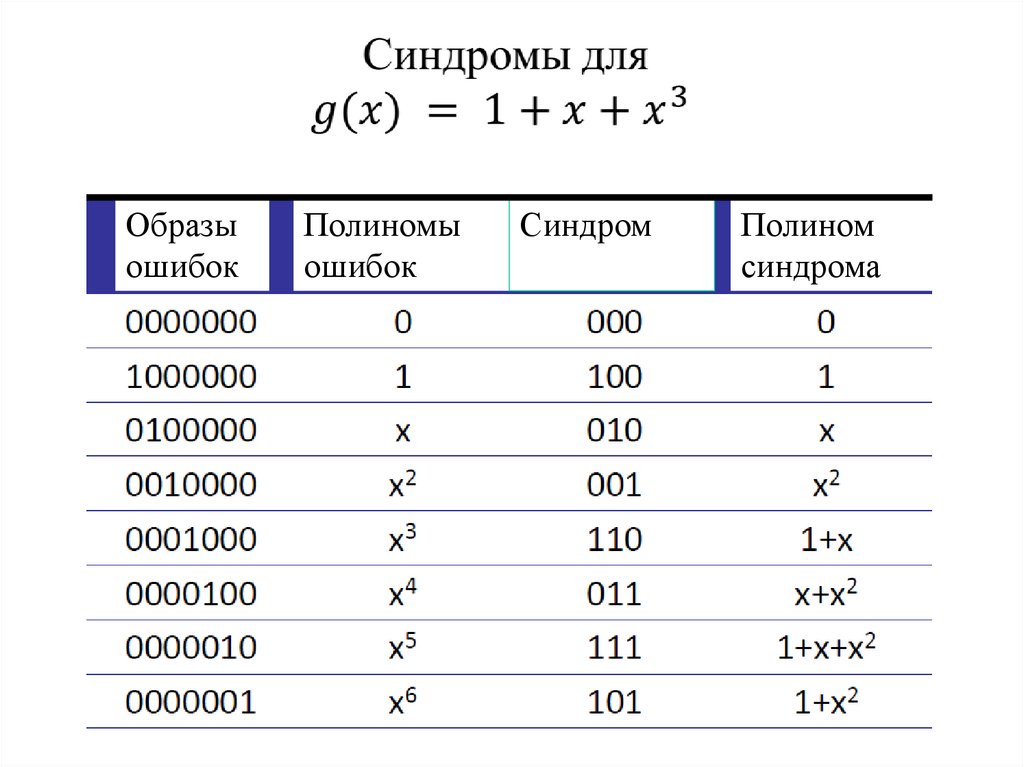
13. Синдромы для g(x) = 1+x+x^3" "

Образы
ошибок
Полиномы
ошибок
Синдром
Полином
синдрома

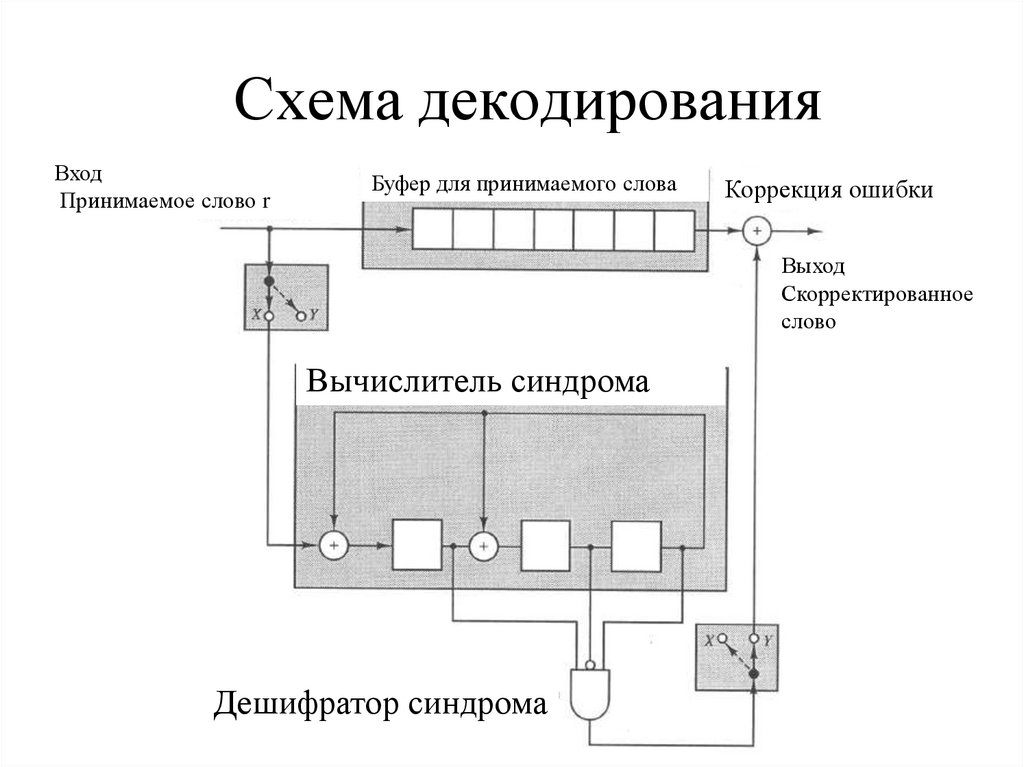
14. Схема декодирования

Вход
Принимаемое слово r
Буфер для принимаемого слова
Коррекция ошибки
Выход
Скорректированное
слово
Вычислитель синдрома
Дешифратор синдрома

15. Вопросы

•?