Комбинаторика

1.

Комбинаторика – это раздел математики, в
котором исследуются и решаются задачи выбора
элементов из исходного множества и расположения
их
в
некоторой
комбинации,
составляемой
по
заданным правилам.
Некоторые
элементы
комбинаторики
были
известны в Индии еще во II в. до н. э.
Как
научная
дисциплина,
сформировалась в XVII в.
комбинаторика

2.

Термин
"комбинаторика"
был
введён
в
математический обиход знаменитым
Готфридом
Вильгельмом
Лейбницем
В 1666 году Лейбниц опубликовал «Рассуждения о
комбинаторном искусстве».
Комбинаторику
он
понимал,
как
составляющую
любого исследования, предполагающего сначала анализ
(расчленение
целого
на
части),
а
затем
синтез
(соединение частей в целое).
Леонард Эйлер рассматривал задачи о разбиении
чисел,
о
квадратов.
построении
магических
и
латинских

3.

В 1713 году было опубликовано сочинение
Якоба
Бернулли
"Искусство
предположений",
в
котором с достаточной полнотой были изложены
известные к тому времени комбинаторные факты.
Сочинение Я. Бернулли превзошло работы его
предшественников
систематичностью,
простотой
методов, строгостью изложения и в течение XVIII века
пользовалось известностью, как учебно-справочное
издание.
Термин «тактика» ввёл в математику английский
математик Джеймс Джозеф Сильвестр в 1861 году.
Сильвестр
определял
тактику
как
раздел
математики, изучающий расположение элементов
друг относительно друга.

4. сочетания

Из n элементов создаются
соединения по k элементов
(k
= n или k < n).
Эти соединения отличаются
друг от друга только самими
элементами.
Количество
сочетаний
можно посчитать по формуле:

5.

Задача 1.
Три друга – Антон, Борис и Виктор – приобрели два
билета на футбольный матч. Сколько существует
различных вариантов посещения футбольного матча для
троих друзей?
►По имеющимся двум билетам на матч могут пойти:
1) либо Антон и Борис;
2) либо Антон и Виктор;
3) либо Борис и Виктор.
Ответ: Три варианта.

6.

Задача 2.
Имеются помидоры (П), огурцы (О), и лук (Л). Сколько
различных салатов можно приготовить, если в каждый из них
должны входить в равных долях 2 различных вида овощей?
Записать все сочетания овощей в составленных салатах.
►Расположим данные овощи по порядку: П, О, Л. Запишем все
сочетания овощей в салатах. Будем брать поочередно каждый овощ
(кроме
последнего)
и
добавлять
к
нему
по
одному
только
последующих, поскольку порядок выбора не важен
ПО
ПЛ
ОЛ
Ответ: 3 вида салатов
из

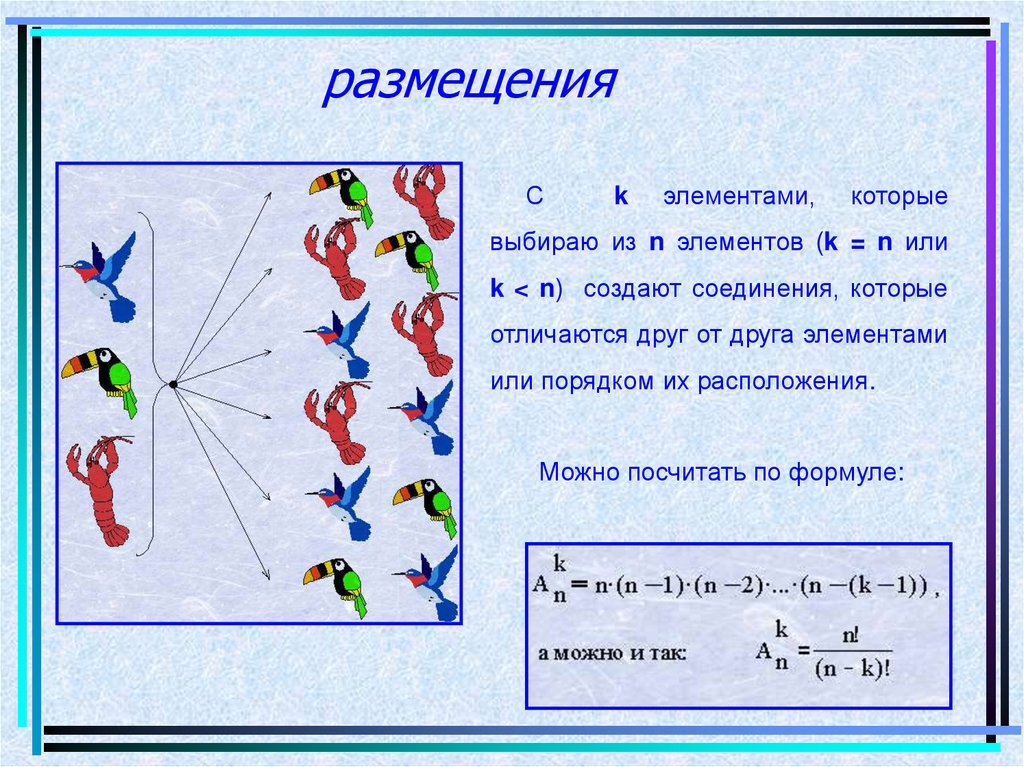
7. размещения

С
k
элементами,
которые
выбираю из n элементов (k = n или
k < n) создают соединения, которые
отличаются друг от друга элементами
или порядком их расположения.
Можно посчитать по формуле:

8.

Задача 3.
Три друга – Антон, Борис и Виктор – приобрели два билета на
футбольный матч на 1-е и 2-е места первого ряда стадиона.
Сколько у друзей есть вариантов (способов) занять эти места на
стадионе? Записать все эти варианты.
► Для удобства перечисления всех возможных вариантов рассаживания
друзей на 1-е и 2-е места будем вместо полных имен мальчиков
записывать лишь их первые буквы. При этом запись АБ будет означать,
что на первом месте сидит Антон, а на втором – Борис. Способ
составления комбинаций будет следующим:
АБ
БА
АВ
ВА
БВ
ВБ
Ответ: 6 способов

9. перестановки

Множество из n элементов
меняют местами. Главное в
этом
деле
-
порядок
элементов.
Число перестановок можно
посчитать по формуле:
Рn = n! , где n! = 1 · 2 · 3 · ... · n

10.

Задача 4.
Антону, Борису и Виктору повезло, и они купили 3 билета на
футбол на 1, 2 и 3 –е места первого ряда стадиона. Сколькими
способами могут занять мальчики эти места.
►Число способов будет таким же, как и задаче 3 из размещений:
АБ
БА
АВ
ВА
БВ
ВБ
Действительно если к каждой паре мальчиков посадить на 3-е место их
друга, ранее не попавшего на мачт, то будут составлены всевозможные
варианты рассаживания мальчиков по трем местам:
АБВ
БАВ
АВБ
ВАБ
БВА
ВБА
Ответ: 6 способов

11.

Задача 5.
Сколько различных трехзначных чисел можно записать с
помощью цифр 1, 2 и 3 при условии, что цифры в числе: 1) должны
быть различными; 2) могут повторяться?
►1)
способ составления трехзначных чисел из 3 различных цифр аналогичен способу
записи троек букв в предыдущей задаче:
123
132
213
231
312
321
Получили 6 чисел.
2) Перебор вариантов можно организовать следующим образом. Выпишем все числа,
начинающиеся с цифры 1 в порядке их возрастания; затем – начинающиеся с цифры 2;
после чего – начинающиеся с цифры 3:
111
121
131
112 113
122 123
132 133
211 212 213
221 222 223
231 232 233
311 312 313
321 322 323
331 332 333
Получим 27 чисел.
Ответ: 1) 6; 2) 27

12.

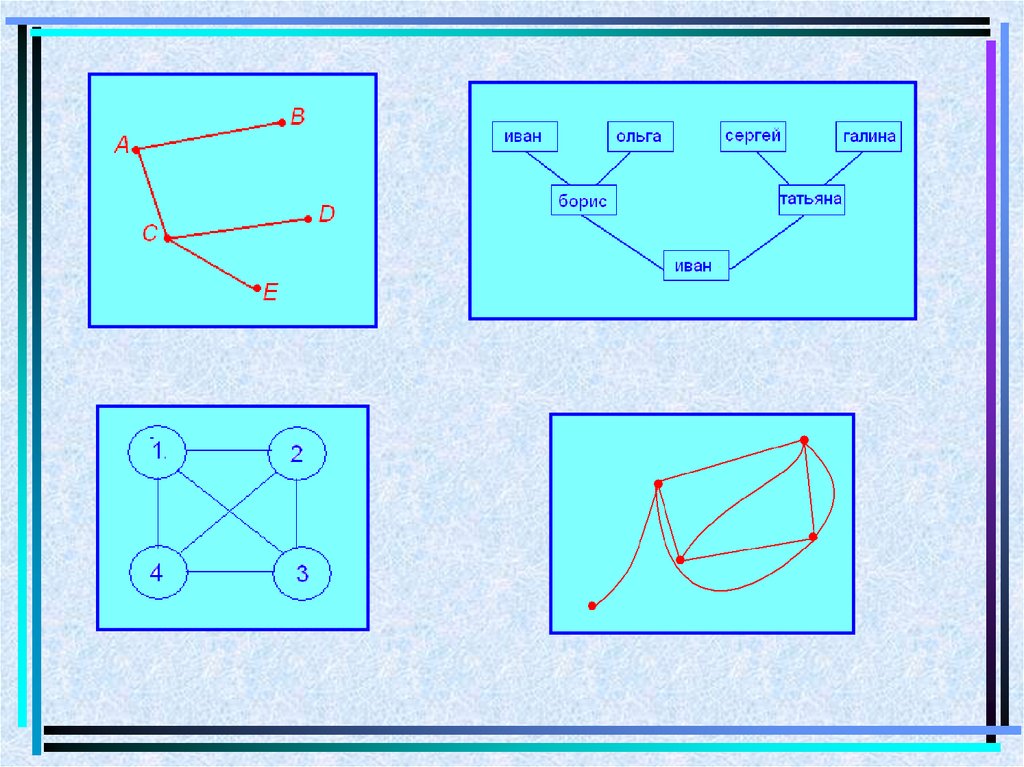
Нередко подсчет вариантов облегчают графы.
Так называемые геометрические фигуры, состоящие из точек
(их называют вершинами) и соединяющих их отрезков (называемых
ребрами графа).
При этом с помощью вершин изображают элементы некоторого
множества (предметов, людей, числовых и буквенных кодов и т. п.), а
с помощью ребер – определенные связи между этими элементами.
Для удобства иллюстрации условия задачи с помощью графа
его вершины-точки могут быть заменены, например, кругами или
прямоугольниками, а ребра-отрезки – любыми линиями.

13.

14.

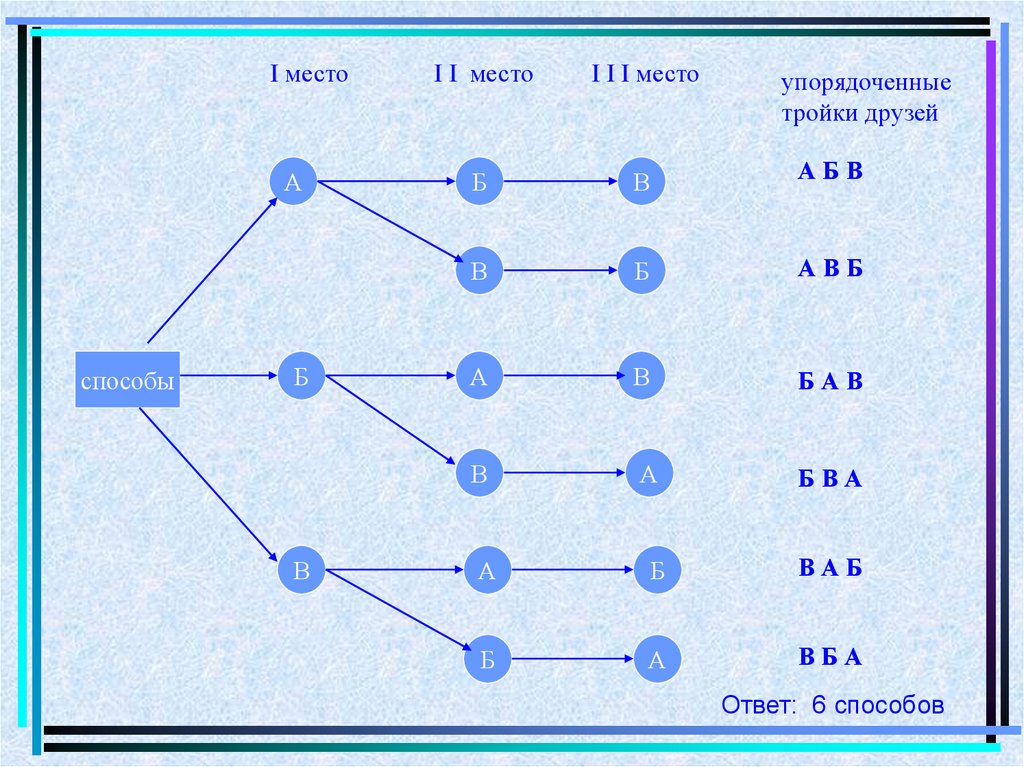
Задачу о способах рассаживания троих друзей на трех местах во
время футбольного матча рассмотрим с помощью графа, называемого
деревом.
Задача 6.
Антону, Борису и Виктору повезло, и они купили 3 билета на
футбол на 1, 2 и 3 –е места первого ряда стадиона. Сколькими
способами могут занять мальчики эти места.
►На 1-е место может сесть любой из троих друзей, на 2-е – любой из
двоих оставшихся, а на 3-е – последний. Сказанное изобразим с
помощью дерева, помещая в вершины графа первые буквы имен
друзей А, Б и В.

15.

I место
А
способы
Б
В
I I место
I I I место
Б
В
АБВ
В
Б
АВБ
А
В
БАВ
В
А
БВА
А
Б
ВАБ
Б
А
ВБА
упорядоченные
тройки друзей
Ответ: 6 способов

16.

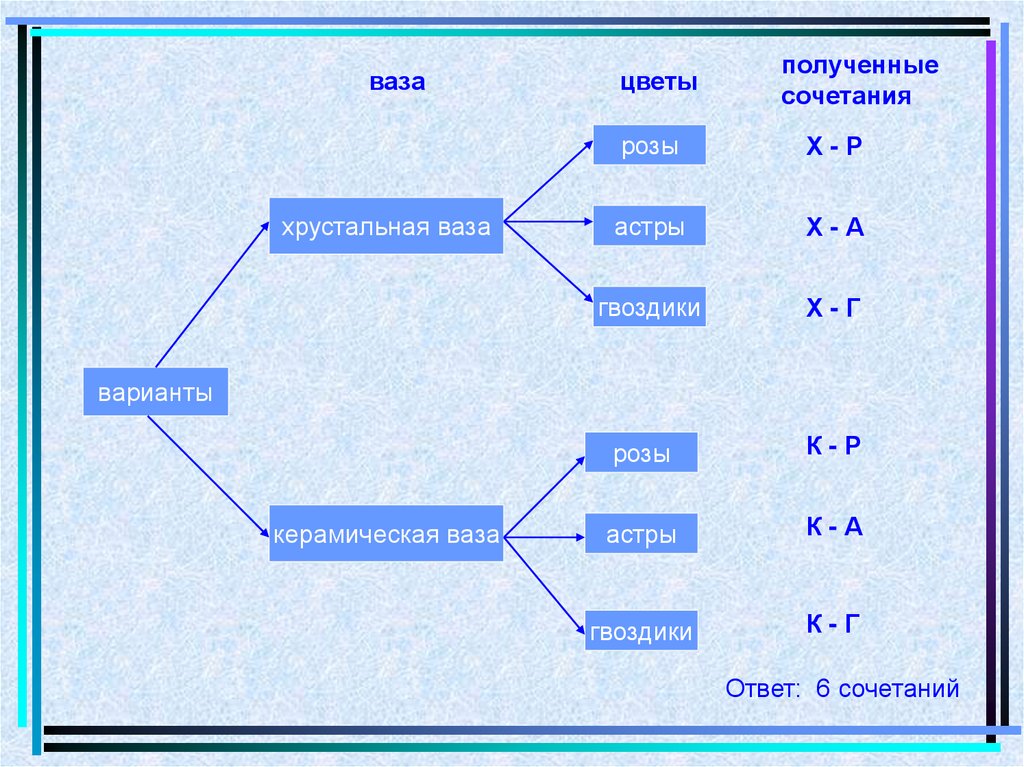
Задача 7.
Маше на день рождения подарили три букета цветов: из роз
(Р), астр (А) и гвоздик (Г). В доме было две вазы: хрустальная (Х) и
керамическая (К). Маша пробовала устанавливать каждый букет в
каждую вазу. Перечислить все полученные сочетания букета с
вазой.
► Нарисуем граф-дерево:

17.

ваза
хрустальная ваза
цветы
полученные
сочетания
розы
Х-Р
астры
Х-А
гвоздики
Х-Г
варианты
керамическая ваза
розы
К-Р
астры
К-А
гвоздики
К-Г
Ответ: 6 сочетаний