Похожие презентации:
Производная функции. Лекция 2
1. Производная функции
Лекция 22. Определение производной
Пусть функция y = f(x) определена в некотором интервале (a; b).Аргументу x придадим некоторое приращение
x x (a; b )
x :
Найдем соответствующее приращение функции:
y f ( x x ) f ( x )
y
Если существует предел
f(x+ Δx )
y
f(x )
0
x
х
x+Δx
х
y
lim
x 0
x
то его называют производной
функции y = f(x) и обозначают
одним из символов:
y ;
f ( x );
dy
dx
3. Определение производной
Итак, по определению:f ( x x ) f ( x )
y lim
x 0
x
Функция y = f(x) , имеющая производную в каждой точке интервала
(a; b), называется дифференцируемой в этом интервале;
операция нахождения производной функции называется
дифференцированием.
Значение производно функции y = f(x) в точке x0 обозначается
одним из символов:
y ( x0 );
f ( x0 );
y x
0
Если функция y = f(x) описывает какой – либо физический процесс,
то f ’(x) есть скорость протекания этого процесса – физический
смысл производной.
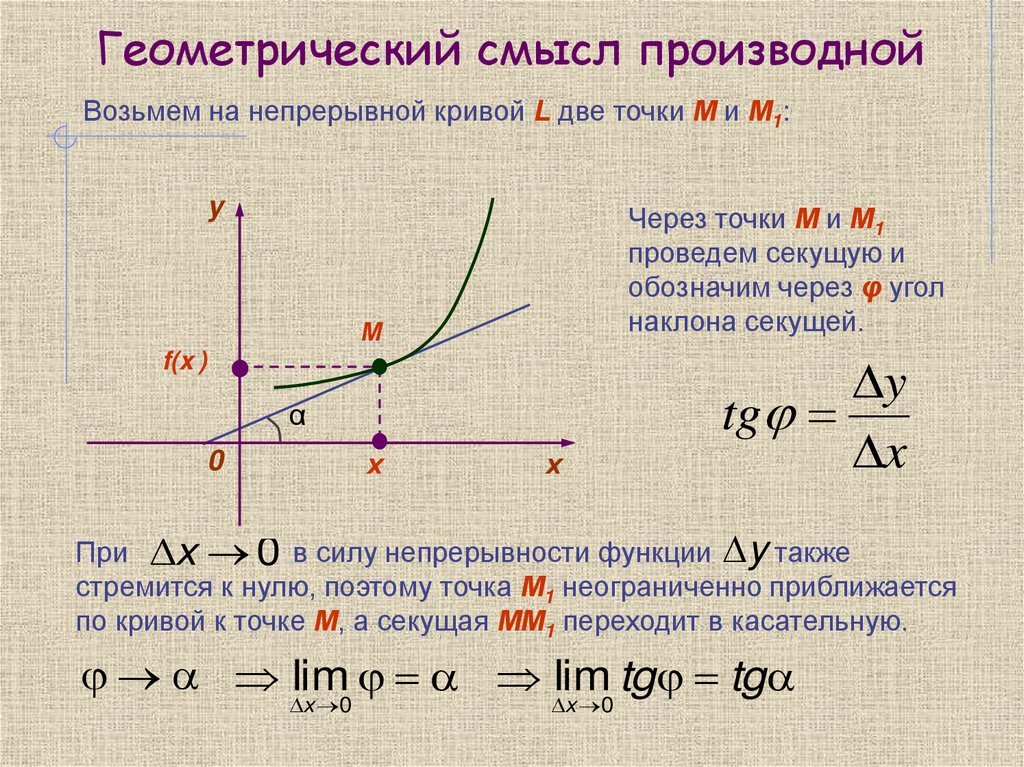
4. Геометрический смысл производной
Возьмем на непрерывной кривой L две точки М и М1:yy
Через точки М и М1
проведем секущую и
обозначим через φ угол
наклона секущей.
М1
f(x+ Δx )
М
f(x )
f(x )
М
y
φ x
α х x+Δx
0
х
0
х
х
y
tg
x
При x 0 в силу непрерывности функции y также
стремится к нулю, поэтому точка М1 неограниченно приближается
по кривой к точке М, а секущая ММ1 переходит в касательную.
lim lim tg tg
x 0
x 0
5. Геометрический смысл производной
f ( x x ) f ( x )y
lim
tg
k
x 0
x
Производная f ’(x) равна угловому коэффициенту касательной к
графику функции y = f(x) в точке,yабсцисса
которой равна x.
Если точка касания М имеет координаты (x0; y0 ), угловой
коэффициент касательной есть k = f ’(x0 ).
Уравнение прямой с угловым коэффициентом:
yy yy00 fк' (( x0-)(xx0 )- x 0 )
f ' ( x0 )
Уравнение
касательной
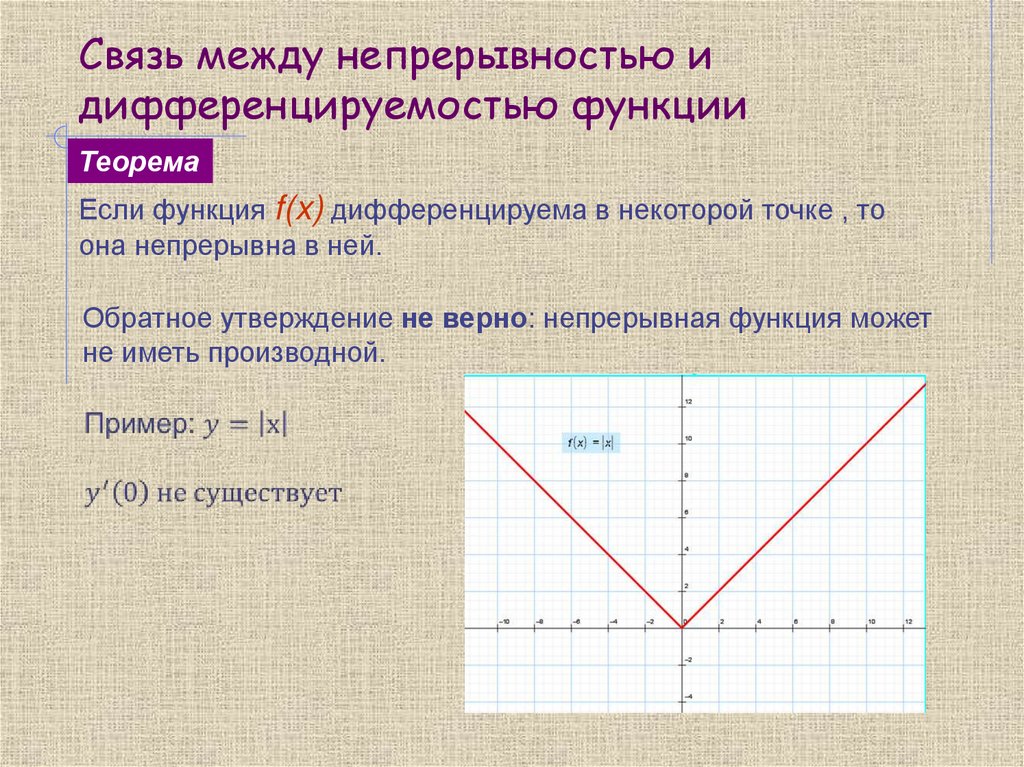
6. Связь между непрерывностью и дифференцируемостью функции
ТеоремаЕсли функция f(x) дифференцируема в некоторой точке , то
она непрерывна в ней.
Обратное утверждение не верно: непрерывная функция может
не иметь производной.
7. Таблица производных
1,
x ln a
1. c ' 0,
4. log a x '
2. ( x n )' nxn 1 ,
ln x ' 1 ,
x ' 2
5. sin x ' cos x,
1
,
x
1
1
' 2 ,
x
x
3. a x ' a x ln a,
x
cos x ' sin x,
1
,
2
cos x
e x ' e x ,
ctgx ' 12 ,
sin x
1
1
6. arcsin x
; arccos x
2
1 x
1 x2
1
1
arctgx
arcctgx
;
2
1 x
1 x2
tgx '
8. Правила дифференцирования
Пусть u(x) , v(x) и w(x) – дифференцируемые в некотороминтервале (a; b) функции, С – постоянная.
(C ) 0
(u v ) u v
(u v ) u v u v (C u ) C u
u u v u v
C
C
v
2
2
v
v
v
v
9. Производная сложной функции
Пусть y = f(u) и u = φ(x) , тогда y = f(φ(x)) – сложная функция спромежуточным аргументом u и независимым аргументом x.
Теорема
Если функция u = φ(x) имеет производную u x в точке x а
функция y = f(u) имеет производную y u в соответствующей точке
u , то сложная функция имеет производную y x , которая
находится по формуле:
y x y u u x
Это правило остается в силе, если промежуточных аргументов
несколько:
y f (u );
u (v );
v g( x )
y x y u uv v x
y f ( (g ( x )))
10. Пример.
1 sin xВычислить производную функции y 3
x ln x
Пример.
1 sin x
y 3
x ln x
(1 sin x) ( x 3 ln x) (1 sin x) ( x 3 ln x)
2
3
x ln x
3
3
3
(sin x) ( x ln x) (1 sin x) (( x ) ln x x (ln x) )
2
3
x ln x
1
cos x x ln x (1 sin x) (3 x ln x x x )
x
2
3
x ln x
3
2
2
3
11. Пример.
Вычислить производную функцииy cos(ln12 x )
Данную функцию можно представить следующим образом:
y cos u; u v 12 ; v ln x
y x y u uv v x
y u sin u sinv 12 sin ln12 x
u 12v 11 12 ln11 x
1
v
x
y sin ln12 x 12 ln11 x
Коротко:
12
12
12
sin(ln
x
)
(ln
x)
y (cos(ln x))
sin(ln x) 12 ln x (ln x)
12
11
1
x
12. Производные высших порядков
Производная y f (x ) функции y f (x ) есть также функцияот x и называется производной первого порядка.
Если функция f (x )
дифференцируема, то ее производная
называется производной второго порядка и обозначается:
y ;
f ( x );
d 2y
dx 2
Итак:
y ( y )
Производная от производной второго порядка, если она существует
называется производной третьего порядка и обозначается:
y ;
f ( x );
d 3y
dx 3
Итак:
y ( y )
Производной n – ого порядка (или n – ой производной)
называется производная от производной n -1 - ого порядка.
y ( n ) ( y ( n 1) )
13. Производные высших порядков
Начиная от производной 4 порядка , производные обозначаютсяримскими цифрами или цифрами в скобках:
или
y (5)
yv
- производная пятого порядка.
Вычислить производную n – ого порядка от функции: y ln( x 1)
x
1
y ln( x 1)
1
( x 1) 1
x 1
x 1
2
3
1
2
y
x
1
1
2
x
1
y x 1 1 x 1 ;
y 1 2 x 1 1 2 3 x 1
y 1 2 3 x 1 1 2 3 4 x 1
4
5
3
4
4
5
y n 1
n 1
n 1 ! x 1 n
14. Производные от функций, заданных параметрически
Пусть функция y = f(x) задана параметрически уравнениями:x x (t )
y y (t )
Производная первого порядка от этой функции
находится по формуле:
y t
y x
x t
Найдем производную второго порядка:
( y x ) t
y x ( y x ) x
xt
Аналогично получаем:
( y x ) t
y x ( y x ) x
xt
y
( 4)
x
( y x ) t
( y x ) x
xt
и т. д.
15. Производные от функций, заданных параметрически
Вычислить производную 3 – ого порядка от функции:x t 2
3
y
1
t
2
3
t
(1 t )
1.5t
y x
2
2t
(t )
( 1.5t )
( y x ) t
y x
(t 2 )
x t
3
1 .5
0.75t 1
2t
1
( y x ) t
(
0
.
75
t
)
y x
x t
(t 2 )
0.75t 2
3
3
2t
4t
16. Дифференциал функции
Пусть функция y = f(x) имеет в некоторой точке х отличнуюот нуля производную, следовательно существует предел:
y
y
f ( x) ( x)
lim
f ( x) 0
x 0
x
x
где
( x ) 0
при
x 0
По теореме о связи
функции, ее предела и
бесконечно малой
функции
y f ( x) x ( x) x
17. Дифференциал функции
y f ( x) x ( x) xПервое слагаемое
f ( x) x называют главной частью
приращения функции.
Дифференциалом функции y = f(x) в точке х называется
главная часть ее приращения:
dy f ( x ) x
Можно доказать, что
dx x
Дифференциал
независимой
переменной
Дифференциал
функции
равен
приращению
этой
равен
произведению
переменной
производной
функции на
dy
дифференциал
f ( x ) переменной
независимой
dy f ( x)dx
dx
18. Геометрический смысл дифференциала
Проведем к графику функции y = f(x) в точке М(x, y) касательнуюРассмотрим ординату
касательной для точки x+Δx.
Из прямоугольного треугольника
AВМ имеем:
y
М1
f(x+ Δx )
y
f(x )
dy
x
α
0
B
М
х
A
x+Δx
tg
х
AB
x
AB tg x
Согласно геометрическому смыслу производной,
tg f (x )
AB f ( x ) x dy
Дифференциал функции y = f(x) в точке x равен приращению
ординаты касательной к графику функции в этой точке, когда x
получает приращение Δx.
19. Приложение дифференциала в приближенных вычислениях
Как известно, приращение функции можно представить в виде:y f ( xdy
) x ( x ) x
Отбрасывая бесконечноdy
малую ( x ) x более высокого порядка,
чем x , получим приближенной равенство:
y dy
Это равенство позволяет с большой точностью вычислять
приращение любой дифференцируемой функции.
f ( x0 x) f ( x0 ) f ( x) x
Формула позволяет приближенно вычислять значение функции в
точке x0+Δx, зная значение функции в точке x0.
20. Приложение дифференциала в приближенных вычислениях
Вычислить приближенно:arctg 1.05
Рассмотрим функцию: y arctg x
arctg ( x0 x ) arctg ( x0 ) arctg ( x0 ) x
Так как
x0 x 1.05
arctg 1
4
то
(arctg x )
x0 1 x 0.05
1
1 x 2
1
arctg (1.05) 0.05 0.81
4 2
(arctg x ) x 1
1
2
21. Исследование функций с помощью производной и построение графиков функций
Схема1. Найти о.о.ф.
2. Найти (если возможно) точки пересечения графика
с осями координат
3. Найти промежутки знакопостоянства функции
4. Исследовать на четность
5. Найти асимптоты графика функции
6. Найти промежутки монотонности, точки экстремума
функции
7. Найти промежутки выпуклости, точки перегиба
графика функции
8. Построить график функции
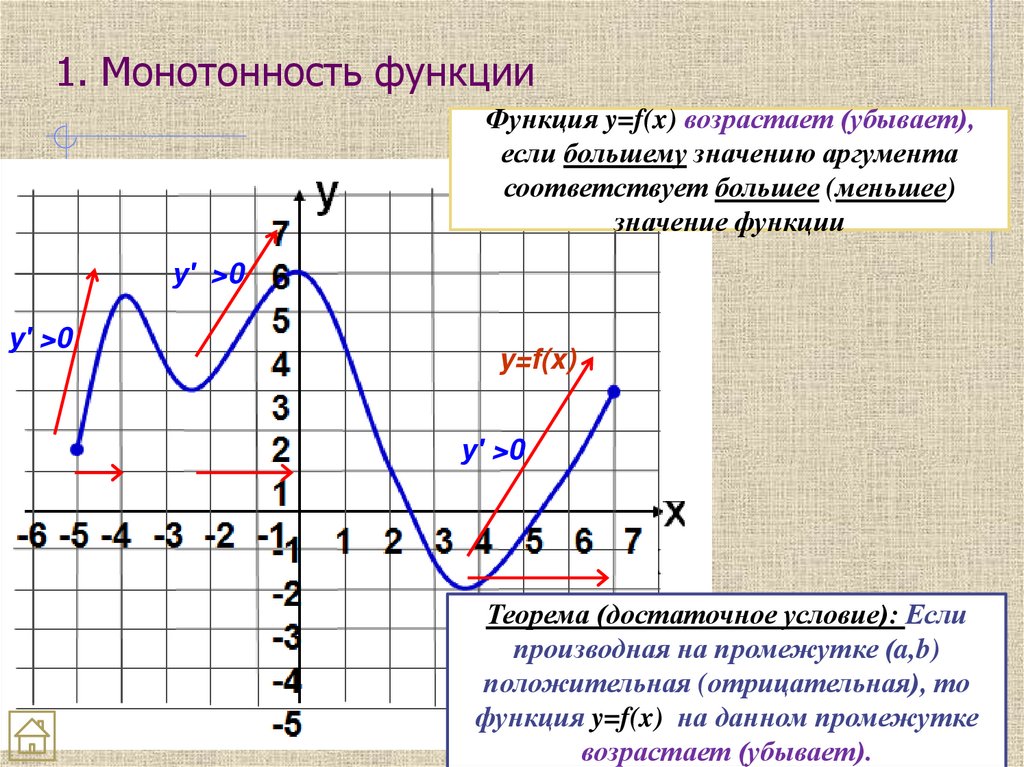
22. 1. Монотонность функции
Функция y=f(x) возрастает (убывает),если большему значению аргумента
соответствует большее (меньшее)
значение функции
у' >0
у' >0
y=f(x)
у' >0
Теорема (достаточное условие): Если
производная на промежутке (a,b)
положительная (отрицательная), то
функция y=f(x) на данном промежутке
возрастает (убывает).
23. Точки экстремума
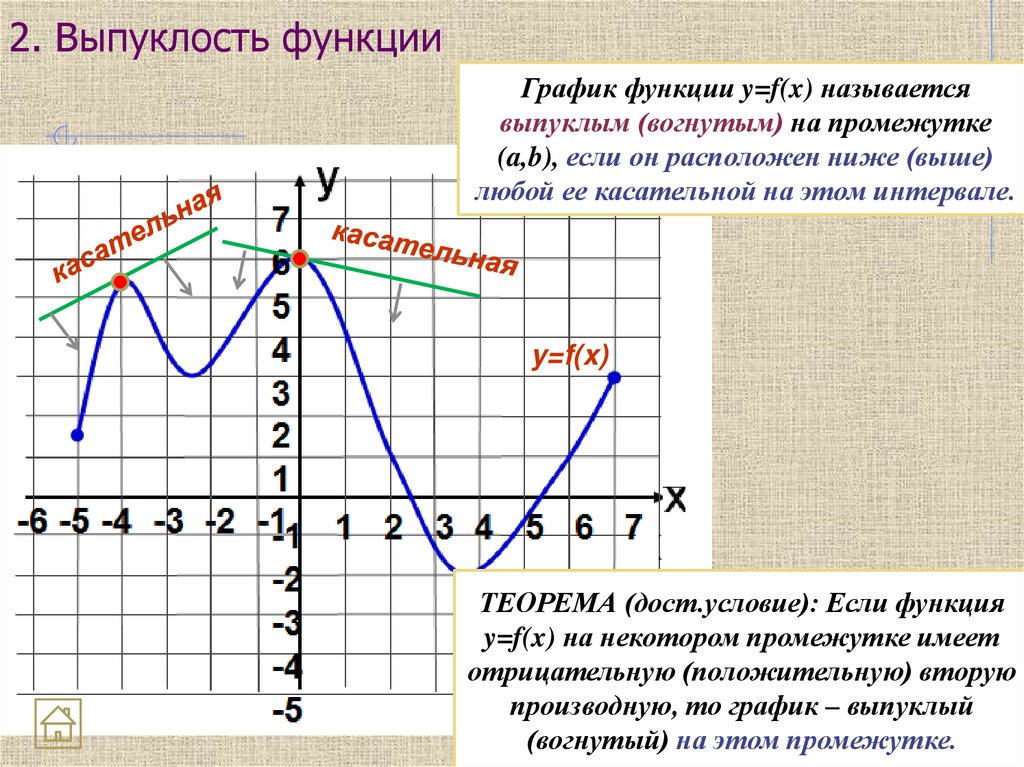
24. 2. Выпуклость функции
График функции y=f(x) называетсявыпуклым (вогнутым) на промежутке
(a,b), если он расположен ниже (выше)
любой ее касательной на этом интервале.
y=f(x)
ТЕОРЕМА (дост.условие): Если функция
y=f(x) на некотором промежутке имеет
отрицательную (положительную) вторую
производную, то график – выпуклый
(вогнутый) на этом промежутке.
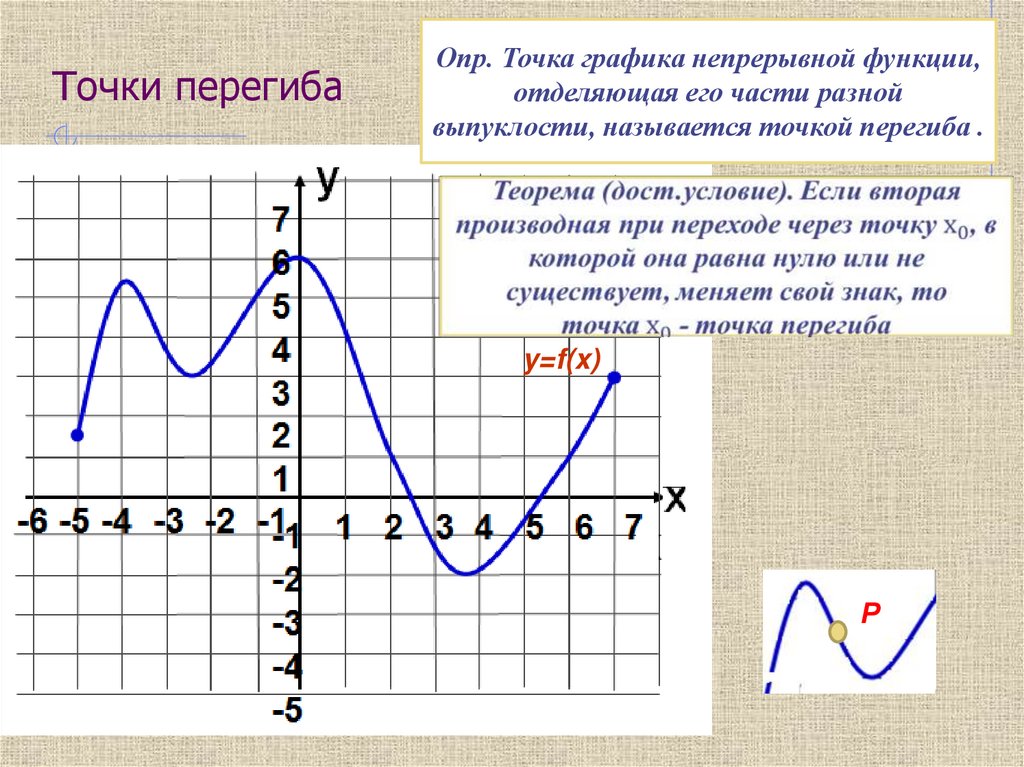
25. Точки перегиба
Опр. Точка графика непрерывной функции,отделяющая его части разной
выпуклости, называется точкой перегиба .
P1
y=f(x)
Р
26. Асимптоты графика функции
Опр. Прямая называется асимптотой графикафункции, если расстояние от точек графика до этой
прямой стремится к 0 при неограниченном удалении
точки графика от начала координат.
Асимптоты бывают вертикальными,
горизонтальными и наклонными.
Опр. Прямая x=a называется вертикальной
асимптотой для y=f(x), если
lim f(x)
x a 0
или
lim f(x)
x a 0
27.
Опр. Наклоннойасимптотой графика
функции y = f (x)
является прямая y=kx+b,
если
существуют конечные
пределы
f ( x)
k lim
,
x
x
b lim f ( x) kx .
x
Горизонтальная асимптота имеет вид y=b и
является частным случаем наклонной асимптоты
при k 0.





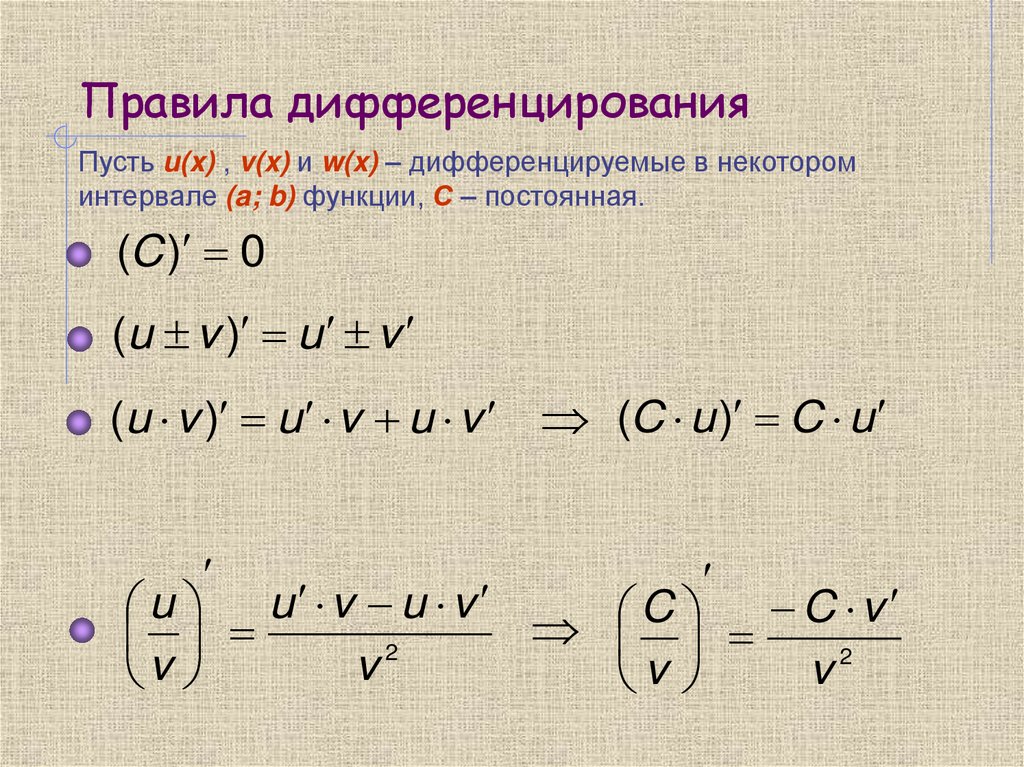
















 Математика
Математика








