Похожие презентации:
Логика как наука
1.
Логика как наукаПреподаватель: Рябов Михаил Александрович
кандидат философских наук, доцент кафедры социологии УдГУ
2.
ОпределениеЛогика – наука о законах и операциях правильного
мышления
Что такое мышление?
Что значит правильное мышление?
2
3.
Когда стали изучать логикуПервый «учебник» по логике
Аристотелем в IV веке до н.э.
был
написан
Он определил предмет логики,
разработал основные принципы,
сформулировал законы и формы
познания
Его логика получила название
«формальной»
3
4.
Аристотелевская логика господствовала в течениепоследующих двух с лишним тысяч лет
Немецкий философ Иммануил Кант
в XVIII веке считал, что со времен
Аристотеля эта наука не сделала ни
шагу
вперед
ввиду
своей
законченности и совершенности
Ситуация меняется с середины XIX
века, с появлением символической
логики
4
5.
Традиционная логика (аристотелевская, формальная)– этап развития логики (IV век до н. э. – конец XIX
века), связанный с изучением и построением правил
преобразования высказываний
Современная логика – этап развития логики (конец
XIX века – XXI век), связанный с проникновением в
неё математических методов и последующим
отделением её от философии
5
6.
Логика и языкЯзык – знаковая система, используемая для целей
коммуникации и познания
Системность языка выражается в наличии в каждом языке
словаря, синтаксиса, семантики и прагматики
Синтаксис – это система правил
преобразования выражений языка
образования
и
Семантика – система правил, определяющих способы
придания значений выражениям языка
6
7.
Все языки могут быть разделены на естественные,искусственные и частично искусственные
Естественные
языки
(повседневные,
складываются стихийно и постепенно
разговорные)
Искусственные языки сознательно создаются людьми для
каких-либо специальных целей: языки математики, логики,
алгоритмические языки, шифры и т.д.
Языки естественных, социальных и гуманитарных наук
относятся к частично искусственным, поскольку включают
специальные термины
7
8.
Функции языкаК основным функциям употребления языка
относятся:
1) Описательная – сообщение о реальном положении
вещей
Описание, соответствующее действительности, истинно;
описание, не отвечающее реальному положение дел, ложно
Иногда допускается, что высказывание может
неопределенным: например, описание будущего
быть
8
9.
2)Эмотивная
–
выражение
определенных
психических состояний, связанных с конкретной
ситуацией
Например: «Рад тебя видеть», «Поздравляю с победой»
3) Декларативная – изменение положения вещей,
существовавшего до высказывания
Например: «Объявляю вас мужем и женой», «Назначаю вас
председателем», «Ухожу в отставку»
9
10.
4) Нормативная – возможность обязать, разрешитьили запретить что-то сделать под угрозой наказания
Например: «Прекратите говорить!»
5) Оценочная – возможность выразить нейтральное,
положительное или отрицательное отношение к
рассматриваемому объекту
Например: «Лучше прийти раньше, чем опоздать»
10
11.
Логическая грамматикаВ грамматике принято выделять различные части речи
(существительное, прилагательное, глагол и т. д.)
Аналогично для логики мы имеем выражения двух типов
Содержательные выражения – имеют содержание,
даже взятые сами по себе
Логические символы – не имеют самостоятельного
содержания и служат для образования одних
содержательных выражений из других
11
12.
Различие между содержательными и логическими частямиможно
уподобить
различию
между
числами
и
арифметическими операциями над ними
Например: 2+3=5
где «2», «3» и «5» играют роль содержательных выражений,
а «+» и «=» – логических символов (логических связок,
функторов)
12
13.
К содержательным частям относятся понятия (имена)и суждения (высказывания)
Понятия: «стул», «стол»
Суждение: «стул стоит на столе»
Логические связки позволяют объединять понятия в
суждения, из суждений строить умозаключения
В языке эти связки выражаются словами:
«…и…», «…или…», «если…, то…», «неверно, что…»
«все… есть…», «некоторые… есть…», «некоторые… не есть…»
13
14.
Наше мышление обычно направлено только на содержание,но чтобы выявить логическую форму рассуждения, надо от
него отвлечься
Для этого понятия и суждения заменяют переменными
Как правило, для обозначения понятий используются
большие буквы второй половины латинского алфавита
Роза – это цветок / (Все) S есть P
У некоторых цветов есть шипы / Некоторые S есть P
Не пойман – не вор / Все S не есть P
14
15.
Для обозначения суждений обычно используются большиебуквы первой половины латинского алфавита
На улице солнечно и тепло / A и B
Если пойдет дождь, то будет сыро / Если A, то B
Для удобства записи логических выражений слова были
заменены специальными символами, например:
ꓵ - «…и…»
ꓴ - «…или…»
AиB/AꓵB
A или B / A ꓴ B
- «если…, то…»
если A, то B / A
B
15
16.
Решение логических задачЗадача 1
Условие задачи. До царя дошла весть, что кто-то из трёх
богатырей убил Змея Горыныча. Приказал царь им всем
явиться ко двору. Молвили богатыри:
Илья Муромец: Змея убил Добрыня Никитич.
Добрыня Никитич: Змея убил Алёша Попович.
Алёша Попович: Я убил змея.
Известно, что только один богатырь сказал правду, а двое
слукавили. Кто убил змея?
16
17.
Первое «решение». Змея убил Добрыня. Тогда Илья сказалправду, а Добрыня и Алёша слукавили
Комментарий. Задача «решена» подбором: приведён
ответ, и доказано, что он удовлетворяет условию. Но
этого недостаточно: надо ещё проверить, единственный
ли он! Поэтому пока задачу нельзя считать решённой
17
18.
Второе решение. Рассмотрим по очереди, кто мог убить змея.Если Илья Муромец, то все трое сказали неправду, что
противоречит условию. Если Добрыня Никитич, то правду
сказал Илья, а Алёша и Добрыня слукавили. Если Алёша, то и
Добрыня, и Алёша сказали правду, а это тоже противоречит
условию. Итак, убить змея мог только Добрыня
Комментарий. Вот теперь задача решена не подбором, а
полным перебором: проверены все возможности, и
доказано, что только одна из них удовлетворяет условию.
Это верное решение. Правда, оно стало длинным
18
19.
Третье решение. Добрыня и Алёша утверждают одно и то же.Но правду сказал лишь один богатырь. Это мог быть только
Илья. Значит, змея убил Добрыня
Комментарий. Эта задача в итоге решена коротко и верно
Ответ: Змея убил Добрыня
19
20.
Задача 2Условие задачи. На острове мудрецов и лжецов есть всего
две деревни. Жители одной из них — мудрецы — всегда
говорят правду. В другой деревне живёт племя лжецов,
которые всегда лгут. Человек говорит: «Я лжец». Является ли
он жителем острова мудрецов и лжецов?
20
21.
Решение. Конечно, мудрец не может так сказать, ведь длянего это было бы ложью. Но и лжец не может так сказать,
ведь для него это было бы правдой. Значит, никакой
островитянин не может назвать себя лжецом.
Ответ: нет
21
22.
Задача 3Условие задачи. Беседуют трое друзей: Белокуров, Рыжов и
Чернов. Брюнет сказал Белокурову: «Любопытно, что один из
нас блондин, другой — брюнет, третий — рыжий, но ни у кого
цвет волос не соответствует фамилии. Какой цвет волос у
каждого из друзей?
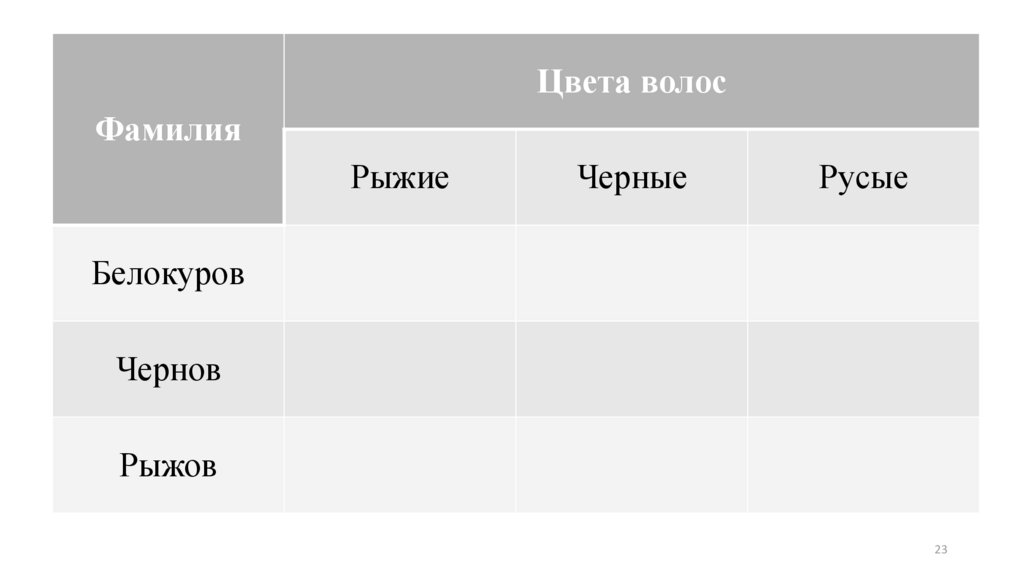
Решение 1. Для решения задачи воспользуемся таблицей 3 х
3, отмечая по горизонталям фамилии, а по вертикалям —
цвета волос беседующих. Обозначим клетки таблицы
буквами Lij, где i — номер столбца таблицы, а j — номер
строки
22
23.
Цвета волосФамилия
Рыжие
Черные
Русые
Белокуров
Чернов
Рыжов
23
24.
По условию задачи Белокуров — не блондин, Чернов — небрюнет, а Рыжов — не рыжий. Это позволяет поставить знак
«–» в клетках L13, L22 и L31. Кроме того, по условию, Белокуров
не брюнет и, значит, в клетке L21, также следует поставить
знак «–»
После этого таблица принимает следующий вид:
24
25.
Цвета волосФамилия
Рыжие
Черные
Русые
Белокуров
—
—
Чернов
—
Рыжов
—
25
26.
Так как между множеством фамилий участников беседы имножеством цветов их волос должно быть взаимно
однозначное соответствие, то, очевидно, в клетках L11 и L23
следует поставить знак «+»
Но тогда в клетках L12 и L33 следует поставить знак «–», а в
оставшейся клетке L32 поставить знак «+» и таблица
принимает следующий вид:
26
27.
Цвета волосФамилия
Рыжие
Черные
Русые
Белокуров
+
—
—
Чернов
—
—
+
Рыжов
—
+
—
27
28.
Ответ: отсюда следует, что у Белокурова волосы рыжие, уЧернова — русые, а у Рыжова — черные
Решение 2. Будем изображать множество друзей и
множество цветов их волос кругами, а элементы множеств —
точками, помещенными в эти круги
28
29.
ЧерновЧёрные
Белокуров
Русые
Рыжов
Рыжие
Множество друзей
Множество цветов волос
29
30.
Так как по условию задачи у Чернова волосы не черные, уБелокурова — не русые, а у Рыжова — не рыжие, то
соединим пунктирными линиями элементы множеств:
«Чернов» и «черные», «Белокуров» и «русые», «Рыжов» и
«рыжие»
Кроме того, известно, что Белокуров не брюнет, то есть у него
волосы не черные. Значит, элементы «Белокуров» и
«черные» также нужно соединить пунктирной линией
В результате будет получен следующий график:
30
31.
ЧерновЧёрные
Белокуров
Русые
Рыжов
Рыжие
Множество друзей
Множество цветов волос
31
32.
Учитывая, что между рассматриваемыми множествамидолжно
быть
взаимно
однозначное
соответствие,
сплошными линиями следует соединить элементы
«Белокуров» и «рыжие», «черные» и «Рыжов»
При этом ясно, что для получения полного решения остается
соединить сплошной линией элементы «Чернов» и «русые»,
и график, дающий решение задачи, имеет вид:
32
33.
ЧерновЧёрные
Белокуров
Русые
Рыжов
Рыжие
Множество друзей
Множество цветов волос
33
































 Математика
Математика Философия
Философия








