Экспериментальное исследование турбулентной динамики и процессов стохастической кластеризации материи в астрофизической плазме

1.

Экспериментальное исследование турбулентной
динамики и процессов стохастической кластеризации
материи в астрофизической плазме с использованием
лабораторных плазменных и теплофизических установок
Будаев В.П., Дедов А.В., Кавыршин Д.И.,
Лисица В.С., Савин С.П., Меньшов И.С., Попов В.Ю., Елецкий А.В.,
Федорович С.Д., Губкин М.К., Лукашевский М.В. и коллеги
Национальный исследовательский университет «МЭИ»,
НИЦ «Курчатовский институт», ИКИ РАН, МГУ,
ИПМ им. Келдыша РАН, ИВТ РАН
«СОВЕЩАНИЕ ПО НАПРАВЛЕНИЮ ЭКСПЕРИМЕНТАЛЬНАЯ
ЛАБОРАТОРНАЯ АСТРОФИЗИКА»
г.САРОВ 18-20/01/2022
[email protected]

2.

План
Актуальность, цель и задачи
Сильная турбулентность плазмы: дальние корреляции,
перемежаемость, супердиффузия, негауссовая статистика
Сравнительное исследование турбулентности и супердиффузии в
астрофизической и лабораторной плазме
Стохастическая кластеризации материи: агломерация ионов и
атомов под влиянием динамики турбулентной плазмы, фрактальный
рост структур, самоподобие
Экспериментальные установки, исполнители
Программа экспериментов на 2022 г
1.
2.
3.
4.
5.
V.P. Budaev , S.P. Savin, L.M Zelenyi, Physics Uspekhi, 181 , 905-952 (2011)
V.P. Budaev, L.M Zelenyi, S.P. Savin , Journal of Plasma Physics, 81, 395810602, (2015)
V.P. Budaev, Physics Letters A. (2017) 381 43 3706-3713.
V.P. Budaev, Symmetry (2021) 13 796.
V.P. Budaev, Physics of Atomic Nuclei (2016) 79(7) 1137-1162.

3.

Актуальность, цель и задачи
Актуальность:
выявление закономерностей тепло-массопереноса в межпланетной среде для целей обеспечения
безопасности космических межпланетных полетов, систематизация экспериментальных
наблюдений топологии и формообразования астрофизических объектов под влиянием
космической плазмы.
Цель исследования:
Экспериментальное исследование универсальных свойств турбулентной динамики, описание
топологии астрофизических объектов, универсальных свойств кластеризации и формообразования
материи как на больших масштабах, так и на микромасштабах с целью систематизации и
выявления закономерностей масштабной инвариантности материи - дилатационных симметрий.
кластеры лития осажденные
из турбулентной плазмы
в установке ПЛМ
туманность Омега
туманность Орион
крабовидная
туманность
Космическая пыль под
микроскопом

4.

Задачи исследования
экспериментальные измерения характеристик турбулентности плазмы в лабораторных
плазменных установках и сравнительный анализ с данными космических спутников;
исследование дальних корреляций и масштабной инвариантности турбулентности плазмы в
неоднородных магнитных полях, экспериментальное определение скейлингов самоподобия и
сравнение со статистическими моделями развитой турбулентности для определения
универсальных закономерностей масштабной инвариантности турбулентности плазмы;
анализ динамики ионов и атомов, в том числе ридберговских, в процессе агломерции под
действием турбулентной плазмы с целью выявления закономерностей масштабной
инвариантности топологической структуры для систематического описания топологии
астрофизических объектов ;
экспериментальные измерения ридберговских состояний атомов в замагниченной лабораторной
плазме, исследование условий формирования молекулярных кластеров, в том числе, из
ридберговских атомов, сравнительный анализ с астрофизическими наблюдениями,
обобщающий анализ данных возможности существования ридберговского вещества;
фрактальный рост агломератов под влиянием динамики турбулентной плазмы;
тепломассоперенос в материалах с фрактальной структурой, сравнительное исследование
супердиффузии в астрофизической и лабораторной плазме;
разработка технологий создания материалов с фрактальной структурой для применения в
ядерных и термоядерных реакторах, биомедицинского применения, разработки компонентов
квантового компьютера, технологий плазменного космического двигателя.

5.

Сильная турбулентность
плазмы: дальние корреляции,
перемежаемость, супердиффузия,
негауссовая статистика
Свойство неизотропности,
нестационарности турбулентности причина формирования структур разных
масштабов, от микромасштабов до
мегамасштабов

6.

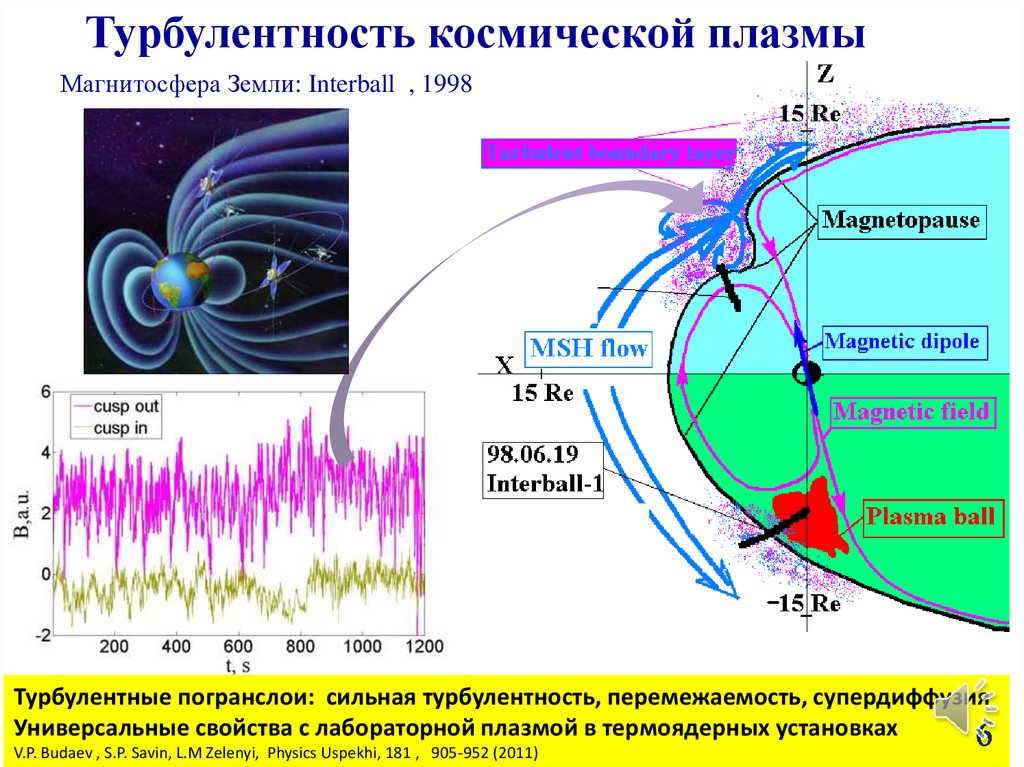
Турбулентность космической плазмы
Магнитосфера Земли: Interball , 1998
Турбулентные погранслои: сильная турбулентность, перемежаемость, супердиффузия
Универсальные свойства с лабораторной плазмой в термоядерных установках
V.P. Budaev , S.P. Savin, L.M Zelenyi, Physics Uspekhi, 181 , 905-952 (2011)

7.

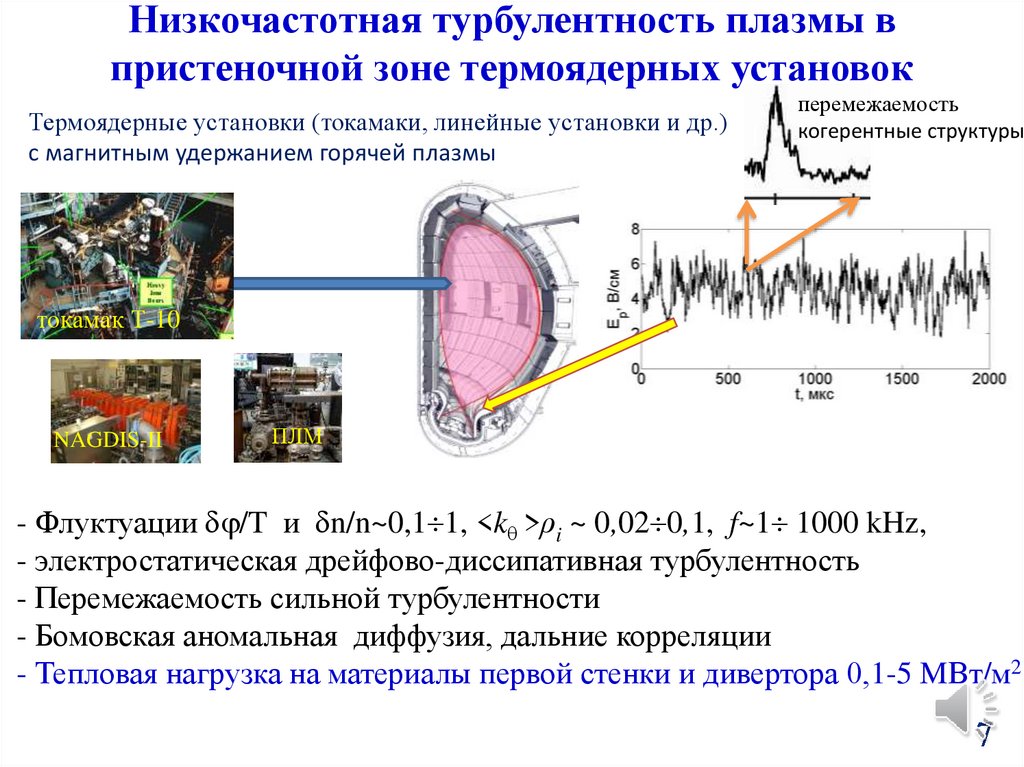
Низкочастотная турбулентность плазмы в
пристеночной зоне термоядерных установок
Термоядерные установки (токамаки, линейные установки и др.)
с магнитным удержанием горячей плазмы
перемежаемость
когерентные структуры
токамак Т-10
NAGDIS-II
ПЛМ
- Флуктуации /T и n/n~0,1 1, <k >ρi ~ 0,02 0,1, f~1 1000 kHz,
- электростатическая дрейфово-диссипативная турбулентность
- Перемежаемость сильной турбулентности
- Бомовская аномальная диффузия, дальние корреляции
- Тепловая нагрузка на материалы первой стенки и дивертора 0,1-5 MВт/м2

8.

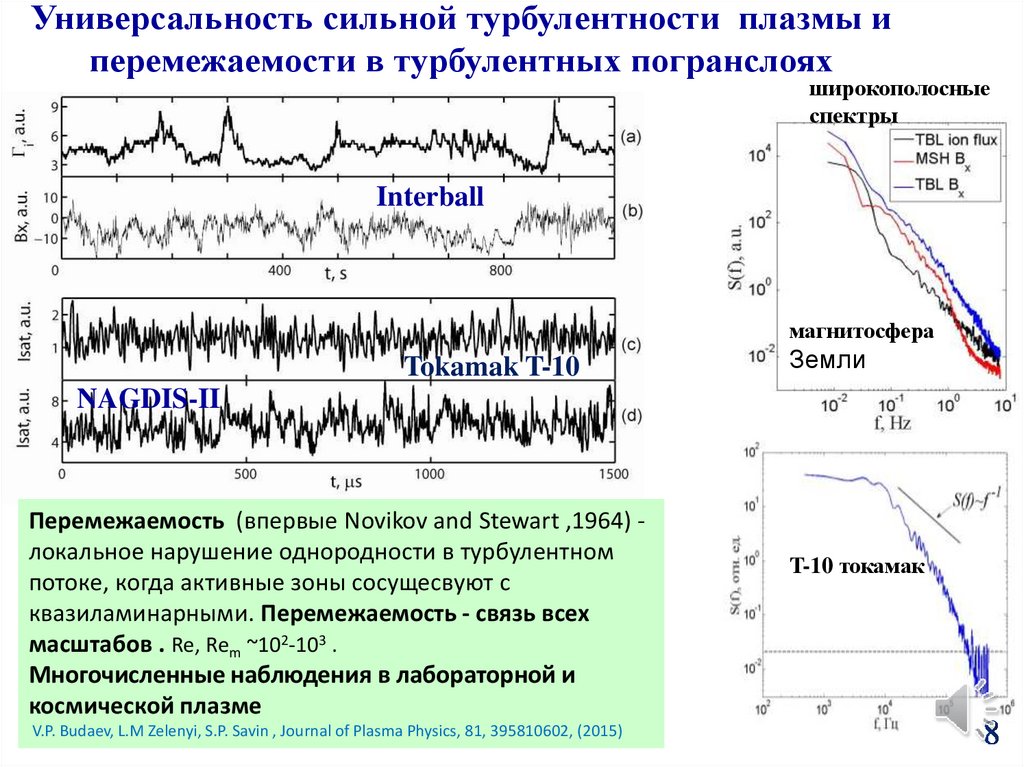
Универсальность сильной турбулентности плазмы и
перемежаемости в турбулентных погранслоях
широкополосные
спектры
Interball
магнитосфера
Tokamak T-10
Земли
NAGDIS-II
Перемежаемость (впервые Novikov and Stewart ,1964) локальное нарушение однородности в турбулентном
потоке, когда активные зоны сосущесвуют с
квазиламинарными. Перемежаемость - связь всех
масштабов . Re, Rem ~102-103 .
Многочисленные наблюдения в лабораторной и
космической плазме
V.P. Budaev, L.M Zelenyi, S.P. Savin , Journal of Plasma Physics, 81, 395810602, (2015)
T-10 токамак

9.

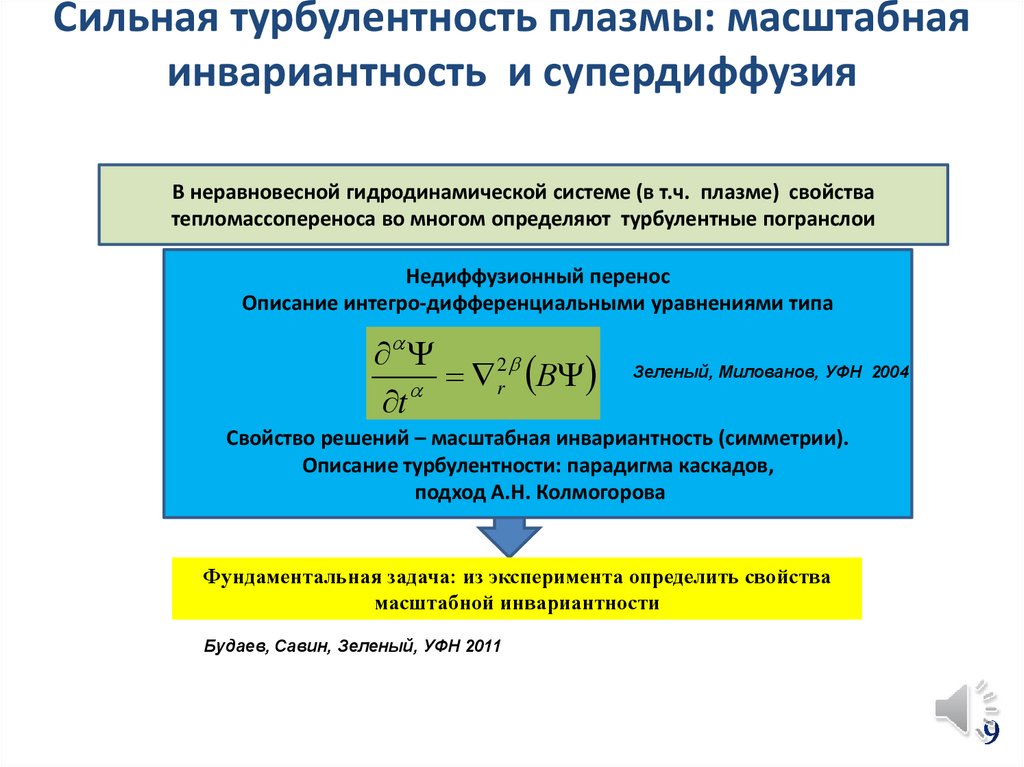
Сильная турбулентность плазмы: масштабная
инвариантность и супердиффузия
В неравновесной гидродинамической системе (в т.ч. плазме) свойства
тепломассопереноса во многом определяют турбулентные погранслои
Недиффузионный перенос
Описание интегро-дифференциальными уравнениями типа
2
r Β
t
Зеленый, Милованов, УФН 2004
Свойство решений – масштабная инвариантность (симметрии).
Описание турбулентности: парадигма каскадов,
подход А.Н. Колмогорова
Фундаментальная задача: из эксперимента определить свойства
масштабной инвариантности
Будаев, Савин, Зеленый, УФН 2011

10.

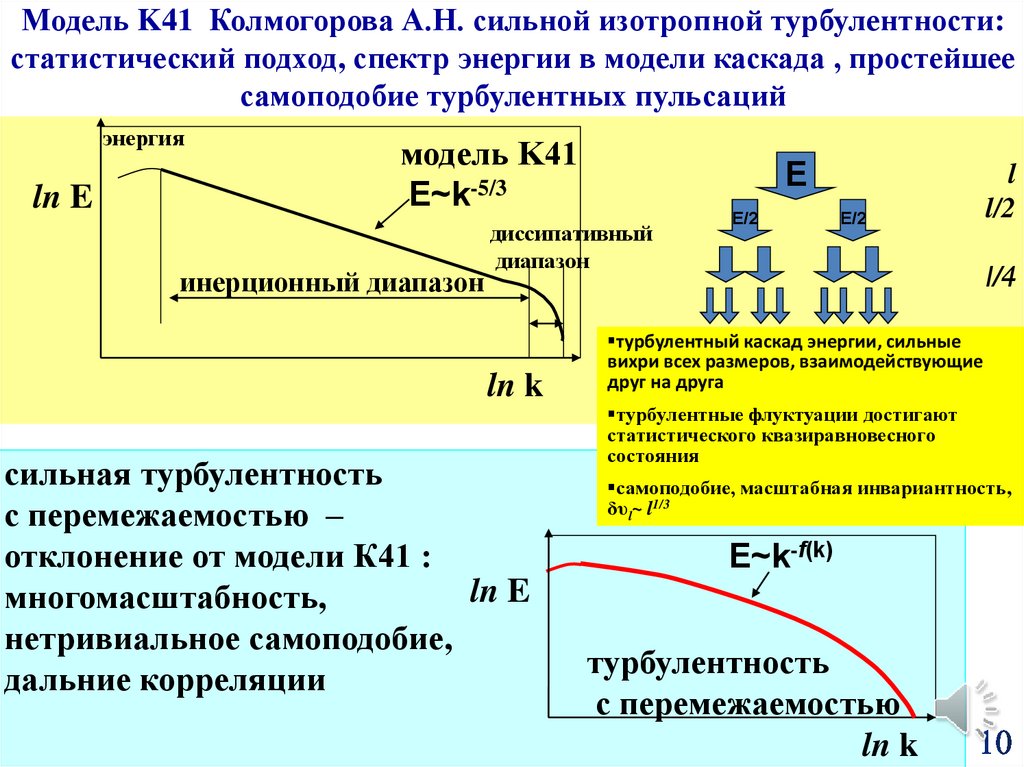
Модель K41 Колмогорова А.Н. сильной изотропной турбулентности:
статистический подход, спектр энергии в модели каскада , простейшее
самоподобие турбулентных пульсаций
энергия
ln E
модель K41
E~k-5/3
инерционный диапазон
E
диссипативный
диапазон
ln k
сильная турбулентность
с перемежаемостью –
отклонение от модели К41 :
ln E
многомасштабность,
нетривиальное самоподобие,
дальние корреляции
E/2
E/2
l
l/2
l/4
турбулентный каскад энергии, сильные
вихри всех размеров, взаимодействующие
друг на друга
турбулентные флуктуации достигают
статистического квазиравновесного
состояния
самоподобие, масштабная инвариантность,
δυl~ l1/3
E~k-f(k)
турбулентность
с перемежаемостью
ln k

11.

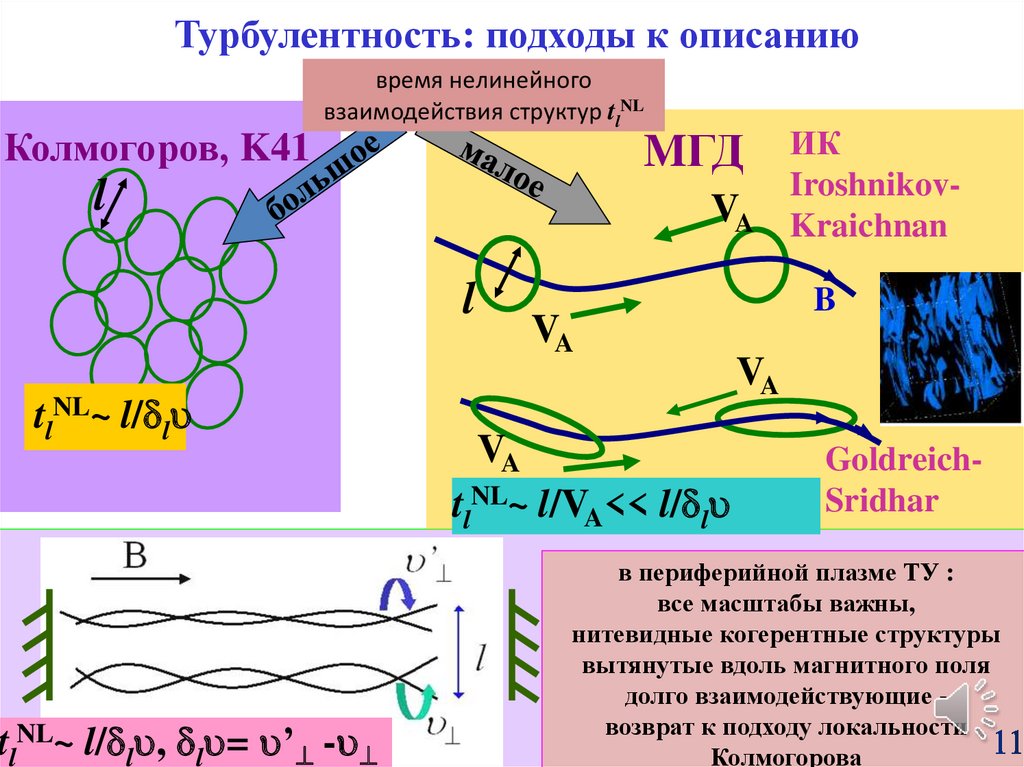
Турбулентность: подходы к описанию
Колмогоров, K41
время нелинейного
взаимодействия структур tlNL
MГД
l
VA
l
tlNL~ l/ l
tlNL~ l/ l , l = ’ -
ИК
IroshnikovKraichnan
B
VA
VA
VA
tlNL~ l/VA<< l/ l
GoldreichSridhar
в периферийной плазме ТУ :
все масштабы важны,
нитевидные когерентные структуры
вытянутые вдоль магнитного поля
долго взаимодействующие возврат к подходу локальности
Колмогорова

12.

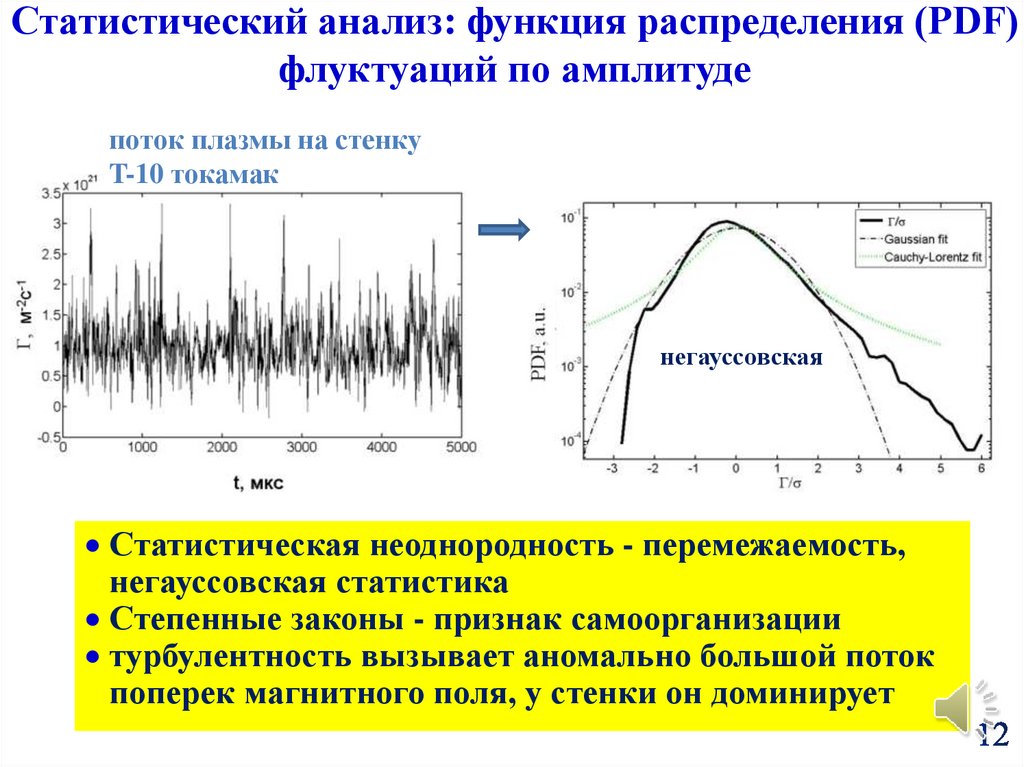
Статистический анализ: функция распределения (PDF)
флуктуаций по амплитуде
поток плазмы на стенку
T-10 токамак
негауссовская
Статистическая неоднородность - перемежаемость,
негауссовская статистика
Степенные законы - признак самоорганизации
турбулентность вызывает аномально большой поток
поперек магнитного поля, у стенки он доминирует

13.

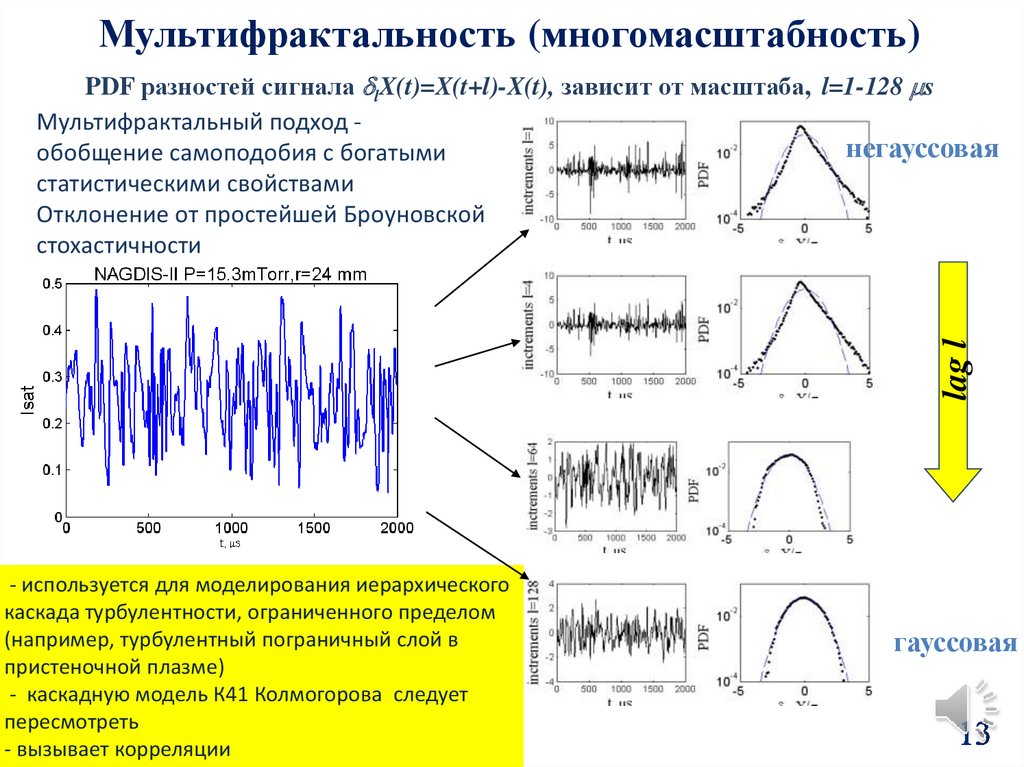
Мультифрактальность (многомасштабность)
lag l
PDF разностей сигнала lX(t)=X(t+l)-X(t), зависит от масштаба, l=1-128 s
Мультифрактальный подход негауссовая
обобщение самоподобия с богатыми
статистическими свойствами
Отклонение от простейшей Броуновской
стохастичности
- используется для моделирования иерархического
каскада турбулентности, ограниченного пределом
(например, турбулентный пограничный слой в
пристеночной плазме)
- каскадную модель К41 Колмогорова следует
пересмотреть
- вызывает корреляции
гауссовая

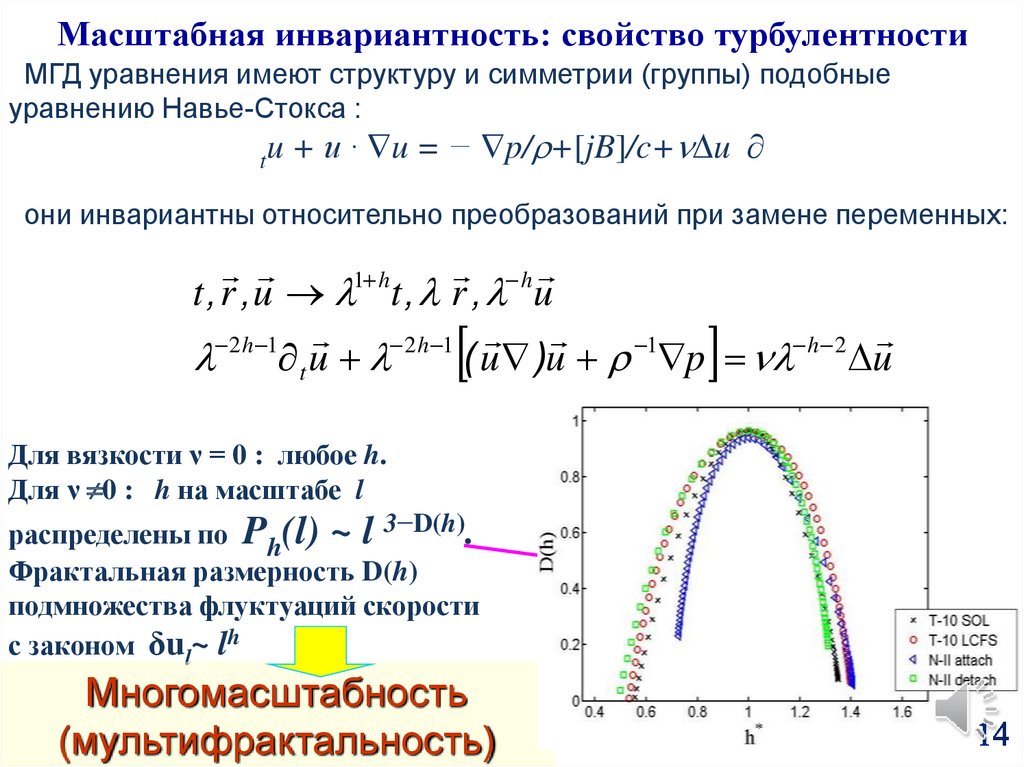
14.

Масштабная инвариантность: свойство турбулентности
МГД уравнения имеют структуру и симметрии (группы) подобные
уравнению Навье-Стокса :
tu
+ u · u = − p/ +[jB]/c+ u ∂
они инвариантны относительно преобразований при замене переменных:
h
1 h
t , r ,u t , r , u
2 h 1
2 h 1
1
h 2
tu
( u )u p u
Для вязкости ν = 0 : любое h.
Для ν 0 : h на масштабе l
распределены по Ph(l) ~ l 3−D(h).
Фрактальная размерность D(h)
подмножества флуктуаций скорости
с законом δul~ lh
Многомасштабность
(мультифрактальность)

15.

Сравнительное исследование
турбулентности и супердиффузии
в астрофизической и
лабораторной плазме

16.

Метод моментов функции распределения
(структурные функции высоких порядков) :
демонстрация обобщенной масштабной инвариантности расширенного самоподобия (ESS )
q
S q ( ) X ( r , t ) ,
X ( r , t ) X ( r , t ) X ( r , t )
9
10
Sq( )~ q/3 гауссовская (для модели K41)
Sq( )~ (q) – негауссовская статистика
Аппроксимация экспериментальных
PDF известными функциями: очень
сложная задача. Альтернативой
является описание неоднородности
турбулентности на различных
масштабах методами моментов PDF
(структурными функциями)
q=7
7
10
q=6
6
10
Броуновский сигнал
q=5
5
Sq( )
.. усреднение
Sq( )
q=8
8
10
10
q=4
4
10
q=3
3
10
q=2
2
10
1
10
0
10 0
10
1
10
2
10
Sq( )
Toкамак T-10
3
10

17.

Метод моментов:
демонстрация обобщенной масштабной инвариантности расширенного самоподобия (ESS )
q
S q ( ) X (r , t ) ~ ( q)
X (r , t ) X (r , t ) X (r , t )
Колмогоров K41 (q)=q/3
q / 3
Sq ( ) S3 ( )
Budaev,Savin,Zelenyi e a PPCF 2008
GSE Bx
TBL MP
Interball,
19.06.1998
q=8
q=7
q=6
q=5
q=4
q=3
q=2
Tokamak T-10
edge plasma
Дальние корреляции и аномальный перенос (супердиффузия) вызваны ESS
С учетом граничных эффектов, универсальность турбулентности

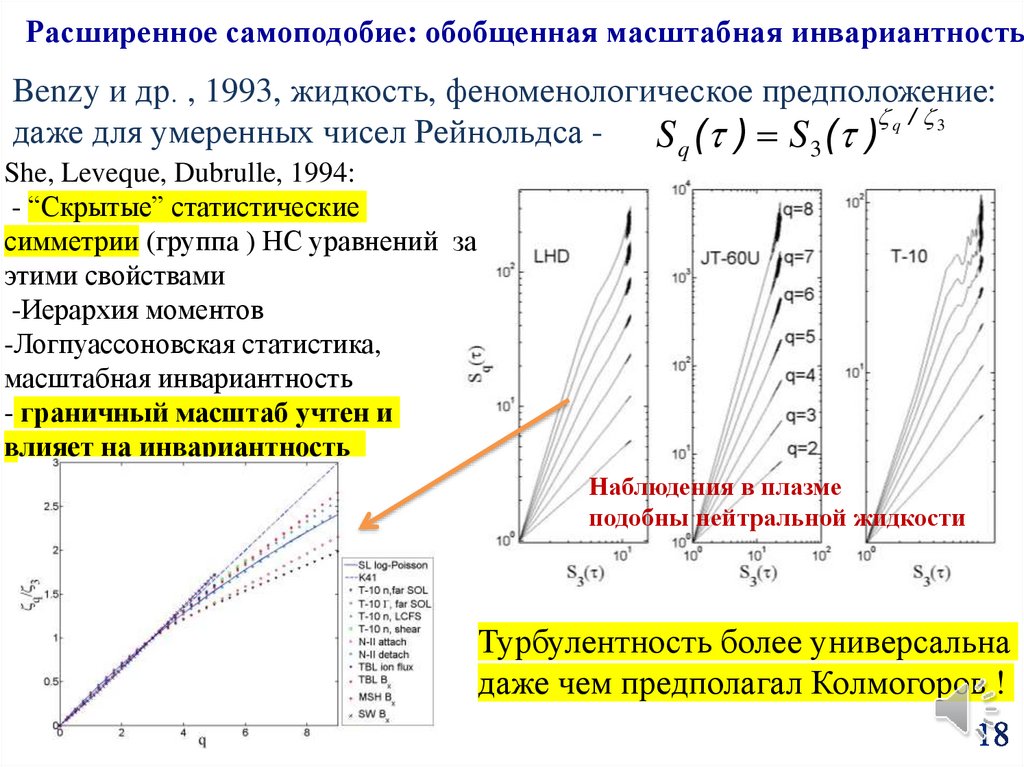
18.

Расширенное самоподобие: обобщенная масштабная инвариантность
Benzy и др. , 1993, жидкость, феноменологическое предположение:
/
даже для умеренных чисел Рейнольдса S q ( ) S3 ( ) q 3
She, Leveque, Dubrulle, 1994:
- “Скрытые” статистические
симметрии (группа ) НС уравнений за
этими свойствами
-Иерархия моментов
-Логпуассоновская статистика,
масштабная инвариантность
- граничный масштаб учтен и
влияет на инвариантность
Наблюдения в плазме
подобны нейтральной жидкости
Турбулентность более универсальна
даже чем предполагал Колмогоров !

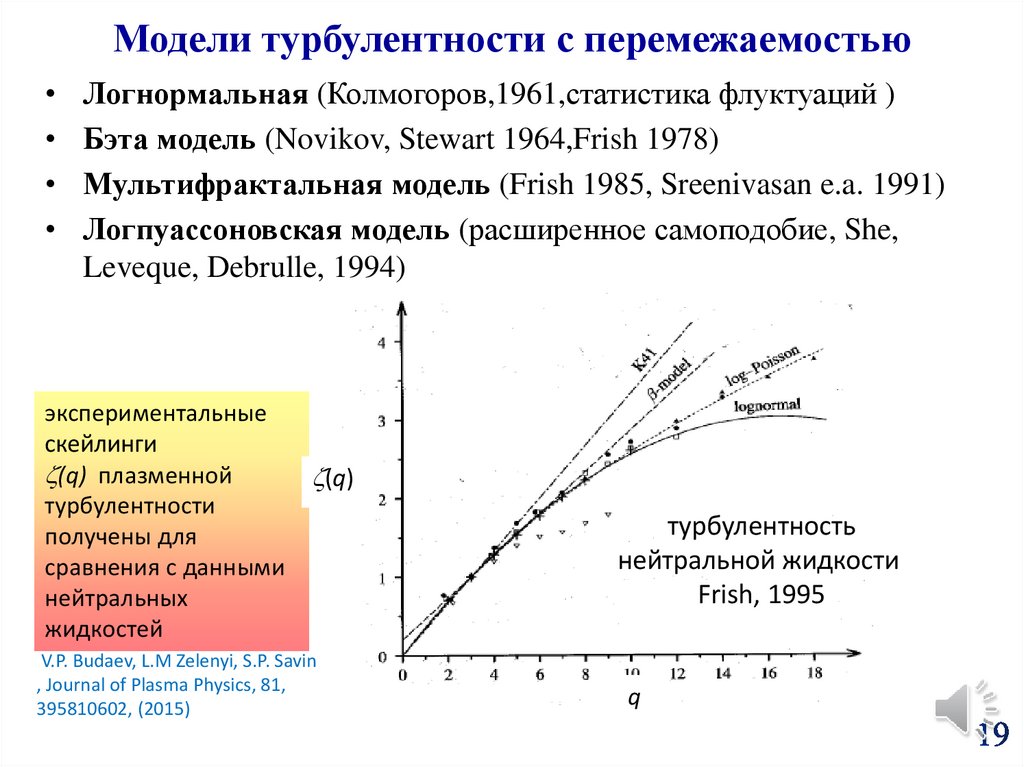
19.

Модели турбулентности с перемежаемостью
Логнормальная (Колмогоров,1961,статистика флуктуаций )
Бэта модель (Novikov, Stewart 1964,Frish 1978)
Мультифрактальная модель (Frish 1985, Sreenivasan e.a. 1991)
Логпуассоновская модель (расширенное самоподобие, She,
Leveque, Debrulle, 1994)
экспериментальные
скейлинги
(q) плазменной
турбулентности
получены для
сравнения с данными
нейтральных
жидкостей
(q)
V.P. Budaev, L.M Zelenyi, S.P. Savin
, Journal of Plasma Physics, 81,
395810602, (2015)
турбулентность
нейтральной жидкости
Frish, 1995
q

20.

Обобщение каскадных моделей турбулентностилогпуассоновская модель с пермежаемостью ,
случайный мультипликативный процесс
Скорость диссипации энергии ε на
масштабах l1 и l2: (l2)=W(l1, l2) ε(l1)
(l)~l (q) , log(Wq(l1, l2) )/log(l2/l1)= (q)
l
q 1
l
q
l
q
l
Aq q 1
l l
,
иерархия моментов
0 1
ln( ) обладает логпуассоновской
статистикой
x e x
( x )
x=ln l / ln .
( x 1)
q
(q ) (1 )
3 1
q
3
1
β - уровень перемежаемости (β=1 → (q)=q/3 колмогоровская модель К41)
Δ - скейлинг наиболее диссипативных перемежаемых структур l ~l – Δ
Изотропная 3D (She -Leveque model): Δ= β=2/3 если диссипативные структуры нитевидные филаменты 1D
S(q,l)~ l (q) , (q) оцениваются из экспериментальных данных

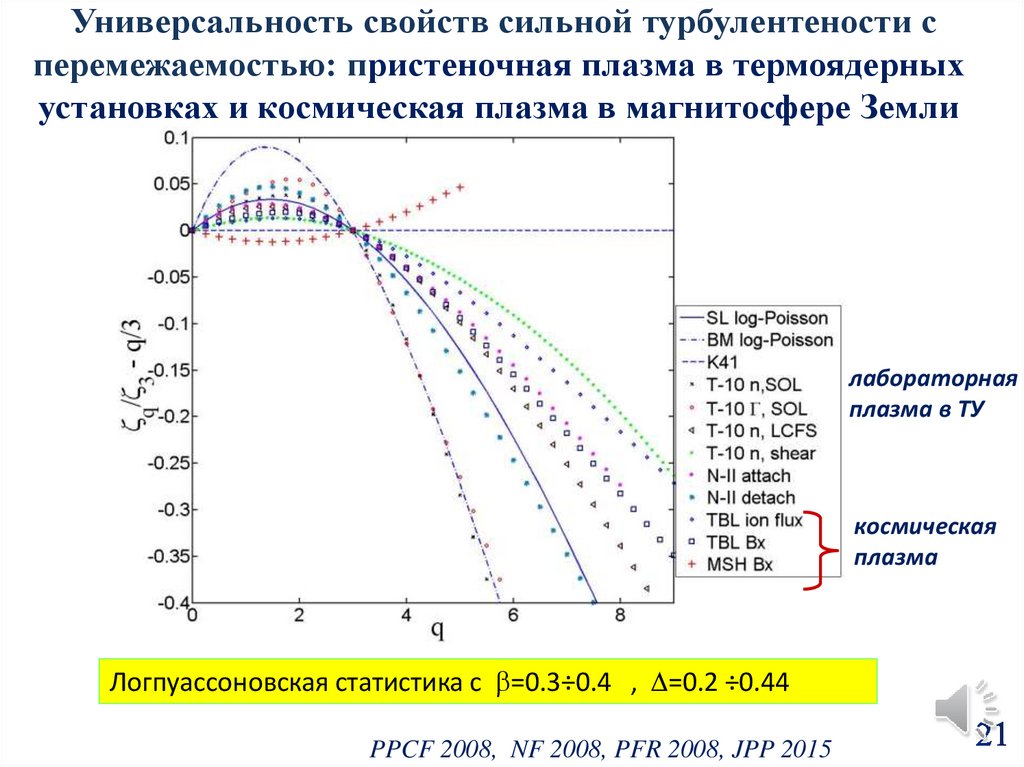
21.

Универсальность свойств сильной турбулентености с
перемежаемостью: пристеночная плазма в термоядерных
установках и космическая плазма в магнитосфере Земли
лабораторная
плазма в ТУ
космическая
плазма
Логпуассоновская статистика с =0.3÷0.4 , =0.2 ÷0.44
PPCF 2008, NF 2008, PFR 2008, JPP 2015

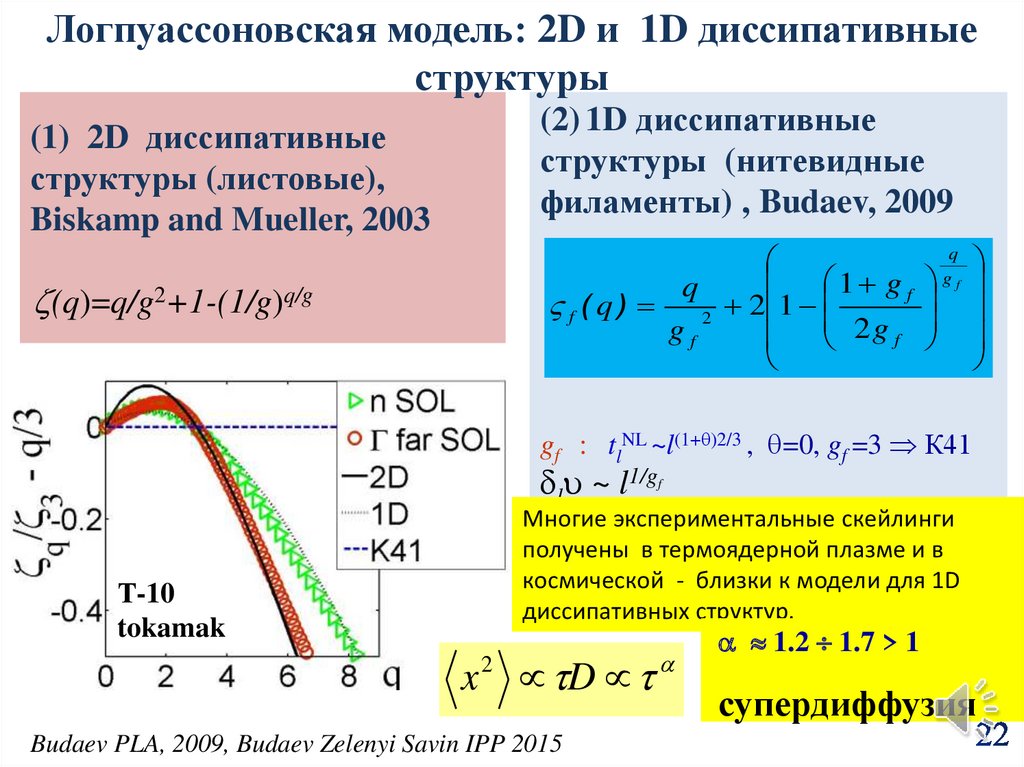
22.

Логпуассоновская модель: 2D и 1D диссипативные
структуры
(2) 1D диссипативные
структуры (нитевидные
филаменты) , Budaev, 2009
(1) 2D диссипативные
структуры (листовые),
Biskamp and Mueller, 2003
1 g f
q
f ( q ) 2 2 1
gf
2g f
(q)=q/g2+1-(1/g)q/g
q
gf
gf : tlNL ~l(1+ )2/3 , =0, gf =3 К41
l ~ l1/g
f
Многие экспериментальные скейлинги
получены в термоядерной плазме и в
космической - близки к модели для 1D
диссипативных структур.
Т-10
tokamak
x D
2
Budaev PLA, 2009, Budaev Zelenyi Savin IPP 2015
1.2 1.7 > 1
супердиффузия

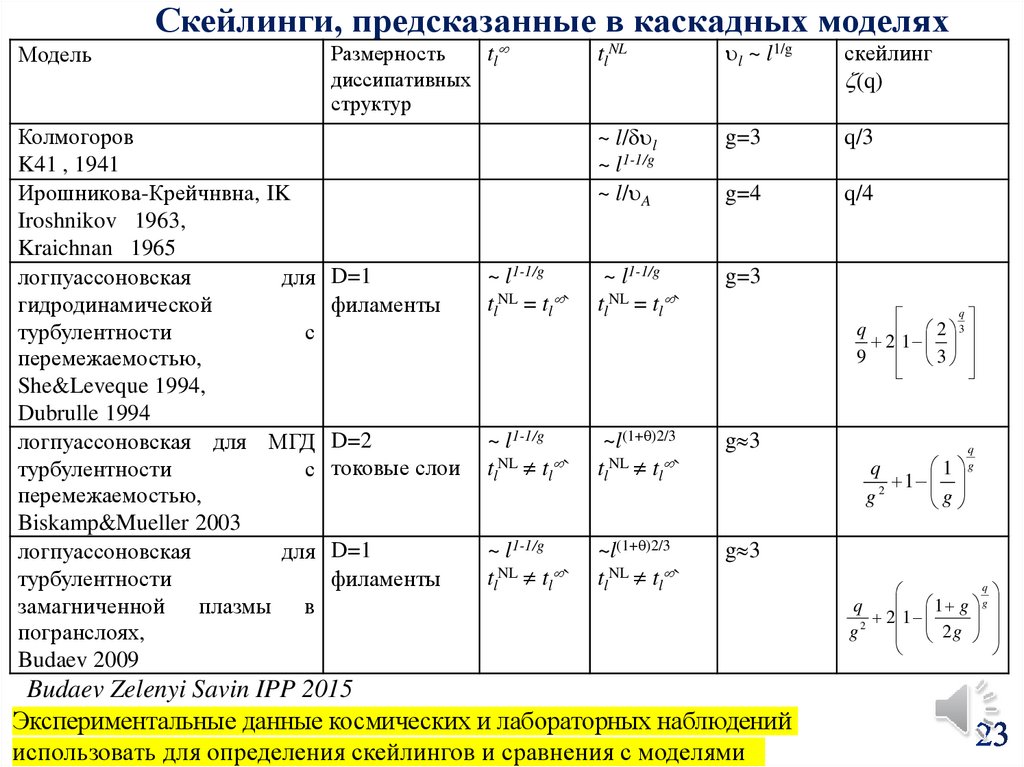
23.

Скейлинги, предсказанные в каскадных моделях
Модель
Колмогоров
K41 , 1941
Ирошникова-Крейчнвна, IK
Iroshnikov 1963,
Kraichnan 1965
логпуассоновская
для
гидродинамической
турбулентности
с
перемежаемостью,
She&Leveque 1994,
Dubrulle 1994
логпуассоновская для МГД
турбулентности
с
перемежаемостью,
Biskamp&Mueller 2003
логпуассоновская
для
турбулентности
замагниченной плазмы в
погранслоях,
Budaev 2009
tl
Размерность
диссипативных
структур
tlNL
l ~ l1/g
скейлинг
q)
~ l/δ l
~ l1-1/g
~ l/ A
g=3
q/3
g=4
q/4
D=1
филаменты
~ l1-1/g
tlNL = tl `
~ l1-1/g
tlNL = tl `
g=3
D=2
токовые слои
~ l1-1/g
tlNL tl `
~l(1+ )2/3
tlNL tl `
g 3
D=1
филаменты
~ l1-1/g
tlNL tl `
~l(1+ )2/3
tlNL tl `
g 3
q
q
2 3
2 1
3
9
1
q
1
2
g
g
Budaev Zelenyi Savin IPP 2015
Экспериментальные данные космических и лабораторных наблюдений
использовать для определения скейлингов и сравнения с моделями
q
g
q
g
1 g
q
2 1
g2
2g

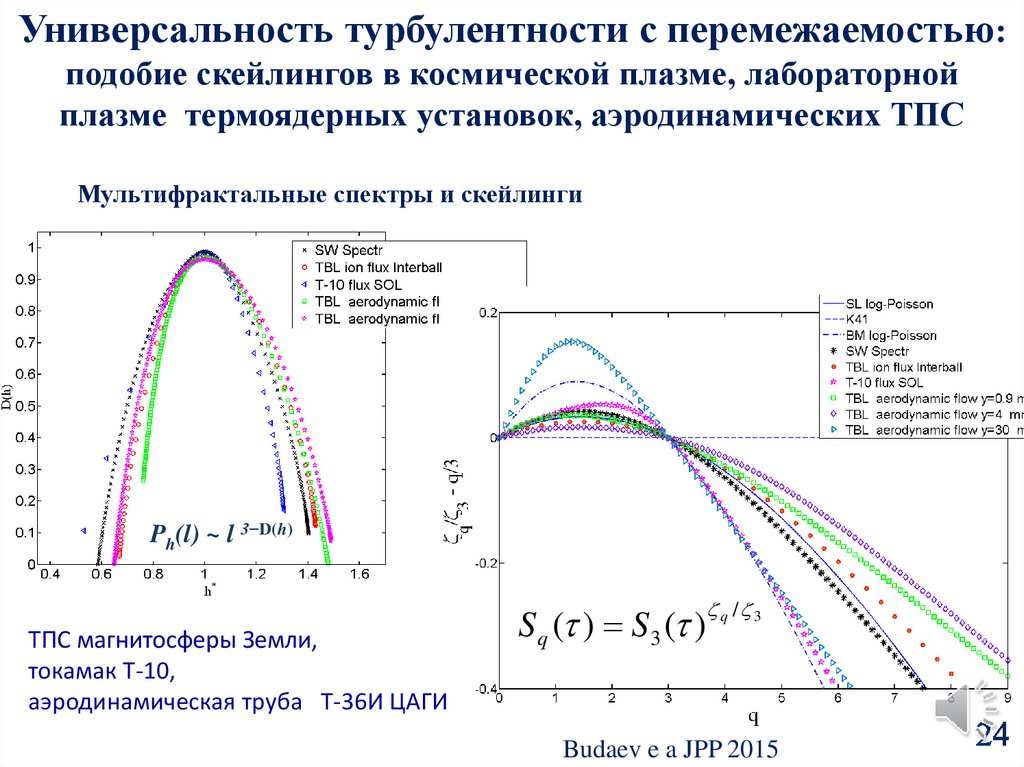
24.

Универсальность турбулентности с перемежаемостью:
подобие скейлингов в космической плазме, лабораторной
плазме термоядерных установок, аэродинамических ТПС
Мультифрактальные спектры и скейлинги
Ph(l) ~ l 3−D(h)
ТПС магнитосферы Земли,
токамак Т-10,
аэродинамическая труба T-36И ЦАГИ
S q ( ) S3 ( )
q / 3
Budaev e a JPP 2015

25.

Стохастическая кластеризации
материи: агломерация ионов и
атомов под влиянием динамики
турбулентной плазмы,
фрактальный рост структур,
самоподобие

26.

Взаимодействие плазма-стенка в термоядерных установках с
магнитным удержанием плазмы : сильная эрозия материалов
W VM-P
Toкамак Т-10, ~1000 разрядов, 1MW ECRH:
растрескивание и дуговые кратеры
Grashin e a FED 146 B (2019) 2100
Эрозия и разрушения материалов под действием плазмы - трещины,
испарение, переосаждение, плавление, дуговые процессы : много процессов
действуют одновременно.
Плазма -стенка: сложная система в неравновесном состоянии

27.

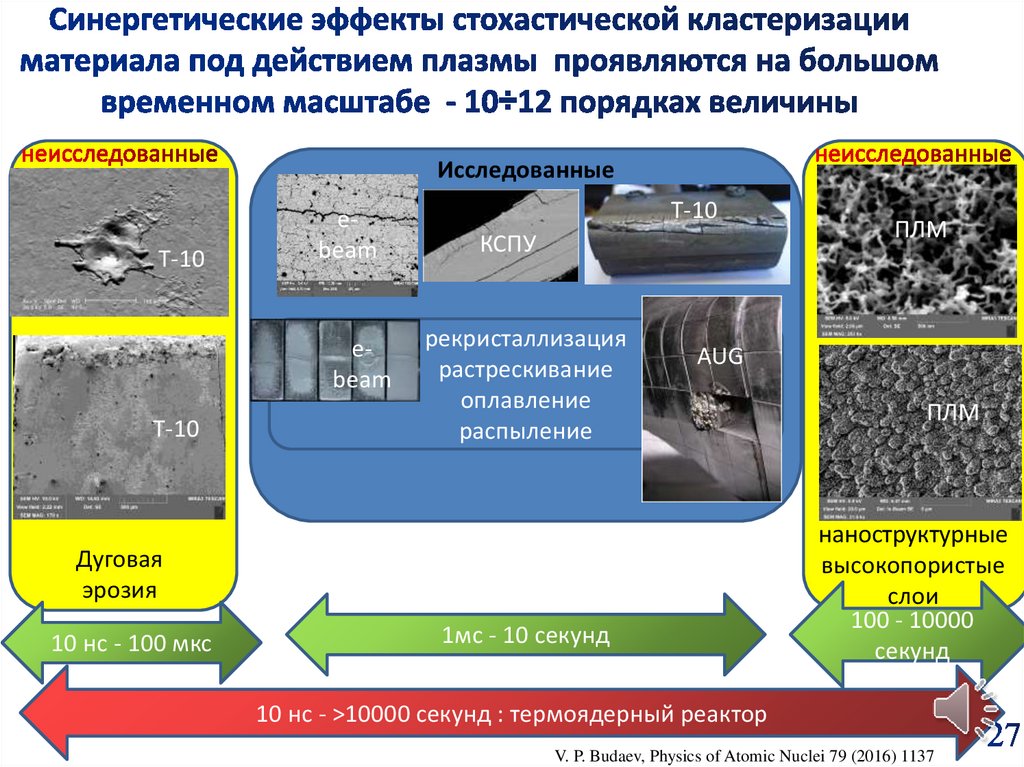
Исследованные
Т-10
ebeam
ebeam
Т-10
Т-10
КСПУ
рекристаллизация
растрескивание
оплавление
распыление
AUG
Дуговая
эрозия
10 нс - 100 мкс
ПЛМ
1мс - 10 секунд
ПЛМ
наноструктурные
высокопористые
слои
100 - 10000
секунд
10 нс - >10000 секунд : термоядерный реактор
V. P. Budaev, Physics of Atomic Nuclei 79 (2016) 1137

28.

Действие плазмы: универсальность роста нано- микроструктурных
кораллоподобных высокопористых поверхностей W, Mo, Ti, Ni, Fe, С
Ti
самоподобная
иерархическая
гранулярность масштабная
инвариантность
, гелиевая плазма ПЛМ Кораллоподобные
структуры типа
«цветная капуста»
W,КСПУ-Т
Mo
гелиевая
плазма
ПЛМ
Углеродные переосажденные
слои, ТокамакT-10
Будаев , Письма в ЖЭТФ, 2017
V.P. Budaev, Symmetry (2021) 13 796.

29.

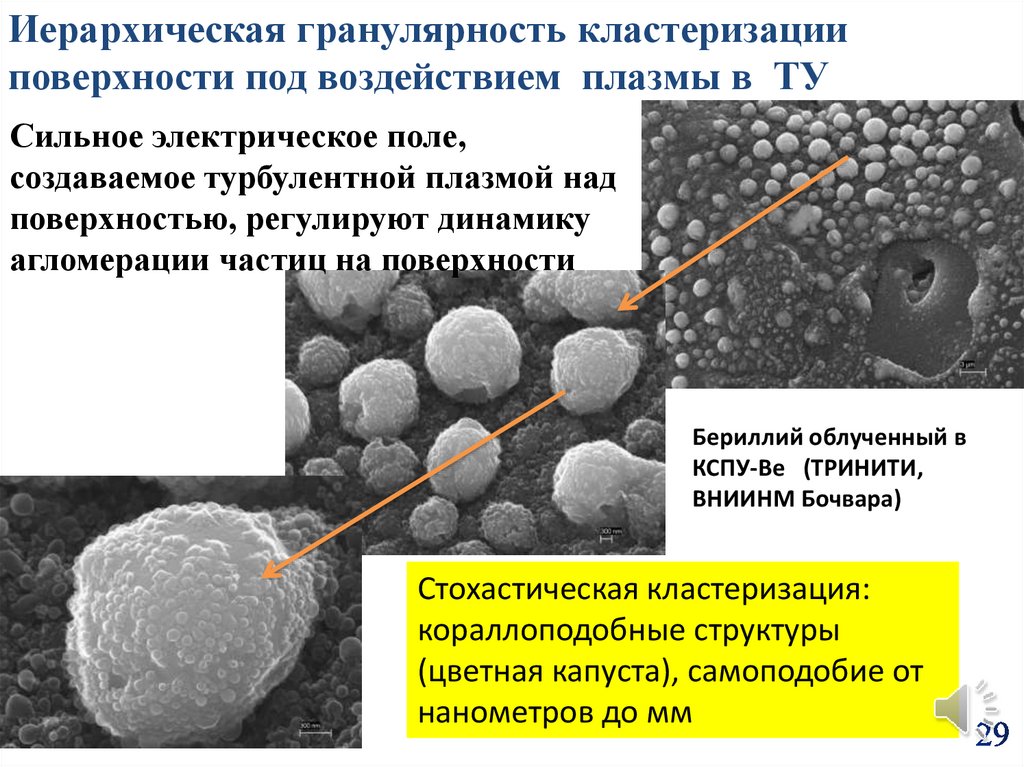
Иерархическая гранулярность кластеризации
поверхности под воздействием плазмы в ТУ
Сильное электрическое поле,
создаваемое турбулентной плазмой над
поверхностью, регулируют динамику
агломерации частиц на поверхности
Бериллий облученный в
КСПУ-Ве (ТРИНИТИ,
ВНИИНМ Бочвара)
Стохастическая кластеризация:
кораллоподобные структуры
(цветная капуста), самоподобие от
нанометров до мм

30.

Дилатационная симметрия- автомодельность
кораллоподобные структуры (цветная капуста)
Ве бериллий
КСПУ
Цветная капуста
• Фракталы – самоподобие при
растяжении-сжатии (масштабная
инвариантность)
• Дилатационные симметрии
отражают свойства уравнений
состояния
• определение:
x ax : h(x) =a-Hh(ax), a>0
Пример: степенные функции и вейвлет
преобразование:
Дилатация:
a=x1/x2
Масштабная инвариантность - фундаментальное свойство структур
материи, в том числе астрофизических объектов. Задача- систематизация
скейлингов автомодельности, поиск универсальности

31.

Фрактальная размерность агломератов,
сформированных при плазменном воздействии
T-10: D = 2.15 2.30
NAGDIS-II
P.V.Romanov et al. J. Nucl. Mat.
307 – 311, 2002, 1294
N.Ohno , DFP
Workshop,
Napa, USA,2005
DIII-D
W.P.West, HIFRM7,
Portland, USA, 2004
QSPA: D = 2.1 2.3 W
1 m
Tore-Supra: D = 2.19
E.Dechlambre , 30th EPS, P3, 169,
St-Peterburg, 2003
Li
Фрактальная размерность D = 2.15 2.30

32.

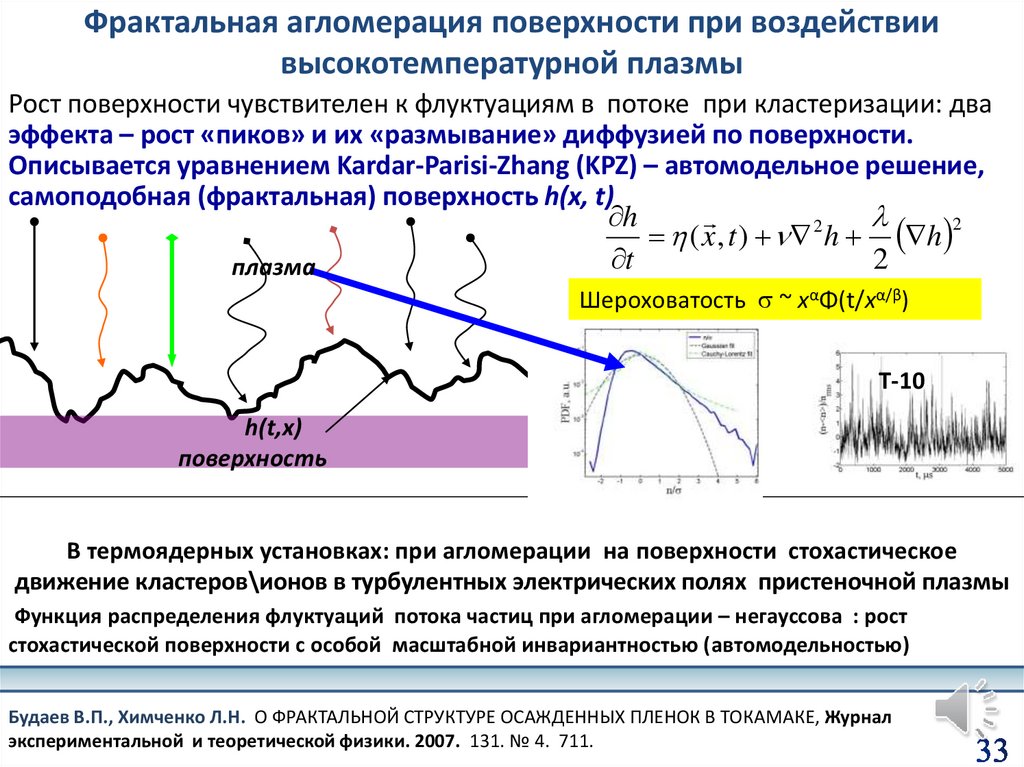
Фрактальная агломерация поверхности при воздействии
высокотемпературной плазмы
Рост поверхности чувствителен к флуктуациям в потоке при кластеризации: два
эффекта – рост «пиков» и их «размывание» диффузией по поверхности.
Описывается уравнением Kardar-Parisi-Zhang (KPZ) – автомодельное решение,
самоподобная (фрактальная) поверхность h(x, t)
плазма
h
2
2
( x , t ) h h
t
2
Шероховатость ~ xαΦ(t/xα/β)
T-10
h(t,x)
поверхность
В термоядерных установках: при агломерации на поверхности стохастическое
движение кластеров\ионов в турбулентных электрических полях пристеночной плазмы
Функция распределения флуктуаций потока частиц при агломерации – негауссова : рост
стохастической поверхности с особой масштабной инвариантностью (автомодельностью)
Будаев В.П., Химченко Л.Н. О ФРАКТАЛЬНОЙ СТРУКТУРЕ ОСАЖДЕННЫХ ПЛЕНОК В ТОКАМАКЕ, Журнал
экспериментальной и теоретической физики. 2007. 131. № 4. 711.

33.

Теоретическое рассмотрение агломерации
Перераспределение массы между кластерами в процессе агломерации
(слипание/распад кластеров разного размера) аналогичен каскадному процессу
передачи энергии в турбулентности
Распределение кластеров по размерам в статистически однородной системе
описывается уравнением Смолуховского для коагуляции :
m1+m2→m
N (m, t )
dm1dm2 K (m1 , m2 ) N (m1 , t )N (m2 , t ) (m m1 m2 ) (m m1 ) (m m2 )
t
2 0
J
J
0 (m m0 ) (m M )
m0
M
формальная аналогия между (1) уравнением для описания нелинейного процесса агрегации-фрагментации и
(2) кинетическим уравнением для изотропной 3-волновой турбулентности, C. Connaughton, e a, PRL (2005)
• Ядро автомодельное:
• K(hm1,hm2,hm)=h K(m1,m2,m), K(m1,m2)~m1 m2 , + = .
• Автомодельные решения: спектр Колмогорова-Захарова
N(m)=Cm-(3+ )/2
Степенные спектры высот стохастической поверхности после
мощного действия плазмы

34.

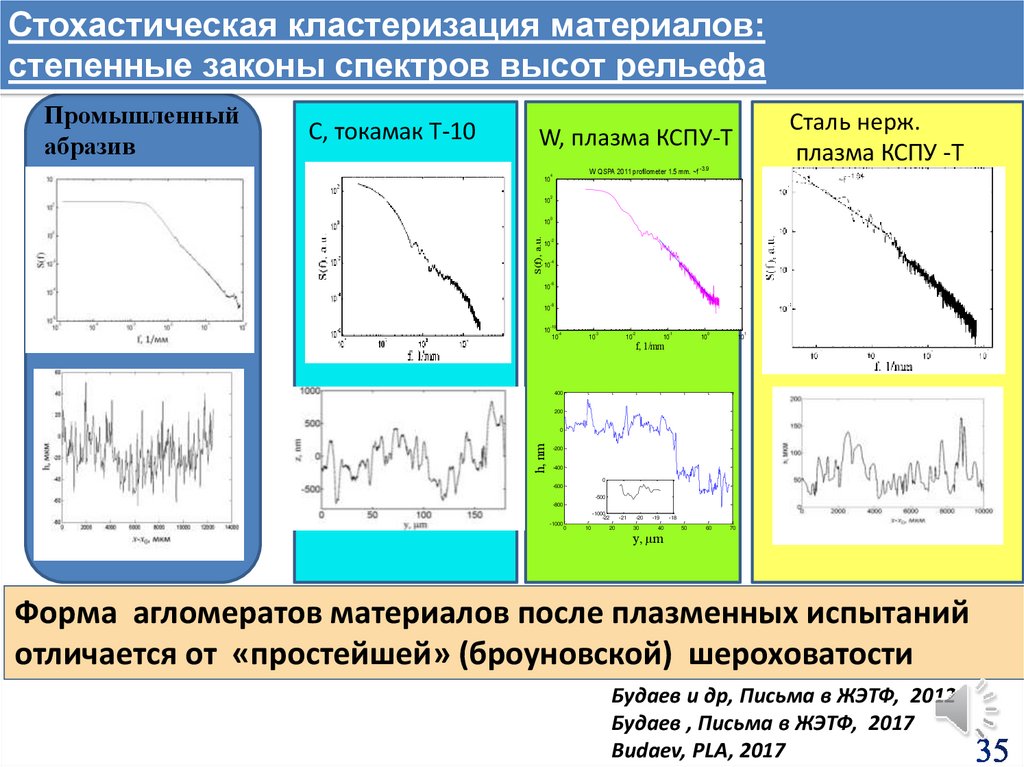
Стохастическая кластеризация материалов:
степенные законы спектров высот рельефа
Промышленный
абразив
C, токамак T-10
Сталь нерж.
плазма КСПУ -T
W, плазма КСПУ-T
W QSPA 2011 profilometer 1.5 mm. ~f -3.9
4
10
2
10
0
S(f), a.u.
10
-2
10
-4
10
-6
10
-8
10
-10
10
-4
-3
10
-2
10
10
-1
0
10
1
10
f, 1/mm
10
400
200
h, nm
0
-200
-400
0
-600
-500
-800
-1000
-22
-1000
0
10
-21
20
-20
30
-19
40
y, m
-18
50
60
70
Форма агломератов материалов после плазменных испытаний
отличается от «простейшей» (броуновской) шероховатости
Будаев и др, Письма в ЖЭТФ, 2012
Будаев , Письма в ЖЭТФ, 2017
Budaev, PLA, 2017

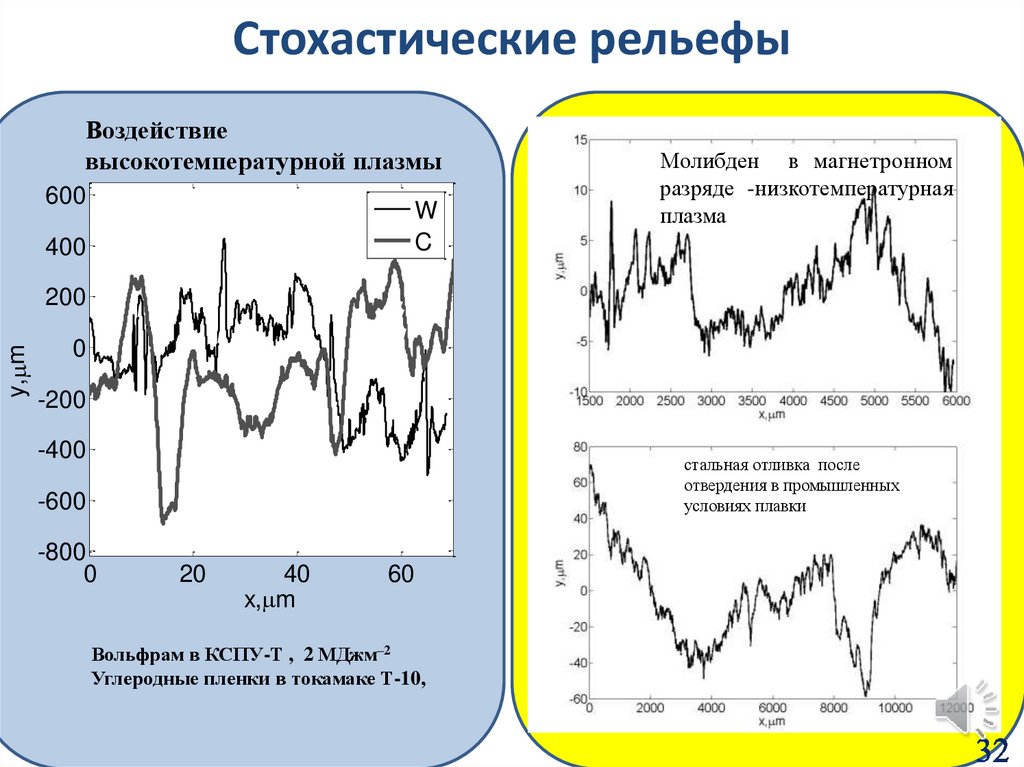
35.

Стохастические рельефы
Воздействие
высокотемпературной плазмы
600
W
C
400
Молибден в магнетронном
разряде -низкотемпературная
плазма
y, m
200
0
-200
-400
стальная отливка после
отвердения в промышленных
условиях плавки
-600
-800
0
20
40
x, m
60
Вольфрам в КСПУ-Т , 2 МДжм–2
Углеродные пленки в токамаке Т-10,

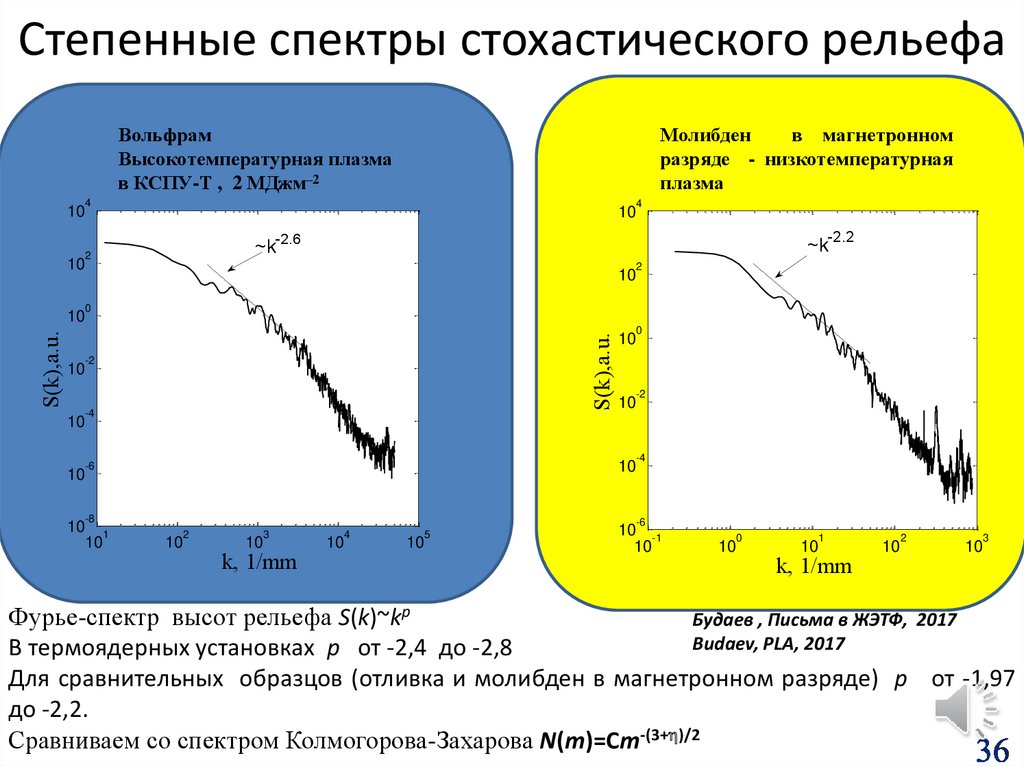
36.

Степенные спектры стохастического рельефа
Молибден
в магнетронном
разряде - низкотемпературная
плазма
Вольфрам
Высокотемпературная плазма
в КСПУ-Т , 2 МДжм–2
4
4
10
10
-2.2
-2.6
~k
~k
2
10
2
10
0
S(k),a.u.
S(k),a.u.
10
-2
10
-4
0
10
-2
10
10
-4
10
-6
10
-8
10 1
10
-6
2
10
3
10
k, 1/mm
4
10
5
10
10 -1
10
0
10
1
10
k, 1/mm
2
10
3
10
Фурье-спектр высот рельефа S(k)~kp
Будаев , Письма в ЖЭТФ, 2017
Budaev, PLA, 2017
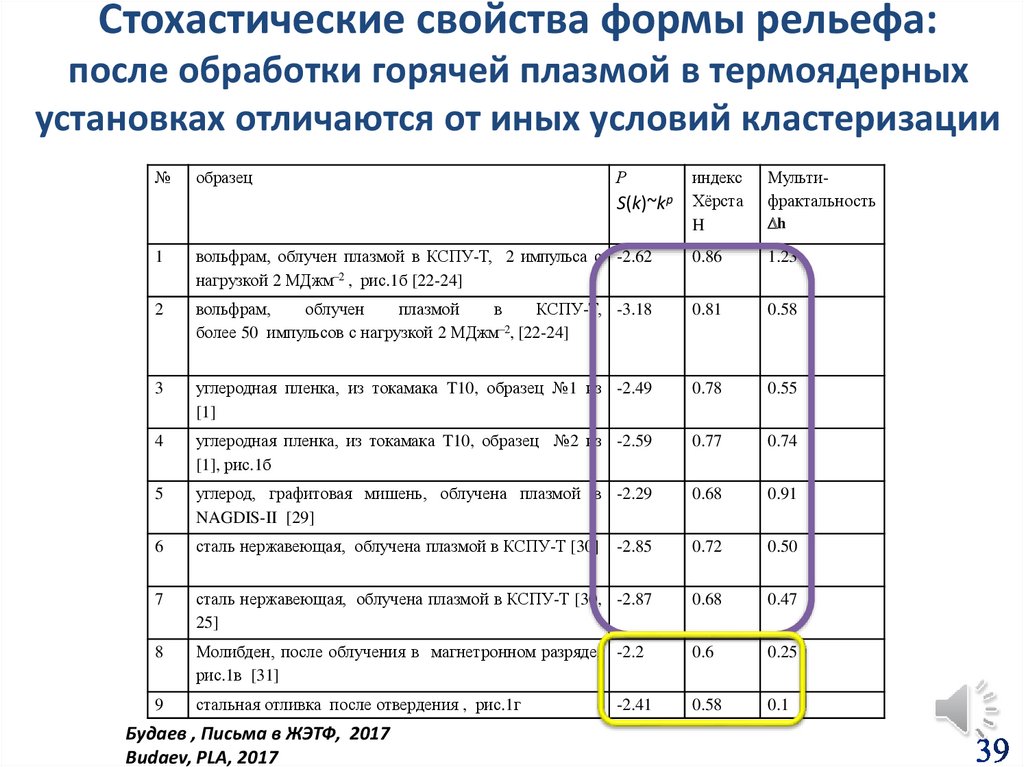
В термоядерных установках р от -2,4 до -2,8
Для сравнительных образцов (отливка и молибден в магнетронном разряде) р от -1,97
до -2,2.
Сравниваем со спектром Колмогорова-Захарова N(m)=Cm-(3+ )/2

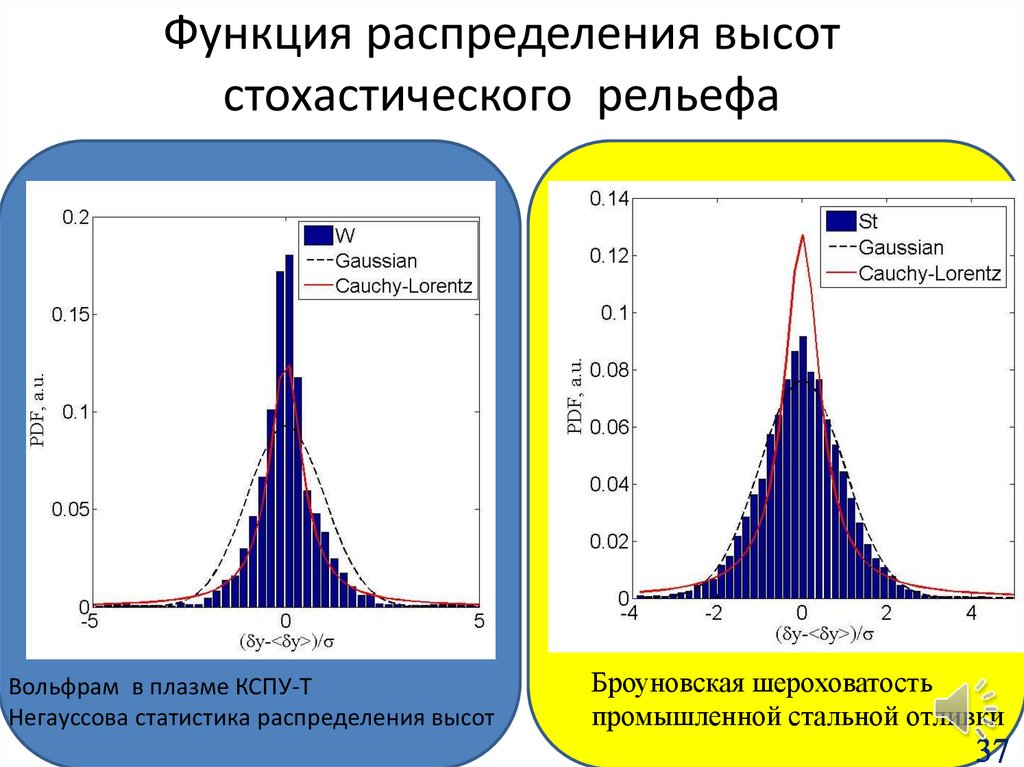
37.

Функция распределения высот
стохастического рельефа
Вольфрам в плазме КСПУ-Т
Негауссова статистика распределения высот
Броуновская шероховатость
промышленной стальной отливки

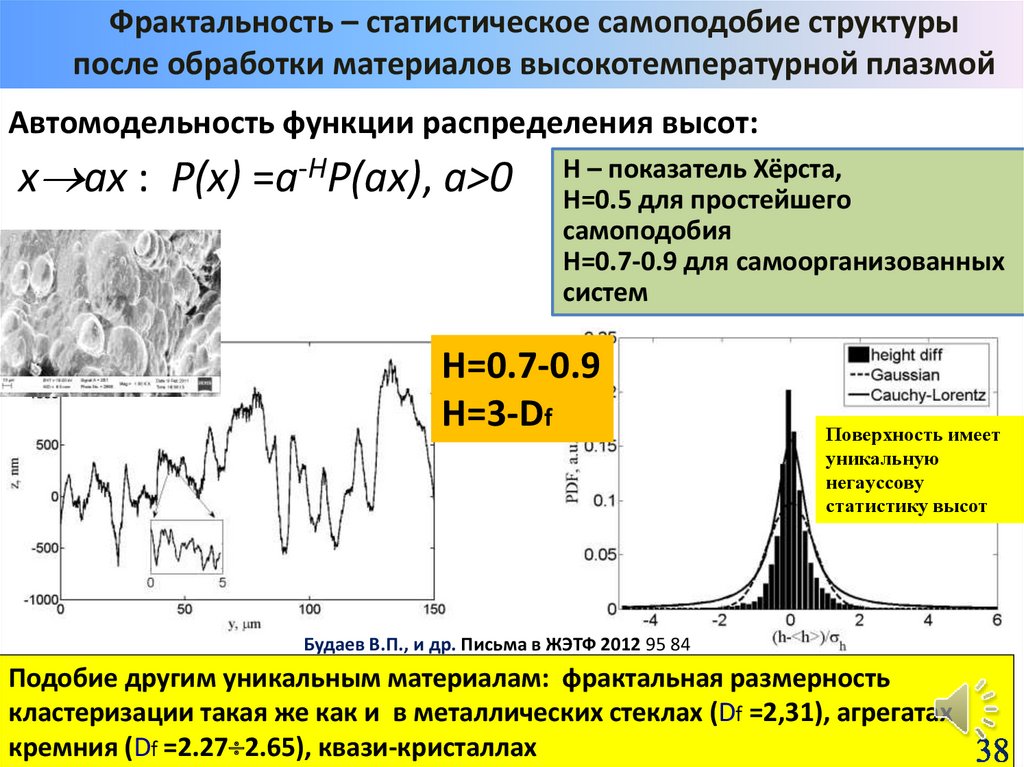
38.

Фрактальность – статистическое самоподобие структуры
после обработки материалов высокотемпературной плазмой
Автомодельность функции распределения высот:
х aх : P(х) =a-HP(aх), a>0
Н – показатель Хёрста,
Н=0.5 для простейшего
самоподобия
Н=0.7-0.9 для самоорганизованных
систем
Н=0.7-0.9
Н=3-Df
Поверхность имеет
уникальную
негауссову
статистику высот
Будаев В.П., и др. Письма в ЖЭТФ 2012 95 84
Подобие другим уникальным материалам: фрактальная размерность
кластеризации такая же как и в металлических стеклах (Df =2,31), агрегатах
кремния (Df =2.27 2.65), квази-кристаллах

39.

Стохастические свойства формы рельефа:
после обработки горячей плазмой в термоядерных
установках отличаются от иных условий кластеризации
№
образец
Р
S(k)~kp
индекс
Хёрста
H
Мультифрактальность
h
1
вольфрам, облучен плазмой в КСПУ-Т, 2 импульса с -2.62
нагрузкой 2 МДжм–2 , рис.1б [22-24]
0.86
1.23
2
вольфрам,
облучен
плазмой
в
КСПУ-Т, -3.18
–2
более 50 импульсов с нагрузкой 2 МДжм , [22-24]
0.81
0.58
3
углеродная пленка, из токамака T10, образец №1 из -2.49
[1]
0.78
0.55
4
углеродная пленка, из токамака T10, образец №2 из -2.59
[1], рис.1б
0.77
0.74
5
углерод, графитовая мишень, облучена плазмой в -2.29
NAGDIS-II [29]
0.68
0.91
6
сталь нержавеющая, облучена плазмой в КСПУ-Т [30]
-2.85
0.72
0.50
7
сталь нержавеющая, облучена плазмой в КСПУ-Т [30, -2.87
25]
0.68
0.47
8
Молибден, после облучения в магнетронном разряде, -2.2
рис.1в [31]
0.6
0.25
9
стальная отливка после отвердения , рис.1г
0.58
0.1
Будаев , Письма в ЖЭТФ, 2017
Budaev, PLA, 2017
-2.41

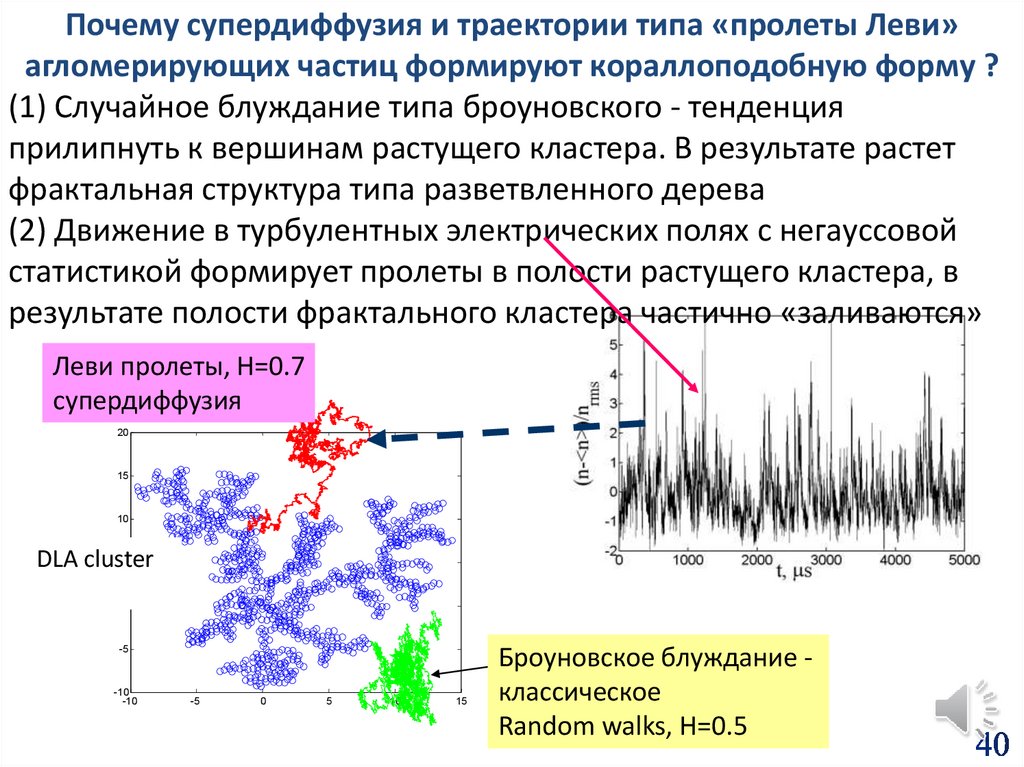
40.

Почему супердиффузия и траектории типа «пролеты Леви»
агломерирующих частиц формируют кораллоподобную форму ?
(1) Случайное блуждание типа броуновского - тенденция
прилипнуть к вершинам растущего кластера. В результате растет
фрактальная структура типа разветвленного дерева
(2) Движение в турбулентных электрических полях с негауссовой
статистикой формирует пролеты в полости растущего кластера, в
результате полости фрактального кластера частично «заливаются»
Леви пролеты, H=0.7
супердиффузия
20
15
10
DLA cluster
5
0
-5
-10
-10
-5
0
5
10
15
Броуновское блуждание классическое
Random walks, H=0.5

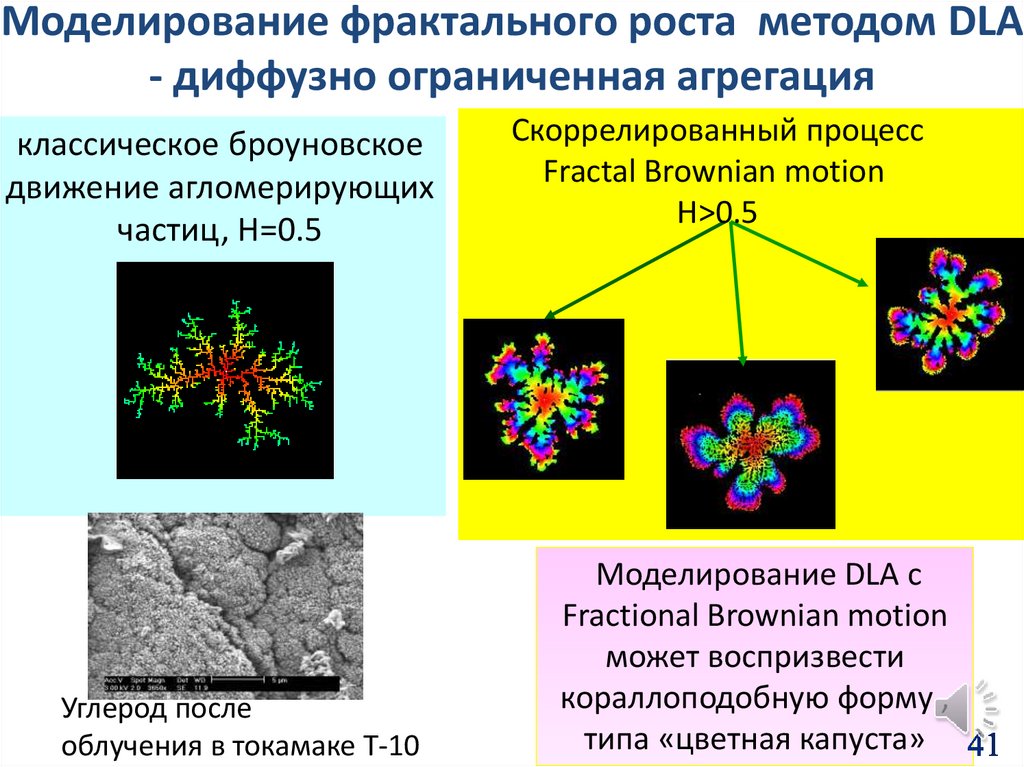
41.

Моделирование фрактального роста методом DLA
- диффузно ограниченная агрегация
классическое броуновское
движение агломерирующих
частиц, H=0.5
Углерод после
облучения в токамаке T-10
Скоррелированный процесс
Fractal Brownian motion
H>0.5
Моделирование DLA c
Fractional Brownian motion
может воспризвести
кораллоподобную форму ,
типа «цветная капуста»

42.

Формообразование в астрофизических объектах: аналогия с
топологией структур из лабораторных плазменных установок с
магнитным удержанием плазмы
астрофизические объекты
Космическая пыль
под микроскопом
лабораторная плазма
пыль
туманность Омега
Туманность «Морской конёк»
в Цефее
T-10 токамак

43.

Ридберговские атомы: кандидатный материал
для фрактального роста агломератов
Be КСПУ
Энергетический спектр атома водорода :
En = –Ry/n2 , где Ry — постоянная Ридберга, n — главное квантовое число . n>>1 - Ридберговские.
Характерный размер атома rn и типичный квазиклассический период обращения электрона Tn:
aB = 0.5·10-10 м — боровский радиус, T1 ~ 10-16 с.
R10=28Å
Моделирование кластеров
из ридберговских атомов:
перекрытие электронных
оболочек
потенциальная энергия
атомов цезия
n
d (нм)
D (см -3 )
1
0.153
2,8 × 10 23
10
15.3
2,8 × 10 17
100
1534
2,8 × 10 11
Оценка при n = 12 время жизни кластера: 25 секунд.
При n = 80 - время жизни, сопоставимое с возрастом Вселенной.
[Л. Холмлид, "Красные смещения в космосе, вызванные вынужденным комбинационным рассеянием света в холодной
межгалактической ридберговской материи, с экспериментальной проверкой". J. Exp. Теор. Phys. ЖЭТФ 100 (2005) 637–644.]
Остается открытым вопрос о метастабильности
атомов и сконденсированной фазы - агломератов
Задача систематизации наблюдений ридберговских состояний атомов
в сравнительном анализе космических данных и лабораторных термоядерных
установках с магнитным удержанием плазмы.

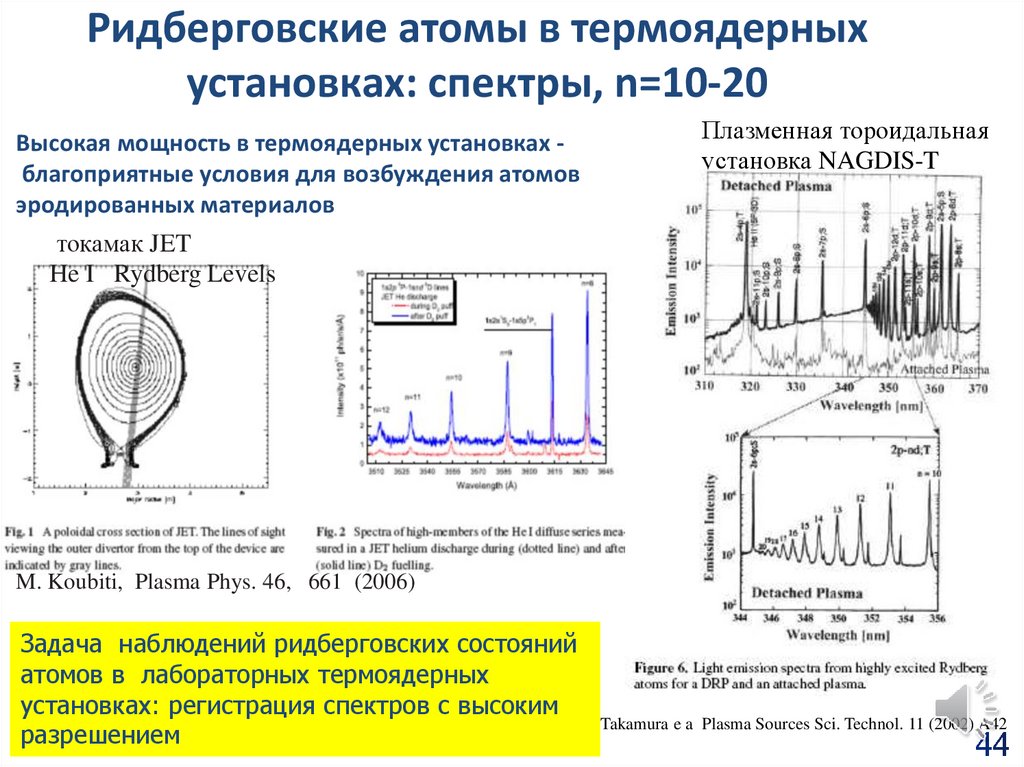
44.

Ридберговские атомы в термоядерных
установках: спектры, n=10-20
Высокая мощность в термоядерных установках благоприятные условия для возбуждения атомов
эродированных материалов
Плазменная тороидальная
установка NAGDIS-T
токамак JET
He I Rydberg Levels
M. Koubiti, Plasma Phys. 46, 661 (2006)
Задача наблюдений ридберговских состояний
атомов в лабораторных термоядерных
установках: регистрация спектров с высоким
разрешением
S Takamura e a Plasma Sources Sci. Technol. 11 (2002) A42

45.

Экспериментальные установки,
исполнители

46.

Научная группа, исполнители
Научная группа коллег из НИУ «МЭИ», ИКИ РАН, НИЦ «Курчатовский институт»,
МГУ, ИПМ им. Келдыша РАН, ИВТ РАН
Будаев В.П., д.ф.-м.н., профессор, НИУ «МЭИ», ИКИ РАН , НИЦ «Курчатовский
институт»
Дедов А.В., д.т.н., член-корреспондент РАН, НИУ «МЭИ»
Лисица В.С., д.ф.-м.н., НИЦ «Курчатовский институт»
Савин С.П., д.ф.-м.н., ИКИ РАН
Меньшов И.С., д.ф.-м.н., профессор, МГУ, ИПМ им. КелдышаРАН,
Попов В.Ю., д.ф.-м.н., профессор, МГУ, ИКИ РАН
Кавыршин Д.И., к.ф.-м.н., НИУ «МЭИ», ИВТ РАН
Елецкий А.В., д.ф.-м.н., профессор, НИУ «МЭИ»,
Федорович С.Д., к.т.н., доцент, НИУ «МЭИ»
Губкин М.К., к.ф.-м.н., доцент, НИУ «МЭИ»
Лукашевский М.В., к.т.н., доцент, НИУ «МЭИ»
студенты, аспиранты 14 человек
Кафедра Общей физики и ядерного синтеза НИУ «МЭИ»

47.

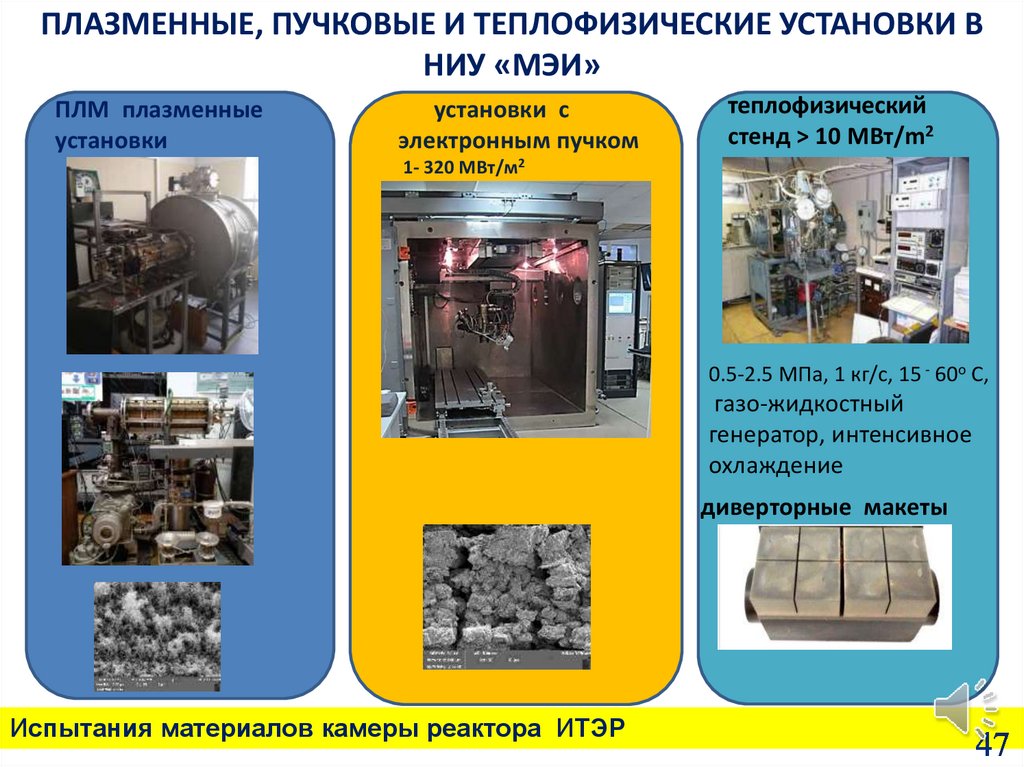
ПЛАЗМЕННЫЕ, ПУЧКОВЫЕ И ТЕПЛОФИЗИЧЕСКИЕ УСТАНОВКИ В
НИУ «МЭИ»
ПЛМ плазменные
установки
установки с
электронным пучком
теплофизический
стенд > 10 MВт/m2
1- 320 MВт/м2
0.5-2.5 MПa, 1 кг/с, 15 - 60o C,
газо-жидкостный
генератор, интенсивное
охлаждение
диверторные макеты
Испытания материалов камеры реактора ИТЭР

48.

Плазменная установка ПЛМ-М в НИУ "МЭИ" (2021) :
исследования турбулентности плазмы, испытания материалов и
технологий плазменного двигателя
Магнитная линейная система мультикасп 8-польный
B = 0.025 Тл на оси, в каспах до 0,2 Тл
ne=1018-1020 м-3,
Te = 1-5 эВ, с фракцией до 50 эВ,
Камера из нерж. стали охлаждаемая
Нагрузка на материал до 10 МВт/м−2
Ионный поток ~ 1023-1025 м−2с−1
Cтационарный разряд до 500 мин
Плазменная установка ПЛМ-М не имеет
аналогов в России, будет в ряду самых
мощных уникальных установок в мире
(MAGNUM-PSI ЕС, MPEX США)
Эксперименты в 2022-2024:
-турбулентность плазмы,спектроскопия, управление турбулентностью
;
- плазменные испытания материалов W, Ti, Li, Sn, B, C ;
-мощная лазерная нагрузка совместно с плазмой: стохастическая
кластеризация материалов;
Лазерный стенд
Nd:YAG LQ529A ,
1064 нм, 10 нс,
0,5 Дж,21 ТВт/м2

49.

Плазменная установка ПЛМ НИУ «МЭИ» (2017) :
исследований плазмы и испытания материалов, W, Mo, Ti, Li, С, Fe
Диаметр камеры – 0,16 м
Длина камеры – 0,8 м
Камера из нерж. стали – двойная с водным охлаждением
безмасляными вакуумными насосами 1х10-6 Торр.
Магнитная линейная система , мультикасп 8-польный
Магнитное поле продольное на оси – до 0,01 Тл, в каспах до
0,2 Тл
Рабочий газ – гелий, аргон, дейтерий
Время стационарного разряда до 200 мин и более
Ток плазменного разряда – до 15 А
Плотность плазмы – до 3х1018 м-3
Электронная температура – до 4 эВ
с фракцией горячих электронов до ~ 30 эВ.
Ионный поток на материальный образец - до 3х10 21м−2с−1
Диагностика – электрические зонды, оптическая,
магнитная, калориметрия
Получение наноструктурированной развитой поверхности тугоплавких материалов при
экспонировании в горячей плазме- формирование фрактальной структуры
Будаев В.П. и др ВАНТ, Сер.Термояд. синтез 2017

50.

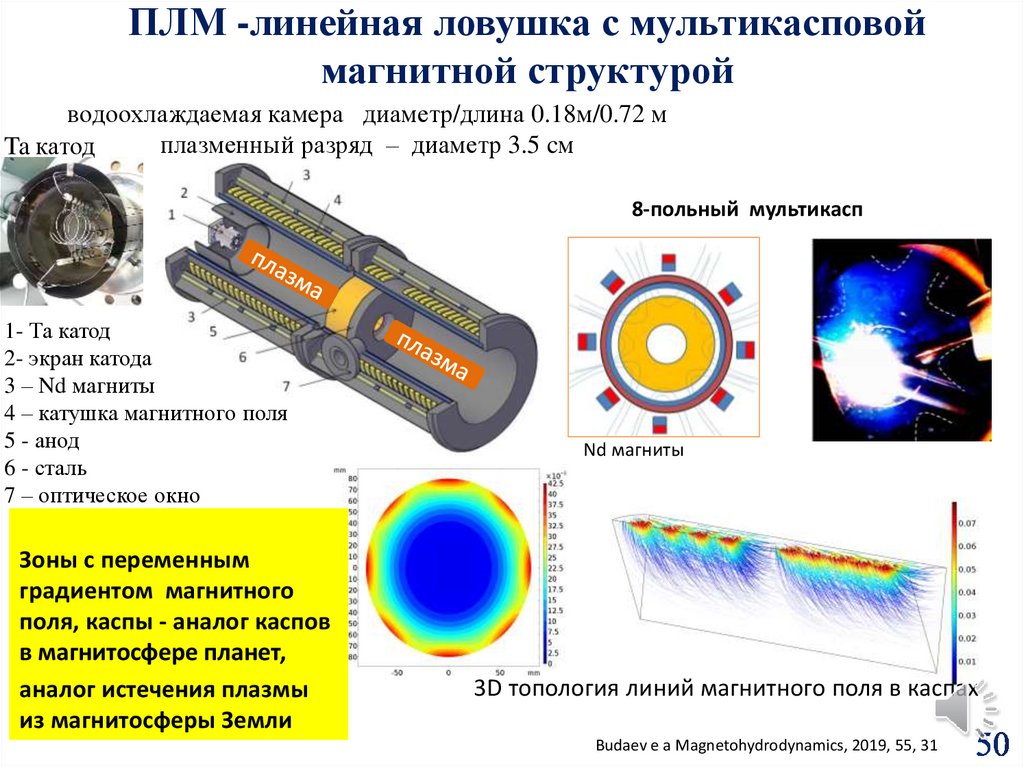
ПЛМ -линейная ловушка с мультикасповой
магнитной структурой
водоохлаждаемая камера диаметр/длина 0.18м/0.72 м
плазменный разряд – диаметр 3.5 cм
Ta катод
8-польный мультикасп
1- Та катод
2- экран катода
3 – Nd магниты
4 – катушка магнитного поля
5 - анод
6 - сталь
7 – оптическое окно cathode,
Зоны с переменным
градиентом магнитного
поля, каспы - аналог каспов
в магнитосфере планет,
аналог истечения плазмы
из магнитосферы Земли
Nd магниты
3D топология линий магнитного поля в каспах
Budaev e a Magnetohydrodynamics, 2019, 55, 31

51.

Стенд мощного лазерного комплекса в
плазменной установке ПЛМ-М
Импульсный лазер Nd:YAG модель LQ529A , λ = 1064 нм ,
энергия импульса 500 мДж; частота повторений 1-10 Гц,
длительность импульса 10 нс.
Фокусировка лазерного пучка 1 - 5 мм2
Испытание W вольфрама с количеством импульсов 1,10
и 100 с энергией импульса 500 мДж при частоте импульсов
1 Гц и длительности лазерного импульса 10 нс.
Плотность мощности пучка - до 21 ТВт/м2
после 1 лазерного импульса
W поверхность
лазер
ПЛМ
после 100 лазерных импульсов

52.

Диагностика плазмы и материалов,
установки в НИУ «МЭИ»
• диагностика плазмы - зонды, болометры,
• оптические измерения - спектрометры,
монохроматор
• анализ структуры материалов - от наномасштабов
до макромасштабов - сканирующий электронный
микроскоп, сканирующий туннельный микроскоп,
просвечивающий электронный микроскоп,
оптический электронный микроскоп, 3D
микроскопия, Нанофаб, рентгеновская
спектроскопия, РФЭС, измерение пористости,

53.

Программа экспериментов на 2022 г
измерение турбулентности плазмы: перенос в турбулентной плазме, свойств
супердиффузии в магнитных полях с различным градиентом - в каспах и
ламинарных зонах, скейлинги турбулентности ( ПЛМ-М, гелиевая плазма);
сравнение со скейлингами астрофизической плазмы солнечного ветра и
магнитосферы Земли (данные Интербола и Кластера);
измерения скейлингов самоподобия морфообразования агломератов лития
при коагуляции под действием турбулентной плазмы (ПЛМ, гелиевая плазма);
сравнение со скейлингами самоподобия астрофизических объектов;
измерения спектров ридберговских атомов в ПЛМ-М гелиевая плазма с
инжекцией лития, бора, углерода; сравнение со спектрами наблюдаемыми в
космической плазме;
исследование влияния возбужденных атомов на кластеризацию при
коагуляции материи: сравнительное измерение характеристик самоподобия
структуры агломератов металлов, сформированных в (i) плазме и (ii)
плазма+мощное лазерное воздействие (ПЛМ-М, гелиевая плазма).

54.

Перспективы применения высокопористых материалов, полученных
после обработки высокотемпературной плазмой
100 nm
новые высокопористые наноструктурные
материалы (С, Ti, W, Ta)
с размером структур < 1 мкм
новые высокопористые W катализаторы разложения
воды на кислород и водород
Литиевые высокопористые материалы для
электродов аккумуляторов большой емкости
Современные кардиостимуляторы ,
нейростимуляторы с биосовместимой
фрактальной структурой с
шероховатостью от нанометров

55.

Выводы
Универсальные свойства сильной турбулентности плазмы, такие как
перемежаемость, негауссова статистика, многомасштабность и мультифрактальность,
аномальный перенос и супердиффузия, наблюдаются в космической плазме магнитосфере Земли и в термоядерных установках с магнитным удержанием плазмы.
Взаимодействие плазмы с материалами в термоядерных установках под действием
высокой тепловой плазменной нагрузки приводит к сильной эрозии и вовлечению
эродированных материалов в процесс стохастической коагуляции, с образованием
нано- и микрометровых агломератов с кораллоподобной структурой и
высокопористых слоев, не наблюдавшихся ранее.
Стохастическая кластеризация и формообразование материи под действием
турбулентной плазмы приводит к иерархической гранулярности - статистическому
самоподобию структур, стоит задача систематизации формообразования на
масштабах от микро- до мегамасштабов.
Программа экспериментов на 2022 год включает эксперименты на плазменных
установках ПЛМ, ПЛМ-М, электронно-пучковых и теплофизических стендах в НИУ
«МЭИ», сравнение скейлингов турбулентности плазмы в лабораторных установках и
магнитосфере Земли, сравнительное исследование фрактальной (самоподобной)
топологии структур астрофизических объектов со структурой стохастических
агломератов из лабораторных плазменных установок с целью выявления влияния
турбулентности на формообразование.

56.

Иван Айвазовский
“Хаос. Сотворение мира”
1841
Спасибо за
внимание!
Результаты, представленные в докладе,
получены в России при выполнении
НИР, в том числе при поддержке проекта
ГК «Росатом» 223-ЕОТП-УТП, РНФ 1719-01469, РФФИ, Госзадания МОН

57.

Аннотация
Исследование фундаментальных свойств турбулентности плазмы является необходимым этапом к описанию астрофизических объектов и универсальных свойств
кластеризации и формообразования материи как на больших масштабах, так и на микромасштабах. Выявление универсальных закономерностей масштабной
инвариантности - дилатационных симметрий обеспечивает систематизацию экспериментальных наблюдений астрофизических объектов, целесообразными
представляются исследования в лабораторных плазменных установках в поддержку такого обобщающего анализа.
В сравнительных исследованиях турбулентности плазмы в магнитосфере Земли и лабораторных термоядерных установках в последние годы достигнут прогресс,
определены характеристики многомасштабной инвариантности (мультифрактальности) турбулентности в погранслоях, такие свойства влияют на условия
тепломассопереноса - формируется супердиффузия. Требуется провести обобщающее исследование на большей экспериментальной базе данных в космической
плазме и в лабораторных установкахдля подтверждения универсальности выявленных закономерностей.
Рассмаривается гипотеза о влиянии закономерностей масштабной инвариантности турбулентной плазмы на формообразование материала при агломерации в
турбулентой плазме, в том числе и в астрофизических объектах. Требуется экспериментальная проверка такой гипотезы, что будет способствовать выявлению
универсальных симметрий масштабной инвариантности астрофизических объектов.
В последние годы обнаружены эффекты стохастической кластеризации поверхности с иерархической гранулярностью (статистическим самоподобием фрактальностью) при воздействии на материал экстремальных плазменно-тепловых нагрузок. Такая структура поверхности твердого тела наблюдается после
воздействия плазмы на материалы в лабораторных термоядерных установках (ТУ), в плазменных, электронно-лучевых и лазерных установках при плазменнотепловых испытаниях мощными пучками и проникающим излучением, где в процесс одновременно вовлечены множественные механизмы эрозии и
переосаждения эродированного материала, плавления, движения и отвердения поверхностных слоев на масштабах от десятков нанометров до сотен
микрометров. Свойства масштабной инвариантности структуры таких материалов определяют связность образца и формирование перколяционного кластера
дефектов и диссипативных структур в широком диапазоне масштабов, начиная от субмикронных масштабов.
Динамика частиц эродированного материала при переосаждении из плазмы и их агломерация на поверхности происходит под действием стохастических
электрических полей, генерируемых турбулентной высокотемпературной плазмой. Особенностью пристеночной плазмы в термоядерных установках является
негауссова статистика флуктуаций электрического поля с дальними корреляциями . Это приводит к росту стохастического рельефа с самоподобной структурой
(иерархическая гранулярность - фрактальность) с негауссовой статистикой высот рельефа, отличающегося от простейшей шероховатости, наблюдаемой в
обычных процессах стохастической агломерации. Доминирующим фактором в таком процессе в термоядерных установках являются коллективные эффекты при
стохастической кластеризации, а не химический элементный состав и физические характеристики твердого материала. Стохастическая фрактальная структура с
иерархической гранулярностью и самоподобием формируется на различных материалах, таких как вольфрам, углеродные материалы и нержавеющая сталь,
которые подвергаются воздействию высокотемпературной плазмы в термоядерных установках. Обсуждаются гипотезы, рассматривающие универсальные законы
фрактального роста .
Неоднородная кластеризация материалов является предметом теорий различной степени сложности, в том числе кинетических моделей, основанных на
уравнении Смолуховского, для описания нерегулярных структур, наблюдаемых в твердых телах и агломератах разных масштабов. Кинетические модели
предлагают описание стохастической кластеризации с автомодельной структурой и рассмотрение степенных решений для числа N агломерирующих кластеров с
массой m , N (m) ~ m- (3+ a) / 2, где a - показатель самоподобия кинетической модели агломерации. Такие степенные законы описывают экспериментально
наблюдаемые характеристики шероховатости материалов после воздействия высокотемпературной плазмы в термоядерных установках. Статистика высот
стохастического рельефа, сформированная в таких условиях, обычно негауссова и функции распределения вероятностей имеют «тяжелые» хвосты, показатель
Херста от 0,68 до 0,86. Это отличает их от броуновских поверхностей с тривиальной стохастической поверхностью. Стохастическая кластеризация материалов из
термоядерных устройств характеризуется мультифрактальной статистикой. Количественные характеристики статистической неоднородности структуры такого
материала, включая мультифрактальный спектр с уширением 0,5 - 1,2, находятся в диапазоне, наблюдаемом для типичных мультифрактальных объектов и
процессов в природе.
Для создания наиболее полной теоретической модели следует привлекать экспериментальные данные о свойствах статистического самоподобия – скейлингах
самоподобия (степенных законах масштабной инвариантности) турбулентности астрофизической и лабораторной плазмы, кластеризации стохастической
поверхности, сформированной под действием турбулентной плазмы. На этом пути важно из эксперимента определить наиболее общие степенные законы,
реализуемые в реальных процессах кластеризации, в том числе ридберговских атомов, которые могут обеспечивать фрактальный рост агломератов.
Обобщающий анализ свойств масштабной инвариантности астрофизических и лабораторных плазменных объектов и агломератов в них будет способствовать
выработке подходов к практической технологии создания материалов с фрактальной структурой для систем интенсивного охлаждения высоконагруженных
компонентов ядерных и термоядерных реакторов, создания материалов для биомедицинского применения, разработки компонентов квантового компьютера.