Основы теории линейного программирования

1.

Лекции № 2 - 3
Филиппова А.С., каф. ИТ, БГПУ
1

2.

ОСНОВЫ ТЕОРИИ ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ
Филиппова А.С., каф. ИТ, БГПУ
2

3.

Джордж Данциг (1914-2005) получил степень бакалавра в области математики
и физики в Мэрилендском университете (1936), а также степень
магистра математики в Мичиганском университете (1938).
После двух лет работы в Бюро трудовой статистики Министерства труда США
он поступил на докторскую программу в области математики в Калифорнийский
университет в Беркли, где изучал статистику под руководством математика Ежи
Неймана. Однажды в 1939 году он опоздал на занятия и ошибочно подумал,
что написанные на доске уравнения — это домашнее задание. Оно было
трудным, но всё-таки Джордж сумел его выполнить. Оказалось, что это были
две нерешённые проблемы статистики, с которыми маститые учёные не могли
справиться в течение многих лет. Эта история стала очень популярной, обросла
легендами и была использована в первых кадрах фильма «Умница Уилл
Хантинг».
Джордж Данциг стал первым лауреатом Теоретической премии фон Неймана (1974). Он
получил Национальную научную медаль США (1975) и стал почётным доктором Мэрилендского
университета в Колледж-Парке (1976). В 1985 году в Израиле удостоен премии Харви.
В 1979 году Общество математического программирования и Общество
промышленной и прикладной математики учредили премию Данцига, которую
вручают каждые три года, начиная с 1982, за оригинальные исследования, внёсшие
выдающийся вклад в математическое программирование.
Филиппова А.С., каф. ИТ, БГПУ
3

4.

Леонид Витальевич Канторович (1912 – 1986)
В возрасте четырнадцати лет поступил в Ленинградский университет.
С 18 лет — преподаватель университета. В 22 года – профессор ЛГУ.
В 23 года ему была присвоена учёная степень доктора физикоматематических наук без защиты диссертации.
В 1938 году, консультируя фанерный трест по проблеме эффективного
использования лущильных станков, Канторович понял, что дело сводится к
задаче максимизации линейной формы многих переменных при наличии
большого числа ограничений в форме линейных равенств и неравенств.
Он модифицировал метод разрешающих множителей Лагранжа для её
решения и понял, что к такого рода задачам сводится колоссальное
количество проблем экономики. В 1939 году опубликовал работу
«Математические методы организации и планирования производства» в
которой описал задачи экономики, поддающиеся открытому им
математическому методу и тем самым заложил основы линейного
программирования.
Филиппова А.С., каф. ИТ, БГПУ
4

5.

Двойственные задачи линейного программирования
Линейное программирование – раздел математики, занимается
изучением экстремальных задач, в которых ищется максимум или
минимум линейной функции в арифметическом конечномерном
векторном пространстве на множестве векторов, удовлетворяющих
конечному числу линейных уравнений и (или) неравенств.
В качестве основной в линейном программировании принята
следующая задача максимизации линейной функции на множестве
решений линейных уравнений и неравенств:
Филиппова А.С., каф. ИТ, БГПУ
5

6.

Основная задача ЛП:
Филиппова А.С., каф. ИТ, БГПУ
6

7.

Основная задача ЛП:
Филиппова А.С., каф. ИТ, БГПУ
7

8.

Основная задача ЛП:
Филиппова А.С., каф. ИТ, БГПУ
8

9.

Основная задача ЛП:
Филиппова А.С., каф. ИТ, БГПУ
9

10.

Основная задача ЛП:
Филиппова А.С., каф. ИТ, БГПУ
10

11.

Основная задача ЛП:
Филиппова А.С., каф. ИТ, БГПУ
11

12.

Основная задача ЛП:
Филиппова А.С., каф. ИТ, БГПУ
12

13.

Основная задача ЛП:
Вектор (2),
удовлетворяющий
условиям (3)–(5),
называется допустимым
Филиппова А.С., каф. ИТ, БГПУ
13

14.

Основная задача ЛП:
Искомый допустимый
вектор, доставляющий
максимум функции (1) –
оптимальным.
Филиппова А.С., каф. ИТ, БГПУ
14

15.

Двойственная задача ЛП:
Филиппова А.С., каф. ИТ, БГПУ
15

16.

Двойственная задача ЛП:
Филиппова А.С., каф. ИТ, БГПУ
16

17.

Двойственная задача ЛП:
Филиппова А.С., каф. ИТ, БГПУ
17

18.

Двойственная задача ЛП:
Филиппова А.С., каф. ИТ, БГПУ
18

19.

Двойственная задача ЛП:
Филиппова А.С., каф. ИТ, БГПУ
19

20.

Двойственная задача ЛП:
Филиппова А.С., каф. ИТ, БГПУ
20

21.

Двойственная задача ЛП:
Вектор (7),
удовлетворяющий
условиям (8)–(10)
называется допустимым
Филиппова А.С., каф. ИТ, БГПУ
21

22.

Двойственная задача ЛП:
Искомый допустимый
вектор, доставляющий
минимум функции (6) –
оптимальным
Филиппова А.С., каф. ИТ, БГПУ
22

23.

Пример. Записать задачу, двойственную к следующей задаче ЛП.
Максимизировать линейную
функцию
μ(x)=2х1 – х2 + 3х3 + х4 – 5х5
на множестве векторов
х=(х1, х2, х3, х4, х5),
удовлетворяющих условиям
х1 ≥ 0, х2 ≥ 0, х4 ≥ 0,
3х1+ х2 – 4х3+
х5 – 6 ≥ 0,
3х2+4х3 – 2х4
+1 ≥ 0,
2х1 + х3 – 3х4 – 2х5 = 0.
Филиппова А.С., каф. ИТ, БГПУ
23

24.

Пример. Записать задачу, двойственную к следующей задаче ЛП.
Максимизировать линейную
функцию
μ(x)=2х1 – х2 + 3х3 + х4 – 5х5
на множестве векторов
х=(х1, х2, х3, х4, х5),
удовлетворяющих условиям
х1 ≥ 0, х2 ≥ 0, х4 ≥ 0,
I= ?; I1= ?; I2= ?;
J= ? ; J1= ?; J2 = ?
3х1+ х2 – 4х3+
х5 – 6 ≥ 0,
3х2+4х3 – 2х4
+1 ≥ 0,
2х1 + х3 – 3х4 – 2х5 = 0.
Филиппова А.С., каф. ИТ, БГПУ
24

25.

Пример. Записать задачу, двойственную к следующей задаче ЛП.
Максимизировать линейную
функцию
μ(x)=2х1 – х2 + 3х3 + х4 – 5х5
на множестве векторов
х=(х1, х2, х3, х4, х5),
удовлетворяющих условиям
х1 ≥ 0, х2 ≥ 0, х4 ≥ 0,
I= ?; I1= ?; I2= ?;
J= ? ; J1= ?; J2 = ?
(4)
(5)
3х1+ х2 – 4х3+
х5 – 6 ≥ 0,
3х2+4х3 – 2х4
+1 ≥ 0,
2х1 + х3 – 3х4 – 2х5 = 0.
Филиппова А.С., каф. ИТ, БГПУ
25

26.

Пример. Записать задачу, двойственную к следующей задаче ЛП.
Максимизировать линейную
функцию
μ(x)=2х1 – х2 + 3х3 + х4 – 5х5
на множестве векторов
х=(х1, х2, х3, х4, х5),
удовлетворяющих условиям
х1 ≥ 0, х2 ≥ 0, х4 ≥ 0,
I={1,2,3}; I1= ?; I2= ?;
(4)
J= ?; J1= ?; J2 = ?
(5)
3х1+ х2 – 4х3+
х5 – 6 ≥ 0,
3х2+4х3 – 2х4
+1 ≥ 0,
2х1 + х3 – 3х4 – 2х5 = 0.
Филиппова А.С., каф. ИТ, БГПУ
26

27.

Пример. Записать задачу, двойственную к следующей задаче ЛП.
Максимизировать линейную
функцию
μ(x)=2х1 – х2 + 3х3 + х4 – 5х5
на множестве векторов
х=(х1, х2, х3, х4, х5),
удовлетворяющих условиям
х1 ≥ 0, х2 ≥ 0, х4 ≥ 0,
I={1,2,3}; I1={3}; I2= ?;
(4)
J= ?; J1= ?; J2 = ?
(5)
3х1+ х2 – 4х3+
х5 – 6 ≥ 0,
3х2+4х3 – 2х4
+1 ≥ 0,
2х1 + х3 – 3х4 – 2х5 = 0.
Филиппова А.С., каф. ИТ, БГПУ
27

28.

Пример. Записать задачу, двойственную к следующей задаче ЛП.
Максимизировать линейную
функцию
μ(x)=2х1 – х2 + 3х3 + х4 – 5х5
на множестве векторов
х=(х1, х2, х3, х4, х5),
удовлетворяющих условиям
х1 ≥ 0, х2 ≥ 0, х4 ≥ 0,
I={1,2,3}; I1={3}; I2={1,2};
J= ?; J1= ?; J2 = ?
3х1+ х2 – 4х3+
х5 – 6 ≥ 0,
3х2+4х3 – 2х4
+1 ≥ 0,
2х1 + х3 – 3х4 – 2х5 = 0.
Филиппова А.С., каф. ИТ, БГПУ
28

29.

Пример. Записать задачу, двойственную к следующей задаче ЛП.
Максимизировать линейную
функцию
μ(x)=2х1 – х2 + 3х3 + х4 – 5х5
на множестве векторов
х=(х1, х2, х3, х4, х5),
удовлетворяющих условиям
х1 ≥ 0, х2 ≥ 0, х4 ≥ 0,
I={1,2,3}; I1={3}; I2={1,2};
J= ?; J1= ?; J2 = ?
(2)
(3)
3х1+ х2 – 4х3+
х5 – 6 ≥ 0,
3х2+4х3 – 2х4
+1 ≥ 0,
2х1 + х3 – 3х4 – 2х5 = 0.
Филиппова А.С., каф. ИТ, БГПУ
29

30.

Пример. Записать задачу, двойственную к следующей задаче ЛП.
Максимизировать линейную
функцию
μ(x)=2х1 – х2 + 3х3 + х4 – 5х5
на множестве векторов
х=(х1, х2, х3, х4, х5),
удовлетворяющих условиям
х1 ≥ 0, х2 ≥ 0, х4 ≥ 0,
I={1,2,3}; I1={3}; I2={1,2};
J={1,2,3,4,5}; J1= ?; J2 = ?
(2)
(3)
3х1+ х2 – 4х3+
х5 – 6 ≥ 0,
3х2+4х3 – 2х4
+1 ≥ 0,
2х1 + х3 – 3х4 – 2х5 = 0.
Филиппова А.С., каф. ИТ, БГПУ
30

31.

Пример. Записать задачу, двойственную к следующей задаче ЛП.
Максимизировать линейную
функцию
μ(x)=2х1 – х2 + 3х3 + х4 – 5х5
на множестве векторов
х=(х1, х2, х3, х4, х5),
удовлетворяющих условиям
х1 ≥ 0, х2 ≥ 0, х4 ≥ 0,
I={1,2,3}; I1={3}; I2={1,2};
J={1,2,3,4,5}; J1=?; J2 ={1,2,4}
3х1+ х2 – 4х3+
х5 – 6 ≥ 0,
3х2+4х3 – 2х4
+1 ≥ 0,
2х1 + х3 – 3х4 – 2х5 = 0.
Филиппова А.С., каф. ИТ, БГПУ
31

32.

Пример. Записать задачу, двойственную к следующей задаче ЛП.
Максимизировать линейную
функцию
μ(x)=2х1 – х2 + 3х3 + х4 – 5х5
на множестве векторов
х=(х1, х2, х3, х4, х5),
удовлетворяющих условиям
х1 ≥ 0, х2 ≥ 0, х4 ≥ 0,
I={1,2,3}; I1={3}; I2={1,2};
J={1,2,3,4,5}; J1={3,5}; J2 ={1,2,4}
3х1+ х2 – 4х3+
х5 – 6 ≥ 0,
3х2+4х3 – 2х4
+1 ≥ 0,
2х1 + х3 – 3х4 – 2х5 = 0.
Филиппова А.С., каф. ИТ, БГПУ
32

33.

Пример. Записать задачу, двойственную к следующей задаче ЛП.
Максимизировать линейную
функцию
μ(x)=2х1 – х2 + 3х3 + х4 – 5х5
на множестве векторов
х=(х1, х2, х3, х4, х5),
удовлетворяющих условиям
х1 ≥ 0, х2 ≥ 0, х4 ≥ 0,
I={1,2,3}; I1={3}; I2={1,2};
J={1,2,3,4,5}; J1={3,5}; J2 ={1,2,4}
I* Минимизировать линейную
функцию
(6)
3х1+ х2 – 4х3+
х5 – 6 ≥ 0,
3х2+4х3 – 2х4
+1 ≥ 0,
2х1 + х3 – 3х4 – 2х5 = 0.
Филиппова А.С., каф. ИТ, БГПУ
33

34.

Пример. Записать задачу, двойственную к следующей задаче ЛП.
Максимизировать линейную
функцию
μ(x)=2х1 – х2 + 3х3 + х4 – 5х5
на множестве векторов
х=(х1, х2, х3, х4, х5),
удовлетворяющих условиям
х1 ≥ 0, х2 ≥ 0, х4 ≥ 0,
I={1,2,3}; I1={3}; I2={1,2};
J={1,2,3,4,5}; J1={3,5}; J2 ={1,2,4}
I* Минимизировать линейную
функцию
(6)
(4)
(5)
3х1+ х2 – 4х3+
х5 – 6 ≥ 0,
3х2+4х3 – 2х4
+1 ≥ 0,
2х1 + х3 – 3х4 – 2х5 = 0.
Филиппова А.С., каф. ИТ, БГПУ
34

35.

Пример. Записать задачу, двойственную к следующей задаче ЛП.
Максимизировать линейную
функцию
μ(x)=2х1 – х2 + 3х3 + х4 – 5х5
на множестве векторов
х=(х1, х2, х3, х4, х5),
удовлетворяющих условиям
х1 ≥ 0, х2 ≥ 0, х4 ≥ 0,
I={1,2,3}; I1={3}; I2={1,2};
J={1,2,3,4,5}; J1={3,5}; J2 ={1,2,4}
I* Минимизировать линейную
функцию
(6)
(4)
(5)
3х1+ х2 – 4х3+
х5 – 6 ≥ 0,
3х2+4х3 – 2х4
+1 ≥ 0,
2х1 + х3 – 3х4 – 2х5 = 0.
Филиппова А.С., каф. ИТ, БГПУ
35

36.

Пример. Записать задачу, двойственную к следующей задаче ЛП.
Максимизировать линейную
функцию
μ(x)=2х1 – х2 + 3х3 + х4 – 5х5
на множестве векторов
х=(х1, х2, х3, х4, х5),
удовлетворяющих условиям
х1 ≥ 0, х2 ≥ 0, х4 ≥ 0,
I={1,2,3}; I1={3}; I2={1,2};
J={1,2,3,4,5}; J1={3,5}; J2 ={1,2,4}
I* Минимизировать линейную
функцию
ν(y)= – 6y1 + y2 + 0 y3
на множестве векторов y=(y1, y2, y3),
3х1+ х2 – 4х3+
х5 – 6 ≥ 0,
3х2+4х3 – 2х4
+1 ≥ 0,
2х1 + х3 – 3х4 – 2х5 = 0.
Филиппова А.С., каф. ИТ, БГПУ
36

37.

Пример. Записать задачу, двойственную к следующей задаче ЛП.
Максимизировать линейную
функцию
μ(x)=2х1 – х2 + 3х3 + х4 – 5х5
на множестве векторов
х=(х1, х2, х3, х4, х5),
удовлетворяющих условиям
х1 ≥ 0, х2 ≥ 0, х4 ≥ 0,
I={1,2,3}; I1={3}; I2={1,2};
J={1,2,3,4,5}; J1={3,5}; J2 ={1,2,4}
I* Минимизировать линейную
функцию
ν(y)= – 6y1 + y2
на множестве векторов y=(y1, y2, y3),
удовлетворяющих условиям:
(8)
у1 ≥ 0, у2 ≥ 0,
3у1 +
2у3+ 2 ≤ 0,
3х1+ х2 – 4х3+
х5 – 6 ≥ 0,
у1 + 3у2
– 1 ≤ 0,
3х2+4х3 – 2х4
+1 ≥ 0,
–4у1 + 4у2 + у3 + 3 = 0,
2х1 + х3 – 3х4 – 2х5 = 0.
– 2у2 – 3у3 + 1 ≤ 0,
Филиппова А.С., каф. ИТ,
37
уБГПУ
– 2у3 – 5=0.
1

38.

Пример. Записать задачу, двойственную к следующей задаче ЛП.
Максимизировать линейную
функцию
μ(x)=2х1 – х2 + 3х3 + х4 – 5х5
на множестве векторов
х=(х1, х2, х3, х4, х5),
удовлетворяющих условиям
х1 ≥ 0, х2 ≥ 0, х4 ≥ 0,
I={1,2,3}; I1={3}; I2={1,2};
J={1,2,3,4,5}; J1={3,5}; J2 ={1,2,4}
I* Минимизировать линейную
функцию
ν(y)= – 6y1 + y2
на множестве векторов y=(y1, y2, y3),
удовлетворяющих условиям:
(8)
у1 ≥ 0, у2 ≥ 0,
3у1 +
2у3+ 2 ≤ 0,
3х1+ х2 – 4х3+
х5 – 6 ≥ 0,
у1 + 3у2
– 1 ≤ 0,
3х2+4х3 – 2х4
+1 ≥ 0,
–4у1 + 4у2 + у3 + 3 = 0,
2х1 + х3 – 3х4 – 2х5 = 0.
– 2у2 – 3у3 + 1 ≤ 0,
Филиппова А.С., каф. ИТ,
38
уБГПУ
– 2у3 – 5=0.
1

39.

Пример. Записать задачу, двойственную к следующей задаче ЛП.
Максимизировать линейную
функцию
μ(x)=2х1 – х2 + 3х3 + х4 – 5х5
на множестве векторов
х=(х1, х2, х3, х4, х5),
удовлетворяющих условиям
х1 ≥ 0, х2 ≥ 0, х4 ≥ 0,
I={1,2,3}; I1={3}; I2={1,2};
J={1,2,3,4,5}; J1={3,5}; J2 ={1,2,4}
I* Минимизировать линейную
функцию
ν(y)= – 6y1 + y2
на множестве векторов y=(y1, y2, y3),
удовлетворяющих условиям:
у1 ≥ 0, у2 ≥ 0,
(9)
3у1 +
2у3+ 2 ≤ 0,
(10)
3х1+ х2 – 4х3+
х5 – 6 ≥ 0,
у1 + 3у2
– 1 ≤ 0,
3х2+4х3 – 2х4
+1 ≥ 0,
–4у1 + 4у2 + у3 + 3 = 0,
2х1 + х3 – 3х4 – 2х5 = 0.
– 2у2 – 3у3 + 1 ≤ 0,
Филиппова А.С., каф. ИТ,
39
уБГПУ
– 2у3 – 5=0.
1

40.

Пример. Записать задачу, двойственную к следующей задаче ЛП.
Максимизировать линейную
функцию
μ(x)=2х1 – х2 + 3х3 + х4 – 5х5
на множестве векторов
х=(х1, х2, х3, х4, х5),
удовлетворяющих условиям
х1 ≥ 0, х2 ≥ 0, х4 ≥ 0,
I={1,2,3}; I1={3}; I2={1,2};
J={1,2,3,4,5}; J1={3,5}; J2 ={1,2,4}
I* Минимизировать линейную
функцию
ν(y)= – 6y1 + y2
на множестве векторов y=(y1, y2, y3),
удовлетворяющих условиям:
у1 ≥ 0, у2 ≥ 0,
(9)
3у1 +
2у3+ 2 ≤ 0,
(10)
3х1+ х2 – 4х3+
х5 – 6 ≥ 0,
у1 + 3у2
– 1 ≤ 0,
3х2+4х3 – 2х4
+1 ≥ 0,
–4у1 + 4у2 + у3 + 3 = 0,
2х1 + х3 – 3х4 – 2х5 = 0.
– 2у2 – 3у3 + 1 ≤ 0,
Филиппова А.С., каф. ИТ,
40
уБГПУ
– 2у3 – 5=0.
1

41.

Пример. Записать задачу, двойственную к следующей задаче ЛП.
Максимизировать линейную
функцию
μ(x)=2х1 – х2 + 3х3 + х4 – 5х5
на множестве векторов
х=(х1, х2, х3, х4, х5),
удовлетворяющих условиям
х1 ≥ 0, х2 ≥ 0, х4 ≥ 0,
I={1,2,3}; I1={3}; I2={1,2};
J={1,2,3,4,5}; J1={3,5}; J2 ={1,2,4}
I* Минимизировать линейную
функцию
ν(y)= – 6y1 + y2
на множестве векторов y=(y1, y2, y3),
удовлетворяющих условиям:
у1 ≥ 0, у2 ≥ 0,
(9)
3у1 +
2у3+ 2 ≤ 0,
(10)
3х1+ х2 – 4х3+
х5 – 6 ≥ 0,
у1 + 3у2
– 1 ≤ 0,
3х2+4х3 – 2х4
+1 ≥ 0,
–4у1 + 4у2 + у3 + 3 = 0,
2х1 + х3 – 3х4 – 2х5 = 0.
– 2у2 – 3у3 + 1 ≤ 0,
Филиппова А.С., каф. ИТ,
41
уБГПУ
– 2у3 – 5=0.
1

42.

Пример. Записать задачу, двойственную к следующей задаче ЛП.
Максимизировать линейную
функцию
μ(x)=2х1 – х2 + 3х3 + х4 – 5х5
на множестве векторов
х=(х1, х2, х3, х4, х5),
удовлетворяющих условиям
х1 ≥ 0, х2 ≥ 0, х4 ≥ 0,
I={1,2,3}; I1={3}; I2={1,2};
J={1,2,3,4,5}; J1={3,5}; J2 ={1,2,4}
I* Минимизировать линейную
функцию
ν(y)= – 6y1 + y2
на множестве векторов y=(y1, y2, y3),
удовлетворяющих условиям:
у1 ≥ 0, у2 ≥ 0,
(9)
3у1 +
2у3+ 2 ≤ 0,
(10)
3х1+ х2 – 4х3+
х5 – 6 ≥ 0,
у1 + 3у2
– 1 ≤ 0,
3х2+4х3 – 2х4
+1 ≥ 0,
–4у1 + 4у2 + у3 + 3 = 0,
2х1 + х3 – 3х4 – 2х5 = 0.
– 2у2 – 3у3 + 1 ≤ 0,
Филиппова А.С., каф. ИТ,
42
уБГПУ
– 2у3 – 5=0.
1

43.

Пример. Записать задачу, двойственную к следующей задаче ЛП.
Максимизировать линейную
функцию
μ(x)=2х1 – х2 + 3х3 + х4 – 5х5
на множестве векторов
х=(х1, х2, х3, х4, х5),
удовлетворяющих условиям
х1 ≥ 0, х2 ≥ 0, х4 ≥ 0,
I={1,2,3}; I1={3}; I2={1,2};
J={1,2,3,4,5}; J1={3,5}; J2 ={1,2,4}
I* Минимизировать линейную
функцию
ν(y)= – 6y1 + y2
на множестве векторов y=(y1, y2, y3),
удовлетворяющих условиям:
у1 ≥ 0, у2 ≥ 0,
(9)
3у1 +
2у3+ 2 ≤ 0,
(10)
3х1+ х2 – 4х3+
х5 – 6 ≥ 0,
у1 + 3у2
– 1 ≤ 0,
3х2+4х3 – 2х4
+1 ≥ 0,
–4у1 + 4у2 + у3 + 3 = 0,
2х1 + х3 – 3х4 – 2х5 = 0.
– 2у2 – 3у3 + 1 ≤ 0,
Филиппова А.С., каф. ИТ,
43
уБГПУ
– 2у3 – 5=0.
1

44.

Пример. Записать задачу, двойственную к следующей задаче ЛП.
Максимизировать линейную
функцию
μ(x)=2х1 – х2 + 3х3 + х4 – 5х5
на множестве векторов
х=(х1, х2, х3, х4, х5),
удовлетворяющих условиям
х1 ≥ 0, х2 ≥ 0, х4 ≥ 0,
I={1,2,3}; I1={3}; I2={1,2};
J={1,2,3,4,5}; J1={3,5}; J2 ={1,2,4}
I* Минимизировать линейную
функцию
ν(y)= – 6y1 + y2
на множестве векторов y=(y1, y2, y3),
удовлетворяющих условиям:
у1 ≥ 0, у2 ≥ 0,
3у1 +
2у3+ 2 ≤ 0,
3х1+ х2 – 4х3+
х5 – 6 ≥ 0,
у1 + 3у2
– 1 ≤ 0,
3х2+4х3 – 2х4
+1 ≥ 0,
–4у1 + 4у2 + у3 + 3 = 0,
2х1 + х3 – 3х4 – 2х5 = 0.
– 2у2 – 3у3 + 1 ≤ 0,
Филиппова А.С., каф. ИТ,
44
уБГПУ
– 2у3 – 5=0.
1

45.

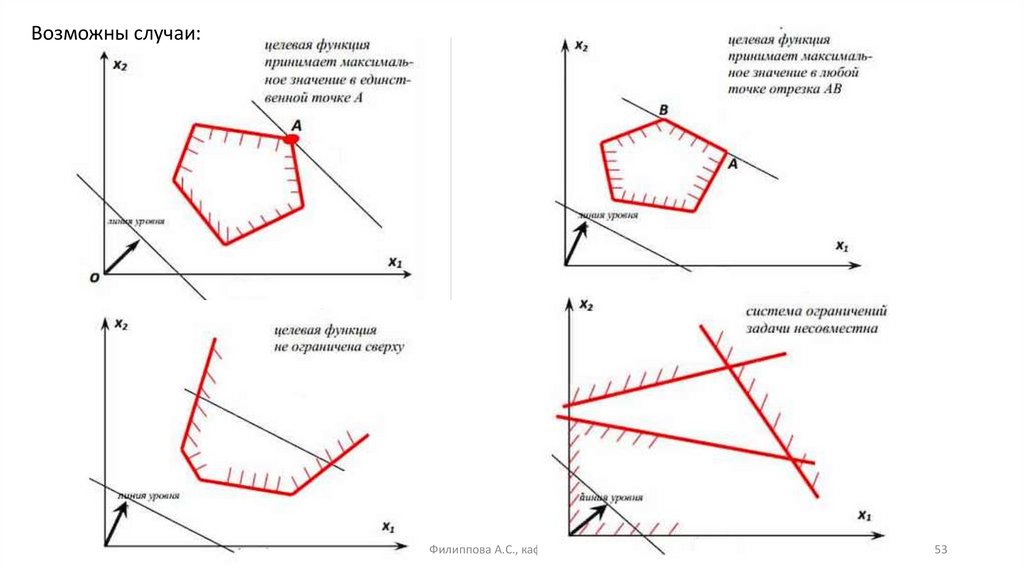
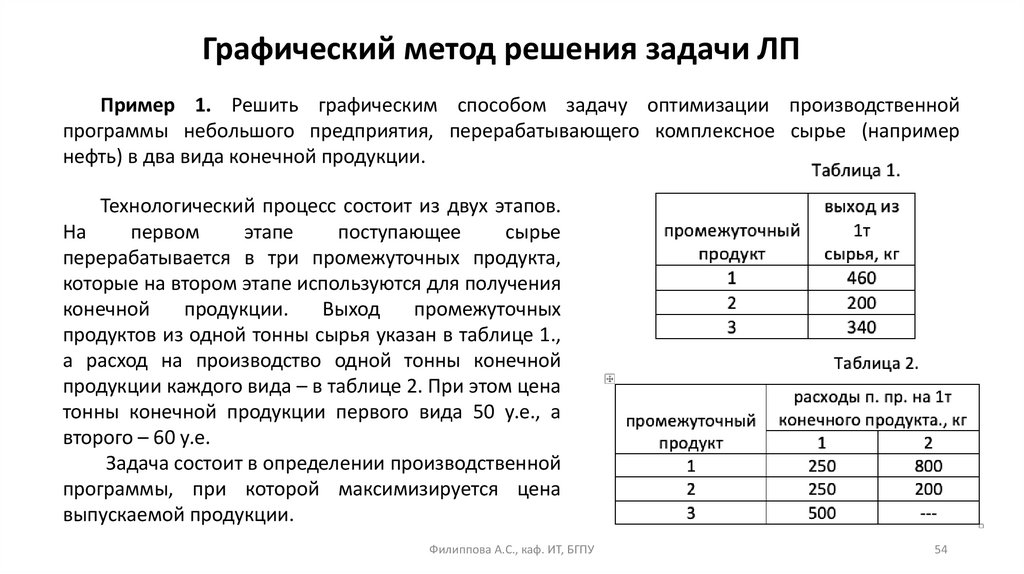
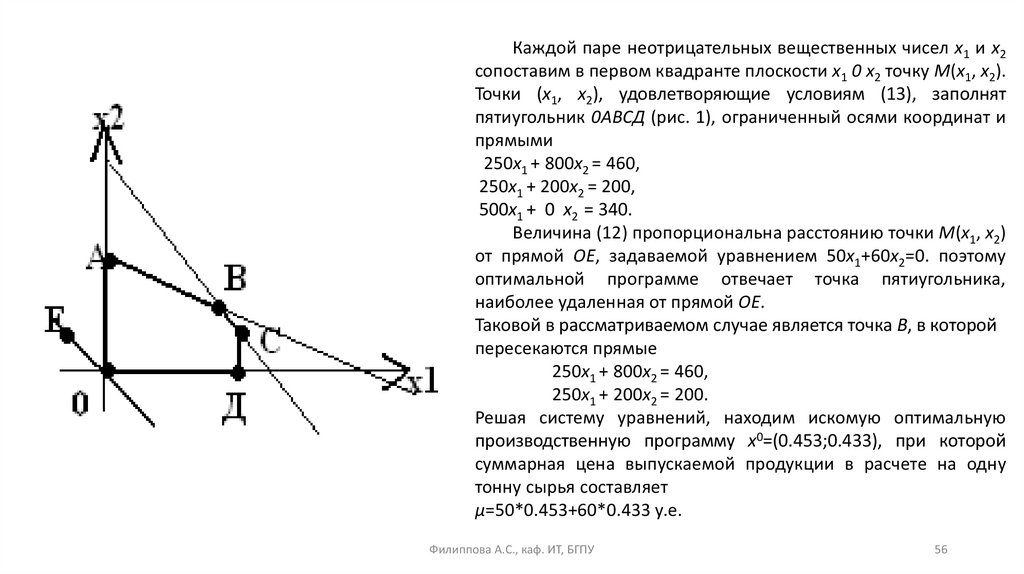
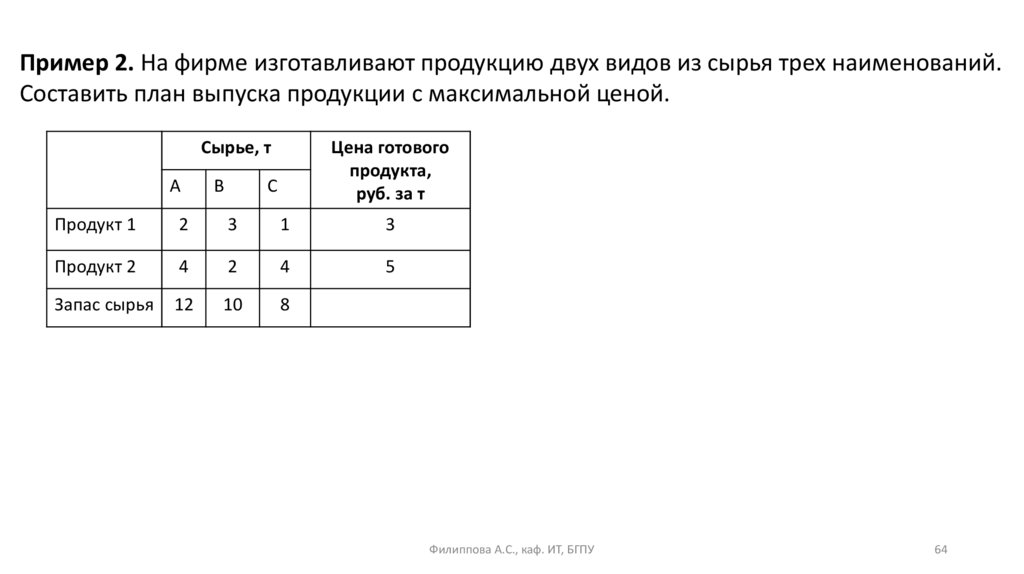
Лемма. Любые допустимые вектора x и y в задачах I и I* для
функций μ(x) и ν(y) удовлетворяют условиям:
μ(x) ≤ ν(y),
при этом равенство достигается тогда и только тогда, когда
допустимые вектора x и y удовлетворяют: