Подобные треугольники

1. Подобные треугольники

2. Девиз урока

- Что есть больше всего на свете? –
Пространство.
- Что быстрее всего? – Ум.
- Что мудрее всего? – Время.
- Что приятнее всего? –
Достичь желаемого.
Фалес Милетский.

3.

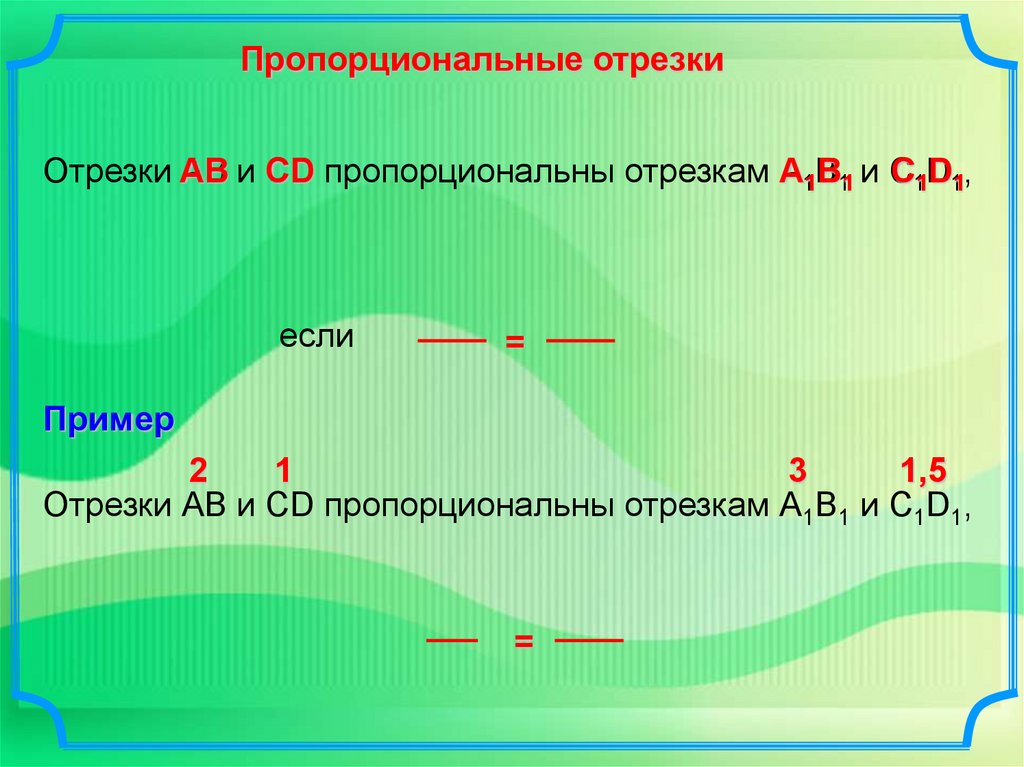
Пропорциональные отрезки
Отрезки АВ и СD пропорциональны отрезкам А1В11 и С
C1D1,
если
=
Пример
2
1
3
1,5
Отрезки АВ и СD пропорциональны отрезкам А1В1 и С1D1,
=

4.

Понятие пропорциональности вводится и для большего
числа отрезков.
Отрезки
АВ,
СD и EF пропорциональны отрезкам А1В11, С
АВ СD
C11D11 и E
E11FF11,
если
=
=

5.

6.

7.

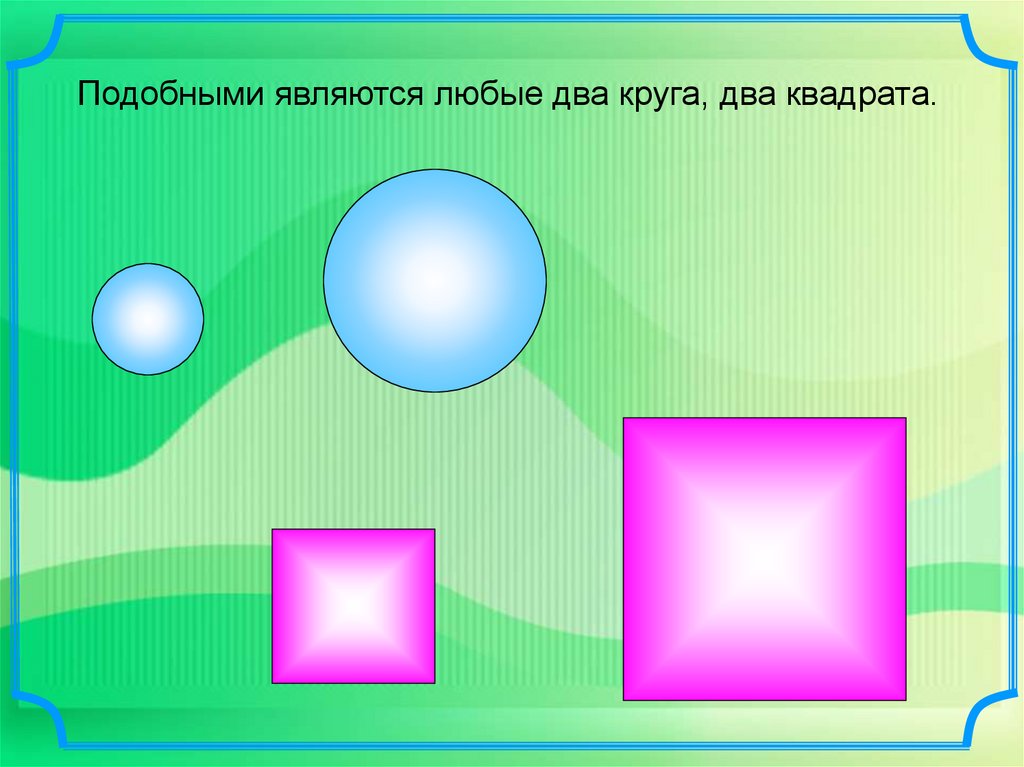
В геометрии фигуры одинаковой формы принято
называть подобными.

8.

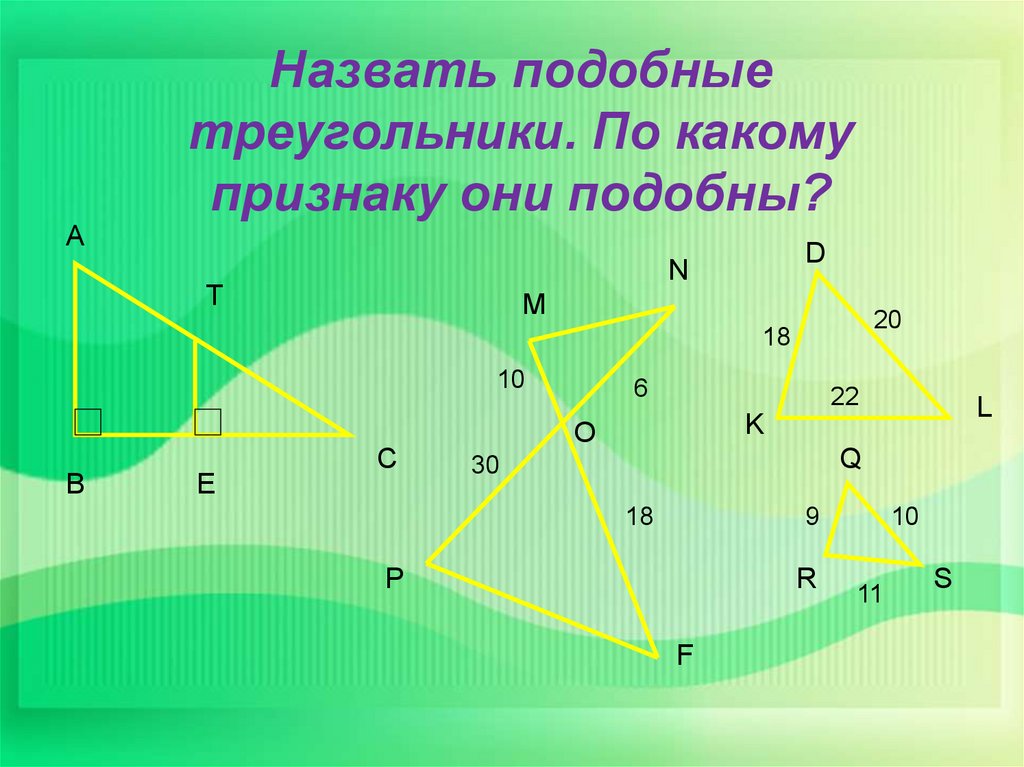
Подобными являются любые два круга, два квадрата.

9. Назвать подобные треугольники. По какому признаку они подобны?

А
Назвать подобные
треугольники. По какому
признаку они подобны?
D
N
Т
М
20
18
10
В
Е
С
6
22
L
K
O
Q
30
18
9
P
R
F
10
11
S

10.

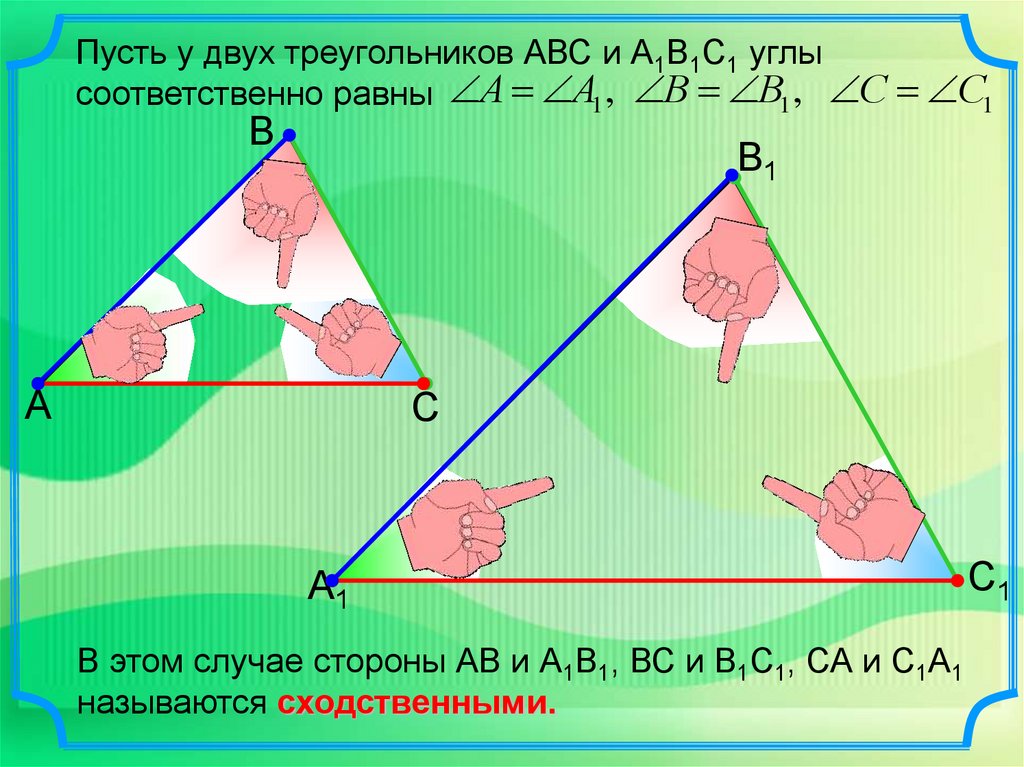
Пусть у двух треугольников АВС и А1В1С1 углы
соответственно равны А А1 , В В1 , С С1
В
В1
А
С
А1
В этом случае стороны АВ и А1В1, ВС и В1С1, СА и С1А1
называются сходственными.
С1

11.

Два треугольника называются подобными, если их
углы соответственно равны и стороны одного
треугольника соответственно пропорциональны
сходственным сторонам другого.
А А1 , В В1 , С С1
В
АВ
ВС
АС
А1 В1 В1С1 А1С1
В1
А
С
А1
С1

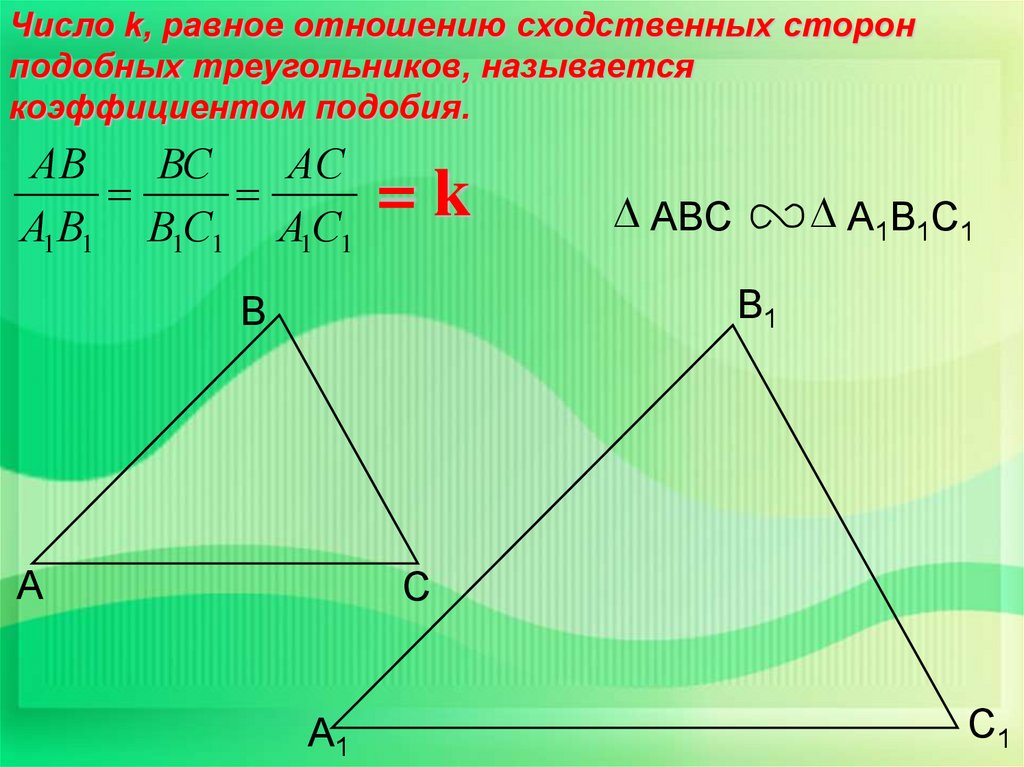
12.

Число k, равное отношению сходственных сторон
подобных треугольников, называется
коэффициентом подобия.
АВ
ВС
АС
А1 В1 В1С1 А1С1
=k
ABC
A1B1C1
В1
В
А
С
А1
С1

13.

Дано:
ABC
ORV
C V
Найти все углы треугольников
A O
B R
В
O
V
800
А
310
АВ
ВС
АС
OR
OV
RV
310
690
69
С
800
R

14.

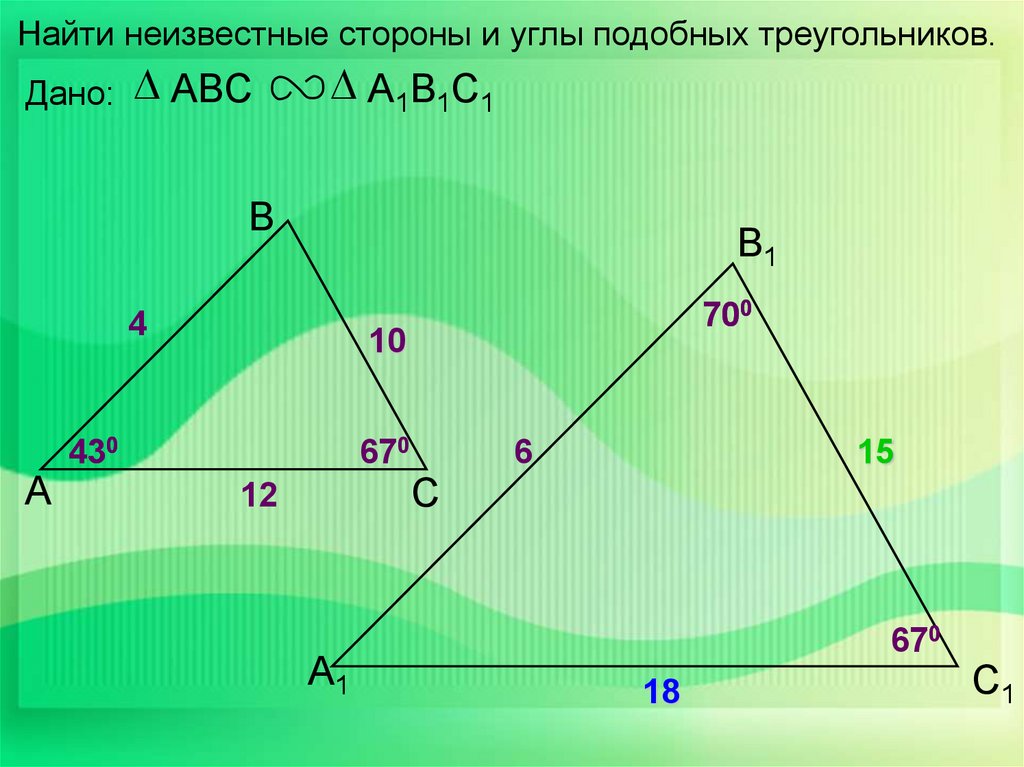
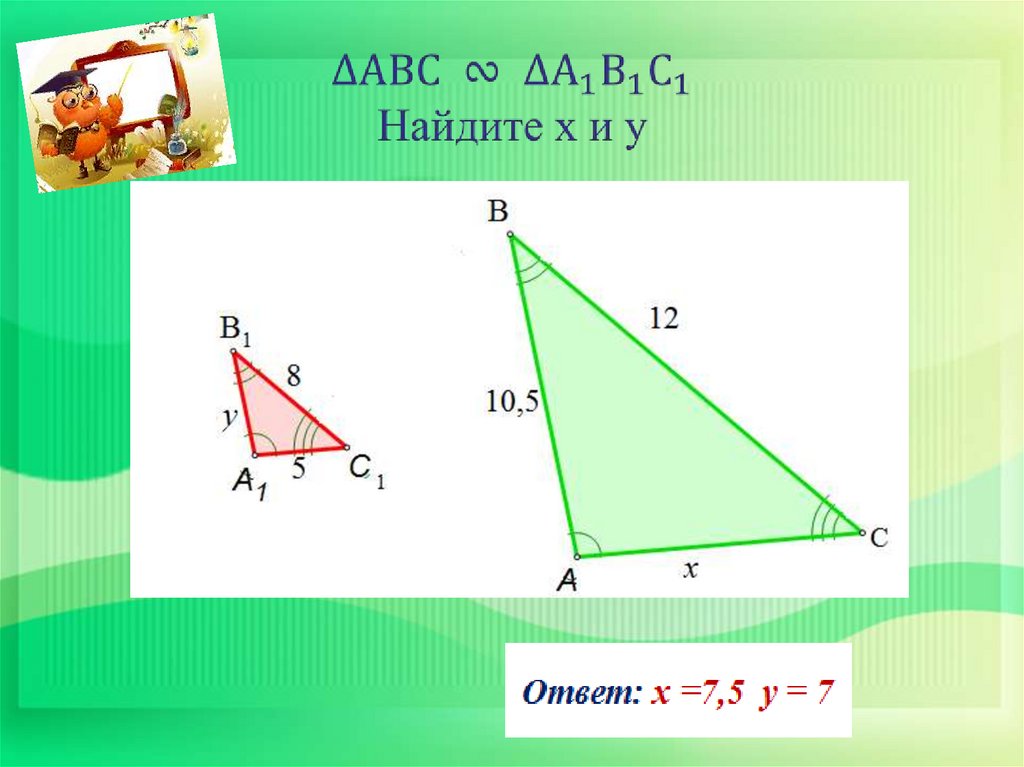
Найти неизвестные стороны и углы подобных треугольников.
Дано:
ABC
А1В1С1
В
В1
4
А
700
10
430
670
12
А1
С
6
15
670
18
С1

15.

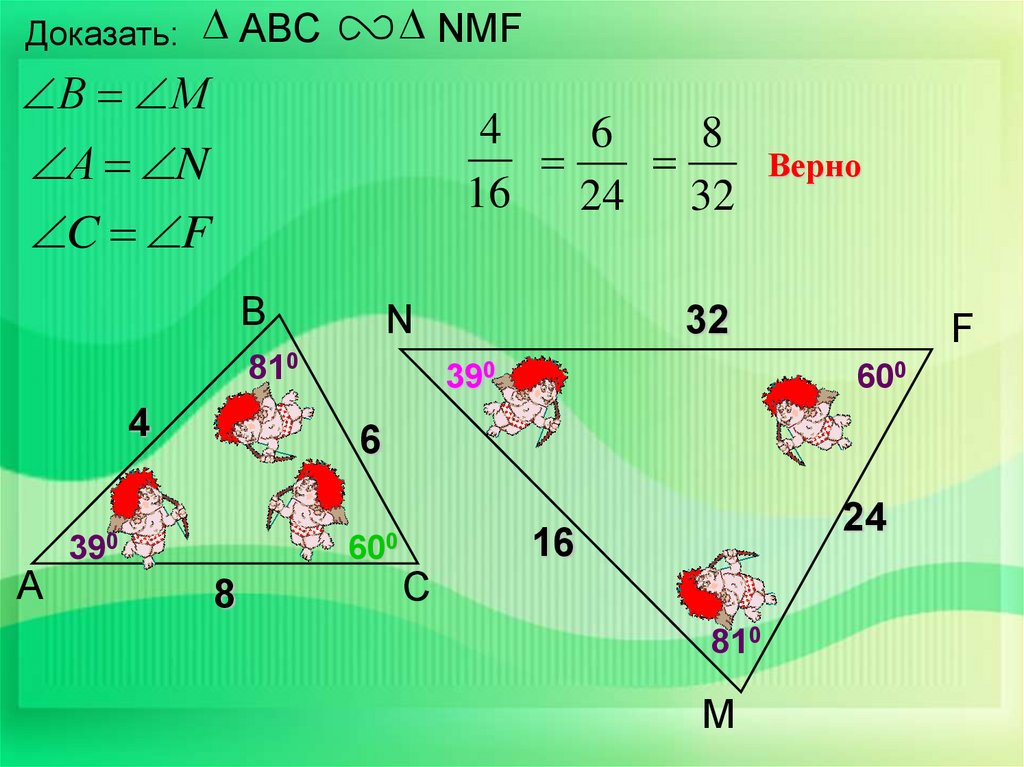
Доказать:
ABC
NMF
В М
4
6
8
16
24 32
А N
C F
В
N
810
4
А
Верно
32
390
F
600
6
390
600
8
24
16
С
810
М

16.

• Чему равно отношение площадей
треугольников, имеющих равные углы?

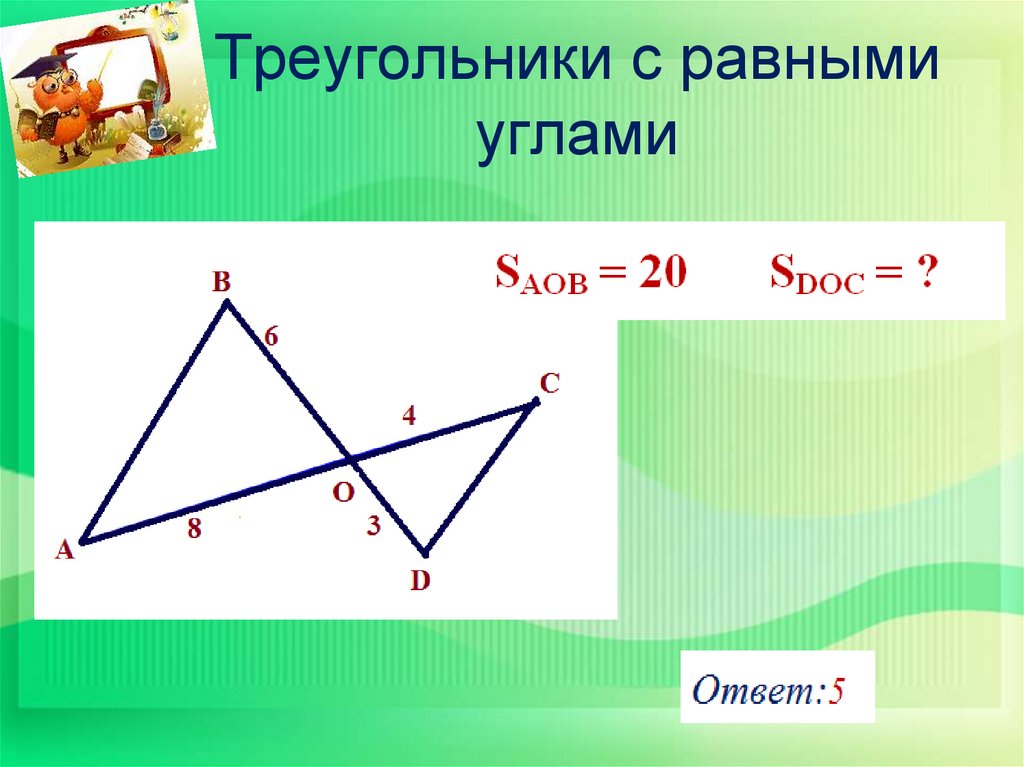
17. Треугольники с равными углами

18. Треугольники с равными углами

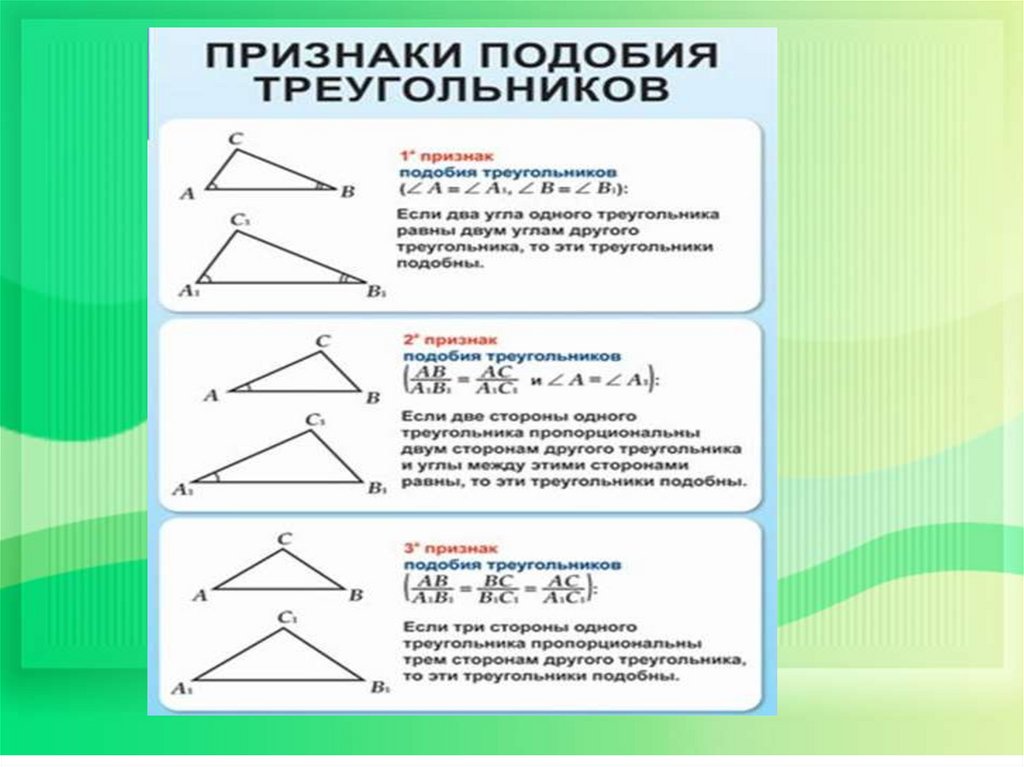
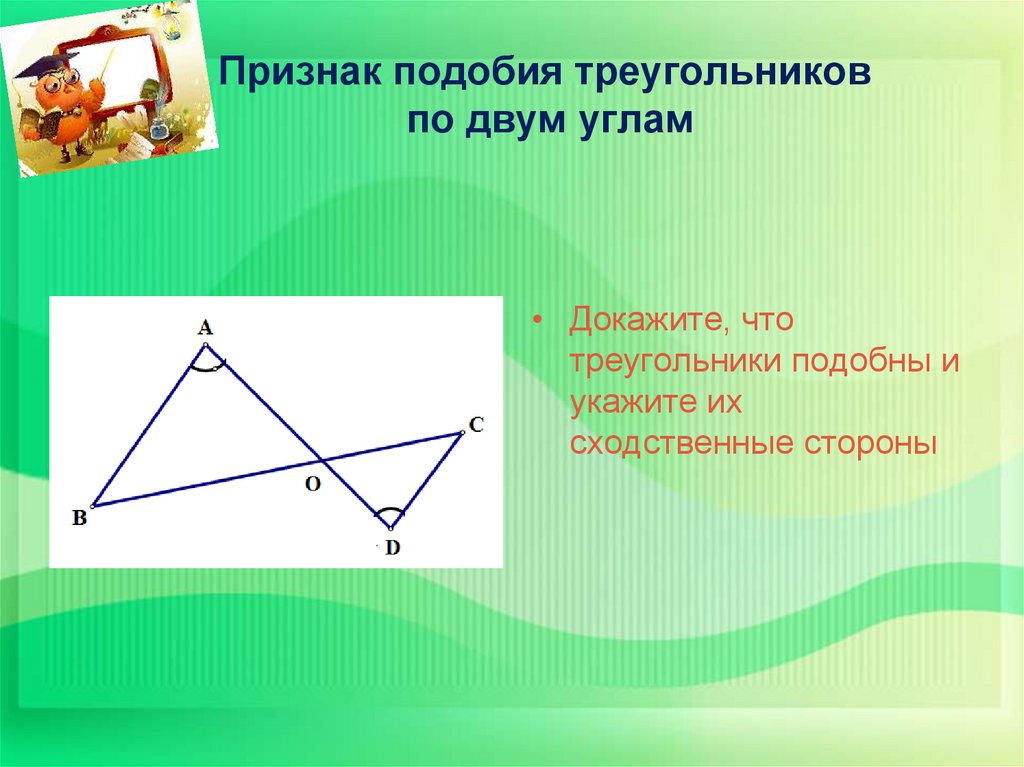
19. Признак подобия треугольников по двум углам

• Докажите, что
треугольники подобны и
укажите их
сходственные стороны

20. Признак подобия треугольников по двум углам

• Докажите, что
треугольники
подобны и укажите
их сходственные
стороны

21.  

22.  

23.

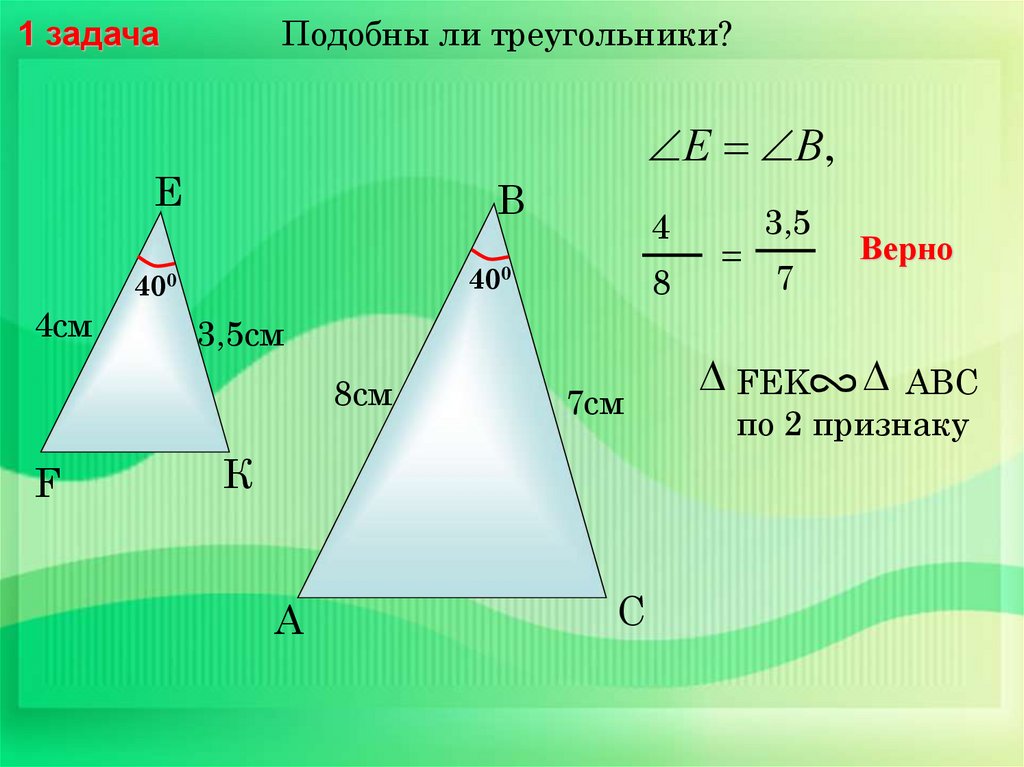
Подобны ли треугольники?
1 задача
Е В,
Е
B
400
400
4см
8
3,5см
8см
F
4
7см
К
A
С
=
3,5
7
FEK
Верно
AВС
по 2 признаку

24.

Подобны ли треугольники?
2 задача
М В ,
B
M
5
10
400
400
=
700
L
K
A
Верно
ABC
по 2 признаку
10см
5см
10
KML
10см
5см
5
C

25.

Реши задачу
1.
R
Являются ли треугольники подобными ?
T
N
S
D
F

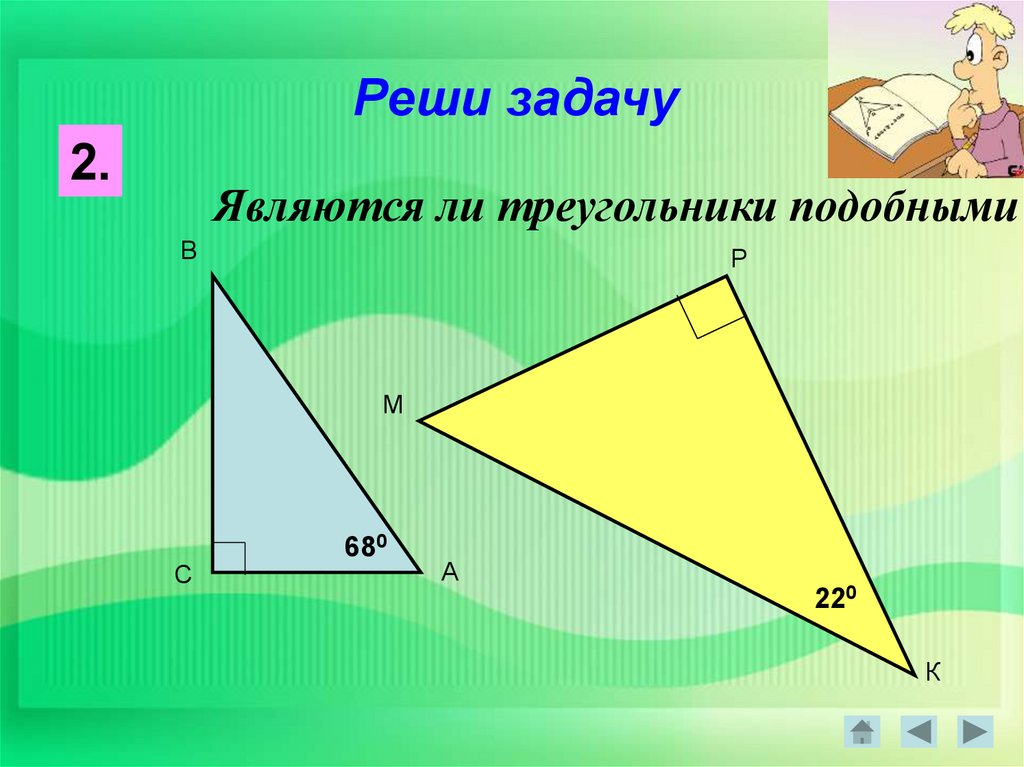
26.

Реши задачу
2.
Являются ли треугольники подобными
В
Р
М
С
680
А
220
К

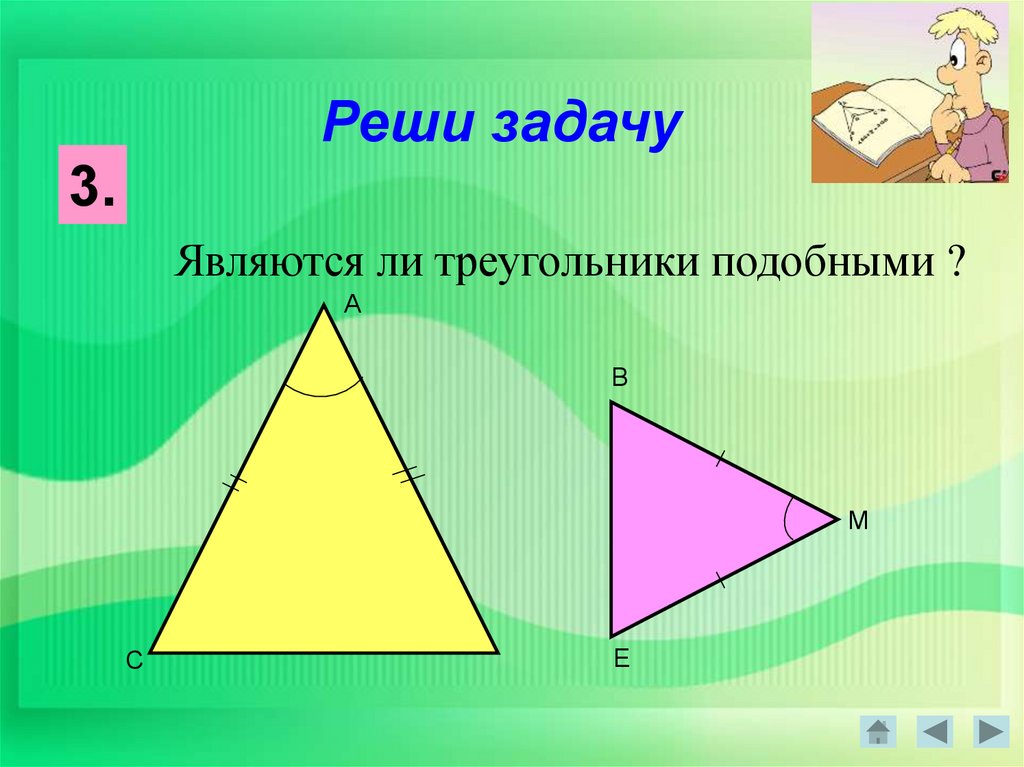
27.

Реши задачу
3.
Являются ли треугольники подобными ?
А
В
М
С
Е

28.

Реши задачу
4.
Назови подобные треугольники и сходственные стороны в них
FN
RS
N
F
A
R
S

29.

Реши задачу
5.
Назови подобные треугольники и сходственные стороны в ни
D
HZ
H
C
Z
K
CK

30.

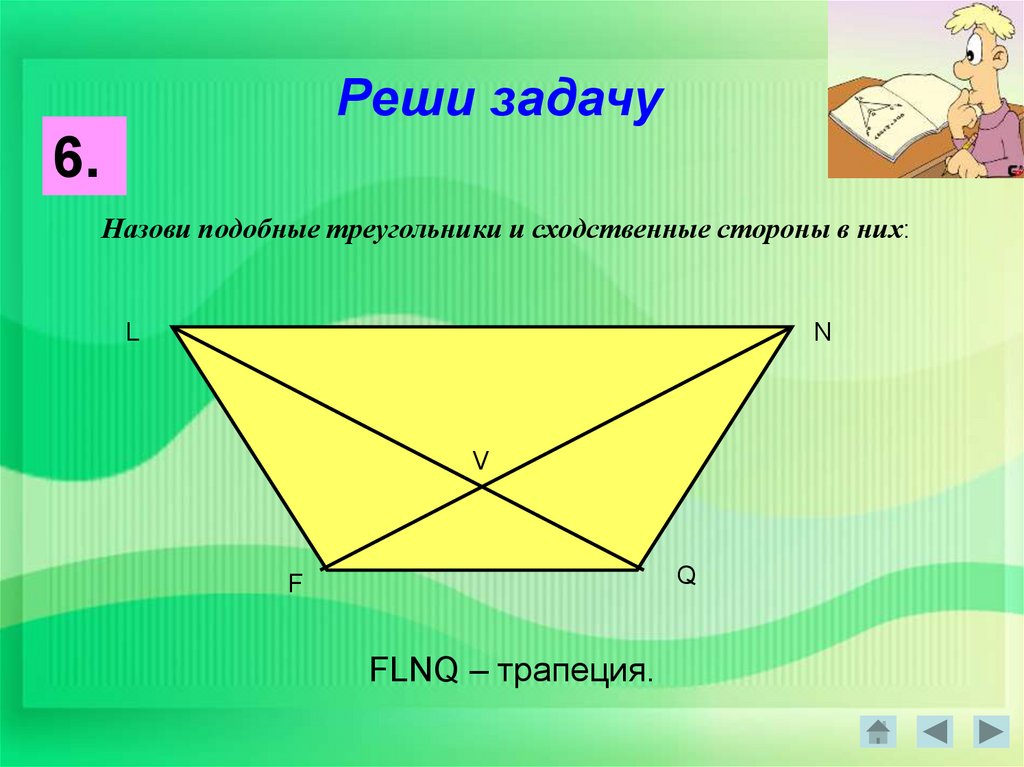
Реши задачу
6.
Назови подобные треугольники и сходственные стороны в них:
L
N
V
Q
F
FLNQ – трапеция.

31.

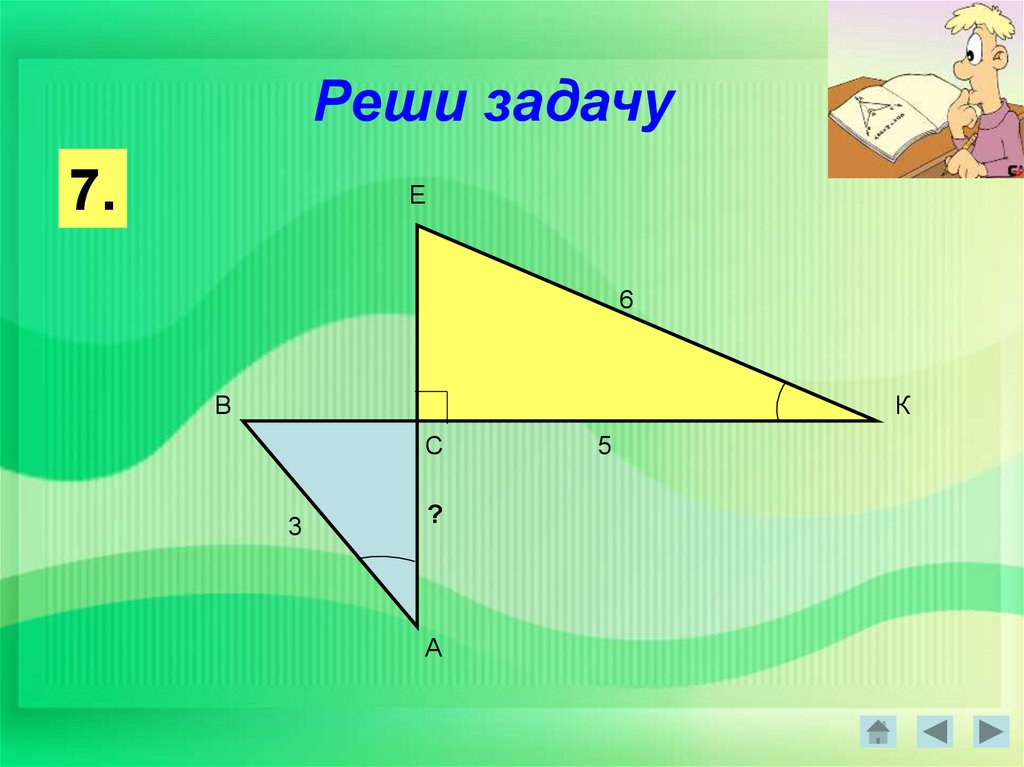
Реши задачу
7.
Е
6
В
К
С
3
?
А
5

32.

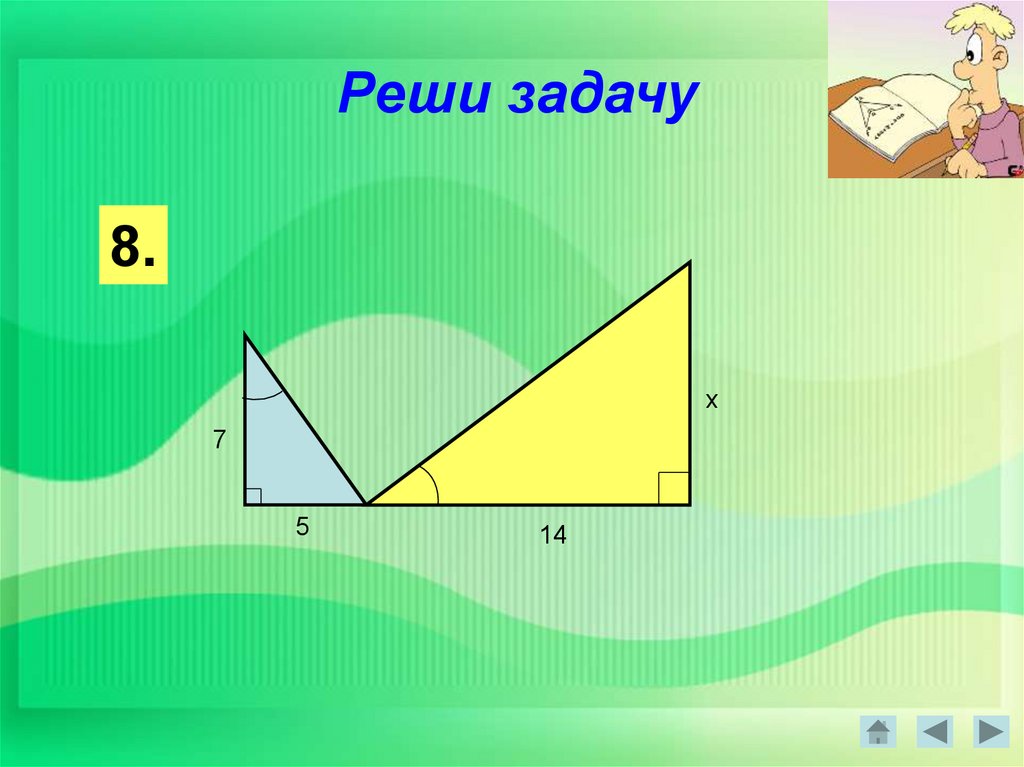
Реши задачу
8.
x
7
5
14

33.

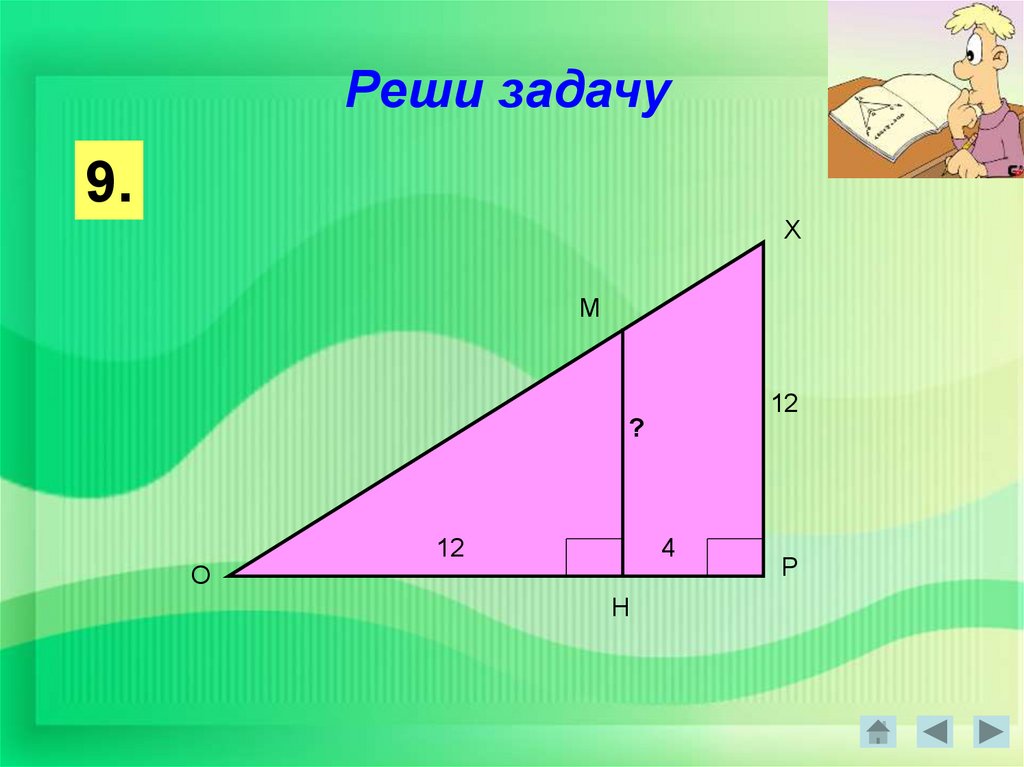
Реши задачу
9.
Х
М
12
?
О
12
4
Н
Р

34.

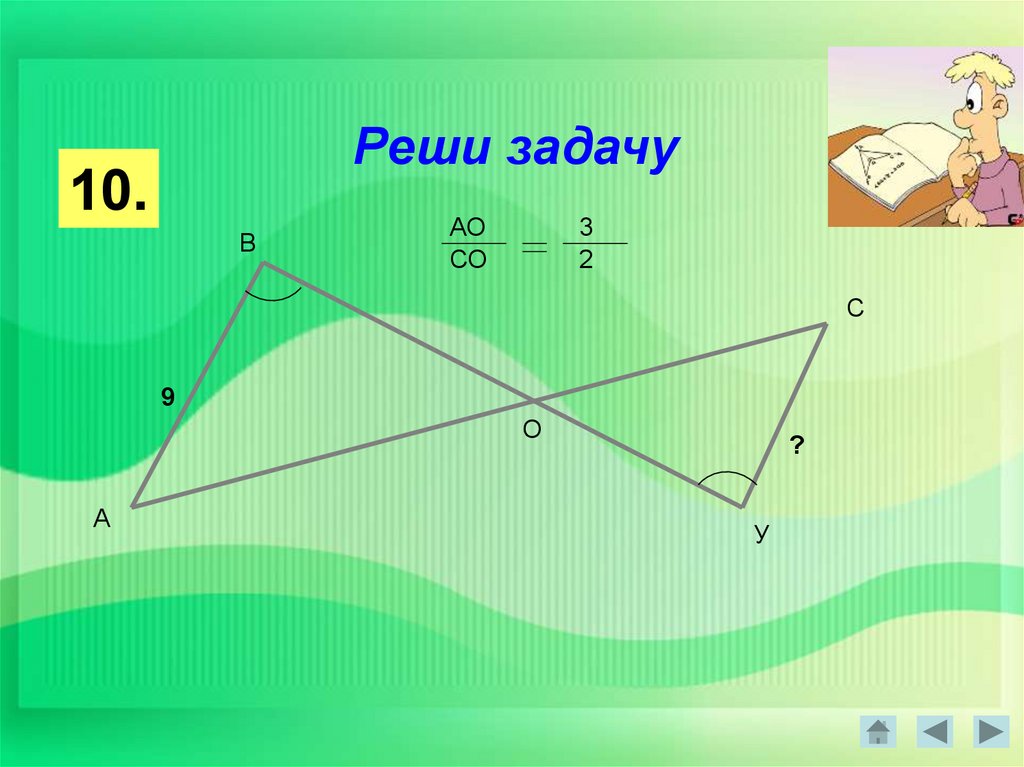
Реши задачу
10.
В
АО
СО
3
2
С
9
О
А
?
У

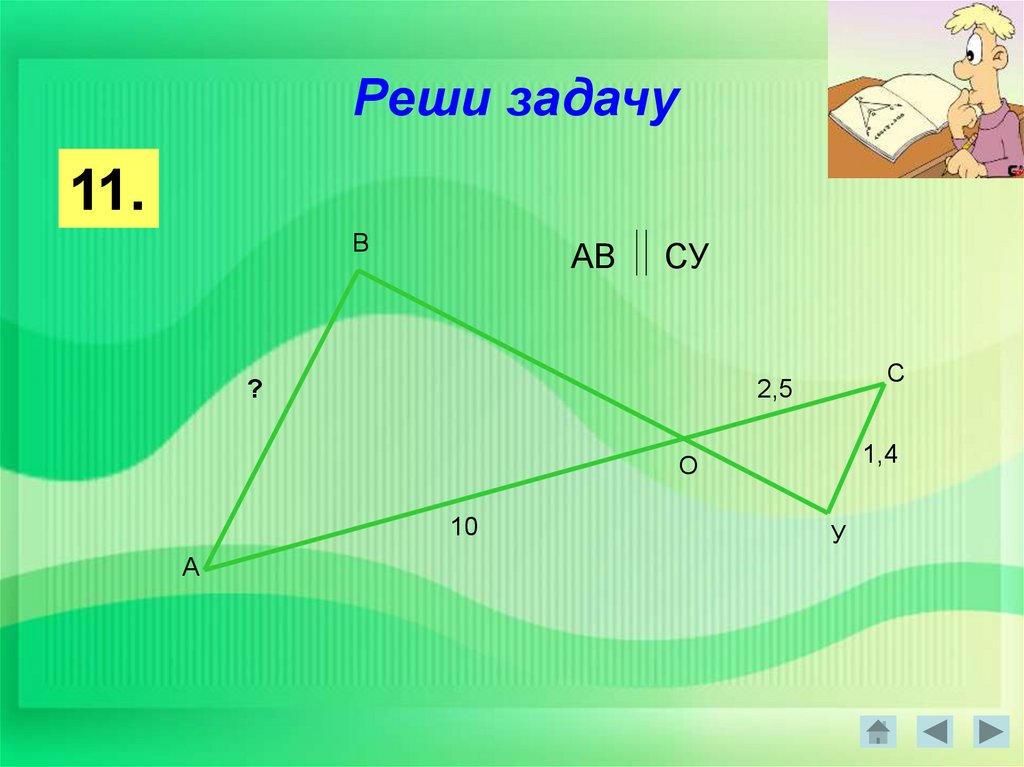
35.

Реши задачу
11.
В
АВ
СУ
?
С
2,5
1,4
О
10
А
У

36.

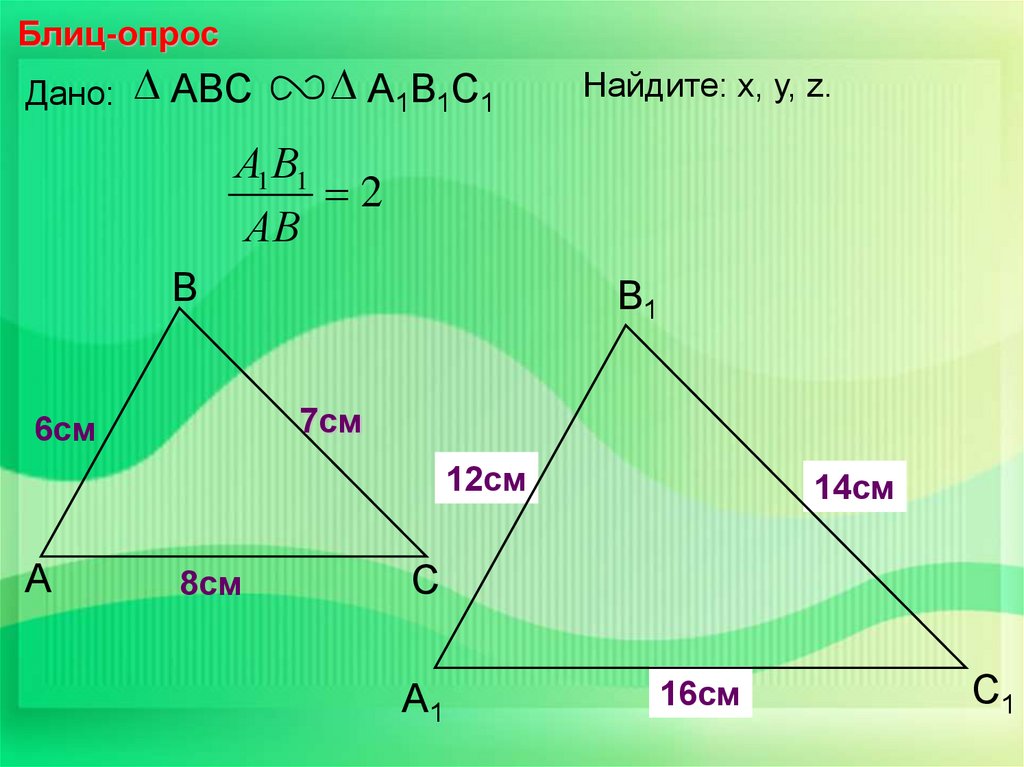
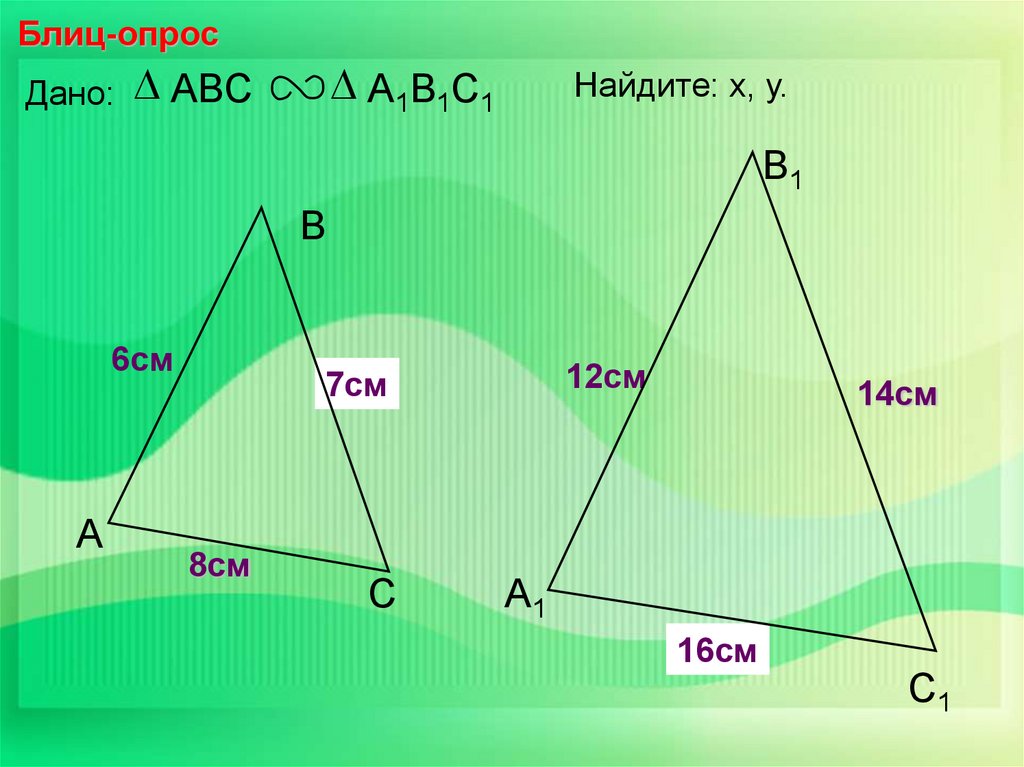
Блиц-опрос
Дано:
ABC
А1В1С1
Найдите: х, у, z.
А1 В1
2
АВ
В
В1
7см
6см
12см
х
А
8см
14см
у
С
А1
16см
z
С1

37.

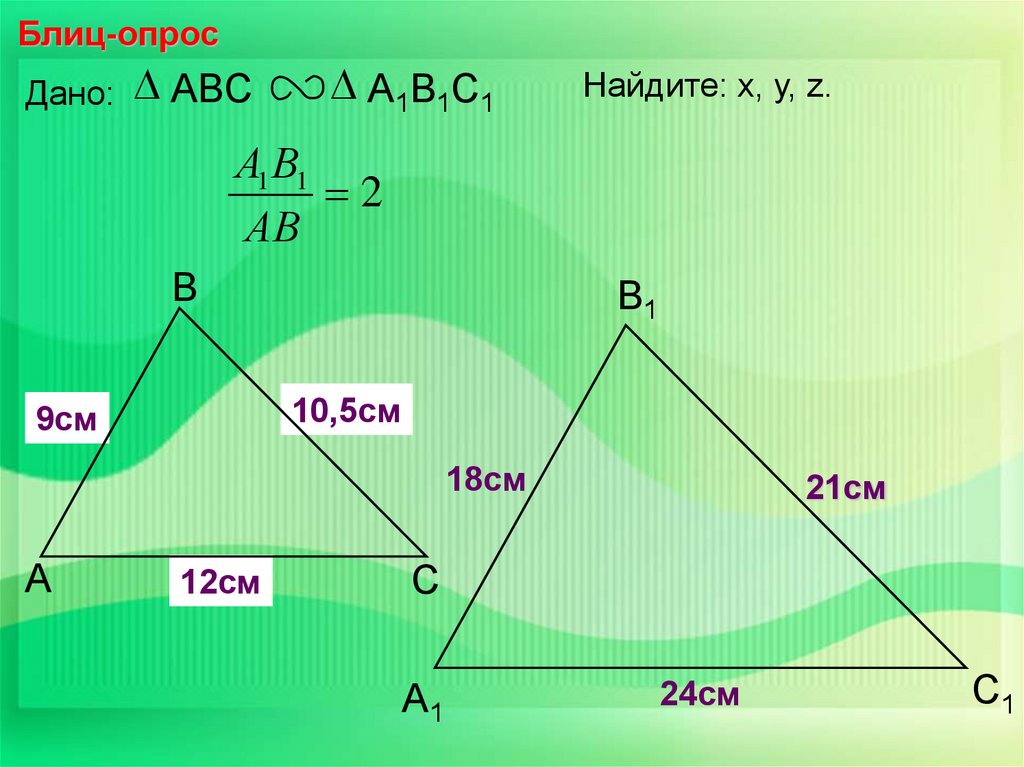
Блиц-опрос
Дано:
ABC
А1В1С1
Найдите: х, у, z.
А1 В1
2
АВ
В
В1
10,5см
у
9смх
18см
А
12см
z
21см
С
А1
24см
С1

38.

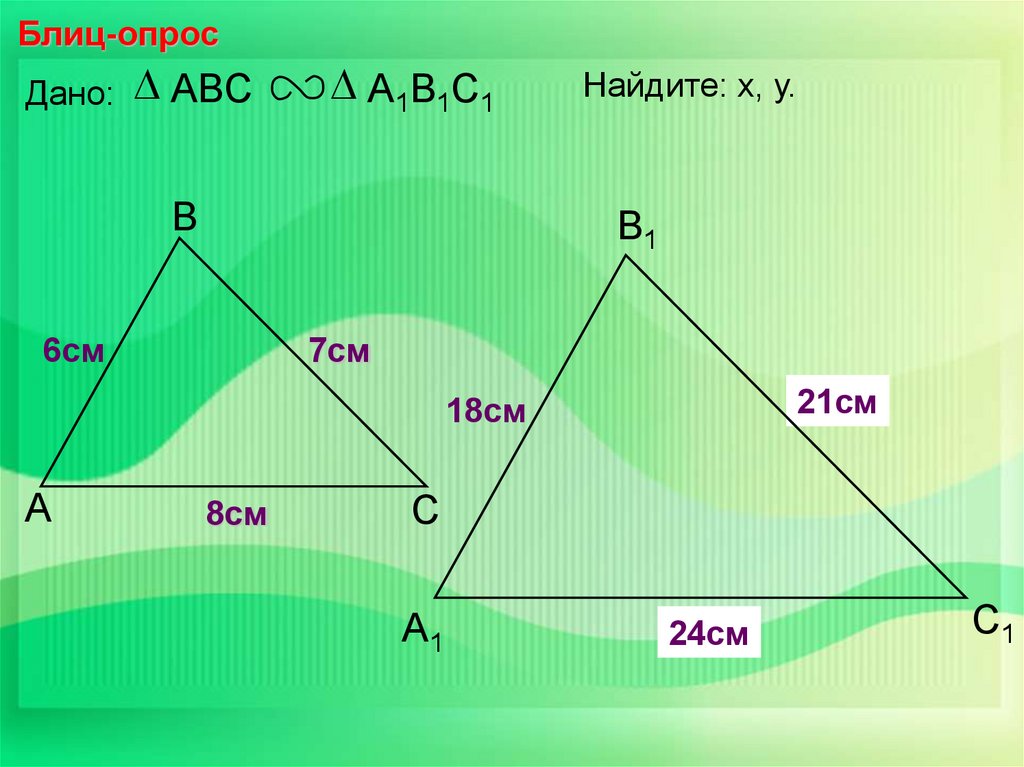
Блиц-опрос
Дано:
ABC
А1В1С1
В
Найдите: х, у.
В1
6см
7см
21см
х
18см
А
8см
С
А1
у
24см
С1

39.

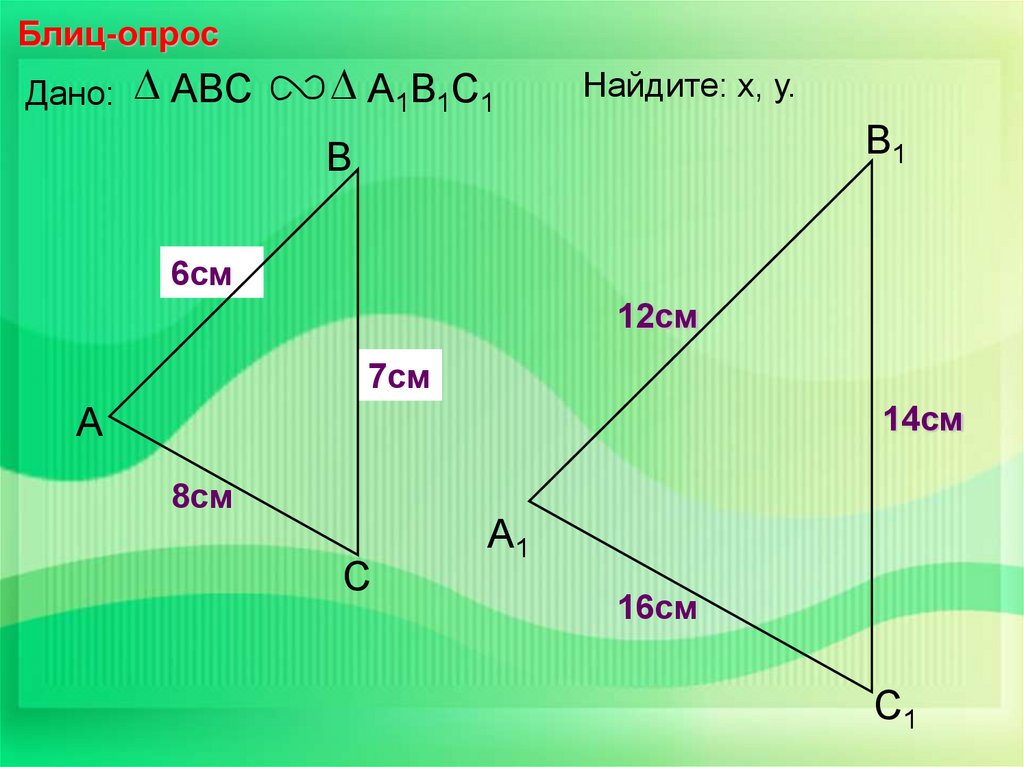
Блиц-опрос
Дано:
ABC
А1В1С1
Найдите: х, у.
В1
В
6см
х
12см
7см
у
А
14см
8см
С
А1
16см
С1

40.

Блиц-опрос
Дано:
ABC
А1В1С1
Найдите: х, у.
В1
В
6см
А
х
7см
8см
С
12см
А1
14см
у
16см
С1

41.

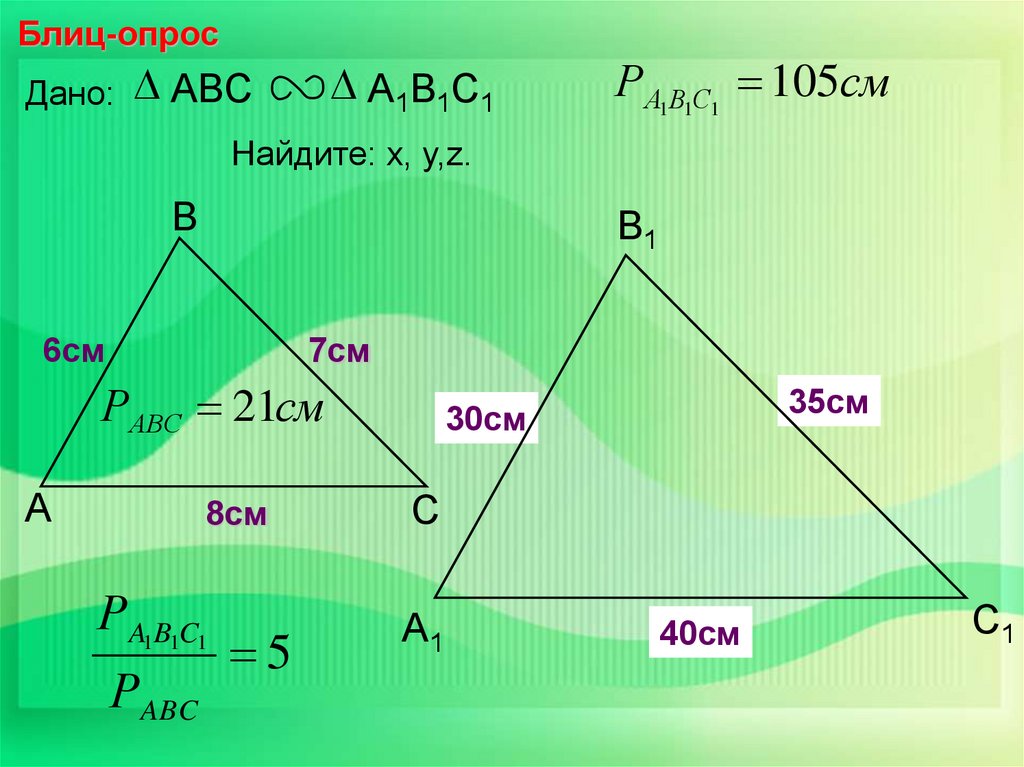
Блиц-опрос
Дано:
ABC
А1В1С1
РА1В1С1 105см
Найдите: х, у,z.
В
В1
6см
7см
РАВС 21см
А
8см
РA1B1C1
РABC
5
35см
y
х
30см
С
А1
z
40см
С1

42.

43.

44.

45.

46.

47.

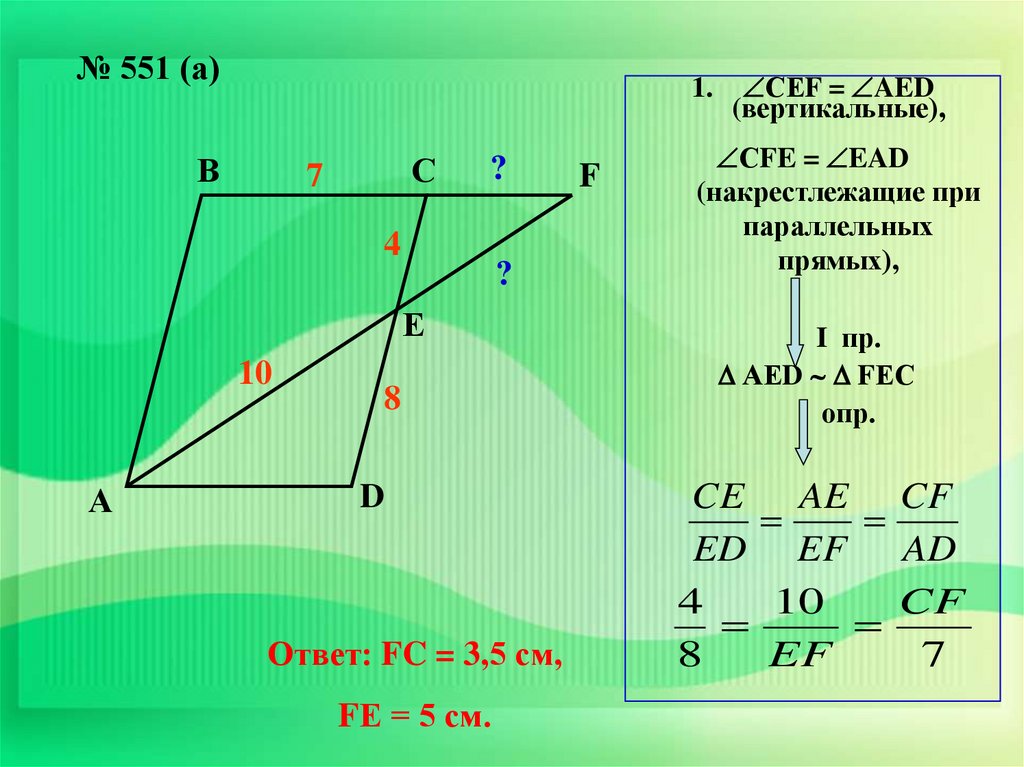
№ 551 (а)
1.
В
С
7
?
4
?
Е
10
А
8
D
Ответ: FC = 3,5 см,
FЕ = 5 см.
F
СЕF = AED
(вертикальные),
СFE = EAD
(накрестлежащие при
параллельных
прямых),
I пр.
АЕD FЕС
опр.
CE AE
ED EF
4
10
8
EF
CF
AD
CF
7

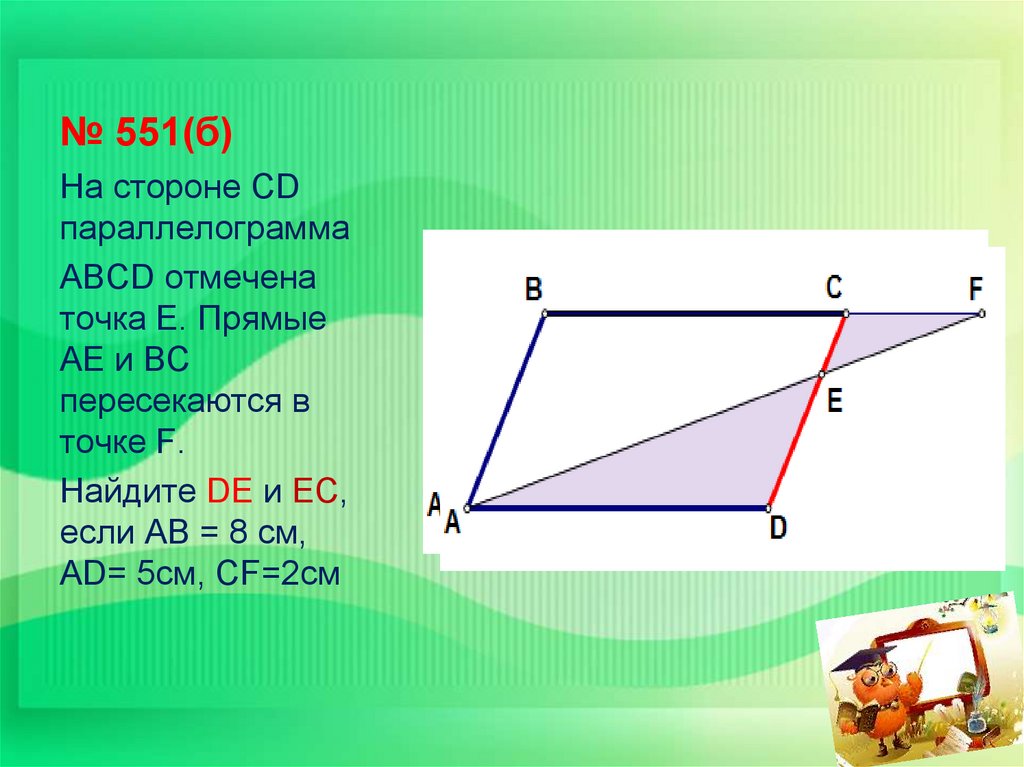
48. № 551(б)

На стороне СD
параллелограмма
ABCD отмечена
точка Е. Прямые
АЕ и ВС
пересекаются в
точке F.
Найдите DЕ и ЕС,
если АВ = 8 см,
AD= 5см, CF=2см

49.

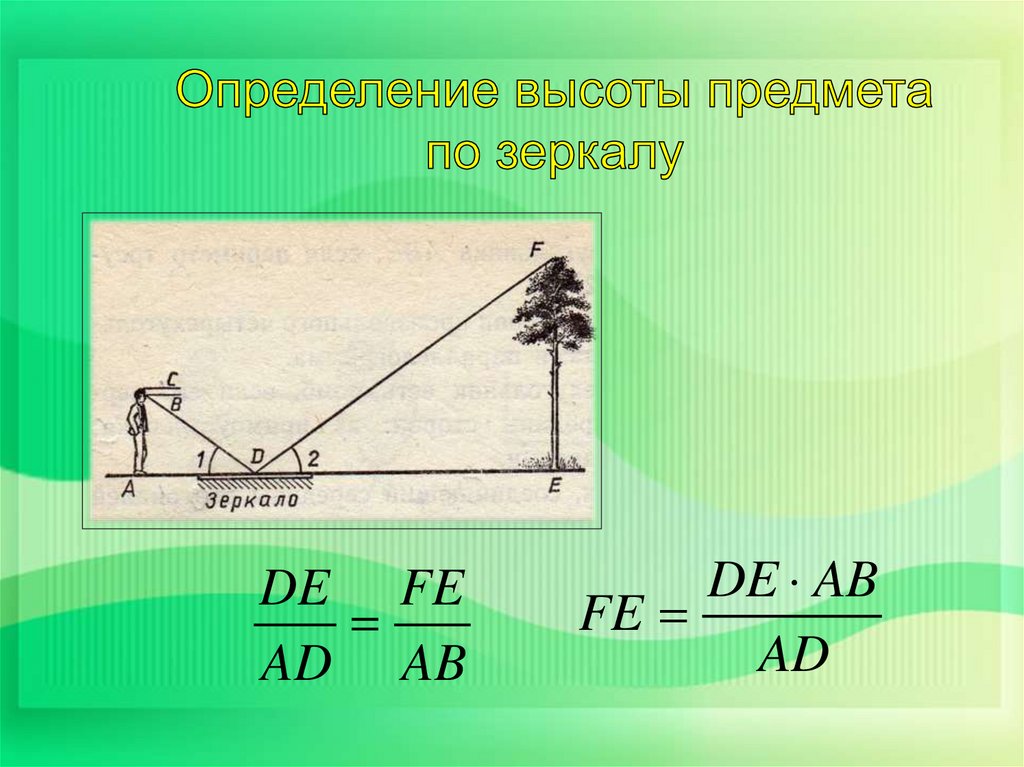
DE FE
AD AB
DE AB
FE
AD

50.

51.

52.

Найдите высоту ели АВ
если:
Высота колышка ab= 10м
Тень ели ВС =45м
Тень шеста bc= 15м
Решение:
АВС ~ abc (объясните почему)
АВ = ВС
ab
bc
AB 45
10 = 15
AB= 30м
Ответ:
Высота ели AB= 30м
Решение задач

53.

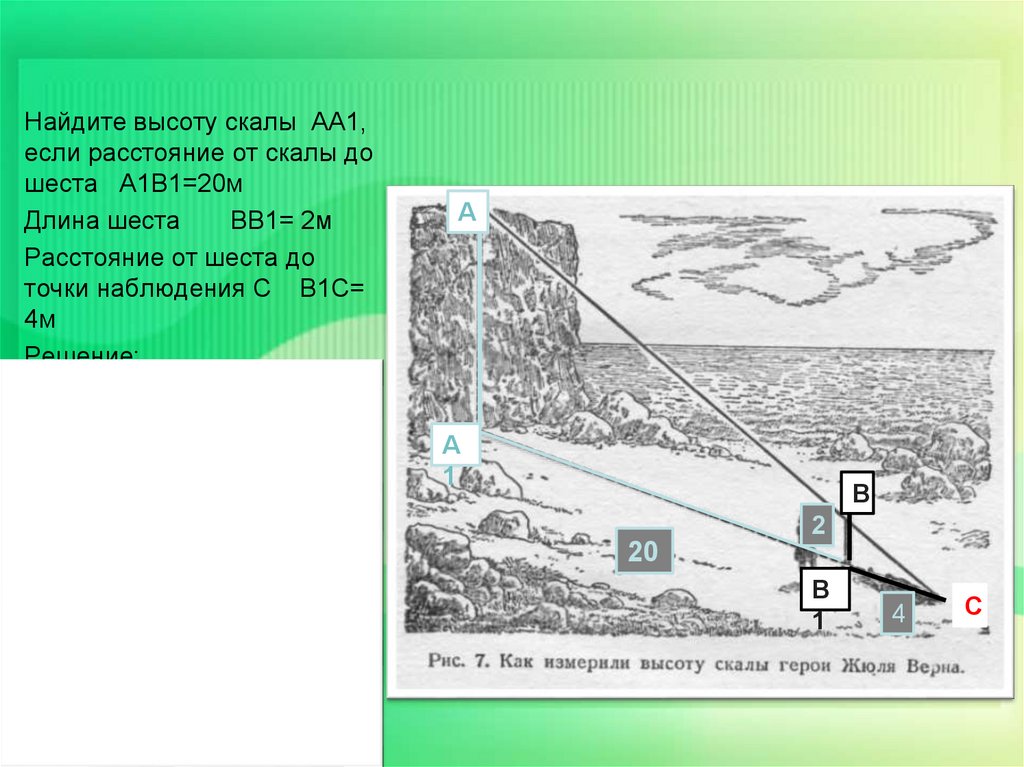
Найдите высоту скалы АА1,
если расстояние от скалы до
шеста А1В1=20м
Длина шеста
ВВ1= 2м
Расстояние от шеста до
точки наблюдения С В1С=
4м
Решение:
АА1 А1С
ВВ1 В1С
АА1
ВВ1 А1С 2 24
12 м
В1С
4
А
А
1
В
2
20
Ответ: Высота скалы равна
12м
В
1
4
С

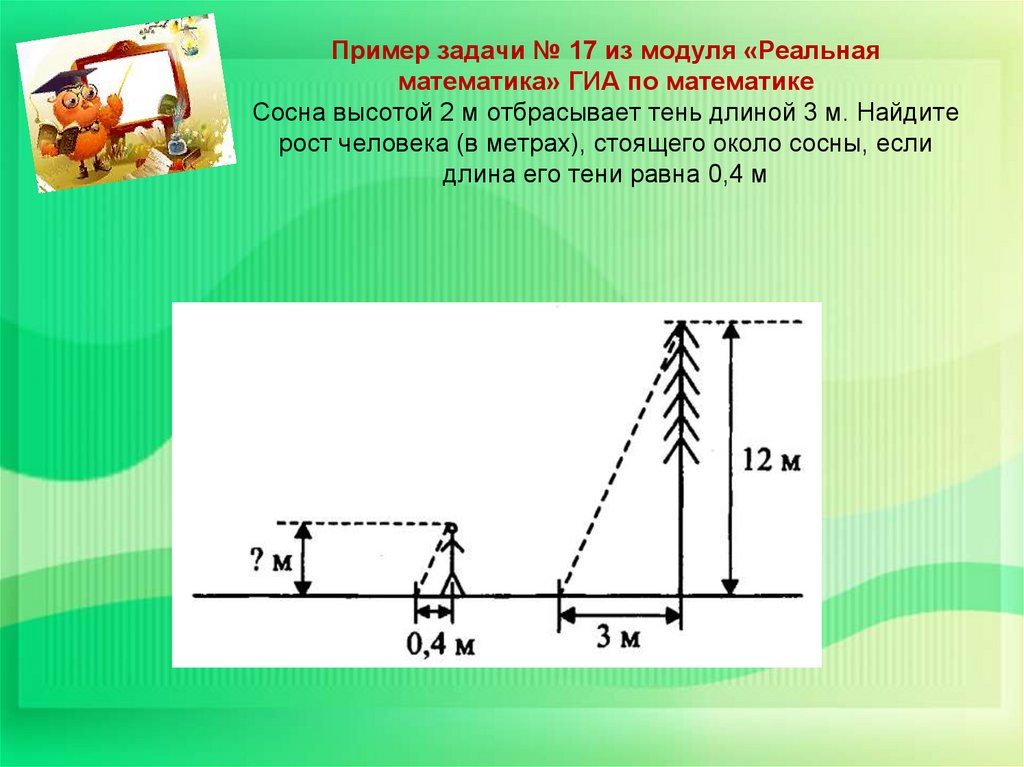
54. Пример задачи № 17 из модуля «Реальная математика» ГИА по математике Сосна высотой 2 м отбрасывает тень длиной 3 м. Найдите

рост человека (в метрах), стоящего около сосны, если
длина его тени равна 0,4 м

55. Пример задачи № 17 из модуля «Реальная математика» ГИА по математике

На сколько метров
поднимется
прикреплённый к
колодезному
журавлю конец
верёвки, если
человек опустил
короткий конец
журавля на 80 см?
Плечи журавля
составляют 2 м и
6 м.

56.

• Подумайте и
скажите,
какие величины
необходимо знать
для нахождения
высоты ели?
• Составьте
пропорцию для её
нахождения;
• Решите задачу.

57.

Чтобы найти ширину реки АВ необходимо
поставить колышек С на продолжение АВ,
вдоль берега отмерить на прямой CF
перпендикулярной АС, расстояние одно в
несколько раз меньше другого. Например
: отмеряют FE в четыре раза меньше ЕС.
По направлению FG, перпендикулярному
к FD отыскивают точку Н из которой точка
Е перекрывает точку А.
Треугольники АСЕ и EFH подобны
(объясните почему). Из подобия
треугольников следует пропорция
AC:FH=CE:EF=4:1.
Значит, измерив FH, можно узнать
искомую ширину реки.
Дано:
CE:EF=4:1 FH=6 м, BC=4 м
Найти: АВ.
Ответ: 20 м.

58. Решение задачи на конкретном примере

• Измерим высоту ели с помощью полученных
знаний о подобных треугольниках. Для этого
сделаем следующее: выйдем на местность,
выберем объект измерения, в нашем случае
ель, на некотором расстоянии от неё
установим шест, в нашем случае Ксюшу =D, и
сфотографируем. Затем измерим расстояние
от объекта до шеста. Но для измерения нам
необходимо знать не только эту величину. Нам
так же потребуется знать расстояние от Ксении
до пересечения гипотенузы с землёй.

59.

– Дано:
СС1- 8м, расстояние от ели до
Ксюши(шеста)
АС-1,5м, рост Ксюши
ВС- 1 м, расстояние от Ксюши до
точки пересечения гипотенузы с
землёй.
А
1
?
– Найти:
А
А1С1- высота ели.
– Решение:
АС*ВС₁
А1С1=1,5*9
ВС
В
= 13,5
=
1
Ответ: высота ели = 13,5м
С
С
1