Похожие презентации:
Техническая механика
1. Техническая механика
2. Раздел 1. Теоретическая механика
Тема 1.2. Связи и их реакции6. Жесткая заделка. Заделка (рис.
1.12) исключает
возможность любых перемещений вдоль осей Ох и Оу, а
также поворот в плоскости хОу. Поэтому такая связь
при
освобождении тела от связи будет заменяться
реакцией R
(или ее
проекциями Rx и Ry и моментом в
заделке МА).
3. Раздел 1. Теоретическая механика
Тема 1.3. Плоская система силСистема сил, линии действия которых лежат в одной
плоскости, называется плоской. На плоскости могут
быть приложены произвольно
расположенные
силы,
пары сил и силы, сходящиеся в одной точке.
Равновесие системы сходящихся сил. Сходящимися
называются
силы,
линии
действия
которых
пересекаются в одной точке (рис. 1.13, а). Существуют
два
метода
сложения
пересекающихся
сил:
геометрический (рис. 1.13, б) и аналитический
(рис. 1.13, в).Геометрический метод сложения
сходящихся сил. От произвольной точки О
откладываем вектор, равный силе j; от конца F
{ откладываем вектор, равный силе F2, и т.д.
(см. рис. 1.13, а, б). Затем, соединяя начало
вектора F{ с концом последнего Fa, получаем
равнодействующую всех сил.
Построенная
фигура
называется
силовым
многоугольником.
4. Раздел 1. Теоретическая механика
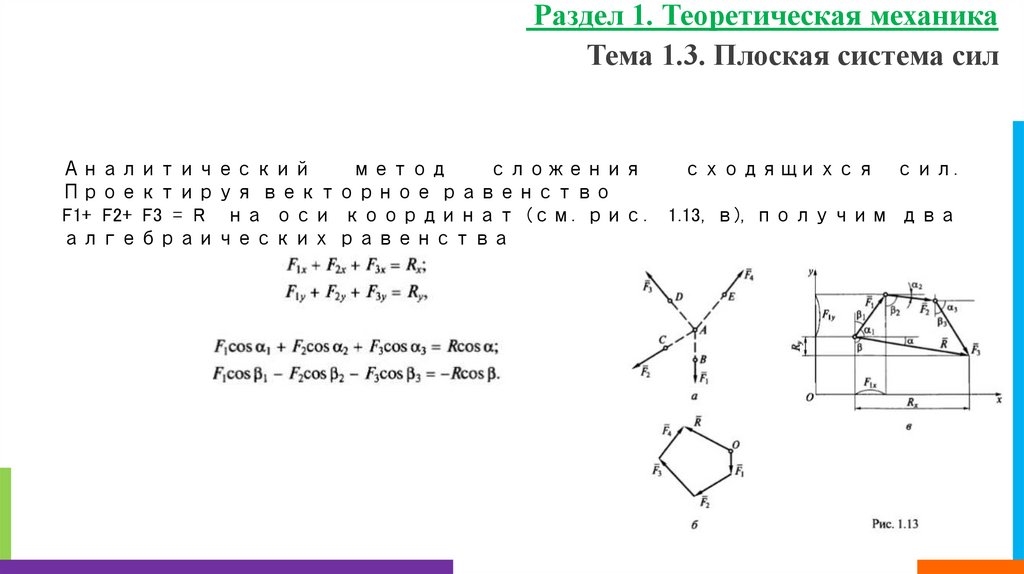
Тема 1.3. Плоская система силАналитический
метод
сложения
Проектируя векторное равенство
F1+ F2+ F3 = R на оси координат (см. рис.
алгебраических равенства
сходящихся
сил.
1.13, в), получим два
5. Раздел 1. Теоретическая механика
Тема 1.3. Плоская система силУсловием
равновесия
системы
сходящихся
сил
является равенство нулю модуля равнодействующей R,
т. е. силовой многоугольник должен быть замкнутым
(при
геометрическом
способе
сложения)
или
(аналитически) проекции равнодействующей силы на
оси координат должны быть равны нулю (Rx = Ry = 0). Отсюда
для плоской системы сходящихся сил получим два
уравнения равновесия этих сил:
Следовательно, для равновесия системы сходящихся
сил необходимо и достаточно, чтобы сумма проекций
всех сил на каждую из осейкоординат была равна нулю.




 Физика
Физика








