Геометрические фигуры

1.

Геометрические
фигуры
Бызова Светлана Анатольевна,
преподаватель,
ГБПОУ АО «Архангельский
государственный многопрофильный
колледж»

2.

Аннотация к подготовленным материалам:
Тема: «Геометрические фигуры»
Интерактивный плакат для студентов 2-х курсов по ЕН.01
«Математика»
Литература: Фрейлах, Наталья Ивановна.
Математика для педагогических училищ : учеб. пособие / Н. И. Фрейлах. – М. : ИД
"Форум" - ИНФРА-М, 2017.
Инструкция:
слайд 3 – щелчок по словам Геометрия, Планиметрия, Стереометрия - выводит их
определения. По всем остальным объектам - гиперссылки.
Слайд 8 – щелчок по словам точка, прямая, плоскость - выводит рисунки.
Слайд 9 – гиперссылка по слову раскрываются переход на слайд 10.
Слайд 11- щелчок по словам Многоугольники, правильные - выводит их определения,
щелчок по словам выпуклые, невыпуклые - выводит рисунки.
Слайд 16 – щелчок по словам Тела вращения - выводит определение, щелчок по
словам цилиндр, конус, шар, сфера - выводит рисунки.
Слайд 17- щелчок по словам Многогранники, правильные - выводит их определения,
щелчок по словам выпуклые, невыпуклые - выводит рисунки. Гиперссылка по
определению правильного многогранника выводит слайд 18.

3.

Это наука о пространственной
форме и количественных
Геометрия
характеристиках предметов
реального мира.
Часть Планиметрия
геометрии, изучающая
фигуры на плоскости.
Основные
фигуры
Многоугольники
Часть Стереометрия
геометрии, изучающая
фигуры в пространстве.
Тела
вращения
Многогранники
Из истории развития
геометрии
Неопределяемые
понятия
Правила построения
геометрии
Вопросы для
самоконтроля

4.

Вопросы для самоконтроля
1. Что изучает геометрия?
2. Что изучает планиметрия?
3. Что изучает стереометрия?
4. Что называется геометрической фигурой?
5. Назовите основные фигуры на плоскости и в пространстве?
6. Дайте определение отрезка?
7. Дайте определение ломаной?
8. Дайте определение угла?
9. Дайте определение многоугольника?
10.Дайте определение треугольника?
11.Перечислите виды треугольников?
12.Дайте определение круга и окружности?
13.Дайте определение многогранника и тела вращения?
14.Приведите классификацию тел вращения?
15.Дайте различные определения куба?

5.

Из истории развития геометрии
Многочисленные памятники письменности свидетельствуют о
том, что уже около 4000 лет назад египтяне имели значительный
запас геометрических сведений, первоначально представлявших
собой набор правил, позволяющих измерять площади земельных
участков, вычислять объемы сосудов, решать задачи,
возникающие в процессе строительных работ. Сохранившиеся
до наших времен и поражающие своим величием храмы и
гробницы египетских фараонов
служат убедительным
подтверждением высокого
уровня геометрических знаний
древних египтян.

6.

Из истории развития геометрии
Развитие мореплавания и торговли привело к
тому, что накопленные египтянами сведения о
свойствах фигур стати в начале VI в. до н. э.
достоянием ученых Древней Греции. Одним из
тех, кто внес огромный вклад в формирование
геометрической науки, был древнегреческий
философ Фалес (ок. 625—547 до н. э.).
Его многочисленные путешествия способствовали
освоению знаний, которыми владели цивилизации Древнего
Вавилона и Египта. Если в Древнем Египте геометрия
носила прикладной характер, то благодаря ученым Древней
Греции она постепенно становилась математической
теорией, способствующей открытию новых геометрических
фактов.

7.

Из истории развития геометрии
Особую роль в развитии геометрии как науки сыграл
древнегреческий ученый Евклид, который жил в Александрии в
III в. до н. э. Его величайшая заслуга состояла в систематизации
накопленного к тому времени богатейшего геометрического
материала и придании изложению геометрии довольно
совершенной логической формы. Основываясь на воззрениях
древнегреческого ученого Аристотеля (ок. 384—322 до н. э.),
Евклид осуществил достаточно логически строгое построение
геометрии. Итогом геометрических исследований,
проведенных ученым, стал научный труд,
состоящий из 15 книг, под общим названием
«Начала», который, по мнению физика XX в.
А. Эйнштейна (1879— 1955), дал человечеству
«уверенность для всей его последующей
деятельности».

8.

Неопределяемые понятия геометрии
Прямая
Точка
Плоскость

9.

Правила построения геометрии
1. Некоторые понятия вводятся без определений.
2. Часть свойств основных понятий раскрывается
через аксиомы.
3. Другие понятия, как правило, раскрываются через
род и видовое отличие, через основные понятия или
уже определенные понятия.
4. Другие свойства понятий формулируются в виде
теорем и доказываются с использованием аксиом и
ранее доказанных теорем.

10.

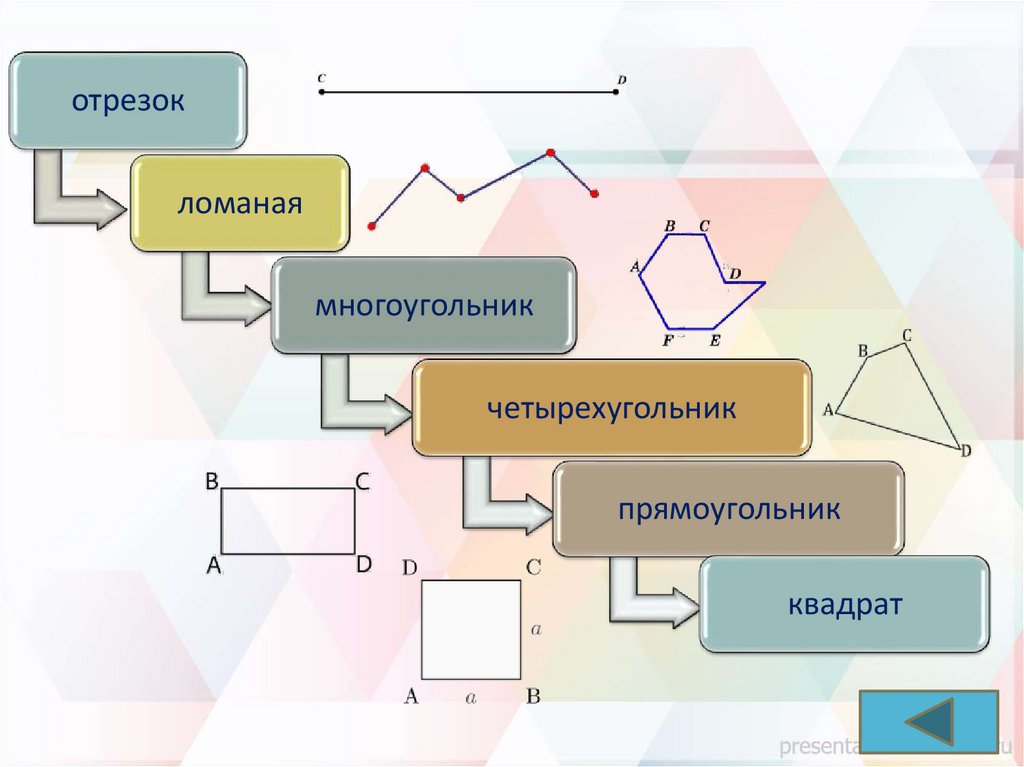
отрезок
ломаная
многоугольник
четырехугольник
прямоугольник
квадрат

11.

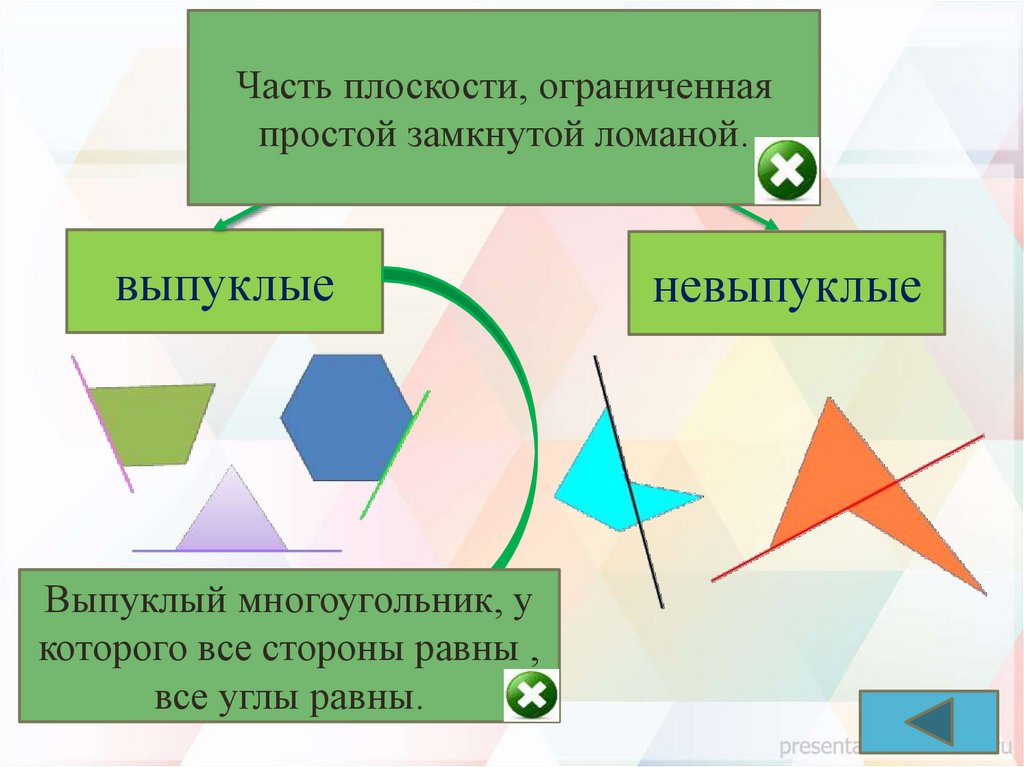
Часть
плоскости, ограниченная
Многоугольники
простой замкнутой ломаной.
выпуклые
Выпуклый многоугольник, у
правильные
которого
все стороны равны ,
все углы равны.
невыпуклые

12.

Основные фигуры
• Отрезком называется часть прямой, которая состоит из всех точек этой
прямой, лежащих между двумя данными её точками.
• Лучом называется часть прямой, которая состоит из всех точек этой
прямой, лежащих по одну сторону от данной её точки. Эта точка
называется начальной точкой луча.
• Углом называется фигура, которая состоит из точки – вершины угла – и
двух различных лучей или отрезков, исходящих из этой точки – сторон
угла.
• Если стороны угла являются дополнительными лучами одной прямой, то
угол называют развёрнутым.
• Два угла называются смежными, если у них одна сторона общая, а
другие стороны этих углов являются дополнительными лучами.
• Угол, равный 90°, называется прямым.
• Угол, меньший 90°, называют острым углом.
• Угол, больший 90° и меньший 180°, называют тупым.
• Два угла называют вертикальными, если стороны одного угла являются
дополнительными лучами сторон другого.

13.

Основные фигуры
• Две прямые называются параллельными, если они не
пересекаются. Для обозначения параллельности прямых
используется знак||.
• Ломаной называется линия, состоящая из отрезков, соединенных
последовательно концами.
• Ломаная называется простой, если она не имеет самопересечений.
• Ломаная называется замкнутой, если у неё концы совпадают.
• Треугольником называется фигура, которая состоит из трёх точек,
не лежащих на одной прямой, и трёх отрезков, попарно
соединяющих эти точки. Точки называются вершинами
треугольника, а отрезки – его сторонами.
• Треугольник называется равнобедренным, если у него две стороны
равны. Эти равные стороны называются боковыми сторонами, а
третья сторона называется основанием треугольника.
• Треугольник, у которого все стороны равны, называется
равносторонним.

14.

Основные фигуры
• Высотой треугольника, опущенной из данной вершины, называется
перпендикуляр, проведённый из этой вершины к прямой, которая
содержит противолежащую сторону треугольника.
• Медианой треугольника, проведённой из данной вершины,
называется отрезок, соединяющий эту вершину с серединой
противолежащей стороны треугольника.
• Биссектрисой треугольника, проведённой из данной вершины,
называется отрезок биссектрисы угла треугольника, соединяющий
эту вершину с точкой на противолежащей стороне.
• Треугольник называется прямоугольным, если у него есть прямой
угол.
• Сторона прямоугольного треугольника, противолежащая прямому
углу, называется гипотенузой, две другие стороны называются
катетами.
• Треугольник называется остроугольным, если все его углы – острые.
Треугольник называется тупоугольным, если у него есть тупой угол.

15.

Основные фигуры
• Параллелограмм – это четырёхугольник, у которого противолежащие
стороны параллельны, т. е. лежат на параллельных прямых.
• Прямоугольник – это параллелограмм, у которого все углы прямые.
• Ромб – это параллелограмм, у которого все стороны равны.
• Квадрат – это прямоугольник, у которого все стороны равны. Можно
также сказать, что квадрат – это ромб, у которого все углы прямые.
• Трапецией называется четырёхугольник, у которого только две
противолежащие стороны параллельны. Эти параллельные стороны
называются основаниями трапеции. Две другие стороны называются
боковыми сторонами.
• Окружностью называется фигура, которая состоит из всех точек
плоскости, равноудалённых от заданной точки. Эта заданная точка
называется центром окружности.
• Расстояние от точек окружности до её центра называется радиусом
окружности. Радиусом называется также отрезок, соединяющий любую
точку окружности с её центром.
• Отрезок, соединяющий две точки окружности, называется хордой. Хорда,
проходящая через центр, называется диаметром окружности.

16.

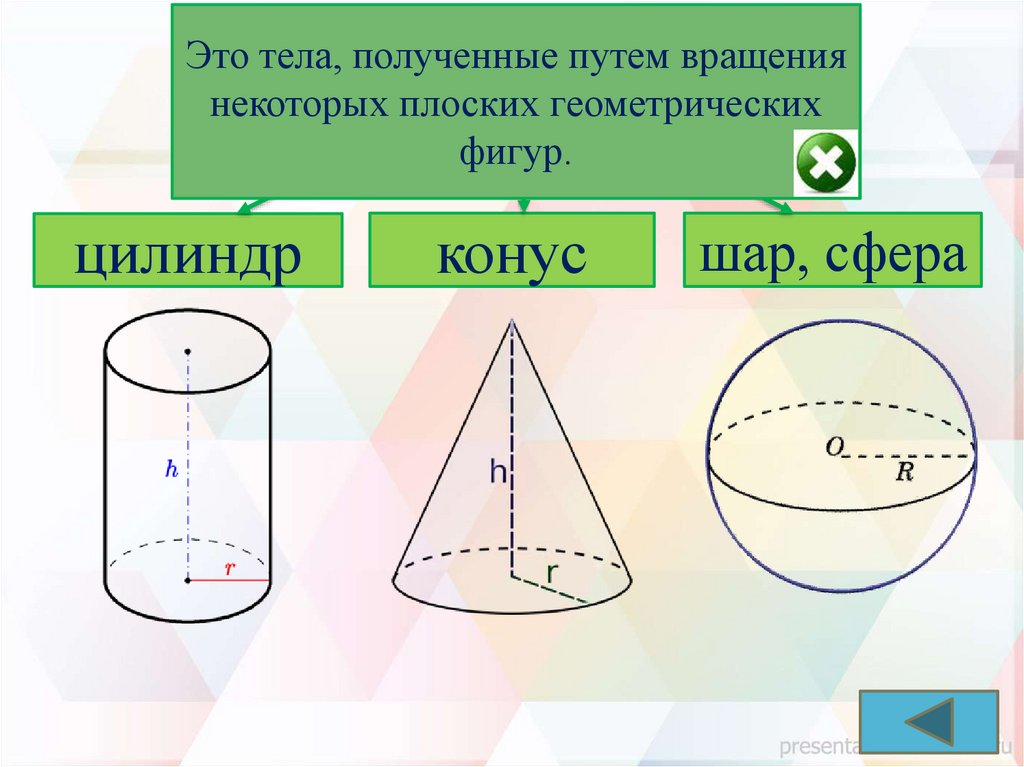
Это тела, полученные путем вращения
Телаплоских
вращения
некоторых
геометрических
фигур.
цилиндр
конус
шар, сфера

17.

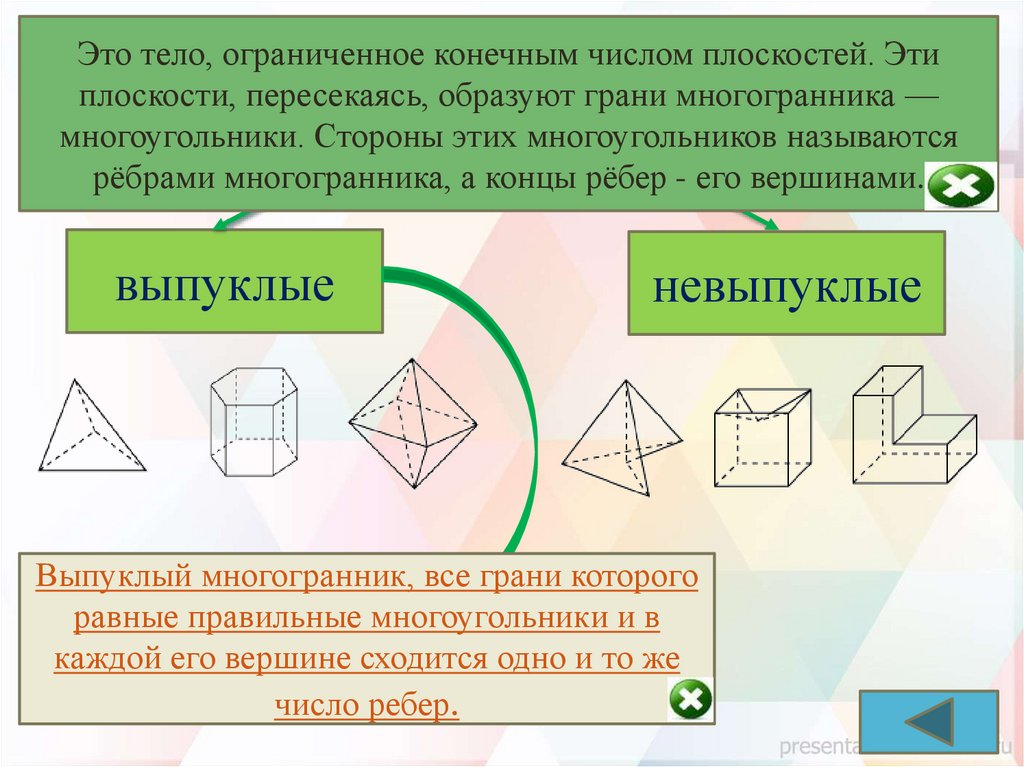
Это тело, ограниченное конечным числом плоскостей. Эти
плоскости, пересекаясь, образуют грани многогранника —
многоугольники. Стороны этих многоугольников называются
рёбрами многогранника, а концы рёбер - его вершинами.
Многогранники
выпуклые
невыпуклые
Выпуклый многогранник, все грани которого
равные правильные многоугольники и в
правильные
каждой
его вершине сходится одно и то же
число ребер.

18.

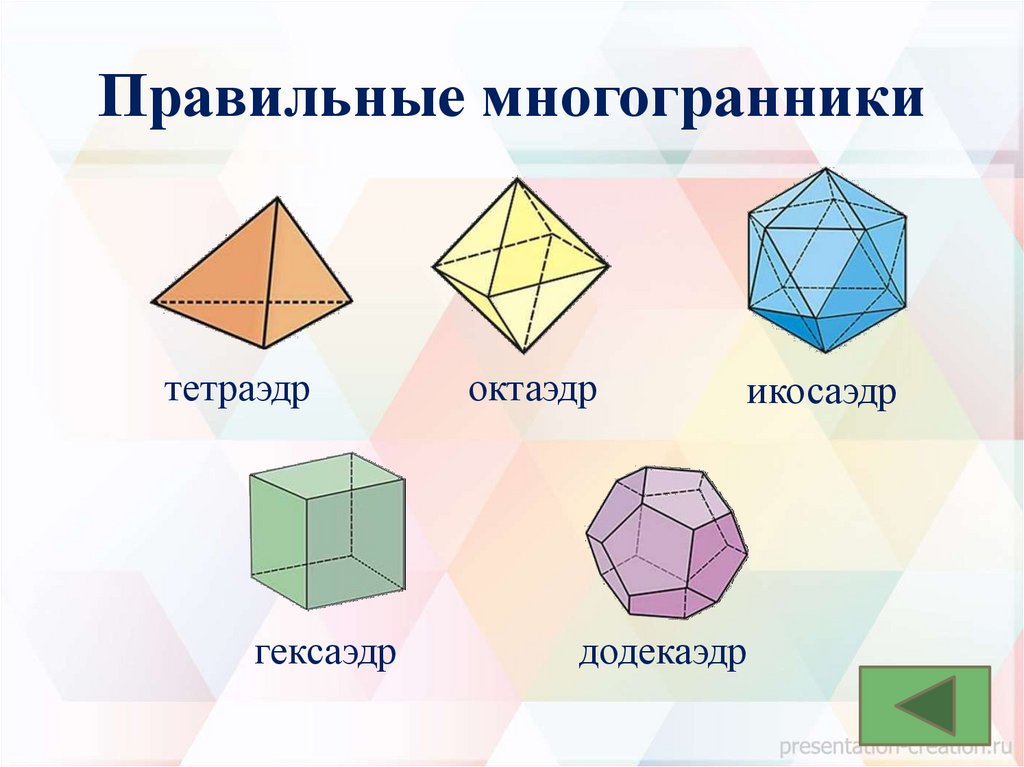
Правильные многогранники
тетраэдр
гексаэдр
октаэдр
икосаэдр
додекаэдр