Похожие презентации:
Теоретическая механика
1.
Национальныйисследовательский
Томский политехнический
университет
Комплект слайд-лекций для технических
специальностей университета
2.
доктор физико-математических наук,профессор Отделения общетехнических дисциплин
Школы базовой инженерной подготовки
Томского политехнического университета
3.
Сходящиеся силыПараллельные силы
4.
1. СИСТЕМА СХОДЯЩИХСЯ СИЛЕсли линии действия всех сил, приложенных
к твердому телу, пересекаются в одной
точке, то система сил называется
СХОДЯЩЕЙСЯ
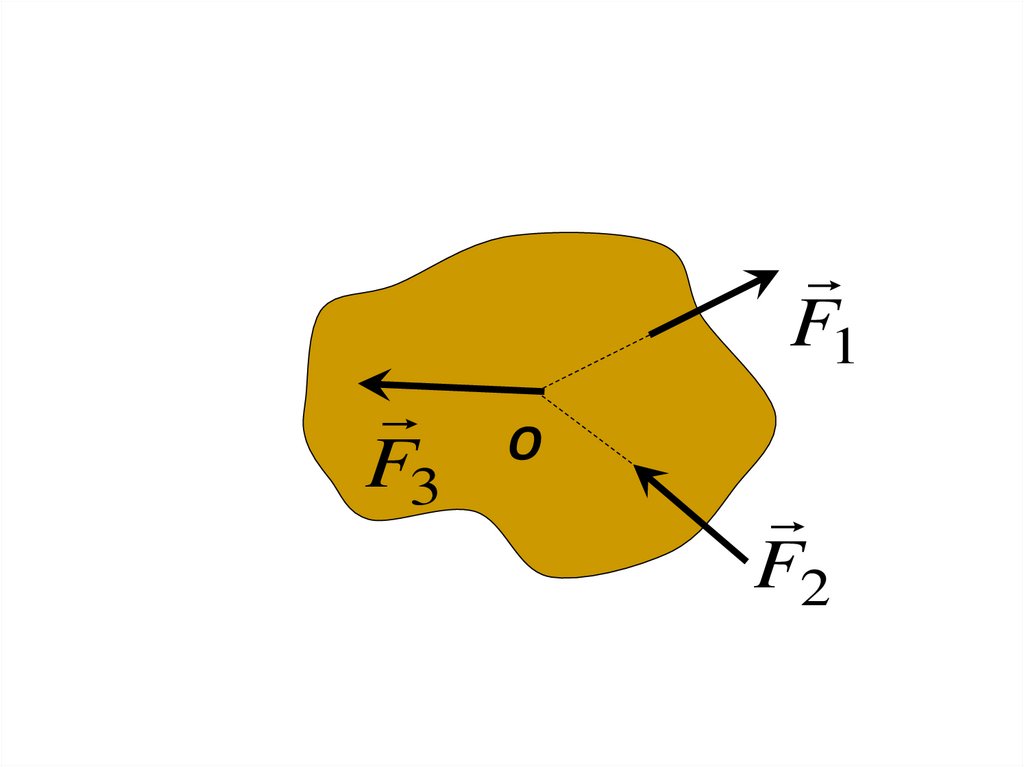
5.
ОF3
F1
F2
6.
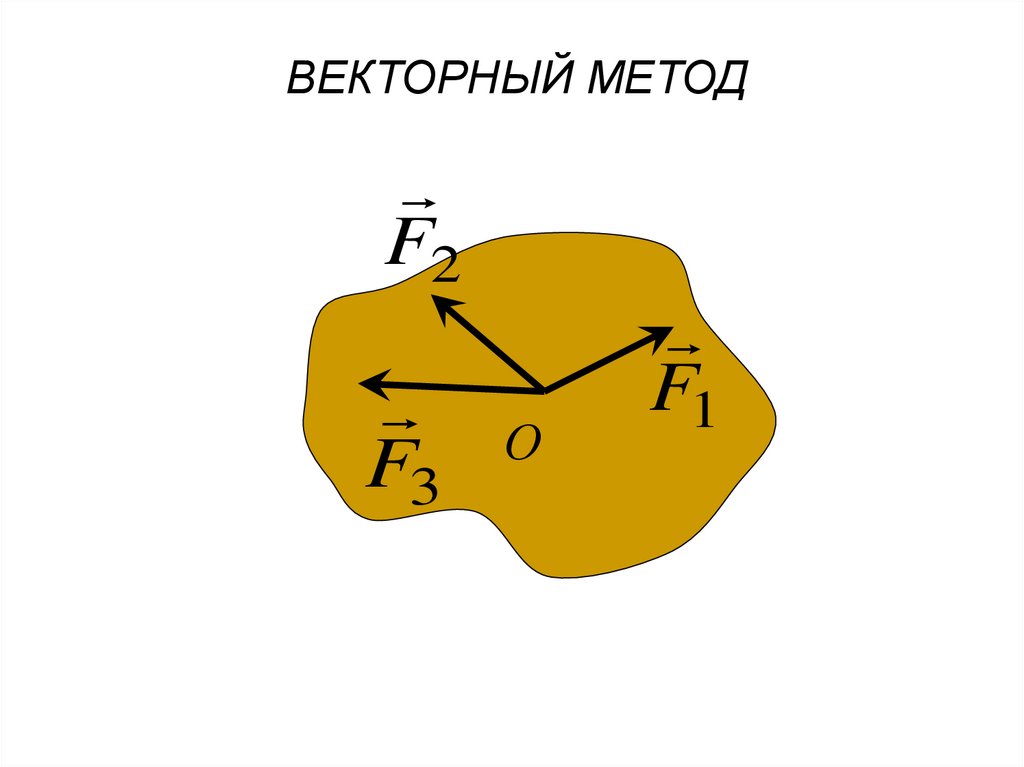
ВЕКТОРНЫЙ МЕТОДF2
О
F3
F1
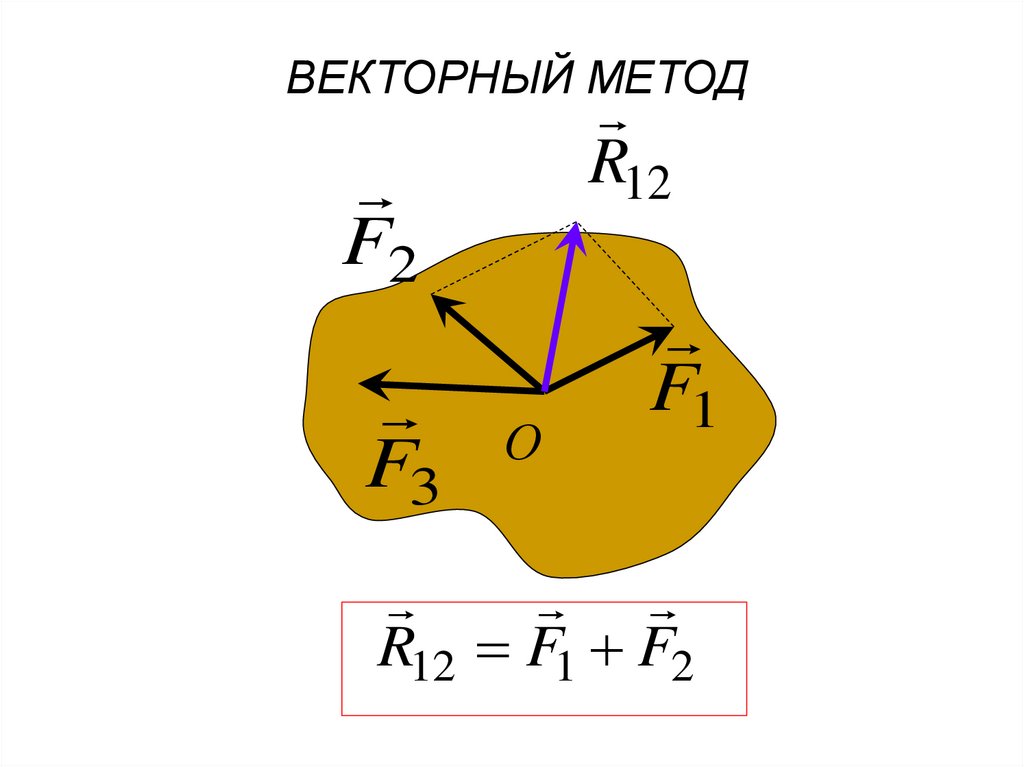
7.
ВЕКТОРНЫЙ МЕТОДR12
F2
О
F3
F1
R12 F1 F2
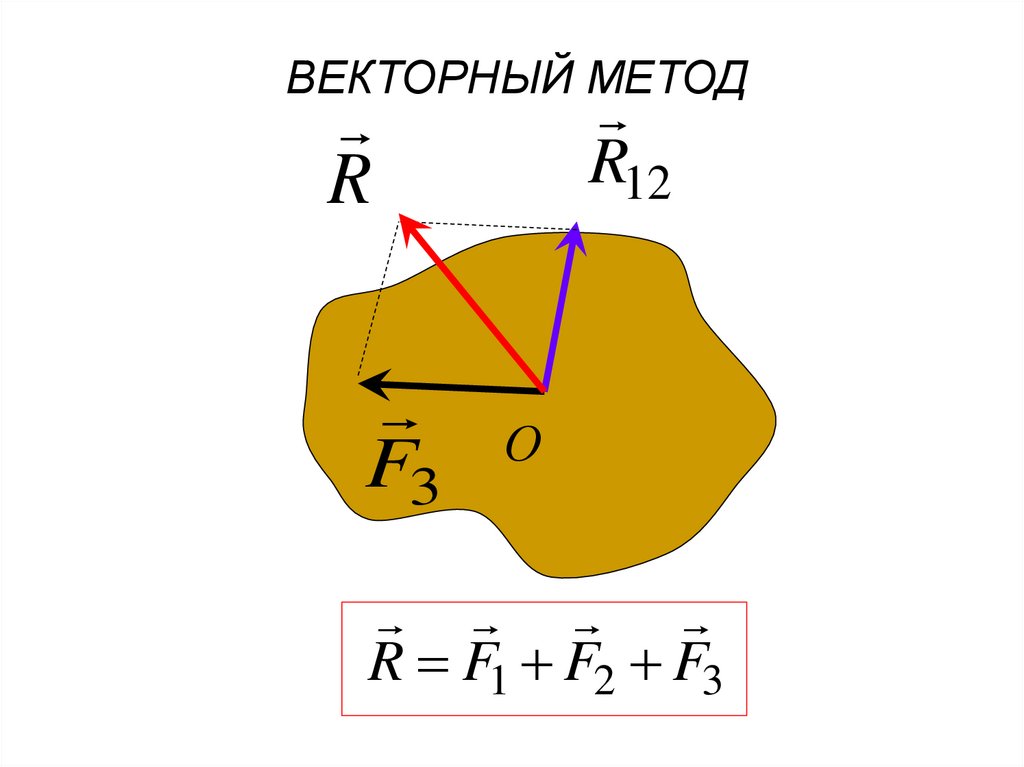
8.
ВЕКТОРНЫЙ МЕТОДR12
R
О
F3
R F1 F2 F3
9.
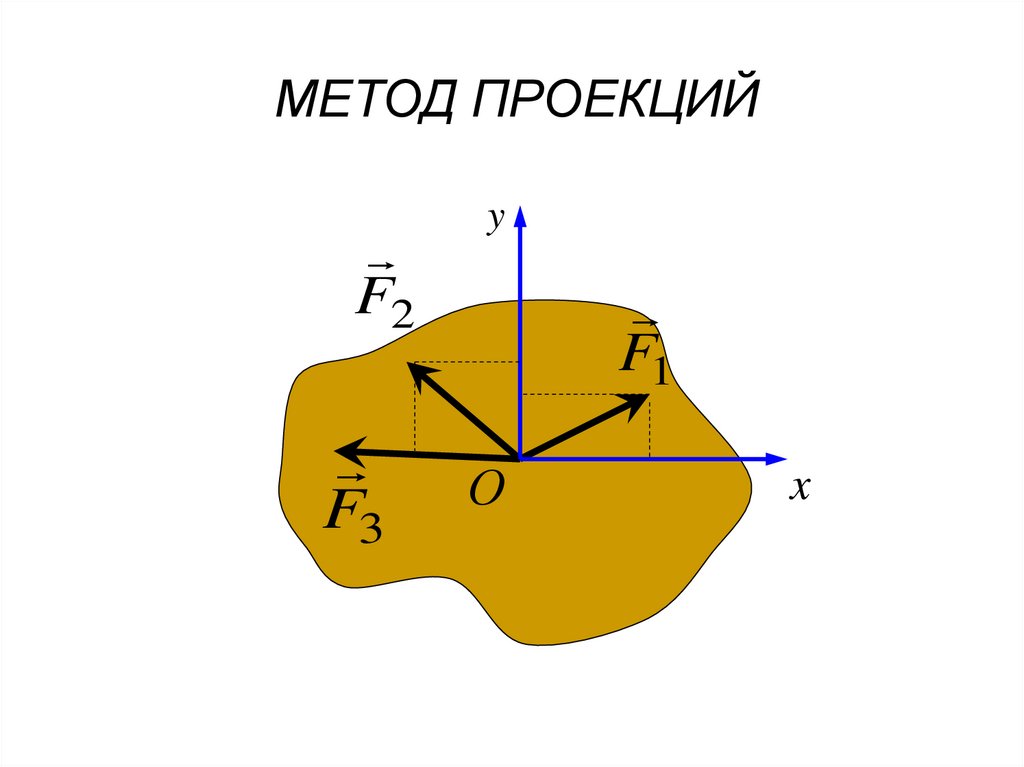
МЕТОД ПРОЕКЦИЙF2
F3
y
F1
О
x
10.
nRx F1x F2 x ... Fnx Fix
i 1
11.
nRx F1x F2 x ... Fnx Fix
i 1
n
R y F1 y F2 y ... Fny Fiy
i 1
12.
nRx F1x F2 x ... Fnx Fix
i 1
n
R y F1 y F2 y ... Fny Fiy
i 1
n
Rz F1z F2 z ... Fnz Fiz
i 1
13.
RF
F
...
F
F
x
1
x
2
x
nx
ix
i 1
n
R y F1 y F2 y ... Fny Fiy
i 1
n
R
F
F
...
F
F
z
1
z
2
z
nz
iz
i 1
2
2
2
R Rx R y R z
n
14.
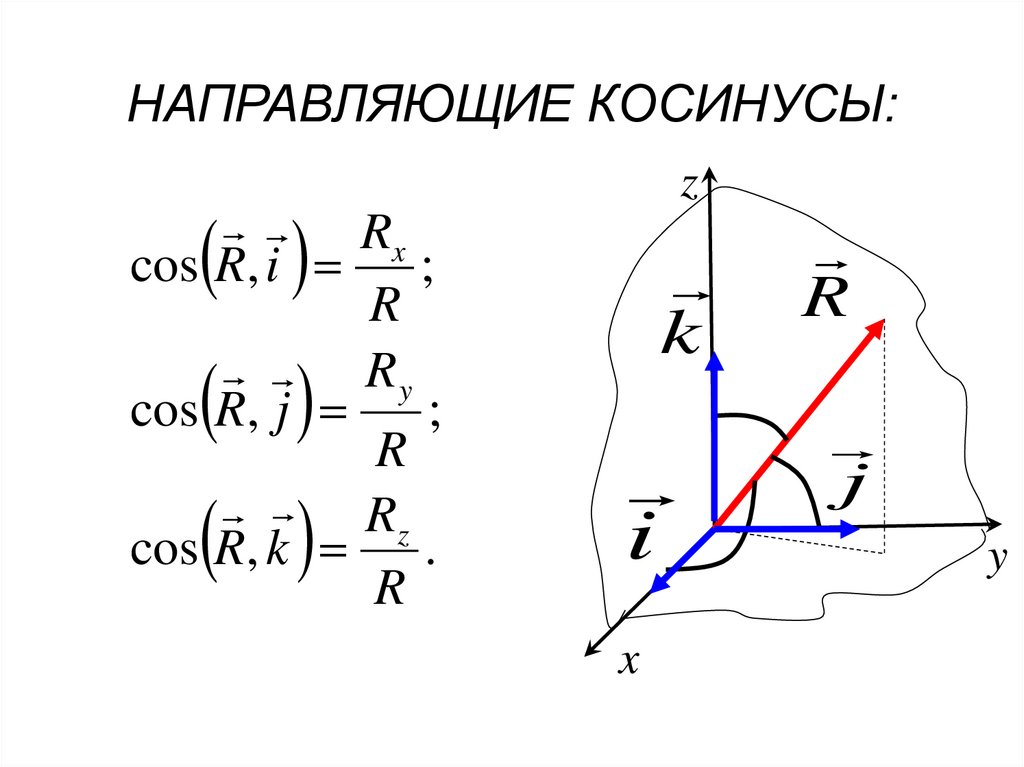
НАПРАВЛЯЮЩИЕ КОСИНУСЫ:z
Rx
cos R, i
;
R
Ry
cos R, j
;
R
Rz
cos R, k .
R
k
i
x
R
j
y
15.
Условие равновесия системысходящихся сил
R F1 F2 .... Fn 0
16.
Условие равновесия системысходящихся сил
R F1 F2 .... Fn 0
Rx F1x F2 x .... Fnx 0;
R y F1 y F2 y .... Fny 0;
Rz F1z F2 z .... Fnz 0.
(1)
(2)
17.
Теорема о трех силах:Если плоская система трех
непараллельных сил находится в
равновесии, то линии действия этих сил
пересекаются в одной точке.
18.
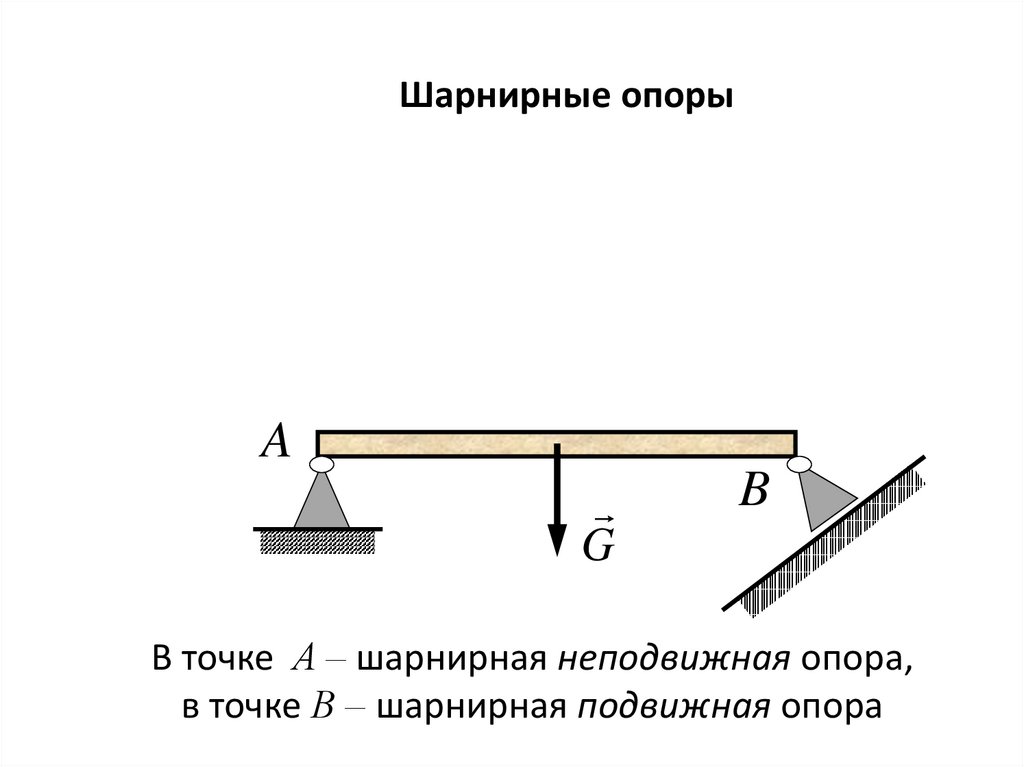
Шарнирные опорыA
G
B
В точке А – шарнирная неподвижная опора,
в точке В – шарнирная подвижная опора
19.
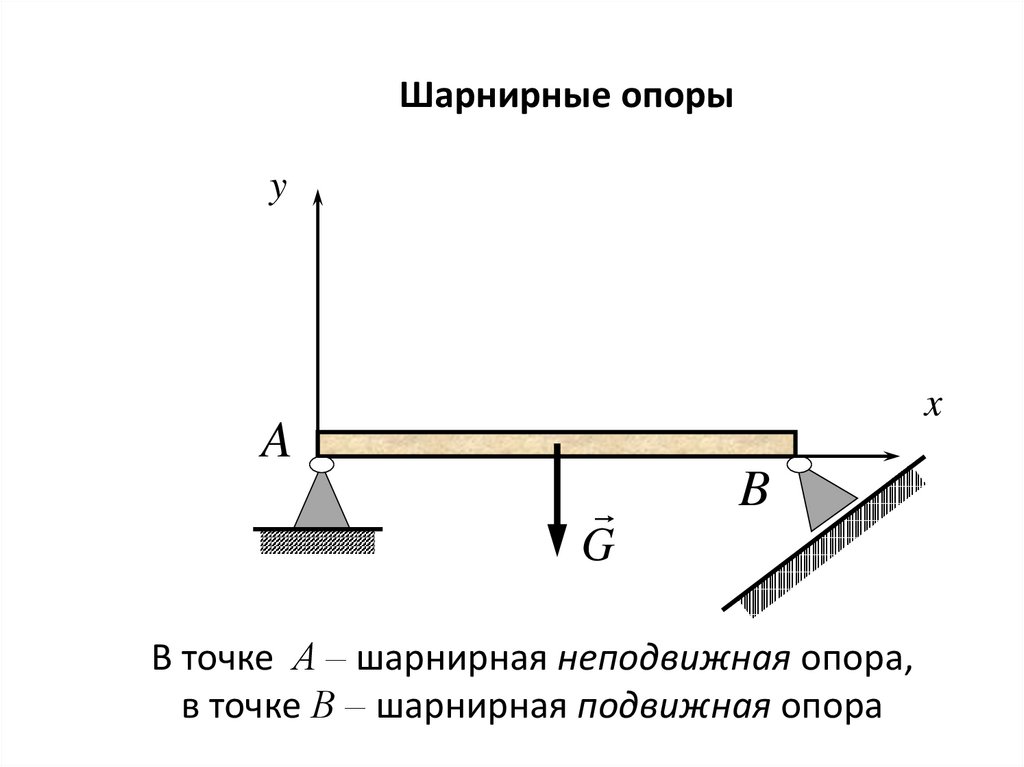
Шарнирные опорыy
x
A
G
B
В точке А – шарнирная неподвижная опора,
в точке В – шарнирная подвижная опора
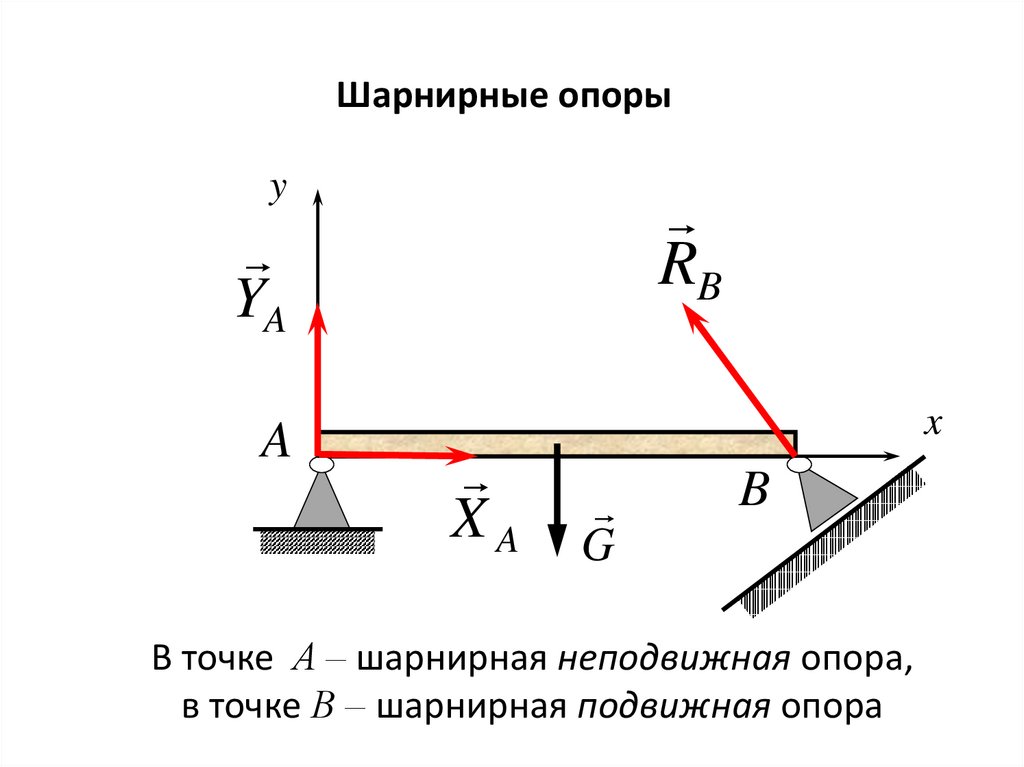
20.
Шарнирные опорыy
RB
YA
A
XA
x
G
B
В точке А – шарнирная неподвижная опора,
в точке В – шарнирная подвижная опора
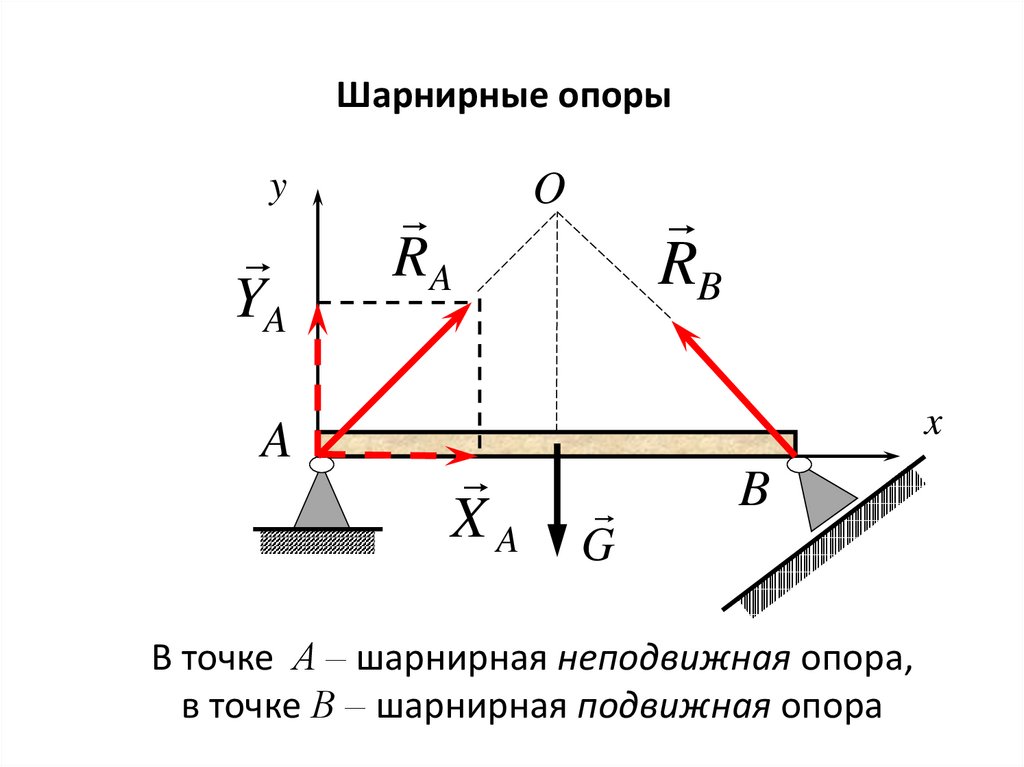
21.
Шарнирные опорыy
YA
A
RA
XA
O
RB
x
G
B
В точке А – шарнирная неподвижная опора,
в точке В – шарнирная подвижная опора
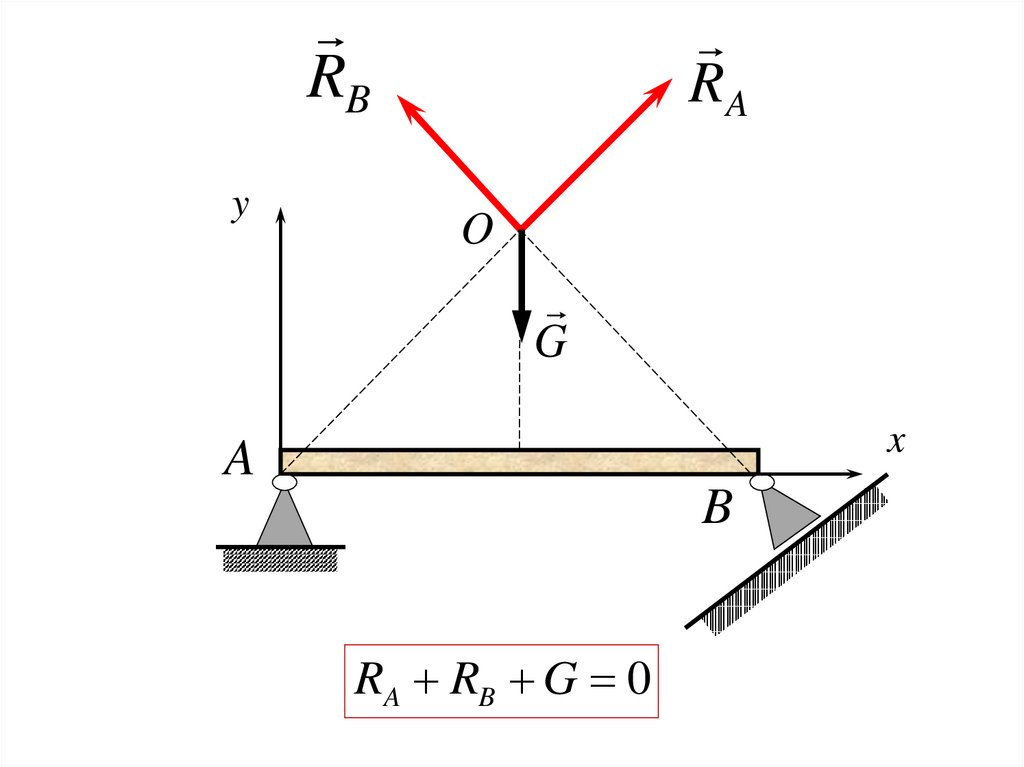
22.
RBy
RA
O
G
x
A
B
RA RB G 0
23.
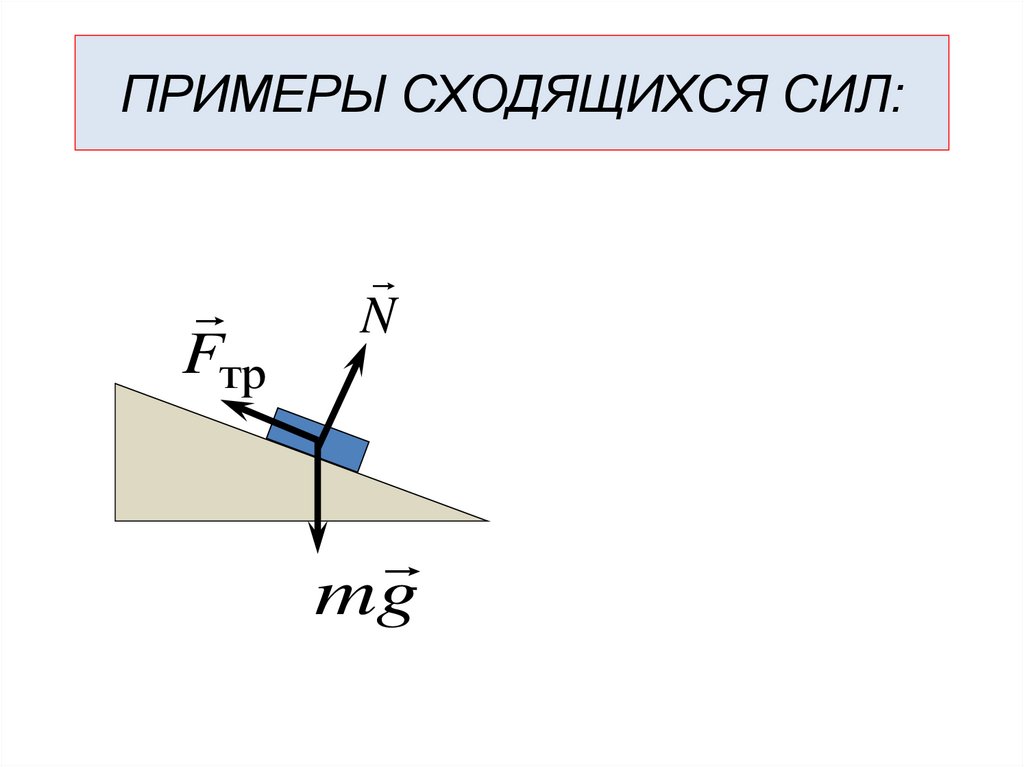
ПРИМЕРЫ СХОДЯЩИХСЯ СИЛ:Fтр
N
mg
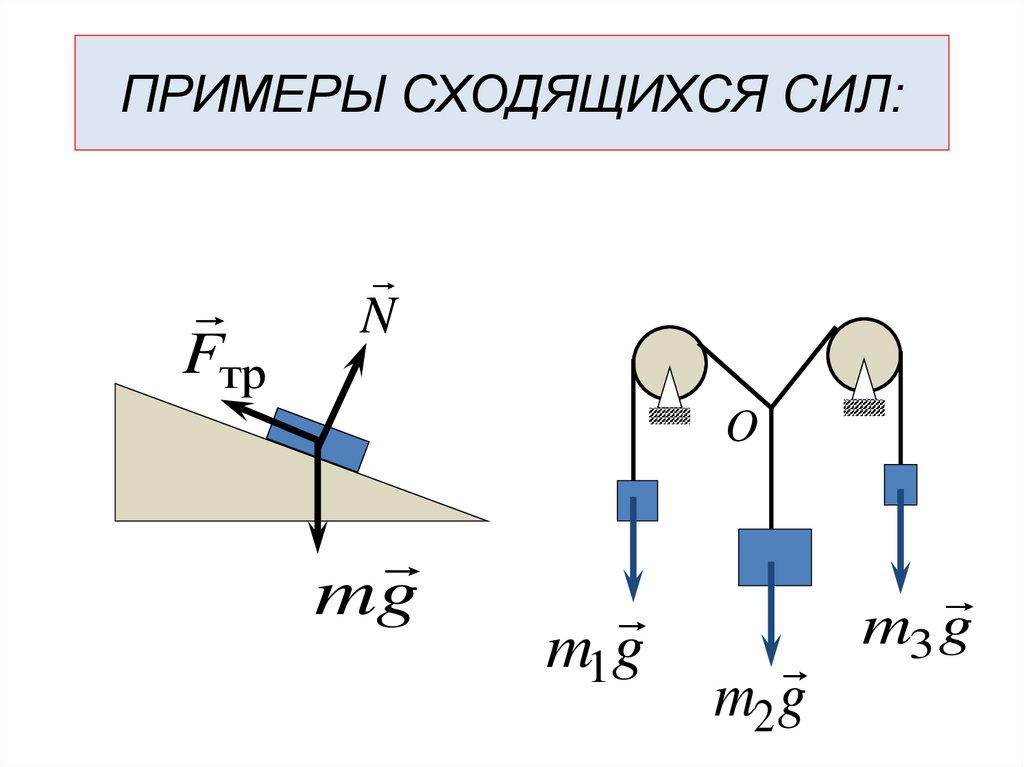
24.
ПРИМЕРЫ СХОДЯЩИХСЯ СИЛ:Fтр
N
O
mg
m1g
m2 g
m3 g
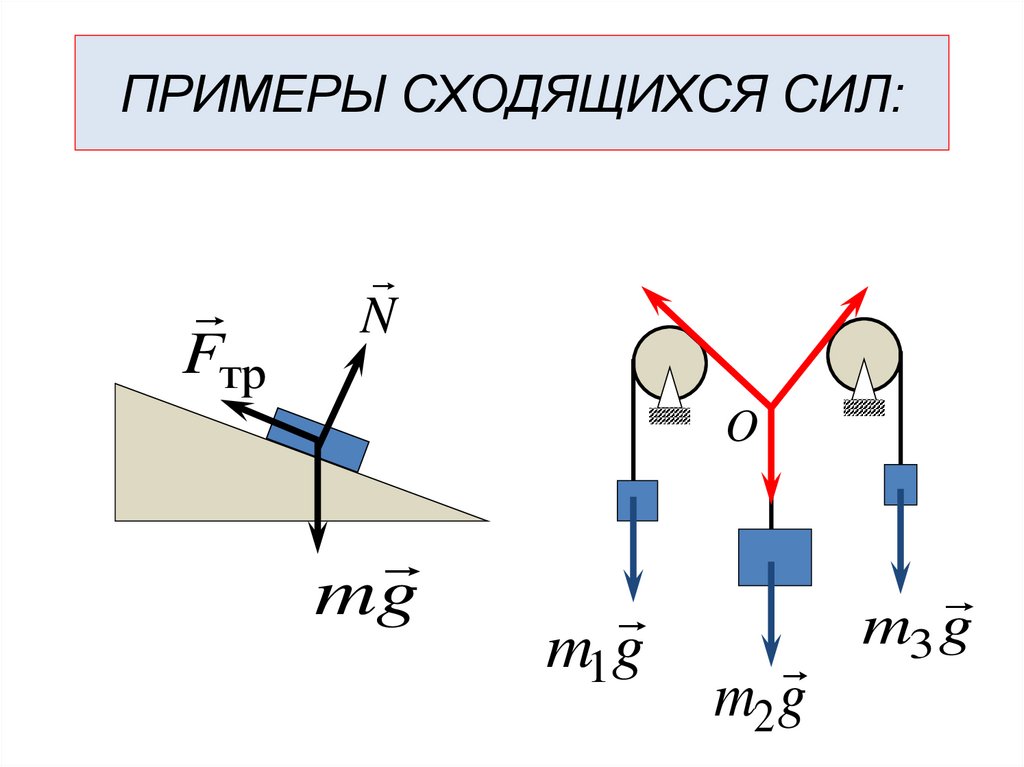
25.
ПРИМЕРЫ СХОДЯЩИХСЯ СИЛ:Fтр
N
O
mg
m1g
m2 g
m3 g
26.
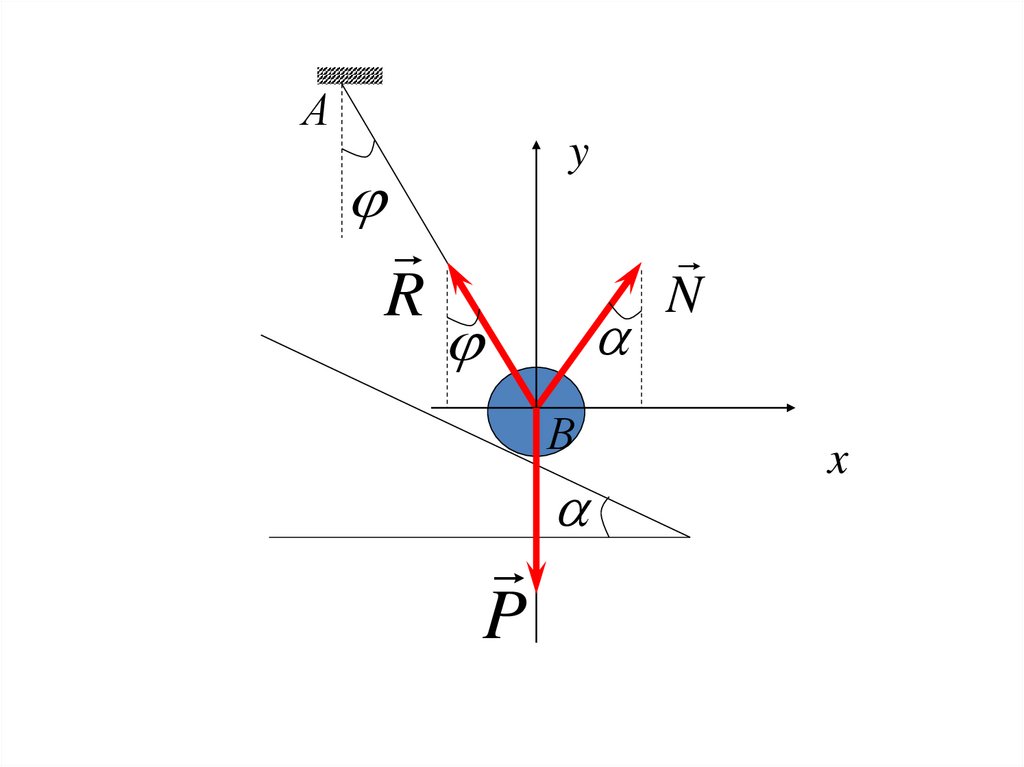
ПримерТяжелый шар весом P подвешен на
стержне АВ, прикрепленном к
неподвижной точке А, и находится в
отклоненном на угол от вертикали
положении на наклонной плоскости,
составляющей угол с горизонтом.
Определить натяжение нити R и
реакцию поверхности N.
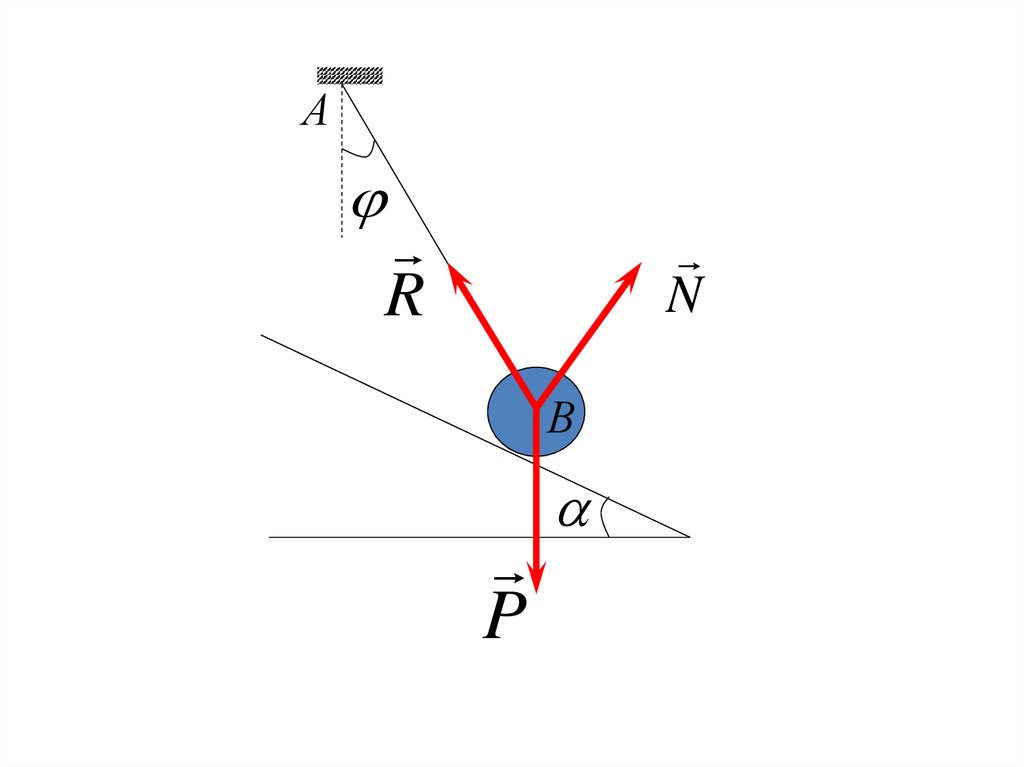
27.
АR
N
В
P
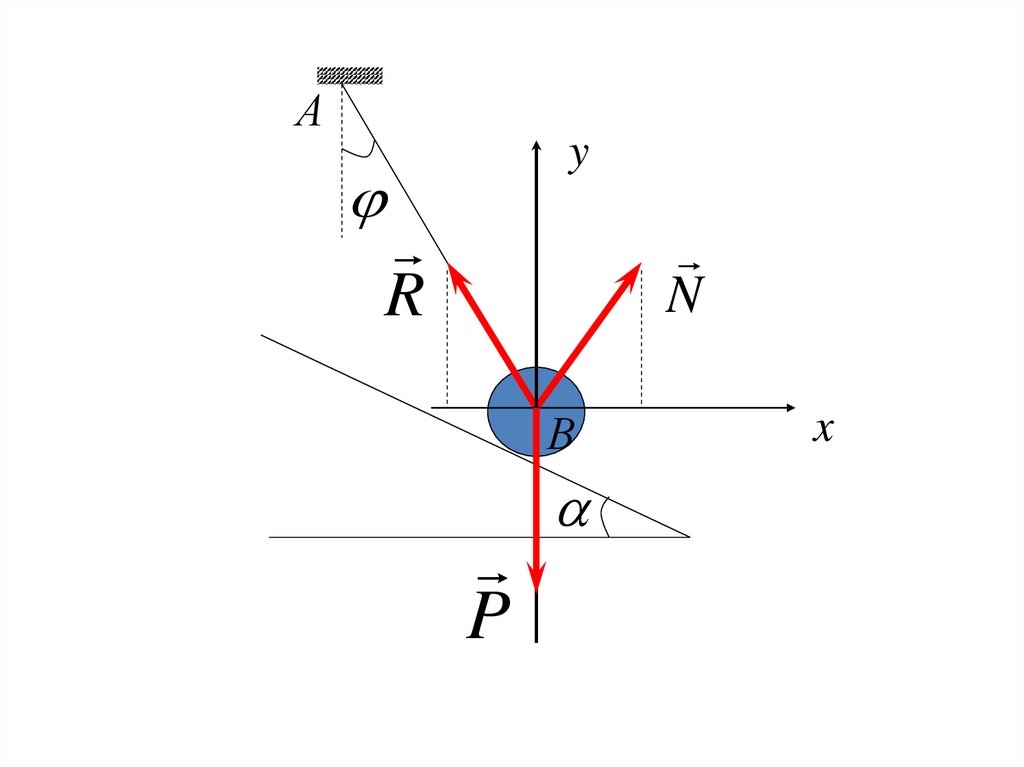
28.
Аy
R
N
В
P
x
29.
Аy
R
В
P
N
x
30.
Условия равновесия:Fix N sin R sin 0
(3)
31.
Условия равновесия:Fix N sin R sin 0
Fiy N cos R cos P 0
(3)
(4)
32.
Условия равновесия:Fix N sin R sin 0
Fiy N cos R cos P 0
R sin
N
sin
(3)
(4)
33.
R sincos R cos P 0
sin
34.
R sincos R cos P 0
sin
P
R
sin ctg cos
35.
R sincos R cos P 0
sin
P
R
sin ctg cos
sin
P
N
sin ctg cos sin
36.
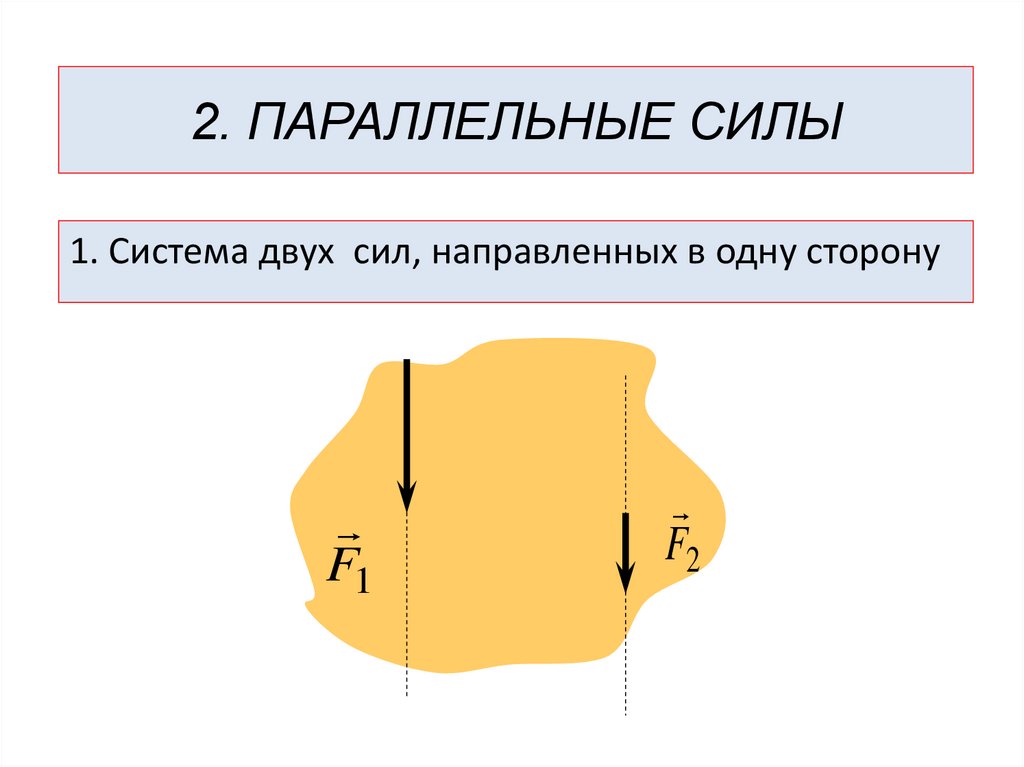
2. ПАРАЛЛЕЛЬНЫЕ СИЛЫ1. Система двух сил, направленных в одну сторону
F1
F2
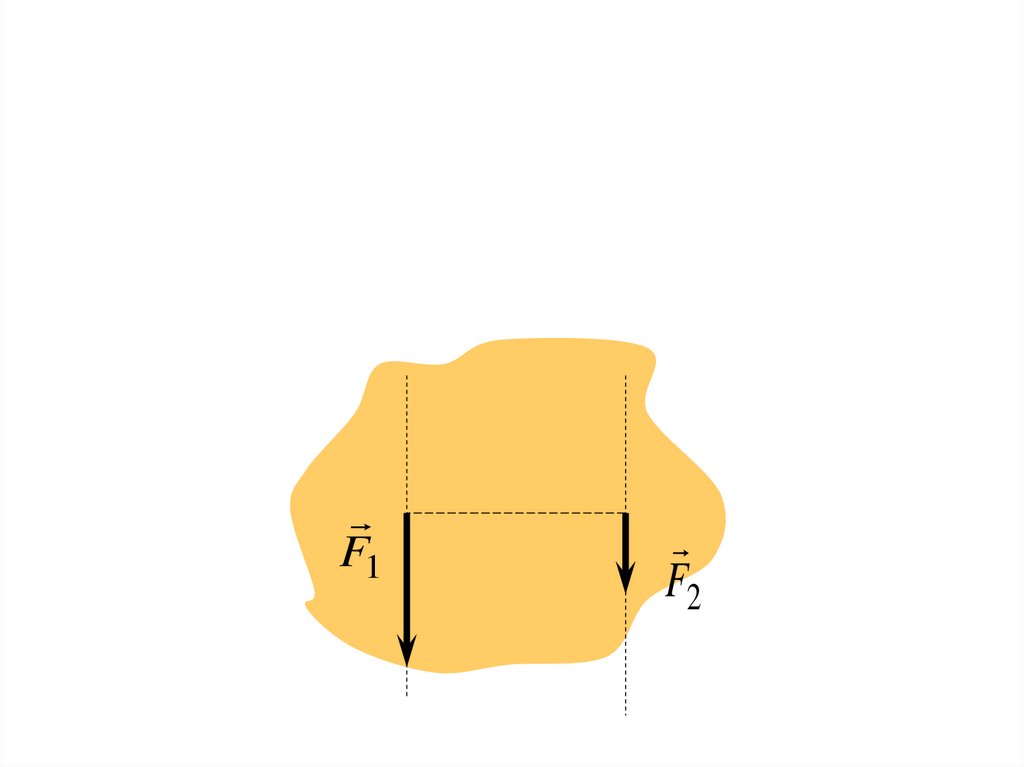
37.
F1F2
38.
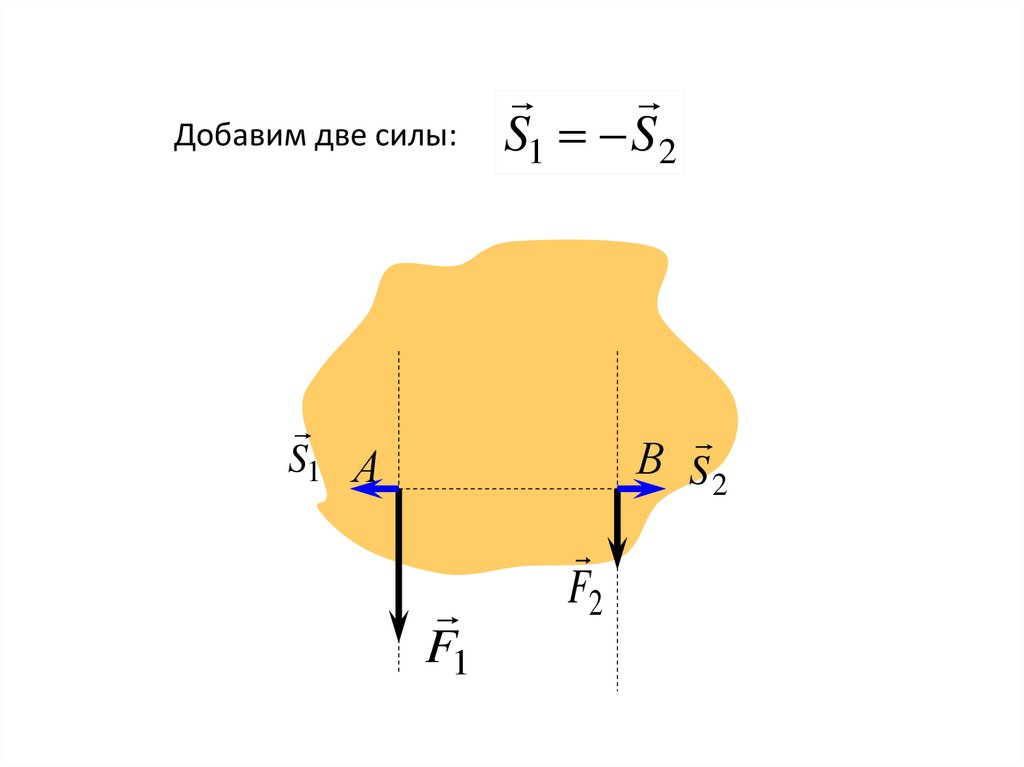
Добавим две силы:S1 S 2
S1 А
В S2
F1
F2
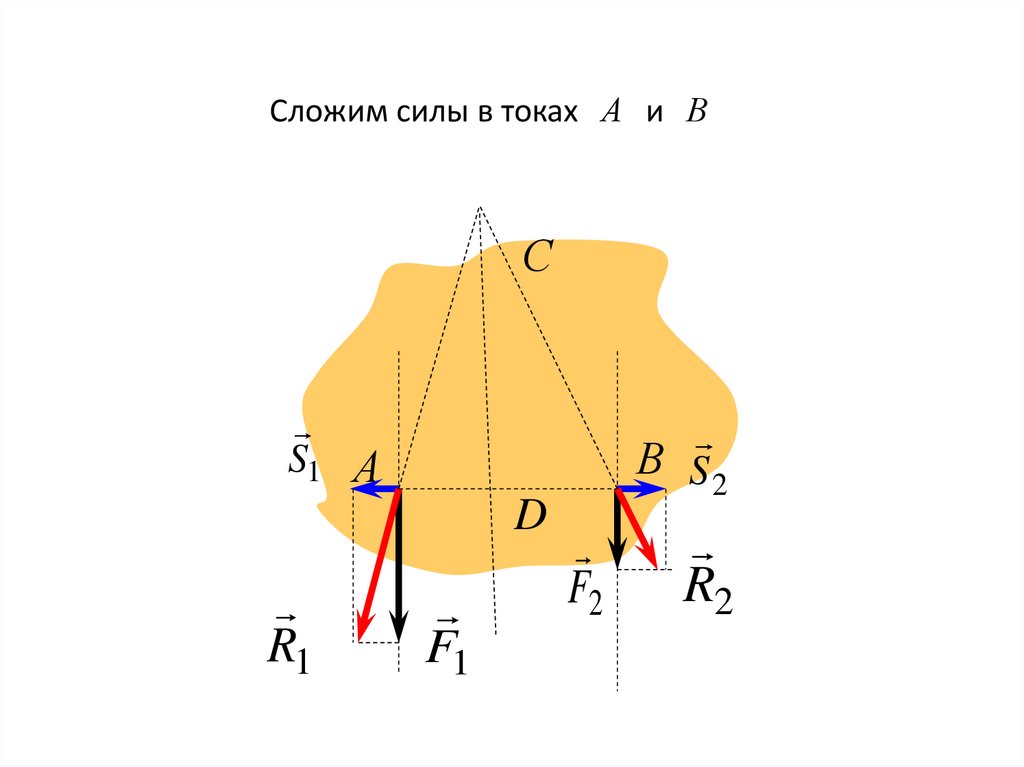
39.
Сложим силы в токах А и ВС
S1 А
D
R1
F1
В S2
F2
R2
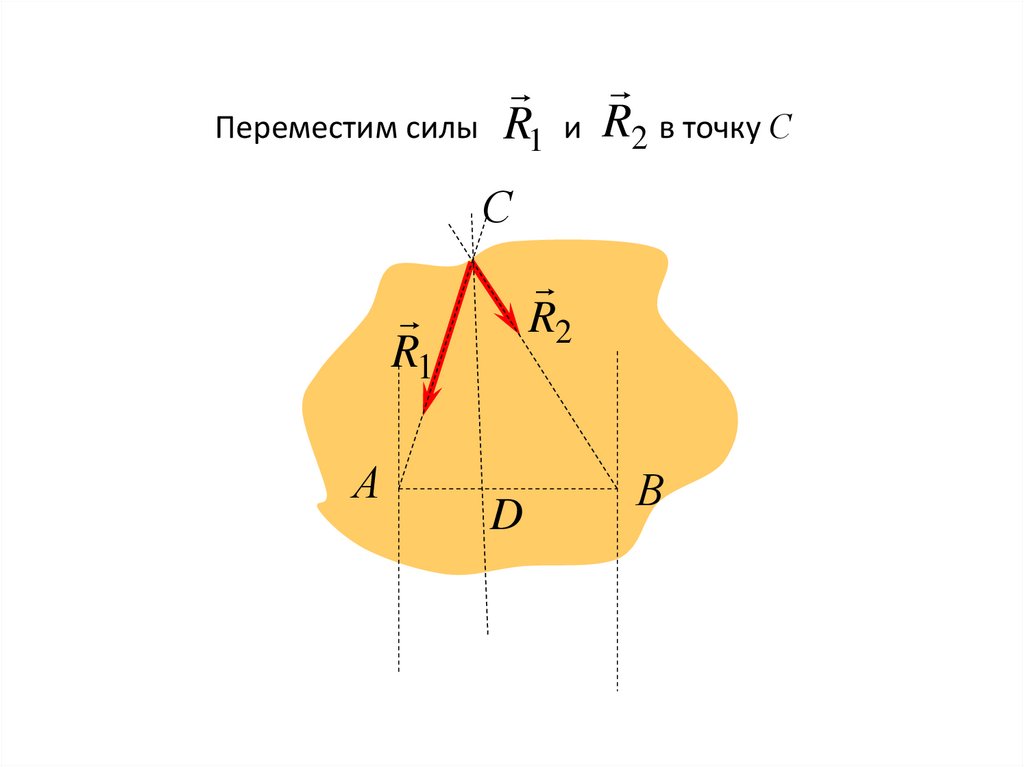
40.
Переместим силыR1
и
R2 в точку С
С
R2
R1
А
D
В
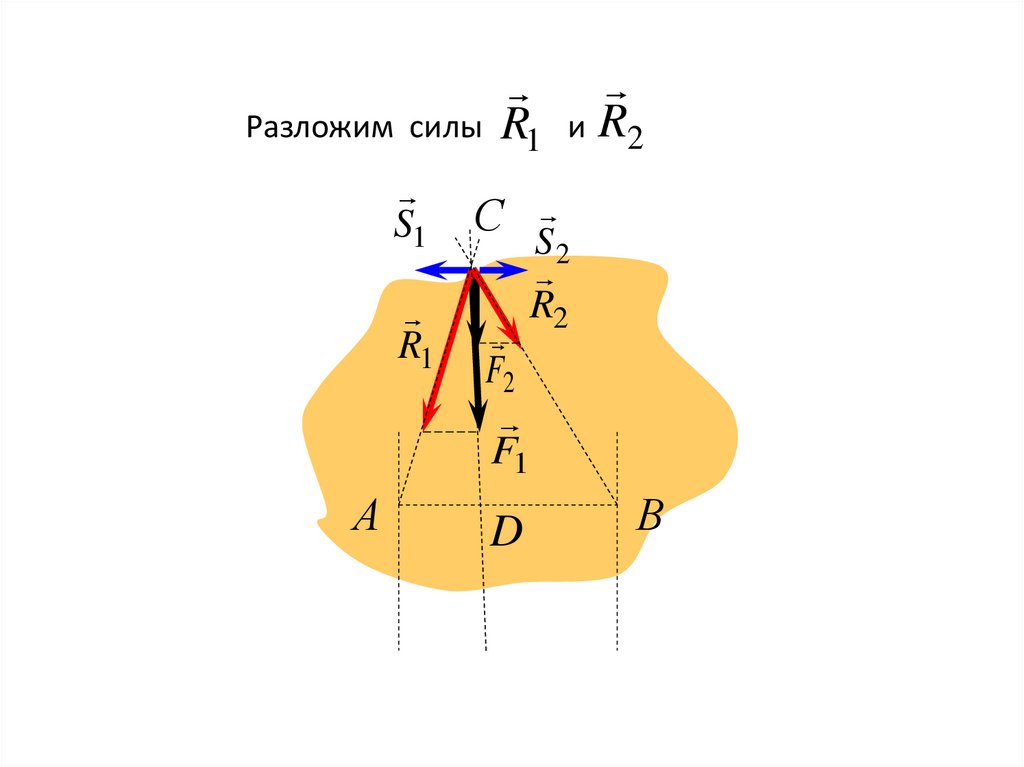
41.
Разложим силыS1
R1
А
R1
и R2
С
F2
F1
D
S2
R2
В
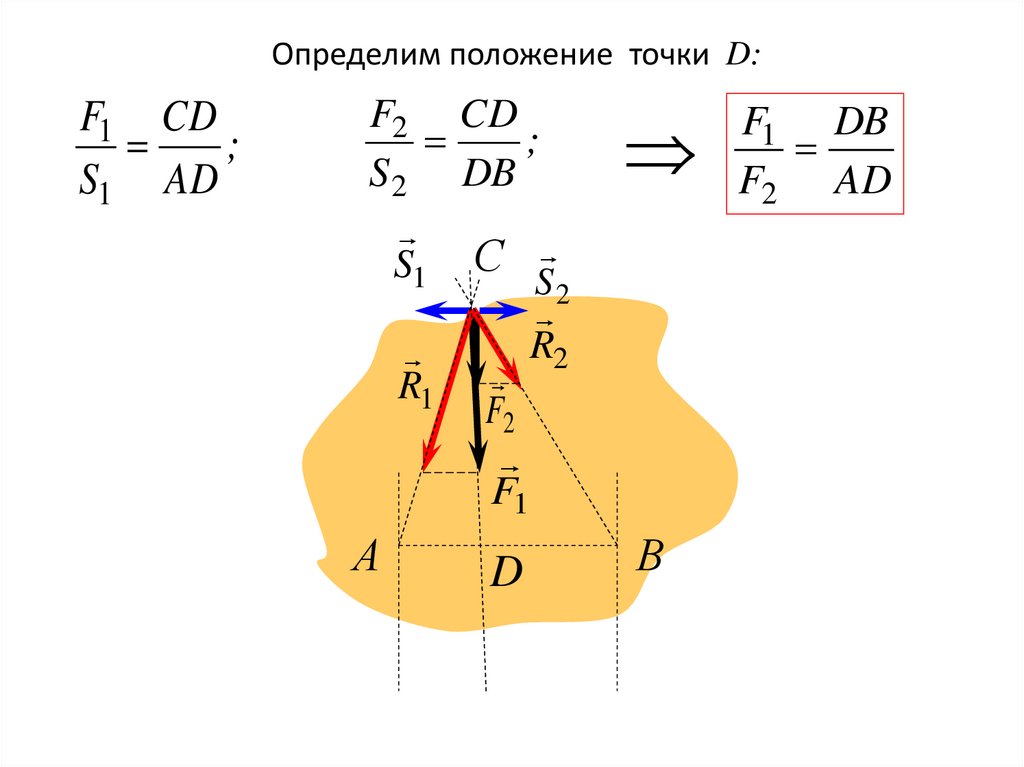
42.
Определим положение точки D:F1 CD
;
S1 AD
F2 CD
;
S 2 DB
S1 С S
2
R2
R1
F2
F1
А
D
В
F1 DB
F2 AD
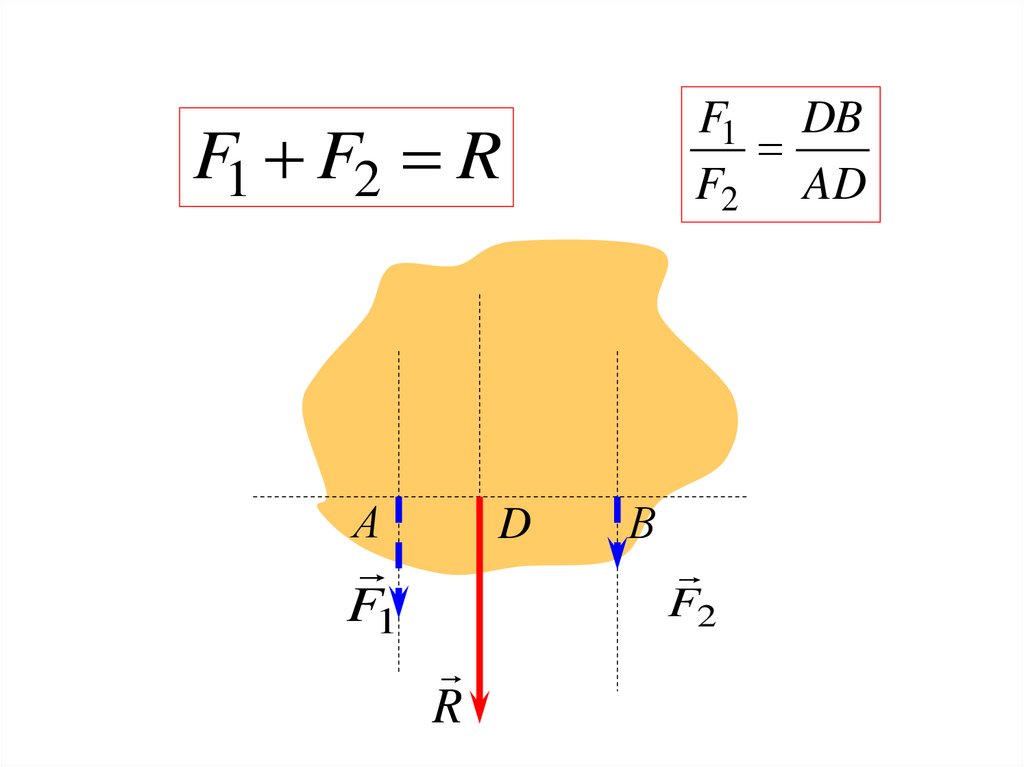
43.
F1 DBF2 AD
F1 F2 R
А
F1
D
R
В
F2
44.
Выводы:В результате сложения двух
однонаправленных параллельных сил
1) получается сила, направленная в ту же
сторону, что и исходные силы, с модулем
равным их сумме;
2)точка приложения результирующей силы
D делит отрезок АВ в отношении обратно
пропорциональном модулям исходных
сил
45.
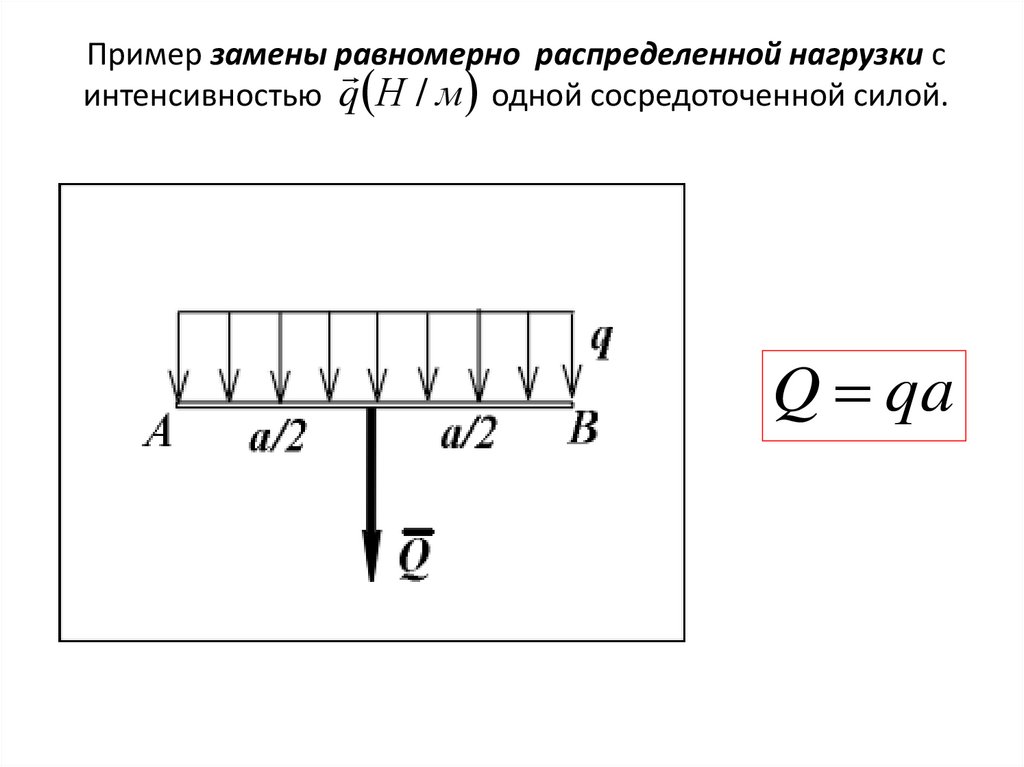
Пример замены равномернораспределенной нагрузки с
интенсивностью q Н / м одной сосредоточенной силой.
Q qa
46.
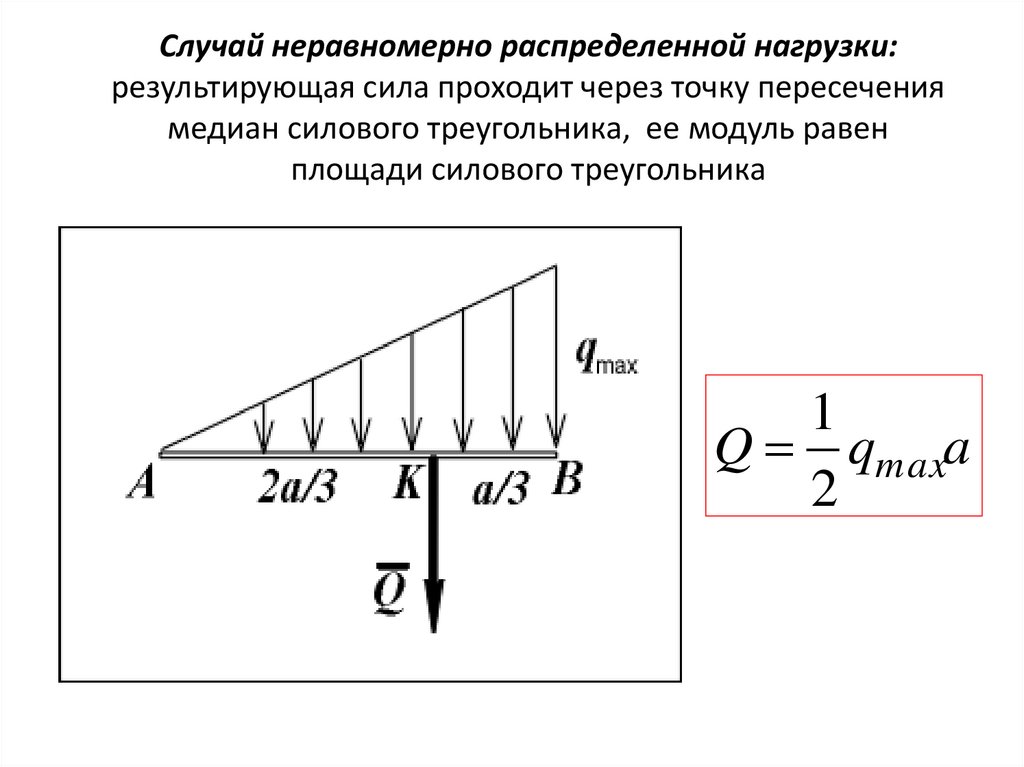
Случай неравномерно распределенной нагрузки:результирующая сила проходит через точку пересечения
медиан силового треугольника, ее модуль равен
площади силового треугольника
1
Q qmaxa
2
47.
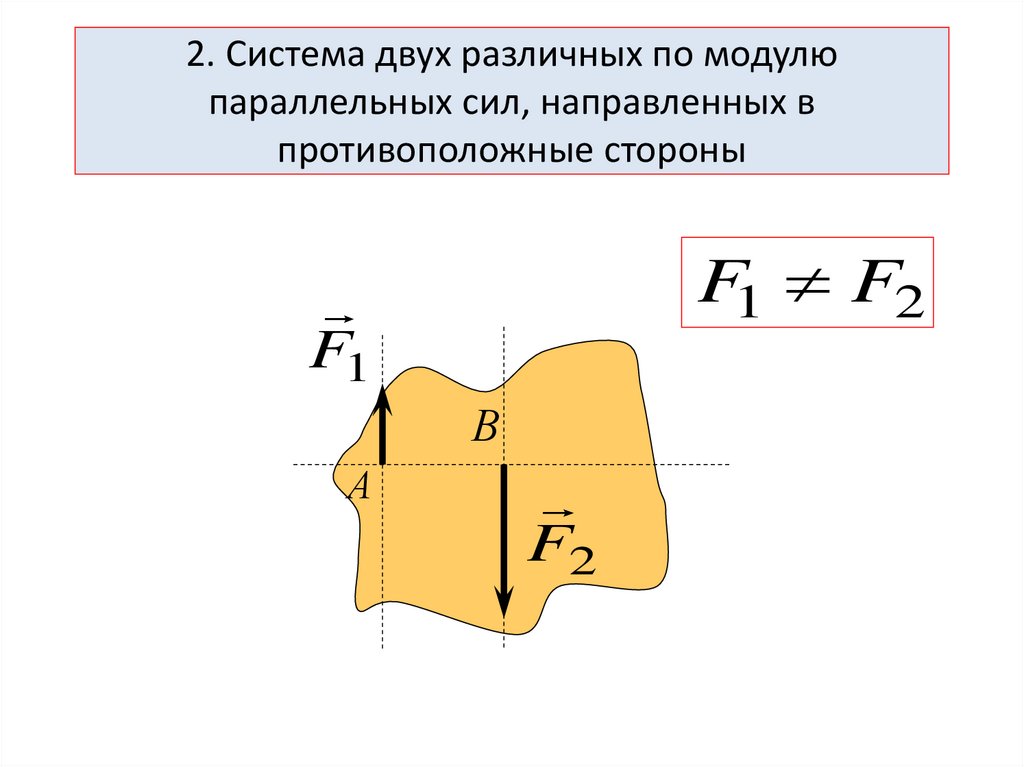
2. Система двух различных по модулюпараллельных сил, направленных в
противоположные стороны
F1 F2
F1
В
А
F2
48.
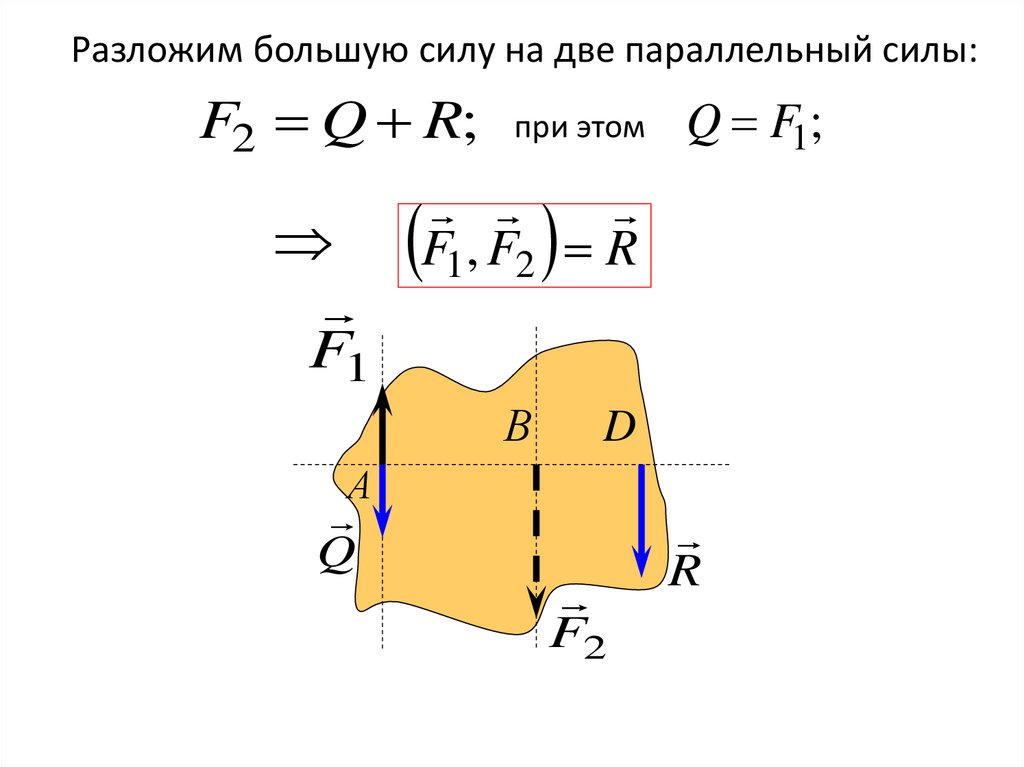
Разложим большую силу на две параллельный силы:F2 Q R;
F1
при этом
Q F1;
F1, F2 R
В
D
А
Q
F2
R
49.
Определение положения точки D:Q BD
;
R AB
50.
Определение положения точки D:Q BD
;
R AB
F1
BD
AB;
F2 F1
51.
Определение положения точки D:Q BD
;
R AB
F1
BD
AB;
F2 F1
F2
BD 1 AB;
F1
52.
Определение положения точки D:Q BD
;
R AB
F1
BD
AB;
F2 F1
F2
BD 1 AB;
F1
F2 AD
F1 BD
53.
Выводы:В результате сложения двух антипараллельных не
равных по модулю сил
1) получается сила, направленная сторону большей
силы, с модулем равным разности исходных сил ;
2)точка приложения результирующей силы D
делит отрезок АВ внешним образом в отношении
обратно пропорциональном модулям исходных
сил
54.
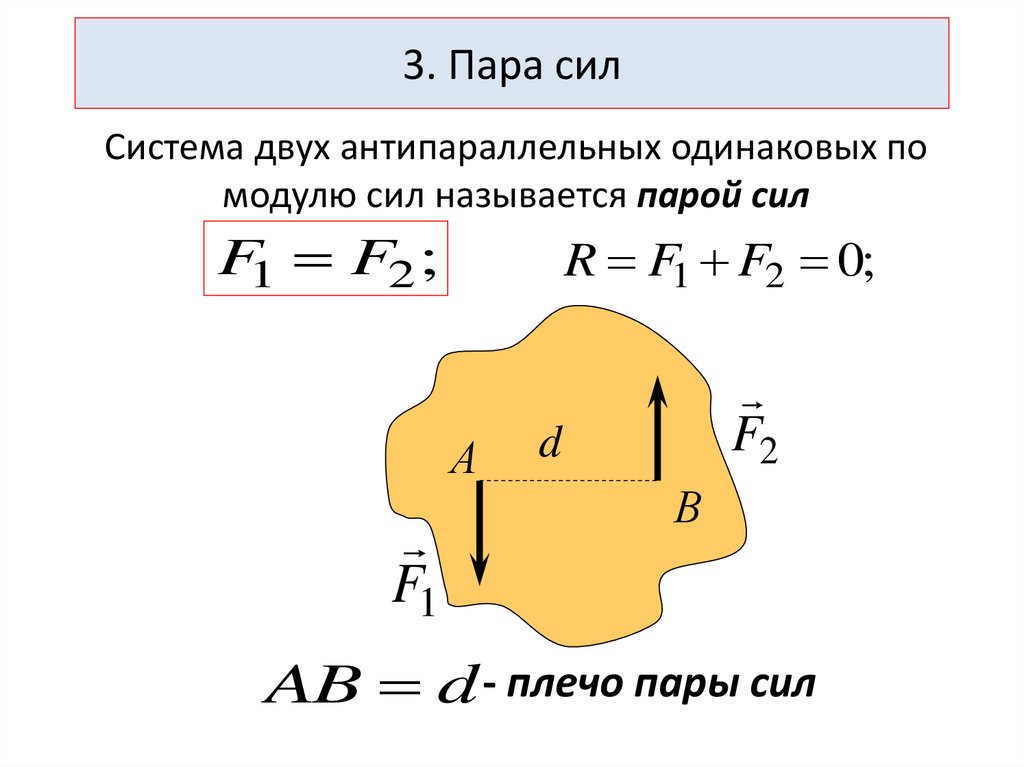
3. Пара силСистема двух антипараллельных одинаковых по
модулю сил называется парой сил
F1 F2 ;
R F1 F2 0;
А
F1
F2
d
В
AB d - плечо пары сил
55.
Пару сил невозможно заменить однойсилой.
Пара сил (наравне с силой) является
самостоятельным элементом статики.
Теория силовых пар рассмотрена в
следующей лекции
56.
Контрольные вопросы1. Приведите пример системы сходящихся
сил, не использованный в лекции.
2. Приведите технический пример
равномерно распределенной нагрузки.
3. Приведите технический пример
неравномерно распределенной нагрузки.
4. Приведите пример возникновения пары
сил.
57.
ТЕСТОВЫЕ ЗАДАНИЯДля самоконтроля знаний рекомендуется
выполнить тестовые задания из учебного
пособия:
Дробчик В.В., Шумский М.П., Дубовик В.А.,
Симанкин Ф.А. Теоретическая механика.
(Статика). Таблица 1.
58.
После просмотра и конспектирования слайд-лекциинеобходимо прочитать указанные страницы
учебников и дополнить конспект наиболее важными
сведениями
1. Теоретическая механика в примерах и задачах,
т.1 (Статика, кинематика), Бать М.И., Джанелидзе
Г.Ю., Кельзон А.С. – М.: Наука, 1967. С. 16-36
2. Тарг С.М. Краткий курс теоретической механики:
Учеб. для втузов.- 10-е изд. – М: ВШ, 1986. С. 1731.
Рекомендованные учебники и учебные пособия выложены в информационном
модуле




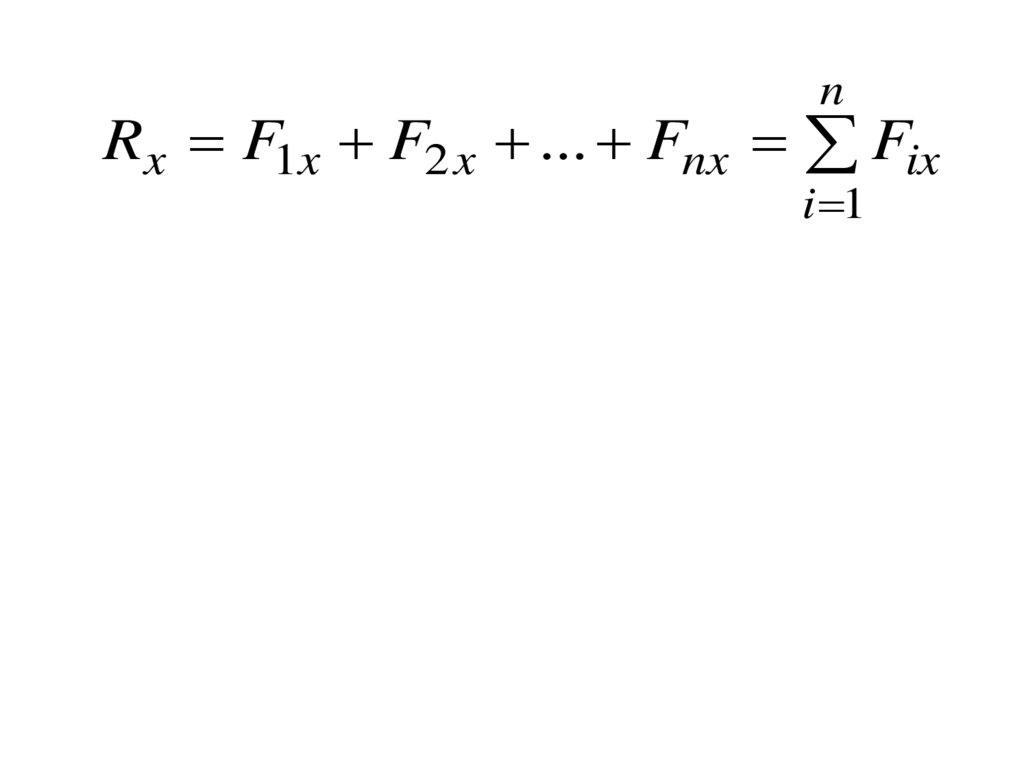
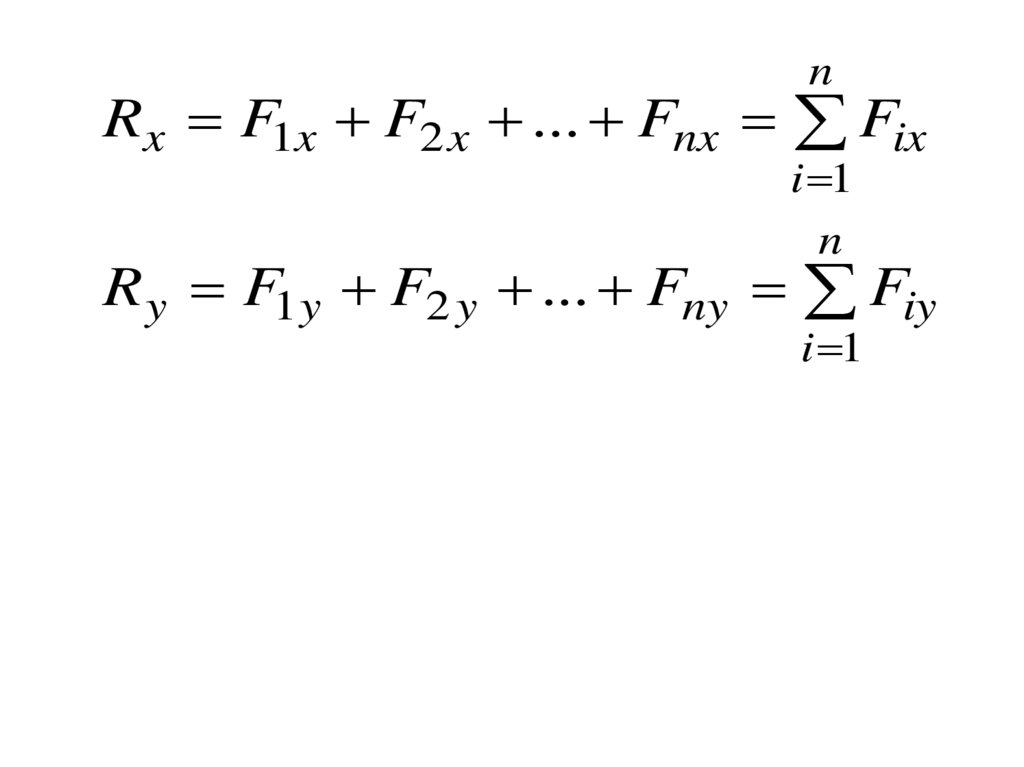
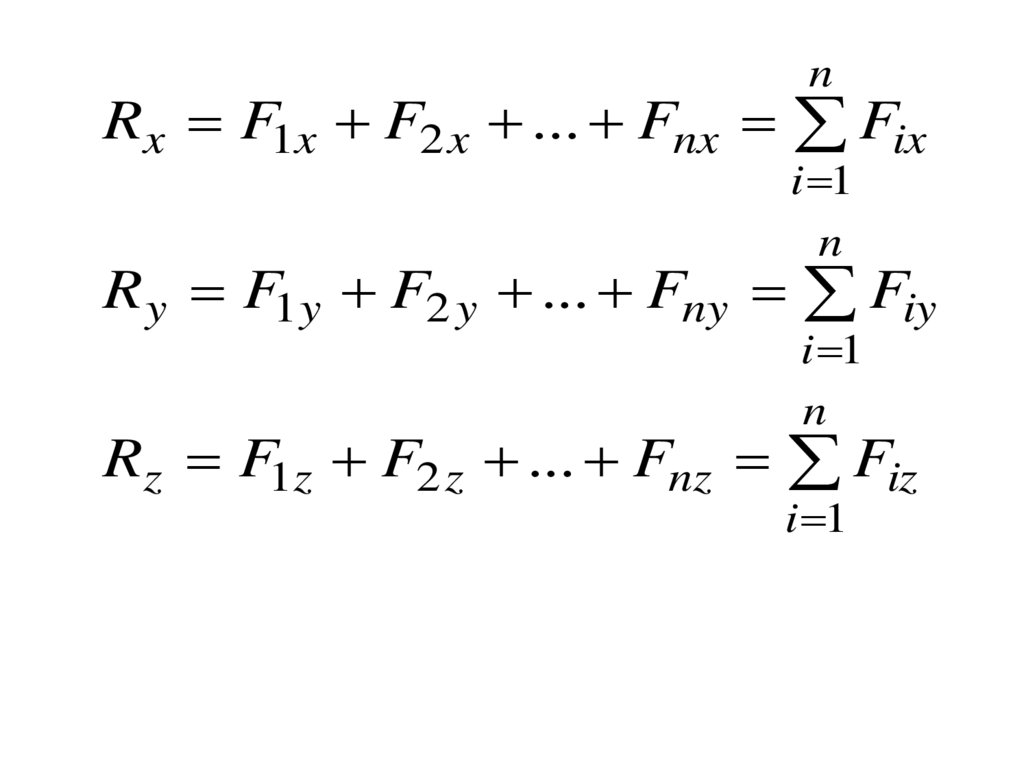
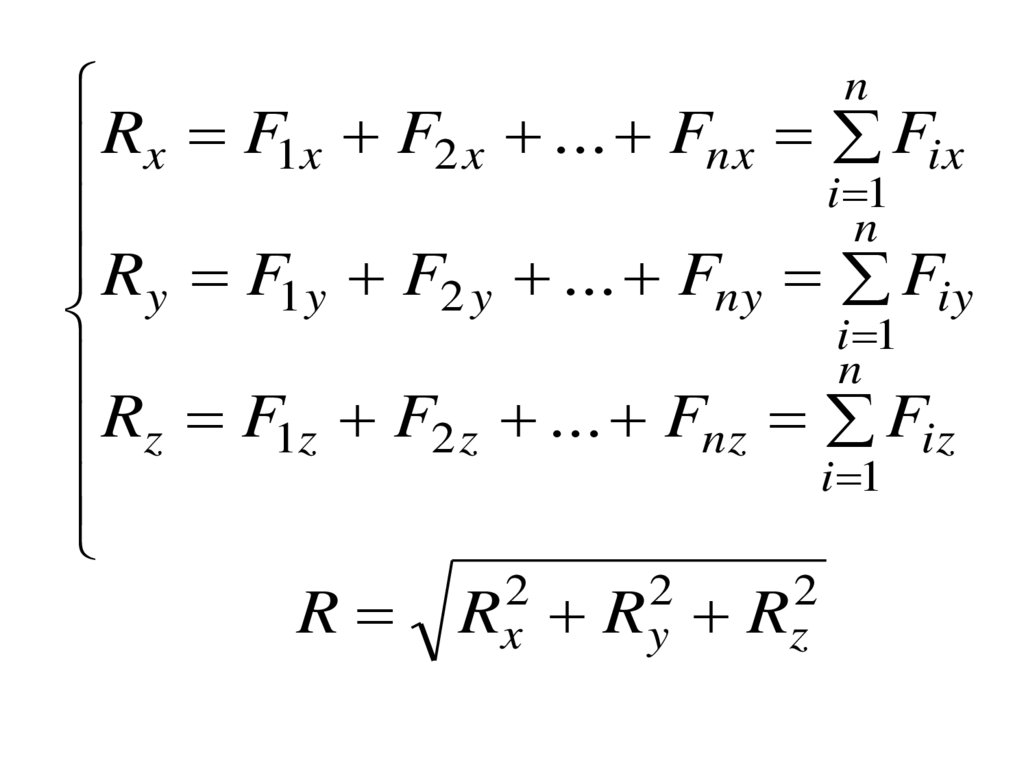




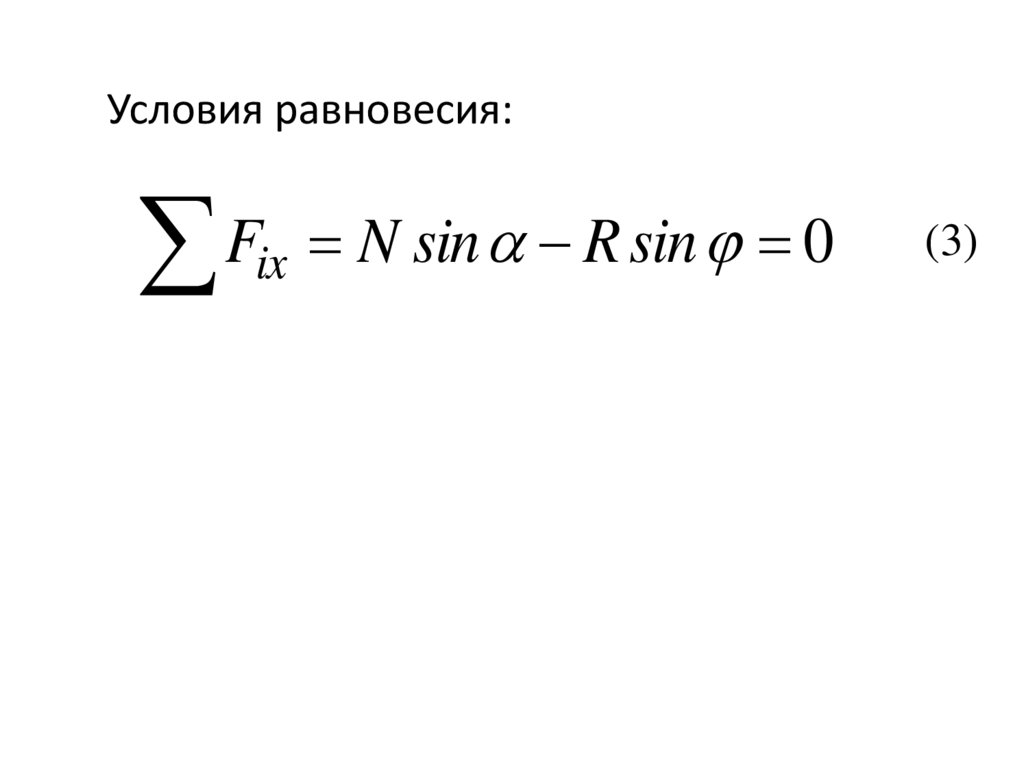

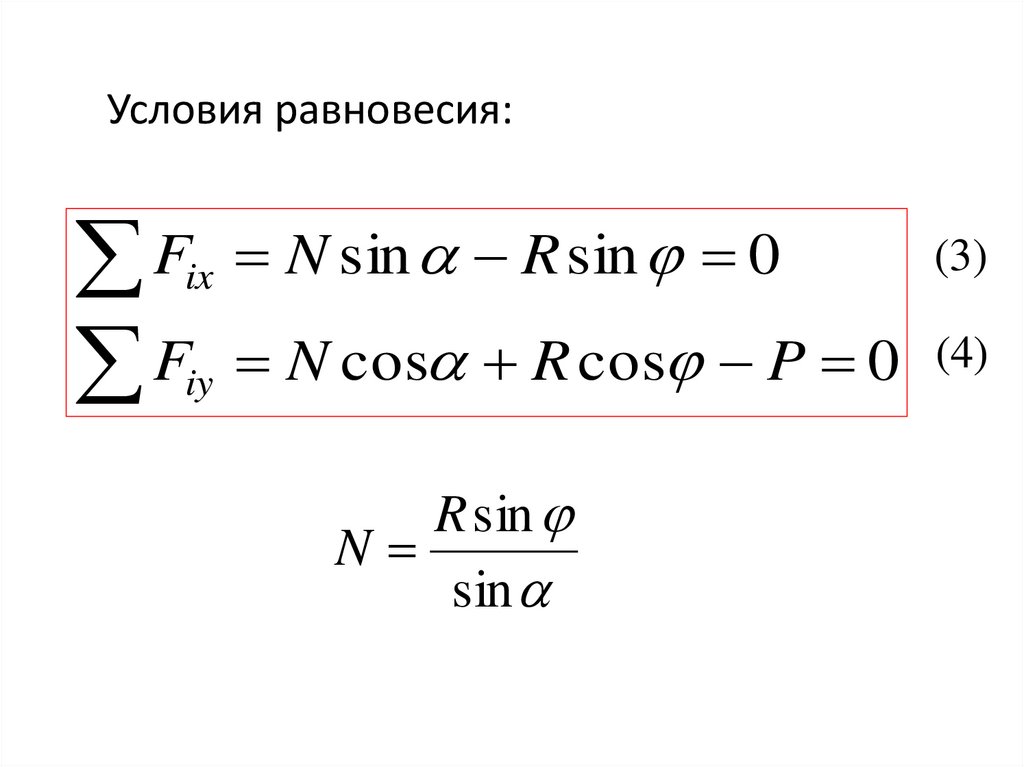
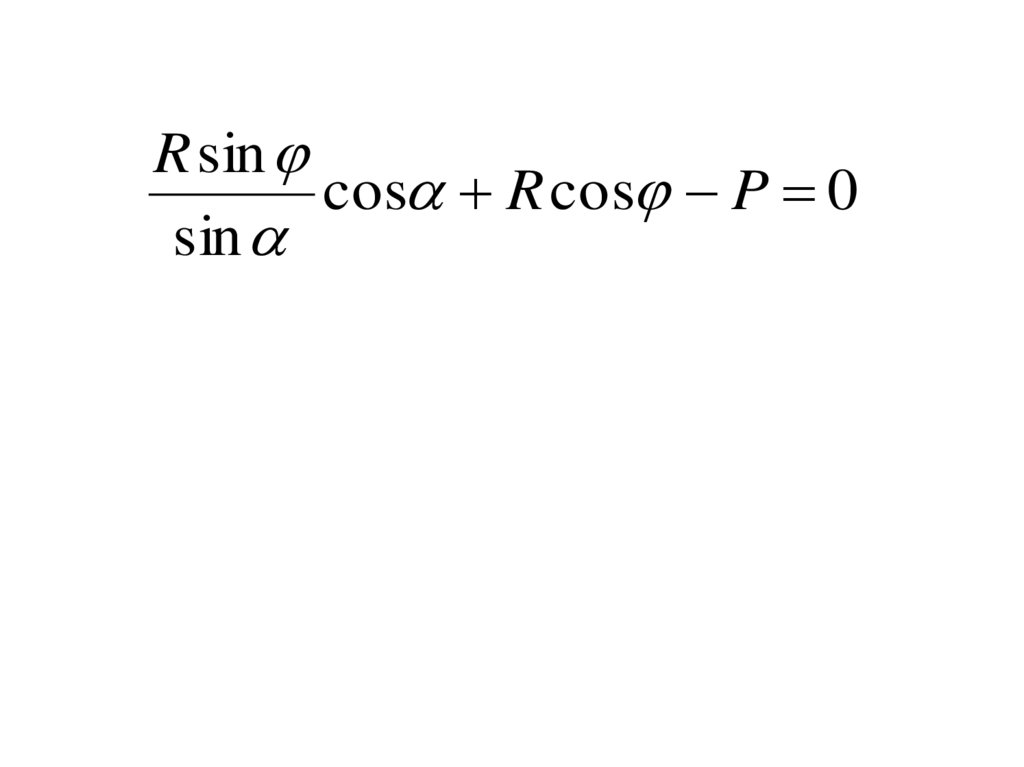












 Физика
Физика








