Похожие презентации:
Производная и дифференциал. Техника дифференцирования элементарных функций
1. Производная и дифференциал.
2. Техника дифференцирования элементарных функций.
c 0, c constx 1
kx b k
1
x
2 x
1
1
2
x
x
1
tan x 2
cos x
sin x cos x
cos x sin x
1
log a x
x ln a
1
ln x
x
1
cot x 2
sin x
3. Правила дифференцирования.
(u v) u v(uv) u v uv
c u ( x)
c u ( x)
uvw
u u v uv
2
v
v
u
1
2
u
u
u vw uv w uvw
4. 1.Применение формул и правил дифференцирования.
32
y
2
x
4
x
5x 3
1. Продифференцировать функцию:
2 x
3
2
3
4 x 5 x 0 2 3x
6 x 2 8x 5
4x 5x 3
y 2 x 4 x 5 x 3 2 x
3
2
2
2
4 2 x 5 1
5. 2. Продифференцировать функцию:
y 2x 3 sin xy 2 x 3 sin x 2 x 3 sin x 2 x 3 sin x
2 x 3 sin x 2 x 3 cos x 2 0 sin x 2 x 3 cos x
2 sin x 2x 3 cos x
6.
3. Продифференцировать функцию: yy
x cos x ln x
x cos x ln x
x cos x ln x
x cos x ln x x cos x ln x
1
cos x ln x x sin x ln x x cos x
x
2 x
1
cos x ln x
x cos x
x sin x ln x
x
2 x
cos x ln x cos x
2 ln x cos x
x sin x ln x
x sin x ln x
2 x
x
2 x
7.
4. Продифференцировать функцию:x3
y
cos x
3
3
x
x cos x x cos x
y
2
cos x
cos x
3
3x cos x x sin x x 3 cos x x sin x
2
cos x
cos 2 x
2
3
2
8.
5. Продифференцировать функцию:tan x
y
7
1
1
tan x 1
1
1
y
tan x tan x
2
2
7
7
7
7
cos
x
7
cos
x
9.
2x xy 3
x
6. Продифференцировать функцию:
1
2
2x x 2x x
y 3
2x x x
1
x
x3
1
2
1
3
2x
7
6
7
1
6
7 6 7 6
y 2 x 2 x 2 x x
6
3
7
6
10.
7. Продифференцировать функцию:y
4
3
x2
y 4 x
2
3
4
x
2
3
4 x
4 x
8
3 3 x5
2
3
y
4
3
x
2
2
3
2 53
8
1
4 x 5
3
3 3
x
8
3x 5 x 2
11. 2.Применение формул и правил дифференцирования.
8. Продифференцировать функцию:y 5 x arcsin x arctan x 3arc cot x
12.
y 5 arcsin x arctan x 3arc cot xx
arcsin x arctan x 3 arc cot x
5
x
1
1
5 ln 5
3
2
2
1 x
1 x2 1 x
x
1
1
3
5 ln 5
2
2
2
1 x
1 x
1 x
x
1
4
5 ln 5
2
2
1
x
1 x
x
1
13.
9. Продифференцировать функцию:y x arccos x
y x arccos x x arccos x x arccos x
1
1 arccos x x
2
1 x
x
arccos x
2
1 x
14.
1 1 exy
x 1 ex
10. Продифференцировать функцию:
1 1 e
y
x
x
1
e
x
1 1 e
x
x 1 e
x
1 1 e
2
x
x
1 e 1 e 1 e
1 e
x
x
x
x 2
1 ex 1 ex 1 ex ex
1 ex 1 ex ex 1 ex
2
2
2
2
x
x
x
x
1 e
1 e
1 e x 1 e x 1 e x
1
2e x
2
2
2
x
x
x
1 e
1 ex
2
15. Производная от сложной функции.
Функция, заданная в виде y=f(g(x)),называется сложнойфункцией, составленной из функций g и f, или
суперпозицией функций g и f. (функция, аргументом
которой служит функция, называется сложной)
элементарная функция
сложная функция
y sin x
y sin x 2 x
аргумент
16.
элементарная функцияy x
3
сложная функция
y 4 x 1
3
y x
y 1 x
y ln x
y ln 2 x 3
2
17. Теорема:
Если функция f(u) дифференцируема по u, афункция u(x) дифференцируема по х, то
производная сложной функции y=f(u(x)) по
независимой
переменной
х
определяется
равенством
y x f u u x
или
y x yu u x
18. Доказательство:
y x yu u xДоказательство:
Пусть дана функция y=f(u(x)).
y
y u
y
u
y x lim
lim
lim
lim
yu u x
x 0 x
x 0 x u
u 0 u x 0 x
y x yu uv v x
19. Примеры. Вычислить производные для функций:
y x yu u xПримеры.
Вычислить производные для функций:
y x 4x 1
1)
y u ,
3
3
u x 4x 1
3
x
y x yu u x u
3
3
2
3
2
4 x 1 3u 3x 4
3 x 4 x 1 3x 4
3
2
2
20.
2)y x yu uv v x
y ln cos 4 x
3
2
y ln cos 4 x ln cos 4 x
3
2
2
3
2
ln cos 4 x
3
2
y ln u, u cos v, v 4 x
3
2
y x yu uv v x ln u cos v 4 x
3
2 1
8 sin v
8
8
sin v 4
tan v tan 4 x
3 u
3 cos v
3
3
21.
2)y ln cos 4 x
3
2
y ln cos 4 x ln cos 4 x
3
2
2
3
2
ln cos 4 x
3
2
2
u
y ln cos 4 x ln cos
4 x ln u
3
u
3
u
u
cos 4 x
2
2
4
x
sin
4
x
cos u u sin u
3
3 cos 4 x
cos 4 x
8
tan 4 x
3
22.
y 2 x 3x 42
3)
y
u
2 x 3x 4 u
2 u
2
2 x
2
3x 4
2 2 x 3x 4
2
4x 3
2 2 x 3x 4
2
23.
y sin x cos x,4
4)
4
f ?
3
4
4
4
y sin x cos x sin x cos x u 4u 3 u
u
u
4
4
3
3
4 sin x sin x 4 cos x cos x
4 sin 3 x cos x 4 cos 3 x sin x
4 sin x cos x sin 2 x cos 2 x 2 sin 2 x
1
2
3
f 2 sin 2 2 sin
2
3
3
3
2
3



















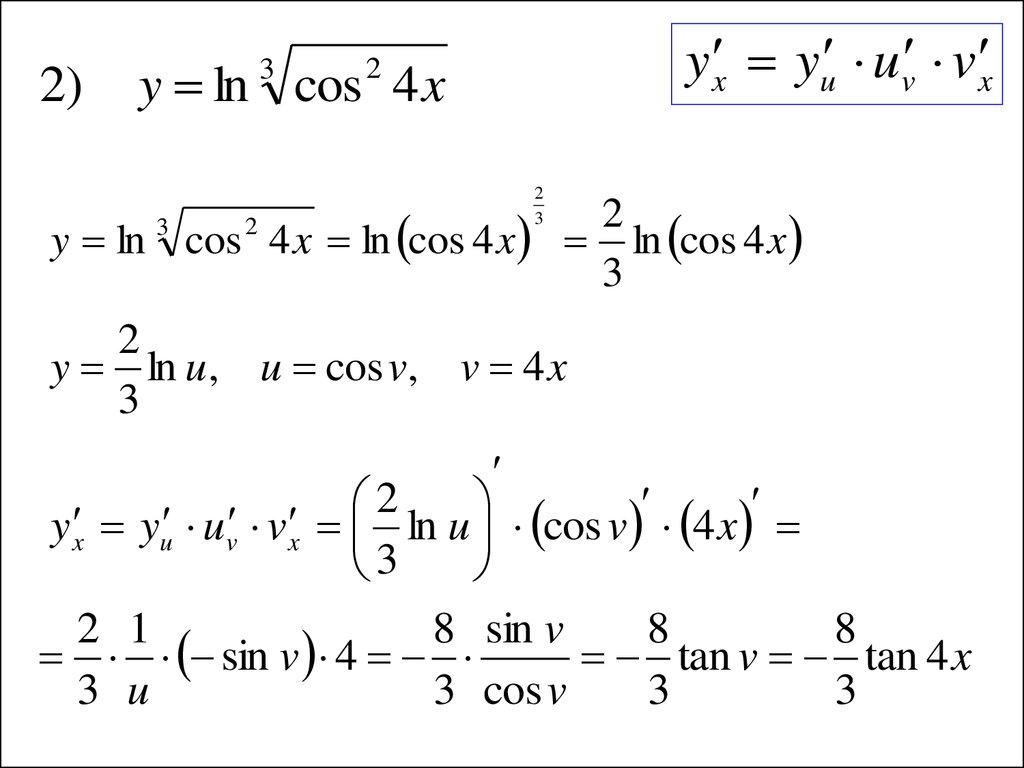
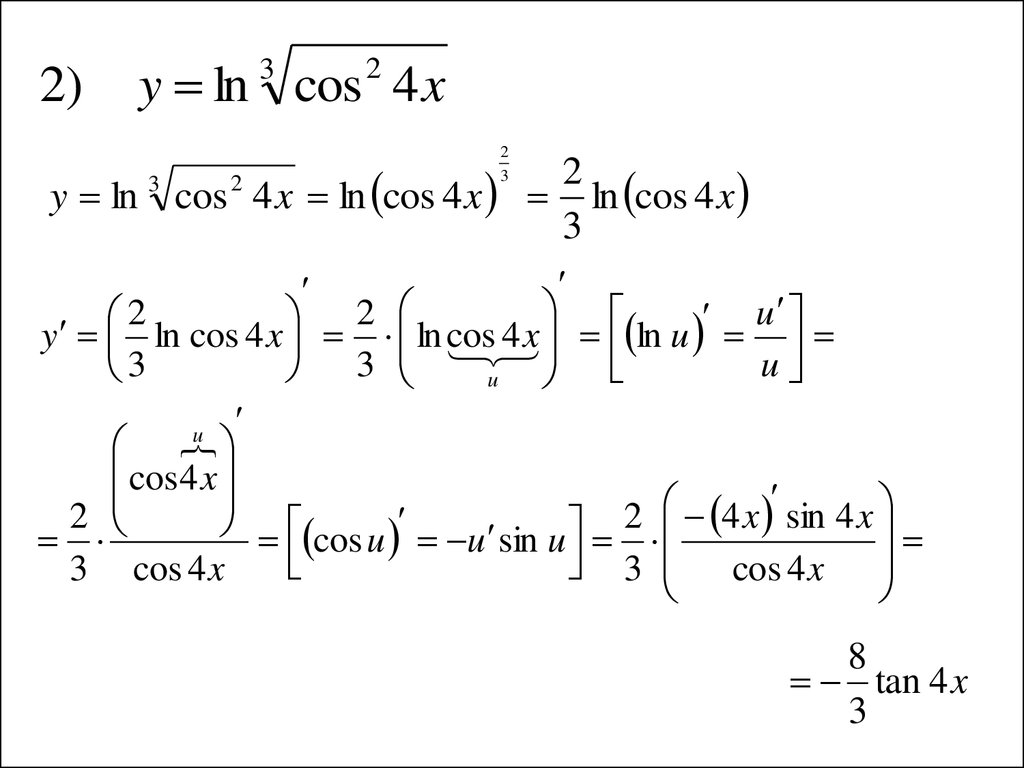
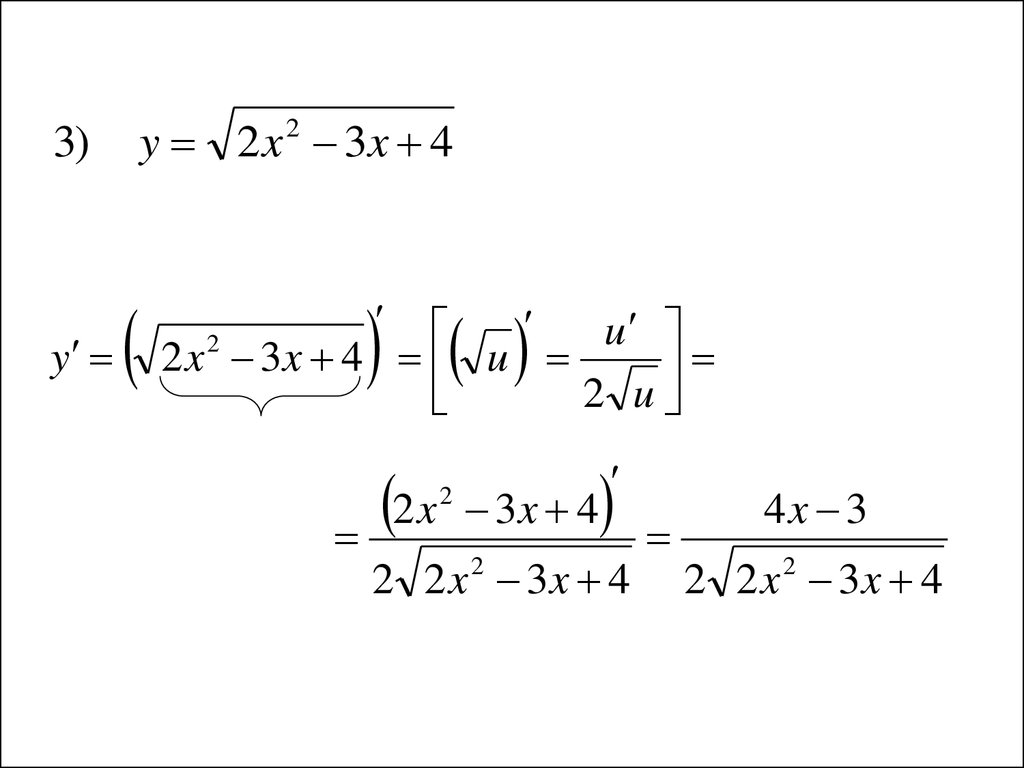
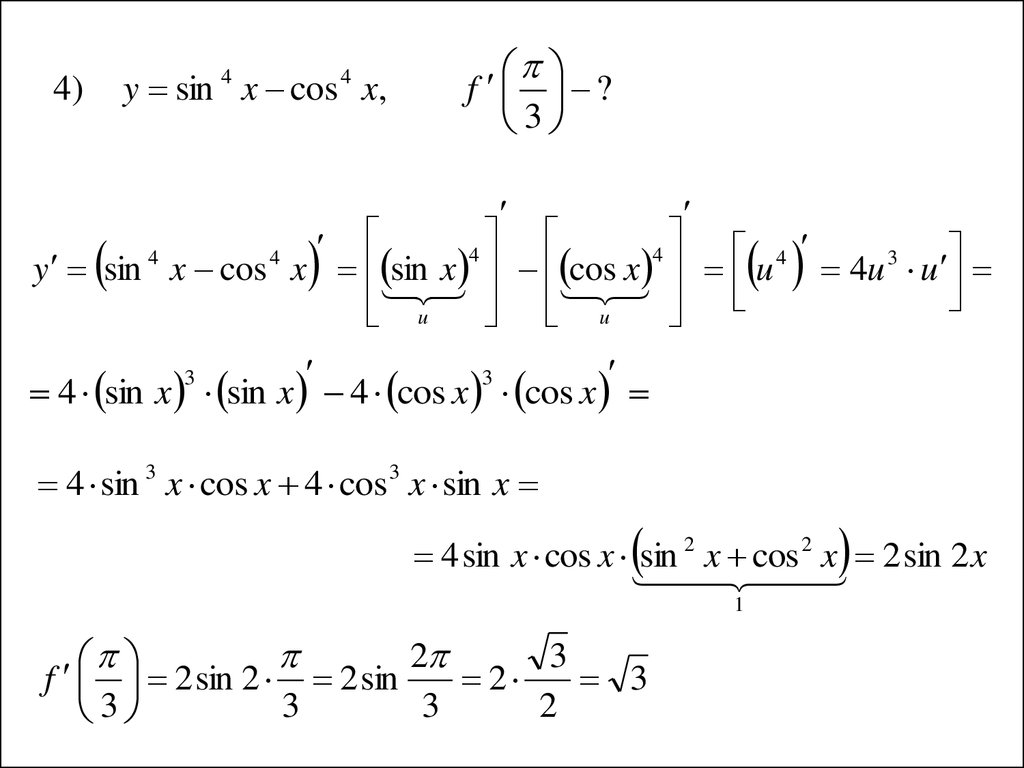
 Математика
Математика








