Похожие презентации:
Перпендикулярность прямой и плоскости
1.
2.
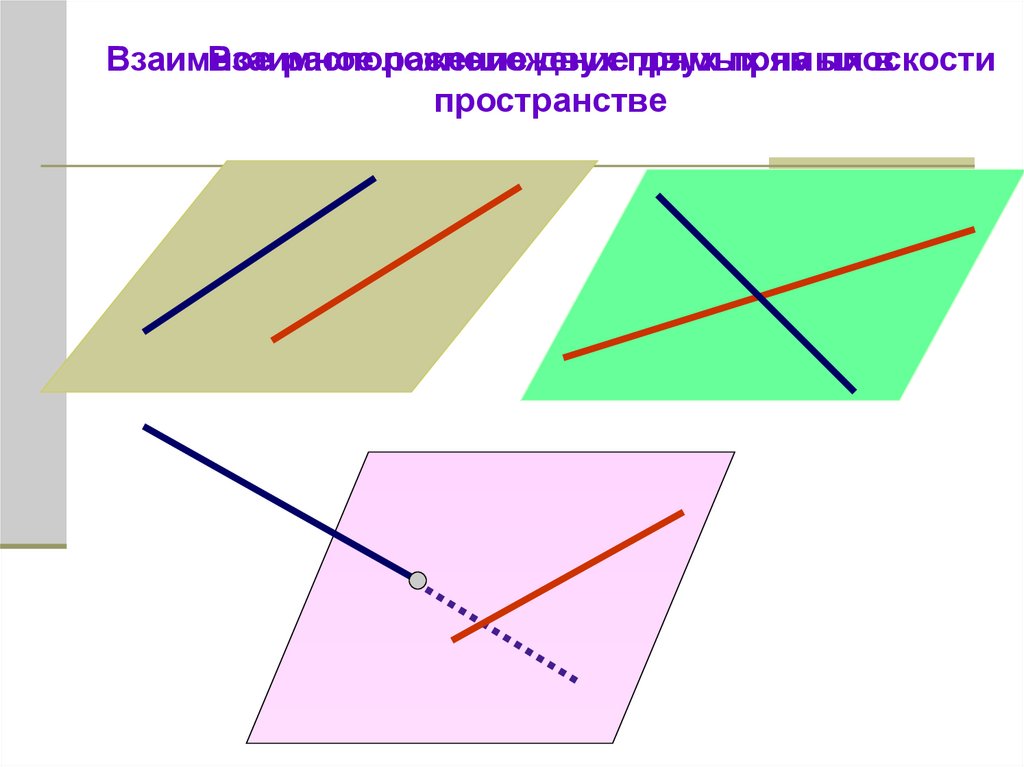
ВзаимноеВзаимное
расположение
расположение
двух прямых
двух прямых
на плоскости
в
пространстве
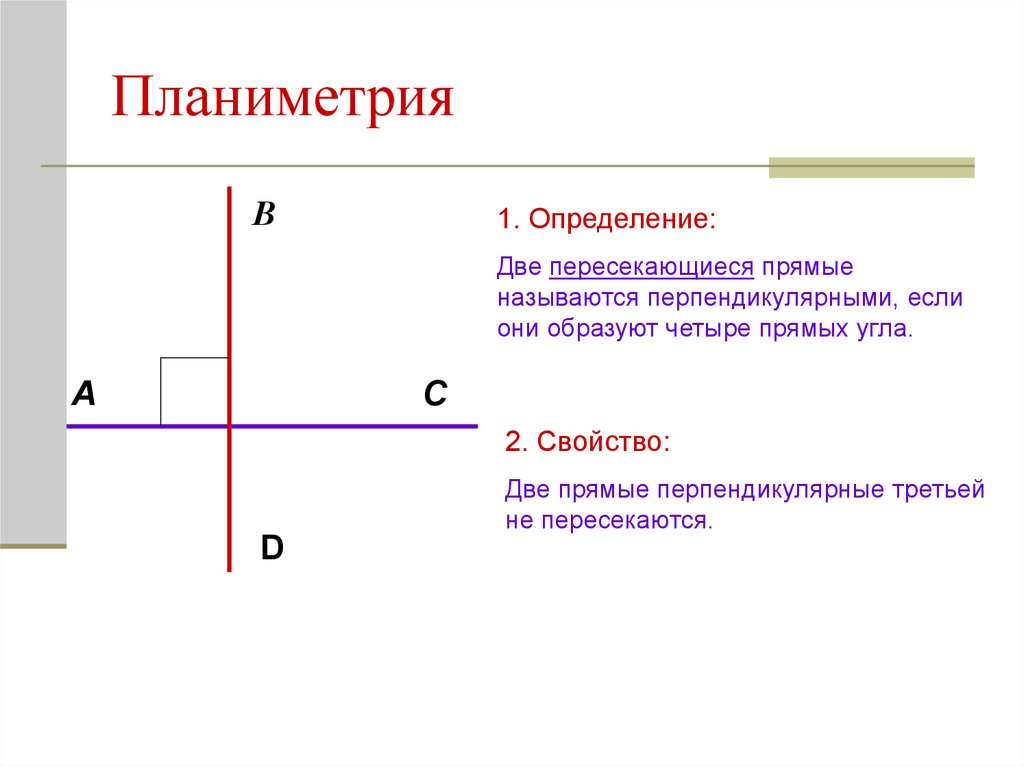
3. Планиметрия
В1. Определение:
Две пересекающиеся прямые
называются перпендикулярными, если
они образуют четыре прямых угла.
С
A
2. Свойство:
Две прямые перпендикулярные третьей
не пересекаются.
D
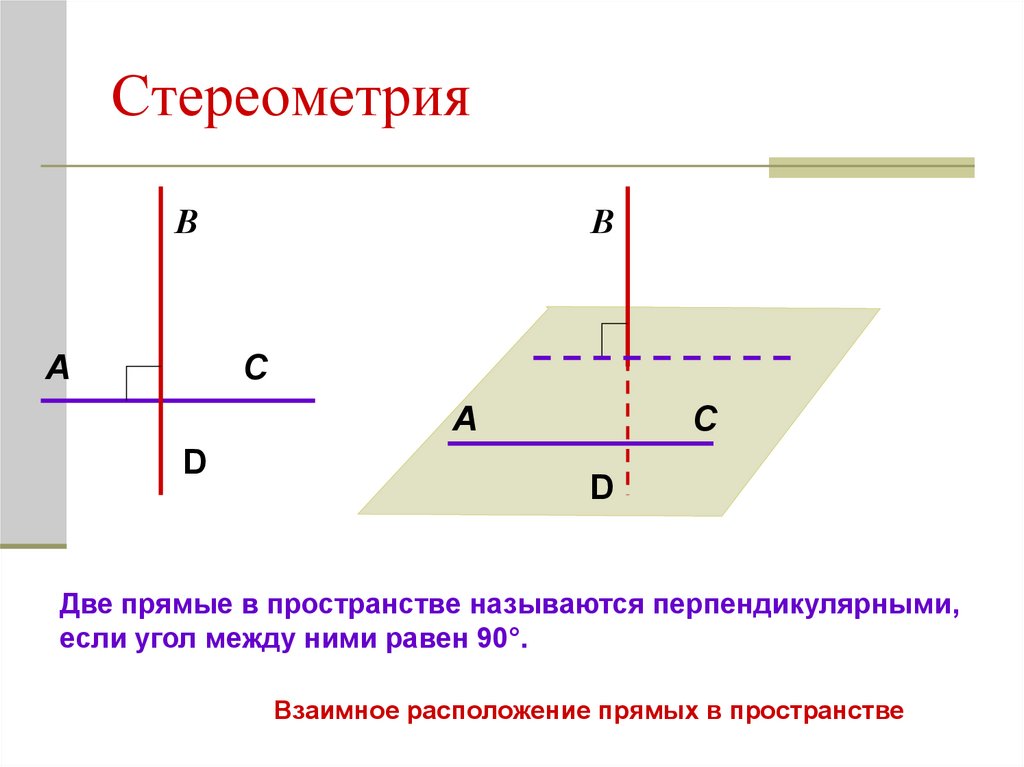
4. Стереометрия
ВВ
С
A
С
A
D
D
Две прямые в пространстве называются перпендикулярными,
если угол между ними равен 90°.
Взаимное расположение прямых в пространстве
5.
Прямые а и b пересекаются.Прямые а и с скрещиваются.
c
а b
b
а с
а
6.
Лемма о перпендикулярности двухпараллельных прямых к третьей
прямой
а
Дано: а с а b
Если одна из bдвух параллельных
прямых
Доказать b с
перпендикулярна к третьей
прямой,
то
и
Доказательство
другая М
прямая перпендикулярна
к этой
А
c
М а; b; с МА а
прямой
МС с
т.к. а с, то АМС 90
(углы с сонаправленными сторонами)
С
а b МА а то МА b
МА b и МС с; АМС 90
(углы с сонаправленными
сторонами)
то bc 90 , т.е. b c
7. Лемма о перпендикулярности двух параллельных прямых к третьей прямой
2. Параллельные прямые,перпендикулярные к
плоскости.
Знать определение прямой перпендикулярной к
плоскости.
Уметь формулировать и доказывать теоремы
прямую и обратную о параллельных прямых.
8. 2. Параллельные прямые, перпендикулярные к плоскости.
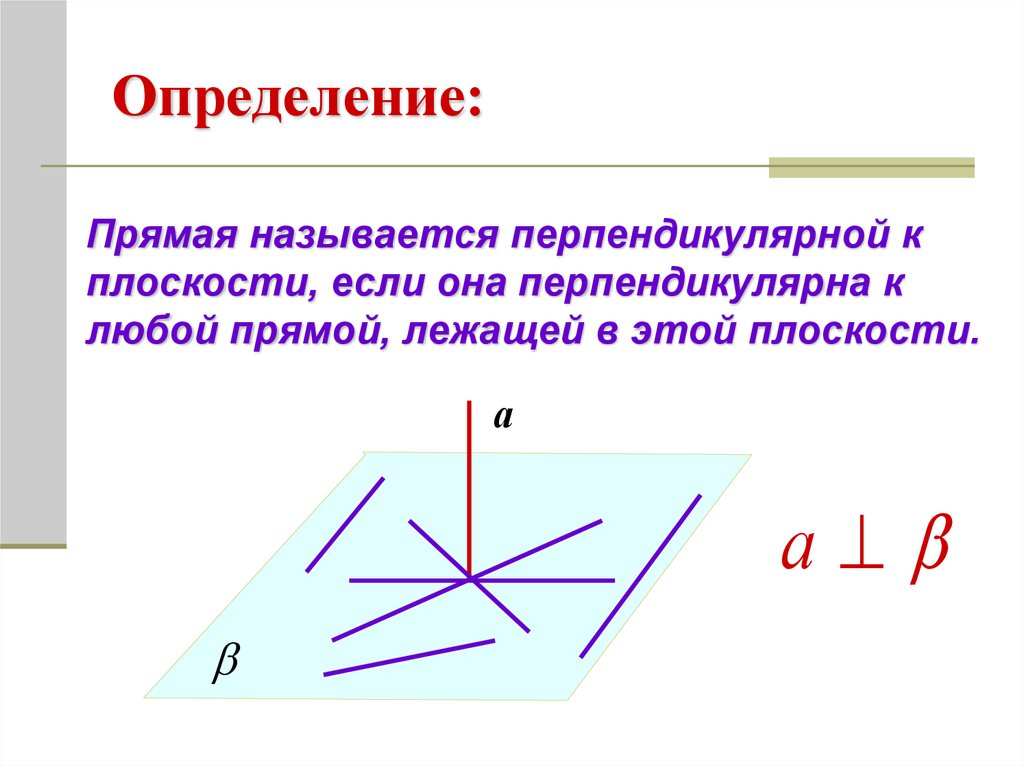
Определение:Прямая называется перпендикулярной к
плоскости, если она перпендикулярна к
любой прямой, лежащей в этой плоскости.
а
а
9. Определение:
Теорема 1Если одна из двух параллельных прямых
перпендикулярна к плоскости, то другая
прямая перпендикулярна к этой плоскости
Дано: а b а
b
Доказать
а
b
Доказательство
x
а , то а x
x
по лемме b x
b
10. Теорема 1
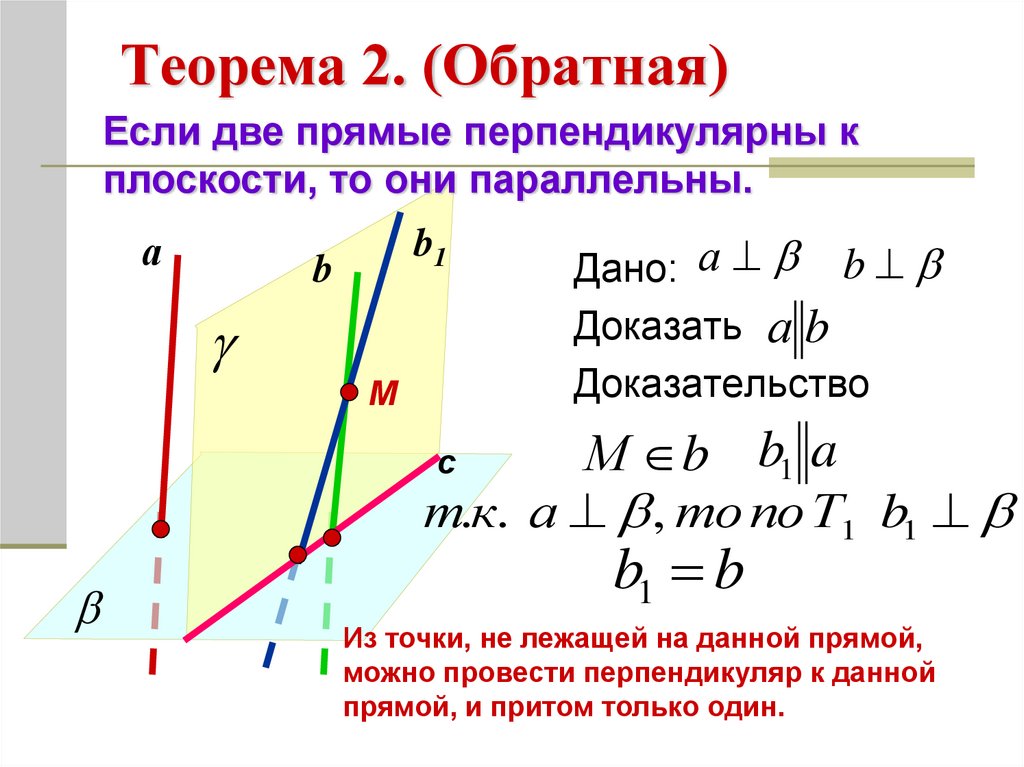
Теорема 2. (Обратная)Если две прямые перпендикулярны к
плоскости, то они параллельны.
а
b1
b
М
Дано: а b
Доказать а b
Доказательство
М b b1 a
т.к. а , то по Т1 b1
с
b1 b
Из точки, не лежащей на данной прямой,
можно провести перпендикуляр к данной
прямой, и притом только один.
11. Теорема 2. (Обратная)
ОДве прямые в пространстве называютсяперпендикулярными, если угол между ними равен
90°.
Л
Если одна из двух параллельных прямых
перпендикулярна к третьей прямой, то и другая
прямая перпендикулярна к этой прямой
О
Прямая называется перпендикулярной к плоскости,
если она перпендикулярна к любой прямой, лежащей
в этой плоскости.
Т1
Если одна из двух параллельных прямых
перпендикулярна к плоскости, то другая прямая
перпендикулярна к этой плоскости
Т2
Если две прямые перпендикулярны к плоскости, то
они параллельны.
12.
Устная работа№1
№2
№3
12.02.2022
Верно ли утверждение: прямая
перпендикулярна к плоскости, если
она перпендикулярна к прямой,
принадлежащей плоскости?
Могут ли быть перпендикулярны
к плоскости две стороны
треугольника одновременно?
Сторона АВ правильного треугольника
АВС лежит в плоскости . Может ли
прямая BC быть перпендикулярна
к этой плоскости?
13
13.
Устная работа№4
№5
№6
12.02.2022
Верно ли утверждение: если прямая
перпендикулярна двум прямым,
лежащим в плоскости, то она
перпендикулярна к данной
плоскости?
Прямая a перпендикулярна
к плоскости , прямая b не
перпендикулярна к плоскости .
Могут ли прямые a и b быть
параллельными?
Верно ли утверждение: если прямая
перпендикулярна к плоскости, то она
перпендикулярна лежащим в этой
плоскости двум сторонам
треугольника?
14
14.
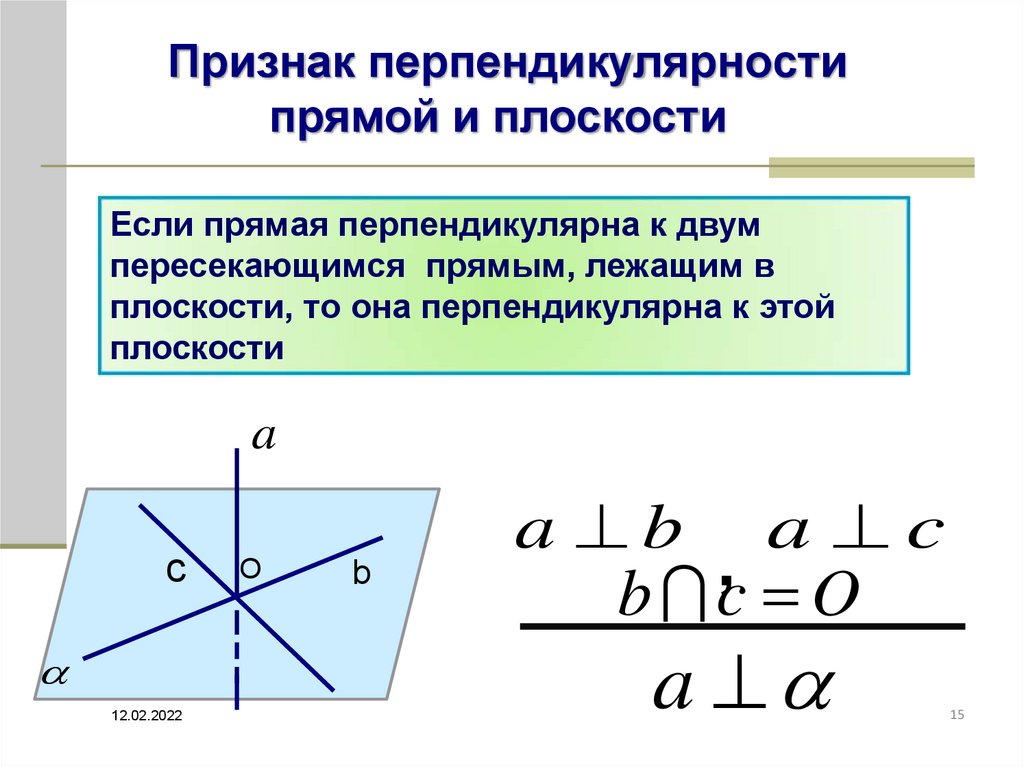
Признак перпендикулярностипрямой и плоскости
Если прямая перпендикулярна к двум
пересекающимся прямым, лежащим в
плоскости, то она перпендикулярна к этой
плоскости
a
c
12.02.2022
O
b
a b a c
,
b c O
a
15
15.
Устная работаС №7
М В
А
D
№8
12.02.2022
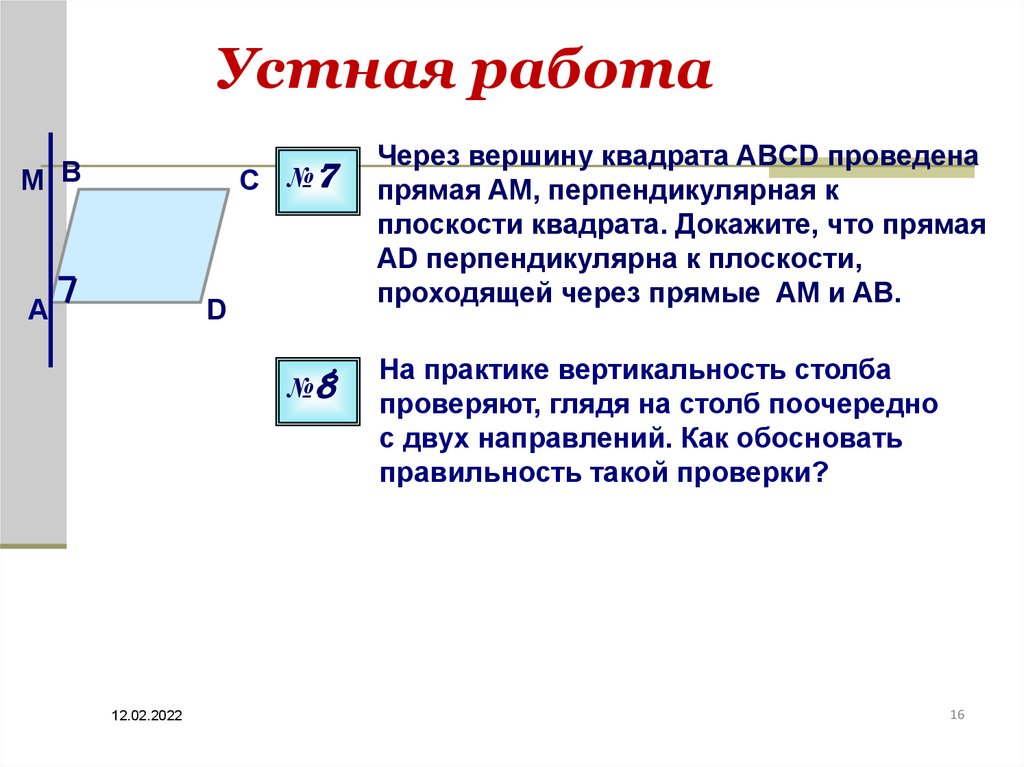
Через вершину квадрата ABCD проведена
прямая AM, перпендикулярная к
плоскости квадрата. Докажите, что прямая
AD перпендикулярна к плоскости,
проходящей через прямые AM и AB.
На практике вертикальность столба
проверяют, глядя на столб поочередно
с двух направлений. Как обосновать
правильность такой проверки?
16
16.
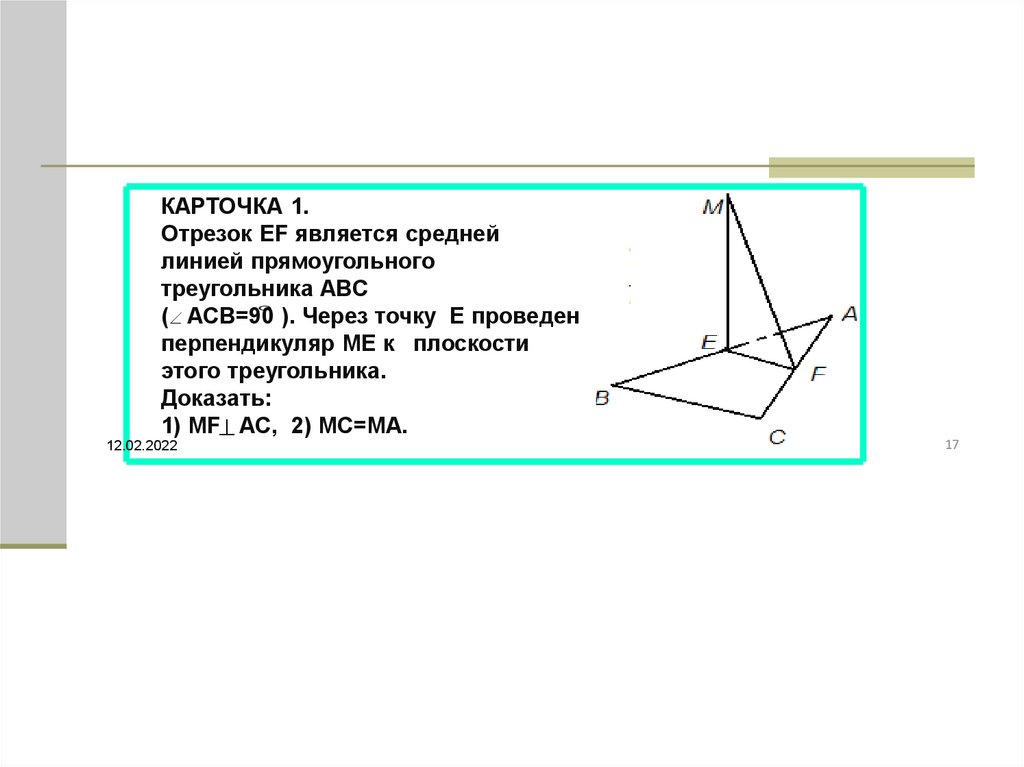
КАРТОЧКА 1.Отрезок EF является средней
линией прямоугольного
треугольника ABC
). Через точку E проведен
( ACB=90
перпендикуляр ME к плоскости
этого треугольника.
Доказать:
1) MF AC, 2) MC=MA.
12.02.2022
17
17.
ВА1
a
12.02.2022
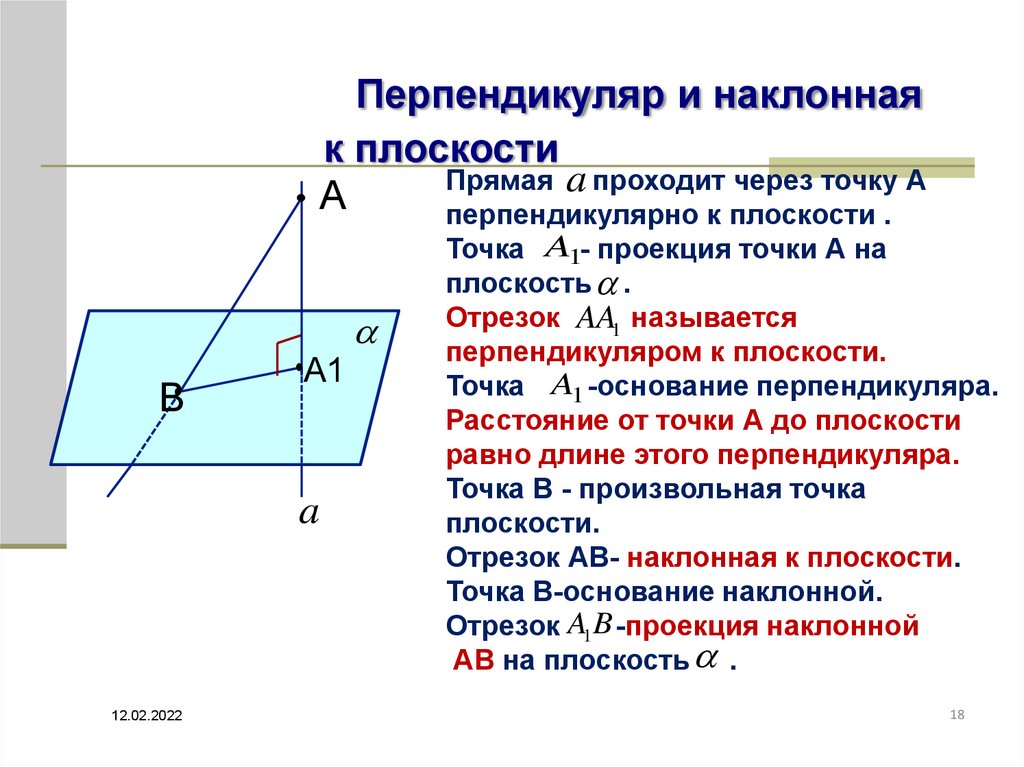
Перпендикуляр и наклонная
к плоскости
Прямая a проходит через точку А
А
перпендикулярно к плоскости .
Точка A1- проекция точки А на
плоскость .
Отрезок AA1 называется
перпендикуляром к плоскости.
Точка A1 -основание перпендикуляра.
Расстояние от точки А до плоскости
равно длине этого перпендикуляра.
Точка В - произвольная точка
плоскости.
Отрезок АВ- наклонная к плоскости.
Точка В-основание наклонной.
Отрезок A1B -проекция наклонной
АВ на плоскость .
18
18.
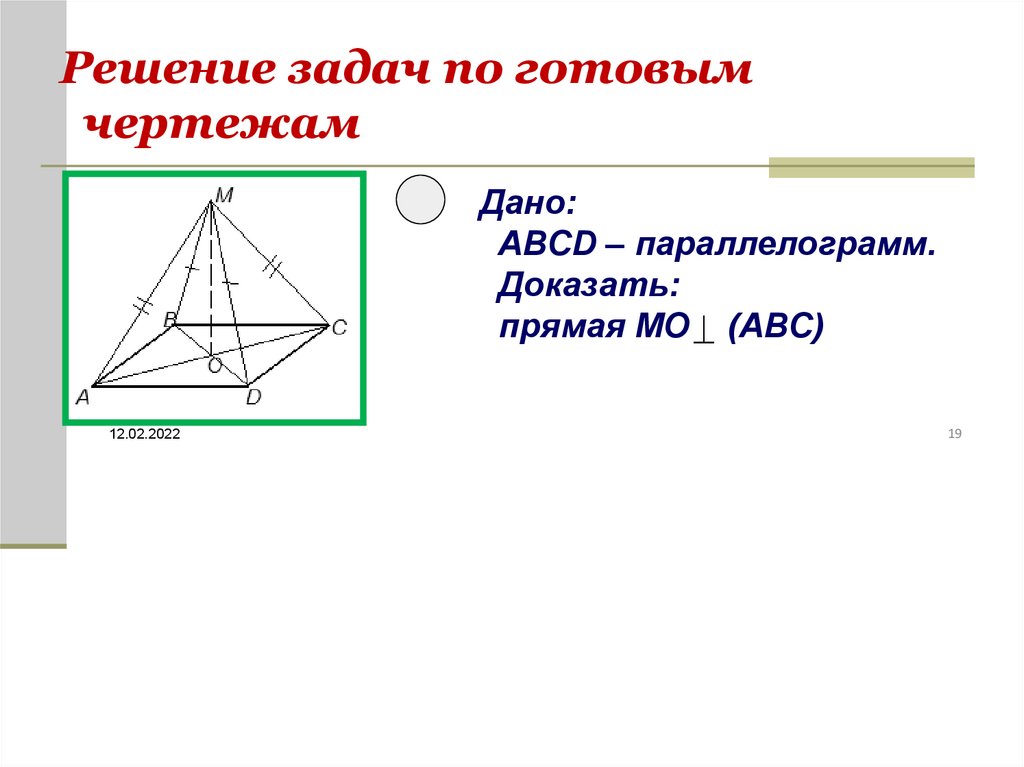
Решение задач по готовымчертежам
Дано:
ABCD – параллелограмм.
Доказать:
прямая MO (ABC)
12.02.2022
19
19. Решение задач по готовым чертежам
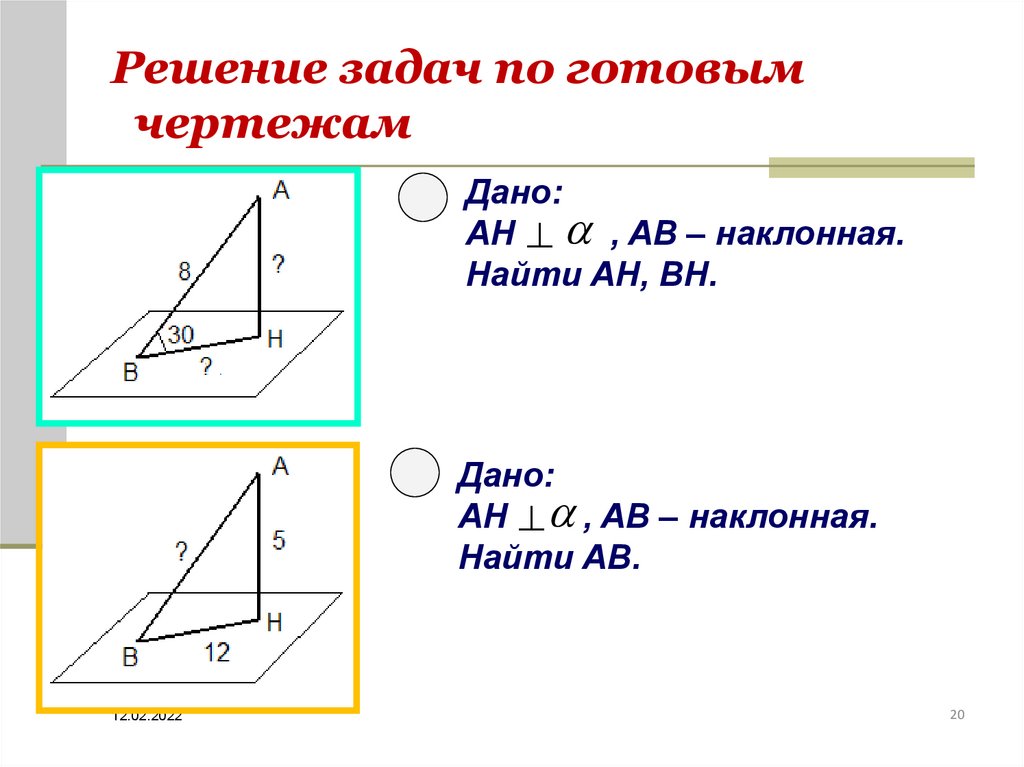
Дано:AH , AB – наклонная.
Найти AН, ВН.
Дано:
AH , AB – наклонная.
Найти AB.
12.02.2022
20
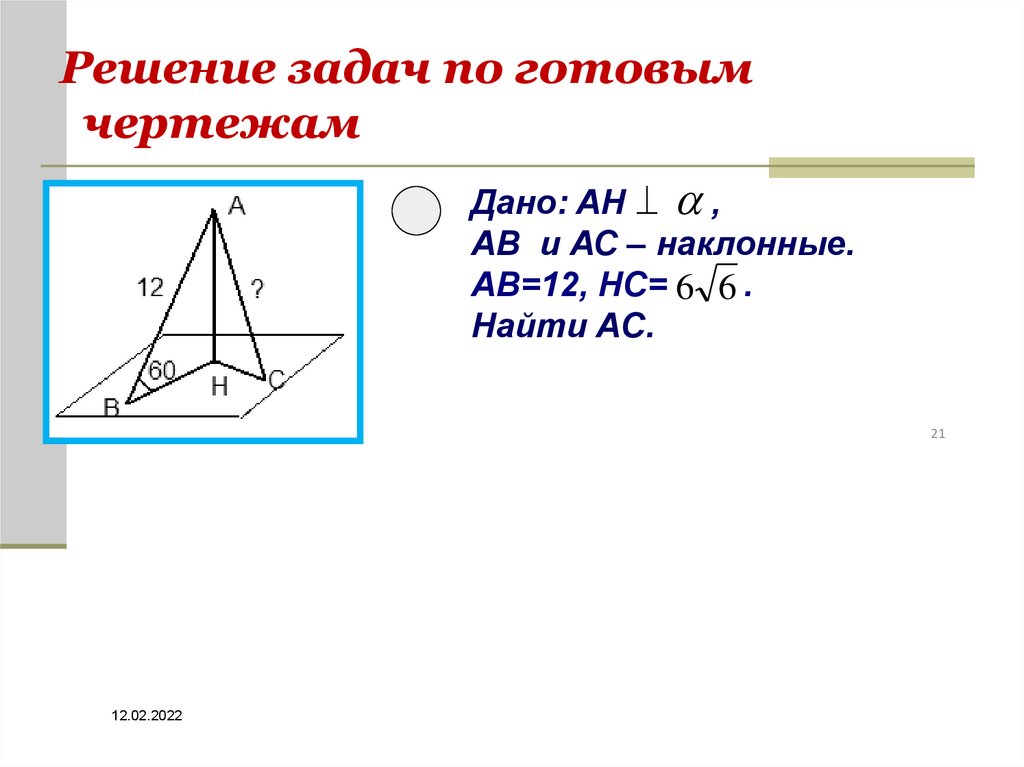
20. Решение задач по готовым чертежам
Дано: AH ,AB и АС – наклонные.
AB=12, HC= 6 6 .
Найти AС.
21
12.02.2022
21. Решение задач по готовым чертежам
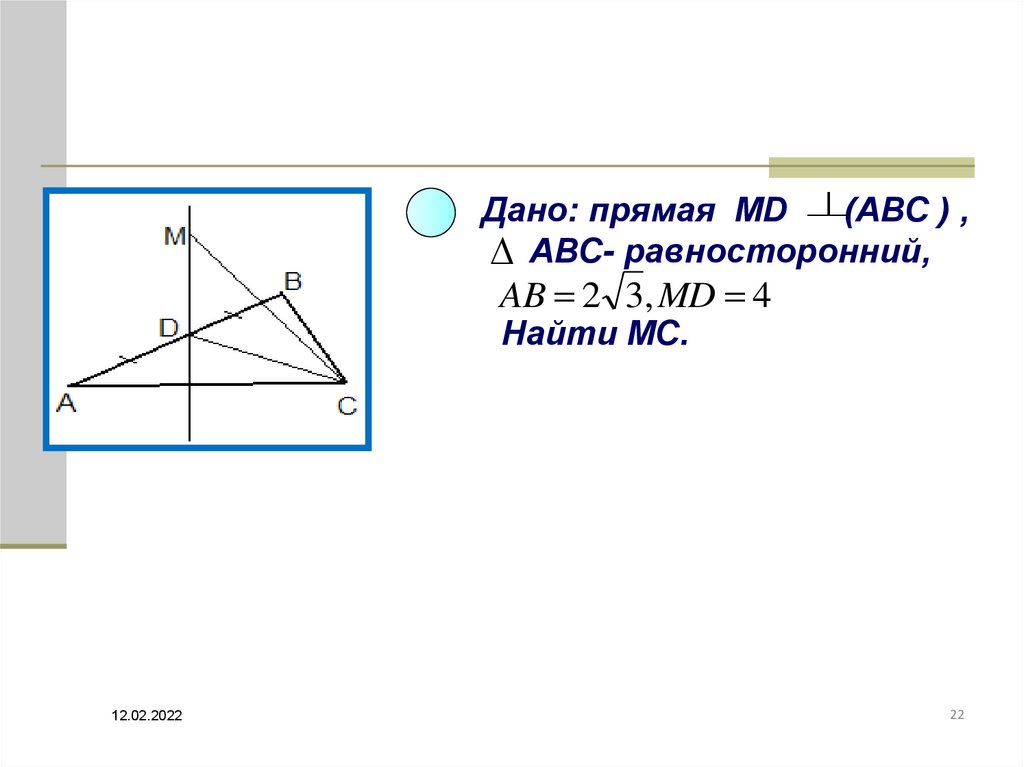
Дано: прямая MD (AВС ) ,АВС- равносторонний,
AB 2 3, MD 4
Найти МС.
12.02.2022
22








 Математика
Математика








