Математическое моделирование

1.

МДК 02.03
Математическое моделирование
(26 ч – ЛПЗ, 4ч – лекция
форма аттестации: комплексный экзамен)

2.

https://www.youtube.com/watch?v=Ru3FFqBc8j0
Канторович Л.В.
1912 – 1986
Советский математик и экономист, один из
создателей линейного программирования.
Лауреат Нобелевской премии по
экономике 1975 года «за вклад в теорию
оптимального распределения ресурсов».
Доктор физико-математических наук,
академик АН СССР, профессор.

3.

Математическое моделирование
Математическая модель – это абстрактная картина
реального мира, в которой интересующие
исследователя отношения между реальными
объектами заменены подходящими отношениями
между математическими объектами.
Математическая модель – это приближенное
описание какого-либо класса явлений внешнего
мира, выраженное с помощью математической
символики.
Процесс математического моделирования – есть
изучение явления с помощью математических
моделей.

4.

Этапы математического
моделирование
I ЭТАП: формулировка законов, связывающих
основные объекты модели.
II ЭТАП: исследование математических задач,
к которым приводят математические
модели.
III ЭТАП: выяснение того, удовлетворяет ли
принятая (гипотетическая) модель критерию
практики
IV ЭТАП: последующий анализ модели и ее
модернизация.

5.

Основные понятия моделирования.
1. Предмет теории моделирования
Модель – это материальный или мысленно-представляемый
объект, который в процессе исследования замещает объекторигинал так, что его непосредственное изучение дает новые
знания об объекте-оригинале.
Моделирование – это замещение одного объекта (оригинала)
другим (моделью) и фиксация и изучение свойств модели.
Теория моделирования – взаимосвязанная совокупность
положений, определений, методов и средств создания моделей.

6.

Основные понятия моделирования.
2. Роль и место моделирования в исследовании
систем
Познание любой системы сводится к созданию ее модели.
Имитационное компьютерное моделирование позволило
занять теории моделей новую ступень в практической
деятельности человечества:
- производство автомобилей;
- выращивание растений;
- функционирование органов человека;
- жизнедеятельность Азовского моря;
- последствия атомной войны;
- и др.

7.

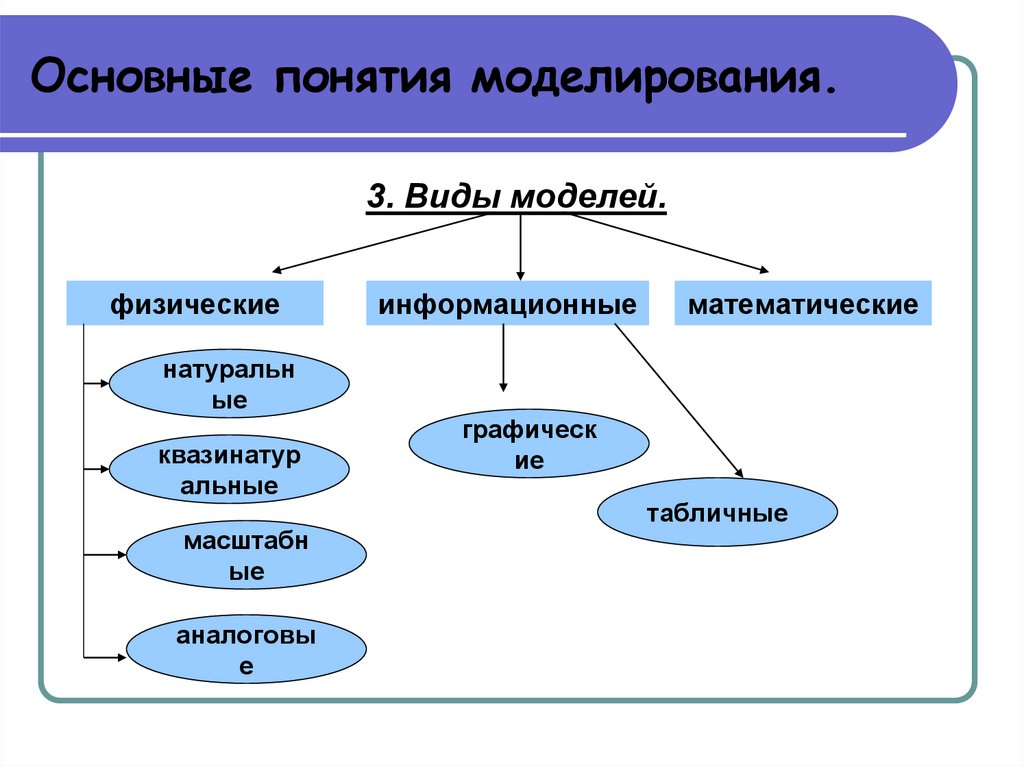
Основные понятия моделирования.
3. Виды моделей.
физические
информационные
математические
натуральн
ые
квазинатур
альные
масштабн
ые
аналоговы
е
графическ
ие
табличные

8.

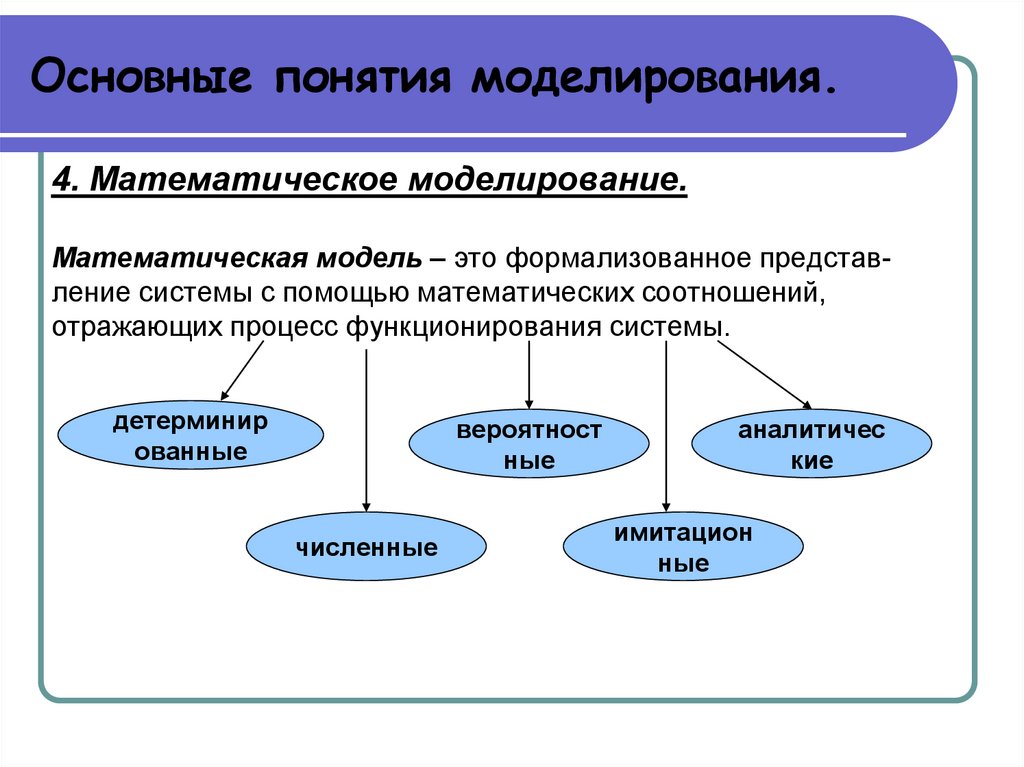
Основные понятия моделирования.
4. Математическое моделирование.
Математическая модель – это формализованное представление системы с помощью математических соотношений,
отражающих процесс функционирования системы.
детерминир
ованные
вероятност
ные
численные
аналитичес
кие
имитацион
ные

9.

Основные понятия моделирования.
5. Аспекты применения математических
методов в решении практических проблем.
1) Совершенствование системы сбора информации о сложном
объекте.
2) Интенсификация и повышение точности технических и
экономических расчетов.
3) Углубление количественного анализа проблем в технических,
экономических и др. приложениях.
4) Решение принципиально новых научных и практических
задач.

10.

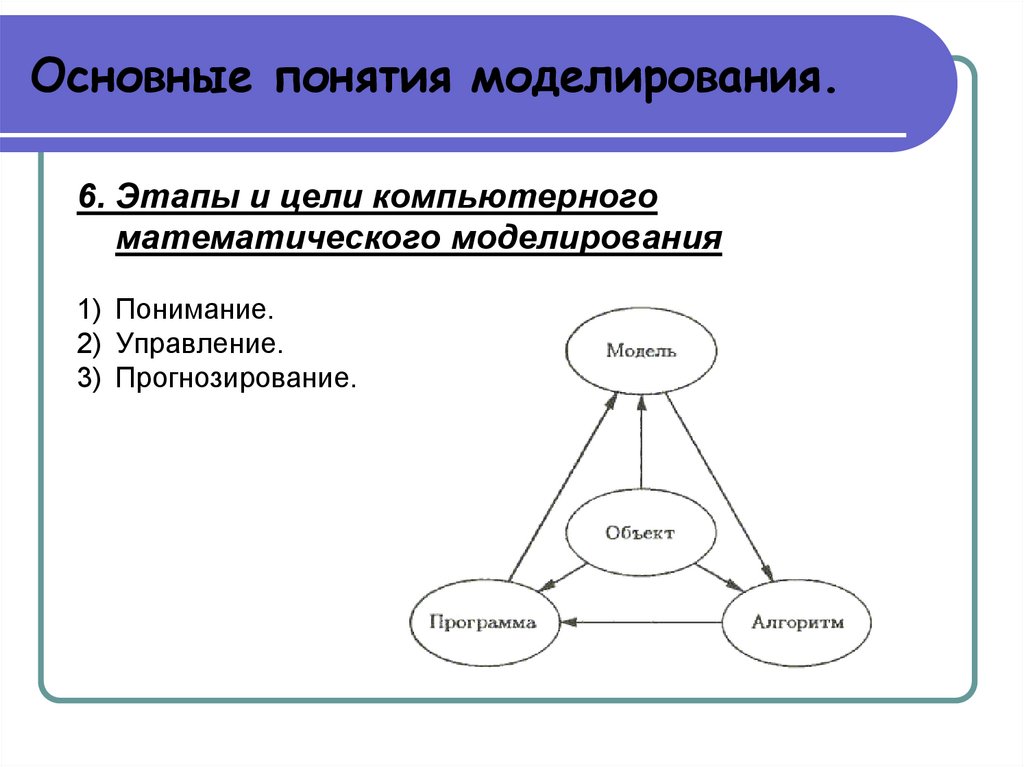
Основные понятия моделирования.
6. Этапы и цели компьютерного
математического моделирования
1) Понимание.
2) Управление.
3) Прогнозирование.

11.

Основные понятия моделирования.
6. Этапы математического моделирования
1) Конструирование модели, формулировка предмодели.
2) Завершение идеализации объекта.
3) Выбор или формулировка законов, которым подчиняется
объект, и его записи в математической форме.
4) Завершение формулировки модели, ее «оснащение».
5) Теоретический анализ модели.
6) Практическое исследование параметров модели и их
фиксирование.

12.

Основные понятия моделирования.
7. Примеры моделей, получаемых из
фундаментальных законов природы.
1) Траектория всплытия подводной лодки
непосредственное применение
закона Архимеда,
определяющего величину
выталкивающей силы, и закона
Ньютона, связывающего силу,
действующую на тело, и его
ускорение, позволяет легко найти
траекторию подлодки.

13.

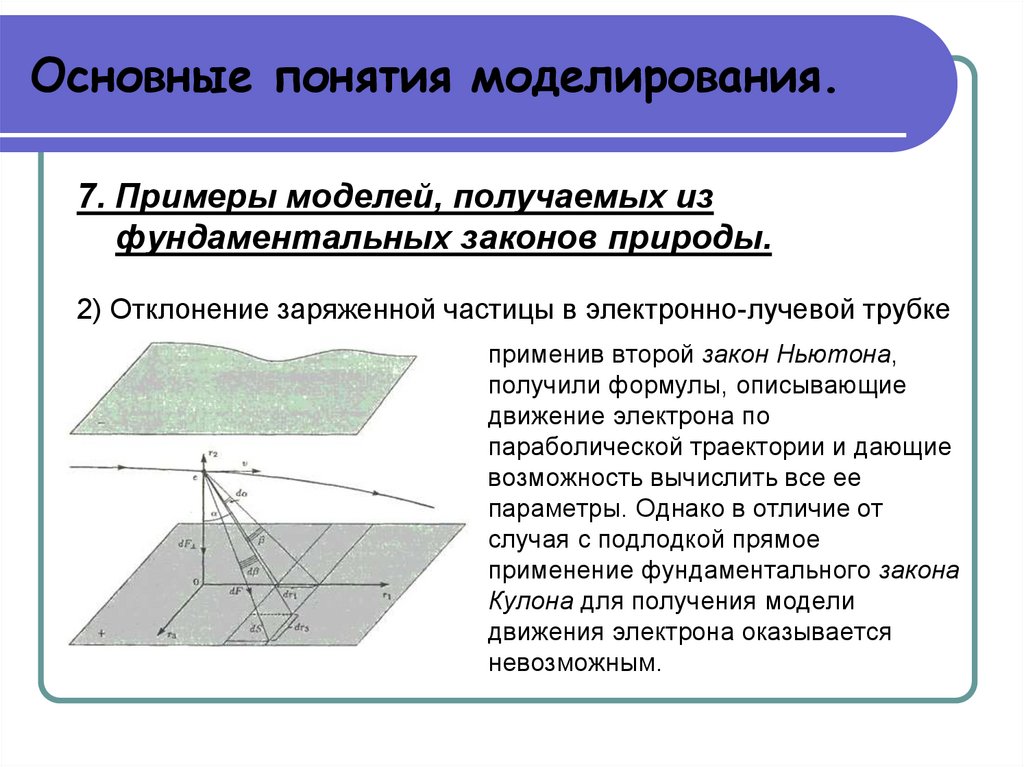
Основные понятия моделирования.
7. Примеры моделей, получаемых из
фундаментальных законов природы.
2) Отклонение заряженной частицы в электронно-лучевой трубке
применив второй закон Ньютона,
получили формулы, описывающие
движение электрона по
параболической траектории и дающие
возможность вычислить все ее
параметры. Однако в отличие от
случая с подлодкой прямое
применение фундаментального закона
Кулона для получения модели
движения электрона оказывается
невозможным.

14.

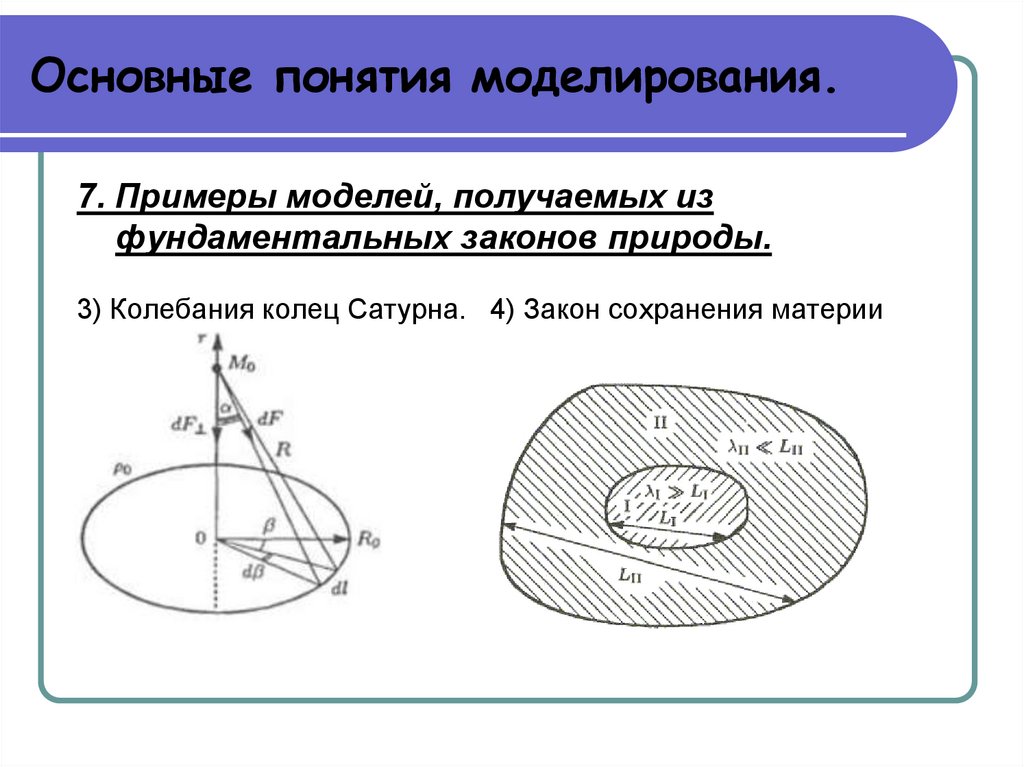
Основные понятия моделирования.
7. Примеры моделей, получаемых из
фундаментальных законов природы.
3) Колебания колец Сатурна. 4) Закон сохранения материи