Основы математической статистики

1. Основы математической статистики

2. План лекции:

1. Задачи математической статистики.
2. Дискретные и интервальные ряды
распределения. Числовые
характеристики.
3. Точечные и интервальные оценки.

3. Что такое математическая статистика?

математическая статистика – это
одновременно искусство и наука
извлечения полезной информации из
данных, полученных в результате
наблюдений или экспериментов

4. Объекты, изучаемые математической статистикой

Генеральная совокупность – конечное или
бесконечное множество объектов, обладающих
определенными математическими свойствами.
Выборка - некоторое число случайным образом
выбранных объектов из конечной или
бесконечной генеральной совокупности; число
выбранных объектов называют объемом
выборки.

5. Какие задачи нас интересуют?

- определение закона распределения
случайной величины по выборочным
данным;
- задача проверки правдоподобия гипотез
(отличия характеристик выборки от
некоторых неслучайных величин; отличия
характеристик нескольких выборок; связь
случайных величин из разных выборок);
- Задача нахождения неизвестных
параметров распределения.

6. Статистическая функция распределения

Пусть имеется некоторая случайная величина Х,
закон распределения которой неизвестен и
требуется проверить гипотезу о том, что эта
случайная величина подчиняется тому или иному
закону. С этой целью над случайной величиной
проводится ряд независимых опытов. В каждом из
них случайная величина Х принимает
определенное значение.
Первичный статистический материал:
совокупность найденных значений Х (простой
статистический ряд).
Эти данные необходимо обрабатывать, но как?

7. Статистическая функция распределения случайной величины Х

F * ( x) P * ( X x)
Рассмотрим эксперимент, который поможет
понять смысл этой функции:
Дана некоторая группа людей, мы измеряем
их рост и пытаемся определить
закономерности распределения людей по
росту.

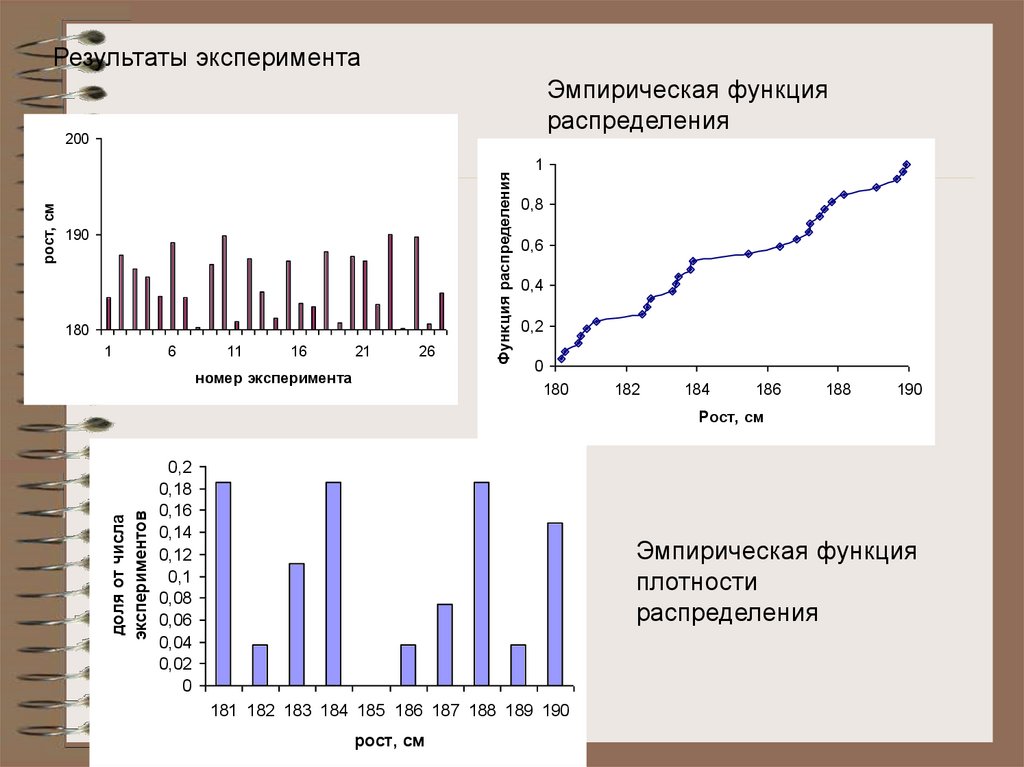
8.

Результаты эксперимента
Эмпирическая функция
распределения
180
1
6
11
16
21
26
номер эксперимента
Функция распределения
190
1
0,8
0,6
0,4
0,2
0
180
182
184
186
188
190
Рост, см
доля от числа
экспериментов
рост, см
200
0,2
0,18
0,16
0,14
0,12
0,1
0,08
0,06
0,04
0,02
0
Эмпирическая функция
плотности
распределения
181 182 183 184 185 186 187 188 189 190
рост, см

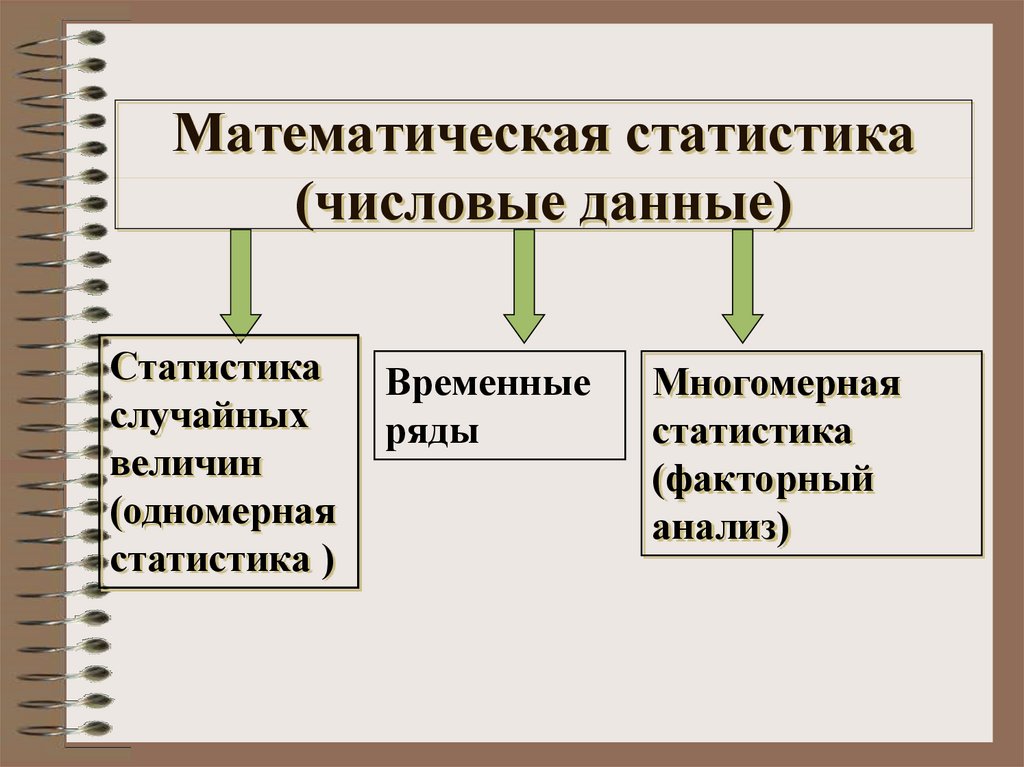
9. Математическая статистика (числовые данные)

Статистика
случайных
величин
(одномерная
статистика )
Временные
ряды
Многомерная
статистика
(факторный
анализ)

10. Задачи одномерной статистики

• Описательная статистика
(представление экспериментальных
данных, определение точечных и
интервальных оценок)
• Проверка статистических гипотез
(о законе распределения, параметрах
распределения)

11.

• Значения изучаемого признака
называются вариантами
• Последовательность вариант,
расположенных в возрастающем
порядке называется
вариационным рядом
Например: 172, 179, 158, 186, 164
Вариационный ряд:
158, 164, 172, 179, 186

12. Непараметрические характеристики

• Me-медиана
Варианта, которая делит ряд пополам
158, 164, 172, 175, 175, 179, 186
при n- нечетном
Ме=175
158, 164, 168, 172, 174, 175, 179, 186
172 174
Me
173
2
при n- четном

13. Непараметрические характеристики

• Mo-наиболее часто встречающаяся
варианта
158, 164, 172, 175, 175, 175, 179, 186
Мо=175
158, 164, 173, 173, 175, 175, 179, 186
173 175
Mo
174
2
бимодальные выборки- если два несмежных
значения имеют одинаковые частоты

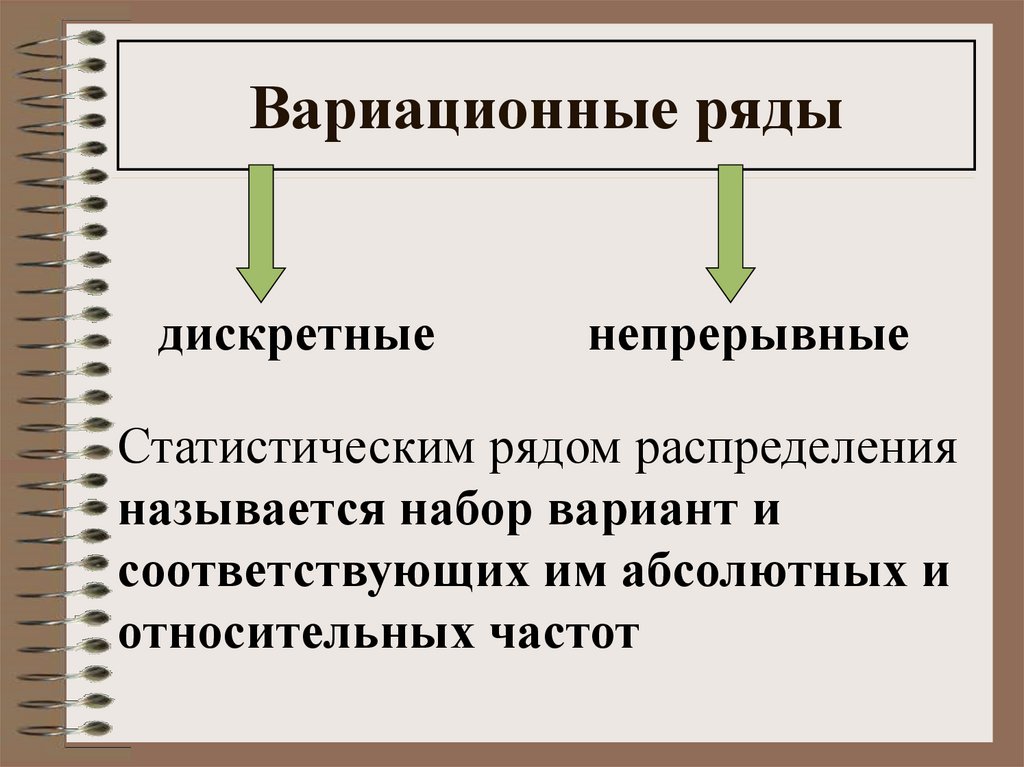
14. Вариационные ряды

дискретные
непрерывные
Статистическим рядом распределения
называется набор вариант и
соответствующих им абсолютных и
относительных частот

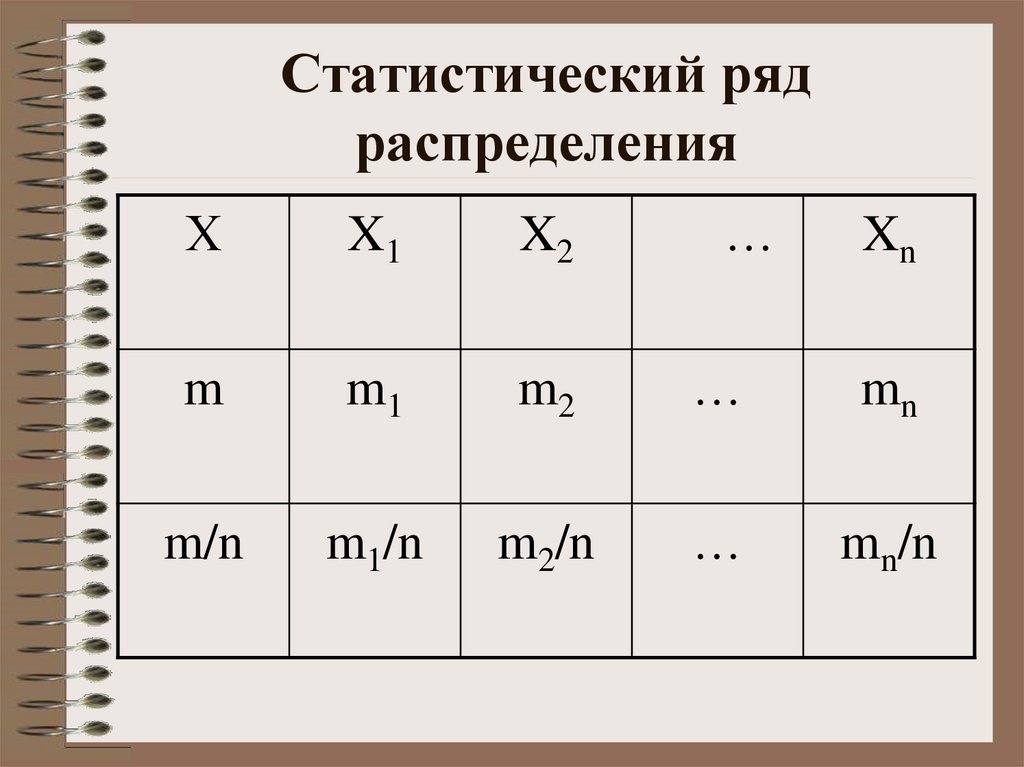
15. Статистический ряд распределения

Х
X1
X2
…
m
m1
m2
…
mn
m/n
m1/n
m2/n
…
mn/n
Xn

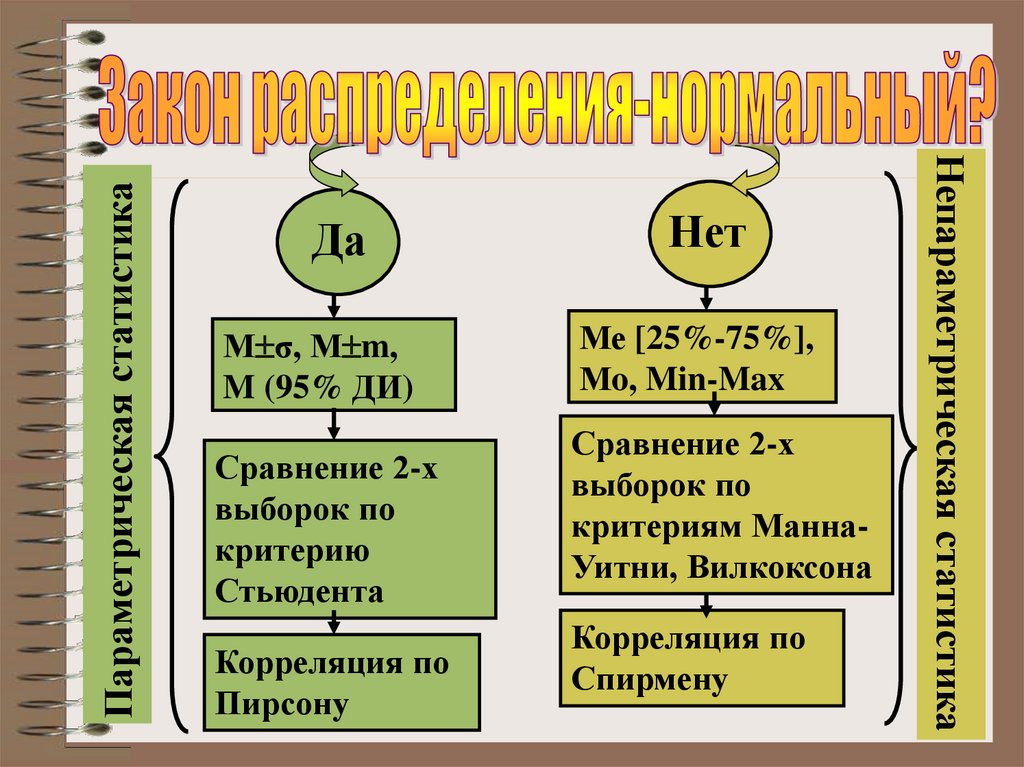
16.

Параметрическая статистика
М σ, М m,
M (95% ДИ)
Сравнение 2-х
выборок по
критерию
Стьюдента
Корреляция по
Пирсону
Нет
Ме [25%-75%],
Мo, Min-Max
Сравнение 2-х
выборок по
критериям МаннаУитни, Вилкоксона
Корреляция по
Спирмену
Непараметрическая статистика
Да

17. Основные этапы исследования:

• Сгруппировать исследуемый ряд по классам.
Подсчитать середины интервалов и частоты
попадания в интервал.
• Построить гистограмму и полигон распределения.
• Найти эмпирическую функцию распределения и
построить ее график.
• Вычислить числовые (точечные) характеристики
распределения.
• Проверить гипотезу о том, что генеральная
совокупность, из которой извлечена выборка,
распределена по нормальному закону, используя
критерии асимметрии и эксцесса.
• Проверить гипотезу о том, что генеральная
совокупность, из которой извлечена выборка,
распределена по нормальному закону, используя
критерий Пирсона 2

18. Ряд распределения студентов по росту

148 158 149 162 170 156 186 151 161
152 171 165 174 157 172 172 177
166 157 149 159 154 164 167 173
176 147 163 185 164 161 153 168
162 184 162 169 154 167 163 166
172 158 155 165 179 165 160 159
169

19. Размах распределения

Из имеющихся значений признака Х
выбирают наименьшее (Хmin),
наибольшее (Хmax), определяют
размах распределения
(Хmax – Хmin)
186-147=39

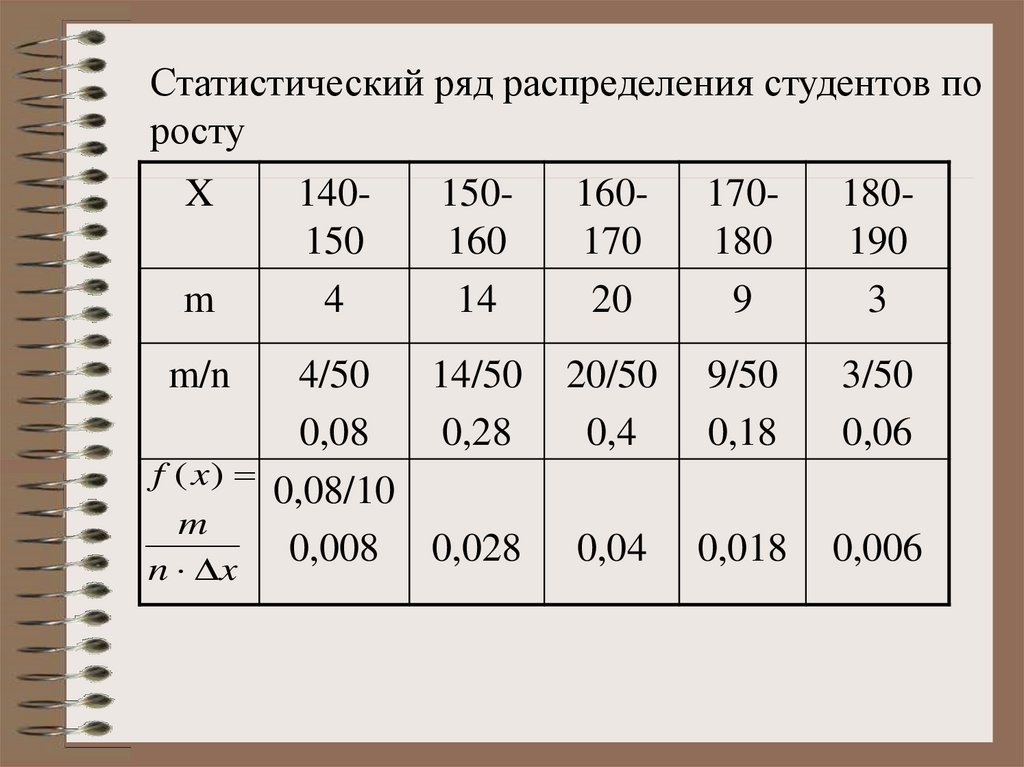
20.

Статистический ряд распределения студентов по
росту
X
150160
14
160170
20
170180
9
180190
3
4/50
14/50
0,08
0,28
f ( x)
0,08/10
m
0,008 0,028
n x
20/50
0,4
9/50
0,18
3/50
0,06
0,04
0,018
0,006
m
m/n
140150
4

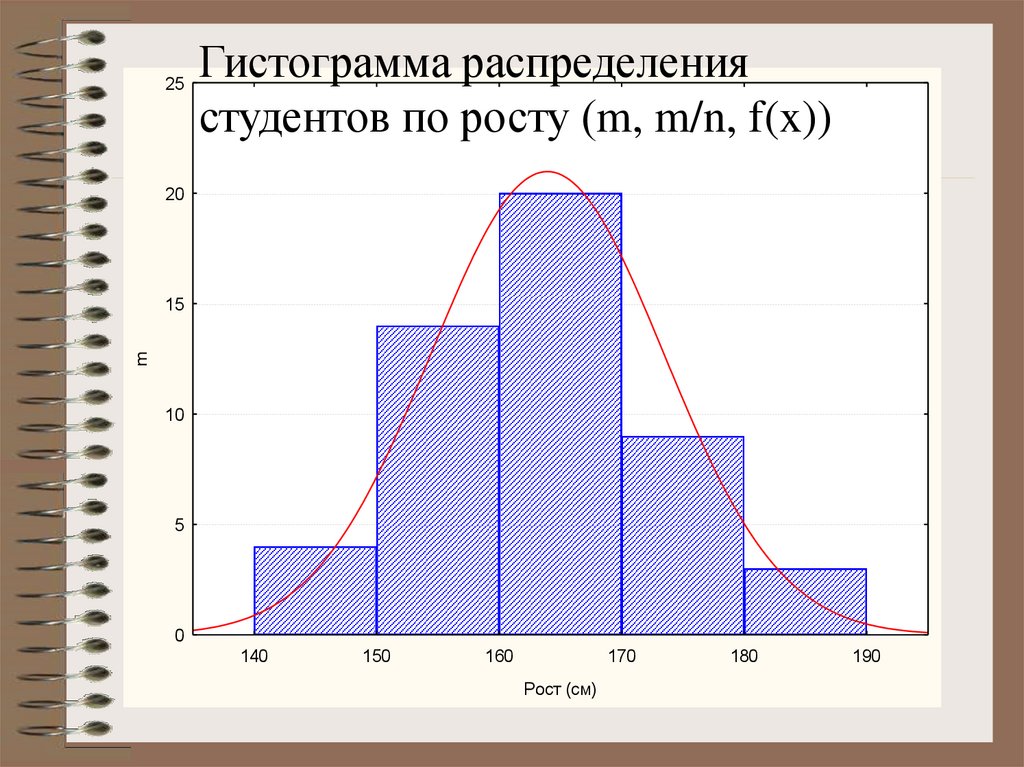
21.

25
Гистограмма распределения
студентов по росту (m, m/n, f(x))
20
m
15
10
5
0
140
150
160
170
Рост (см)
180
190

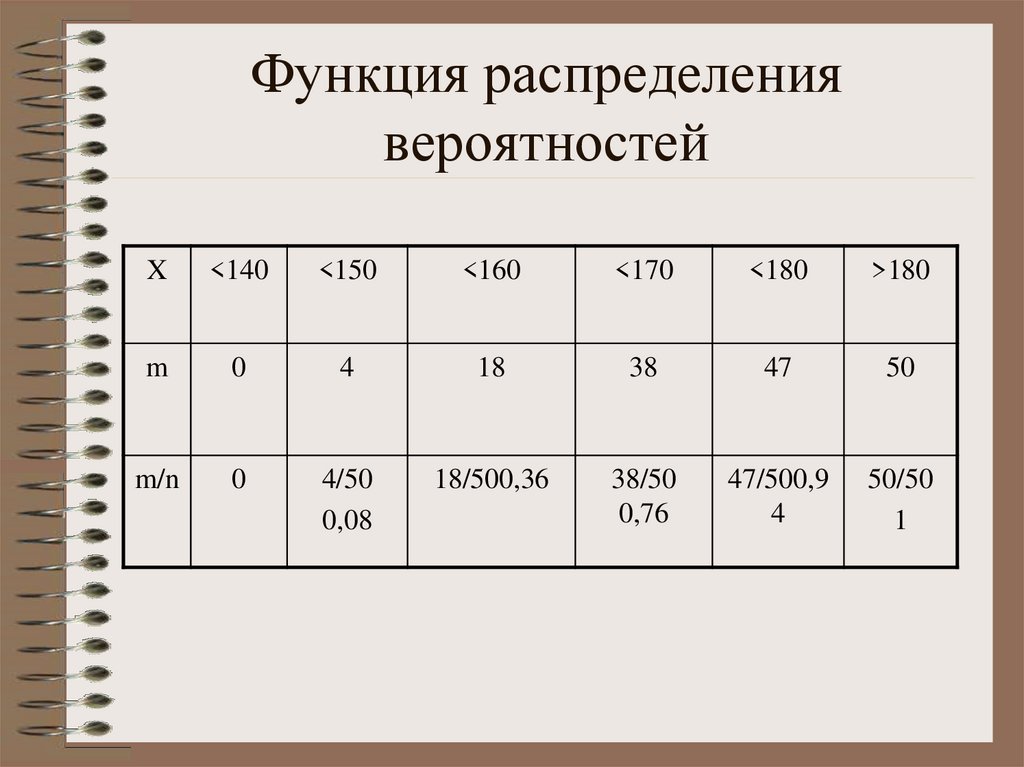
22. Функция распределения вероятностей

X
<140
<150
<160
<170
<180
>180
m
0
4
18
38
47
50
m/n
0
4/50
0,08
18/500,36
38/50
0,76
47/500,9
4
50/50
1

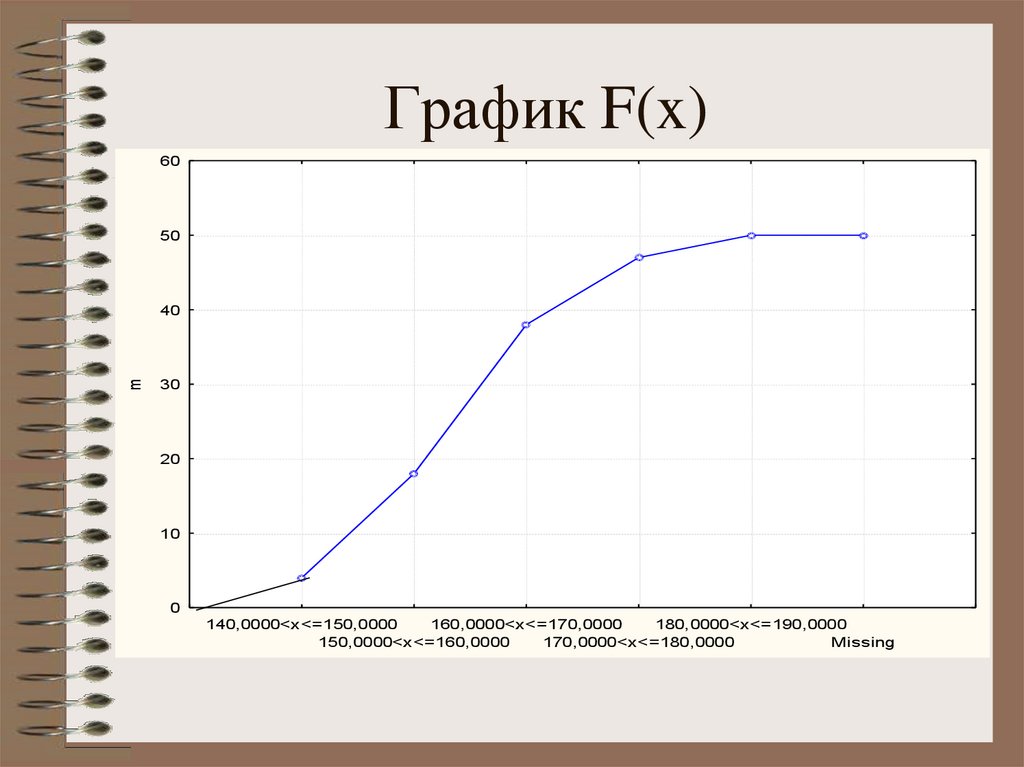
23. График F(x)

60
50
m
40
30
20
10
0
140,0000<x<=150,0000
160,0000<x<=170,0000
180,0000<x<=190,0000
150,0000<x<=160,0000
170,0000<x<=180,0000
Missing

24. Точечные характеристики

n
m1x1 m 2 x 2 ... m n x n
X
n
x
n
D( x)
i 1
i
2
X mi
n
( x) D( x)
xm
i 1
i
n
i

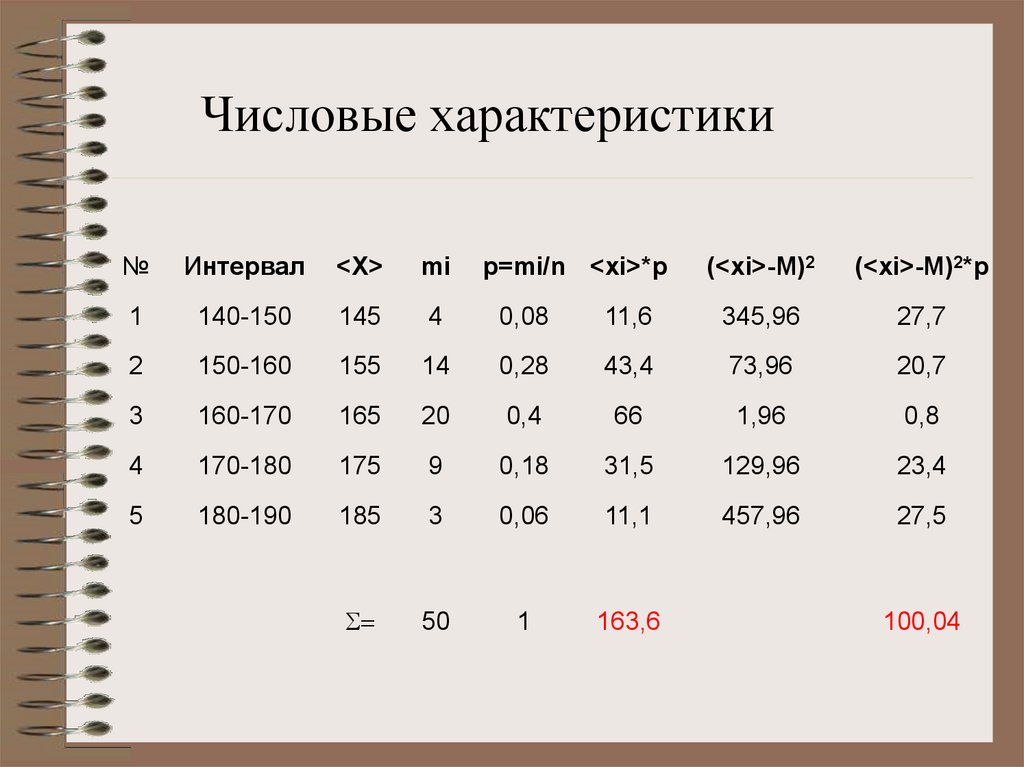
25.

Числовые характеристики
№
Интервал
<X>
mi
p=mi/n <xi>*p
(<xi>-M)2
(<xi>-M)2*p
1
140-150
145
4
0,08
11,6
345,96
27,7
2
150-160
155
14
0,28
43,4
73,96
20,7
3
160-170
165
20
0,4
66
1,96
0,8
4
170-180
175
9
0,18
31,5
129,96
23,4
5
180-190
185
3
0,06
11,1
457,96
27,5
S
50
1
163,6
100,04

26.

X 163,6 см
D(X)=100
σ=10 см

27. Числовые характеристики статистического распределения

1 n
M [ X ] 184.89
Среднее
M [ X ] X (i )
n
i 1
дисперсия
1 n
D[ X ] ( X (i ) M [ X ]) 2
n i 1
D[ X ] 10.55
Свойства точечных оценок:
Оценка называется несмещённой, если ее математическое
ожидание равно оцениваемому параметру генеральной
совокупности
Оценка называется эффективной, если она обладает минимальной
дисперсией среди всех возможных несмещенных точечных оценок.
Оценка называется состоятельной, если она по вероятности с
увеличением объема выборки n стремится к параметру генеральной
совокупности

28.

• Доверительный интервал для роста студентов
с вероятностью p=0,95 ( =0,05);
• M(x)=163,6 см, σ=10 см
Δх=1,96 10 20 см
Следовательно, рост студентов находится в
интервале: 163,6-20<x<163,6+20=
143,6 см<x<183,6 см

29. РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА:

Основная литература:
Павлушков И.В. Основы высшей
математики и математической статистики.
М., ГЭОТАР-Медиа, 2005, с.251-269.
Ремизов А.Н., Максина А.Г. Сборник задач
по медицинской и биологической физике.
М., Дрофа, 2001.
Учебно–методические пособия:
Шапиро Л.А., Шилина Н.Г. Руководство к
практическим занятиям по медицинской и
биологической статистике Красноярск:
ООО «Поликом». – 2003.