Похожие презентации:
Java. Массивы
1.
JavaМассивы
2.
МассивыМассив – это группа однотипных элементов,
имеющих общее имя и расположенных в
памяти рядом.
Особенности:
• все элементы имеют один тип
• весь массив имеет одно имя
• все элементы расположены в памяти друг
за другом
Примеры:
• список учеников в классе
• школы в городе
• данные о температуре воздуха за год
2
3.
Массивыa
НОМЕР
массив
0
1
5
10
a[0]
a[1]
22
15
15
элемента массива
(ИНДЕКС)
3
4
20
25
ЗНАЧЕНИЕ
a[2]
a[3]
элемента
a[4]
массива
ЗНАЧЕНИЕ
элемента массива: 15
!
a[2]
НОМЕР (ИНДЕКС)
элемента массива: 2
Нумерация элементов массива в Java
начинается с НУЛЯ!
3
4.
Определение массиватип[] имяМассива = new тип[количество элементов];
для объявленного имениМассива, зарезервируем
память при помощи ключевого слова new.
Примеры:
int[] myFirstArray = new int[15];
double[] an = new double[in.nextInt()];
Как получить длину массива в Java?
int arrLength = ИМЯ МАССИВА.length;
Как получить индекс последнего элемента
массива?
int lastElem = arr[arr.length - 1];
5.
Объявление массивовЕще примеры:
int[] cats = new int[6];
cats[3] = 5;
cats[5] = 7;
С присвоением начальных значений:
int[] arr = {0, 1, 2, 3, 4};
double[] arrDouble;
arrDouble = {3.14, 2.71, 0, -2.5, 99.123};
!
Все численные типы инициализируются
нулями; boolean – false, остальные типы null
5
6.
Заполнение массиваЗаполнение массива числами, вводимыми с
клавиатуры.
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int[] arr = new int[n];
for (int i = 0; i < n; i++){
arr[i] = in.nextInt();
}
Заполнение массива квадратами.
int n = in.nextInt();
int[] myFirstArray = new int[n];
for(int i = 0; i < n; i++){
myFirstArray[i] = i*i;
7.
Как заполнить массив случайными числами?for(int i = 0; i < arr.length; i++){
arr[i] =(int) round( random() * 100);
System.out.print(arr[i] + " ");
}
Вывод элементов массива
for (int i = 0; i < n; i++) {
System.out.print(arr[i] + " ");
}
Нахождение суммы элементов.
int sum = 0;
for(int i = 0; i < arr.length; i++){
sum += arr[i];
}
8.
Задача №112279. Чётные и нечётныеНапишите программу, которая заполняет массив из N элементов
случайными целыми числами в диапазоне [ A , B ] и определяет
количество чётных и количество нечётных элементов этого
массива.
int a = in.nextInt();
int b = in.nextInt();
int n = in.nextInt();
int[] arr = new int[n+1];
int count=0;
for(int i = 0; i < arr.length; i++){
arr[i] =(int)round( random() *(b-a))+ a;
if (arr [i]%2 == 0) count++;
}
System.out.println(count +" "+ (n-count));
9.
Максимальный элементint max = Integer.MIN_VALUE;
for (int i = 0; i < n; i++) {
arr[i] = in.nextInt();
if (arr[i] > max) {
max = arr[i];
}
}
System.out.println(max);
Дополнение: min = Integer.MAX_VALUE;
10.
Максимальный элементДополнение: как найти номер максимального
элемента?
max = a[0]; // пока A[0]– максимальный
iMax = 0;
for (int i=1; i < n; i++ ) //проверяем остальные
if ( a[i] > a[iMax]
max
) { // нашли новый
max = a[i];
// запомнить a[i]
iMax = i;
// запомнить i
}
?
Как упростить?
По номеру элемента iMax всегда можно найти его
значение a[iMax]. Поэтому везде меняем max на
a[iMax] и убираем переменную max.
10
11.
МассивыЧасть II
Обработка массивов
12.
Удаление элементадан массив А:
3 5 6 8 12 15 17 18 20 25
Элемент который нужно
удалить
k =3
2. 3 5 6 12 15 17 18 20 25 25
1.
int k = in.nextInt();
for (int i = k; i < n-1 ; i++) {
arr[i] = arr[i+1];
}
n--;
13.
Вставка элементадан массив А:
3 5 6 8 12 15 17 18 20 25
0
Элемент на место которого
нужно вставить новый
k =3
2. 3 5 6 x 8 12 15 17 18 20 25
1.
int k = in.nextInt();
for (int i = n; i > k ; i--) {
arr[i] = arr[i-1];
}
n++;
14.
Циклический сдвиг I способ0
1
2
3
…
N-2 N-1
3 5 8 1 … 9 7
5 8 1 … 9 7 3
Алгоритм:
1. определить сколько раз необходимо
произвести одноэлементный сдвиг k %= n;
2. k раз применить одноэлементный сдвиг
Одноэлементный сдвиг :
temp = a[0];
for ( i = 0; i < n-1; i ++) {a[i] = a[i+1];}
a[n-1] = temp;
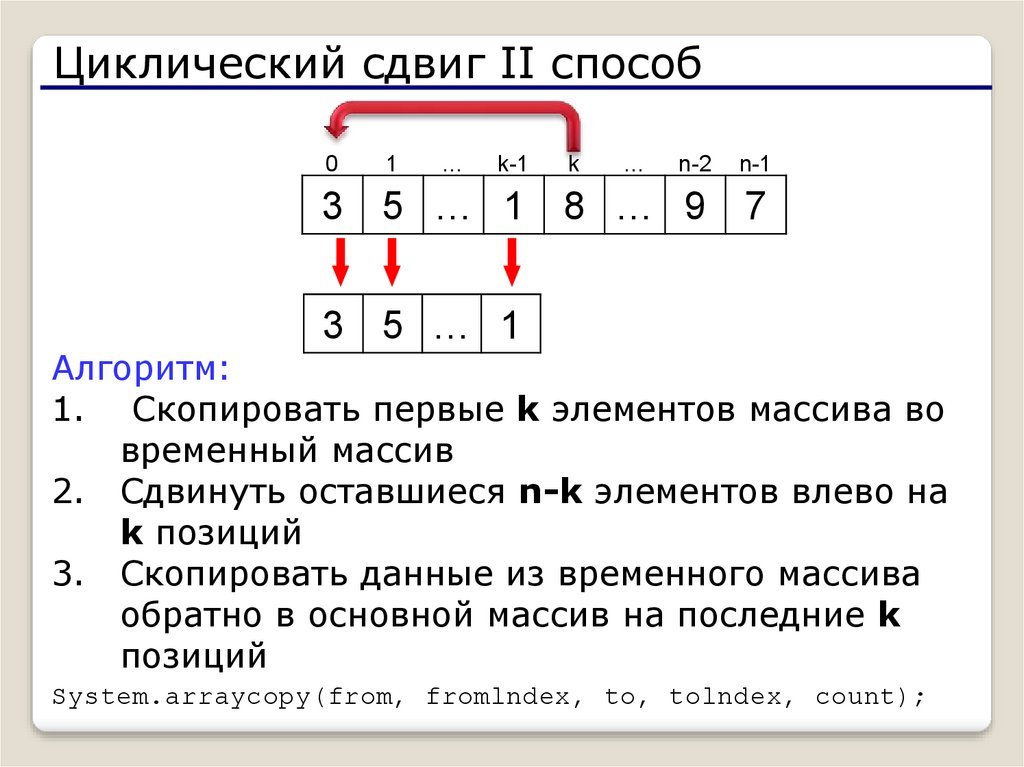
15.
Циклический сдвиг II способ0
1
…
k-1
k
…
n-2
n-1
3 5 … 1 8 … 9 7
3 5 … 1
Алгоритм:
1. Скопировать первые k элементов массива во
временный массив
2. Сдвинуть оставшиеся n-k элементов влево на
k позиций
3. Скопировать данные из временного массива
обратно в основной массив на последние k
позиций
System.arraycopy(from, fromlndex, to, tolndex, count);
16.
Реверс массиваЗадача: переставить элементы массива в обратном
порядке (выполнить инверсию).
0
1
…
N-2 N-1
3 5 … 9 7
0
1
…
N-2 N-1
7 9 … 5 3
сумма индексов N-1
Алгоритм:
поменять местами a[0] и a[n-1], a[1] и a[n-2],…
Псевдокод:
for ( i = 0; i < n / 2; i++ )
// a[i]
a[n-1-i]
16
17.
Циклический сдвиг III способАлгоритм:
1. отразить элементы массива(0, k-1)
2. отразить элементы массива (k, n-1)
3. отразить элементы массива (0, n-1)
18.
Циклический сдвиг отражениями0
L
R
left = 0; right = k - 1;
count = (right - left+1)/2;
for(int i = 0; i < count; i++) {
temp = arr[left + i];
arr[left + i] = arr[right - i ];
arr[right - i ] = temp ;
}
left = k; right = n - 1;
count = (right - left+1)/2;
***
left = 0; right = n - 1;
count = (right - left+1)/2;
***
N-1
***
18
19.
public static void main(String[] args) throwsIOException {
Scanner sc = new Scanner(new
File("input.txt"));
int[] a = new int[100000];
int n = 0;
while (sc.hasNextInt()) {
a[n] = sc.nextInt();
n++;
}
sc.close();
PrintWriter output = new PrintWriter(new
File("output.txt"));
for (int i = 0; i < n; i++) {
output.print(a[i] + " ");
}
output.close();
}
20.
МассивыЧасть III
Поиск в массиве
21.
indexX – номернужного
в массиве
indexX = -1; // пока не нашли элемента
...
Линейный поиск
for ( i = 0; i < n;i ++) // цикл по всем элементам
if ( a[i] == X )
// если нашли, то ...
indexX = i;
// ... запомнили номер
if (indexX < 0) System.out.print("Не нашли...")
else
System.out.print (indexX );
?
Что можно улучшить?
Улучшение: после
того, как нашли X,
выходим из цикла.
indexX = -1;
for ( i = 0; i < n; i ++)
if ( a[i] == X ) {
indexX = i;
break; //выход из цикла
break;
}
21
22.
Двоичный поискx=7
1. Выбрать средний элемент
a[middle] и сравнить с X.
2. Если x = a[middle],
нашли (выход).
3. Если x < a[middle],
искать дальше в первой
половине.
4. Если x > a[middle],
искать дальше во второй
половине.
1
1
1
2
2
2
3
3
3
4
4
4
5
5
5
6
6
7
7
7
8
8
8
8
9
9
9
10
10
10
11
11
11
12
12
12
13
13
13
14
14
14
15
15
15
16
16
16
4
X<8
X>4
X>6
6
6
23.
Двоичный поиск0
L
m
R
N-1
iX = -1;
left = 0; right = n-1; //ищем от A[0] до A[N-1]
while ( left<=right ){
номер среднего элемента
middle = (right + left) / 2;
if (x == a[middle]) {
если нашли …
iX = middle ;
break;
выйти из цикла
сдвигаем границы
}
if (x < a[middle]) right = middle - 1;
else left = middle + 1;
}
if (iX < 0) System.out.print("Не нашли...")
else
System.out.print (iX);
23
24.
Задача №672. Провода.Входные данные
Дано N проводов длиной L1, L2, ..., LN сантиметров. Требуется с
помощью разрезания получить из них K равных отрезков как можно
большей длины. В первой строке находятся числа N и К. В
следующих N строках - L1, L2, ..., LN, по одному числу в строке.
int l = 0, r = sumL /k + 1, s; //sumL- сумма
длин проводов
while (l < r - 1) {
int m = (l + r) / 2;
for (int i = 0; i < N; i++)
s += arr[i] / m;
if (s >= k)
l = m;
else
r = m;
}
System.out.println(l);
25.
Слияние двух упорядоченных массивов0
1
2
3
4
5
6
1 3 3 5 7 56 70
0
1
2
3
2
4
6
8 95
9
10
4
0
1
2
3
4
5
6
7
8
11
1
2
3
3
4
5
6
7
8 56 70 95
Алгоритм
1.Создаем массив с длиной n+m элементов.
2. Заполняем массив c следующим образом:
• Сравниваем между собой a[i] и b[j]
• В массив с помещаем меньший из них
• Индексы увеличиваем на 1
3. Повторяем шаг 2 до тех пор пока не
достигнут конец одного из массивов
26.
int n = in.nextInt();int m = in.nextInt();
int[] a = new int[n];
int[] b = new int[m];
int[] c = new int[n + m];
{заполнение массивов a и b}
int iA=0; iB=0; iC=0;
while (iA< n && iB< m){
if (a[iA] < b[iB])
c[iC++] = a[iA++];
else
c[iC++] = b[iB++];
}
for (int i=iA; i<n; i++ )
c[iC++] = a[i];
for (int i=iB; i<m; i++ )
c[iC++] = b[i];
27.
МассивыЧасть IV
Квадратичные
сортировки массивов
28.
СортировкаСортировка – это расстановка элементов массива
в заданном порядке (по возрастанию, убыванию,
последней цифре, сумме делителей, …).
Задача: переставить элементы массива в порядке
возрастания.
сложность
O(N2)
Алгоритмы:
• простые и понятные, но неэффективные для больших
массивов
метод пузырька
сложность O(N·logN)
метод выбора
время
• сложные, но эффективные
«быстрая сортировка» (Quick Sort)
сортировка «кучей» (Heap Sort)
сортировка слиянием
пирамидальная сортировка
O(N2)
O(N·logN)
28
N
29.
Программа (1-ый проход)0
1
…
N-2
N-1
5
2
…
6
3
сравниваются пары
a[0] и a[1],
a[1] и a[2]
…
a[n-2] и a[n-1]
a[j] и a[j+1]
for( j = 0; j < n-1 ; j++ )
if ( a[j] > a[j+1] ) {
temp = a[j];
a[j] = a[j+1];
a[j+1] = temp;
}
29
30.
Программа (следующие проходы)2-ой проход
0
1
…
N-2
N-1
!
a[n-1] уже на своем
месте!
for ( j = 0; j < n-2 ; j++ )
if ( a[j] > a[j+1] ) {
temp = a[j];
a[j] = a[j+1];
a[j+1] = temp;
}
(i+1)-ый проход
for (int j = 0; j < n - i - 1; j++)
...
30
31.
Программа сортировки “пузырьком”public static void main(String[] args){
int n = in.nextInt();
// описать, заполнить массив
// вывести исходный массив
for (int i = 0; i < n - 1; i++){
for (int j = 0; j < n - i - 1; j++)
{
if (a[j] > a[j + 1])
Меняем
{
a[j] и a[j+1]
temp = a[j];
a[j] = a[j + 1];
a[j + 1] = temp;
}
}}
// вывести полученный массив
}
31
32.
Программа сортировки “пузырьком”int n = in.nextInt();
// описать, заполнить массив
boolean flag;
int i = 0;
do{
flag = false;
for (int j = 0; j < n - i - 1; j++) {
if (mass[j] > mass[j + 1]) {
flag = true;
temp = mass[j];
mass[j] = mass[j + 1];
mass[j + 1] = temp;
}
}
i++;
} while (flag );
32
33.
Сортировка подсчетомАлгоритм:
1. Создаем дополнительный массив count. Его
длина зависит от диапазона чисел
исходного массива.
2. Для каждого a[i] увеличить count[a[i]] на
единицу.
3. Распечатываем массив count следующим
образом: i-й элемент печатаем count[i] раз
for (int i = 0; i < n; i++) {
count[a[i]]++;
}
for (int i = 0; i < count.length; i++)
for (int j = 0; j < count[i]; j++)
System.out.print(i + " ");
34.
Задача №3044. Сортировка подсчетомВходные данные
На вход программе сначала подается значение n ≤ 100000 –
количество элементов в массиве. В следующей строке входных
данных расположены сами элементы массива – целые числа, по
модулю не превосходящие 10000.
int n = in.nextInt();
int[] a = new int[n];
{заполнение массива a}
int[] count = new int[20001];
for (int i = 0; i < n; i++) {
count[a[i] + 10000]++;
}
for (int i = 0; i < count.length; i++) {
for (int j = 0; j < count[i]; j++) {
System.out.print(i - 10000 + " ");
}
}
35.
Сортировка “выбором”Алгоритм (на примере сортировки по
убыванию)
1.
2.
3.
4.
Выбрать минимальный (максимальный)
элемент массива
Поменять его местами с последним
(первым) элементом: теперь самый
маленький (большой) на своем месте
Уменьшить количество
рассматриваемых элементов на 1
Повторить действия 1-3 с
оставшимися элементами (теми,
которые еще не стоят на своих
местах)
35
36.
Сортировка “выбором”int iMax;
for (int i = 0; i <= n-1; i++) {
iMax = i;
for (int j = i+1; j < n; j++) {
if (mass[j] > mass[iMax]){
iMax = j;
}
}
temp = mass[iMax];
mass[iMax] = mass[i];
mass[i] = temp;
}
36
37.
Сортировка “выбором”int iMax;
for (int i = n - 1; i >= 0; i--) {
iMax = i;
for (int j = i; j >= 0; j--) {
if (mass[j] > mass[iMax]){
iMax = j;
}
}
if (iMax != i){
temp = mass[iMax];
mass[iMax] = mass[i];
mass[i] = temp;
}
}
37
38.
Сортировка вставкойАлгоритм:
1.
На k-ом шаге считаем, что часть массива,
содержащая элементы [0, k-1] уже
упорядочена, то есть
a[0] <= a[1] <= ... <= a [k-1]
2.
Берем k-ый элемент и подбираем для него
место в отсортированном массиве такое,
чтобы после его вставки упорядоченность
не нарушилась. То есть необходимо найти
j, которое удовлетворяло бы условиям:
0<=j<=k-1, a[j] <= a[k] <= a[j+1]
3.
Вставляем элемент a[k] на найденное
место.
39.
Сортировка вставкойАлгоритм:
1. Просматриваем элементы массива
(упорядоченного), двигаясь от конца к
началу массива (то есть от
k-1 до 0)
2. Просматриваем пока не будет выполнено
одно из условий:
a) найдем a[j]<x (будем вставлять между a[j-1]
и a[j]
b) достигнут левый конец упорядоченной части
массива (тогда необходимо х вставить на
нулевое место)
3.
Пока условие 2 не выполнено будем
смещать просматриваемые элементы на 1
позицию вправо, в результате чего в
отсортированной части будет освобождено
место под Х.
40.
for (int i = 1;i < n ;i++) {int j = i; x = a[i]
while (j > 0 && x < a[j - 1]
a[j] = a[j - 1];
j--;
}
a[j] = x;
}
){







































 Программирование
Программирование








