Пилотажно-навигационные параметры. Тема 1.2

1.

Направление 24.03.02
«Системы управления движением и навигация»
Датчики авионики
Тема 1.2 ГОСТ 20058-80. Основные
пилотажно-навигационные параметры.
Системы координат
Тимофеев Константин Николаевич
доц., к. т. н
2022

2.

Литература
1. ГОСТ 20058-80 ДИНАМИКА
ЛЕТАТЕЛЬНЫХ АППАРАТОВ В АТМОСФЕРЕ
2.Авиационные приборы: учеб. пособие /
В.А. Прилепский. – Самара: Изд-во
Самарского университета, 2016. – 316 с.

3.

ГОСТ 20058-80

4.

5.

6.

7.

8.

Основные пилотажнонавигационные параметры

9.

Движение самолета в пространстве состоит из
поступательного и углового движений.
Поступательное движение самолета относительно
заданной системы отсчета О0X0Y0Z0 определяется
линейными координатами:
H – высотой полета,
L – пройденным расстоянием,
Z – боковым отклонением.
9

10.

На рис. изображена система координат OXДYДZД, которая
движется поступательно с центром масс самолета относительно
системы отсчета О0X0Y0Z0.
Рис. Система координат поступательного движения самолета
10

11.

Высоты различают как
- абсолютную (H) – отсчитывается от уровня моря,
- относительную (Hотн) – отсчитывается от выбранного
уровня (от места взлета или посадки), и
-истинную (Hист) – отсчитывается от места, где
находится самолет в текущий момент времени.
11

12.

Угловое положение самолета в пространстве определяется угловыми
координатами
При этом вводится связанная система
координат OXYZ, в которой ось OX направлена по продольной оси
самолета, OY – вертикально вверх, OZ – в сторону правого крыла (рис).
Рис. Угловая система координат движения самолета
12

13.

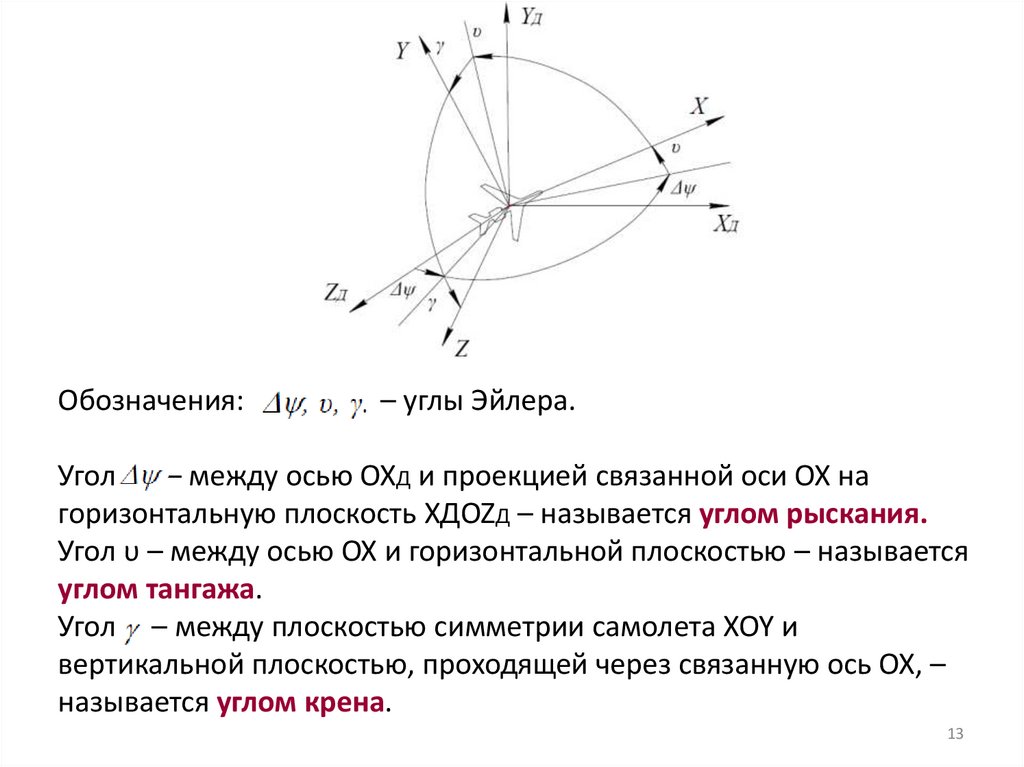
Обозначения:
– углы Эйлера.
Угол
– между осью OXД и проекцией связанной оси OX на
горизонтальную плоскость XДOZД – называется углом рыскания.
Угол υ – между осью OX и горизонтальной плоскостью – называется
углом тангажа.
Угол – между плоскостью симметрии самолета XOY и
вертикальной плоскостью, проходящей через связанную ось OX, –
называется углом крена.
13

14.

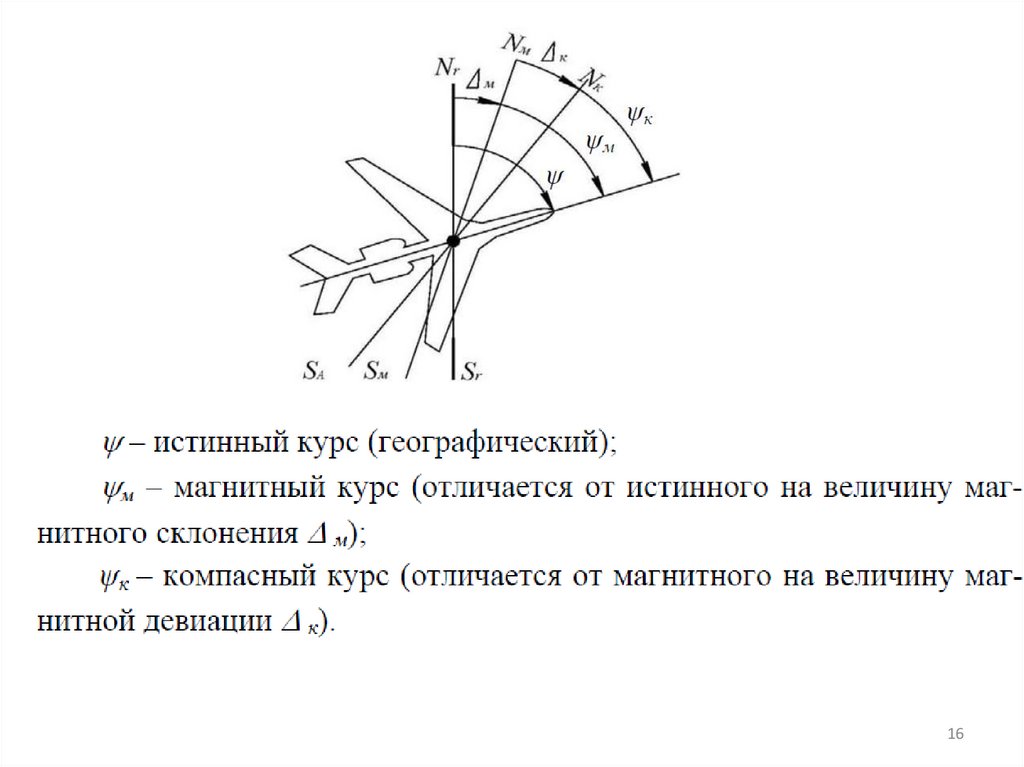
Направление полета самолета относительно земной системы координат определяется курсом ψ самолета: это угол, отсчитывается по
часовой стрелки между направлением меридиана и проекцией продольной оси самолета на плоскость горизонта (рис.).
Рис. Система координат направления полета самолета
14

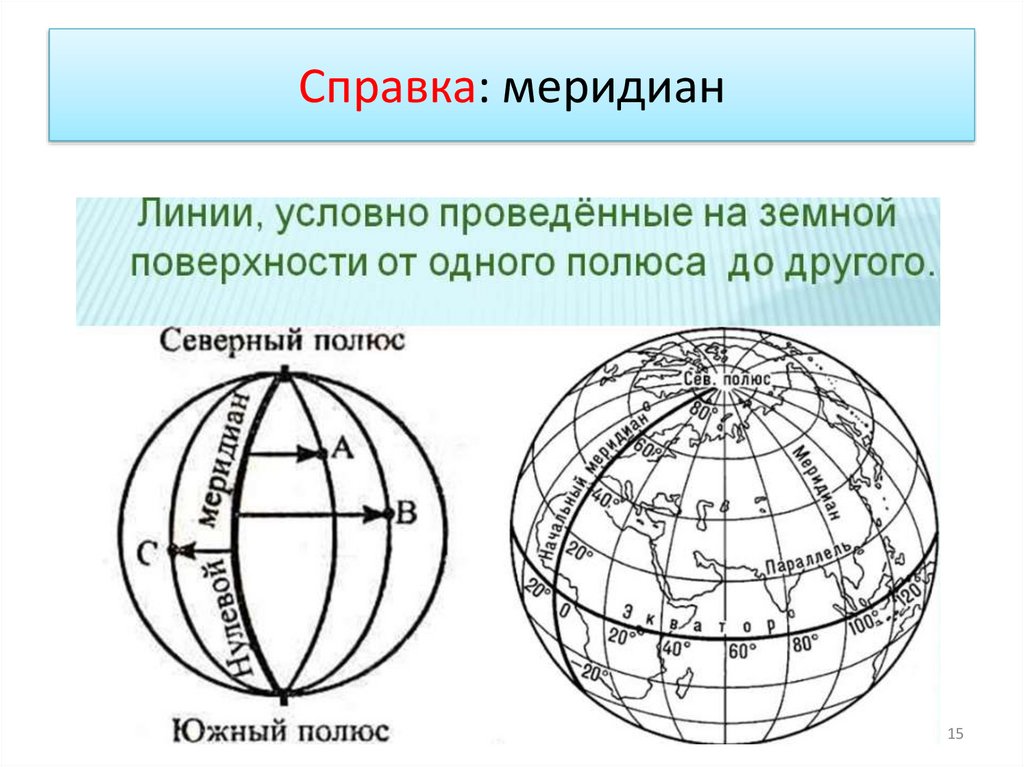
15.

Справка: меридиан
15

16.

16

17.

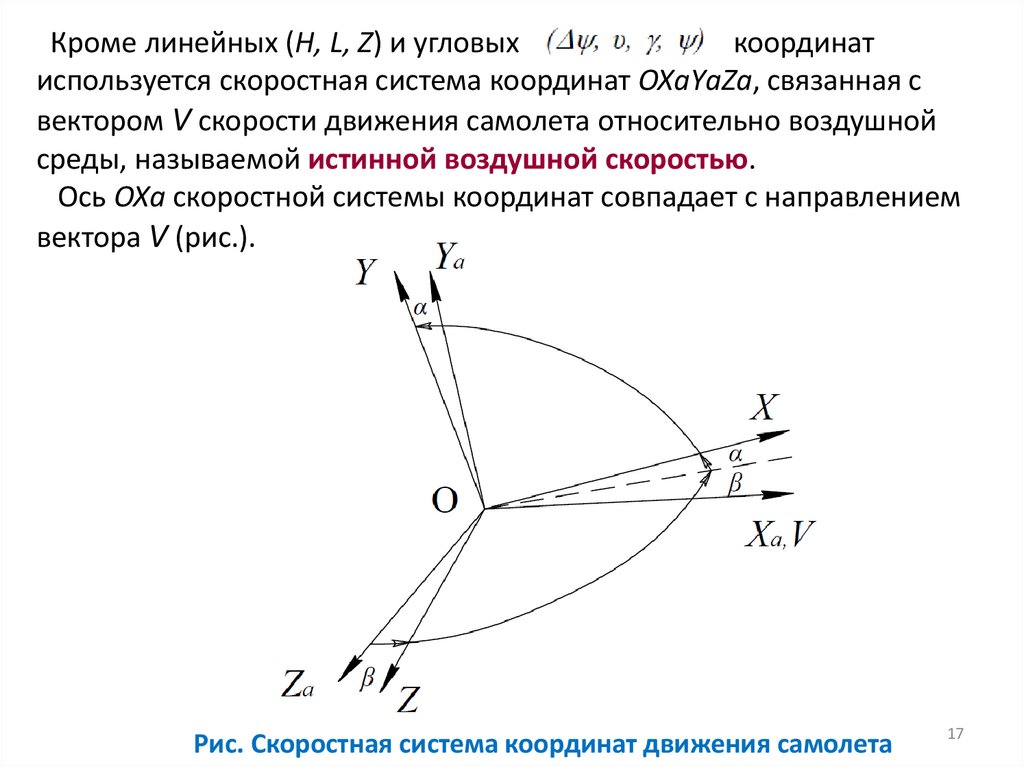
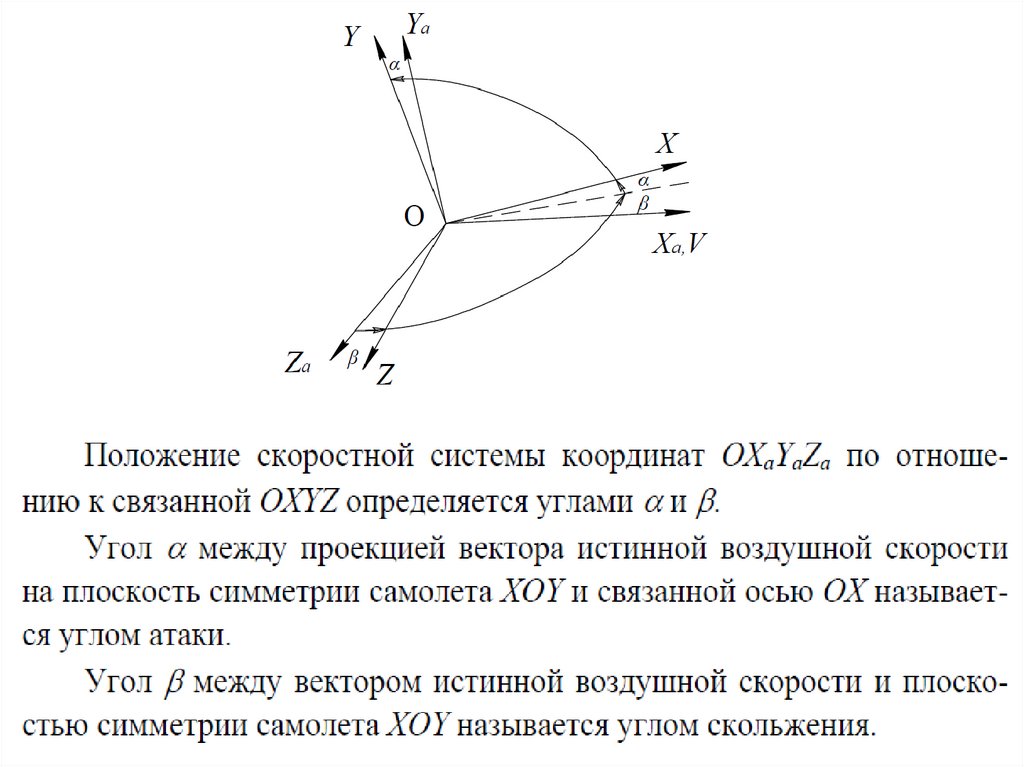
Кроме линейных (H, L, Z) и угловых
координат
используется скоростная система координат OXаYаZа, связанная с
вектором V скорости движения самолета относительно воздушной
среды, называемой истинной воздушной скоростью.
Ось OXа скоростной системы координат совпадает с направлением
вектора V (рис.).
Рис. Скоростная система координат движения самолета
17

18.

18

19.

Также, используются такие скорости полета, как
• индикаторная (приборная),
• путевая и
• вертикальная.
Индикаторная Vи – это истинная воздушная скорость,
приведенная к нормальной плотности воздуха.
Путевая Vп – это горизонтальная составляющая скорости
самолета относительно земли. При наличии ветра путевая
скорость равна геометрической сумме горизонтальных
составляющих истинной воздушной скорости и скорости ветра.
Вертикальная скорость – это вертикальная составляющая
скорости движения самолета относительно земли.
19

20.

20

21.

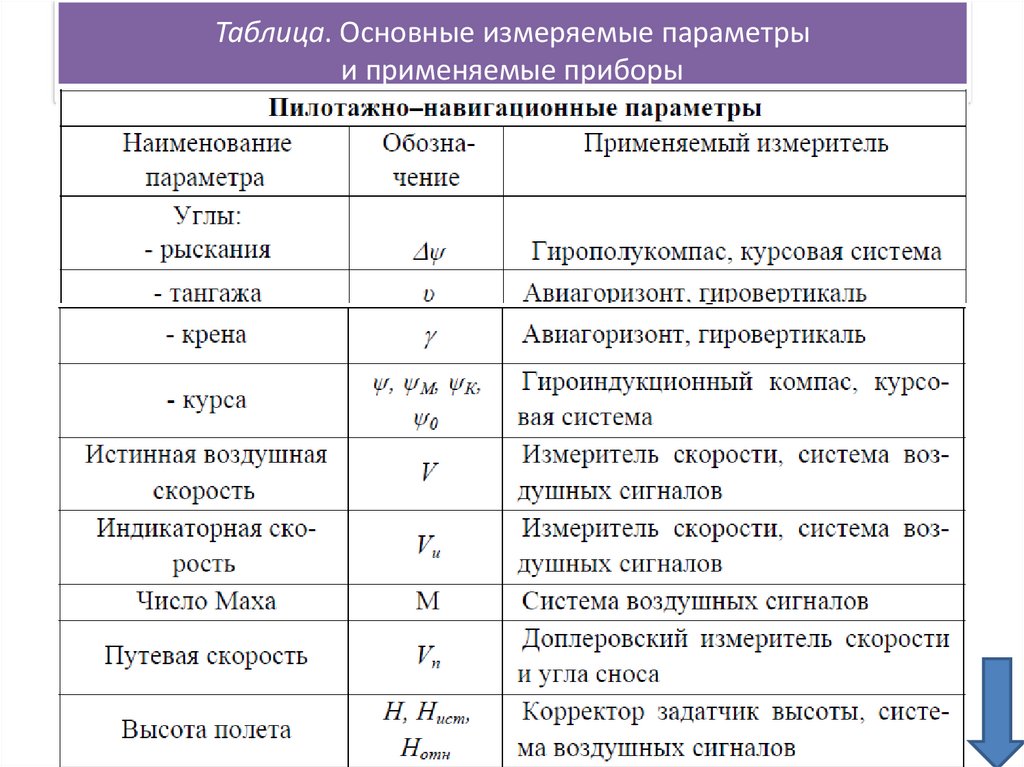
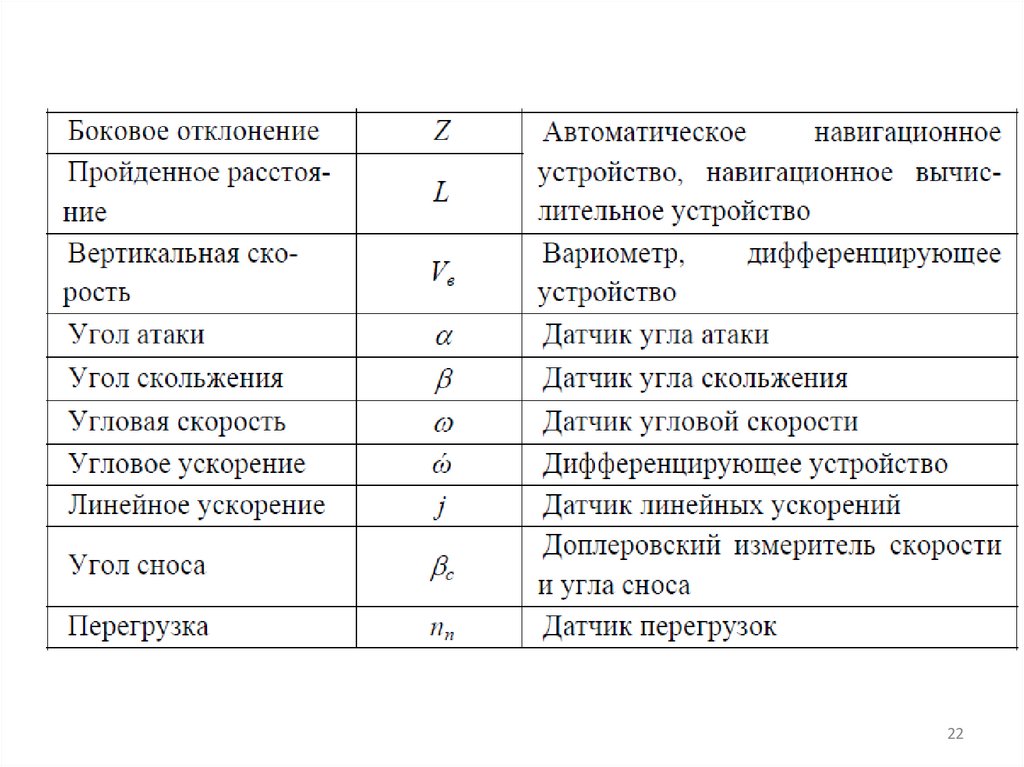
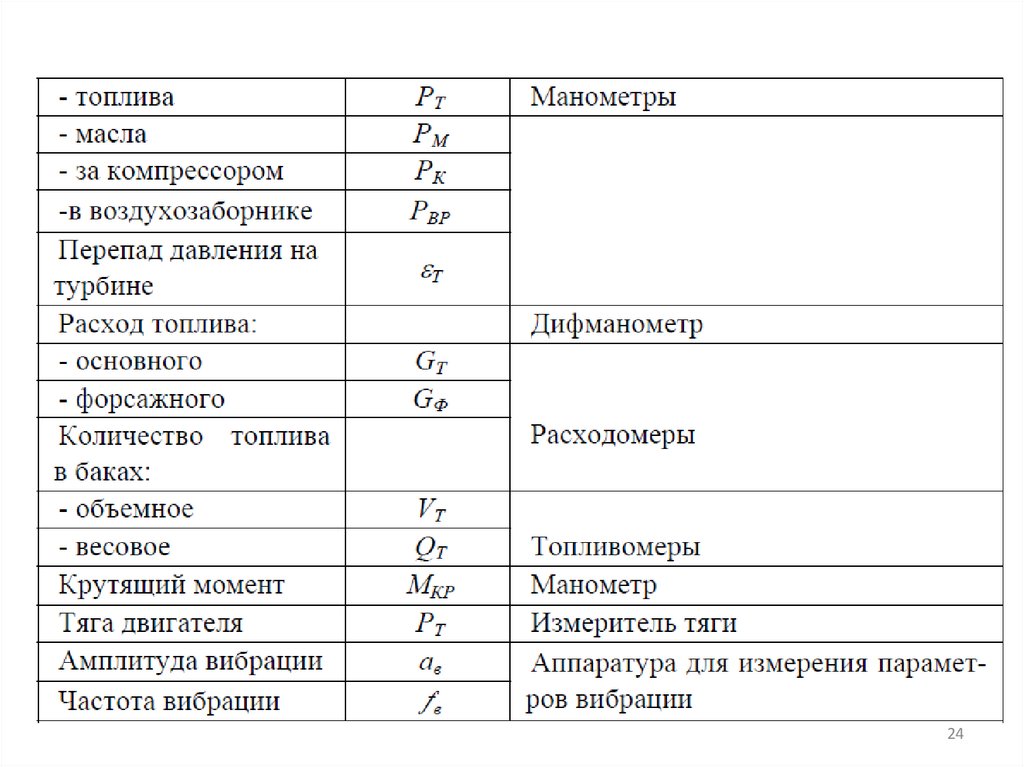
Таблица. Основные измеряемые параметры
и применяемые приборы
21

22.

22

23.

23

24.

24

25.

Таблица. Параметры окружающей среды
25

26.

Системы координат,
применяемые в воздушной
навигации

27.

Терминология. Траектория и линия пути
Пространственное место самолета (ПМС) – точка в
пространстве, в которой в данный момент времени находится
центр масс ВС.
Место самолета (МС) – проекция ПМС на земную поверхность
Траектория – линия, описываемая ПМС при его движении.
Линия пути – линия, описываемая МС при его движении
(проекция траектории на земную поверхность).
Линия заданного пути (ЛЗП) - это линия, по которой
должно перемещаться МС в соответствии с планом полета
линия фактического пути (ЛФП) – по которой оно
перемещается на самом деле в данном полете.
27

28.

При работе с наземными и техническими средствами
самолетовождения приходится использовать различные
системы координат, основными из которых являются
географическая, ортодромная, полярная системы
координат.
Географические системы координат.
Достоинством таких систем является то, что они являются
едиными для всей Земли: координаты точки однозначно
определяют ее местоположение.
Но они неудобны для определения местоположения ВС
относительно заданной траектории. Например, зная широту
и долготу, невозможно сразу сказать, находится ВС на ЛЗП
или уклонилось от нее.
28

29.

Бывает 3 вида географических координат:
1) На эллипсоиде задается система геодезических координат (сетка
меридианов и параллелей) и координаты любой точки
определяются геодезическими координатами (широтой B и
долготой L).
29

30.

2) Если очень высокая точность решения навигационных задач не
требуется, то Землю можно рассматривать как сферу. В этом случае
используется нормальная сферическая система координат, полюсы
которой совпадают с географическими полюсами нашей планеты, т.е.
точками, в которых оси вращения Земли пересекает ее поверхность.
Система координат на сфере строится с помощью больших кругов.
3) Астрономическая система координат, в которой астрономическая
широта - угол, заключенный между плоскостью экватора и отвесной
линией в данной точке.
Различия между геодезическими, нормальными
сферическими и астрономическими координатами невелико не более нескольких угловых минут. Поэтому, когда различие между
этими системами координат не грает роли, их объединяют общим
названием географических координат.
30

31.

Ортодромические системы координат
Ортодро́ мия, ортодро́ ма (от др.-греч. «ὀρθός» — «прямой» и
«δρόμος» — «бег», «путь») в геометрии — кратчайшая линия
между двумя точками на поверхности вращения, частный
случай геодезической линии.
В навигации ортодромия — название кратчайшего
расстояния между двумя точками на поверхности Земли.
В самолётовождении, где Земля принимается за шар,
ортодромия представляет собой дугу большого круга.
Через две точки на земной поверхности, расположенные
не на противоположных концах одного диаметра Земли,
можно провести только одну ортодромию.
31

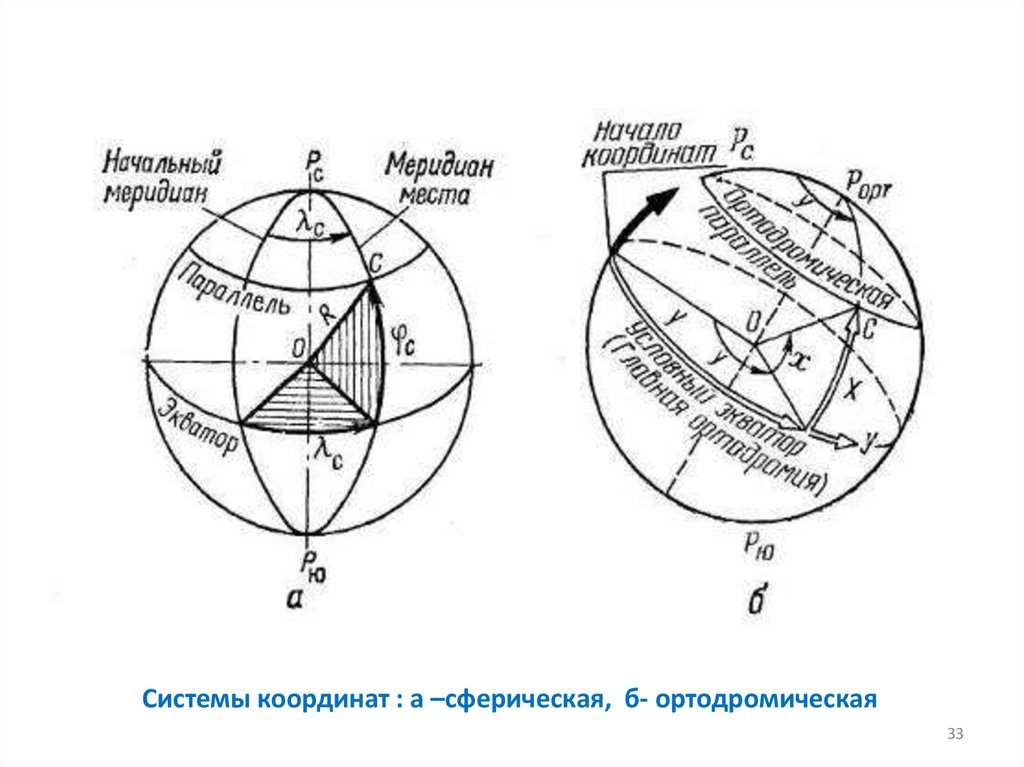
32.

Ортодромические системы координат являются
обобщающим случаем сферических координат.
Вместо «настоящих» меридианов и параллелей, как в
географических системах, используются меридианы и
параллели условные, наиболее удобно расположенные
относительно маршрута полета.
В ортодромических системах осями являются две ортодромии,
перпендикулярные друг другу в начале системы координат.
В зависимости от того, как направлены эти оси и где
расположено начало системы координат, различают две их
группы: главноортодромическая и частноортодромическая.
32

33.

Системы координат : а –сферическая, б- ортодромическая
33

34.

Эта система координат нашла широкое применение в современных
устройствах счисления пути. В ортодромической системе координат
одна из дуг большого круга (обычно совмещаемая с линией
заданного пути), играет роль условного экватора.
Другая дуга большого круга, лежащая в плоскости
перпендикулярной плоскости условного экватора (обычно это
дуга, проходящая через исходный пункт маршрута (ИПМ), играет роль условного начального меридиана.
На различных полетных картах ортодромия на расстояниях до
1000—1200 км практически совпадает с прямой.
34

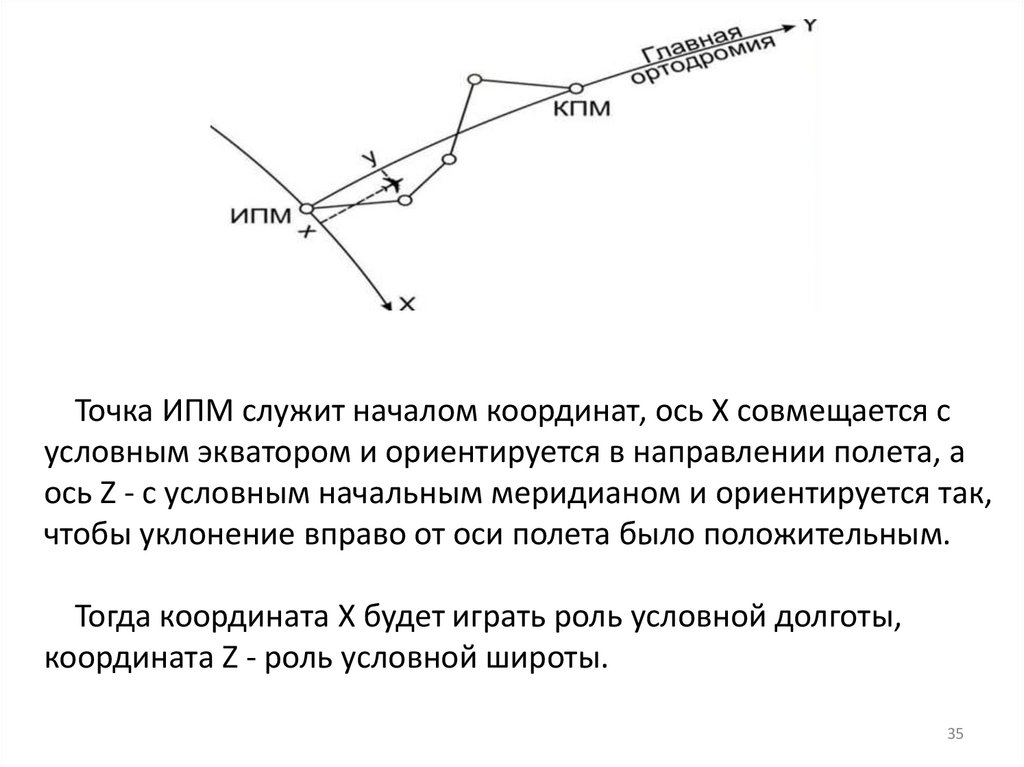
35.

Точка ИПМ служит началом координат, ось X совмещается с
условным экватором и ориентируется в направлении полета, а
ось Z - с условным начальным меридианом и ориентируется так,
чтобы уклонение вправо от оси полета было положительным.
Тогда координата X будет играть роль условной долготы,
координата Z - роль условной широты.
35

36.

Особенностью системы является то, что вблизи условного
экватора условные меридианы и параллели образуют
практически прямоугольную сетку, что позволяет при
незначительных отклонениях от ортодромии не учитывать
сферичность Земли и от решения задач на сфере переходить к
решению задач на плоскости.
Важным преимуществом этой системы является возможность
ее применения в любых районах земного шара.
Ортодромическая система координат наиболее полно
соответствует условиям применения гироскопических
курсовых приборов, обеспечивающих полет по
ортодромической линии пути.
36

37.

Для повышения точности самолетовождения и упрощения
решения многих навигационных задач полеты необходимо
выполнять по ортодромии.
Ортодромия пересекает меридианы под разными углами, и
полет по этой линии с помощью магнитного компаса
невозможен.
Для полета по ортодромии определяются ортодромические
путевые углы относительно опорных меридианов.
По ортодромическим путевым углам рассчитываются
ортодромические курсы с учетом влияния ветра, которые
выдерживаются с помощью специальных курсовых устройств,
таких, как курсовая система (ТКС-П), ГМК -1, гирополукомпас
ГПК-52 астрономический компас ДАК-ДБ-5Б и др.
37

38.

При полете самолета с ортодромическим или условным
курсом линия фактического пути на карте изображается
прямой линией, т. е. так же, как и линия заданного пути.
Положение самолета относительно линии заданного пути
(ЛЗП) в этом случае можно точно определить по пеленгам
радиотехнических средств, расположенных в поворотных
пунктах маршрута.
Сравнивая ортодромический пеленг с ортодромическим
путевым углом, можно безошибочно установить наличие
уклонения самолета от ЛЗП.
38

39.

Полярная система координат
В полярной системе координат определяются полярные
координаты объекта (самолета, радиостанции, ориентира и
т. д.) относительно какой-либо заранее оговоренной или
подразумеваемой точки (как бы полюса этой системы
координат).
Этой точкой обычно бывает радиомаяк или самолет.
Нельзя говорить о полярных координатах радиомаяка
относительно самого радиомаяка или о координатах
самолета относительно самого себя. Поэтому, когда говорят
о полярных координатах ВС, начало координат
подразумевается в другой точке (обычно, радиомаяке), и
наоборот, полярные координаты радиомаяка могут быть
указаны относительно самолета.
39

40.

Координатами в полярной системе являются
дальность и пеленг
Дальность (D) – расстояние от начала системы координат до
объекта (точки).
Различают наклонную дальность, измеренную по прямой от
радиомаяка до рассматриваемой точки (например, до МПС) и
горизонтальную, от радиомаяка до точки на земной
поверхности под самолетом, то есть до МС.
Наклонная дальность всегда больше горизонтальной, а
совпадает с ней, когда рассматриваемая точка (например,
самолет) находится на поверхности земли.
Наклонная дальность непосредственно измеряется
радионавигационными системами.
Горизонтальная дальность используется для определения
МС на карте.
40

41.

Пеленг – угол в горизонтальной плоскости между
направлением, принятым за начало отсчета и направлением
на объект.
Пеленг отсчитывается по часовой стрелке и измеряется от 0
до 360°.
Если объект находится к северу, его пеленг составляет 0°,
если к востоку – 90°, к югу – 180°, а к западу – 270°.
Часто вместо специфического навигационного термина
«пеленг» используется общепринятое (например, в
географии) слово «азимут».
41

42.

42

43.

Инерциальная система координат
Все существующие системы отсчета делятся на инерциальные
и на неинерциальные.
Инерциальная система отсчета (ИСО) лежит в основе
механики Ньютона.
В системах отсчета, строящихся по типу инерциальности,
свободные тела движутся прямолинейно и равномерно (при
отсутствии внешнего воздействия), либо не движутся совсем.
Применение Земли в качестве ИСО, несмотря на
приближённый его характер, широко распространено в
навигации.
43

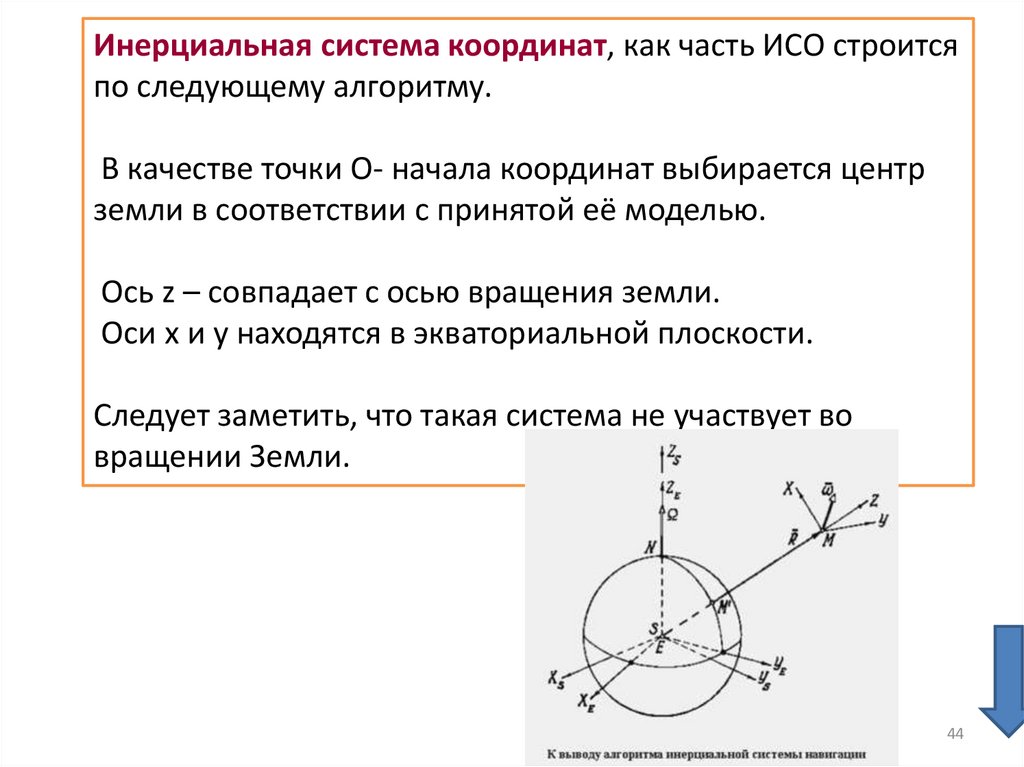
44.

Инерциальная система координат, как часть ИСО строится
по следующему алгоритму.
В качестве точки O- начала координат выбирается центр
земли в соответствии с принятой её моделью.
Ось z – совпадает с осью вращения земли.
Оси x и y находятся в экваториальной плоскости.
Следует заметить, что такая система не участвует во
вращении Земли.
44

45.

45

46.

46