Похожие презентации:
Центр тяжести
1.
Национальныйисследовательский
Томский политехнический
университет
Комплект слайд-лекций для технических
специальностей университета
2.
доктор физико-математических наук,профессор Отделения общетехнических дисциплин
Школы базовой инженерной подготовки
Томского политехнического университета
3.
Центр тяжести и центр масс4. ЦЕНТР ТЯЖЕСТИ
zΔVi
Pi
0
x
y
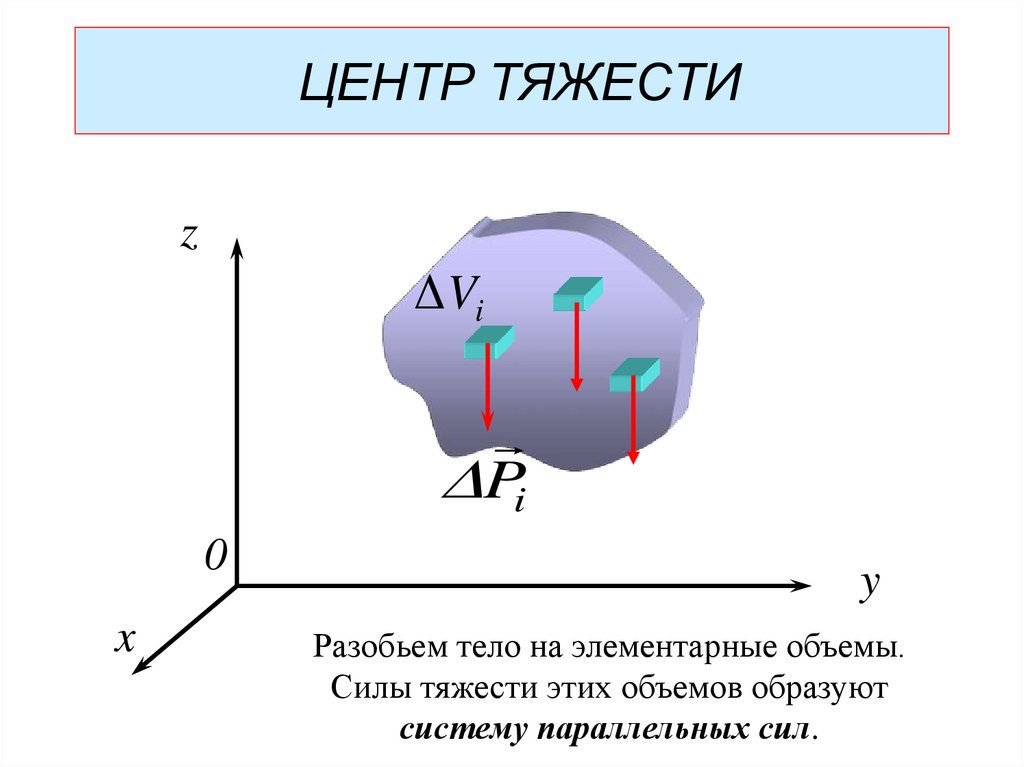
Разобьем тело на элементарные объемы.
Силы тяжести этих объемов образуют
систему параллельных сил.
5.
ЦЕНТР ТЯЖЕСТИz
ΔVi
ri
Pi
0
x
y
Положение каждого элементарного объема
характеризуется радиус-вектором ri
6.
Сила тяжести элементарного объема:Pi i gi ΔVi
(1)
i - удельная плотность тела
g i -ускорение свободного падения в данной
точке
7.
Положение центра тяжести тела определяетсярадиус-вектором:
ΔPi ri
n
rc
i 1
n
ΔP
i 1
i
8.
Положение центра тяжести тела определяетсярадиус-вектором:
n
rc
ΔPi ri
i 1
n
ΔPi
i 1
n
i gi ΔVi ri
i 1
n
i gi ΔVi
i 1
(2)
9.
Если поле силы тяжести однородное:g const
то
n
rc
i ΔVi ri
i 1
n
i ΔVi
i 1
n
Δmi ri
i 1
n
Δmi
i 1
В этом случае центр тяжести и центр
масс совпадают
(3)
10.
Центром масс называется центр параллельныхсил, пропорциональных массе
11.
Центром масс называется центр параллельныхсил, пропорциональных массе
Если требуется определить центр масс дискретной
системы материальных точек:
m1r1 m2 r2 .... mn rn
rc
m1 m2 .... mn
12.
Для сплошных тел:1
rc
r dm
m m
(4)
13.
Для сплошных тел:1
rc
r dm
m m
(4)
Для сплошных и однородных тел:
const
1
rc
r
dV
V V
(5)
14.
В скалярном виде для сплошныходнородных тел:
1
xc
xdV
V V
1
yc
ydV
V V
1
zc
zdV
V V
(6)
15.
Для пластин:V Sh,
h const
h – толщина, S - площадь пластины
1
rc
r dS
S S
1
xc
xdS
S S
(7)
1
(8)
yc
ydS
S
S
16.
Для материальных линий:V al ,
a const
а – площадь поперечного сечения
материальной линии
1
rc r dl
l l
1
xc xdl
l l
1
yc ydl
l l
(9)
1
zc zdl (10)
l l
17. Методы вычисления центра тяжести:
• Метод симметрии• Метод разбиения
• Метод отрицательных масс
18. Метод симметрии
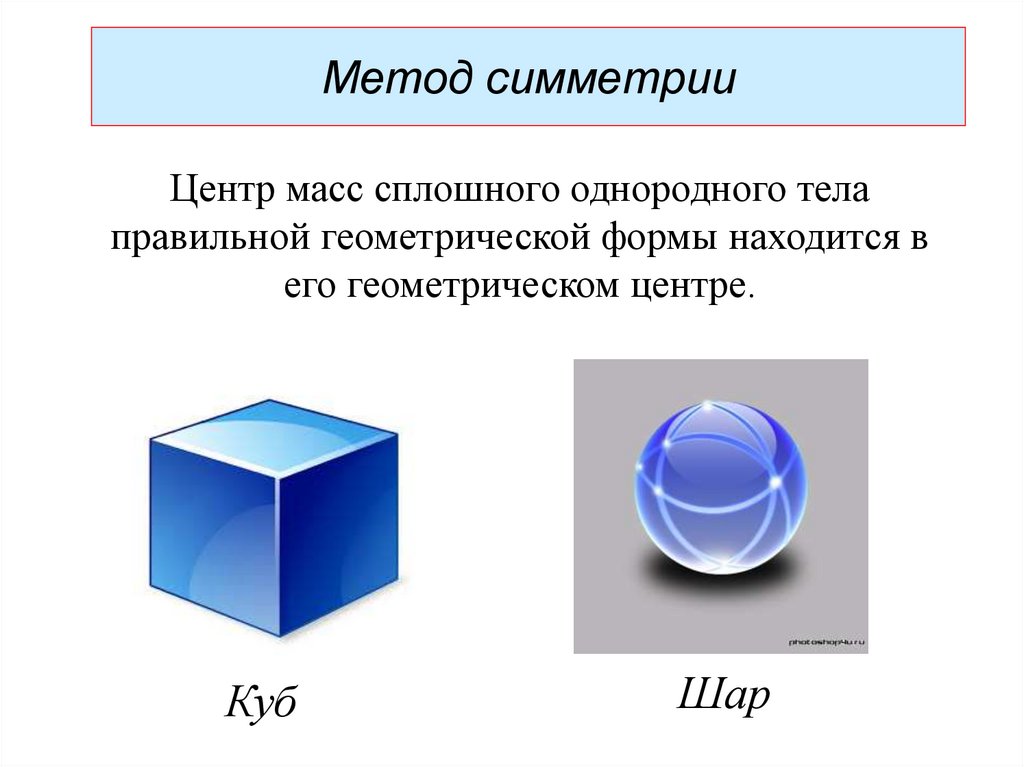
Центр масс сплошного однородного телаправильной геометрической формы находится в
его геометрическом центре.
Куб
Шар
19. Метод разбиения (пример 1)
ВА
D
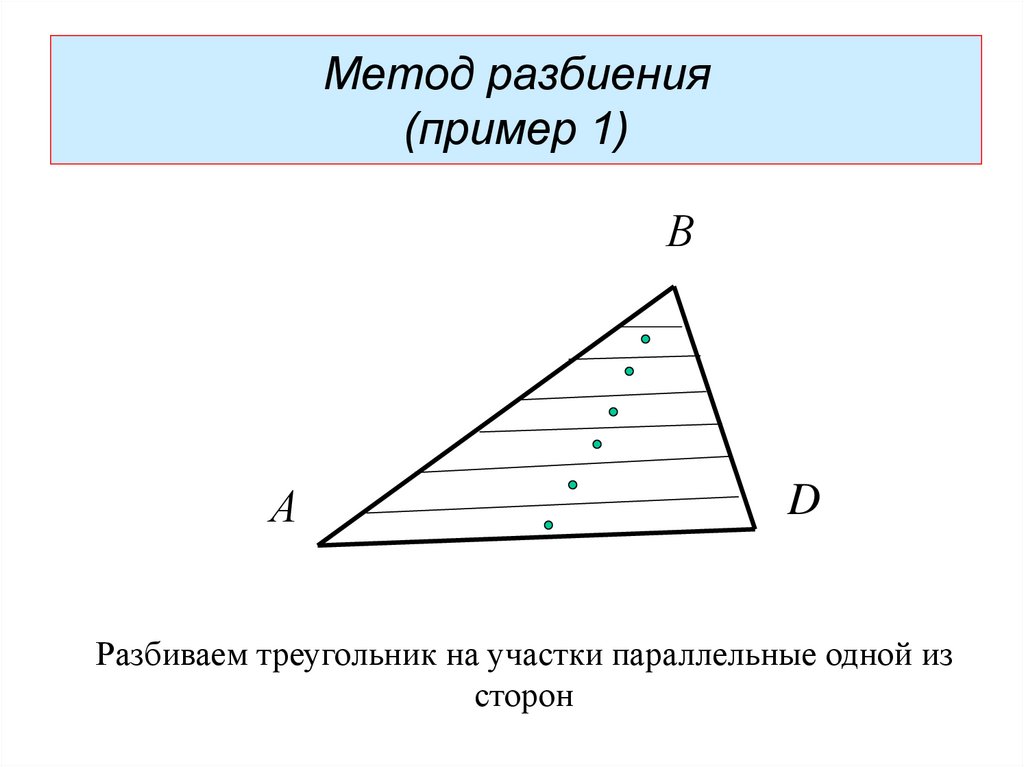
Разбиваем треугольник на участки параллельные одной из
сторон
20.
ВК - медианаВ
D
А
К
Соединяем линией центры масс всех участков
21.
ВК, AN, CM - медианыВ
М
C
N
D
А
К
C- центр масс находится на пересечении медиан
треугольника
22. Метод разбиения (Пример 2)
0x
Требуется определить цент масс пластинки,
представленной на рисунке
23.
Метод разбиения(Пример 2)
x2
0
x1
x
Разбиваем пластинку на простые геометрические фигуры.
Из соображений симметрии определяем положение
центра масс каждой фигуры. Координаты центров масс
всех выделенных фигур определяются в одной системе
отсчета.
24.
Метод разбиения(Пример 2)
x2
0
x1
x
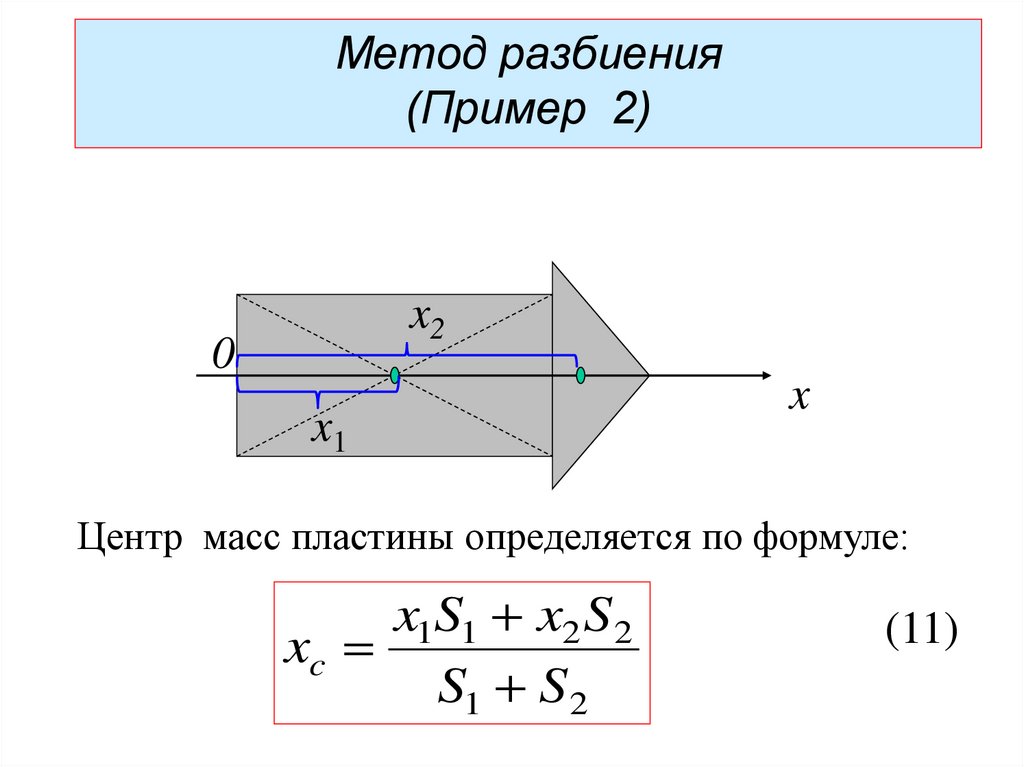
Центр масс пластины определяется по формуле:
x1S1 x2 S 2
xc
S1 S 2
(11)
25.
Метод разбиения(Пример 3)
y
O
x
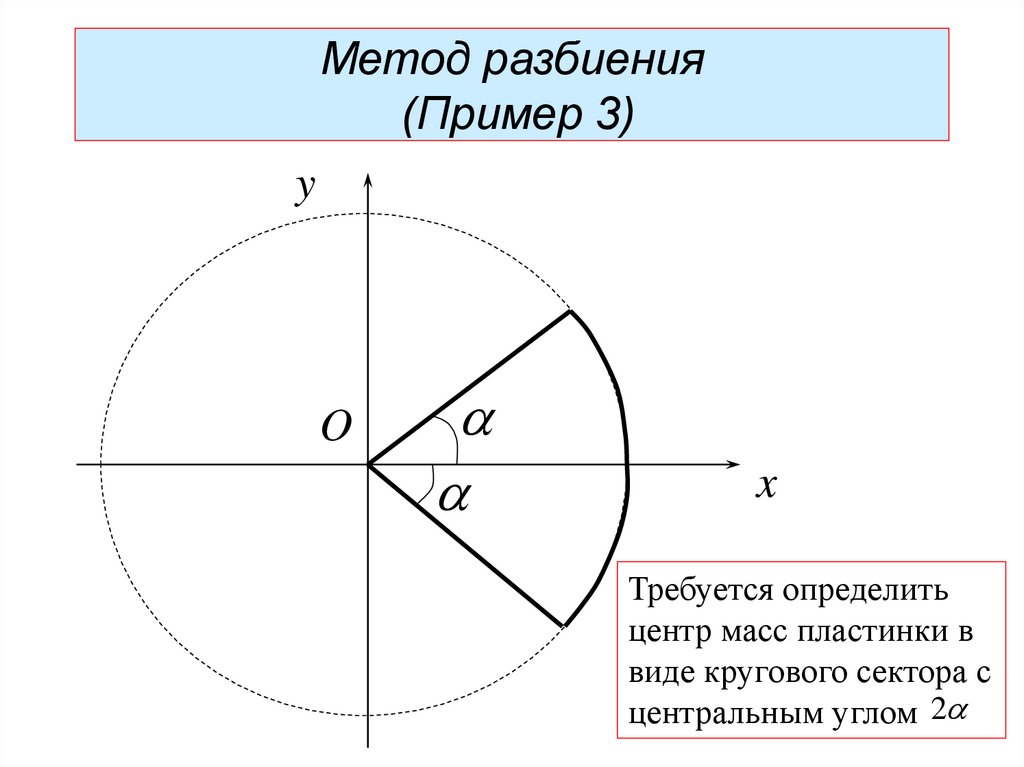
Требуется определить
центр масс пластинки в
виде кругового сектора с
центральным углом 2
26.
Метод разбиения(Пример 3)
y
O
R
*
x
Разбиваем пластину на
элементарные секторы
(треугольники)
27.
Метод разбиенияМетод разбиения (3)
(Пример 3)
y
O
N
R
*
x
Соединяем центры
элементарных секторов
28.
Метод разбиения(Пример 3)
y
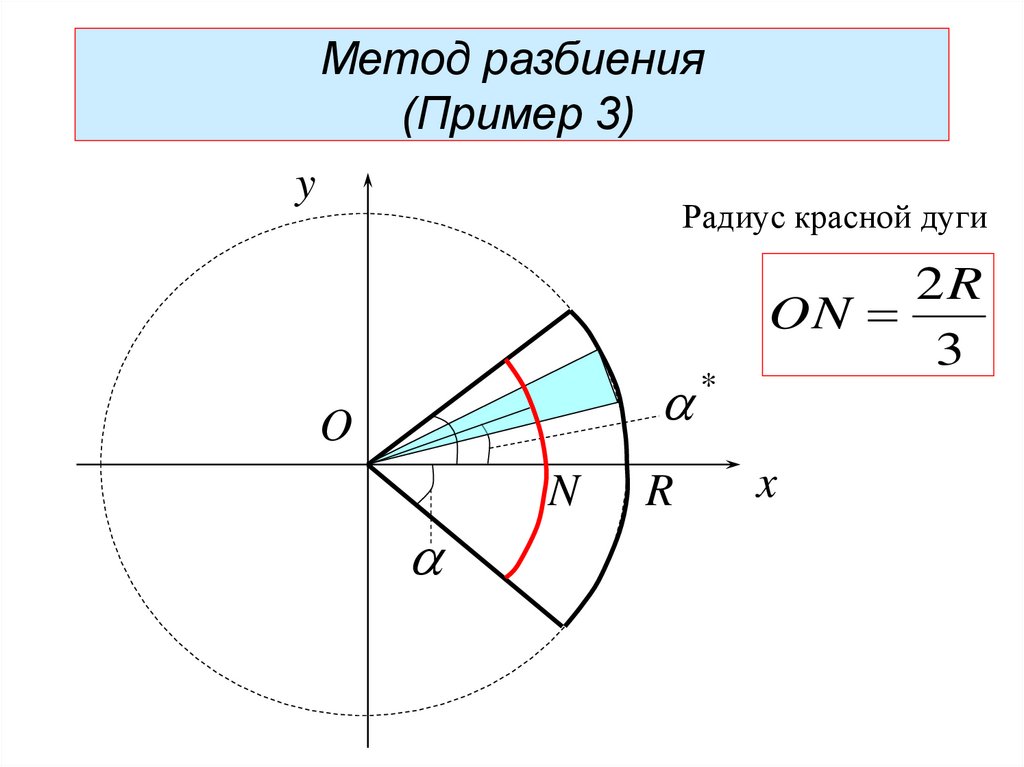
Радиус красной дуги
O
N
R
*
2R
ON
3
x
29.
Метод разбиения(Пример 3)
y
O
x
N
R
*
2R
ON
3
x
Координата центра масс
произвольного треугольника:
2
x R cos *
3
30.
Длина красной дуги:2
l R 2
3
31.
2l R 2
3
Длина красной дуги:
1
3
xc xdl
l l
4 R
1
2
2
*
R cos dl
3
cos
dl
*
32.
2l R 2
3
Длина красной дуги:
1
3
xc xdl
l l
4 R
1
2
Так как
2
*
R cos dl
3
cos
*
dl
2
*
dl R d
3
33.
1xc
3
2 R sin
R cos d 3
*
*
Положение центра масс кругового сектора
определяется по формуле:
2R sin
xc
3
(12)
Положение центра масс дуги радиуса R:
xc
R sin
(13)
34.
Метод отрицательных массy
R
r
O
a
x
Требуется определить центр масс пластинки с вырезом.
35.
S1 R - площадь большого круга2
36.
S1 R2
S2 r
2
- площадь большого круга
- площадь вырезанного круга
37.
S1 R2
S2 r
2
- площадь большого круга
- площадь вырезанного круга
x1 0 -координата центра масс большого
круга (без выреза)
x2 a
- координата центра масс выреза
38.
В соответствие с идеей метода площадь (масса)выреза считается отрицательной.
Координата центра масс пластины с вырезом:
x1S1 x2 S2
xc
S1 S2
(13)
В данном случае:
2
ar
xc 2 2
R r
(14)
39.
yR
r
O
C
xC
a
x
Значение xC получилось отрицательным,
следовательно центр масс пластины расположен
левее точки О.
40.
КОНТРОЛЬНЫЕ ВОПРОСЫ:1. Приведите пример когда положение центра
тяжести и центра масс тела не совпадают ?
2. Можно ли применить понятие «центр тяжести»
к планете?
3. Приведите пример применения метода
симметрии, не использованный в лекции.
4. Приведите пример использования метода
отрицательных масс.
41.
ТЕСТОВЫЕ ЗАДАНИЯДля самоконтроля знаний рекомендуется
выполнить тестовые задания из учебного пособия:
Дробчик В.В., Шумский М.П., Дубовик В.А.,
Симанкин Ф.А. Теоретическая механика.
(Статика). Таблица 14.
42.
После просмотра и конспектирования слайд-лекциинеобходимо прочитать указанные страницы
учебников и дополнить конспект наиболее важными
сведениями
1. Тарг С.М. Краткий курс теоретической механики:
Учеб. для втузов.- 10-е изд. – М: ВШ, 1986.
С. 86-94.




































 Физика
Физика








