Похожие презентации:
8. Оценивание случайных погрешностей измерения
1.
1Оценивание случайных
погрешностей измерения
2.
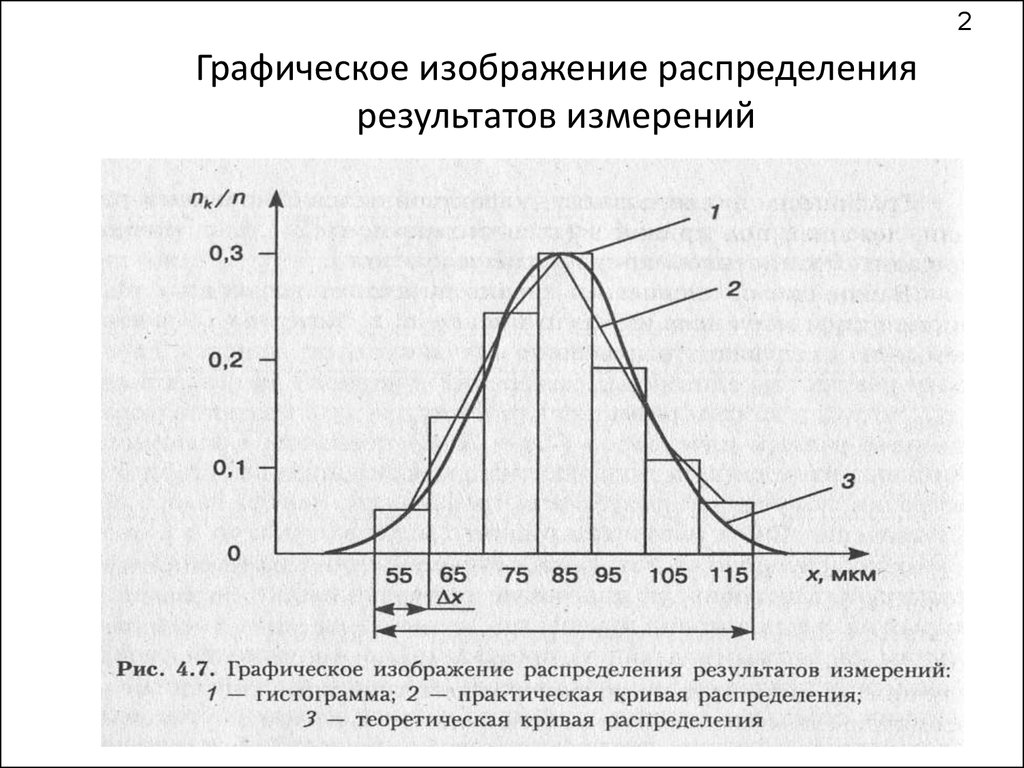
2Графическое изображение распределения
результатов измерений
3.
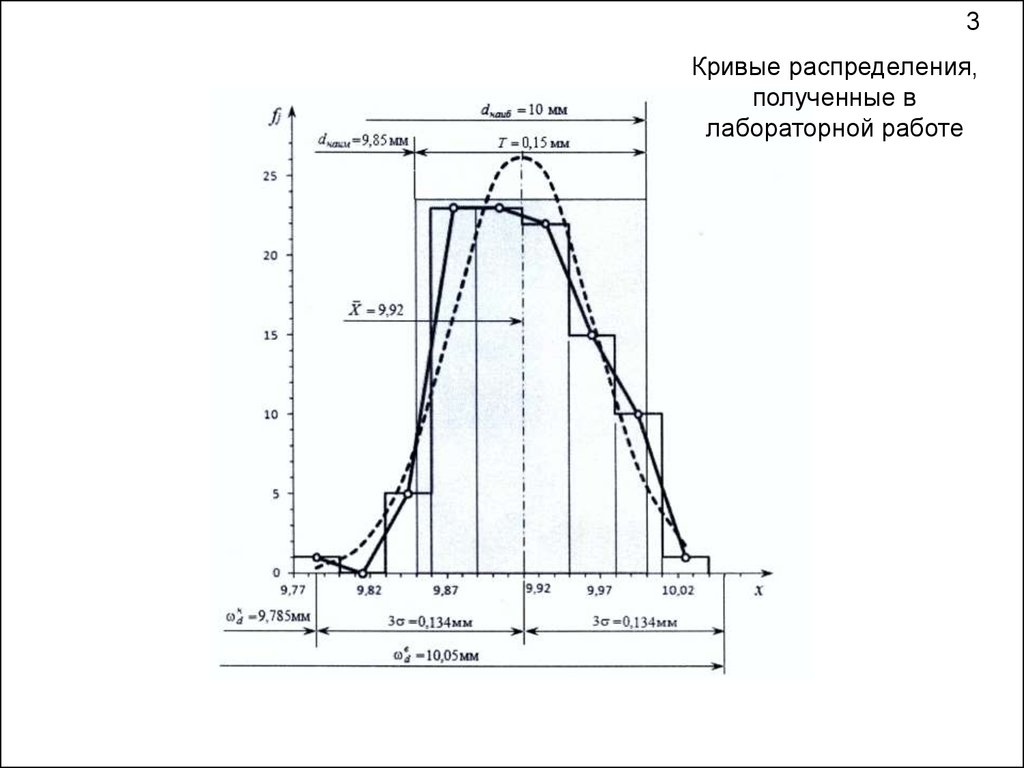
3Кривые распределения,
полученные в
лабораторной работе
4.
Числовые характеристики случайныхвеличин
Математическое ожидание
mx x
x
f ( x)dx,
- случайная величина
Дисперсия
Dx
x m x f ( x)dx,
4
5.
5Среднее квадратическое отклонение
случайной величины
Dx
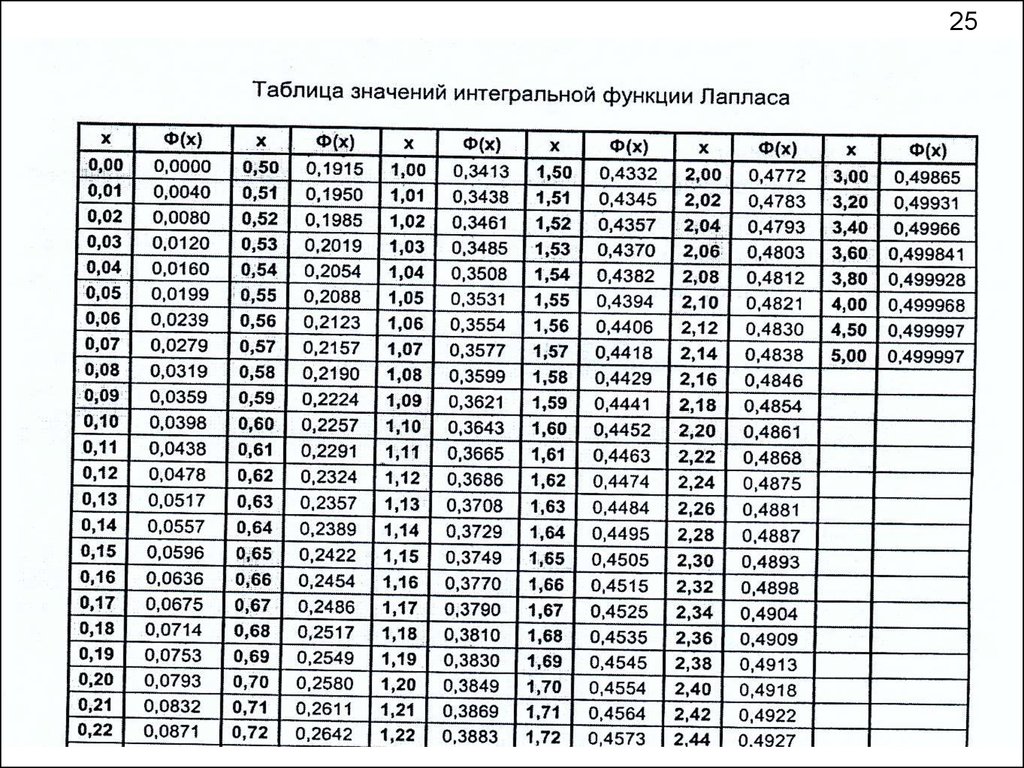
Функция Лапласа
1 z 0,5z 2
0 z
dz
e
2 0
0 0 0;
0 z 0 z ;
0 0,5 0 0,5
равенства,
справедливые для
функции Лапласа
6.
6Правило трёх сигм
mx 3
7.
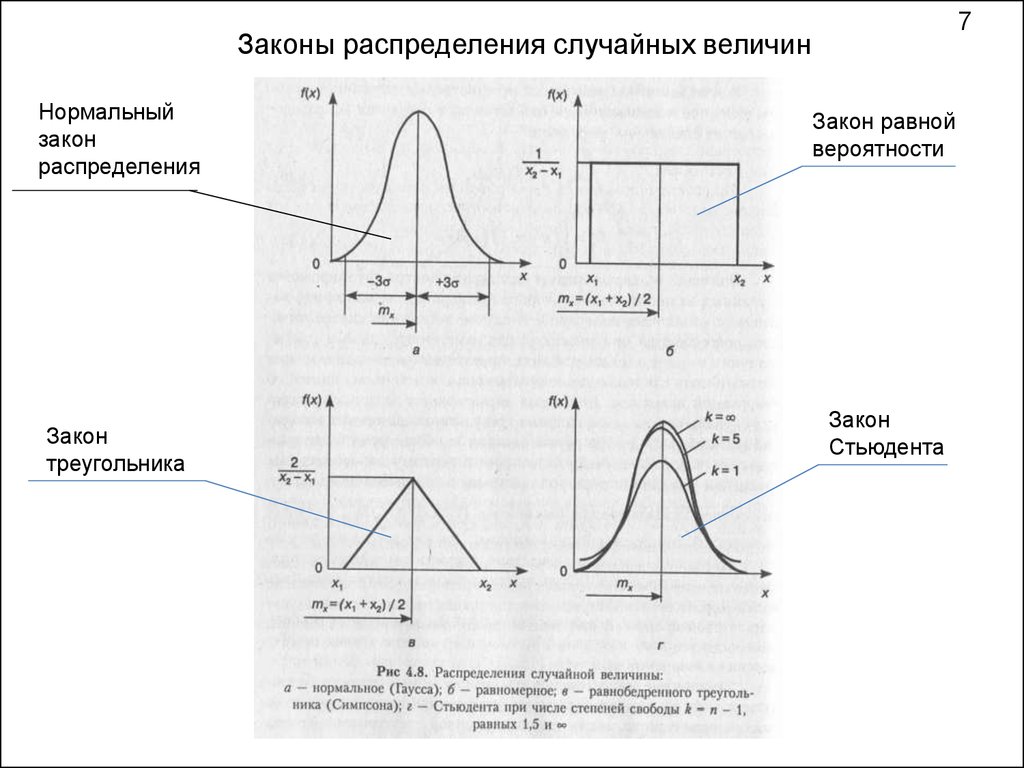
7Законы распределения случайных величин
Нормальный
закон
распределения
Закон
треугольника
Закон равной
вероятности
Закон
Стьюдента
8.
8Закон равной вероятности
9.
9Закон равнобедренного треугольника
10.
10Распределение Стьюдента
11.
11Точечная оценка математического ожидания – среднее
арифметическое значение измеряемой величины
1 n
x xi ,
n i 1
где n – число единичных измерений;
xi – результат i – го единичного измерения.
12.
12Точечная оценка дисперсии
~
1 n
2
D x
(
x
x
)
i
n 1 i 1
_
Среднее квадратическое отклонение результатов измерений
~
S x D x
_ 2
1 n
xi x
n 1 i 1
13.
13Средняя квадратическая погрешность (отклонение)
результата измерений среднего арифметического
2
1 n
Sx
xi x
Sx
n n n 1 i 1
14.
Определение доверительного результата измерений14
P xн x x в 1 q
P – вероятность того, что истинное значение
измеряемой величины
находится в заданных пределах;
q – уровень значимости
Предельные значения случайной величины
xн x z p S x
xв x z p S x
z p - аргумент функции Лапласа
z pSx
0 z
, отвечающий вероятности Р/2
доверительные границы погрешности результата измерений
15.
15Полученный доверительный интервал результата измерений
P x z p Sx x x z p Sx 2 0 z
16.
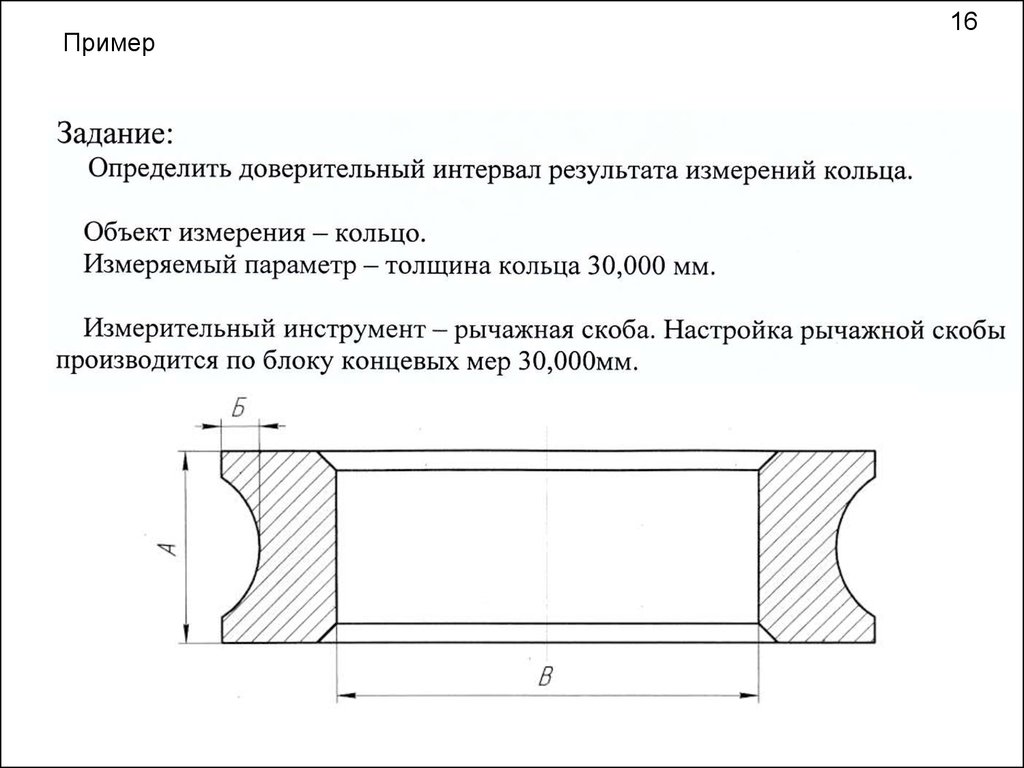
Пример16
17.
1718.
18Настройка рычажной скобы



















 Промышленность
Промышленность