Криволинейное движение КМ по твердой опорной поверхности

1.

Криволинейное движение КМ по
твердой опорной поверхности
1. Способы поворота и условия поворотливости КМ

2.

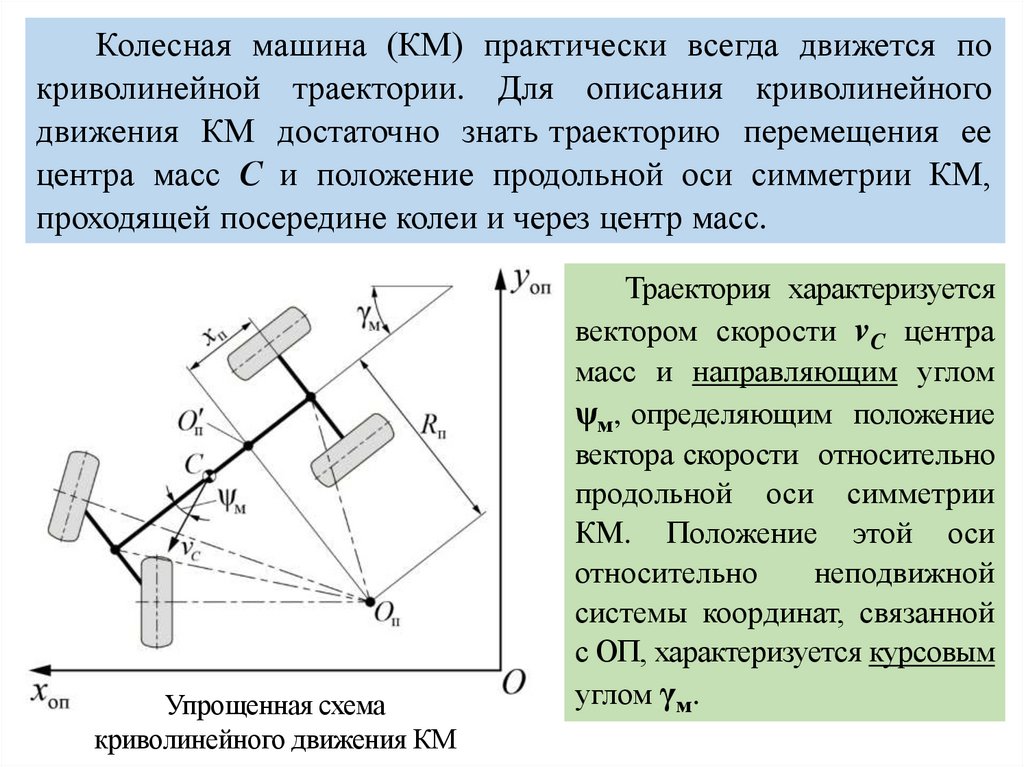
Колесная машина (КМ) практически всегда движется по
криволинейной траектории. Для описания криволинейного
движения КМ достаточно знать траекторию перемещения ее
центра масс С и положение продольной оси симметрии КМ,
проходящей посередине колеи и через центр масс.
Упрощенная схема
криволинейного движения КМ
Траектория характеризуется
вектором скорости vC центра
масс и направляющим углом
ψм, определяющим положение
вектора скорости относительно
продольной оси симметрии
КМ. Положение этой оси
относительно
неподвижной
системы координат, связанной
с ОП, характеризуется курсовым
углом γм.

3.

Принято выделять условно прямолинейное движение по
траектории с кривизной 1 / R п < 0,002 м-1 (радиус поворота
Rп > 500 м), а все остальное относить к криволинейному
движению.
Признаком криволинейного движения является отличие по
величине и направлению скоростей движения различных точек
колесной машины.
Траектория движения КМ изменяется в результате:
• действий водителя;
• в результате воздействий внешней среды;
• изменения параметров самой КМ в процессе движения.

4.

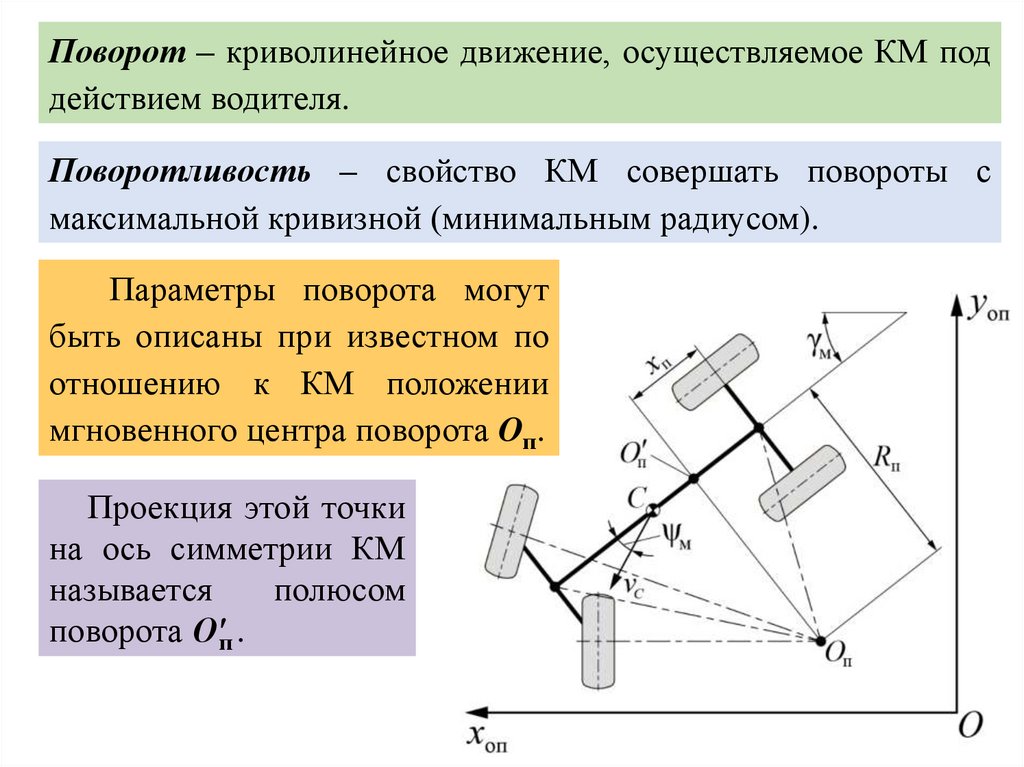
Поворот – криволинейное движение, осуществляемое КМ под
действием водителя.
Поворотливость – свойство КМ совершать повороты с
максимальной кривизной (минимальным радиусом).
Параметры поворота могут
быть описаны при известном по
отношению к КМ положении
мгновенного центра поворота Oп.
Проекция этой точки
на ось симметрии КМ
называется
полюсом
поворота О'п .

5.

Rп
xп
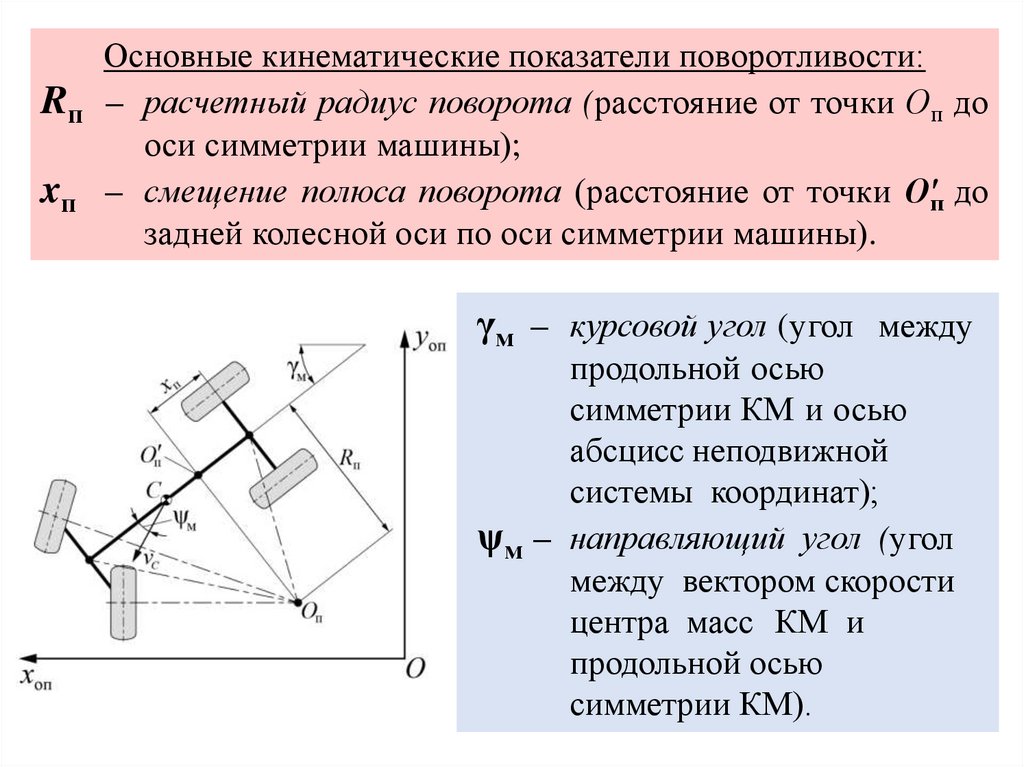
Основные кинематические показатели поворотливости:
– расчетный радиус поворота (расстояние от точки Оп до
оси симметрии машины);
– смещение полюса поворота (расстояние от точки О'п до
задней колесной оси по оси симметрии машины).
γм – курсовой угол (угол между
продольной осью
симметрии КМ и осью
абсцисс неподвижной
системы координат);
ψм – направляющий угол (угол
между вектором скорости
центра масс КМ и
продольной осью
симметрии КМ).

6.

В зависимости от решаемых задач оперируют такими
понятиями, как:
минимальный радиус поворота Rп1н – расстояние от точки
Оп до оси следа переднего наружного колеса при
максимальных углах поворота управляемых колес (этот
радиус обычно приводят в технической характеристике
КМ),
радиус кривизны траектории RпC – расстояние от точки Оп
до центра масс С.
Различают следующие виды поворотливости:
статическая – поворот с постоянным и минимальным радиусом
при постоянной скорости движения;
динамическая – поворот с переменными радиусом и скоростью,
с учетом времени поворота и изменения траектории движения.

7.

Процесс поворота состоит из трех этапов:
1) вход в поворот – увеличение кривизны траектории движения
центра масс;
2) равномерный поворот – движение с постоянной кривизной
траектории;
3) выход из поворота – уменьшение кривизны траектории
движения и возвращение к прямолинейному движению.
2
1
3

8.

КМ могут совершать поворот тремя основными способами:
1) поворотом плоскостей
вращения колес
управляемых осей
относительно продольной
оси КМ на разные углы
(классический поворот)
2) поворотом плоскостей
вращения колес
управляемых осей
относительно продольной
оси КМ на одинаковый угол
(поворот сочлененных КМ)
3) изменением
линейных скоростей
колес наружного и
внутреннего бортов
(бортовой поворот)

9.

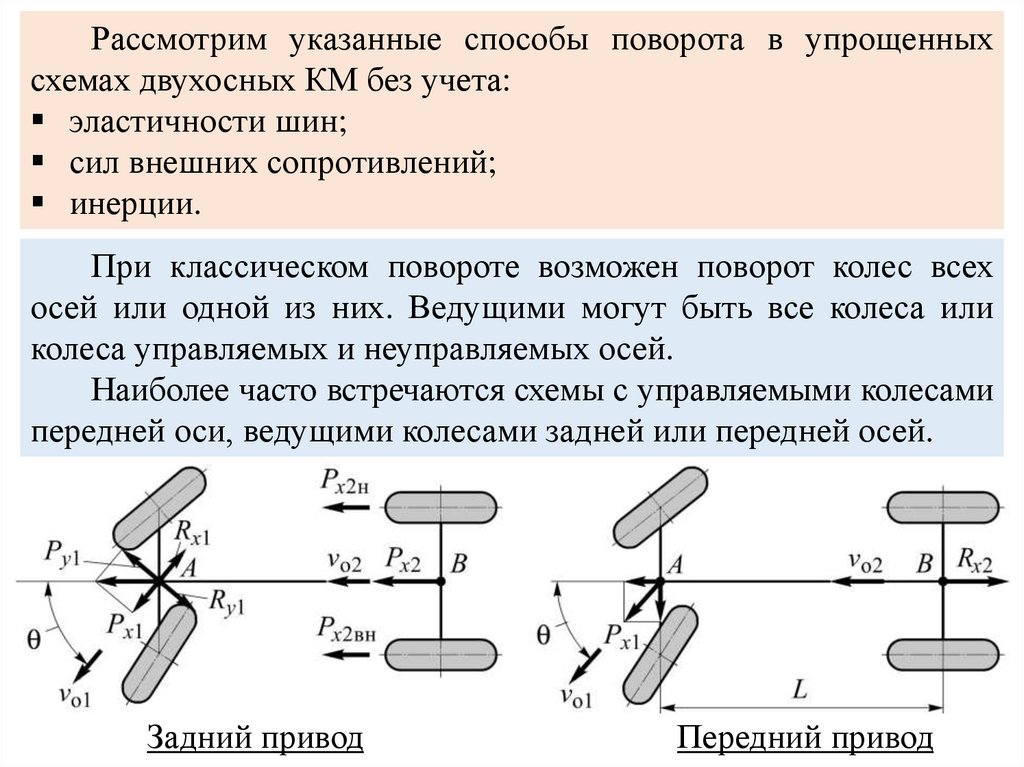
Рассмотрим указанные способы поворота в упрощенных
схемах двухосных КМ без учета:
эластичности шин;
сил внешних сопротивлений;
инерции.
При классическом повороте возможен поворот колес всех
осей или одной из них. Ведущими могут быть все колеса или
колеса управляемых и неуправляемых осей.
Наиболее часто встречаются схемы с управляемыми колесами
передней оси, ведущими колесами задней или передней осей.
Задний привод
Передний привод

10.

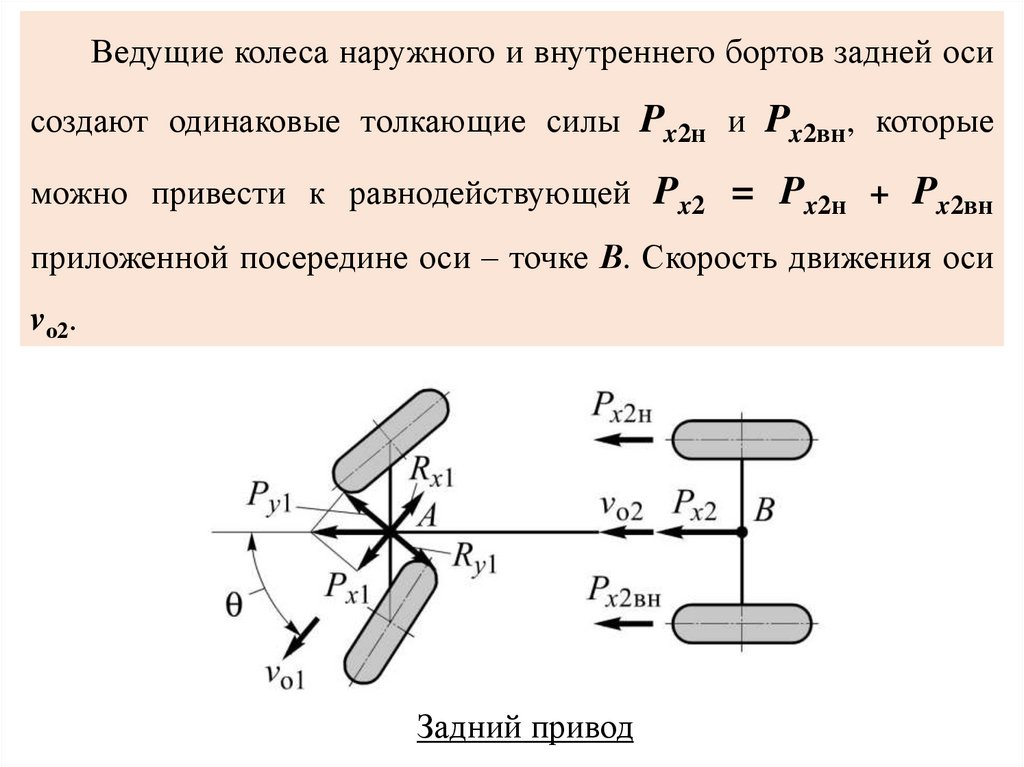
Ведущие колеса наружного и внутреннего бортов задней оси
создают одинаковые толкающие силы Px2н и Px2вн, которые
можно привести к равнодействующей Px2 = Px2н + Px2вн
приложенной посередине оси – точке В. Скорость движения оси
vо2.
Задний привод

11.

Поскольку внешних сил нет, то посередине передней оси (в
точке А) от корпуса будет действовать та же толкающая сила Px2,
которую можно разложить на две составляющие:
параллельную плоскости вращения колеса Px1 = Px2·cos θ
перпендикулярную плоскости вращения колеса Py1 = Px2·sin θ
Задний привод

12.

Задний привод
Перемещению колеса по направлению действия силы Px1
препятствует сила сопротивления качению Pfx1 = f1·Rz1, а по
направлению
действия
силы
Py1 – сила сопротивления
движению Pfy1 = φ1·Rz1. В большинстве случаев f1 << φ1,
поэтому Pfx1 << Pfy1 и центр передней оси перемещается по
направлению действия силы Px1 со скоростью vо1.

13.

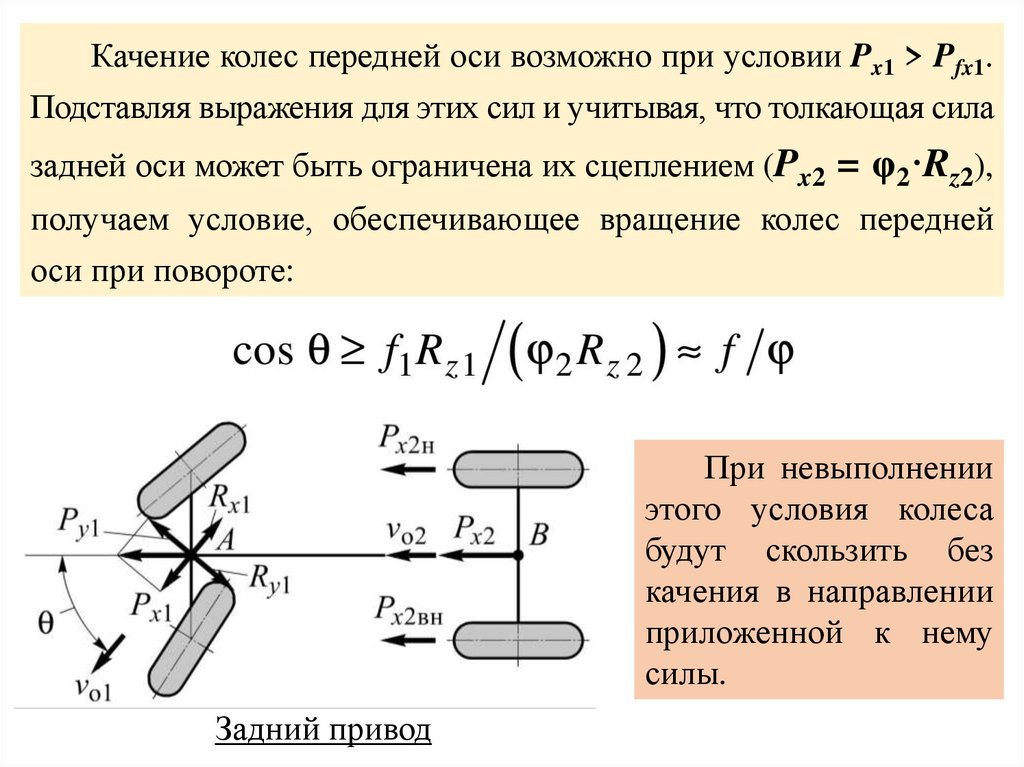
Качение колес передней оси возможно при условии Px1 > Pfx1.
Подставляя выражения для этих сил и учитывая, что толкающая сила
задней оси может быть ограничена их сцеплением (Px2 = φ2·Rz2),
получаем условие, обеспечивающее вращение колес передней
оси при повороте:
При невыполнении
этого условия колеса
будут скользить без
качения в направлении
приложенной к нему
силы.
Задний привод

14.

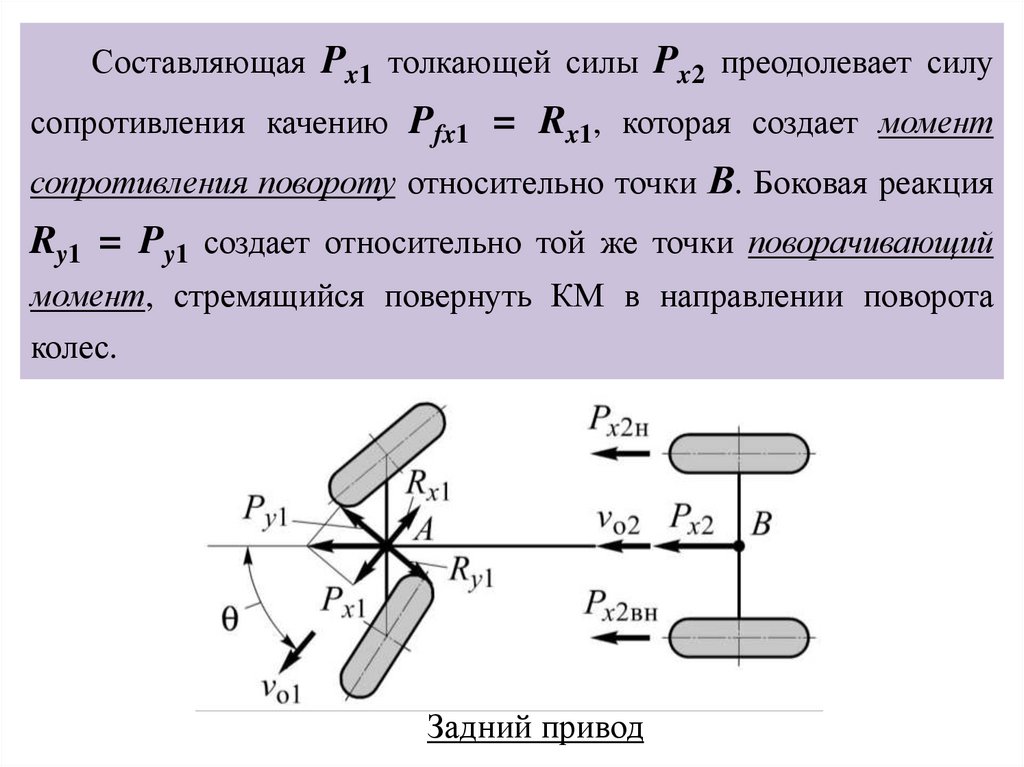
Составляющая Px1 толкающей силы Px2 преодолевает силу
сопротивления качению Pfx1 = Rx1, которая создает момент
сопротивления повороту относительно точки В. Боковая реакция
Ry1 = Py1 создает относительно той же точки поворачивающий
момент, стремящийся повернуть КМ в направлении поворота
колес.
Задний привод

15.

Во второй схеме (передний привод) составляющая Px1·cos θ
силы тяги колес передней оси толкает колеса задней оси,
преодолевая их сопротивление качению. Составляющая Px1·sin θ
на плече L создает поворачивающий момент.
Передний привод
Качение передних колес при такой схеме не ограничено
углами поворота управляемых колес.

16.

Поворот
сочлененных
машин
происходит
как
и
при
классическом способе, но с той разницей, что колеса одной оси по
отношению к другим изменяют плоскость своего вращения
одновременно с поворотом одной части КМ по отношению к
другой. Возможен поворот одной оси или секций.
Поворот передней оси
Поворот секции

17.

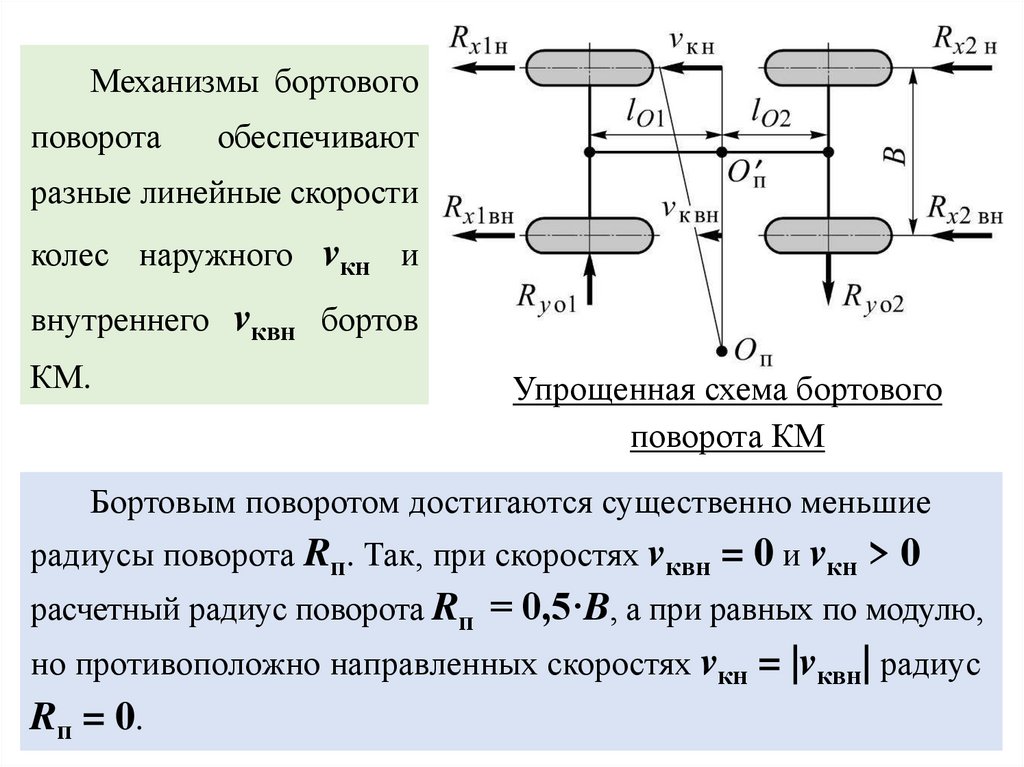
Механизмы бортового
поворота
обеспечивают
разные линейные скорости
колес наружного vкн и
внутреннего vквн бортов
КМ.
Упрощенная схема бортового
поворота КМ
Бортовым поворотом достигаются существенно меньшие
радиусы поворота Rп. Так, при скоростях vквн = 0 и vкн > 0
расчетный радиус поворота Rп = 0,5·B, а при равных по модулю,
но противоположно направленных скоростях vкн = |vквн| радиус
Rп = 0.

18.

Рассмотренные упрощенные схемы дают только качественное
представление о процессе поворота, т. е. каким образом КМ может
его совершить. При повороте на КМ действуют дополнительные
силы и моменты, увеличивающие сопротивление движению и
приводящие к необходимости увеличения силы тяги на колесах.
Для обеспечения поворота КМ с заданным радиусом должны
выполняться как минимум два условия:
1) создание достаточной силы тяги ведущих колес, способной
преодолеть возросшую по сравнению с прямолинейным
движением силу сопротивления движению;
2) отсутствие скольжения (буксования) колес не менее двух осей,
из которых хотя бы одна должна быть осью с управляемыми
колесами.

19.

Первое условие можно приближенно записать в безразмерном
виде:
где fкрив – коэффициент сопротивления движению КМ при
криволинейном движении.
Второе условие обеспечивается, когда суммарная реакция в
пятне контакта RΣ не превосходит реакции по сцеплению RΣϕ :
где

20.

При бортовом повороте неизбежно боковое скольжение колес,
поэтому поворотливость КМ определяется условием

21.

Кинематические и силовые параметры
колесного движителя при криволинейном
движении и действии боковой силы

22.

В общем случае на колесо кроме сил Px и Pz действует
боковая сила Py, существенно изменяющая параметры его
взаимодействия с ОП.

23.

Для описания движения колеса
используют две системы координат:
OкXкYкZк – связана с центром
обода;
OшXшYшZш – связана с центром
контакта шины с ОП, на оси
которых проецируют силы Pi,
действующие от корпуса КМ, и
реакции Ri, возникающие со
стороны ОП.
Реакции Ri создают следующие моменты:
1) сопротивления качению Мf = Rz·aш ;
2) опрокидывающий Мопр = Rz·q ;
3) стабилизирующие поперечный Мст y = Ry·e и продольный Мст х = Rx·d ;
4) крутящий Мк = Rx·rк0.

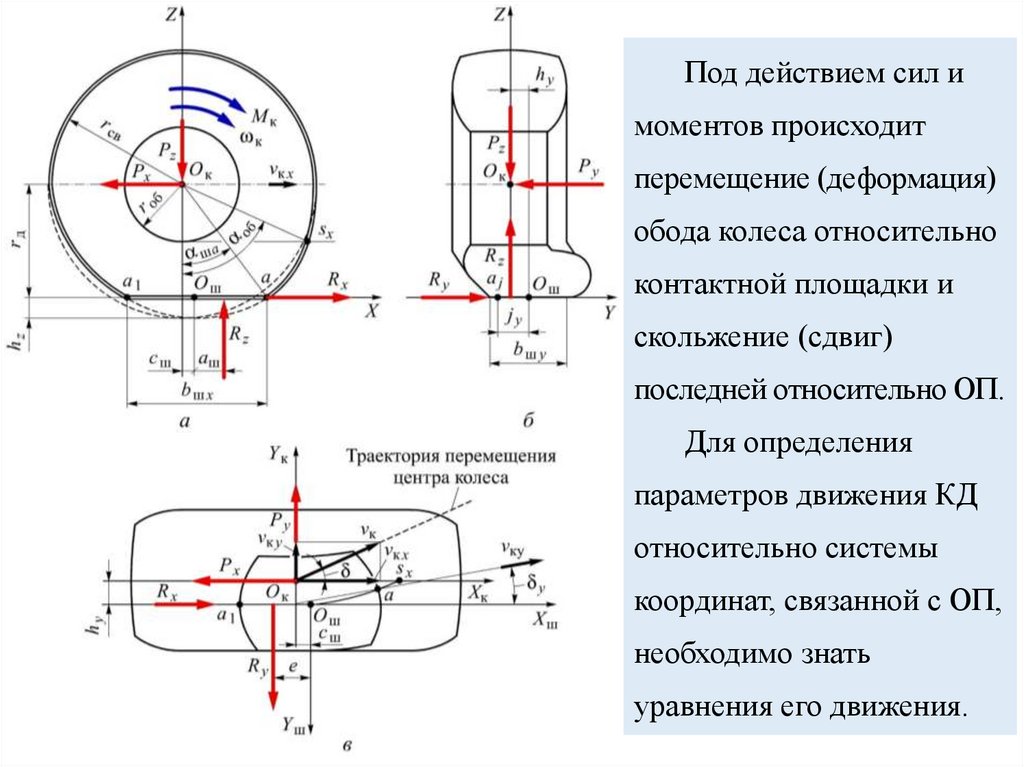
24.

Под действием сил и
моментов происходит
перемещение (деформация)
обода колеса относительно
контактной площадки и
скольжение (сдвиг)
последней относительно ОП.
Для определения
параметров движения КД
относительно системы
координат, связанной с ОП,
необходимо знать
уравнения его движения.

25.

Выделяют следующие случаи движения колеса под действием
приложенных к нему сил:
1) перемещение центра Oк относительно неподвижной точки
контактной площадки Oш (радиальная, боковая и окружная
деформации колеса);
2) сдвиг jx и jy контактной площадки соответственно в продольном
и поперечном направлениях;
3) перемещение центра обода Oк в продольной плоскости движения
под углом δ к плоскости симметрии колеса – оси Xк (увод колеса);
4) поворот колеса вокруг вертикальной или наклоненной оси Zк на
угол поворота θк относительно продольной оси КМ;
5) поворот плоскости колеса относительно продольно-вертикальной
плоскости на угол γкy поперечного наклона (развала).

26.

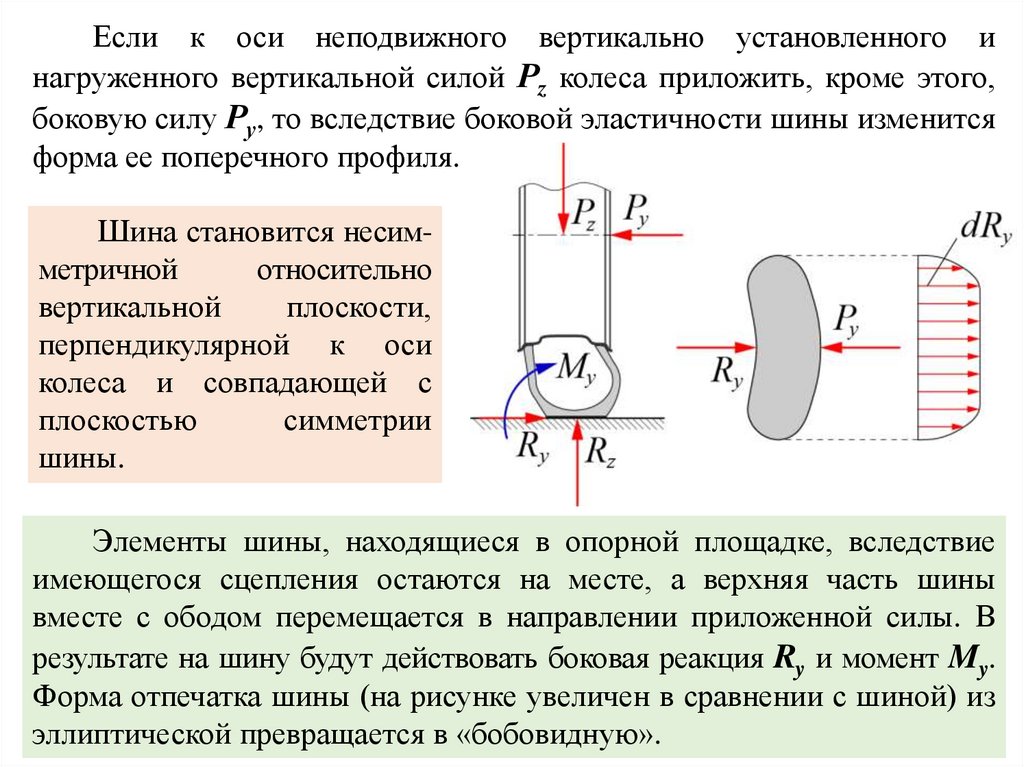
Если к оси неподвижного вертикально установленного и
нагруженного вертикальной силой Рz колеса приложить, кроме этого,
боковую силу Ру, то вследствие боковой эластичности шины изменится
форма ее поперечного профиля.
Шина становится несимметричной
относительно
вертикальной
плоскости,
перпендикулярной к оси
колеса и совпадающей с
плоскостью
симметрии
шины.
Элементы шины, находящиеся в опорной площадке, вследствие
имеющегося сцепления остаются на месте, а верхняя часть шины
вместе с ободом перемещается в направлении приложенной силы. В
результате на шину будут действовать боковая реакция Ry и момент My.
Форма отпечатка шины (на рисунке увеличен в сравнении с шиной) из
эллиптической превращается в «бобовидную».

27.

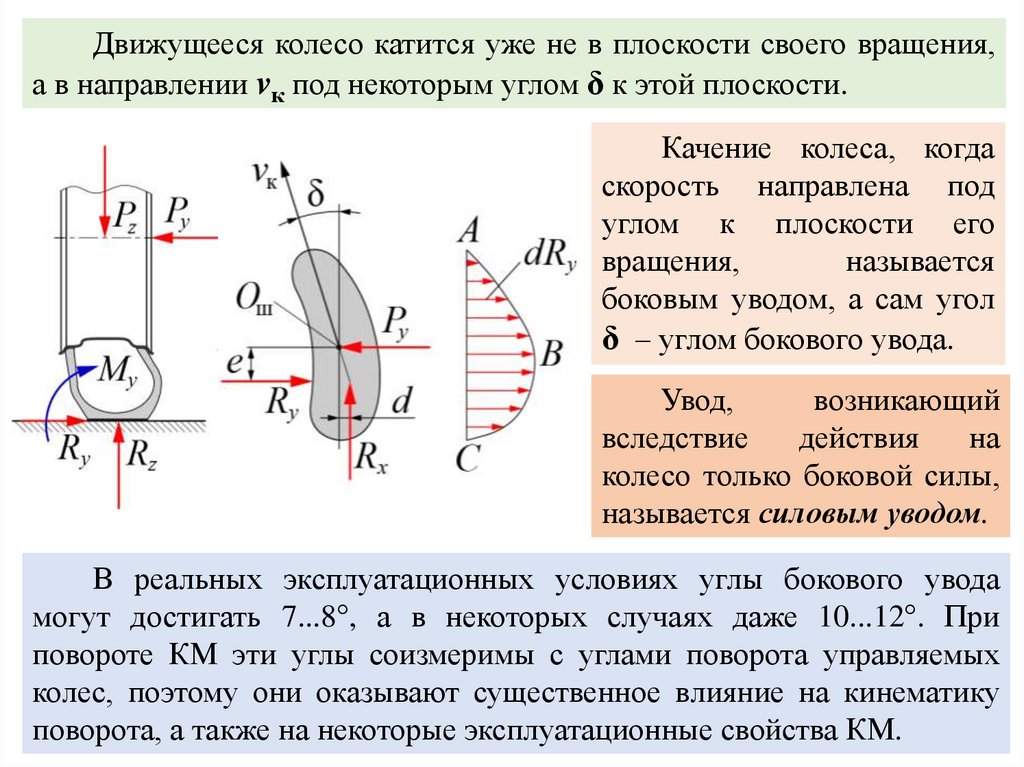
Движущееся колесо катится уже не в плоскости своего вращения,
а в направлении vк под некоторым углом δ к этой плоскости.
Качение колеса, когда
скорость направлена под
углом к плоскости его
вращения,
называется
боковым уводом, а сам угол
δ – углом бокового увода.
Увод,
возникающий
вследствие
действия
на
колесо только боковой силы,
называется силовым уводом.
В реальных эксплуатационных условиях углы бокового увода
могут достигать 7...8°, а в некоторых случаях даже 10...12°. При
повороте КМ эти углы соизмеримы с углами поворота управляемых
колес, поэтому они оказывают существенное влияние на кинематику
поворота, а также на некоторые эксплуатационные свойства КМ.

28.

Эпюру элементарных боковых касательных сил можно заменить
равнодействующей реакцией Ry, которая вследствие неравносторонности треугольника ABC смещена относительно оси колеса на
величину плеча е. Вследствие этого боковая сила Ру и равная ей
реакция Ry создают момент относительно вертикальной оси. Этот
момент направлен таким образом, что стремится повернуть колесо в
нейтральное положение, соответствующее прямолинейному движению
КМ, т.е. оказывает сопротивление повороту колеса. По этой причине
его называют стабилизирующим моментом (Mст y).
Продольная реакция Rx вследствие
«искривления»
отпечатка
также
смещается от его центра в направлении
реакции Ry. Создается момент на плече d,
но этот момент существенно меньше
момента, создаваемого боковой силой на
плече е.

29.

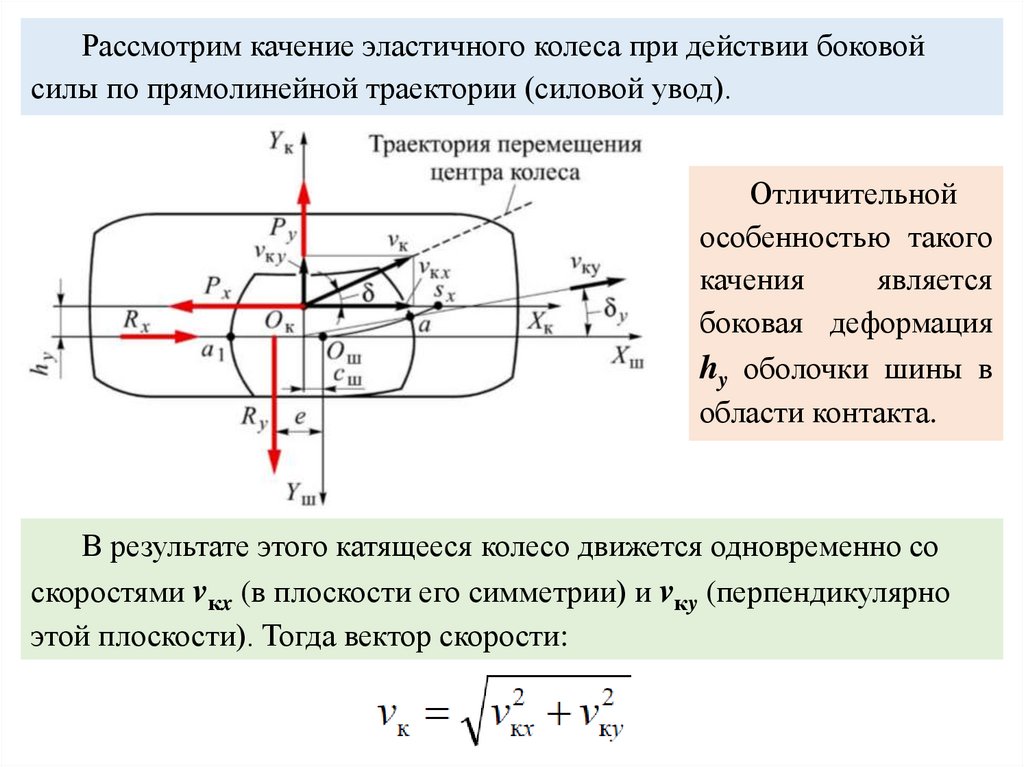
Рассмотрим качение эластичного колеса при действии боковой
силы по прямолинейной траектории (силовой увод).
Отличительной
особенностью такого
качения
является
боковая деформация
hy оболочки шины в
области контакта.
В результате этого катящееся колесо движется одновременно со
скоростями vкx (в плоскости его симметрии) и vкy (перпендикулярно
этой плоскости). Тогда вектор скорости:

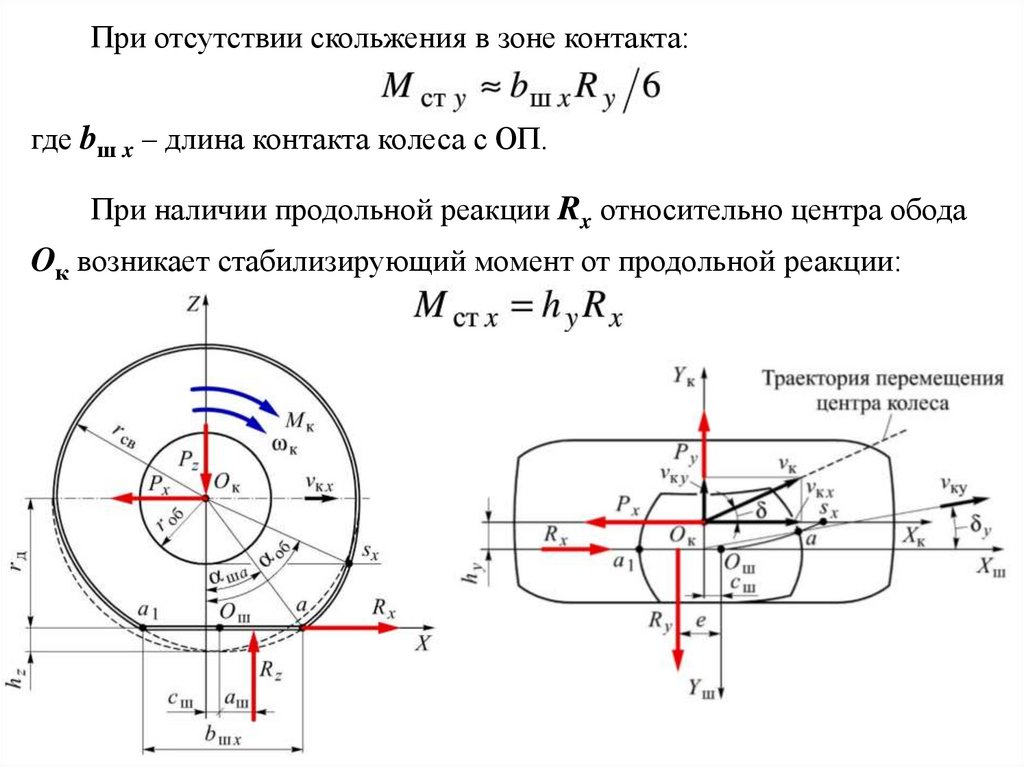
30.

При отсутствии скольжения в зоне контакта:
где bш x – длина контакта колеса с ОП.
При наличии продольной реакции Rx относительно центра обода
Oк возникает стабилизирующий момент от продольной реакции:

31.

При действии силы Px = Rx центр обода смещается в продольном
направлении на величину сш и упругий стабилизирующий момент
шины от боковой реакции изменяется:
Суммарный стабилизирующий момент шины равен сумме
моментов от продольной Rx и боковой Ry реакций:
При значительной боковой силе или малом
коэффициенте сцепления в боковом направлении
φy поверхность контакта может скользить в
боковом направлении на величину бокового
сдвига jy.

32.

В этом случае составляющая vк y скорости центра колеса состоит
из упругой скорости vк уy и скорости скольжения vк yj.
Первая обусловлена упругой деформацией шины в боковом
направлении dhy (перемещением центра обода относительно центра
контакта),
вторая
–
боковым
сдвигом
jy контакта (боковым
перемещением центра контакта относительно ОП).
Суммарный угол бокового увода, вызванный действием боковой
силы Py, также имеет упругую δу и сдвиговую δj составляющие:
Боковая деформация dhy и упругая составляющая угла увода δу
(при отсутствии бокового скольжения) зависят от конструктивных
особенностей колес, давления воздуха pw, а также сил Pz и Py.

33.

Изменение деформаций шин в зависимости от нагрузки и давления воздуха:
а – для шин 1200×500–508 (1), 9.75–18 (2); 12.00–18 (3), 12.00–20 (4);
б, в – для шины 1300×530–533 при pw = 0,35 МПа (б) и Pz = 40 кН (в)

34.

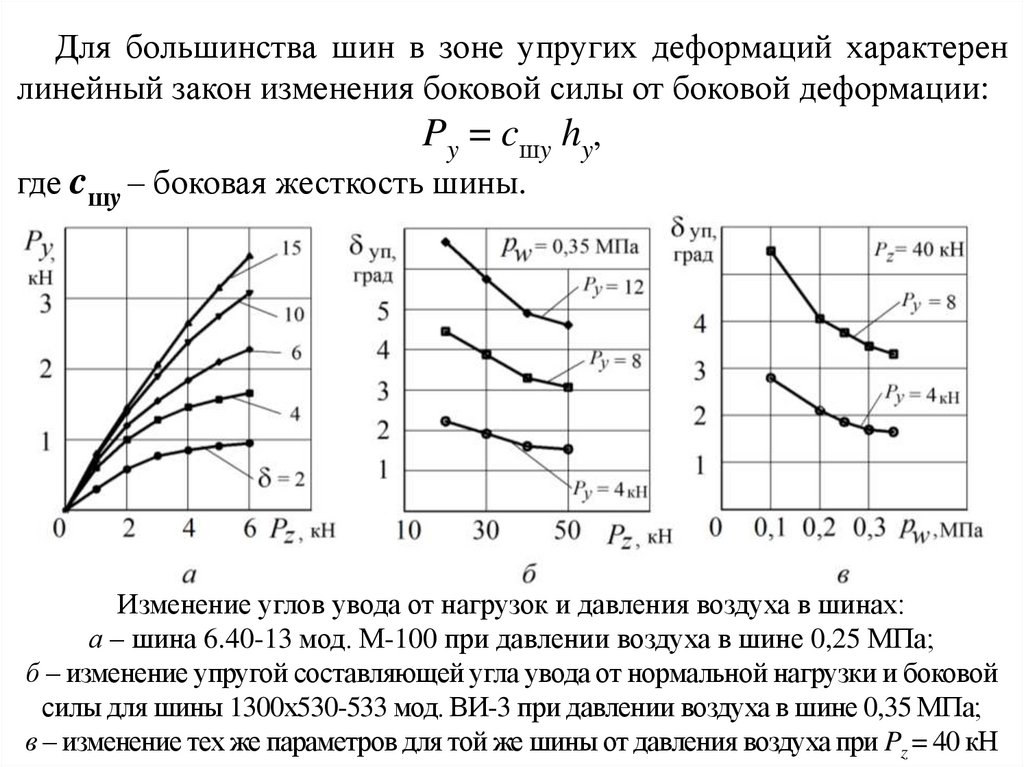
Для большинства шин в зоне упругих деформаций характерен
линейный закон изменения боковой силы от боковой деформации:
Py = cшy hy,
где cшy – боковая жесткость шины.
Изменение углов увода от нагрузок и давления воздуха в шинах:
а – шина 6.40-13 мод. М-100 при давлении воздуха в шине 0,25 МПа;
б – изменение упругой составляющей угла увода от нормальной нагрузки и боковой
силы для шины 1300х530-533 мод. ВИ-3 при давлении воздуха в шине 0,35 МПа;
в – изменение тех же параметров для той же шины от давления воздуха при Pz = 40 кН

35.

В теории колесных машин наиболее часто для описания
взаимосвязи боковой силы Py и реализуемого угла увода δ (с
учетом боковой деформации шины и ее проскальзывания
относительно опорной поверхности) используется уравнение:
Py = ky δ,
где ky – коэффициент сопротивления боковому
(нелинейный коэффициент пропорциональности).
уводу
Коэффициент сопротивления боковому уводу ky зависит от
многих конструктивных и эксплуатационных условий. Наиболее
строгой и досконально разработанной теорией по определению
ky в различных условиях эксплуатации колеса является теория
нелинейного увода, разработанная Д.А. Антоновым.

36.

Согласно теории нелинейного бокового увода действительное
значение
ky
определяется
относительно
некоторого
фиксированного значения ky0 с помощью коэффициентов
коррекции qi, учитывающих изменение эксплуатационных
параметров качения колеса (давления воздуха, нормальной и
продольной нагрузки, коэффициента сцепления и т. д.):
ky = ky0 qw qRz qRx qφ.
При отсутствии скольжения в зоне контакта значения ky
достаточно стабильны и определяются исключительно
параметрами
шины,
влияние
опорной
поверхности
незначительно.
При достижении определенного значения суммарной реакции
RΣ в плоскости контакта , зависящей от нормальной нагрузки Pz
и сцепления шины с ОП, начинается боковое и продольное
скольжение шины к зоне контакта.

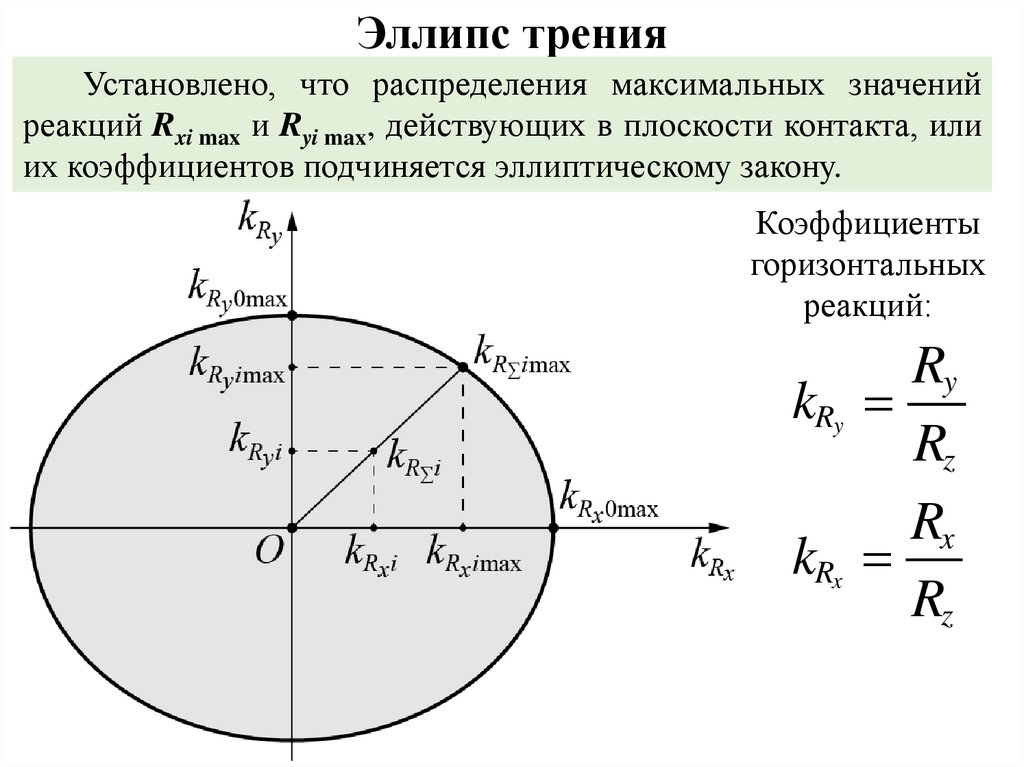
37.

Эллипс трения
Установлено, что распределения максимальных значений
реакций Rxi max и Ryi max, действующих в плоскости контакта, или
их коэффициентов подчиняется эллиптическому закону.
Коэффициенты
горизонтальных
реакций:
Ry
kRy
Rz
Rx
kRx
Rz

38.

Эллипс трения
Коэффициенты максимальных реакций в точках пересечения
эллипса с его осями, т. е. при Ry = 0 и Rx = 0, называют
коэффициентами сцепления в продольном и боковом
направлениях:
kRy 0max φy
kRx 0max φx

39.

Эллипс трения
Уравнение связи предельных значений коэффициентов:
Предельные значения проекций на оси X и Y:
В большинстве случаев kRx0
max
kRy0
max,
причем в
зависимости от типа шины и вида ОП различны соотношения
между ними.

40.

На диаграмме распределения продольных и боковых реакций
при качении радиальной шины с Рz = 3,2 кН видно, что до δ = 3°
изменение продольной реакции Rx незначительно сказывается на
значении Ry.
Максимальная продольная реакция в тяговом (Rx > 0) режиме
обычно больше, чем в тормозном (Rx < 0).
Распределение продольных и боковых реакций при качении радиальной
шины с различными углами увода

41.

При Rx = const с увеличением угла увода δ реакция Ry
возрастает, стабилизируясь при δ > 8°. Подтверждением этому
служит зависимость kу(δ).
Видно, что при угле
увода δ > 4° значения kу
монотонно
убывают,
однако при малых δ в
некоторых
случаях
отмечается
и
незначительный рост.
Изменение коэффициента
сопротивления боковому уводу шин
1200х500-508 (1) и 6.00-16 (2)

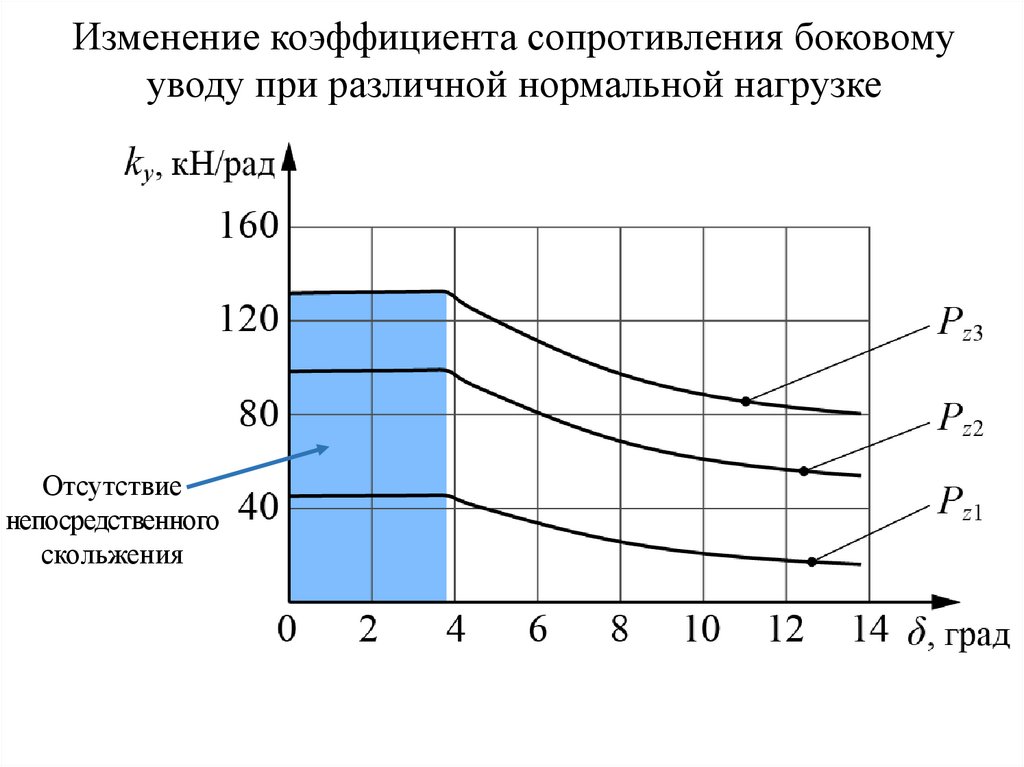
42.

Изменение коэффициента сопротивления боковому
уводу при различной нормальной нагрузке
Отсутствие
непосредственного
скольжения

43.

Изменение продольной реакции Rx в наибольшей мере
сказывается на суммарном стабилизирующем моменте шины
МстΣ, чем на коэффициенте сопротивления боковому уводу kу.
Изменение суммарного стабилизирующего момента шины и
коэффициента сопротивления боковому уводу от относительной
продольной реакции и угла увода

44.

На коэффициент сопротивления боковому уводу ky в
большей степени влияют: нормальная нагрузка Рz, давление
воздуха в шине pw, коэффициент трения скольжения шины
по опорной поверхности μск и угол увода δ.

45.

При оценке устойчивости, управляемости и маневренности
КМ необходимо выделить два случая движения:
1) движение КМ с большими углами поворота управляемых
колес, большими углами увода и невысокими скоростями;
2) движение КМ с большими скоростями и относительно
малыми углами поворота управляемых колес и увода.
В первом случае наиболее важными являются вопросы,
связанные с определением продольных и боковых сил,
моментов сопротивления повороту, положения мгновенного
центра поворота. При этом необходимо также учитывать
скольжение в зоне контакта колеса.
Во втором случае скольжением в зоне контакта в
большинстве случаев пренебрегают и рассматривают
неустановившиеся (переходные) процессы при кривизне
траектории, близкой к нулю.

46.

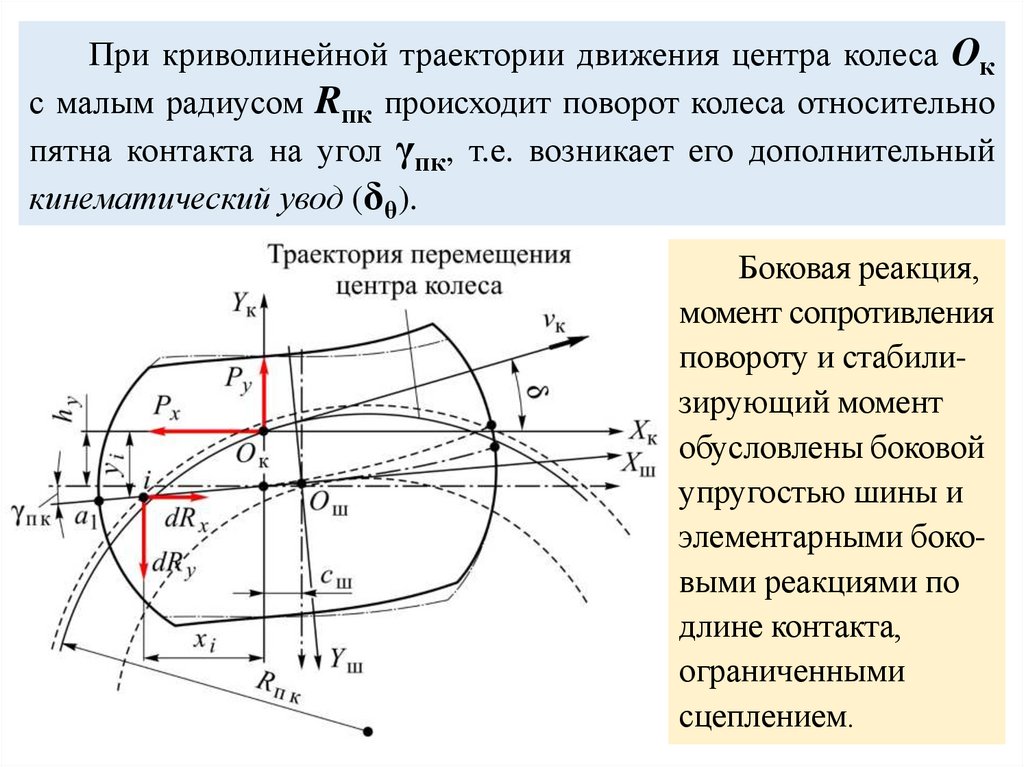
При криволинейной траектории движения центра колеса Ок
с малым радиусом Rпк происходит поворот колеса относительно
пятна контакта на угол γпк, т.е. возникает его дополнительный
кинематический увод (δθ).
Боковая реакция,
момент сопротивления
повороту и стабилизирующий момент
обусловлены боковой
упругостью шины и
элементарными боковыми реакциями по
длине контакта,
ограниченными
сцеплением.

47.

В упрощенной расчетной схеме проекцию плоскости
симметрии жесткого обода на горизонтальную плоскость в зоне
контакта можно представить отрезком длиной l = bшx. Радиусы
кривизны Rпк0, Rпкl центра и начала контакта, а также его длина
l определяют угол αl , в пределах которого происходит изменение
боковых перемещений i-х точек контакта в зависимости от угла
поворота θк, относительно плоскости прямолинейного качения.
При качении и повороте
обода шина деформируется в
боковом направлении, а точка
входа в контакт не имеет боковых
перемещений.
При отсутствии скольжения
точки контакта шины с ОП
неподвижны и поворот обода
происходит относительно них.

48.

Рассматривается кинематический увод при повороте колеса. В
основном изменяется и оценивается момент сопротивления
повороту, причем его величина зависит от радиуса поворота (при
радиусе более 3 м он имеет малое значение).
Для оценки момента сопротивления повороту может быть
использована зависимость:
M сп θ
где
M спθ0
0,925 0,15 Rпк0 bш y
Mсп θ 0 – момент сопротивления повороту колеса на месте;
bш y и Fш – ширина и площадь контакта, соответственно.
M спθ0 0,375 φ Rz Fш

49.

Суммарный угол δΣ, обусловленный углами силового δP y и
кинематического δθ увода:
При прямолинейном
движении КМ угол
кинематического увода
равен углу схождения
колеса:

50.

Для обеспечения устойчивого прямолинейного движения КМ
и уменьшения колебаний колес их устанавливают с развалом и
схождением.
При наклоне плоскости колеса
относительно продольно-вертикальной
плоскости на угол поперечного наклона
(развала) γкy вследствие боковой
деформации
шины
возникает
дополнительная боковая реакция:
и возрастает суммарная боковая реакция:

51.

Для определения боковой реакции по углу увода (Ry = kyγδ)
необходимо корректировать коэффициент ky, полученный при γкy = 0.
Однако в большинстве случаев вводят понятие угла
кинематического увода δγ наклоненного колеса. Такое колесо
всегда стремится катиться с уводом в сторону наклона под углом
где kγ – коэффициент пропорциональности, определяемый
экспериментальным путем, kγ = 0,15...0,25 ≈ 0,2.
При действии внешней боковой силы и наклоне колеса
суммарная боковая реакция определяется выражением
Экспериментально установлено, что при угле γкy = 10°
коэффициент ky уменьшается не более чем на 5 %.

52.

Для компенсации влияния развала колеса используют еще и
соответствующее схождение, добиваясь при этом, чтобы боковая
реакция в контакте стала равной нулю (Ry = 0). Тогда угол
схождения колеса
Правильно установленное на КМ с развалом и схождением
колесо всегда катится с уводом, но при отсутствии боковой
реакции в контакте. Это позволяет не учитывать углы установки
колес в расчетах КМ.
При уравновешенности боковых реакций от наклона и
схождения колеса на него действует стабилизирующий момент,
обусловленный разными точками приложения указанных
реакций в контакте колеса с ОП.

53.

При оценке маневренности КМ большое значение имеют
затраты энергии на криволинейное движение, а также моменты и
силы, действующие на колеса. Упрощенные уравнения
мощностного и силового балансов при криволинейном движении
колеса имеют вид
где

54.

Рассмотренные выше зависимости Ry(δ) справедливы для
установившегося криволинейного движения. Однако в ряде
процессов, связанных с управляемостью КМ, необходимо
учитывать влияние кривизны траектории колеса. Для этого
предпочтительнее использовать теорию качения эластичного
колеса, разработанную М.В. Келдышем.
Рассмотрим наиболее простой случай: угол развала γк y = 0,
скольжение в зоне контакта отсутствует (SбΣ = 0), деформации
шины малы, нормальная реакция Rz = const, а продольная Rx = 0,
т.е. свободный режим качения.
Боковая
сила
в
зоне
упругих
определяется линейным уравнением
боковых
деформаций
.

55.

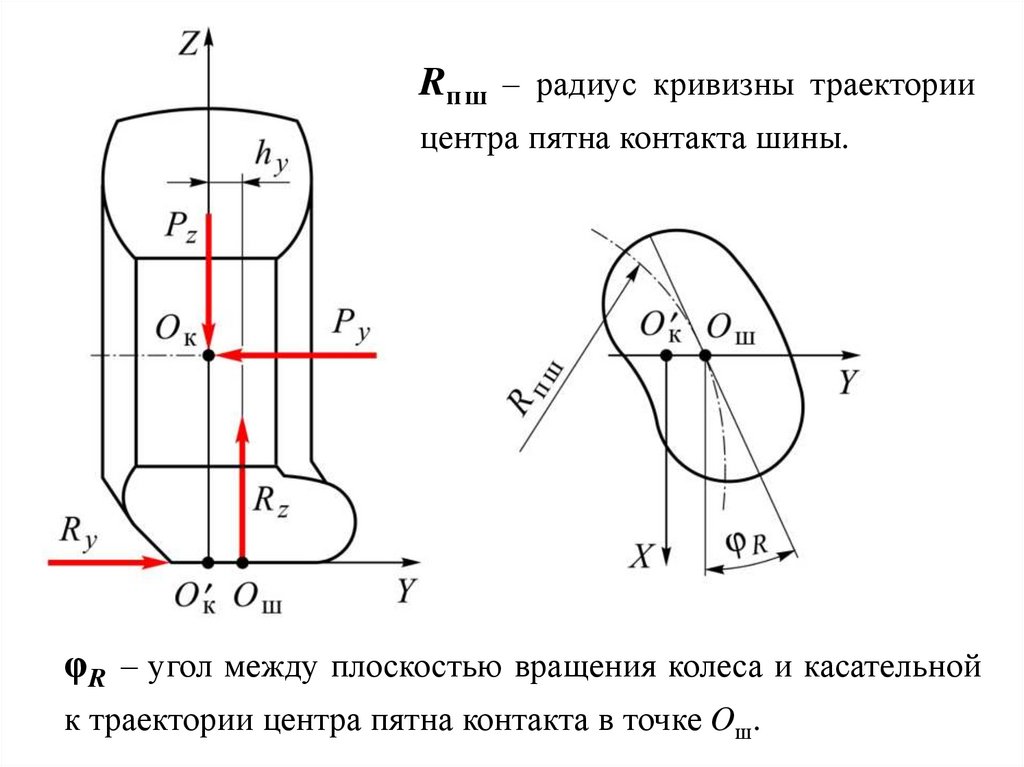
Rп ш – радиус кривизны траектории
центра пятна контакта шины.
φR – угол между плоскостью вращения колеса и касательной
к траектории центра пятна контакта в точке Oш.

56.

Кривизна траектории качения шины:
α и β – постоянные коэффициенты;
hy – перемещение цента обода колеса (точка Oк) относительно
центра пятна контакта (точка Oш).
В общем случае неустановившегося движения устанавливается
связь между силой и кинематическими параметрами:
bшx – длина контакта шины с ОП.