Учебные дисциплины: ППП, «Физические основы микро- и наноэлектроники» 2

1.

Учебные дисциплины: ППП, «Физические
основы микро- и наноэлектроники» 2

2.

Электропроводность полупроводников
В отсутствие внешнего поля свободные электроны и дырки находятся в
равновесном состоянии и совершают (при температуре ) хаотическое
движение в объеме полупроводника, средняя тепловая скорость носителей
заряда
велика (например, при T 0K ).
Электроны и дырки испытывают рассеяние - изменяют направление и
скорость своего движения при столкновениях с узлами кристаллической
решетки, дефектами решетки, атомами примесей.
В результате рассеяния устанавливается равновесное их распределение, при
этом средняя скорость движения носителей заряда в любом направлении .
0
При воздействии электрического поля на полупроводник средняя скорость
движения носителей заряда становится не равной нулю ( 0) в
направлении, определяемом направлением напряженности электрического
поля Е, она называется дрейфовой скоростью. Движение носителей заряда
под воздействием электрического поля называется дрейфом.
2

3.

Электропроводность полупроводников
jn en nE
,
, (3.1)
nE n E
. (3.2)
jn en n E
. (3.3)
Сравнивая выражение (3.3) с выражением для закона Ома в дифференциальной форме
-
где
n
jn n E
Уд
электрическая проводимость, найдем выражение для проводимости:
n en n
n p e n n p p
, (3.4)
3

4.

Выражение (3.4) справедливо при значениях напряженности поля E , не
превышающих некоторое критическое значение E
, т. е. при , при
кр
которых подвижности носителей заряда не зависят от напряженности
электрического поля и остаются постоянными.
При E Eкр носители заряда приобретают за время свободного пробега
между столкновениями дрейфовую составляющую скорости, сравнимую со
скоростью теплового движения
.
При этом происходит насыщение скорости дрейфа, она перестает возрастать
вследствие увеличения числа столкновений в единицу времени. Поэтому при
E Eкр
с ростом напряженности подвижность уменьшается, эта
зависимость выражается эмпирической формулой
0 Eкр / E 1 / 2
где
- подвижность, соответствующая критической напряженности, т.
0
е. по существу ее номинальное значение.
Подвижности электронов и дырок несколько различаются из-за разницы их
эффективных масс: n . p Как следует из (3.2), чем больше
подвижность, тем больше дрейфовая скорость носителей заряда и тем
выше быстродействие полупроводникового прибора.
4

5.

Подвижность носителей заряда зависит от многих факторов,
важнейшими из которых являются:
температура T ,
концентрация примесных атомов N
и напряженность электрического поля при E E кр
.
Зависимость подвижности от температуры определяется
преобладающим механизмом рассеяния носителей заряда, под
которым понимаются действия или последовательность действий,
приводящие к рекомбинации.
Основные из механизмов рассеяния - на тепловых колебаниях решетки и
ионизированных примесях, учитывая, что первый из них является
определяющим при высоких, а второй - при низких температурах.
Движение электронов в полупроводнике удобно описывать, пользуясь
понятием средней длины свободного пробега
, равной
среднему пути, который проходит электрон между двумя
последовательными актами рассеяния. Если электрон уже в единичном
акте рассеяния полностью потерял свою скорость в первоначальном
направлении, то
5

6.

где
- средняя скорость движения электрона;
- среднее
время релаксации, равное среднему времени свободного пробега
электрона.
Время релаксации характеризует скорость установления равновесного
состояния в системе, выведенной из этого состояния. Время релаксации
количественно определяется как время, в течение которого разность
неравновесной и равновесной концентраций
уменьшается в
n
n
0
раз .
Часто, однако, для того чтобы скорость в направлении первоначального
движения стала равной нулю, требуется не одно, а в среднем
е
столкновений электрона с рассеивающими центрами. При этом средний
путь
(3.5)
L
Из (3.5) можно определить среднее время релаксации
/
(3.6)
Величина называется эффективностью столкновений. В квантовой механике
дается выражение для подвижности через введенные с помощью (3.5) и (3.6)
параметры. Подвижность электронов в невырожденном полупроводнике
n
e
mn
(3.7)
6

7.

Установление зависимости подвижности от температуры сводится к
определению температурной зависимости параметров и .
Рассеяние на тепловых колебаниях решетки (на фононах).
Подобно тому, как электромагнитное поле излучения можно трактовать как
набор световых квантов — фотонов, поле упругих колебаний, заполняющих
кристалл, можно считать совокупностью квантов нормальных колебаний
решетки - фононов.
Аналогично фотону фонон обладает не только энергией, но и импульсом.
Однако фононы не являются частицами в обычном смысле. Появляясь в
результате квантования нормальных колебаний, они представляют собой
корпускулярный аспект описания коллективных волновых движений,
охватывающих кристалл.
Средняя длина свободного пробега электронов должна, очевидно, быть
обратно пропорциональна концентрации фононов n ф , т. е.
~ 1 /.n
ф
Известно, что при высоких температурах nф ~ T , поэтому
~ 1/ T (3.8)
В области высоких температур фононы обладают импульсом, по порядку
величины равным импульсу электронов проводимости, что делает возможным
прекращение движения электрона в данном направлении уже в единичном
акте его столкновения с фононом, поэтому
1 .
7

8.

Подставив (3.8) в (3.7) и учитывая, что средняя скорость , получим
n ~ T
3 / 2
Рис. 3.1. Рассеяние
носителей заряда на
тепловых колебаниях
решетки
при различных
температурах (T2 T1 );
A1 и A2 - амплитуды
колебаний узлов решетки
при температурах T1 и T2
.
8

9.

Рассеяние на ионизированных примесях.
Из всех примесей, содержащихся в полупроводниковом кристалле,
наибольшее влияние на рассеяние носителей заряда оказывают
ионизированные примеси. Это связано с тем, что кулоновское поле,
созданное такой примесью, действует на большом расстоянии и вызывает
отклонение траектории носителей, движущихся даже сравнительно далеко от
атома примеси
при рассеянии на примесных атомах должна быть обратно
Величина
пропорциональна концентрации этих атомов
и не зависеть от температуры
N
~ 1 / N const
(3.9)
Решение задачи об определении эффективности столкновений носителей
заряда с ионизированными атомами примесей приводит к следующему
2
результату
4
~ mn
(3.10)
Ze
Ze -
где - относительная диэлектрическая проницаемость полупроводника;
заряд ионизированной примеси.
9

10.

Из (3.10) следует, что чем выше скорость движения носителей заряда, больше их
эффективная масса и сильнее ослабляется поле в кристалле (чем выше
), тем
слабее носители отклоняются полем заряженной примеси, поэтому требуется
большее число столкновений для прекращения движения в первоначальном
направлении. С увеличением же заряда рассеивающего иона Ze число
столкновений
должно, естественно, уменьшаться.
Так как в невырожденном полупроводнике
(3.11)
~T2
~ T
, то
Подставляя (3.9) и (3.11) в (3.7), получим
n ~ T 3/ 2
10

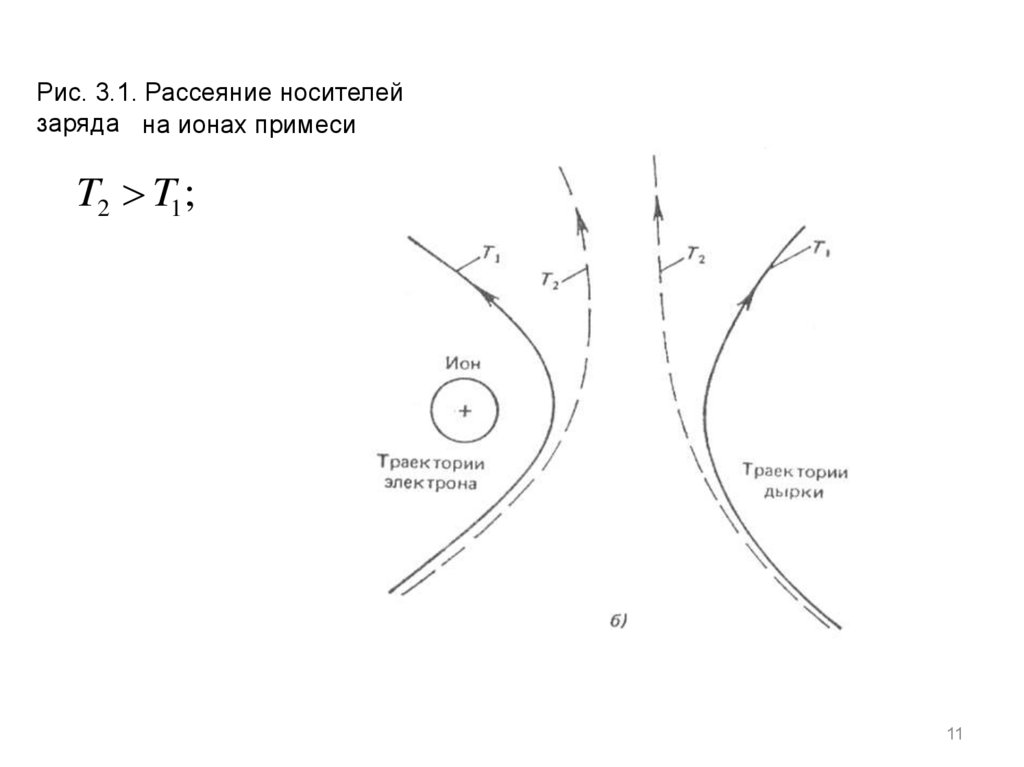
11.

Рис. 3.1. Рассеяние носителей
заряда на ионах примеси
T2 T1;
11

12.

На рис. 3.2 показаны кривые температурной зависимости подвижности
при различных значениях концентрации легирующей примеси в
невырожденном полупроводнике.
Рис. 3.2. Зависимость
подвижности носителей
заряда от температуры в
невырожденном
полупроводнике при
различных концентрациях
примеси:
N'Д N Д
12

13.

Зависимость подвижности от концентрации легирующей примеси
Зависимость подвижности от концентрации легирующей примеси N сложная
и в целом аналитически не описывается.
p для кремния приведены на
Экспериментальные зависимости
n и
рис.3.3. Примеси являются центрами рассеяния в полупроводнике,
увеличение их концентрации приводит к уменьшению средней длины
свободного пробега носителей (3.9), а значит - к снижению их подвижностей.
Рис. 3.3. Зависимость
подвижности электронов и
дырок в кремнии от
концентрации легирующей
примеси N при
T 293K
13

14.

Подвижность при одновременном действии нескольких механизмов
рассеяния.
Два или более механизмов рассеяния носителей заряда могут действовать
одновременно. Необходимо оценить их совместное влияние на подвижность.
Рассмотрим некоторое количество носителей заряда, например электронов,
в полупроводнике, которые рассеиваются за время dt.
Вероятность того, что электроны рассеиваются за время dt по i-ому
механизму равна dt/τi , где τi – среднее время между двумя
последовательными актами рассеяния по i-ому механизму.
Полная вероятность рассеяния электронов за интервал времени dt
равна dt/ τ , где τ – среднее время рассеяния, обусловленное одновременным
действием всех механизмов рассеяния. В то же время, она равна сумме
вероятностей рассеяния по всем действующим механизмам, то есть
n
dt/ τ = Σ dt/τi.
i=1
Здесь n – число действующих в полупроводнике механизмов рассеяния.
14

15.

Из полученного выражения можно сделать следующие выводы:
- среднее время рассеяния τ, обусловленное всеми механизмами рассеяния,
действующими одновременно, меньше времени рассеяния, обусловленного
каким-либо одним из действующих механизмов;
- среднее время рассеяния τ определяется наименьшим временем рассеяния,
из всех времён рассеяния τi, характеризующих различные механизмы
рассеяния.
С учётом выражений (3.6), (3.7) можно записать для подвижности
n
1/ μ = Σ 1/ μ i.
i=1
Здесь μi – подвижность, определяемая i-ым механизмом рассеяния. Отсюда
следует, что результирующее значение подвижности μ определяется тем
механизмом рассеяния, которому соответствует наименьшее τi.
15

16.

i
Собственная электропроводность полупроводников
Полупроводники высокой степени очистки при не слишком низких
температурах обладают собственной электрической проводимостью
i
.
Поскольку в собственном полупроводнике концентрации свободных
электронов и дырок равны: n p n то (3.4) можно переписать в виде .
l
i eni n p
С учетом выражений (2.38), (2.39) и (2.42), определяющих
собственная электрическая проводимость
2 mn m p kT
g
exp
n
p
i 2e
2
2kT
h
3/ 2
ni
,
g
0 exp 2kT
(3.12)
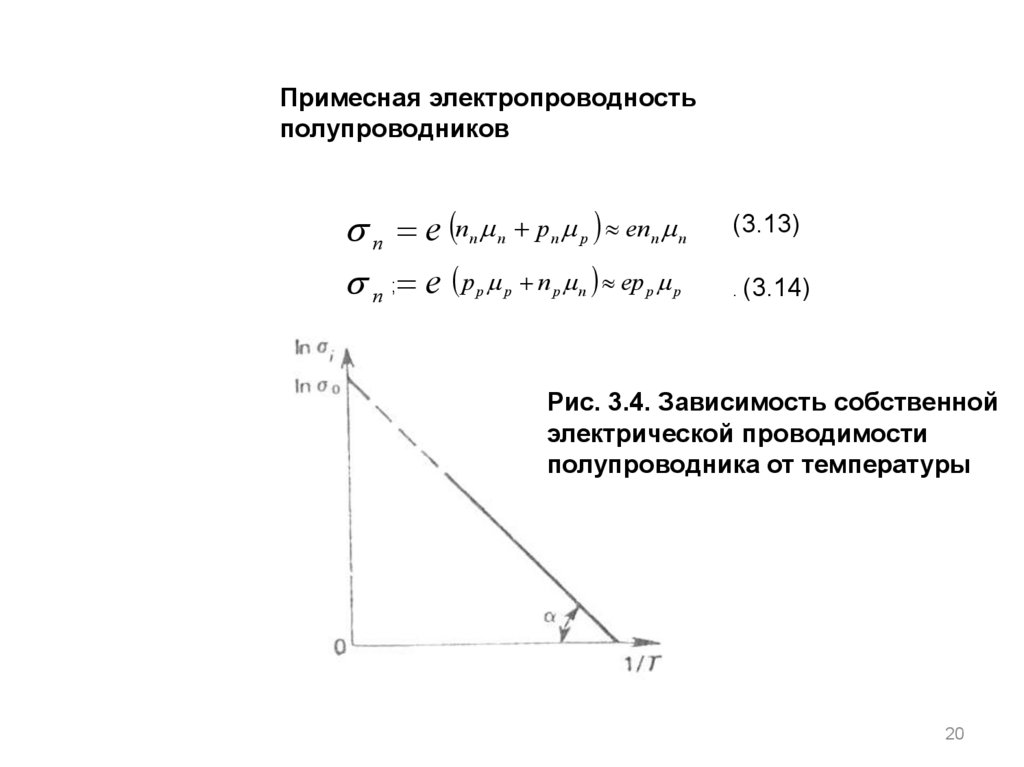
Из (3.12) видно, что при T i 0 . На рис.3.4 зависимость
представлена в логарифмических координатах . При заданной
температуре концентрация носителей заряда и электрическая
проводимость собственного полупроводника определяются шириной его
запрещенной зоны .
16

17.

Рис. 3.4. Зависимость собственной электрической проводимости
полупроводника от температуры
17

18.

.
Рис. 3.2. Зависимость подвижности носителей заряда от температуры в
невырожденном
полупроводнике при различных концентрациях примеси
N'Д N Д
18

19.

.
Рис. 3.3. Зависимость подвижности электронов
в кремнии от концентрации легирующей примеси
n
N
и дырок
p
при
T 293K
19

20.

Примесная электропроводность
полупроводников
n e n
n ; e p
n
p
n
p
p n p enn n
(3.13)
n p n ep p p
. (3.14)
Рис. 3.4. Зависимость собственной
электрической проводимости
полупроводника от температуры
20

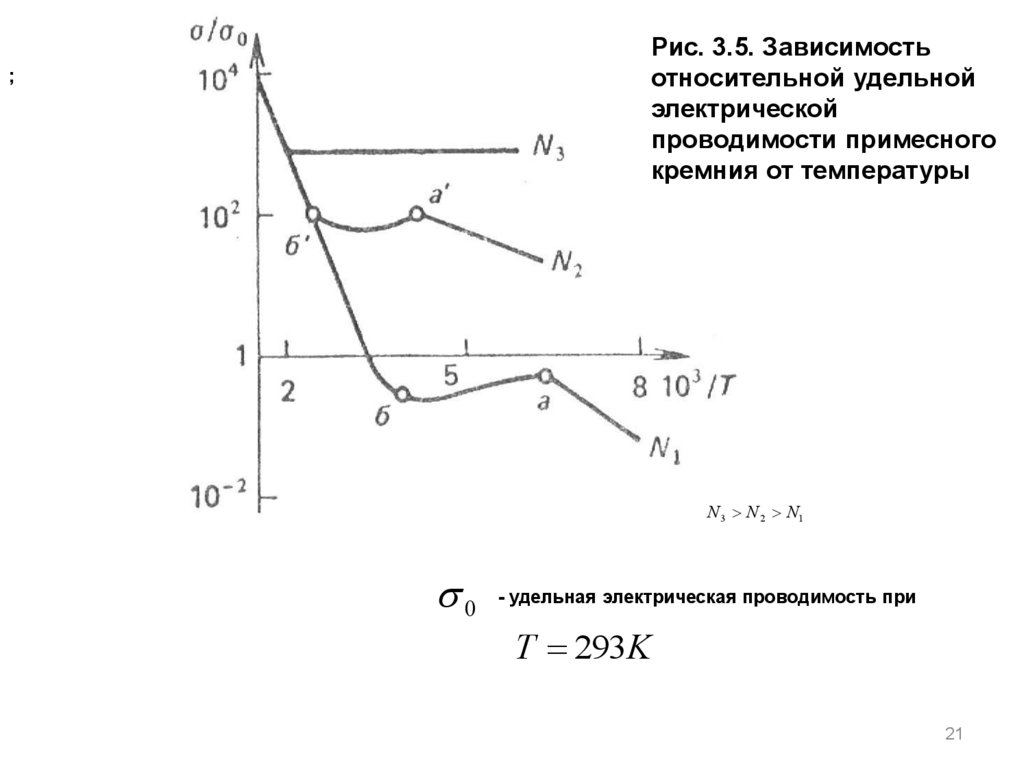
21.

Рис. 3.5. Зависимость
относительной удельной
электрической
проводимости примесного
кремния от температуры
;
N 3 N 2 N1
0
- удельная электрическая проводимость при
T 293K
21

22.

Неравновесные носители заряда и их основные
характеристики.
Воздействие света, электрического поля и других
факторов может привести к появлению дополнительных,
избыточных по отношению к равновесным, концентраций
свободных носителей заряда, их называют
неравновесными носителями заряда.
Они являются дополнительными по отношению к
равновесным и созданы под действием внешнего фактора
(например излучения).
При неизменной интенсивности внешнего фактора в
полупроводнике устанавливается стационарное состояние,
при котором скорости генерации и рекомбинации
носителей заряда равны.
22

23.

В этих условиях концентрации избыточных носителей заряда равны:
и p n n n и p p p , где
0
0
n
постоянные концентрации электронов и дырок при наличии внешнего
фактора;
то же, в отсутствие внешнего фактора, т. е.
0 и p0
равновесные концентрации.
Если в полупроводнике нет объемного заряда, то выполняется условие
его электрической нейтральности:
n
.
n p
Различают низкий и высокий уровни возбуждения полупроводника. При низком
уровне возбуждения концентрация избыточных носителей заряда много меньше
концентрации основных носителей, но может значительно превышать
концентрацию неосновных носителей. При высоком уровне возбуждения
концентрация избыточных носителей заряда значительно выше равновесных.
После прекращения воздействия внешнего фактора, вызывающего генерацию
избыточных носителей заряда, их концентрации из-за рекомбинации быстро
23
уменьшаются и достигают равновесных значений.

24.

Скорость, с которой протекает рекомбинация, определяется временем
жизни неравновесных носителей заряда
.
Время жизни - это среднее время существования носителя заряда
(электрона, дырки) от его возникновения (генерации) до исчезновения
(рекомбинации, захвата ловушкой).
Рассмотрим, от каких факторов зависит . Выделим в
полупроводнике плоскопараллельный слой толщиной (рис. 3.6),
перпендикулярный направлению движения электрона.
В смысле захвата электрона каждую дырку можно рассматривать
как сферу радиуса r , при попадании в которую электрон
испытывает столкновение и захватывается дыркой.
Сечение захвата электрона дыркой :
A r 2
n
Электрон, проходя через слой и попадая в один из таких дисков,
будет захвачен дыркой.
Обозначим площадь выделенного слоя S , объем этого слоя
,
число дырок в нем: pSdx , где p - концентрация дырок.
Суммарная площадь захвата электрона дырками при прохождении
им слоя толщиной dx :
Sdx
S захв Аn pSdx
24

25.

Рис. 3.6. К определению времени
жизни электронов.
25

26.

Вероятность того, что электрон при прохождении испытывает
столкновение с дыркой:
Wn S захв / S An pdx
Учитывая, что
(3.17)
dx n dt
, разделим левую и правую части (3.17) на
и найдем вероятность столкновения электрона с
dt
дыркой в единицу времени:
Pn An p n
Такое столкновение заканчивается рекомбинацией, поэтому Pn
представляет собой вероятность рекомбинации электрона в
единицу времени.
Величина n , обратная Pn , представляет собой среднее
время жизни электрона в свободном состоянии:
1
1
n
Pn An n p
(3.18)
26

27.

Аналогичное выражение можно записать для среднего времени
жизни дырок:
1
1
p
Pp Ap p n
(3.19)
A p - сечение захвата дырки электроном; p - скорость
где
движения дырки относительно электронов;
- концентрация
электронов.
В полупроводниках захватывать электроны могут не только дырки, но и
различные локальные центры, создающие в запрещенной зоне
дискретные уровни. Произведение сечения захвата на скорость
движения носителя заряда, усредненное по всем носителям в зоне,
называется коэффициентом рекомбинации , т. е. для электронов и
дырок можно записать
n
n An n
(3.20)
p Ap p
(3.21)
27

28.

n
1
np
1
p
pn
Скорость рекомбинации измеряется числом носителей заряда,
ежесекундно рекомбинирующих в единице объема полупроводника.
Для неравновесных носителей заряда она равна произведению
вероятности рекомбинации носителя в единицу времени на
избыточную концентрацию. Для электронов и дырок скорость
рекомбинации
дn
n
Rn
Pn n
n p n
дt
n
дp
p
Rp
Pp p
p n p
дt
p
28

29.

Механизмы рекомбинации
С точки зрения механизма протекания различают рекомбинацию:
межзонную, через локальные уровни и поверхностную.
Межзонная рекомбинация. При межзонной (непосредственной)
рекомбинации происходит переход электрона из зоны
проводимости непосредственно на свободный уровень валентной
зоны.
При таком переходе освобождается энергия, примерно равная
ширине запрещенной зоны, которая может выделяться в виде
кванта излучения (фотона) или превращаться в энергию тепловых
колебаний решетки (фононов).
В соответствии с этим различают межзонную рекомбинацию:
излучательную и фононную.
Вероятность межзонной рекомбинации очень мала, более
вероятны переходы носителей заряда через локальные уровни,
расположенные в запрещенной зоне.
29

30.

Рекомбинация через локальные уровни.
На рис. 3.7, а, б показаны энергетические диаграммы
полупроводника, содержащего глубокий локальный уровень
мелкие локальные уровни ' л и ' ' л .
л
и
Захват электрона глубоким уровнем отображается переходом 1 (рис.
3.7,а).
30

31.

После захвата электрон может быть переброшен обратно в зону
проводимости (переход 3) или перейти в валентную зону, что
эквивалентно захвату заполненным локальным уровнем дырки из
валентной зоны (переход 2). Первый из этих процессов - обратный
тепловой переброс электрона - в рекомбинации роли не играет, второй
процесс приводит к рекомбинации электрона и дырки.
Для мелких локальных уровней вероятность обратного теплового
переброса электрона очень велика. Поэтому в этом случае процесс
сводится к энергичному обмену электронами локального уровня
и зоны проводимости, локального уровня и валентной. Такие
локальные уровни принято называть центрами прилипания.
При наличии глубокого локального уровня. Для осуществления теплового
переброса в зону проводимости (переход 3 на рис. 3.7, а) электрон должен
поглотить одновременно несколько фононов, так как энергии одного фонона
для этого недостаточно. Поэтому вероятность теплового переброса электрона в
зону проводимости незначительна.
Более вероятен переход электрона в валентную зону (переход 2),
заканчивающийся его рекомбинацией с дыркой. Вероятность встречи дырки с
локализованным неподвижным электроном значительно выше вероятности
встречи с подвижным электроном. Поэтому глубокие локальные уровни
31
являются эффективными центрами рекомбинации.

32.

Поверхностная рекомбинация
Следует учитывать, что приповерхностный слой имеет особую зонную
структуру (много локальных энергетических уровней), а значит, и
отличные от объёмных количественные параметры.
Если рабочий участок полупроводниковой пластины частично
расположен в объеме, а частично - в приповерхностном слое, то
время жизни неравновесных носителей заряда связано с временами
их жизни в объеме
и у поверхности
соотношением:
s
v
1/ 1/ v 1/ s
Как правило, из-за большой концентрации ловушек вблизи поверхности
s v поэтому
ближе к
s.
Рассмотрим полупроводник, в запрещенной зоне которого имеется
поверхностный рекомбинационный центр s . Пусть в нем
равномерно по всему объему генерируются неравновесные носители
заряда, обозначим их избыточные концентрации через n и p .
32

33.

Наличие у поверхности полупроводника уровня s , выполняющего
роль «стока» для неравновесных носителей заряда, приводит к
возникновению направленных потоков носителей к поверхности,
пропорциональных значениям их избыточной концентрации
jn / e Sn n
j
j p / e S p p
где , n , j p - плотности тока электронов и дырок;
- заряд
электрона; ,
, S
- коэффициенты пропорциональности.
Sn
p
В условиях равновесия ток через поверхность равен нулю, поэтому
эти плотности тока равны друг другу. Число носителей заряда,
ежесекундно рекомбинирующих в единице площади поверхности:
e
qS j p / e jn / e Sn n S p p
(3.25)
Из (3.25) видно, что S n и S p выражают относительную долю избыточных
носителей заряда, ежесекундно рекомбинирующих в единице площади
поверхности полупроводника, эти коэффициенты имеют размерность скорости и
называются скоростями поверхностной рекомбинации электронов и дырок.
Связь между скоростью поверхностной рекомбинации и временем жизни в
(3.25)
общем случае установить трудно.

34.

.
V0
.
Работа выхода и контактная разность
потенциалов
Положительные ионы, образующие
решетку металла, создают внутри него
электрическое поле с положительным
потенциалом, периодически
изменяющимся при движении вдоль
прямой, проходящей через узлы
решетки .
Этим изменением пренебрегают и
считают потенциал вл всех точках
одинаковым и равным V 0
Свободный электрон в таком поле имеет потенциальную энергию
eV0
34

35.

Движение носителей заряда в полупроводниках.
Движение носителей заряда в полупроводнике в общем случае
обусловлено двумя процессами: диффузией под действием градиента
их концентрации и дрейфом под действием электрического поля.
Полный ток, таким образом, состоит из четырёх составляющих.
Запишем выражение для его плотности:
j n j nE j nD j pE j pD
j pE - дрейфовые, а j nD , j pD - диффузионные составляющие
,
где j nE,
плотности тока электронов и дырок, соответственно.
Уравнение непрерывности.
Поведение неравновесных носителей заряда в полупроводниках
описывается уравнением непрерывности. Рассмотрим его
содержание.
Предположим, что в полупроводнике p - типа в направлении оси
существует градиент концентрации электронов dn / dx 0 и
действует электрическое поле напряженностью E x . Выделим в
полупроводнике слой толщиной dx , расположенный перпендикулярно
оси
с площадью поперечного сечения 1м x 1м (рис. 3.9).
x
x
35

36.

Рис. 3.9. К выводу уравнения
непрерывности
36

37.

Объем этого слоя равен dx . Концентрации носителей заряда
зависят от двух переменных - координаты x и времени t .
Обозначим концентрацию электронов в слое в момент времени
через n x, t , а в момент времени t dt - через n x, t dt
Изменение числа электронов в слое за время dt составит
.
t
.
дn
n x, t dt n x, t dx dtdx
дt
Оно вызывается протекающими в слое процессами генерации и
рекомбинации, а также диффузией и дрейфом носителей заряда.
В результате генерации за время dt в слое объемом dx
ионизирующий фактор создает g dx dt электронов, где g
скорость генерации электронов.
Вследствие рекомбинации в единицу времени в единице объема
n n0
полупроводника исчезнет свободных электронов
R
За время в объеме убыль электронов составит:
n n0
n
n
dxdt
37

38.

x
Наличие градиента концентрации и внешнего поля в направлении оси
приведет к тому, что поток электронов J n x , втекающий в слой dx, будет
не равен потоку J n x dx , вытекающему из слоя.
Изменение числа электронов за время dt , вызванное различием этих
потоков, описывается соотношением
J n x J n x dx dt дJ n dxdt
дx
Полное изменение числа электронов в слое за время dt составит
дJ n
n n0
дn
dtdx
dtdx
g
дt
n
дx
Сократив обе части этого уравнения на dtdx , получим уравнение
непрерывности для избыточных электронов
дn
дJ n
n n0
g
дt
дx
n
(3.26)
38

39.

Аналогичное уравнение можно получить для избыточных дырок:
дJ p
дp
p p0
g
дt
дx
p
(3.27)
Преобразуем выражения (3.26) и (3.27). Поток электронов
удобно выразить через плотность тока: J j / e , где
n
n
заряд электрона.
Плотность дрейфового тока электронов:
Jn
e
j nE en n E x
где n - подвижность электронов, а
- их концентрация.
Плотность тока, обусловленного диффузией электронов,
пропорциональна градиенту концентрации:
n
j nD
дn
eDn
дx
39
-

40.

Коэффициент пропорциональности D n называется коэффициентом
диффузии.
Плотность тока, обусловленного дрейфом и диффузией электронов,
дn
j n e n n E x Dn
дx
Аналогичное выражение можно получить для плотности тока дырок
дp
j p e p p E x D p
дx
Знак минус у диффузионной составляющей плотности тока дырок
указывает на то, что направление диффузионного тока
противоположно градиенту их концентрации. Заменив в (3.26), (3.27)
потоки J n и J p плотностями тока, получим уравнения
непрерывности в виде:
p p0
дp
д2 p
дp
Dp 2 Ex p
g
дt
дx
p
2
дx
n n
дn
д n
дn
Dn 2 E x n
g
дt
дx
n
дx
(3.28)
0
(3.29)
40

41.

Диффузионная длина носителей заряда
Используем уравнение непрерывности для решения задачи о
распределении неравновесных носителей заряда вдоль
полупроводника, на одном конце которого поддерживается постоянная
избыточная концентрация электронов n n n
.
0
0
dp
dn
0
Для стационарного случая, когда dt 0 и dt
, при
условии, что электрическим полем E x
и генерацией
носителей заряда в объеме полупроводника можно пренебречь,
выражение (3.28) принимает вид
d 2 n n n0
2
Dn n
dx
(3.34)
Запишем граничные условия этого дифференциального уравнения:
при
,
(n n0 ) n0 и при x (n n0 ) 0
Решение уравнения
(3.34) записывается так:
x
x 0
n n n0 n0 exp
D
n n
(3.35)
41

42.

Выражение (3.35) определяет закон убывания концентрации
избыточных носителей заряда вдоль полупроводника в стационарных
условиях.
Dn n имеет размерность длины, причем на
Величина
протяжении отрезка длиной D концентрация избыточных
n n
носителей заряда уменьшается в e раз .
Эта величина называется диффузионной длиной электронов:
Ln Dn n
(3.36)
Аналогично можно записать выражение для диффузионной длины
дырок:
L p D p p
(3.37).
Диффузионные длины - средние расстояния, на которых
концентрации неравновесных носителей заряда (электронов,
дырок) при их движении уменьшаются в е раз ( е – основание
42
натурального логарифма, примерно равное 2.72).

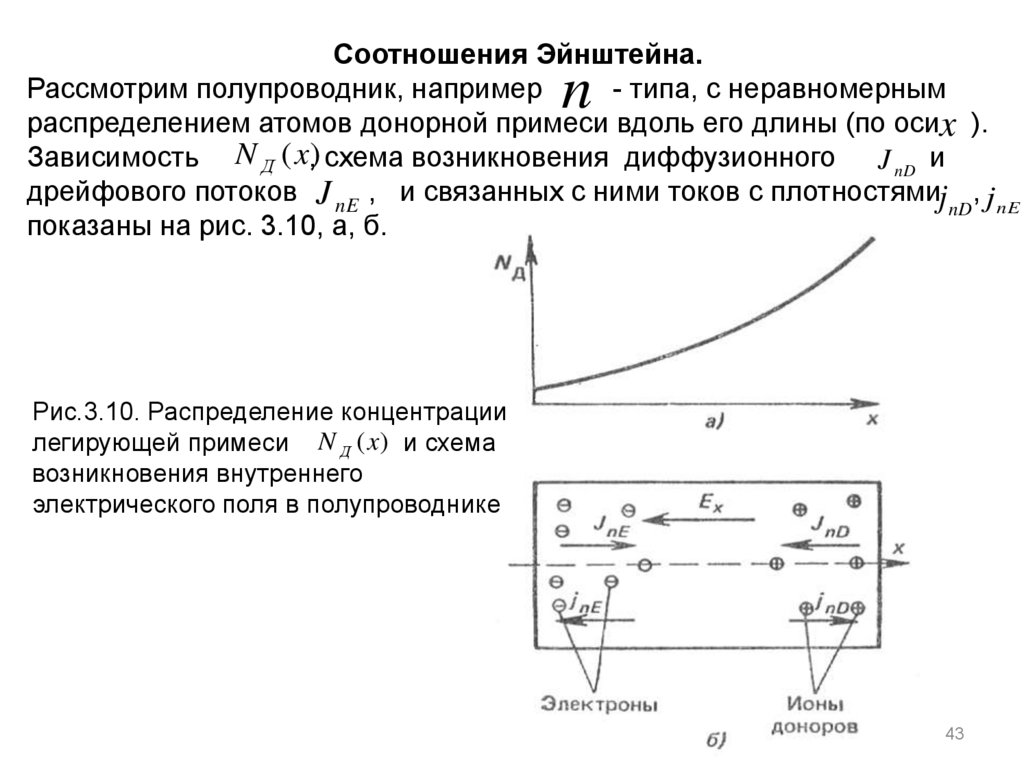
43.

Соотношения Эйнштейна.
Рассмотрим полупроводник, например
- типа, с неравномерным
распределением атомов донорной примеси вдоль его длины (по осиx ).
Зависимость N Д (x,) схема возникновения диффузионного J nD и
дрейфового потоков J nE , и связанных с ними токов c плотностямиj nD, j nE
показаны на рис. 3.10, а, б.
n
Рис.3.10. Распределение концентрации
легирующей примеси N Д (x) и схема
возникновения внутреннего
электрического поля в полупроводнике
43

44.

В результате диффузионного перетекания электронов появляются
нескомпенсированные объемные заряды: положительный заряд
ионизированных атомов доноров - в областях, из которых электроны
ушли, и отрицательный заряд электронов - в областях с низкой
концентрацией доноров, куда электроны пришли.
Образование объемных зарядов сопровождается возникновением
внутреннего (статического) электрического поля - встроенного
электрического поля, образующегося в объёме полупроводника,
имеющего неравномерное распределение легирующей примеси по
координате, с напряженностью E x и дрейфового тока, направленного
противоположно диффузионному. При достижении равновесного
состояния диффузионный и дрейфовый токи уравниваются:
en n E x
dn
eDn
dx
(3.30)
44

45.

Электроны, находящиеся в электрическом поле E x , обладают
потенциальной энергией, равной - e (x ), где (x ) - потенциал поля в
точке x .
В соответствии с законом больцмановского распределения, в условиях
равновесия концентрация электронов в области, охватывающей точку x
, равна n( x) c exp e ( x) , где c - коэффициент пропорциональности.
kT
Найдем производную
dn / dx
d ( x )
Ex
dx
, учтя, что
dn
e ( x) e
c exp
Ex
dx
kT kT
(3.31)
Подставив (3.31) в (3.30), получим:
kT
Dn
n T n
e
(3.32)
Аналогичное выражение можно записать для коэффициента диффузии
дырок:
kT
(3.33)
D
p
e
p
T
p
45

46.

Выражения (3.32) и (3.33) называются соотношениями Эйнштейна.
Они связывают коэффициенты диффузии носителей заряда с их
подвижностями. Поверхностные явления в полупроводниках.
Все энергетические уровни, разрешенные в полупроводниковом кристалле
неограниченных размеров, разрешены и в ограниченном кристалле.
Обрыв решетки приводит к тому, что вблизи поверхности кристалла
появляются разрешенные дискретные энергетические уровни или зоны в тех
областях энергии, которые запрещены для неограниченного кристалла.
Электроны, занимающие эти уровни, не могут проникать внутрь кристалла и
локализуются у его поверхности. Такие уровни называются поверхностными или
уровнями Тамма. Поверхностные уровни могут служить донорами,
акцепторами и центрами прилипания. Заполнение акцепторных уровней
означает локализацию электронов, а удаление электронов с донорных
уровней – локализацию дырок на этих уровнях, в результате чего
происходит заряжение поверхности отрицательным или положительным
зарядом.
В соответствии с условием электрической нейтральности оно должно
сопровождаться возникновением в приповерхностном слое объемного заряда,
нейтрализующего поверхностный заряд. Это осуществляется притяжением к
поверхности носителей заряда со знаком, противоположным знаку заряда на
поверхности, и отталкиванием носителей заряда одного с нею знака. В результате
приповерхностный слой полупроводника оказывается обедненным носителями
заряда одного знака с поверхносностным зарядом и обогащенным носителями
46
заряда противоположного знака.

47.

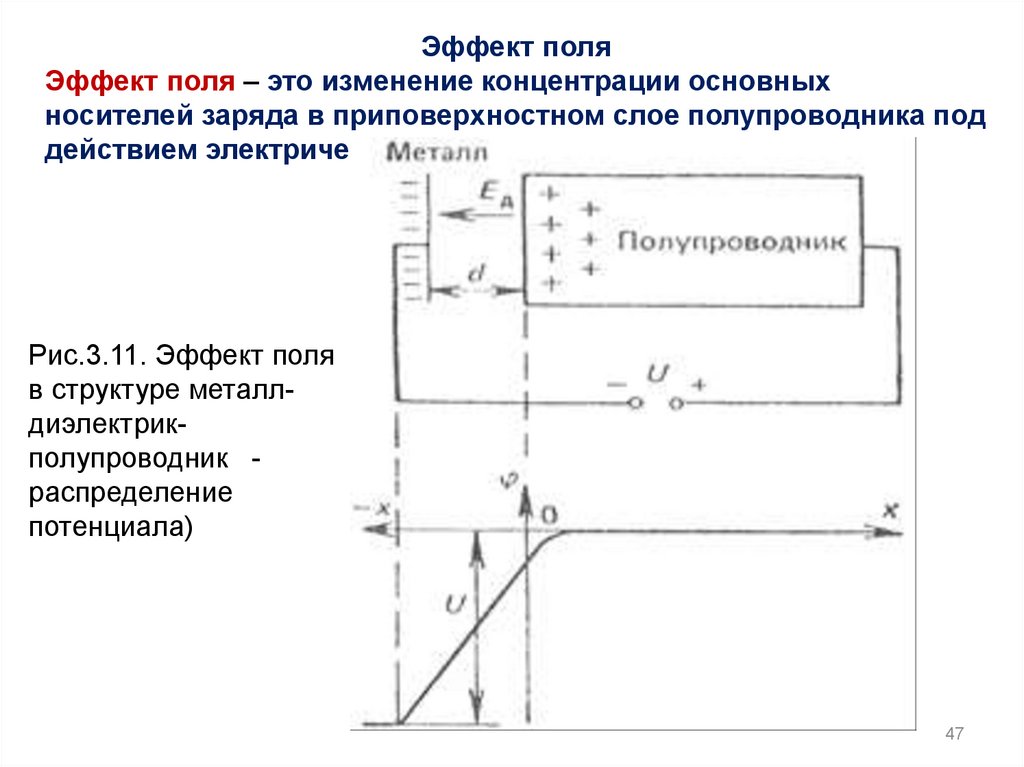
Эффект поля
Эффект поля – это изменение концентрации основных
носителей заряда в приповерхностном слое полупроводника под
действием электрического поля.
Рис.3.11. Эффект поля
в структуре металлдиэлектрикполупроводник распределение
потенциала)
47

48.

На металл подаётся положительный или отрицательный потенциал.
Заряд в полупроводнике, равный по значению и противоположный по
знаку заряду на металлической пластине, не находится на поверхности, а
сосредоточивается в его приповерхностном слое.
В металлах, имеющих очень высокую концентрацию носителей заряда ,
нейтрализация поверхностного заряда происходит уже на расстоянии, равном
нескольким параметрам решетки ~ 10 28 м 3 .
В полупроводниках область объемного заряда простирается на
6
значительную глубину ~ 10 м и более.
Обычно её принимают равной так называемой дебаевской длине
экранирования L
, определяемой как расстояние, на протяжении
D
которого потенциал поля в веществе со свободными носителями заряда
уменьшается в e раз . Расчеты показывают, что
1/ 2
1/ 2
для собственного полупроводника:
0 kT
LD 2
2e ni
0 T
2eni
Для примесного полупроводника с концентрацией ионизированной
примеси N
0 Т
LD
eN
1/ 2
48

49.

Поскольку N ni , значение LD в примесных полупроводниках много
меньше, чем в собственных.
Например, в собственном кремнии LD 14 мкм, а в примесном
22
3
кремнии с N Д 10 м LD 0,04
мкм при температуре T 300К.
Заряжение поверхности полупроводника вызывает возникновение
разности потенциалов между его поверхностью и объемом.
Следствием этого является искривление энергетических зон у
поверхности.
При заряжении поверхности отрицательным зарядом энергетические
зоны изгибаются вверх, так как при перемещении электрона из объема к
поверхности его энергия увеличивается.
При заряжении поверхности положительным зарядом зоны
изгибаются вниз. Изгиб простирается в глубь полупроводника примерно
на величину .LD .
Концентрации электронов и дырок в приповерхностном слое
полупроводника описываются соотношениями
i
n ni exp F
kT
(3.38)
i F
p ni exp
kT
(3.39)
49

50.

Из (3.38) и (3.39) видно, что если в приповерхностной области
полупроводника середина запрещенной зоны i располагается ниже
n ni p . Следовательно,
уровня Ферми, т. е. F t то
полупроводник в этой области обладает электропроводностью - типа.
n
В области, в которой i F , концентрации
полупроводник ведет себя как собственный.
n p ni
и
В области, в которой уровень Ферми F i , концентрации p ni n
и полупроводник имеет электропроводность
- типа.
p
Таким образом, могут иметь место обеднение, обогащение и
инверсия (рис. 3.12, а – в) – явления в приповерхностном слое
полупроводника, происходящие под действием электрического
поля, заключающиеся в уменьшении концентрации основных
носителей заряда, её увеличении или изменении типа
электропроводности, соответственно.
50

51.

Рис. 3.12.
Образование в
приповерхностной
области
полупроводника под
влиянием заряда на
поверхности
обеднённого (а) ,
инверсного (б) и
обогащённого (в)
слоев
51

52.

Обедненная область появляется в случае, когда на поверхности
полупроводника возникает заряд, по знаку совпадающий с основными
носителями заряда, а по значению - не настолько большой, чтобы вызвать
пересечение кривой, соответствующей середине запрещенной зоны , с
уровнем Ферми (рис. 3.12, а). Вызванный зарядом на поверхности изгиб
зон приводит к увеличению расстояния от уровня Ферми до дна зоны
проводимости в полупроводнике п - типа и до потолка валентной зоны в
полупроводнике р - типа. Увеличение этого расстояния сопровождается
обеднением приповерхностной области основными носителями заряда,
концентрация которых, как и концентрация неосновных носителей заряда,
оказывается много меньше концентрации примесных атомов (ионов
примеси). Заряд ионов примеси в приповерхностной области оказывается
нескомпенсированным зарядом подвижных носителей.
Инверсная область в приповерхностном слое полупроводника возникает
при высокой плотности поверхностного заряда, по знаку совпадающего с
основными носителями заряда (рис. 3.12, б). Кривая, соответствующая
середине запрещенной зоны , в этом случае пересекает уровень Ферми и
располагается выше его в полупроводнике п- типа и ниже - в полупроводнике
р- типа. Расстояние от уровня Ферми до потолка валентной зоны в
полупроводнике п - типа оказывается меньше расстояния до дна зоны
проводимости.
52

53.

Вследствие этого концентрация неосновных для полупроводника п- типа
носителей заряда - дырок в приповерхностном слое оказывается выше
концентрации основных носителей заряда - электронов, и тип
электропроводности в нем изменяется.
В полупроводнике р - типа расстояние от уровня Ферми до дна зоны
проводимости оказывается меньше расстояния до потолка валентной зоны,
вследствие чего концентрация неосновных носителей заряда – электронов в
приповерхностном слое оказывается выше концентрации основных носителей
заряда - дырок, и тип электропроводности в нем изменяется. Описанное
явление называется инверсией, а слои, в которых оно имеет место, —
инверсными.
Обогащенная область появляется в приповерхностном слое в случае,
когда знак поверхностного заряда противоположен знаку основных носителей
заряда в полупроводнике (рис. 3.12, в). Под влиянием заряда на поверхности
происходит притяжение к ней основных носителей и обогащение ими
приповерхностного слоя. Такие слои называются обогащенными.
53

54.

Большинство изделий микроэлектроники представляют собой
сугубо неоднородные структуры, важнейшими элементами
которых являются контакты: металл - полупроводник и двух
полупроводников с различным типом электропроводности ( р-п
переход).
Для анализа явлений, протекающих в приконтактных областях
удобно воспользоваться понятиями работы выхода и
контактной разности потенциалов.
Положительные ионы, образующие решетку металла, создают внутри
него электрическое поле с положительным потенциалом, периодически
изменяющимся при движении вдоль прямой, проходящей через узлы
решетки (рис. 3.13, а). В первом приближении этим изменением
пренебрегают и считают потенциал во всех точках металла одинаковым
и равным V 0 .
Свободный электрон в таком поле имеет потенциальную энергию eV
0
. На рис. 3.13, б показано изменение этой энергии при переходе из
металла в вакуум 0 , которое происходит на протяжении отрезка
, равного примерно параметру решетки. Металл является для
электрона потенциальной ямой, которую он не может свободно 54
покинуть.
0

55.

Рис. 3.13. К определению работы
выхода из металла (а, б) и
полупроводника (в).
55

56.

Для выхода электрона из металла требуется затрата определенной
энергии, называемой работой выхода. Даже при температуре T 0K
электроны в металле занимают все нижние энергетические уровни
потенциальной ямы вплоть до уровня Ферми поэтому для их
освобождения требуется энергия, меньшая 0
. Наименьшая
энергия требуется для удаления электронов с уровня FM (рис. 3.13,
б), её называют термодинамической работой выхода.
При температуре T 0 в зоне проводимости появляются электроны,
занимающие энергетические уровни выше уровня Ферми FM . Удаление
электронов с уровней, лежащих выше уровня FM , требует меньшей
затраты энергии, а с уровней, лежащих ниже уровня FM , - большей
затраты энергии, чем их удаление с уровня Ферми ; при таких удалениях
нарушается равновесное состояние системы. Учитывая это
обстоятельство, условились и при температурах T 0K работу
выхода отсчитывать от уровня Ферми до нулевого уровня. Еще
сложнее оказывается определение работы выхода из полупроводника.
Выход электронов здесь возможен из зоны проводимости с затратой
энергии ВН, с примесных уровней (зон) и различных уровней валентной
зоны с затратами энергии ПР , 1 , 2 и т.д. (рис. 3.13, в).
56

57.

К определению работы выхода из
металла и полупроводника
Рис. 3.13. К определению работы
выхода из металла (а, б) и
полупроводника (в).
57

58.

Поэтому и для полупроводника за работу выхода П принимают
энергетическое расстояние от уровня Ферми до нулевого
уровня, хотя на самом уровне на нём нет электронов. Работу выхода
обычно измеряют в электрон-вольтах (эВ). Отношение работы выхода,
к заряду электрона представляет собой потенциал выхода.
Контакт металл-металл.
Рассмотрим процессы, возникающие при контакте двух металлов (рис.
3.14). Работы выхода электронов из первого и второго металлов,
обозначим 1 и 2 , энергии Ферми FM 1и FM 2 (рис 3.14, а).
Приведем металлы в контакт, сблизив их на расстояние, при котором
возможен эффективный обмен электронами. В начальный момент
контакта из-за наличия разности уровней Ферми возникает
преимущественный переход электронов из второго металла в
первый, при этом они заряжаются. Этот переход прекращается
после выравнивания уровней Ферми. Между проводниками
устанавливается равновесие (рис. 3.14, б), оно сопровождается
возникновением между заряженными проводниками контактной
разности потенциалов 0, которая создает для электронов,
переходящих из второго металла в первый, энергетический барьер,
равный e 0 . В условиях равновесия высота барьера
58

59.

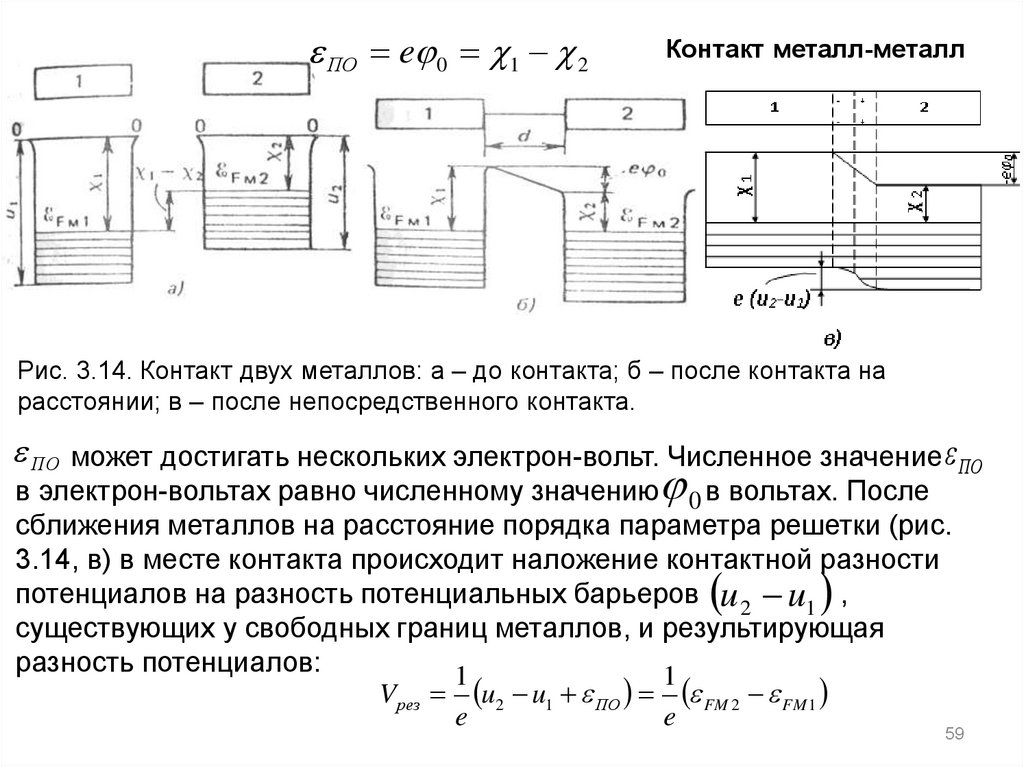
ПО e 0 1 2
Контакт металл-металл
Рис. 3.14. Контакт двух металлов: а – до контакта; б – после контакта на
расстоянии; в – после непосредственного контакта.
ПО может достигать нескольких электрон-вольт. Численное значение ПО
в электрон-вольтах равно численному значению 0 в вольтах. После
сближения металлов на расстояние порядка параметра решетки (рис.
3.14, в) в месте контакта происходит наложение контактной разности
потенциалов на разность потенциальных барьеров u 2 u1 ,
существующих у свободных границ металлов, и результирующая
разность потенциалов:
1
1
V рез u2 u1 ПО FM 2 FM 1
e
e
59

60.

Иногда V называют внутренней контактной разностью потенциалов.
рез
Электрическое поле существует лишь в тонком пограничном слое между
металлами, в котором и сосредоточена вся контактная разность потенциалов.
Контакт металл-полупроводник
На рис. 3.15 показаны энергетические диаграммы металла и полупроводника
n - типа до контакта (а) и после него (б, в) . Установление равновесия между
металлом и полупроводником происходит путем обмена электронами между
ними. Поскольку уровень Ферми в металле FM расположен ниже, чем в
полупроводнике, поток электронов из полупроводника будет преобладать над
их встречным потоком из металла в начальный момент после электрического
соединения металла и полупроводника, расположенных на некотором
расстоянии d друг от друга.
Металл начнет заряжаться отрицательно, и его уровень Ферми FM будет
подниматься, а полупроводник будет заряжаться положительно, и его уровень
Ферми F будет опускаться.
Равновесие наступит при установлении этих уровней на одной высоте, оно
будет сопровождаться возникновением потенциального барьера для
электронов, идущих из полупроводника в металл
ПО e 0 M П
где 0- контактная разность потенциалов между металлом и полупроводником,
и
M , П - работы выхода электрона из металла и полупроводника.
60

61.

Контакт металл-полупроводник
Рис. 3.15. Контакт полупроводника с металлом: а – до контакта; б – после
контакта на расстоянии; в – после непосредственного контакта
d 2 П e
2
dx
0
П (d П ) 0
d П
dx
x d n
0
e2
П ( x)
N Д ( d П x) 2
2 0
1/ 2
2 0 ПО
dП
N e2
Д
( x)
n( x) nn 0 exp П
kT61

62.

Отличие рассматриваемого случая от предыдущего - контакта двух
металлов - состоит в том, что полупроводник, как правило, имеет
существенно меньшую концентрацию свободных электронов,
чем металл. Вследствие этого толщина слоя полупроводника, из
которого уходят электроны, может оказаться во много раз
больше, чем в металле.
Приповерхностный слой полупроводника значительной толщины
оказывается обедненным электронами. В нем образуется
неподвижный положительный заряд ионизированных доноров,
обеспечивающий выравнивание энергетических уровней Ферми
полупроводника и металла. Этот слой называется обедненным
или областью объемного заряда. В нем и сосредоточивается
контактное поле (рис. 3.15, в).
Наличие поля в контактной области приводит к искривлению всех
энергетических уровней полупроводника. В слое, в котором действует
контактное поле, энергия становится функцией координат электрона.
Например, в зоне проводимости характер изменения энергии электрона
таков, что в области объемного заряда на него действует сила,
стремящаяся вытолкнуть электрон из этого слоя.
62

63.

Преодоление этой силы требует затраты определенной работы,
которая переходит в потенциальную энергию электрона П (x) .
Максимального значения П ( x) ПО
потенциальная энергия
электрона достигает на границе раздела металл - полупроводник.
Для определения вида функции воспользуемся известным из
электростатики уравнением Пуассона, связывающим потенциал
поля с объемной плотностью неподвижных зарядов (x ) ,
создающих это поле. Выразив потенциал (x ) через потенциальную
энергию электрона в поле e (x) , запишем уравнение
П
Пуассона
d 2 П
e
2
dx
0
(3.40)
Если предположить, что в обедненном слое все донорные атомы
ионизированы и освободившиеся электроны ушли в металл, то eN Д
, где N Д - концентрация доноров в полупроводнике. Поскольку на
расстояниях контактное поле в полупроводнике отсутствует,
граничными условиями дифференциального уравнения (3.40)
d П
являются:
П (d П ) 0
dx
x d n
0
63

64.

В результате, решение уравнения (3.40) будет следующим
e2
П ( x)
N Д ( d П x) 2
2 0
(0)
(3.41)
П
ПО
M
П .
При x 0 получим
Подставив
в (3.41), найдем толщину обедненного слоя:
ПО
1/ 2
2 0 ПО
dП
N e2
Д
(3.42)
Таким образом, глубина проникновения контактного поля в полупроводник тем
больше, чем больше разность работ выхода полупроводника и металла и
меньше концентрация легирующей примеси в полупроводнике.
Концентрация электронов в приконтактной области:
,
( x)
n( x) nn 0 exp П
kT
- равновесная концентрация электронов в объеме
nn 0
где
полупроводника.
Нами был рассмотрен случай контакта полупроводника - типа с металлом,
64
когда соотношение их работ выхода
П M .

65.

M П концентрация электронов в
При обратном соотношении
приконтактной области полупроводника не уменьшается, а увеличивается,
становясь равной:
П ( x)
n( x) nn 0 exp
kT
Такой приконтактный слой полупроводника называется обогащенным.
В случае контакта металла,` с полупроводником р - типа обедненный слой
`
образуется
при
,
а
обогащенный
при
,
M
П
M
П
`
где
П - работа выхода полупроводника р - типа.
Энергетические диаграммы контактов металл - полупроводник показаны на
рис. 3.16, а - д.
65

66.

Рис. 3.16. Образование объединённых (а, б) и обогащённых (в, г) слоёв при
контакте металла с полупроводником п - типа (а, в) и р - типа (б, г)
66

67.

Степень искривления энергетических зон вблизи поверхности (рис. 3.16)
характеризуется величиной равновесного поверхностного потенциала
φs0 = - е ·εп0.
Если пренебречь ролью поверхностных состояний, то величина φs0 будет
равна контактной разности потенциалов металла и полупроводника.
Выпрямляющие контакты металл-полупроводник
Оба контакта, показанные на рис. 3.16, а, б, характеризуются наличием
обедненных слоев в приконтактном слое полупроводника. В них
концентрация основных носителей мала по сравнению с равновесной,
сохраняющейся вдали от контакта. Следовательно, такой приконтактный
слой обладает повышенным удельным электрическим сопротивлением и
поэтому определяет сопротивление всей системы. Потенциальный барьер
в приконтактном слое называют барьером Шотки.
Так, если напряжение приложено плюсом к металлу, а минусом к
полупроводнику, то потенциальный барьер в контакте на рис. 3.16, б
повышается. Тогда приконтактный слой еще больше обедняется основными
носителями заряда — дырками и, следовательно, будет иметь повышенное
сопротивление по сравнению с равновесным. Значит, напряжение с этой
полярностью является для данного контакта обратным.
67

68.

В контакте на рис.3.16, а при той же полярности напряжения
потенциальный барьер понижается, приконтактный слой обогащается
основными носителями — электронами и его сопротивление будет меньше
равновесного. Значит, напряжение с этой полярностью является для
данного контакта прямым.
Таким образом, контакты, показанные на рис. 3.16, а, б, обладают
выпрямляющими свойствами и могут быть основой диодов. Такие диоды,
использующие барьеры Шотки, называют диодами Шотки.
Вариантом выпрямляющих контактов является контакт, в котором вблизи
границы с металлом образуется инверсный слой, т. е. слой с
противоположным типом проводимости
Рис. 3.16.
Образование инверсного слоя при
контакте металла с полупроводником
п- типа (д.)
Толщина инверсионного слоя мала (не
превышает 1—2 нм)
д)
68

69.

Невыпрямляющие контакты металл-полупроводник
Пусть для контакта металла с полупроводником р-типа имеет место
неравенство: разность потенциалов металл-полупроводник φM-П < 0 , а для
контакта с полупроводником n-типа — неравенство φM-П > 0.
В первом случае электроны будут переходить из полупроводника в металл и
зоны искривятся «вверх», а во втором случае электроны будут переходить из
металла в полупроводник и зоны искривятся «вниз».
В таких контактах вблизи границы в полупроводнике накапливаются
основные носители, т. е. получаются обогащенные слои. Их протяженность
определяется дебаевской длиной, т. е. составляет сотые доли микрометра.
Как видно из рис. 3.16, в, г, мы приняли очень небольшие контактные разности
потенциалов, поэтому искривление зон незначительное и полупроводники
остаются невырожденными.
Если принять значения φM-П ≥ 0,1 В, то искривление зон будет значительно
сильнее и вблизи границы уровень Ферми будет проходить через
соответствующую разрешенную зону. На этом участке полупроводник
превращается в полуметалл с ничтожным удельным сопротивлением.
Независимо от того, вырождается или не вырождается полупроводник,
наличие обогащенного слоя означает, что сопротивление системы в
целом определяется нейтральным слоем полупроводника и,
следовательно, не зависит ни от величины, ни от полярности
приложенного напряжения. Такие невыпрямляющие комбинации металла с
полупроводником называют омическими контактами.
69

70.

Омические контакты осуществляются в местах присоединения выводов к
полупроводниковым слоям. Получение омических контактов — задача не
менее важная, чем получение выпрямляющих контактов. Помимо двусторонней
проводимости, важным свойством омического контакта является ничтожное
время жизни избыточных носителей в обогащенном слое. Поэтому при анализе
полупроводниковых приборов обычно считают, что концентрации избыточных
носителей на омическом контакте равны нулю.
В изделиях микроэлектроники в настоящее время наиболее
распространенным металлом омических контактов является алюминий.
Его напыляют на поверхность и затем «вжигают» на небольшую глубину при
повышенной температуре.
Если кремний р-типа, то алюминий, будучи акцептором, при нагреве
(вжигании) дополнительно легирует приповерхностный слой, что способствует
повышению проводимости омического контакта
Если же кремний п-типа, то при вжигании акцепторные атомы алюминия могут
перекомпенсировать основные донорные атомы и тогда приповерхностный
слой кремния превратится в дырочный. В результате вместо омического
контакта получится паразитный р—п-переход. Вероятность такого случая
тем больше, чем меньше концентрация доноров, т. е. при высоком удельном
сопротивлении электронного кремния. Чтобы этого избежать, поверхность пкремния дополнительно легируют донорами, формируя приконтактный
сильно легированный n+-слой, в котором перекомпенсация доноров
атомами алюминия исключается.
70

71.

Контакт двух примесных полупроводников с различным типом
электропроводности называется электронно-дырочным или
р-п переходом.
Полупроводниковая структура в месте перехода разделяется
плоскостью на две области: р- и п- типов, каждую из которых при
анализе будем считать однородной, т.е. имеющей постоянное
значение концентрации легирующей примеси по объему.
Возможны два основных случая: концентрация доноров в побласти равна концентрации акцепторов в р- области, что
соответствует симметричному переходу,
и NД
N в случае несимметричного перехода.
A
Если в плоскости контакта концентрация легирующей примеси
изменяется скачком от N Д к N A , то такой переход
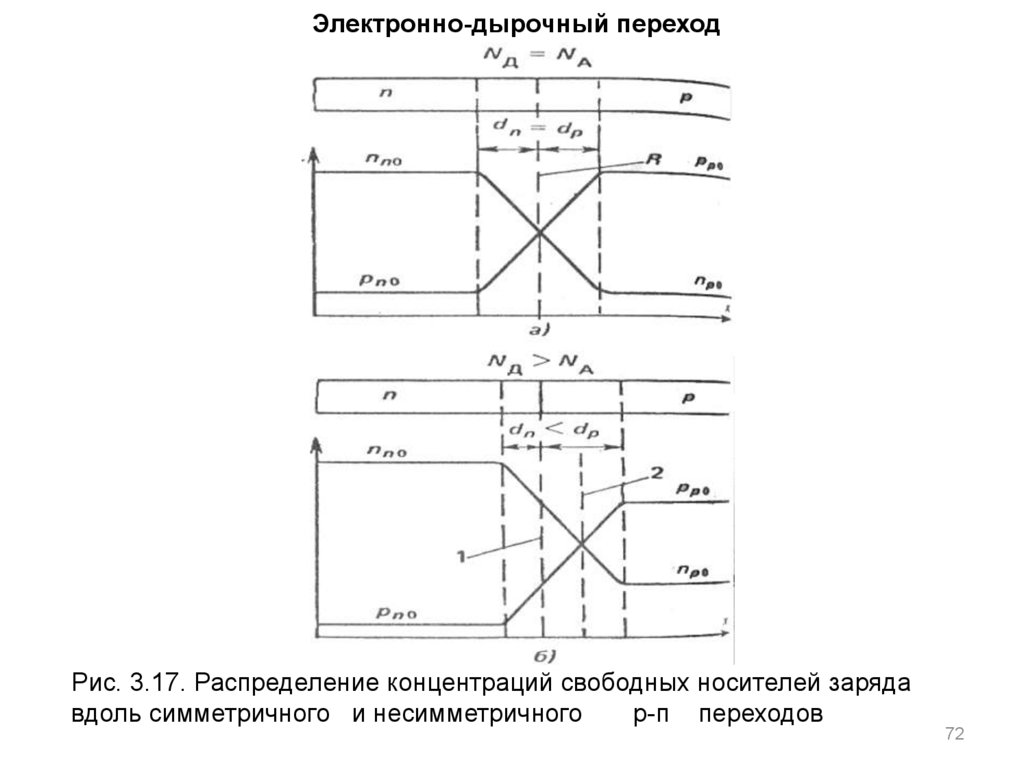
называется резким или ступенчатым. На рис. 3.17, а, б показано
распределение концентраций свободных носителей заряда вдоль
симметричного и несимметричного переходов.
71

72.

Электронно-дырочный переход
Рис. 3.17. Распределение концентраций свободных носителей заряда
вдоль симметричного и несимметричного
р-п переходов
72

73.

Поскольку электроны и дырки представляют собой свободные
подвижные носители заряда, то их концентрации не могут изменяться
скачком как для жестко связанных с кристаллической решеткой атомов
доноров и акцепторов. Эти изменения происходят в некоторой узкой
области. Кривые распределения равновесных концентраций электронов
и дырок будут симметричны на основании условия: n p n p n 2
n0 n0
p0 p0
i
. Прологарифмировав это выражение, найдем:
lg nn 0 lg p n 0 lg p p 0 lg n p 0
lg ni
2
2
т.е. уровень lg ni
лежит посередине уровней логарифмов
концентраций электронов и дырок в обеих областях. На рис 2.17, а, б
концентрации носителей заряда по оси ординат отложены в
логарифмическом масштабе. Р-п переход представляет собой
область, обедненную носителями заряда.
73

74.

В симметричном р-п переходе концентрации свободных носителей
заряда выравниваются в плоскости раздела р и п областей (рис. 3.17,
а).
В несимметричном р-п переходе плоскость, в которой происходит
выравнивание концентраций, не совпадает с плоскостью раздела
областей, а сдвинута по отношению к ней в менее легированную
область из двух областей п- и р- (в р-область на рис. 3.17, б). С этой
точки зрения различают металлургический (плоскость 1) и
физический (плоскость 2) переходы.
Слой между плоскостями 1 и 2 имеет измененный тип
электропроводности по отношению к исходному, до осуществления
контакта между областями, и называется инверсным. В дальнейшем
для простоты будем рассматривать симметричный резкий
переход. При этом каждую из областей будем считать достаточно
протяженной, чтобы можно было не учитывать краевые эффекты.
р-п переход в состоянии равновесия
В состоянии равновесия, когда к переходу не приложено внешнее
напряжение, через него проходят одновременно четыре различных
тока. Запишем их, пользуясь величинами плотностей токов , т. е. токов,
74
протекающих через поперечное сечение единичной площади :

75.

1) j pD - диффузионная составляющая плотности тока дырок,
обусловленная их движением из р-области в п-область ;
2) j nD - диффузионная составляющая плотности тока электронов,
связанная с движением электронов из п-области в р-область .
Обе эти составляющие связаны с диффузионным движением основных
носителей заряда. Если бы не было фактора, ограничивающего
диффузионное движение носителей заряда, оно продолжалось бы до
тех пор, пока концентрации электронов и дырок в обеих областях не
выровнялись бы.
Таким фактором является внутреннее электрическое поле в области
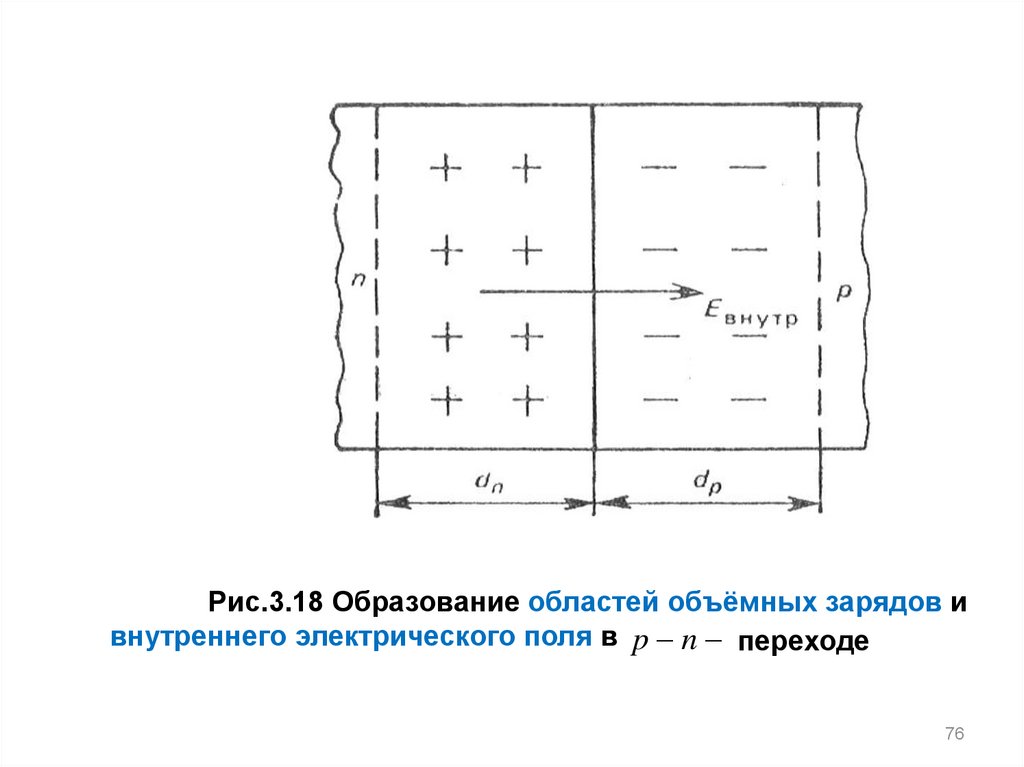
перехода. Образование этого поля связано с тем, что носители заряда,
диффундируя в соседнюю область (электроны в р- область, дырки в побласть), оставляют в покинутых ими областях неподвижные ионы
доноров и акцепторов. В результате п-область, прилегающая к
плоскости раздела, заряжается положительно, а р-область отрицательно, возникают два слоя объемных зарядов.
Между этими слоями существует внутреннее электрическое поле с
напряженностью E в нутр (рис. 3.18).
75

76.

Рис.3.18 Образование областей объёмных зарядов и
внутреннего электрического поля в p n переходе
76

77.

Преодолеть тормозящее действие этого поля и проникнуть в соседнюю
область совершающие диффузионное движение носители заряда могут
только в том случае, если они обладают достаточно большой энергией.
В то же время внутреннее электрическое поле подхватывает
неосновные носители заряда в каждой области, которые, совершая
тепловое движение, попадают на границы областей объемных зарядов,
и переносит их в соседнюю область. Поэтому к указанным
диффузионным токам, проходящим через переход, добавляются еще
два:
pE - дрейфовая составляющая плотности тока дырок из п3)
области в р-область ;
4)
- дрейфовая составляющая плотности тока электронов
j
j nE
из р-области в п-область .
В состоянии равновесия сумма всех четырех составляющих
4
плотности тока j 0
, или полный ток через переход I
i
.
i 1
0
77

78.

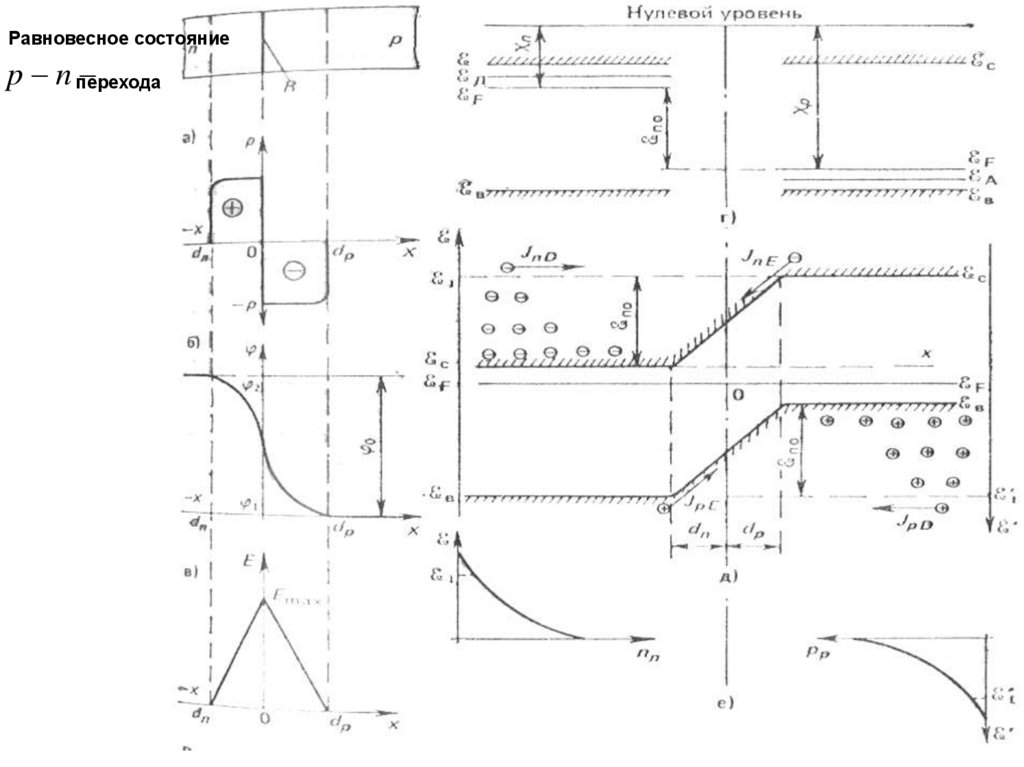
На рис. 3.19, а показано распределение плотности объёмного
заряда в области перехода. Здесь d n , d p - границы областей
объемного заряда в п- и р- областях. Поскольку концентрации
подвижных носителей заряда в области перехода снижены, при
расчетах их обычно не учитывают.
Заряды в обеих областях равны по значению и противоположны по
знаку. За пределами областей, при x d n и x d p , концентрации
свободных носителей заряда становятся соизмеримыми с
концентрациями ионов примеси, n n N Д и p p N A , поэтому 0 .
На рис.3.19, б приведен график изменения потенциала
в
области перехода. Максимальная скорость изменения потенциала
соответствует плоскости раздела р- и п- областей. За пределами
областей положительного и отрицательного объёмных зарядов
потенциал имеет постоянные значения:
2 - в
п- области и
- в р- области, между областями
1
0 2 1
существует контактная разность потенциалов
.
В одномерном случае напряженность электрического поля связана с
потенциалом следующим образом:
d
E
зависимость в области перехода показана рис. 3.19, в.
(3.43)
dx
78

79.

Заряжение п- области положительно вызывает снижение всех ее
уровней, в том числе и уровня Ферми. Наоборот, заряжение р- области
отрицательно вызывает повышение всех ее уровней. Перетекание
электронов из п - области в р - область и дырок в обратном
направлении происходит до тех пор, пока уровни Ферми в этих
областях не установятся на одной высоте.
Энергетические диаграммы п- и р- областей до приведения их в
контакт показаны на рис. 3.19, г, а на рис. 3.19, д приведена
энергетическая диаграмма перехода после установления равновесия
между п- и р- областями. Диффузионный переход из п- области в робласть совершают электроны с энергией 1 .
`
`
А из р-области в п-область переходят дырки с энергией
.
1
Распределение по энергиям электронов в зоне проводимости и дырок в
валентной зоне для невырожденных полупроводников подчиняется
статистике Максвелла – Больцмана:
F
n ~ exp
kT
F `
p ~ exp
kT
79

80.

Равновесное состояние
p n перехода
80

81.

То есть, с ростом энергии экспоненциально убывает количество
носителей заряда, обладающих этой энергией (рис. 3.19, е). Таким
образом, высота энергетического барьера между п- и робластями существенно влияет на количество носителей заряда,
способных осуществить диффузионный переход в соседнюю
область. С повышением высоты барьера это количество
экспоненциально уменьшается, со снижением - увеличивается.
Дрейфовое движение осуществляется носителями заряда, которые
можно, прибегая к аналогии, представить скатывающимися с
энергетической горки. Чтобы скатиться, им достаточно очутиться на
её краю. Дырки “скатываются” из п-области в р-область, электроны –
из р-области в п-область. Состоянию равновесия между и
областями соответствует равновесный энергетический барьер
(рис 3.19, д). Его высоту можно определить из выражения:
ПО p n Fn Fp
где p ,
- работа выхода, а Fp ,
n
Ферми, соответственно, в р- и п- областях.
Fn
- положение уровня
81

82.

С помощью соотношений (2.36) для
nn 0
и
,
n p0
, учитывая что
Fp Fn П 0
и приняв за начало отсчета уровень с 0 , получим:
П0
p p0
nn 0 p p 0
nn 0
kT ln
kT ln
kT ln
n p0
pn0
ni2
(3.44)
nn0 pn0 p p 0 n p 0 ni . Поскольку П 0 e 0 ,
Здесь учтено, что
где e - заряд электрона, а 0
- контактная разность потенциалов
между п- и р- областями, получим для
0
2
p p0
nn 0 p p 0
nn 0
0 T ln
T ln
T ln
n p0
pn0
ni2
где
(3.45)
T kT / e - температурный потенциал.
82

83.

Из (3.44) и (3.45) следует, что значения П 0 и
0 в переходе будут
тем выше, чем больше различие в концентрациях носителей с зарядом
одного знака в п- и р- областях.
При увеличении степени легирования областей уровень Ферми в побласти Fn c , в р- области Fp В , а высота
энергетического барьера
П0 g
.
Из рис. 3.19, д видно, что высота энергетического барьера между
областями изменяется не мгновенно, а на протяжении области
объемного заряда, называемой обедненным слоем d d n d p.
Для определения вида функции П x воспользуемся уравнением
Пуассона (3.40). При вычислении объемной плотности заряда x
будем считать все примесные атомы ионизированными, не будем
учитывать подвижные носители заряда в обедненном слое. В этом
случае для п - области x 0 получим n eN Д en n 0 , а для робласти x 0 :
.
p eN А ep p 0
83

84.

При указанных допущениях и резком переходе решение уравнения
Пуассона для толщины области объемного заряда
будет
иметь вид:
d
2 0
nn 0 p p 0
d dn d p 2 П0
e
n
p
n0 p0
1/ 2
(3.46)
d
Значение
тем больше, чем ниже концентрация основных
носителей заряда в п- и р- областях. Если одна из них легирована
менее сильно, чем другая, то практически вся область объемного
заряда локализуется в ней. Например, если nn 0 p p 0
, то
2 0 П 0
d dp 2
e p
p0
1/ 2
(3.47)
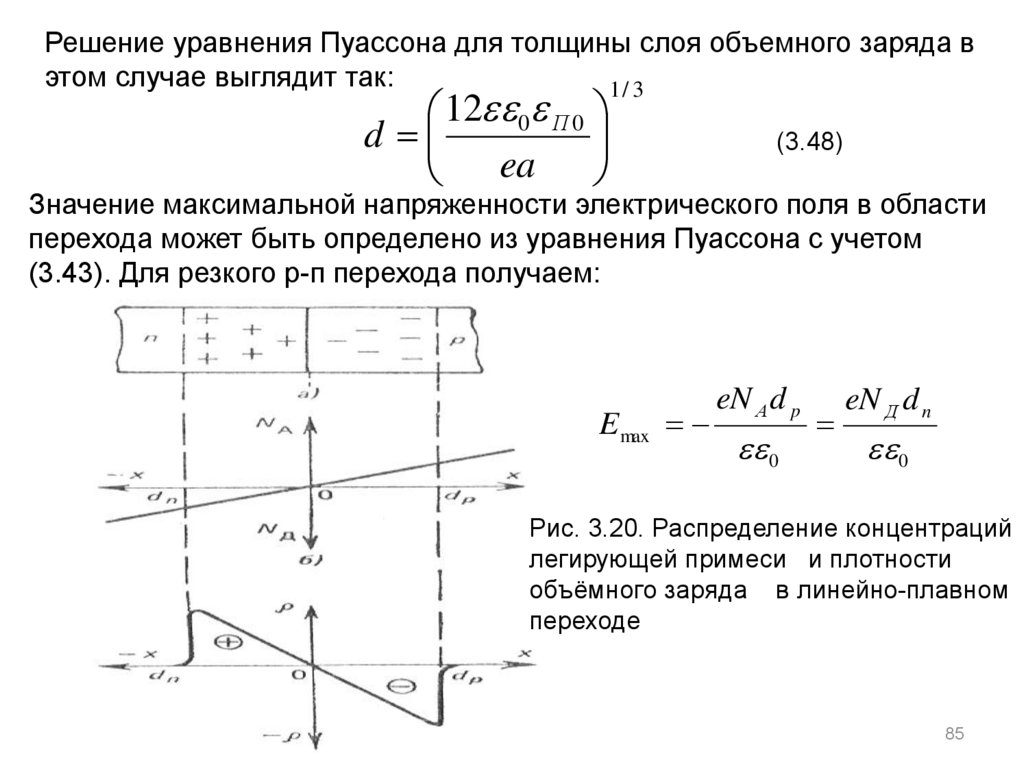
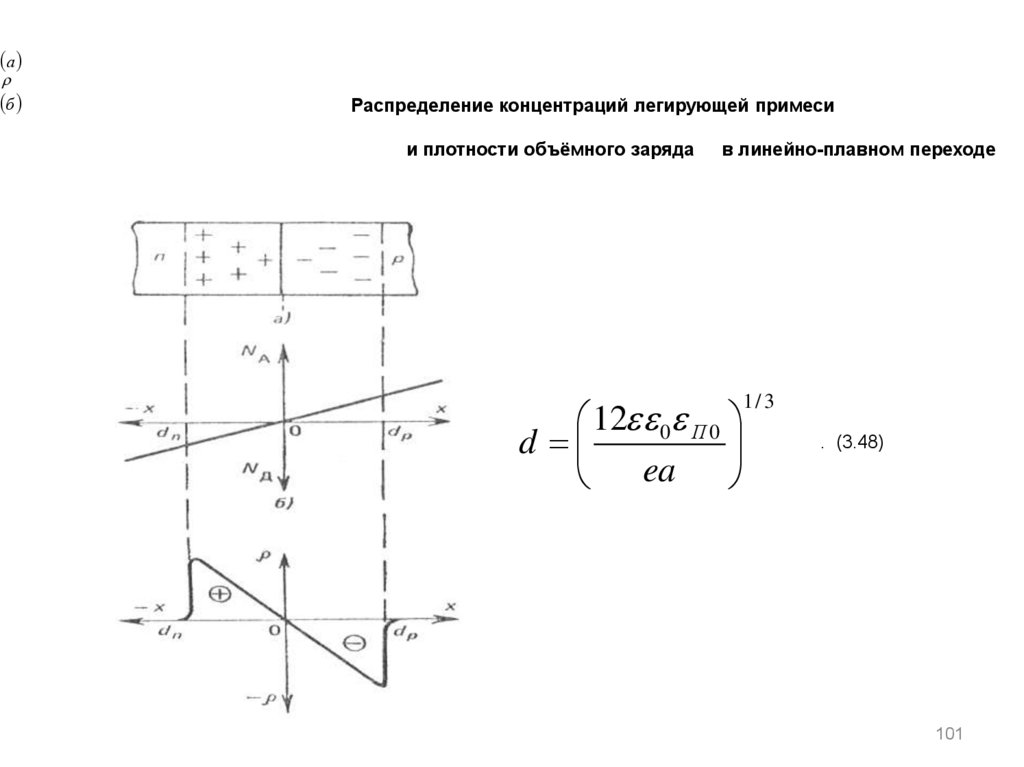
На рис. 3.20, а, б показано распределение концентраций легирующей
примеси и плотности объемного заряда x в так называемом
линейно-плавном переходе. При этом изменение концентрации
примеси
N x ax , где a grad N x const .
84

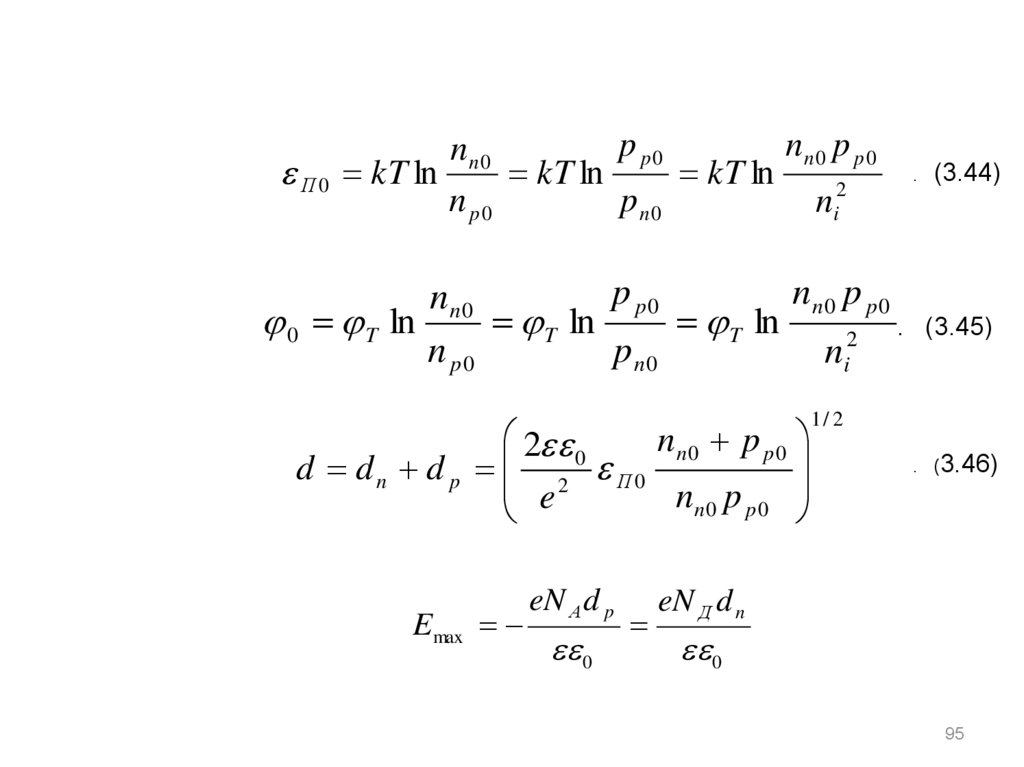
85.

Решение уравнения Пуассона для толщины слоя объемного заряда в
этом случае выглядит так:
1/ 3
12 0 П 0
d
ea
(3.48)
Значение максимальной напряженности электрического поля в области
перехода может быть определено из уравнения Пуассона с учетом
(3.43). Для резкого р-п перехода получаем:
E max
eN А d p
0
eN Д d n
0
Рис. 3.20. Распределение концентраций
легирующей примеси и плотности
объёмного заряда в линейно-плавном
переходе
85

86.

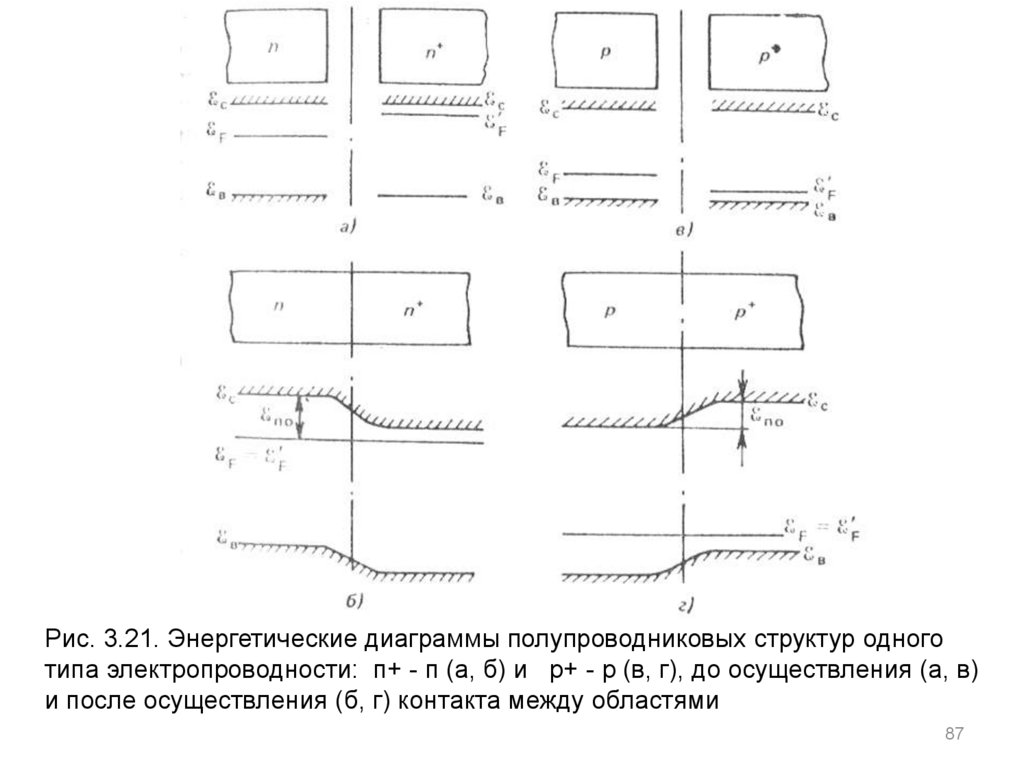
Контакт между полупроводниками одного типа электропроводности.
Контакты полупроводников одного типа электропроводности, но
различной степени легирования обозначают п-п+ и р-р+ . Знак +
относится к области с более высокой концентрацией примеси (степенью
легирования). На рис. 3.21 показаны энергетические диаграммы таких
контактов до осуществления контакта и после его установления в
состоянии равновесия.
Как и для обычных переходов, высота равновесного энергетического
барьера определяется концентрациями основных носителей заряда
П0
nn 0
kT ln
nn 0
П 0 kT ln
p p 0
для п+ - п перехода,
для р+ - р
перехода.
p p0
При контакте однотипных полупроводников не образуется слой с
малой концентрацией носителей заряда. Поэтому сопротивление
структуры определяется в основном сопротивлением ее высокоомной
области.
86

87.

Рис. 3.21. Энергетические диаграммы полупроводниковых структур одного
типа электропроводности: п+ - п (а, б) и р+ - р (в, г), до осуществления (а, в)
и после осуществления (б, г) контакта между областями
87

88.

Такие переходы не обладают выпрямляющим эффектом, другим их
важным свойством является отсутствие инжекции неосновных
носителей заряда из низкоомной области в высокоомную.
Инжекция и экстракция неосновных носителей заряда
Приложение к переходу внешнего напряжения изменяет высоту
потенциального барьера перехода и соотношение между
диффузионными и дрейфовыми токами.
Через переход начинает течь результирующий ток. Если внешнее
напряжение приложено плюсом к р-слою, то высота
потенциального барьера снижается (см. рис. 3.25, б) и ток через
переход возрастает. Напряжение такой полярности называется
прямым.
Если к р-слою внешнее напряжение приложено минусом, то
высота потенциального барьера возрастет (см. рис. 3.25, в) и ток
через переход уменьшается. Такая полярность напряжения
называется обратной.
88

89.

С приложением к переходу прямого напряжения, вследствие
снижения высоты барьера, из п-области в р-область будут
переходить (диффундировать) электроны, а из р-области в побласть - дырки. При этом вблизи границ перехода концентрация
неосновных носителей заряда - электронов в р-области и дырок
в п- области – становится больше равновесной.
Избыточные неосновные носители заряда диффундируют в глубь р- и
п-областей и рекомбинируют там.
Повышение концентрации неосновных носителей заряда в р- и
п- областях при прямых напряжениях называется инжекцией.
Снижение концентрации неосновных носителей при обратных
напряжениях – экстракцией.
Соотношение между равновесными концентрациями основных и
неосновных носителей заряда в р- и п- областях (рис. 3.22, б)
получим из (3.45):
n p0
nn 0
pn0
e 0
exp
p p0
kT
(3.49)
89

90.

Рис. 3.22. Инжекция неосновных
носителей заряда. Модель
несимметричного диода: Wn W p ,
n p (а), распределение
концентрации носителей заряда
в состоянии равновесня (б), при
инжекции (в) и экстракции (г)
90

91.

В типичном случае п- и р- области полупроводниковых диодов
геометрически и физически резко несимметричны (рис. 3.22. а, б).
Из соотношения (3.54) видно, что при N Д nn 0 N А p p 0
n область будет инжектировать гораздо больше, чем р- область,
т.е. концентрация инжектируемых неосновных носителей заряда в
высокоомном р- слое будет значительно больше, чем концентрация
в
n слое.
Следовательно, в диодах несимметричной конструкции инжекция
носит односторонний характер и главную роль играют носители
заряда, инжектируемые из сильнолегированного (низкоомного)
слоя в слаболегированный (высокоомный) слой.
Сильнолегированный инжектирующий слой называют эмиттером, а
слаболегированный слой, в который инжектируются неосновные
носители заряда, - базой.
Уровнем инжекции
называется отношение концентрации избыточных
неосновных носителей заряда к равновесной концентрации основных
носителей (рис. 3.22, в):
n p 0 n p 0
p p0
n p 0
(3.55)
NА
91

92.

Электроны, инжектированные в р-область, диффундируя в глубь
этой области, рекомбинируют с дырками (основными носителями
заряда р-области), вследствие чего их концентрация постепенно
снижается. Подставляя в (3.35) n p 0 из (3.50), получим
аналитическое выражение для распределения инжектированных в робласть электронов:
n p x n p 0 n p 0 exp eU / kT 1 exp x / Ln
(3.56)
Аналогично, используя (2.51), для дырок можно записать выражение:
p p x p n 0 p n 0 exp eU / kT 1 exp x / L p
(3.57)
Графики функций и при инжекции приведены на рис. 3.22, в.
Инжектированные носители создают вблизи перехода избыточные
заряды, которые компенсируются приходящими из глубины р- и побластей основными носителями. Поэтому на расстояниях Ln
и Lp
концентрации основных носителей заряда p p x и n n x превышают
равновесные (рис. 3.22, в).
92

93.

С приложением к диоду обратного смещения р- и п- области
вблизи перехода обедняются неосновными носителями заряда
(рис. 3.22, г). Это связано с тем, что электроны р- области,
Ln , могут
находящиеся на расстоянии диффузионной длины
попадать в поле перехода и перебрасываться в п- область.
В результате концентрация неосновных носителей заряда в р- области
вблизи перехода снижается. Аналогично дырки п- области могут
перебрасываться полем перехода в р- область. Поэтому
концентрация неосновных носителей заряда вблизи перехода
снижается и определяется выражениями
n p 0 n p 0 exp eU / kT
(3.58)
pn 0 pn 0 exp eU / kT
(3.59)
В направлении от границ обедненного слоя концентрация неосновных
носителей заряда возрастает, приближаясь к равновесной. Составляя на
основе соотношений (3.58), (3.59) уравнения, аналогичные (3.56) и
(3.57), получим аналитические выражения для распределения
неосновных носителей заряда при экстракции:
93

94.

n p x n p 0 n p 0 exp eU / kT 1 exp x / Ln
(3.60)
p n x p n 0 p n 0 exp eU / kT 1 exp x / L p
(3.61)
Графики функций и при экстракции приведены на рис. 3.22, г.
94

95.

П0
p p0
nn 0 p p 0
nn 0
kT ln
kT ln
kT ln
n p0
pn0
ni2
p p0
nn 0 p p 0
nn 0
0 T ln
T ln
T ln
.
2
n p0
pn0
ni
2 0
nn 0 p p 0
d dn d p 2 П0
e
n
p
n
0
p
0
E max
eN А d p
0
.
(3.44)
(3.45)
1/ 2
. (3.46)
eN Д d n
0
95

96.

Общая структура дисциплины
Физические основы микро- и наноэлектроники
Модуль 1: Введение
Модуль 2: Основы физики полупроводников
Модуль 3: Кинетические явления в полупроводниках
Модуль 4: Основы физики полупроводниковых приборов
Модуль 5: Перспективные направления микроэлектроники и основы наноэлектроники

97.

Модуль 1:Введение
Состав модуля 1:
•этапы и направления развития электроники
• микро- и наноэлектроника
• изделия элементной базы
Модуль 2: Основы физики полупроводников
Состав модуля 2:
• электрон в атоме и твёрдом теле
• основы зонной теории
• носители заряда в металлах и полупроводниках
• дисперсные соотношения и кривые

98.

Модуль 3: Кинетические явления в полупроводниках
Состав модуля 3:
• электропроводность твёрдых тел
• рекомбинационные эффекты
• контактные явления
• импульсные свойства диодов
Модуль 4:Основы физики полупроводниковых приборов
Состав модуля 4:
• разновидности диодов
• принцип работы усилительного прибора
• биполярные транзисторы
• полевые транзисторы
• тиристоры
• проводники коммутационных цепей

99.

Модуль 5: Перспективные направления микроэлектроники и
основы наноэлектроники
Состав модуля 5:
• фотоэлектронные приборы
• направления функциональной микроэлектроники
• наноматериалы и наноприборы
• изделия микросистемной техники
99

100.

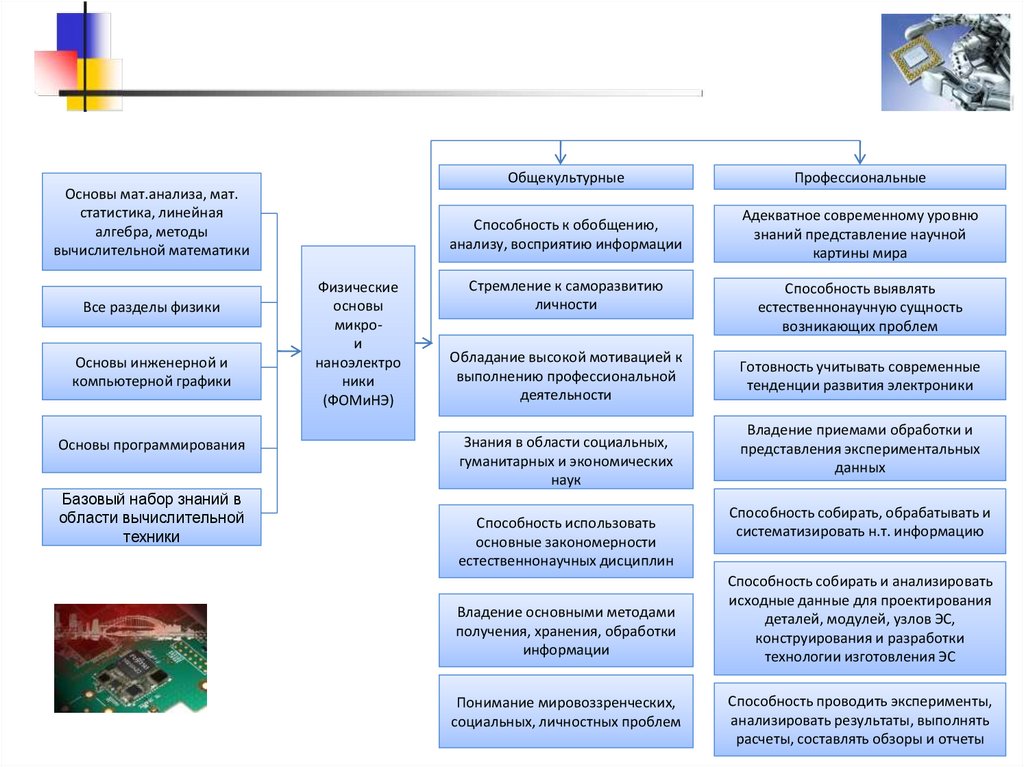
Основы мат.анализа, мат.
статистика, линейная
алгебра, методы
вычислительной математики
Все разделы физики
Основы инженерной и
компьютерной графики
Основы программирования
Базовый набор знаний в
области вычислительной
техники
Физические
основы
микрои
наноэлектро
ники
(ФОМиНЭ)
Общекультурные
Профессиональные
Способность к обобщению,
анализу, восприятию информации
Адекватное современному уровню
знаний представление научной
картины мира
Стремление к саморазвитию
личности
Обладание высокой мотивацией к
выполнению профессиональной
деятельности
Знания в области социальных,
гуманитарных и экономических
наук
Способность использовать
основные закономерности
естественнонаучных дисциплин
Владение основными методами
получения, хранения, обработки
информации
Понимание мировоззренческих,
социальных, личностных проблем
Способность выявлять
естественнонаучную сущность
возникающих проблем
Готовность учитывать современные
тенденции развития электроники
Владение приемами обработки и
представления экспериментальных
данных
Способность собирать, обрабатывать и
систематизировать н.т. информацию
Способность собирать и анализировать
исходные данные для проектирования
деталей, модулей, узлов ЭС,
конструирования и разработки
технологии изготовления ЭС
Способность проводить эксперименты,
анализировать
результаты, выполнять
100
расчеты, составлять обзоры и отчеты

101.

а
б
Распределение концентраций легирующей примеси
и плотности объёмного заряда
в линейно-плавном переходе
12 0 П 0
d
ea
1/ 3
. (3.48)
101