Таблицы истинности, функции, логические операции

1. Алгебра логики

ТАБЛИЦЫ ИСТИННОСТИ,
ФУНКЦИИ
ЛОГИЧЕСКИЕ ОПЕРАЦИИ

2. ТАБЛИЦЫ ИСТИННОСТИ, ФУНКЦИИ

На основе логической связи между простыми высказываниями, входящими в состав
сложного, делается логический вывод. Для получения логического вывода составляют
таблицу истинности, в которой перечисляют все комбинации значений (значение – это
“истина” или “ложь”) простых высказываний и, реализуя логическую связь, получают
результат, анализируя который определяют все истинные значения сложного
высказывания.
Пример:
Дано сложное высказывание: “Ученик прогулял урок и получил двойку”.
Здесь связка “и” реализует конъюктивную связь двух высказываний. Составим таблицу
истинности:
Прогулял урок
Получил двойку
Прогулял урок и
получил двойку
Ложь
Ложь
Ложь
Ложь
Истина
Ложь
Истина
Ложь
Ложь
Истина
Истина
Истина
Логический вывод: анализируя данные
таблицы истинности, видим, что
сложное высказывание, состоящее из
двух простых, истинно, если оба
простых истинны.

3. ТАБЛИЦЫ ИСТИННОСТИ, ФУНКЦИИ

Для выражения логических связей, которые существуют между высказываниями,
используется язык формул (подобно тому, как в математике используется язык формул для
выражения отношений).
В алгебре логики сложное высказывание, в котором простые высказывания заменены на
логические переменные (значениями переменных могут быть только 0 и 1), логические
связки – на математические символы, превращается в логическую функцию.
Пример:
Высказывание “Все мышки и кошки с хвостами” запишется в виде: х1 х2.
Логические переменные х1, х2 связаны между собой конъюктивно. То есть получаем
логическую функцию:
F(х1,х2) = х1 х2
Запишем:
Сложное высказывание является логической (булевой) функцией некоторых двоичных аргументов простых высказываний, которую можно получить при помощи логических операций.
Основная задача алгебры логики заключается в том, чтобы определить истинность или ложность
сложного высказывания на основании истинности или ложности входящих в него простых
высказываний.
Таблица соответствия возможных значений аргумента (входных двоичных переменных) значениям
функции, называется таблицей истинности.
Количество возможных наборов аргументов равно 2n, где n – число аргументов.

4. ЛОГИЧЕСКИЕ ОПЕРАЦИИ

Проанализируем известные нам логические связи с учётом вышесказанного, учитывая, что в
терминах алгебры логики логическая связь – это логическая функция.
Простейшие логические операции (И, ИЛИ, НЕ) можно пояснить с помощью диаграмм,
предложенных английским логиком Эйлером-Венном.
Инверсия
Первая из этих операций - отрицание некоторого высказывания. Она называется инверсией.
Круг на рисунке обозначает высказывание А, тогда отрицанию этого высказывания
соответствует остальная площадь четырёхугольника, т.е. всё, что не относится к А.
Примеры высказываний:
“Неверно, что 2 2 = 5”; “Завтра мы не пойдём на улицу”.
В этих примерах отрицание высказываний реализуется связками “неверно, что…” и “не”.
Данное высказывание истинно, когда его отрицание ложно и наоборот.
Логическая Функция - F(А) = А
ТАБЛИЦА ИСТИННОСТИ ОПЕРАЦИИ ОТРИЦАНИЯ:
А
⌉А
1
0
0
1
Логический вывод: инверсия переменной истинна тогда и только тогда,
когда переменная ложна.

5. ЛОГИЧЕСКИЕ ОПЕРАЦИИ

Конъюнкция
Возьмём теперь в качестве высказывания А утверждение "Пасмурно", а в качестве
высказывания В - утверждение "Идёт дождь". Если даны два высказывания А и В, то можно
определить функцию "А и В" – “Пасмурно и идёт дождь”.
Эта логическая операция называется конъюнкцией или логическим И.
На рисунке площадь, принадлежащая обоим кругам, должна соответствовать
высказыванию А В. Общая для обоих кругов площадь охватывает всё то, что относится
одновременно и к А и к В.
Высказывание А В “Пасмурно и идёт дождь” может быть истинным лишь тогда, когда
истинны оба входящие в него высказывания. Если хотя бы одно из них ложно, то и результат
будет ложным.
Логическая функция: F(А,В) = А В
ТАБЛИЦА ИСТИННОСТИ ОПЕРАЦИИ КОНЪЮНКЦИЯ:
А
В
А⋀В
0
0
0
0
1
0
1
0
0
1
1
1
Логический вывод: конъюнкция логических переменных истинна тогда и
только тогда, когда все логические переменные истинны.

6. ЛОГИЧЕСКИЕ ОПЕРАЦИИ

Дизъюнкция
Два высказывания А и В могут быть связаны словом ИЛИ. В результате поучается новая
функция "А или В". Эта операция носит название дизъюнкции.
Значение ИЛИ поясняет рисунок. Функция "А или В" изображается площадью,
объединяющей оба круга. Заштрихованная область на диаграмме содержит всё то, что
принадлежит А и В, причём "и" следует понимать здесь в смысле объединения или
суммирования.
Пример высказывания: “В природе бывает, что солнце при дожде светит или прячется в тучах”.
В этом высказывании связка “или” реализует дизъюнкцию, при этом сложное высказывание
истинно, если истинно хотя бы одно из простых высказываний, в том числе если истинны сразу
ТАБЛИЦА ИСТИННОСТИ ОПЕРАЦИИ ДИЗЪЮНКЦИЯ:
оба высказывания.
В этих соотношениях находит выражение особенность сложения чисел
Логическая функция: F(А,В) = А В 1 и 0. Поэтому дизъюнкцию называют иногда также
логическим сложением или логической суммой.
А
В
А⋁В
0
0
0
0
1
1
1
0
1
1
1
1
Логический вывод: дизъюнкция логических переменных истинна тогда и
только тогда, когда истинна хотя бы одна логическая переменная.

7. ЛОГИЧЕСКИЕ ОПЕРАЦИИ

Неравнозначность
Неравнозначность, называемая иногда исключающее ИЛИ, выражается
словосочетанием "или…, или" ("либо…, либо").
Пример высказывания: “В этом году летом мы либо поедем к морю, либо будем жить на даче”.
Связка “либо…либо” реализует строгую дизъюнкцию, при этом сложное
высказывание истинно, только если одно из простых высказываний истинно, но не оба
сразу.
Логическая функция: F(А,В) = А В
ТАБЛИЦА ИСТИННОСТИ ОПЕРАЦИИ НЕРАВНОЗНАЧНОСТЬ:
А
В
А⊕В
0
0
0
0
1
1
1
0
1
1
1
0
Логический вывод: строгая дизъюнкция логических переменных истинна
тогда и только тогда, когда истинна хотя бы одна из логических переменных.

8. ЛОГИЧЕСКИЕ ОПЕРАЦИИ

Импликация
Импликация - это одна из самых важных операций логики высказываний. Эта
операция выражается словосочетанием "если…, то…".
Пример высказывания: “Если будет хорошая погода, то мы пойдём в лес”.
Здесь связка “если…то” реализует импликацию, при этом первую часть высказывания
– “Если будет хорошая погода” – называют основанием, а вторую – “мы пойдём в лес” –
следствием.
Высказывание такого типа ложно только в одном случае – если истинно условие и
ложно заключение.
Логическая функция: F(А,В) = А В
ТАБЛИЦА ИСТИННОСТИ ОПЕРАЦИИ ИМПЛИКАЦИЯ:
А
В
А→В
0
0
1
0
1
1
1
0
0
1
1
1
Логический вывод: импликация двух логических переменных ложна тогда и
только тогда, когда условие истинно, а заключение ложно.

9. ЛОГИЧЕСКИЕ ОПЕРАЦИИ

Эквивалентность
Операция эквивалентность (двойная импликация) обозначается знаками .
Пример высказывания: “Я куплю радиоприёмник тогда и только тогда, когда получу премию”.
В этом примере связка “…тогда и только тогда…когда…” помогает выразить взаимную
обусловленность событий. Данное сложное высказывание будет истинным, когда
простые высказывания либо оба истинны, либо оба ложны.
Логическая функция: F(А,В) = А В
ТАБЛИЦА ИСТИННОСТИ ОПЕРАЦИИ ЭКВИВАЛЕНТНОСТЬ:
А
В
А↔В
0
0
1
0
1
0
1
0
0
1
1
1
Логический вывод: эквивалентность двух логических переменных истинна тогда и только
тогда, когда обе переменные одновременно истинны или одновременно ложны.

10. ЛОГИЧЕСКИЕ ОПЕРАЦИИ

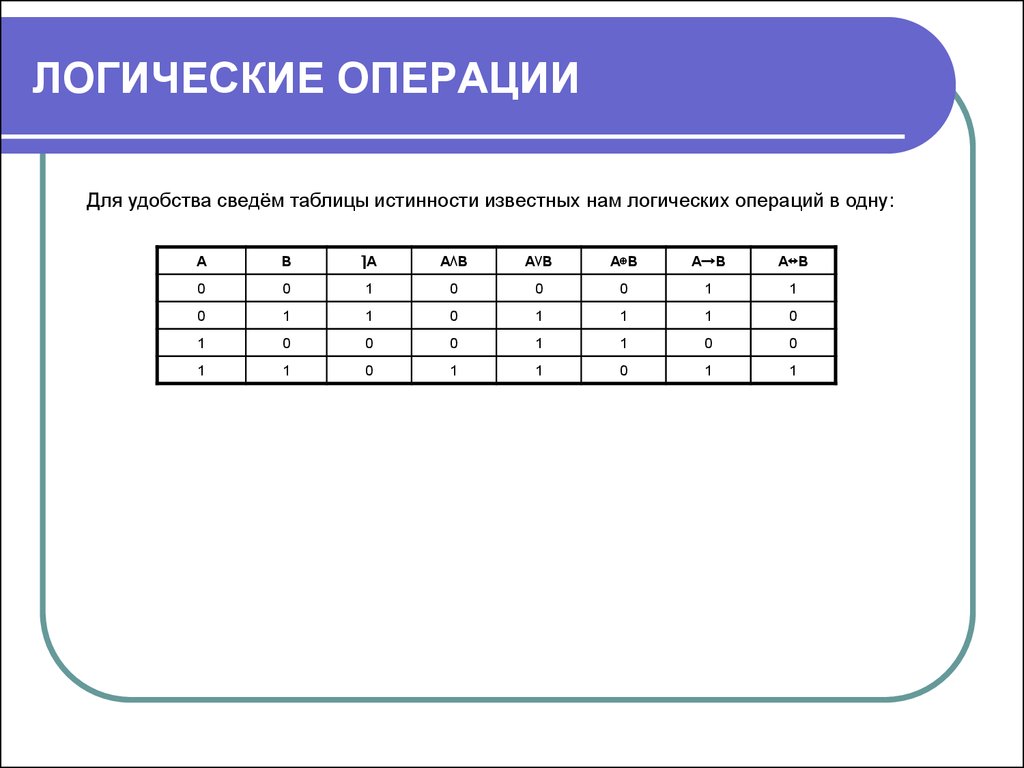
Для удобства сведём таблицы истинности известных нам логических операций в одну:
А
В
⌉А
А⋀В
А⋁В
А⊕В
А→В
А↔В
0
0
1
0
0
0
1
1
0
1
1
0
1
1
1
0
1
0
0
0
1
1
0
0
1
1
0
1
1
0
1
1

11. ФОРМУЛЫ АЛГЕБРЫ ЛОГИКИ

Используя основные логические операции, можно построить более сложные высказывания,
например;
(А В) (А В) (А С),
(А А) (В АС),
( (А В) С).
Указанные высказывания называются формулами алгебры высказываний. Эти формулы
состоят из простых высказываний А, В, …, знаков логических операций и скобок.
ПОСЛЕДОВАТЕЛЬНОСТЬ ВЫПОЛНЕНИЯ ОПЕРАЦИЙ
Скобки указывают последовательность выполнения операций. При отсутствии скобок
первой всегда выполняется операция отрицания, затем конъюнкция (логическое
произведение), дизъюнкция (логическое сложение) и неравнозначность, затем
импликация и эквивалентность:
⌉;
;
+ , ;
.
Пример. Какие из приведённых ниже выражений являются формулами логики высказываний, а какие нет?
А + В;
(+ p + q);
p q r;
(p + q) r.