Похожие презентации:
Формирование растра. Понятие связности пикселей. Растровое представление отрезка. Алгоритмы растризации
1.
Приднетровский государственный университет им. Т.Г. ШевченкоИнженерно-технический институт
Кафедра “Программное обеспечение вычислительной техники
и автоматизированных систем
Башкатов А.М.
Компьютерная графика
Для студентов направлений: “Программная инженерия”,
“Информатика и вычислительная техника”,
“Информационные системы и сети”
Лекция 4.
Формирование растра. Понятие связности пикселей.
Растровое представление отрезка. Алгоритмы растризации.
Построение кривых различных порядков.
Закраска области цветом. Заполнение многоугольников
Тирасполь, 2019
2.
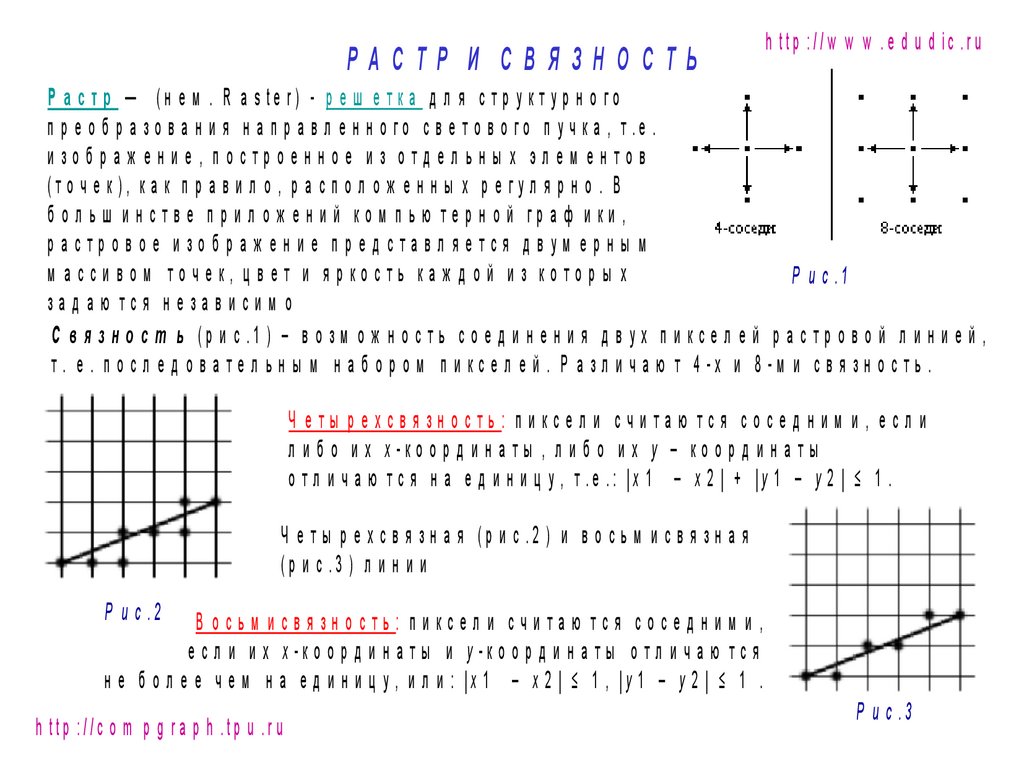
РАСТР И СВЯЗНО СТЬh ttp :// w w w . e d u d ic .r u
Р а с т р — (н е м . R a s te r) - р е ш е т к а д л я с т р у к т у р н о г о
п р е о б р а з о в а н и я н а п р а в л е н н о го с в е т о в о го п у ч к а , т .е .
изображ ение, построенное из отдельны х эл ем ентов
(т о ч е к ), к а к п р а в и л о , р а с п о л о ж е н н ы х р е гу л я р н о . В
б о л ь ш и н с тв е п р и л о ж е н и й ко м п ь ю те р н о й гр а ф и ки ,
растровое изоб раж ение пред ставл яется д вум ерны м
м ассивом точек, ц вет и ярко сть каж д ой из котор ы х
Р и с .1
задаю тся независим о
С в я з н о с т ь (р и с .1 ) – в о з м о ж н о с т ь с о е д и н е н и я д в у х п и к с е л е й р а с т р о в о й л и н и е й ,
т . е . п о с л е д о в а т е л ь н ы м н а б о р о м п и к с е л е й . Р а з л и ч а ю т 4 -х и 8 -м и с в я з н о с т ь .
Ч еты рехсвязность: пиксел и считаю тся сосед ним и, есл и
л и б о и х x -ко о р д и н а т ы , л и б о и х y – ко о р д и н а т ы
о т л и ч а ю т с я н а е д и н и ц у , т .е .: |x 1 – x 2 | + |y 1 – y 2 | ≤ 1 .
Ч е т ы р е х с в я з н а я (р и с .2 ) и в о с ь м и с в я з н а я
(р и с .3 ) л и н и и
Р и с .2
В осьм исвязность: пиксел и считаю тся сосед ним и ,
е с л и и х x -к о о р д и н а т ы и y -к о о р д и н а т ы о т л и ч а ю т с я
н е б о л е е ч е м н а е д и н и ц у , и л и : |x 1 – x 2 | ≤ 1 , |y 1 – y 2 | ≤ 1 .
h ttp ://c o m p g ra p h .tp u .ru
Р и с .3
3.
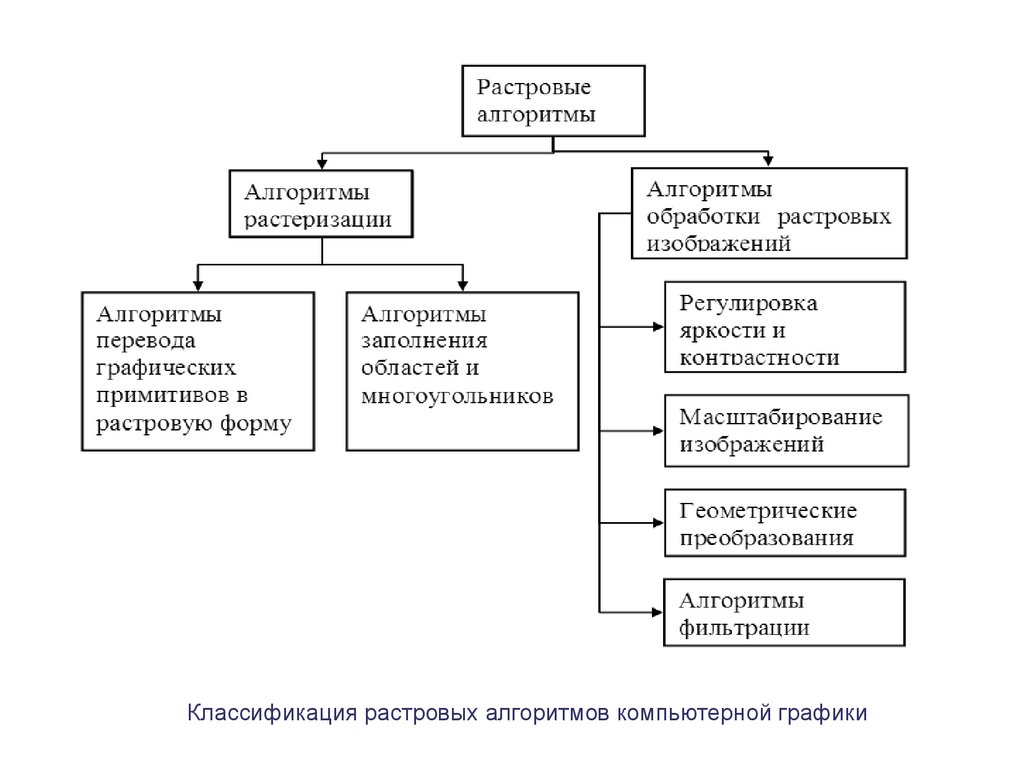
Классификация растровых алгоритмов компьютерной графики4.
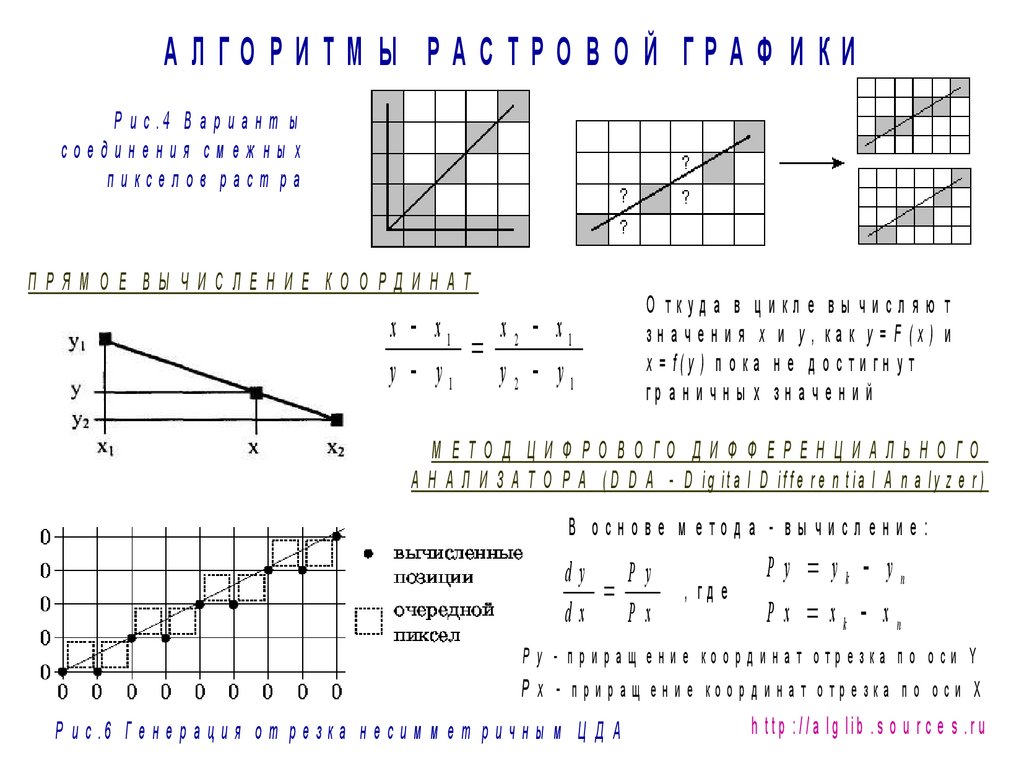
АЛГО РИТМ Ы РАСТРО ВО Й ГРАФ ИКИР и с .4 В а р и а н т ы
соединения см еж ны х
пикселов раст ра
П РЯМ О Е ВЫ ЧИСЛЕН И Е КО О РД ИН АТ
x x1
x 2 x1
y y1
y 2 y1
О ткуд а в ц икл е вы числ яю т
з н а ч е н и я x и y , ка к y = F (x ) и
x = f(y ) п о к а н е д о с т и г н у т
гр а н и ч н ы х зн а ч е н и й
М ЕТО Д Ц И Ф РО ВО ГО ДИ Ф Ф ЕРЕН Ц И АЛЬН О ГО
А Н А Л И З А Т О Р А ( D D A - D ig ita l D iffe r e n tia l A n a ly z e r )
В основе м етода - вы числение:
dy
Py
dx
Px
, гд е
P y yk yn
P x xk xn
P y - при ращ ени е коо рд инат отрезка по оси Y
P x - при ращ ение коо рд инат отрезка по оси X
Р и с .6 Г е н е р а ц и я о т р е з к а н е с и м м е т р и ч н ы м Ц Д А
h ttp :// a lg lib .s o u r c e s .r u
5.
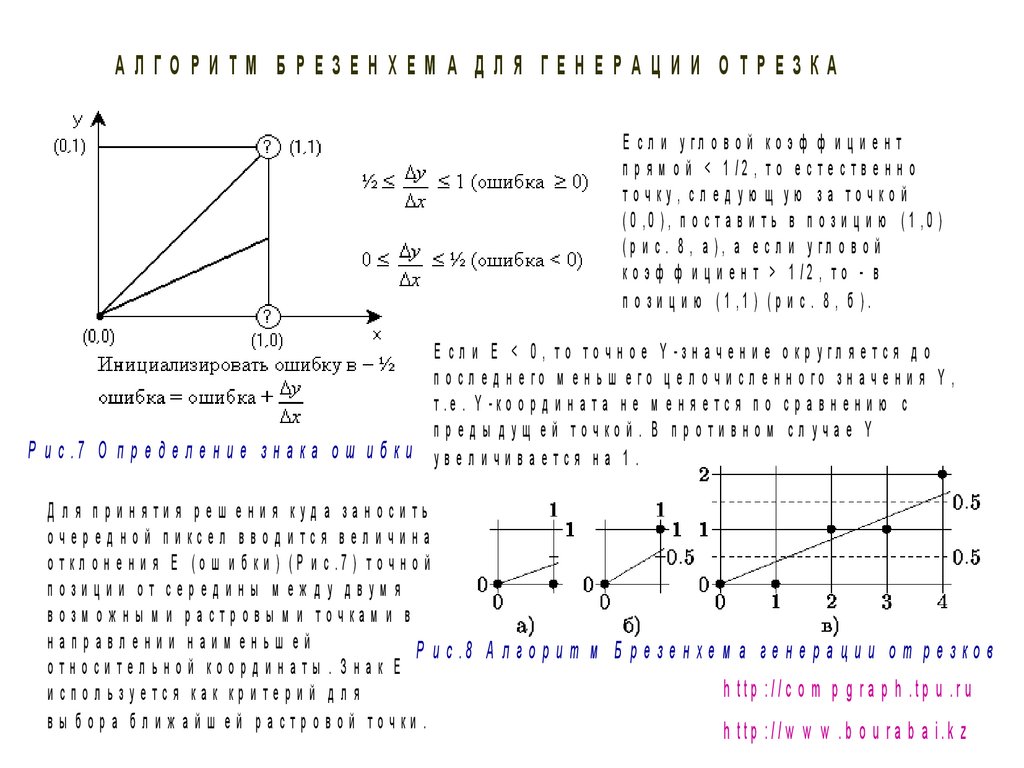
АЛГО РИТМ БРЕЗЕНХЕМ А ДЛЯ ГЕНЕРА ЦИИ О ТРЕЗКАЕ с л и у гл о в о й ко э ф ф и ц и е н т
п р я м о й < 1 /2 , т о е с т е с т в е н н о
точку, сл ед ую щ ую за точко й
(0 ,0 ) , п о с т а в и т ь в п о з и ц и ю (1 ,0 )
(р и с . 8 , а ), а е с л и у гл о в о й
к о э ф ф и ц и е н т > 1 /2 , т о - в
п о з и ц и ю (1 ,1 ) (р и с . 8 , б ).
Р и с .7 О п р е д е л е н и е з н а к а о ш и б к и
Е с л и Е < 0 , т о т о ч н о е Y -з н а ч е н и е о к р у гл я е т с я д о
п о с л е д н е го м е н ь ш е го ц е л о ч и с л е н н о го з н а ч е н и я Y ,
т .е . Y -к о о р д и н а т а н е м е н я е т с я п о с р а в н е н и ю с
пр ед ы д ущ ей точкой . В пр о ти в но м сл уча е Y
увеличивается на 1.
Д ля принятия реш ения куд а заносить
очеред ной пи ксел ввод и тся вел ичина
о т к л о н е н и я Е (о ш и б к и ) (Р и с .7 ) т о ч н о й
позиции от серед ины м еж д у двум я
возм ож ны м и растровы м и точкам и в
направлении наим еньш ей
Р и с .8 А л г о р и т м Б р е з е н х е м а г е н е р а ц и и о т р е з к о в
относительной координаты . Знак Е
h ttp ://c o m p g ra p h .tp u .ru
и спол ьзуется как кри тери й д л я
вы б ора бл и ж айш ей растр о вой точки .
h ttp :// w w w .b o u r a b a i.k z
6.
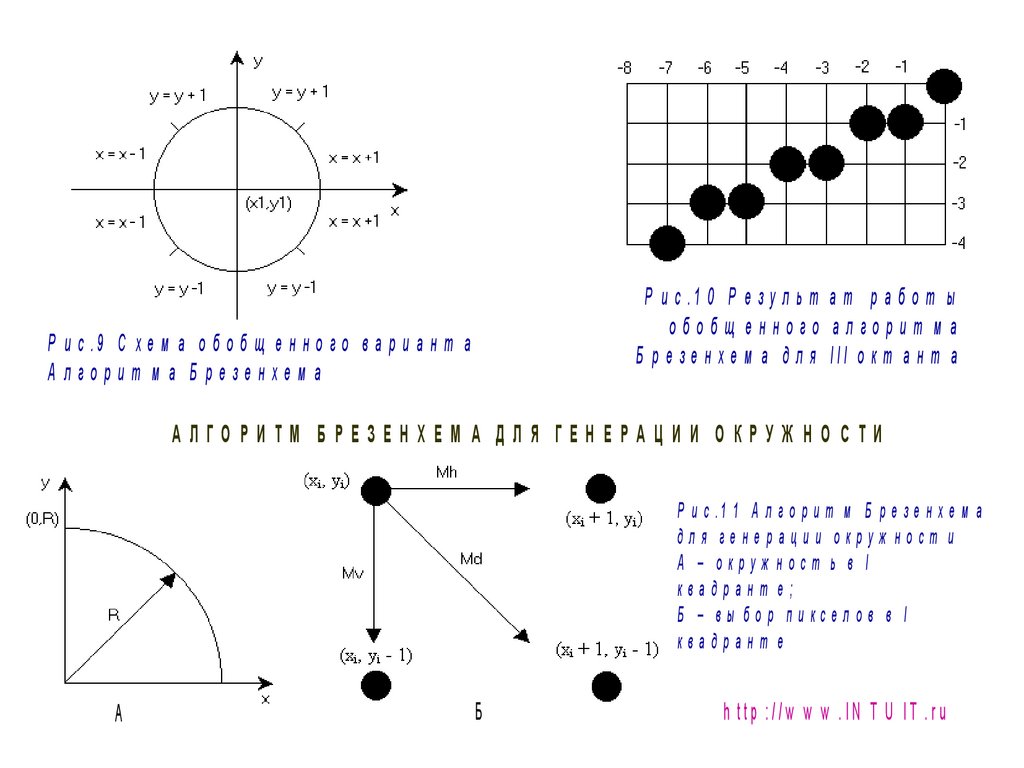
Р и с .1 0 Р е з у л ь т а т р а б о т ыобобщ енного алгорит м а
Б р е з е н х е м а д л я III о к т а н т а
Р и с .9 С х е м а о б о б щ е н н о г о в а р и а н т а
А лгорит м а Б резенхем а
АЛГО РИ ТМ Б РЕЗЕН ХЕМ А Д ЛЯ ГЕН ЕРА Ц И И О КРУЖ Н О С ТИ
Р и с .1 1 А л г о р и т м Б р е з е н х е м а
для генерации окруж ност и
А – окруж ност ь в I
квадрант е;
Б – вы бор пикселов в I
квадрант е
А
Б
h ttp ://w w w .IN T U IT .ru
7.
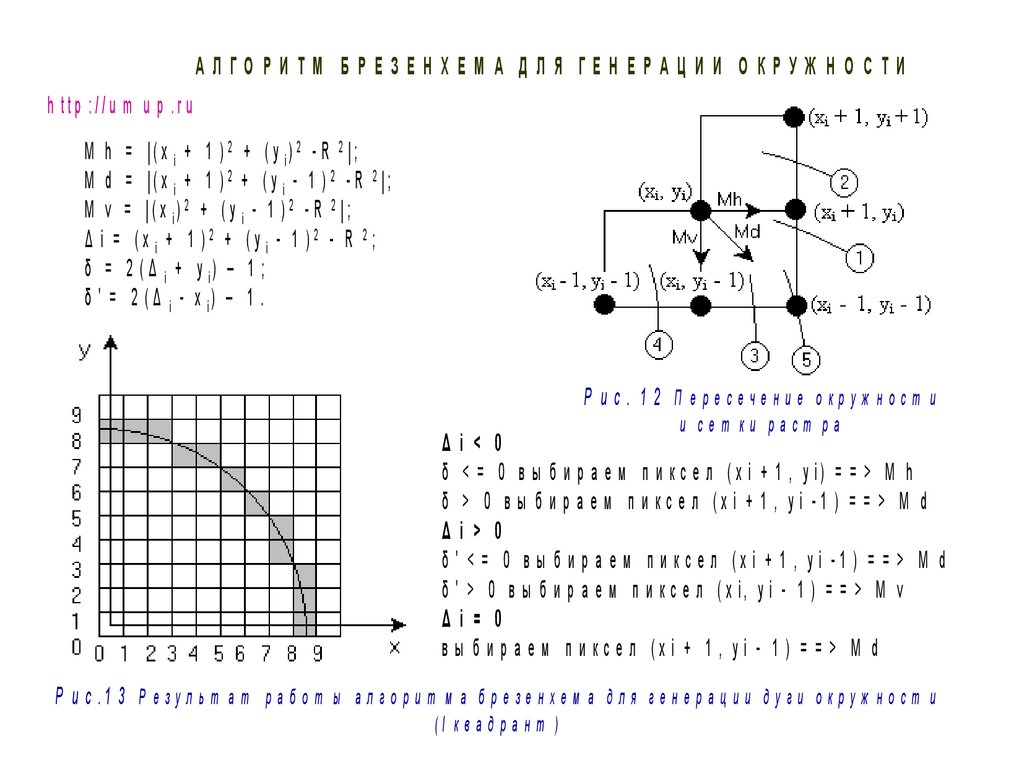
АЛГО РИ ТМ Б РЕЗЕН ХЕМ А Д ЛЯ ГЕНЕРА Ц И И О КРУЖ Н О С ТИh ttp ://u m u p .ru
M h = | ( x i + 1 ) 2 + ( y i) 2 - R 2 | ;
M d = |( x i + 1 ) 2 + ( y i - 1 ) 2 - R 2 |;
M v = | ( x i) 2 + ( y i - 1 ) 2 - R 2 | ;
Δ i = (x i + 1 )2 + (y i - 1 )2 - R 2;
δ = 2 ( Δ i + y i) – 1 ;
δ ' = 2 ( Δ i - x i) – 1 .
Р ис. 1 2 П ересечение окруж ност и
и сет ки раст ра
Δi < 0
δ < = 0 в ы б и р а е м п и к с е л ( x i + 1 , y i) = = > M h
δ > 0 в ы б и р а е м п и к с е л (x i + 1 , y i -1 ) = = > M d
Δi > 0
δ ' < = 0 в ы б и р а е м п и кс е л (x i + 1 , y i -1 ) = = > M d
δ ' > 0 в ы б и р а е м п и к с е л ( x i, y i - 1 ) = = > M v
Δi = 0
в ы б и р а е м п и к с е л (x i + 1 , y i - 1 ) = = > M d
Р и с .1 3 Р е з у л ь т а т р а б о т ы а л г о р и т м а б р е з е н х е м а д л я г е н е р а ц и и д у г и о к р у ж н о с т и
(I к в а д р а н т )
8.
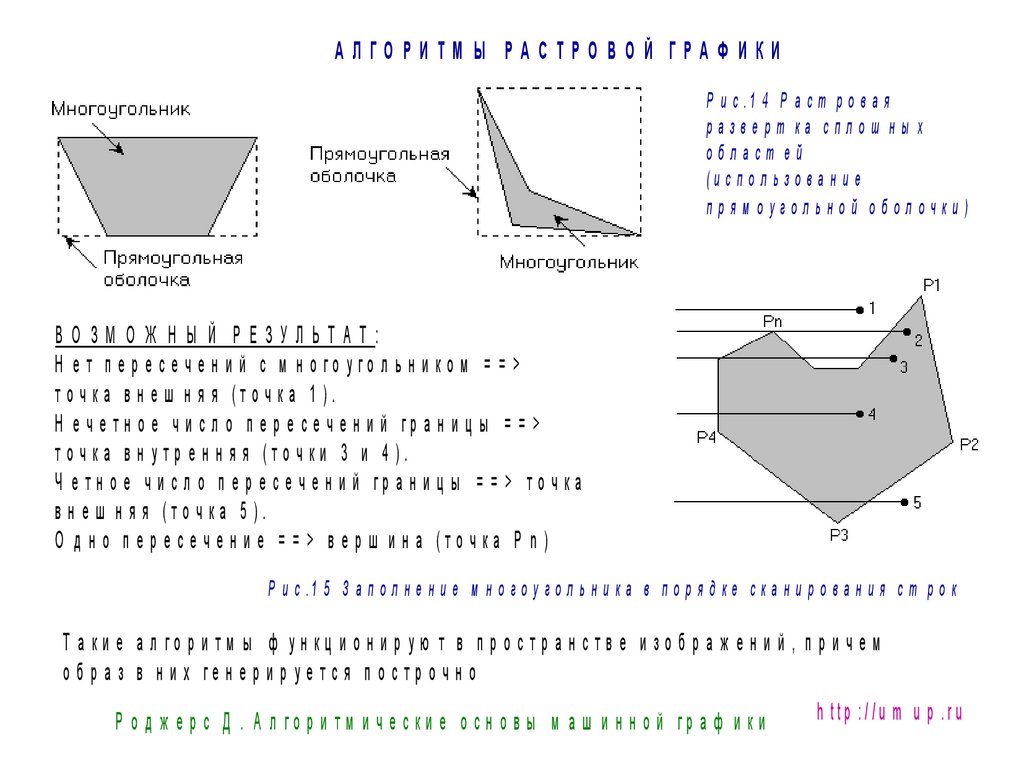
А ЛГО РИ ТМ Ы РА С ТРО ВО Й ГРА Ф И КИР и с .1 4 Р а с т р о в а я
разверт ка сплош ны х
област ей
(и с п о л ь з о в а н и е
прям оугольной оболочки)
ВО ЗМ О Ж Н Ы Й РЕЗУЛЬТАТ:
Н е т п е р е с е ч е н и й с м н о го уго л ь н и ко м = = >
т о ч к а в н е ш н я я (т о ч к а 1 ).
Н е ч е тн о е ч и с л о п е р е с е ч е н и й гр а н и ц ы = = >
т о ч к а в н у т р е н н я я (т о ч ки 3 и 4 ).
Ч е тн о е ч и с л о п е р е с е ч е н и й гр а н и ц ы = = > то ч ка
в н е ш н я я (т о ч к а 5 ).
О д н о п е р е с е ч е н и е = = > в е р ш и н а (т о ч к а P n )
Р и с .1 5 З а п о л н е н и е м н о г о у г о л ь н и к а в п о р я д к е с к а н и р о в а н и я с т р о к
Т а ки е а л го р и тм ы ф ун кц и о н и р у ю т в п р о с тр а н с тв е и зо б р а ж е н и й , п р и ч е м
о б р а з в н и х ге н е р и р уе т с я п о с тр о ч н о
Р о д ж е р с Д . А л го р и тм и ч е с ки е о с н о в ы м а ш и н н о й гр а ф и ки
h ttp ://u m u p .ru
9.
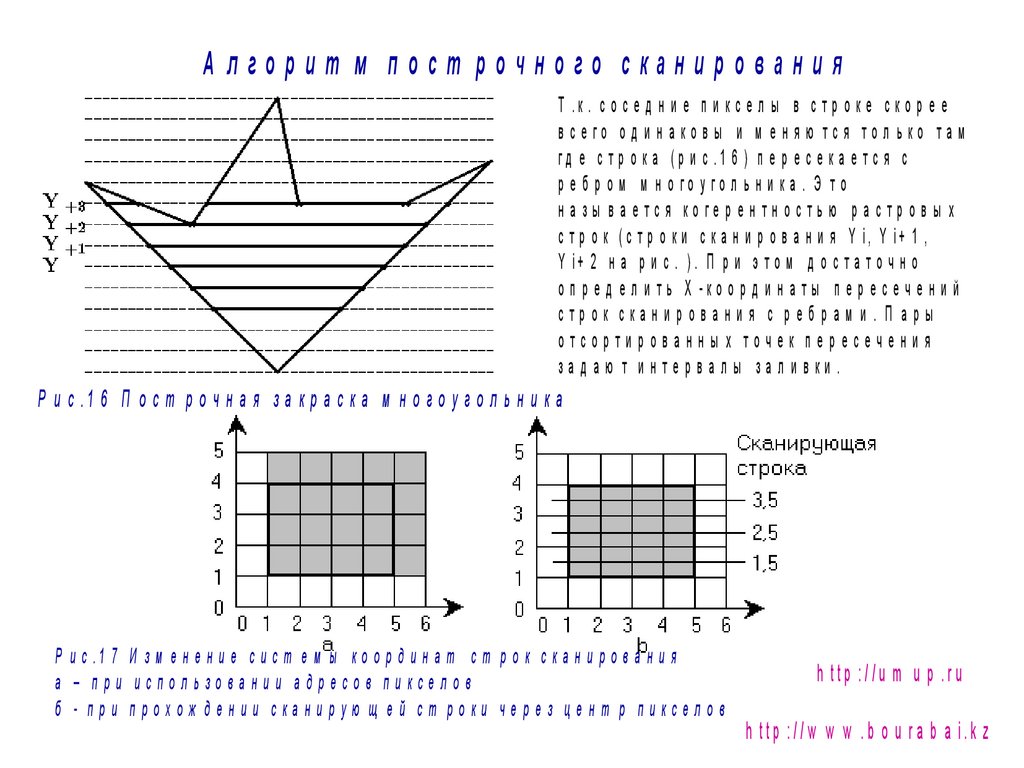
А лгорит м пост рочного сканированияТ .к . с о с е д н и е п и к с е л ы в с т р о к е с к о р е е
в с е го о д и н а к о в ы и м е н я ю т с я то л ь ко т а м
гд е с т р о к а (р и с .1 6 ) п е р е с е к а е т с я с
р е б р о м м н о го у го л ь н и ка . Э т о
н а з ы в а е т с я ко ге р е н тн о с т ь ю р а с т р о в ы х
с т р о к ( с т р о к и с к а н и р о в а н и я Y i, Y i+ 1 ,
Y i+ 2 н а р и с . ) . П р и э т о м д о с т а т о ч н о
о п р е д е л и т ь X -ко о р д и н а т ы п е р е с е ч е н и й
строк сканирования с ребрам и. П ары
отсортированны х точек пересечения
зад аю т и нтервал ы зал и вки .
Р и с .1 6 П о с т р о ч н а я з а к р а с к а м н о г о у г о л ь н и к а
Р и с .1 7 И з м е н е н и е с и с т е м ы к о о р д и н а т с т р о к с к а н и р о в а н и я
а – при использовании адресов пиксел ов
б - при прохож дении сканирую щ ей ст роки через цент р пикселов
h ttp ://u m u p .ru
h ttp :// w w w . b o u r a b a i.k z
10.
А лгорит м ы заполнения раст ровы х област ейР и с .1 8 Т и п ы о б л а с т е й :
В нут ренне
определенная област ь
Гранично
определенная област ь
О снованы на анализе зон:
- г р а н и ч н о -о п р е д е л е н н ы х , т .е .
з а д а в а е м ы е с в о е й (з а м кн у т о й )
гр а н и ц е й та к, ч то ко д ы п и кс е л о в
гр а н и ц ы о тл и ч н ы о т ко д о в
внутр енн ей , пе рекр аш и вае м ой
обл асти;
- в н у т р е н н е -о п р е д е л е н н ы х ,
нарисованны х одним заданны м
код ом пиксел а. П ри зал и вке этот
код зам е няется н а н овы й код
закраски
Н а ко д ы п и кс е л ы в н у т р е н н е й ч а с т и о б л а с ти н а л а га ю т с я д в а у с л о в и я - о н и д о л ж н ы б ы ть
о т л и ч н ы о т ко д а п и кс е л о в гр а н и ц ы и ко д а п и кс е л а п е р е кр а с ки . Е с л и в н у тр и гр а н и ч н о о п р е д е л е н н о й о б л а с ти и м е е т с я е щ е о д н а гр а н и ц а , н а р и с о в а н н а я п и кс е л а м и с те м ж е
ко д о м , ч то и в н е ш н я я гр а н и ц а , то с о о тв е тс тв у ю щ а я ч а с ть о б л а с ти н е д о л ж н а
перекраш иваться
Р и с .1 9 В а р и а н т ы
связност и зон
заполнения
h ttp ://u m u p .ru
h ttp :// w w w . b o u r a b a i.k z
11.
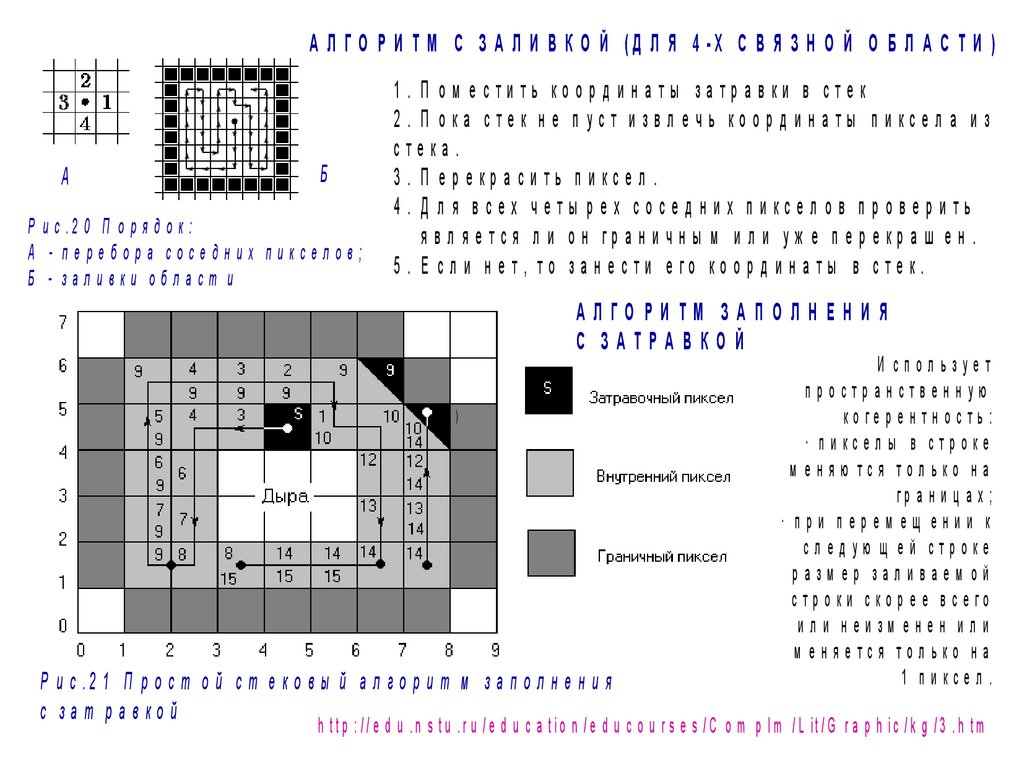
А Л Г О Р И Т М С З А Л И В К О Й (Д Л Я 4 -Х С В Я З Н О Й О Б Л А С Т И )А
Б
Р и с .2 0 П о р я д о к :
А - перебора соседних пикселов;
Б - заливки област и
1. П ом естить коорд инаты затравки в сте к
2. П ока стек не п уст извл ечь коорд инаты пиксел а из
стека.
3. П ерекрасить пиксел .
4. Д л я всех четы рех сосед них пиксел ов проверить
я в л я е тс я л и о н гр а н и ч н ы м и л и уж е п е р е кр а ш е н .
5 . Е с л и н е т , то за н е с ти е го ко о р д и н а ты в с те к.
АЛГО РИ ТМ ЗАП О ЛН ЕН И Я
С ЗАТРАВКО Й
a)
Р и с .2 1 П р о с т о й с т е к о в ы й а л г о р и т м з а п о л н е н и я
с зат равкой
И спользует
пространственную
ко ге р е н т н о с т ь :
· пи ксел ы в строке
м еняю тся тол ько на
гр а н и ц а х ;
· при перемещ ении к
след ую щ ей строке
разм ер заливаем ой
с тр о ки с ко р е е в с е го
или неизм енен или
м еняется тол ько на
1 пи ксел .
h tt p : // e d u .n s tu .r u / e d u c a tio n / e d u c o u r s e s /C o m p Im /L it/G r a p h ic /k g /3 .h tm
12.
АЛГО РИТМЗАТРАВО ЧНО ГО
ЗАПО ЛНЕНИЯ
М НО ГО УГО ЛЬНИКА
Р и с .2 2 П О Р Я Д О К Р А Б О Т Ы
АЛ ГО РИ ТМ А
a – пом ещ ение в ст ек
зат равочного пиксела;
b – з а п о л н е н и е н а 3 -е й
сканирую щ ей ст роке;
c - // - // - н а 4 -о й ;
d - // - // - н а 5 -о й ;
e – извлечение пиксела 2 и
з а в е р ш е н и е (з а п о л н е н и е
с т е к а ). Ц и к л .
h tt p : // e d u .n s tu .r u / e d u c a tio n /e d u c o u r s e s /C o m p Im /L it /G r a p h ic /k g /3 .h tm
13.
http://www.chinapads.ruКРИВЫЕ БЕЗЬЕ
Кривая Безье — параметрическая кривая, задаваемая выражением
где
Р
i
— функция компонент векторов опорных вершин, а
— базисные функции
кривой Безье, называемые также полиномами Бернштейна.
n
n!
где i i ! ( n i ) ! — число сочетаний из n по i, где n — степень полинома, i — порядковый
опорной вершины.
номер
Историческая справка
Кривые Безье или Кривые Бернштейна-Безье были разработаны в 60-х годах XX века
независимо друг от друга Пьером Безье из автомобилестроительной компании «Рено» и
Полем де Кастельжо из компании «Ситроен», где применялись для проектирования кузовов
автомобилей.
Несмотря на то, что открытие де Кастельжо было сделано несколько ранее Безье, его
исследования не публиковались и скрывались компанией как производственная тайна до
конца 1960-х.
Кривая Безье является частным случаем многочленов Бернштейна, описанных Сергеем
Натановичем Бернштейном в 1912 году.
Впервые кривые были представлены широкой публике в 1962 году французским
инженером Пьером Безье, который, разработав их независимо от де Кастельжо,
использовал их для компьютерного проектирования автомобильных кузовов. Кривые были
названы именем Безье, а именем де Кастельжо назван разработанный им рекурсивный
способ определения кривых.
Впоследствии это открытие стало одним из важнейших инструментов систем
автоматизированного проектирования и программ компьютерной графики.
14.
http://www.chinapads.ruВиды кривых Безье
Линейные кривые
При n = 1 кривая представляет собой отрезок прямой линии, опорные точки P 0 и P1 определяют его начало и конец. Кривая задаётся уравнением:
Квадратичные кривые
Квадратичная кривая Безье задаётся 3-мя опорными точками: P0, P1 и P2.
Квадратичные кривые Безье в составе сплайнов используются для описания формы
символов в шрифтах TrueType и в SWF файлах.
Кубические кривые
В параметрической форме кубическая кривая Безье описывается следующим уравнением:
Кубическая кривая Безье
Четыре опорные точки P0, P1, P2 и P3, заданные в 2-х
или 3-мерном пространстве определяют форму кривой.
Линия берёт начало из точки P0 направляясь к P1 и
заканчивается в точке P3 подходя к ней со стороны P2.
Т.е. кривая не проходит через точки P1 и P2, они
используются для указания её направления. Длина
отрезка между P0 и P1 определяет, как скоро кривая
повернёт к P3.
15.
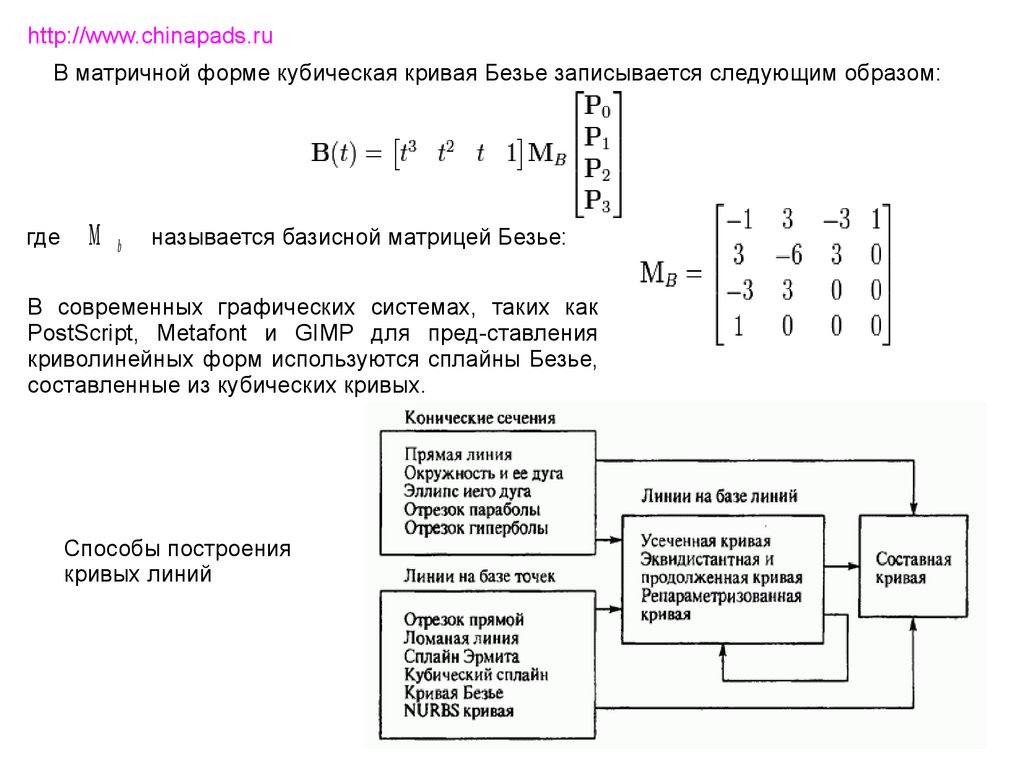
http://www.chinapads.ruВ матричной форме кубическая кривая Безье записывается следующим образом:
где
М
b
называется базисной матрицей Безье:
В современных графических системах, таких как
PostScript, Metafont и GIMP для пред-ставления
криволинейных форм используются сплайны Безье,
составленные из кубических кривых.
Способы построения
кривых линий
16.
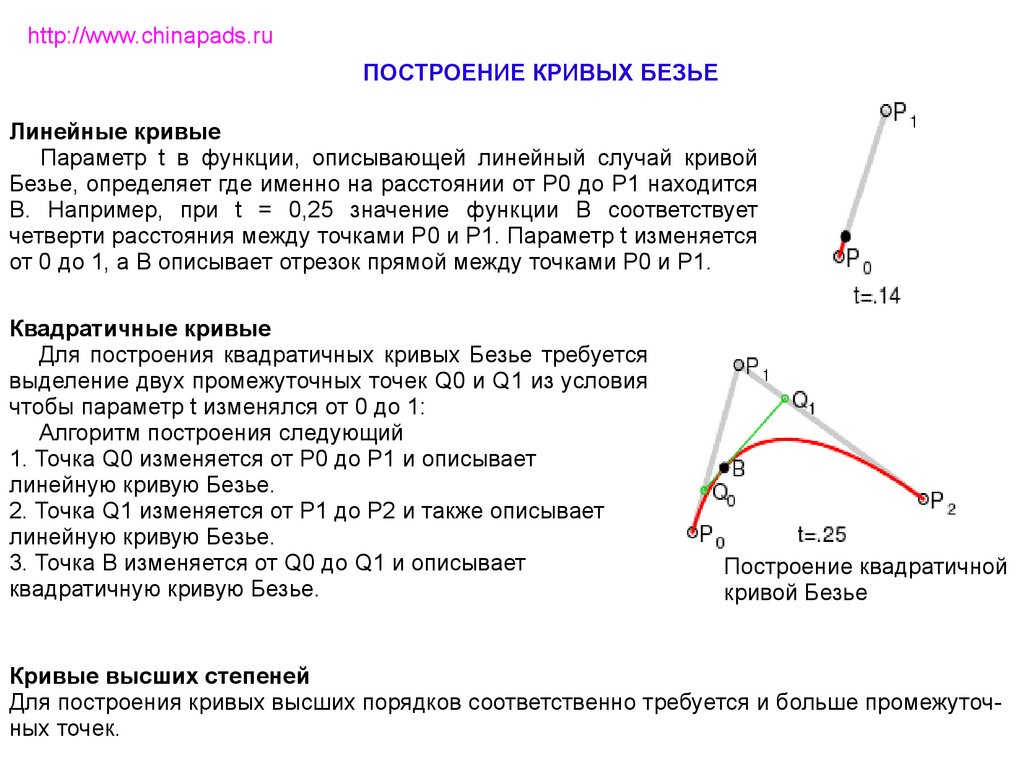
http://www.chinapads.ruПОСТРОЕНИЕ КРИВЫХ БЕЗЬЕ
Линейные кривые
Параметр t в функции, описывающей линейный случай кривой
Безье, определяет где именно на расстоянии от P0 до P1 находится
B. Например, при t = 0,25 значение функции B соответствует
четверти расстояния между точками P0 и P1. Параметр t изменяется
от 0 до 1, а B описывает отрезок прямой между точками P0 и P1.
Квадратичные кривые
Для построения квадратичных кривых Безье требуется
выделение двух промежуточных точек Q0 и Q1 из условия
чтобы параметр t изменялся от 0 до 1:
Алгоритм построения следующий
1. Точка Q0 изменяется от P0 до P1 и описывает
линейную кривую Безье.
2. Точка Q1 изменяется от P1 до P2 и также описывает
линейную кривую Безье.
3. Точка B изменяется от Q0 до Q1 и описывает
квадратичную кривую Безье.
Построение квадратичной
кривой Безье
Кривые высших степеней
Для построения кривых высших порядков соответственно требуется и больше промежуточных точек.
17.
Для кубической кривой это промежуточные точки Q0, Q1 и Q2, описывающие линейные кривые, а такжеточки R0 и R1, которые описывают квадратичные кривые: более простое уравнение
p0q0/p0q1=q1p1/p1p2=bq0/q1q0
Построение кубической кривой Безье
Для кривых четвёртой степени это будут точки Q0, Q1, Q2 и Q3,
описывающие линейные кривые, R0, R1 и R2, которые
описывают квадратичные кривые, а также точки S0 и S1,
описывающие кубические кривые Безье:
Построение кривой Безье
4-й степени
Свойства кривой Безье
- непрерывность заполнения сегмента между начальной и конечной точками;
- кривая всегда располагается внутри фигуры, образованной линиями, соединяющими контрольные
точки;
- при наличии только двух контрольных точек сегмент представляет собой прямую линию;
- прямая линия образуется при коллинеарном размещении управляющих точек;
- кривая Безье симметрична, то есть обмен местами между начальной и конечной точками не влияет на
форму кривой;
- масштабирование и изменение пропорций кривой Безье не нарушает ее стабильности, так как она с математической точки зрения «аффинно инвариантна»;
- изменение координат хотя бы одной из точек ведет к изменению формы всей кривой Безье;
- степень кривой всегда на одну ступень ниже числа контрольных точек. Например, при трех
контрольных точках форма кривой — парабола;
-окружность не может быть описана параметрическим уравнением кривой Безье;
- невозможно создать параллельные кривые Безье, за исключением тривиальных случаев.






 Математика
Математика








