Модели и методы интервального программирования

1. Модели и методы интервального программирования

2. Следует повторить

• определение выпуклого множества, конуса,
выпуклого конуса,
• необходимое и достаточное условие
выпуклости конуса, определение крайнего
вектора для выпуклого конуса, конической
оболочки, многогранного конуса.
• основные ограничения, прямые ограничения
• Нормаль
• Активные, пассивные ограничения
• Теорема Куна-Таккера
• выпуклое множество

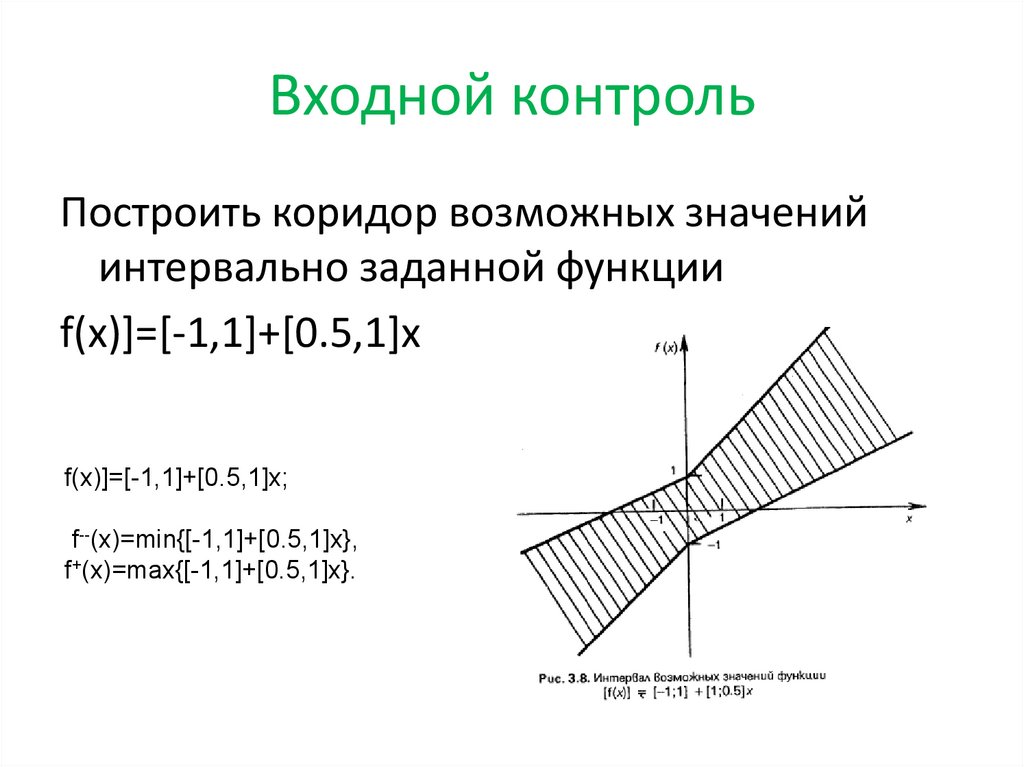
3. Входной контроль

Построить коридор возможных значений
интервально заданной функции
f(x)]=[-1,1]+[0.5,1]x

4. Входной контроль

Построить коридор возможных значений
интервально заданной функции
f(x)]=[-1,1]+[0.5,1]x
f(x)]=[-1,1]+[0.5,1]x;
f--(x)=min{[-1,1]+[0.5,1]x},
f+(x)=max{[-1,1]+[0.5,1]x}.

5. План лекции

1. Элементы интервальной математики
2. Задача интервального линейного
программирования (ЗИЛП)
3. Постановки и детерминированные
эквиваленты ЦФ и ограничений
4. Единственность решения задачи
линейного программирования с
интервальной ЦФ
5. Алгоритм определения единственности
решения ЗЛП с интервальной ЦФ

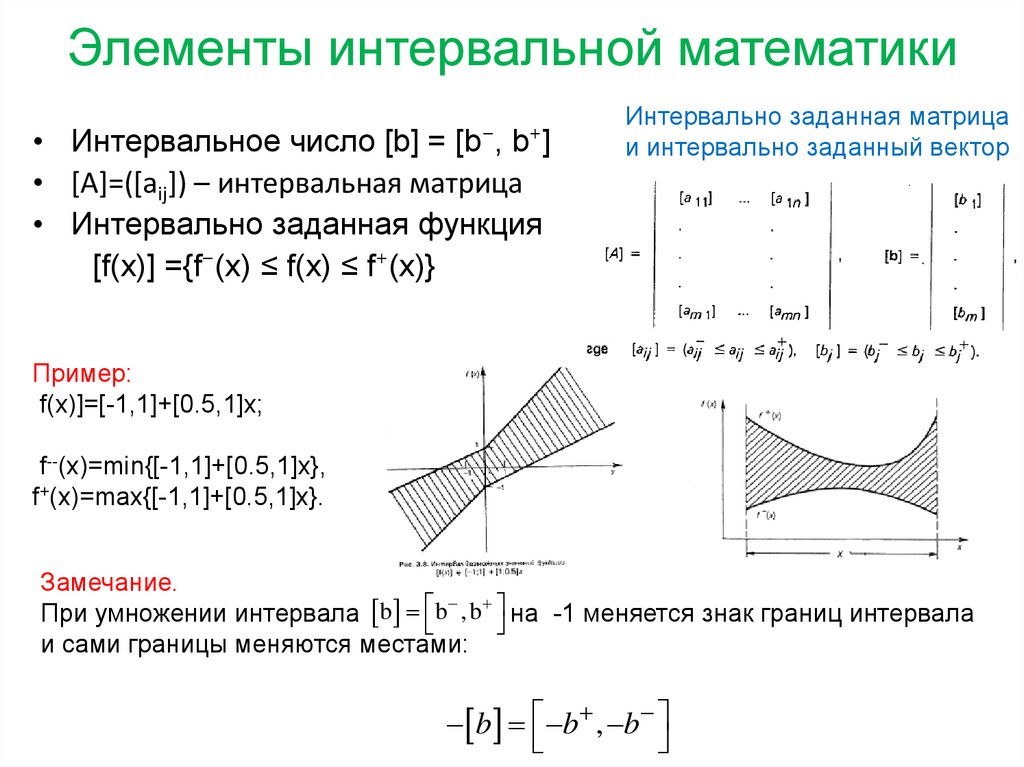
6. Элементы интервальной математики

• Интервальное число [b] = [b⁻, b⁺]
• [A]=([aij]) – интервальная матрица
• Интервально заданная функция
[f(x)] ={f⁻(х) ≤ f(x) ≤ f⁺(x)}
Интервально заданная матрица
и интервально заданный вектор
Пример:
f(x)]=[-1,1]+[0.5,1]x;
f--(x)=min{[-1,1]+[0.5,1]x},
f+(x)=max{[-1,1]+[0.5,1]x}.
Замечание.
При умножении интервала b b ,b на -1 меняется знак границ интервала
и сами границы меняются местами:
b b , b

7. Задачи интервального программирования с линейными ограничениями

[f (x)] min
[A]x [b],
x 0.

8. ЗИЛП

• Интервально заданная функция
[f(x)]=[c`x] → max(min)
• Ограничения с интервальными
коэффициентами [A]x ≤ [b]
• Х >=0 – детерминированный → [c`x] = [c]`x
c `x min
[A]x [b],
x 0.

9. Постановки ЗИЛП

Модели ограничений
1. x₁ = { x ≥ 0 | при ∀ A ∈ [A],
∀ b ∈ [b] верно Ax ≤ b } (жёсткое ограничение)
2. х₂ = { x ≥ 0; ∀ A ∈ [A], ∃ b ∈ [b]: Ax ≤ b }
3. х₃ = { x ≥ 0: ∃ A ∈ [A], ∀ b ∈ [b]: Ax ≤ b }
4. х₄ = { x ≥ 0: ∃ A ∈ [A], ∃ b ∈ [b]: Ax ≤ b } (мягкое
ограничение)
(b b )
5. х₅ = { x ≥ 0: A x b } где b
2

10. Детерминированные эквиваленты ограничений

1. х₁ = { x ≥ 0: A⁺x ≤ b⁻ }
2. х₂ = { x ≥ 0: A⁺x ≤ b⁺ }
3. х₃ = { x ≥ 0: A⁻x ≤ b⁻ }
4. х₄ = { x ≥ 0: A⁻x ≤ b⁺ }
5. х₅ = { x ≥ 0: A x b
A (aij ) : aij
ij
ij
a a
2
Соотношение между множествами x₁ - х₅:
x₁ ⊂ х₅ ⊂ х₄
}

11. Пример

12.

Утверждение 1. При любом выборе f(x) согласно условию
f x f x f x
(*)
вариация экстремального значения критерия ограничена
пределами
f (x 0 ) f (x 0 ) f (x 0 ), f x f x (1*)
где
х0 / argmin f / (x), х0 argmin f (x)
x X
x X
Доказательство. Для x X , f x [ f x ] выполнено (*). Покажем, что
min f x min f x .
От противного. Пусть выполнено обратное:
f x0 min f x min f x f x0
Тогда f ( x) min f ( x) min f ( x) f ( x0 ), x X .
Возьмем x x0 : f ( x0 ) f ( x0 ) , что противоречит (*). Значит, (1*) верно.
Аналогично доказывается f(x0-)<= f(x0).

13. Постановки и детерминированные эквиваленты ЦФ

1. Минимаксная: минимальная реализация функции на max.
min [c]`x → max,
c ⁻ x → max
Максиминная: максимальная реализация функции на min.
max [c]`x → min,
c⁺x → min
Принцип пессимистический. Применяется, когда необходимо обеспечить гарантированный
результат. Эта постановка ориентирована на наихудший случай, особенно в случае допустимой
области X1
2. Миниминная:
min [c]`x → min,
Максимаксная:
max [c]`x → max,
c ⁻ x → min
c⁺x → max
Принцип оптимистический. Если использовать область X4, то буде получено минимально
(максимально) возможное значение критерия
3. В среднем
[ c ]`x → max:
((c⁻+c⁺)/2)*x → max
Наиболее естественно использовать Х5.
4. Многокритериальная
f₁(x) → max
…………….
fm(x) → max
fi(x) ∈ [f⁻(x), f ⁺(x)]

14. Постановки и детерминированные эквиваленты ЦФ

Постановка
Модель
Детерминированны
й эквивалент
Минимаксная:
минимальная
реализация функции на
max
min [c]`x → max
c ⁻ x → max
Миниминная
min [c]`x → min
c ⁻ x → min
В среднем
[c ]`x → max
((c⁻+c⁺)/2)*x → max
Многокритериальная
f₁(x) → max
…………….
fm(x) → max
fi(x) ∈ [f⁻(x), f ⁺(x)]

15.

Основы выпуклого анализа
Выпуклым конусом, порожденным конечной системой
элементов
x k ( x k ,.., x k ), (k 1, 2,..., l )
1
n
пространства R n называется множество элементов ,
определяемых формулой
x 1x1 2 x2 ... m xm , i 0
При этом элементы x k ( x1k ,.., xnk ), (k 1, 2,..., l ) называются
образующими элементами конуса.
Опр. Пусть Х – произвольное множество из R n .
Конической оболочкой множества Х называется
множество всех неотрицательных линейных комбинаций
K
K0 x j x j
j 1
точек x X .
Коническая оболочка является наименьшим выпуклым
конусом, содержащим множество Х.
j

16.

Опр. Выпуклый конус K Rn называется многогранным,
если для заданного конечного множества векторов
A [a1 ,.., am ] ai R n
любая точка x K является их неотрицательной линейной
комбинацией
m
K {x R n ; x A j a j : j 0, j 1, m}
i 1
Столбцы матрицы А будут крайними векторами.
Пример: Определить, принадлежит ли вектор х=(1,1,1) конусу с крайними
векторами
2
1
0.5
a1 0 , a2 1 , a3 1
0.5
4
0.5
Составим матрицу
a1
Решение
a2
A x1 , x2 , x3 и решим систему x A a , a , a
1
2
3
1 1
a3 2 1
1
3
x0 A 1a1 2 a2 3a3
(6 / 27;3 / 27; 24 / 27) . Так как 0 , то
да, принадлежит.

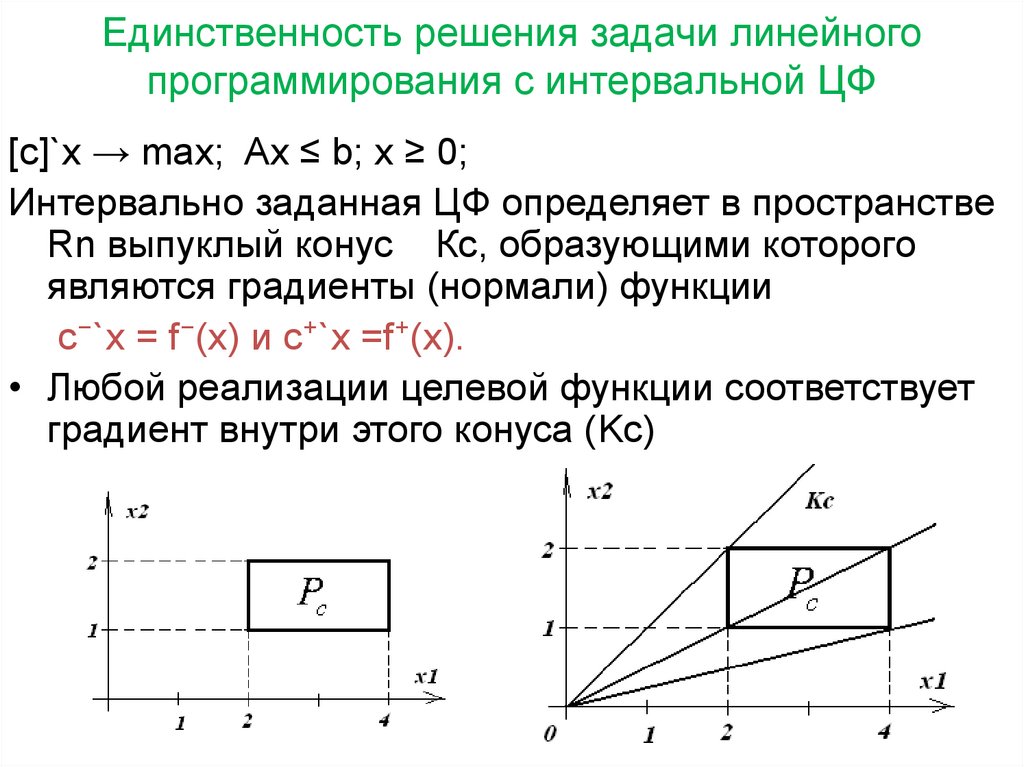
17. Единственность решения задачи линейного программирования с интервальной ЦФ

[c]`x → max; Ax ≤ b; x ≥ 0;
Интервально заданная ЦФ определяет в пространстве
Rn выпуклый конус Кс, образующими которого
являются градиенты (нормали) функции
c⁻`x = f⁻(x) и c⁺`x =f⁺(x).
• Любой реализации целевой функции соответствует
градиент внутри этого конуса (Kc)

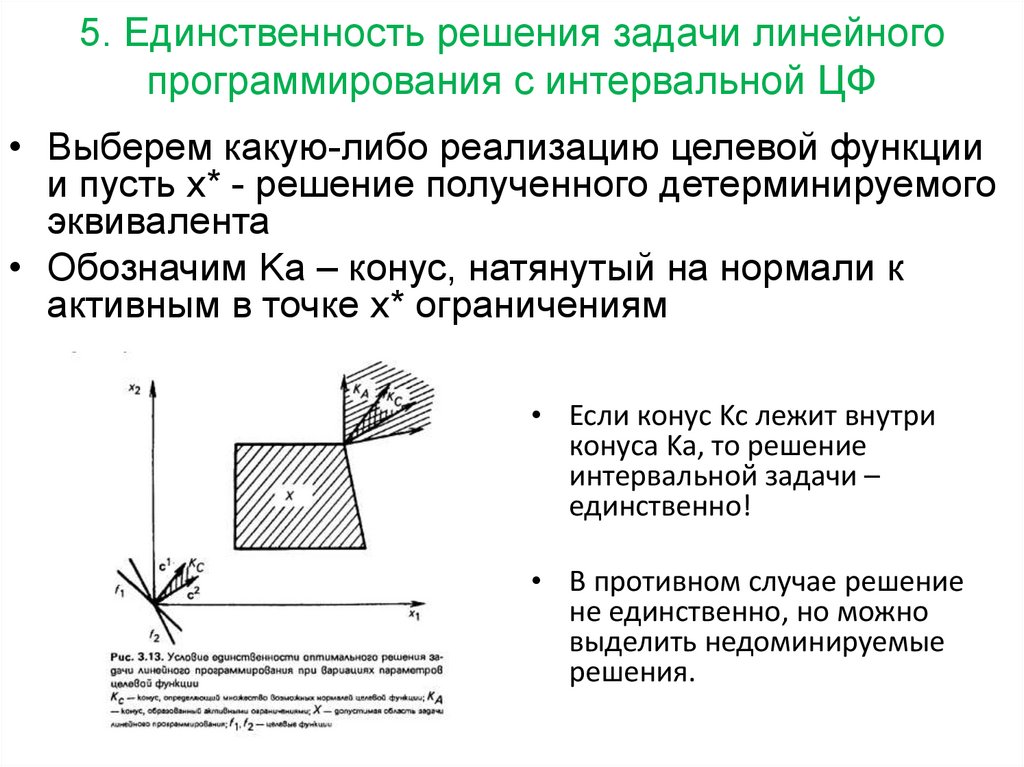
18. 5. Единственность решения задачи линейного программирования с интервальной ЦФ

• Выберем какую-либо реализацию целевой функции
и пусть х* - решение полученного детерминируемого
эквивалента
• Обозначим Ka – конус, натянутый на нормали к
активным в точке х* ограничениям
• Если конус Kc лежит внутри
конуса Ka, то решение
интервальной задачи –
единственно!
• В противном случае решение
не единственно, но можно
выделить недоминируемые
решения.

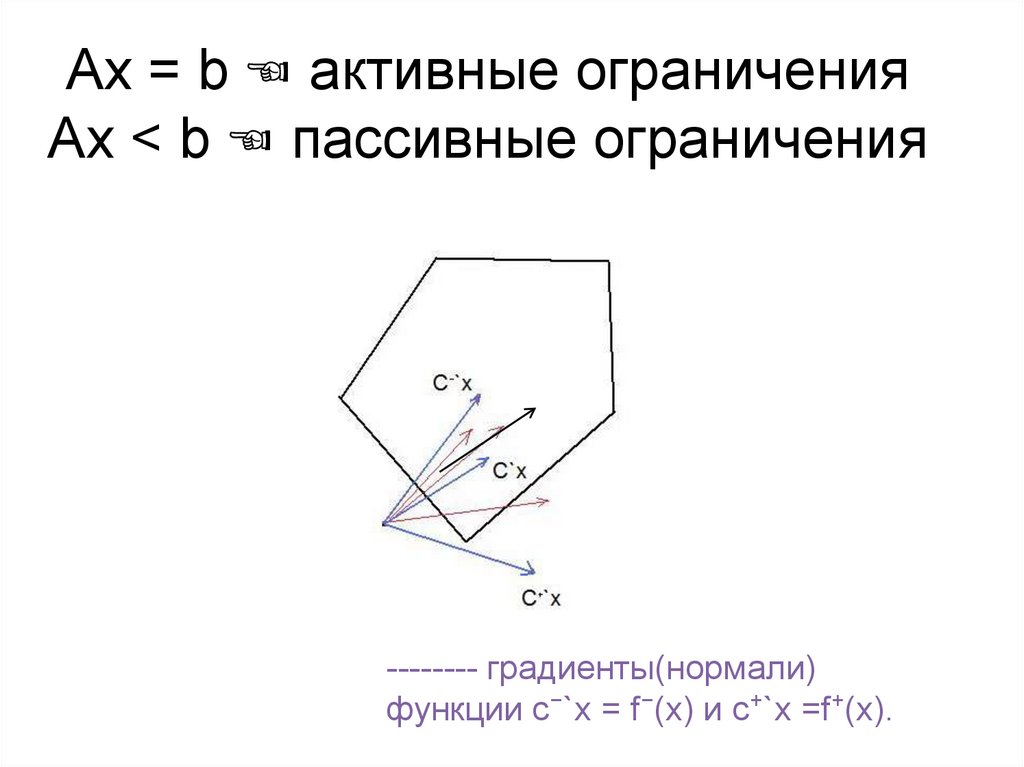
19. Аx = b ☜ активные ограничения Ax < b ☜ пассивные ограничения

Аx = b ☜ активные ограничения
Ax < b ☜ пассивные ограничения
-------- градиенты(нормали)
функции c⁻`x = f⁻(x) и c⁺`x =f⁺(x).

20. 6. Алгоритм определения единственности решения

21. 6. Алгоритм определения единственности решения

22.

Пример №1
Решить задачу интервального программирования
[c] x max,
5x1 3x2 2.5x3 150,
x1 x2
x3 40,
x3 10,
x j 0, j 1, 3.
n
[
c
]
R
Где
- интервальный вектор коэффициентов целевой
функции, проверить единственность ее решения.

23.

Постановка задачи
[8.4; 8.5] x1 [2.7; 2.8] x 2 [2.2; 2.3] x 3 max,
5 x1 3 x 2 2.5 x 3 150,
x1 x 2
x 3 40,
x 3 10,
x j 0, j 1,3.
Решение задачи
1.Детерминированный эквивалент (максиминная модель ).
{8.5 x1 2.8 x 2 2.3 x3 } min,
5 x1 3 x 2 2.5 x3 150,
x1 x 2
x3 40,
x3 10,
x j 0, j 1,3.

24.

2. Решение задачи:
17.5
x 12.5
10
f 206.75
3. Проверка единственности решения.
3.1 Сформируем матрицу
Mc R
n 2 n
из векторов c j [c], j 1,2 n
8.4 8.4 8.4 8.4 8.5 8.5 8.5 8.5
M c 2.7 2.8 2.7 2.8 2.7 2.8 2.7 2.8
2.2 2.2 2.3 2.3 2.2 2.2 2.3 2.3

25.

3.2 Формируем ЗЛП с коэффициентами из
первого столбца
8.4
c1 2.7
2.2
(c ) x max,
1
Ax b,
x 0
8.4 x1 2.7 x 2 2.2 x3 max,
5 x1 3 x 2 2.5 x3 150,
x1 x 2
x3 40,
x3 10,
x j 0, j 1,3.

26.

8.4
Вектору c1 2.7 соответствует оптимальный план:
2.2
17.5
1
x 12.5
10
Активными в точке
X
f 202 .75
1
являются ограничения (1), (2), (3).

27.

3.3. Для решения
x
1
формируем матрицу
MA
Строки которой – векторы нормали активных
ограничений в точке
x
1
5 1 0
M A 3 1 0
2 .5 1 1

28.

3.4. Решаем матричное уравнение
M A M c
55.6 55.9 55.85 56.15 56.1 56.4 56.35 56.65
13.3 13.4 13.4 13.5 13.4 13.5 13.5 13.6
2 .2 2 .2
2
.
3
2
.
3
2
.
2
2
.
2
2
.
3
2
.
3
.
3.5. Т.к. Все
решение задачи!
0 , то x
1
- единственное

29. Резюме

сущность задач принятия решений в условиях
интервальной неопределенности
различия в основных постановках задач интервального
программирования
Основные модели задачи интервального
программирования с линейными ограничениями (модели
ограничений, модели критерия)
Детерминированные эквиваленты задач интервального
программирования