Похожие презентации:
Установление преемственных связей в обучении рассуждениям и доказательству в процессе реализации требований ФГОС
1. Установление преемственных связей в обучении рассуждениям и доказательству в процессе реализации требований ФГОС ООО
продолжениеСветлана Иосифовна Смирнова
24.06.2016
1
2.
Ученик достигает пониманияматематики, если в процессе
обучения он принимает активное
участие в развитии математических
идей, процедур, в построении (пусть
и маленьких, локальных) математических теорий
А.А. Столяр
2
3. Примеры локальных теорий
Игра«Кирпичики»
Б. П. Никитин. Ступеньки творчества,
или Развивающие игры.
3
4.
45. Установление отношения длин ребер
1:2:45
6.
Видспереди
Вид
сбоку
Вид
сверху
6
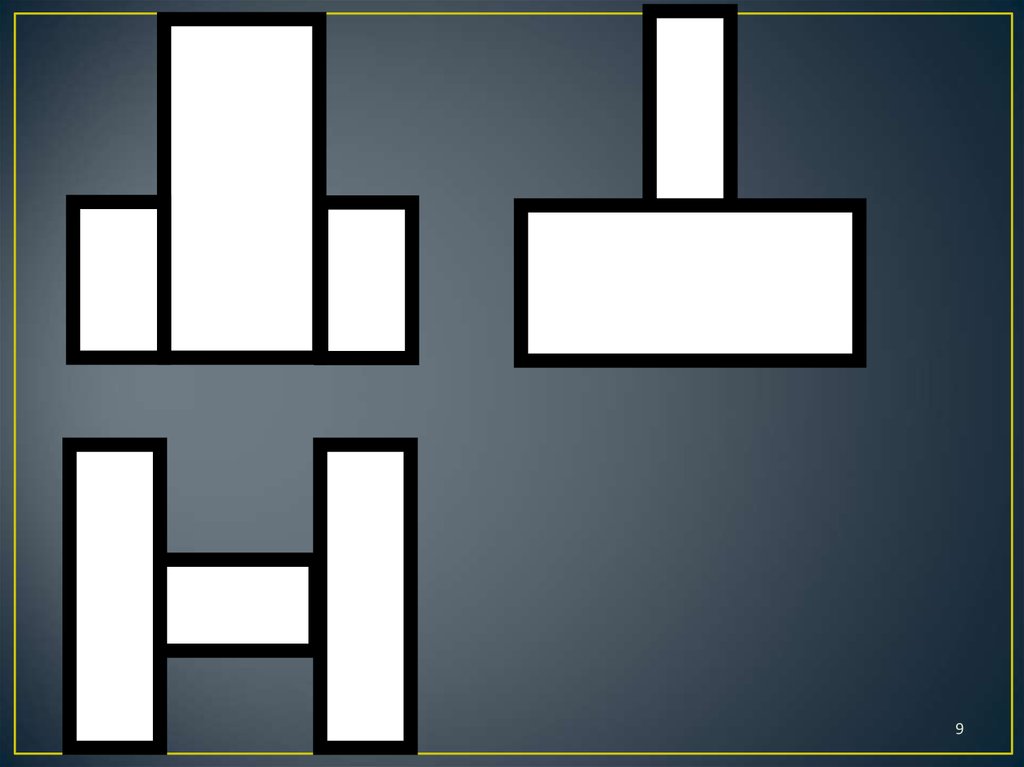
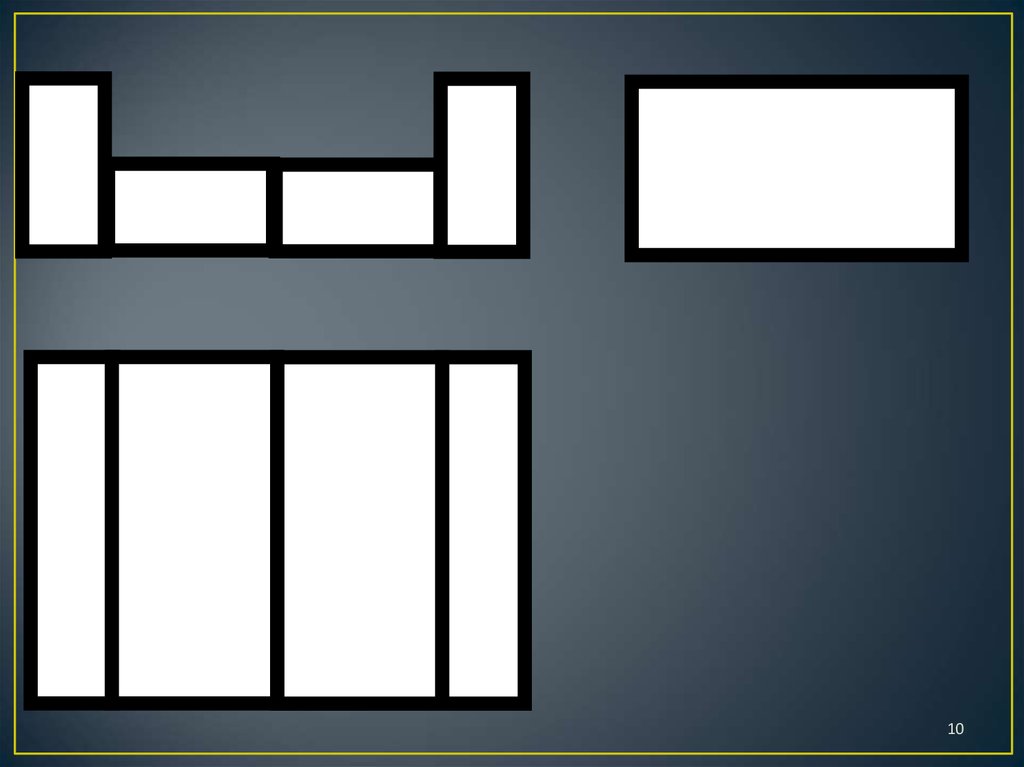
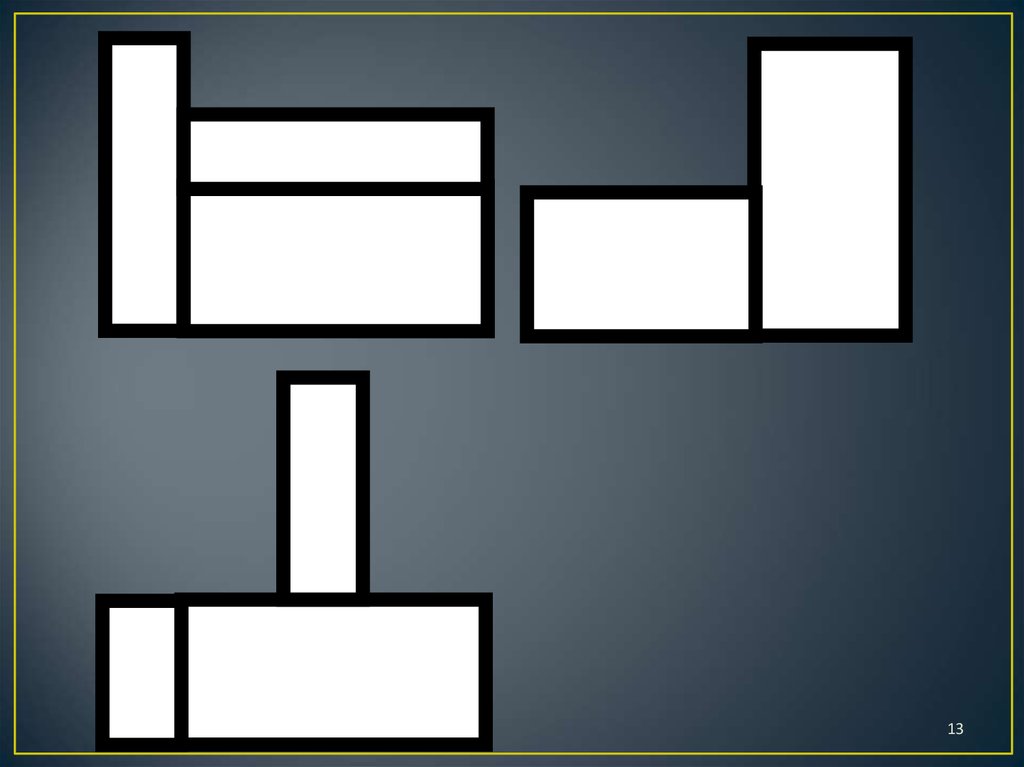
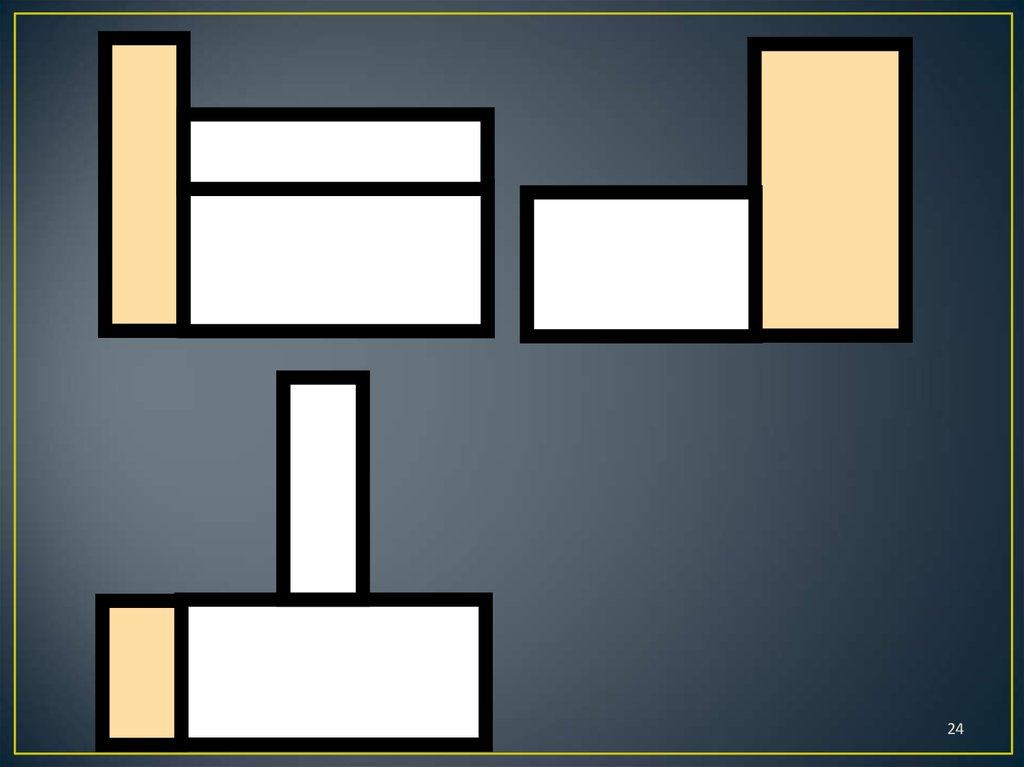
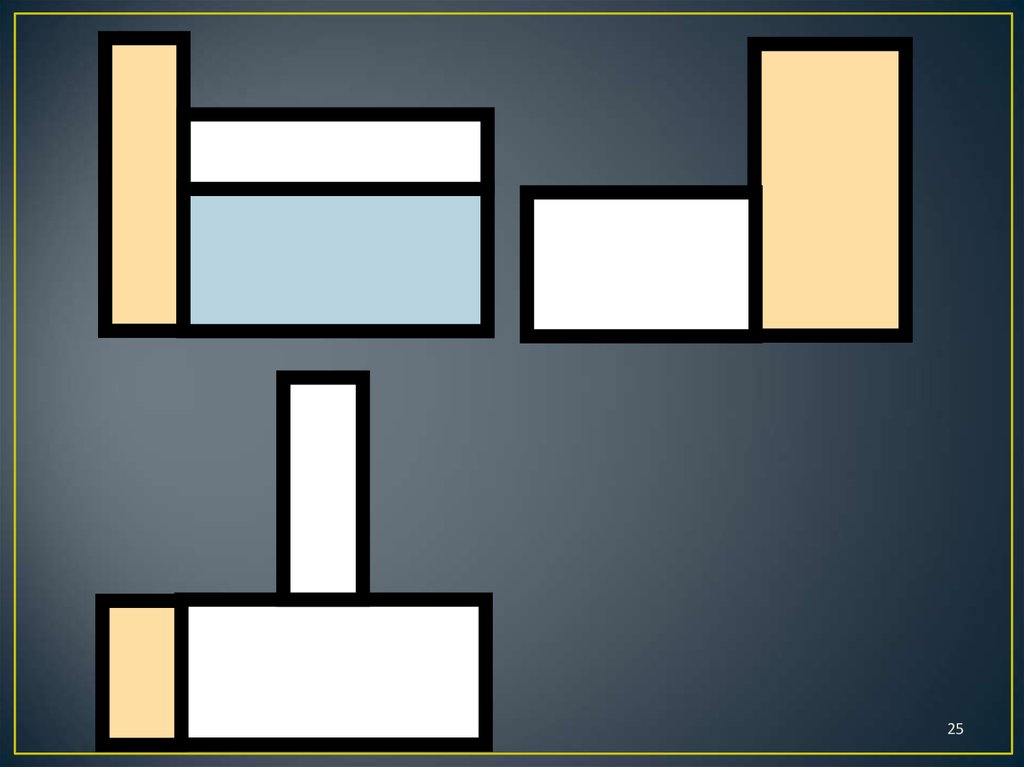
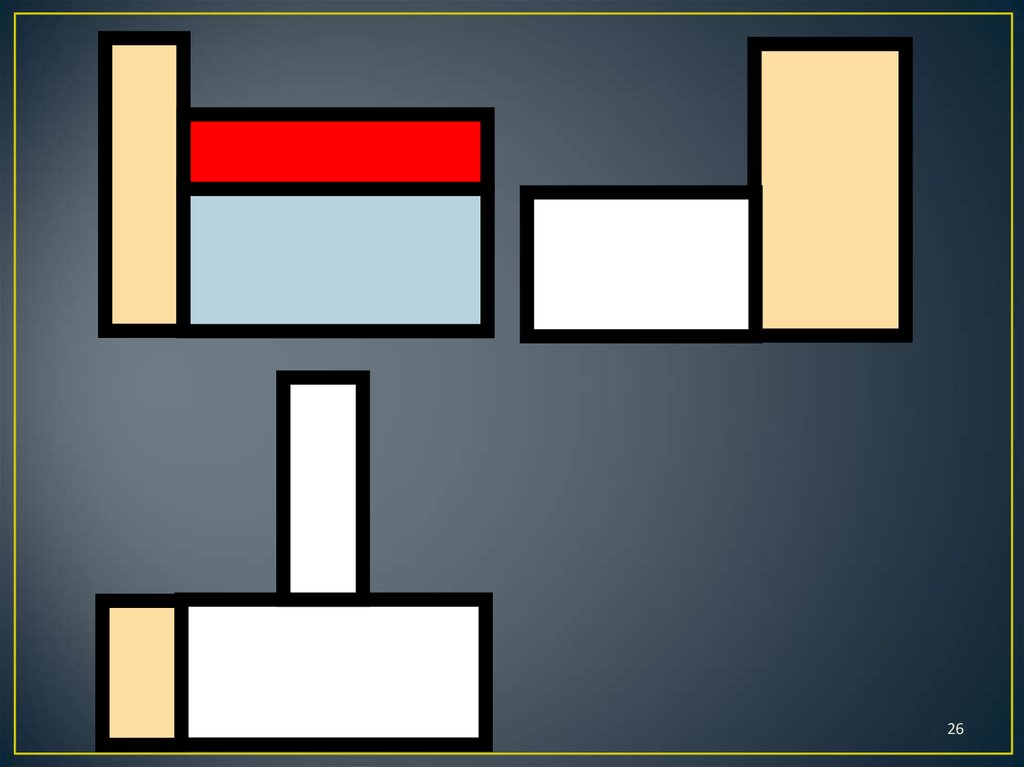
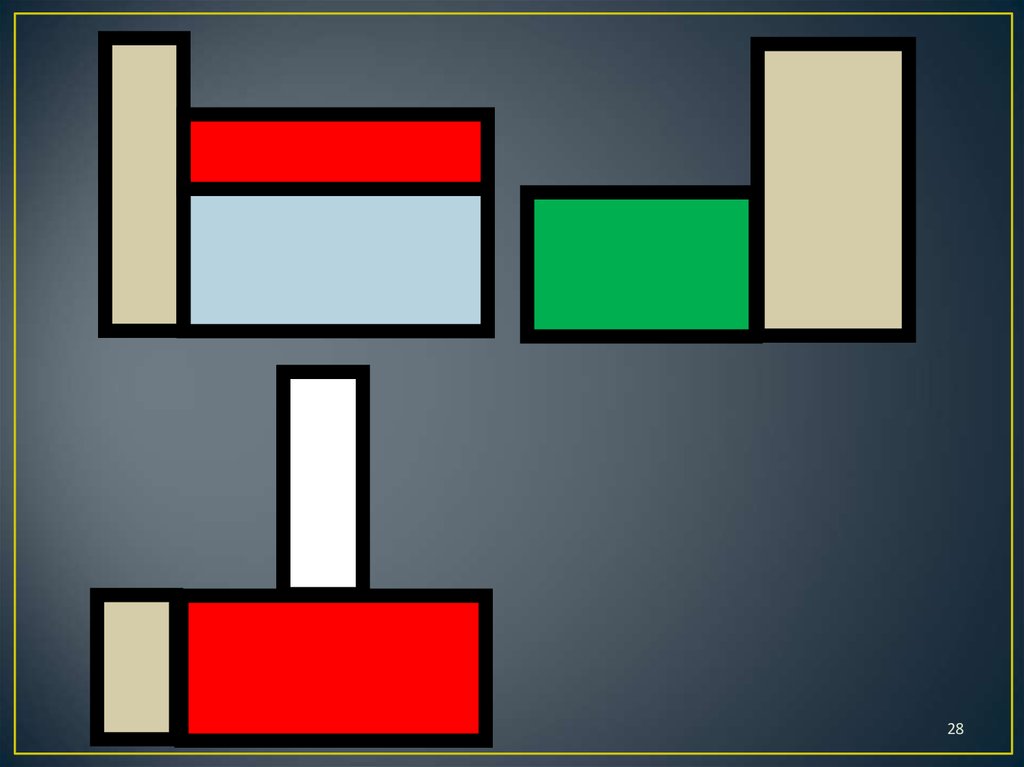
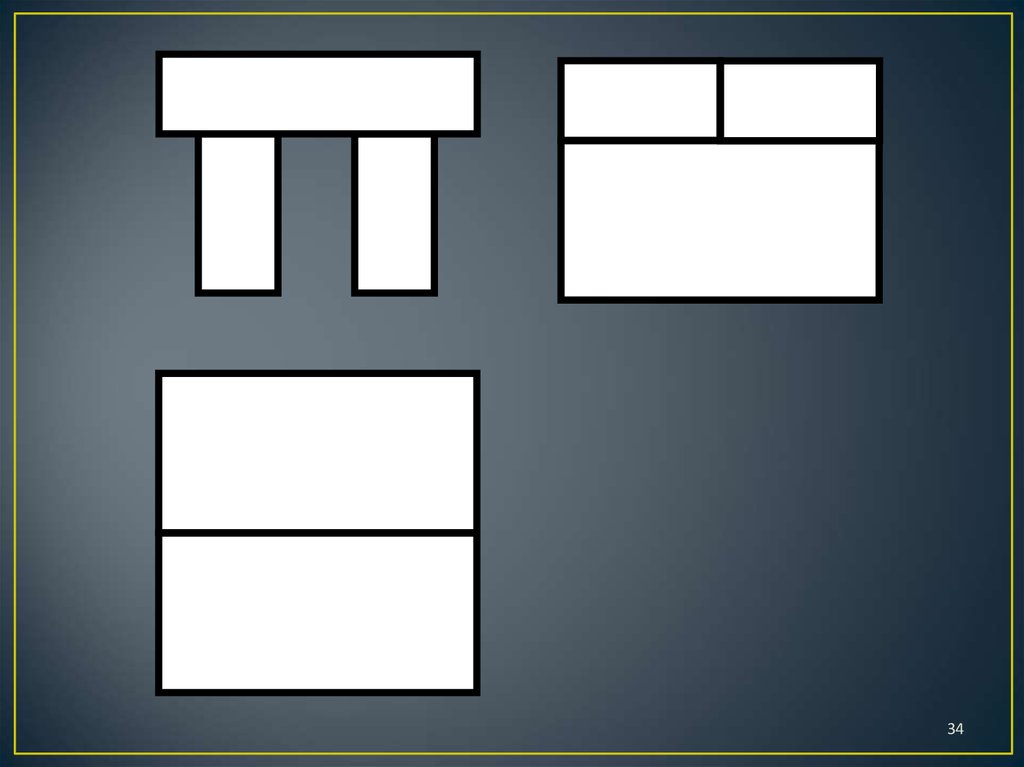
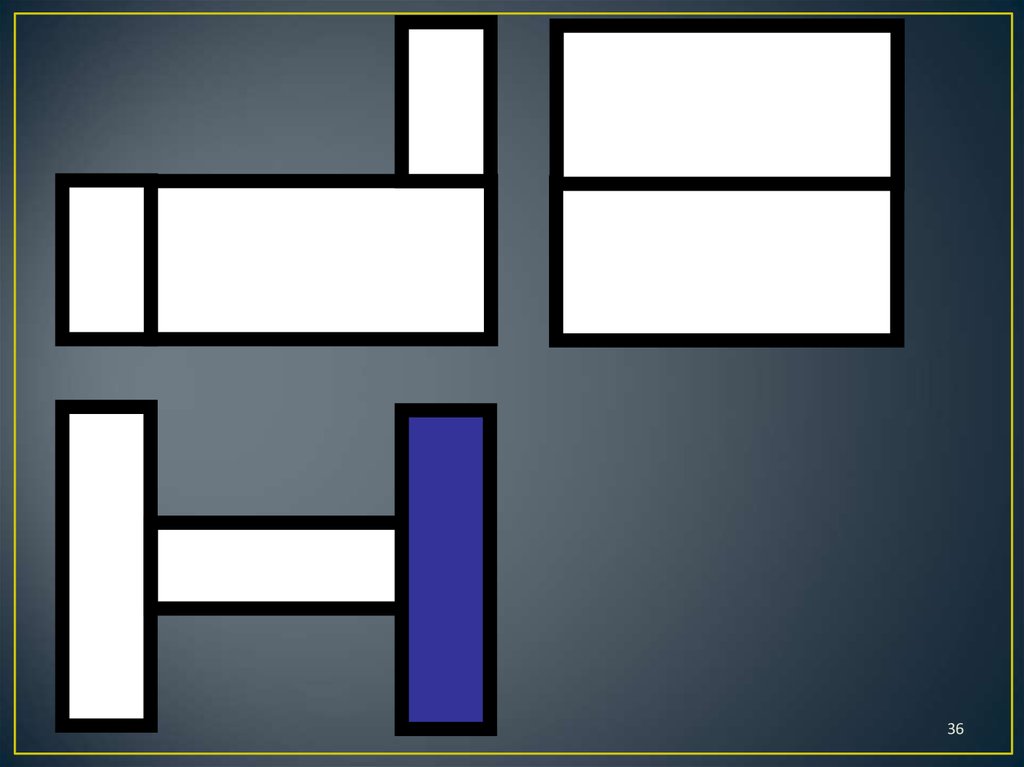
7. Правила игры
1. Определить по чертежу, сколько кирпичиковпотребуется для построения конструкции.
Обосновать.
2. Построить конструкцию, взяв количество
кирпичиков, определенное на первом шаге.
3. Проверить правильность построения, сравнив
виды конструкции и чертеж.
4. Сделать вывод.
7
8.
89.
910.
1011.
1112.
1213.
1314.
1415.
1516.
1617.
1718.
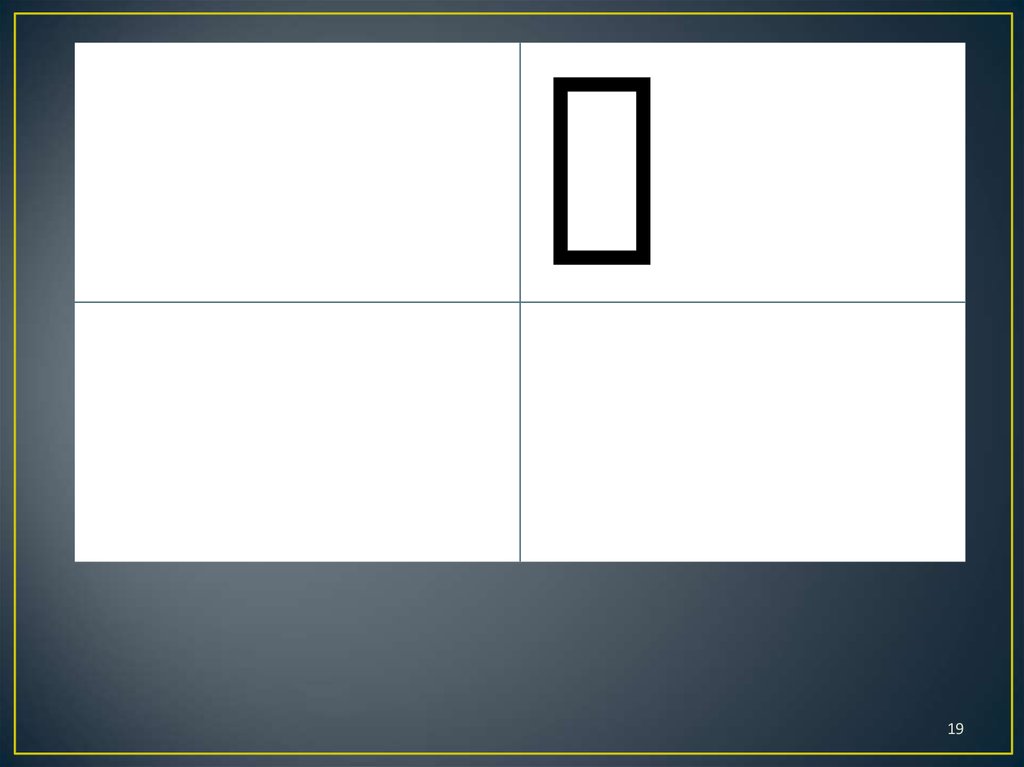
1819.
1920.
Если на виде спереди изображена большаягрань горизонтально, то на виде сверху
будет средняя грань горизонтально, а на
виде сбоку – маленькая грань вертикально.
20
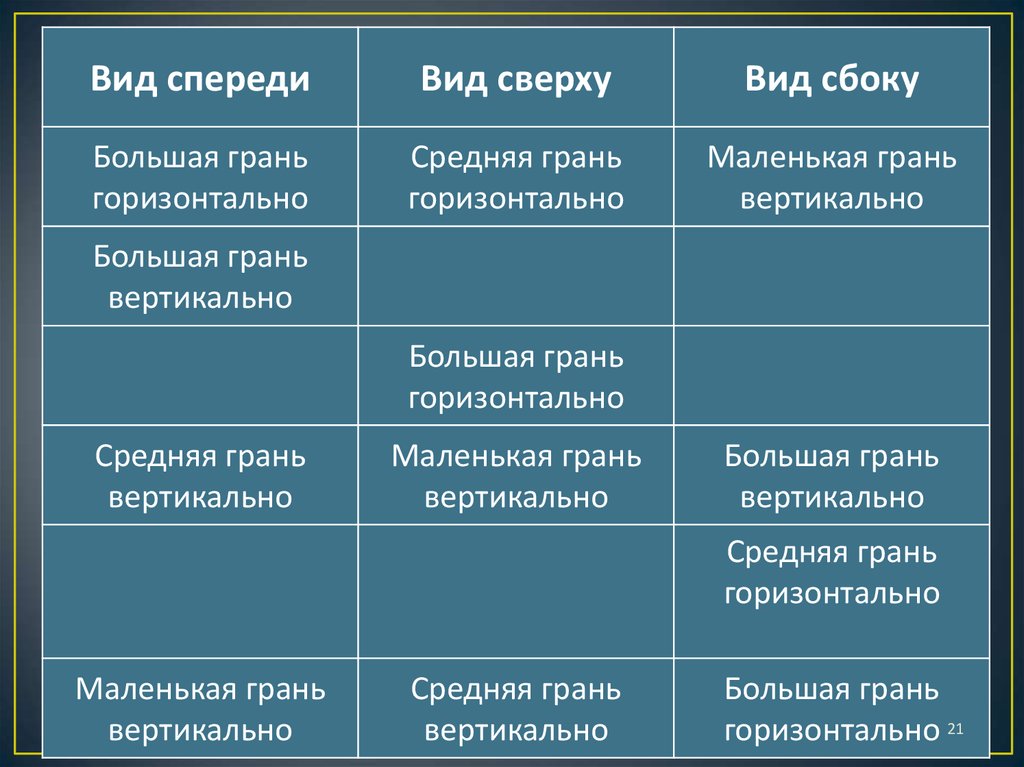
21.
Вид спередиВид сверху
Вид сбоку
Большая грань
горизонтально
Средняя грань
горизонтально
Маленькая грань
вертикально
Большая грань
вертикально
Большая грань
горизонтально
Средняя грань
вертикально
Маленькая грань
вертикально
Большая грань
вертикально
Средняя грань
горизонтально
Маленькая грань
вертикально
Средняя грань
вертикально
Большая грань
горизонтально 21
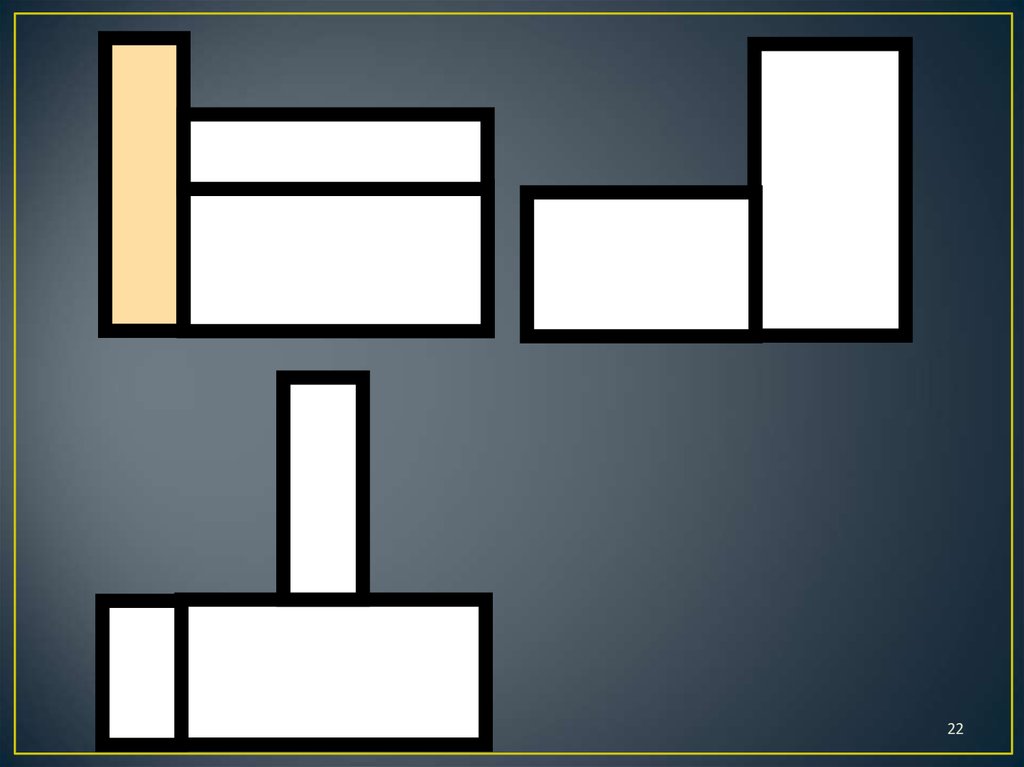
22.
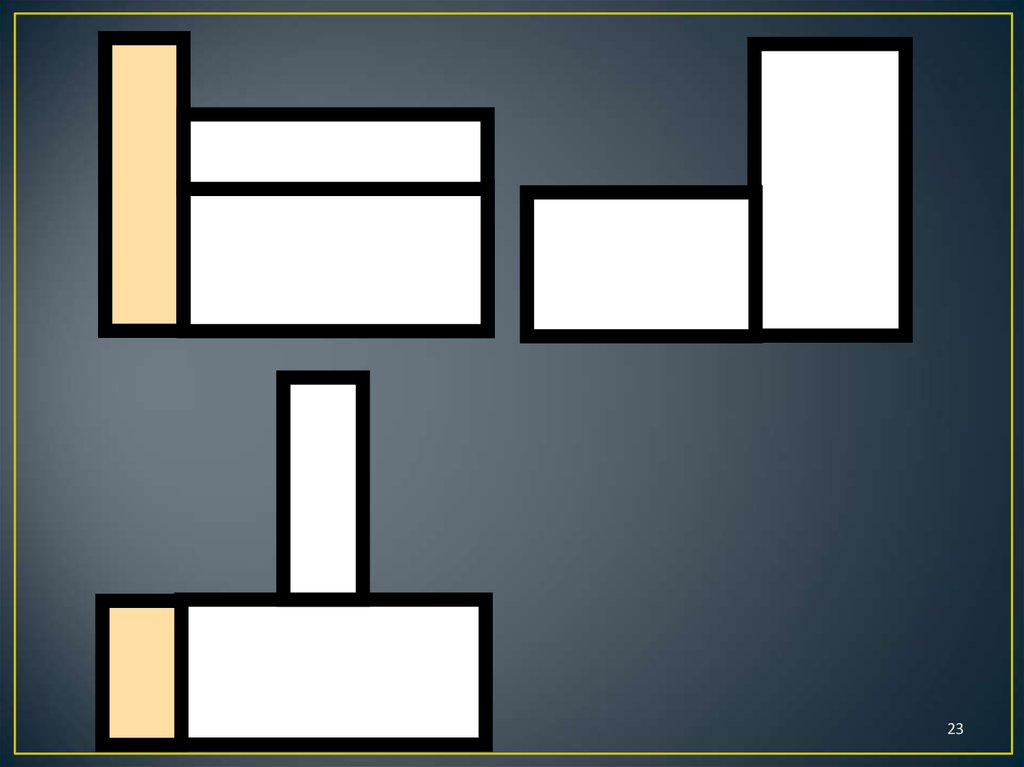
2223.
2324.
2425.
2526.
2627.
2728.
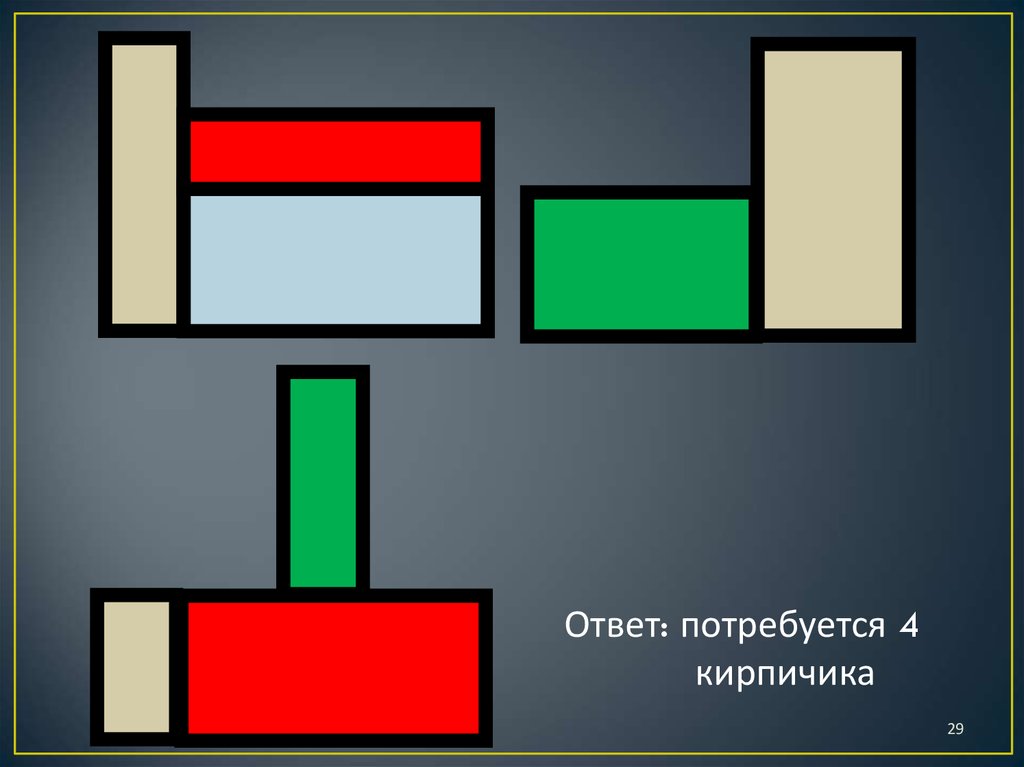
2829.
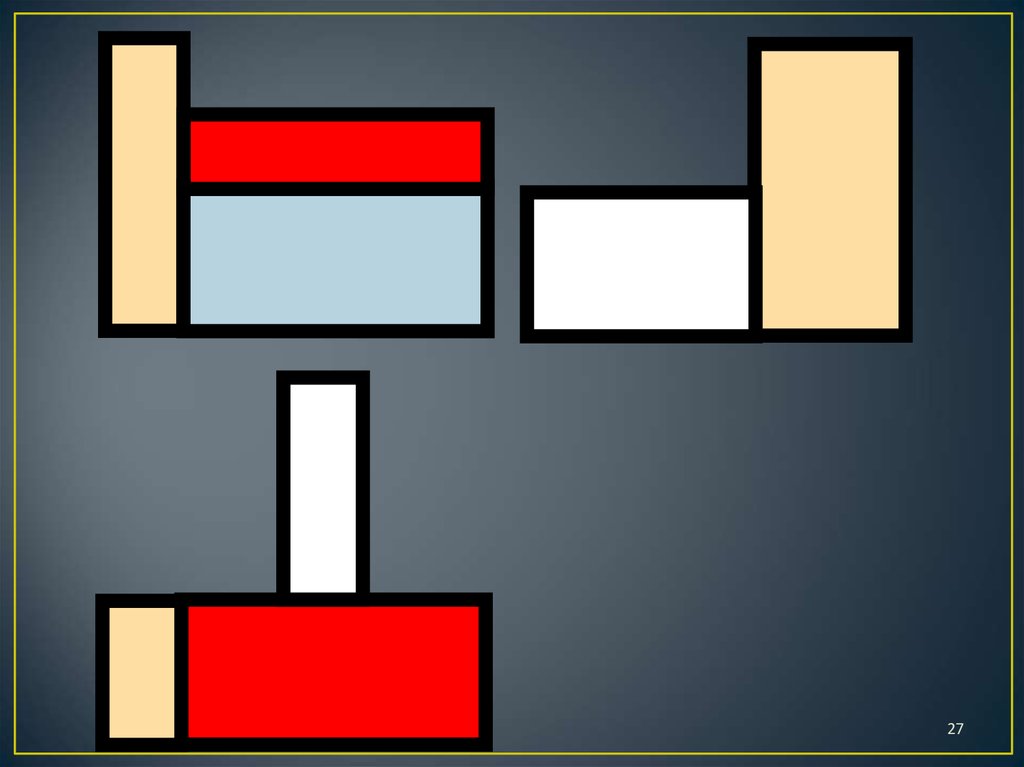
Ответ: потребуется 4кирпичика
29
30. Этапы построения теории «Кирпичики»
1.Мотивация обоснованиясуждений
2.Построение мини теории
30
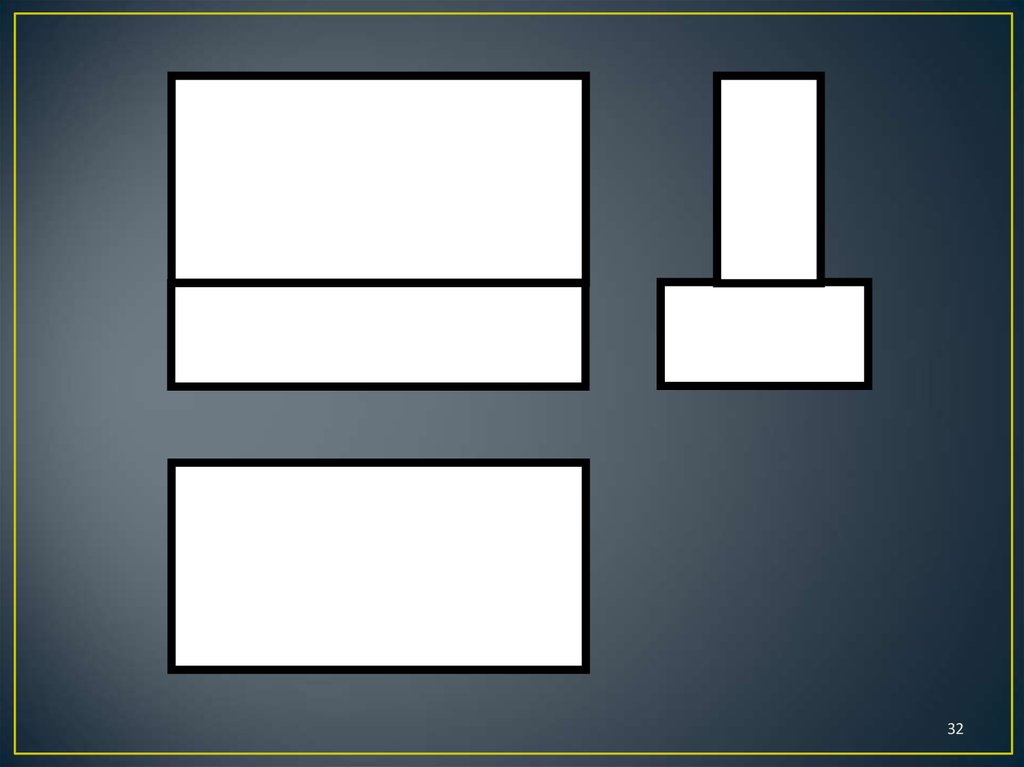
31.
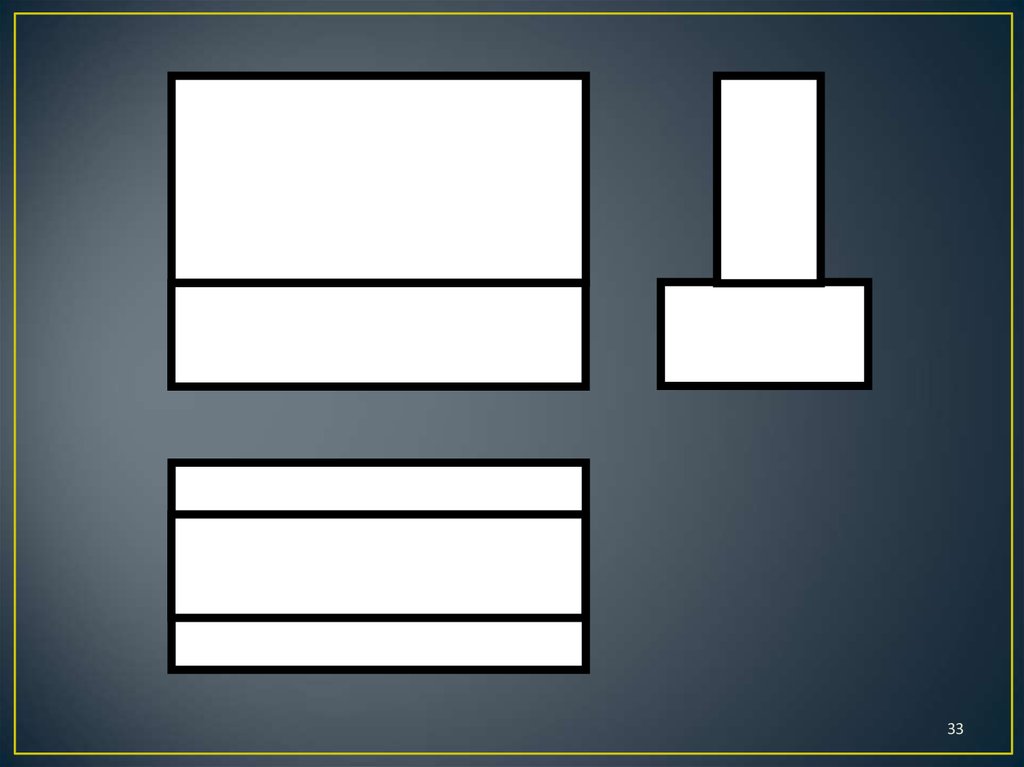
3132.
3233.
3334.
3435.
3536.
3637. Планирование
№занятия
Основное содержание
1
1. Знакомство с прямоугольным параллелепипедом и его
элементами.
2. Формирование представлений о чертеже. Знакомство с
правилами игры «Кирпичики».
2
1. Закрепление представлений о чертеже.
2. Построение простейших конструкций.
3
4
5
1. Мотивация проведения рассуждений в случае более
сложной конструкции.
2. Введение терминологии.
1. Введение правил расположения граней кирпичика на
чертеже.
2. Построение простейших рассуждений.
Выполнение разнообразных заданий с применением
введённых терминов и правил.
37
38. Проверьте себя!
3839.
3940. Решите задачи
1. Докажите, что при любом натуральномчисле k произведение (5k + 2) · (3k – 1)
выражается четным числом.
2. Выберите из таблицы пять чисел, сумма
которых равна 20:
1 1 1 1
3
5
7
3
5
7
3
5
7
3
5
7
3. Можно ли указать такое целое значение a,
при котором значение суммы a2 + a + 1
делится нацело на 2014?
41. Локальная теория «Четные и нечетные числа»
4142. Является ли четным число:
• 26• 128
• 1234567890
• 2481
42
43.
• ОПРЕДЕЛЕНИЕ 1. Четным называетсянатуральное число, десятичная запись
которого оканчивается цифрой 0, 2, 4, 6
или 8. Число 0 – четное.
• ОПРЕДЕЛЕНИЕ 2. Нечетным называется
натуральное число, десятичная запись
которого оканчивается цифрой 1, 3, 5, 7
или 9.
43
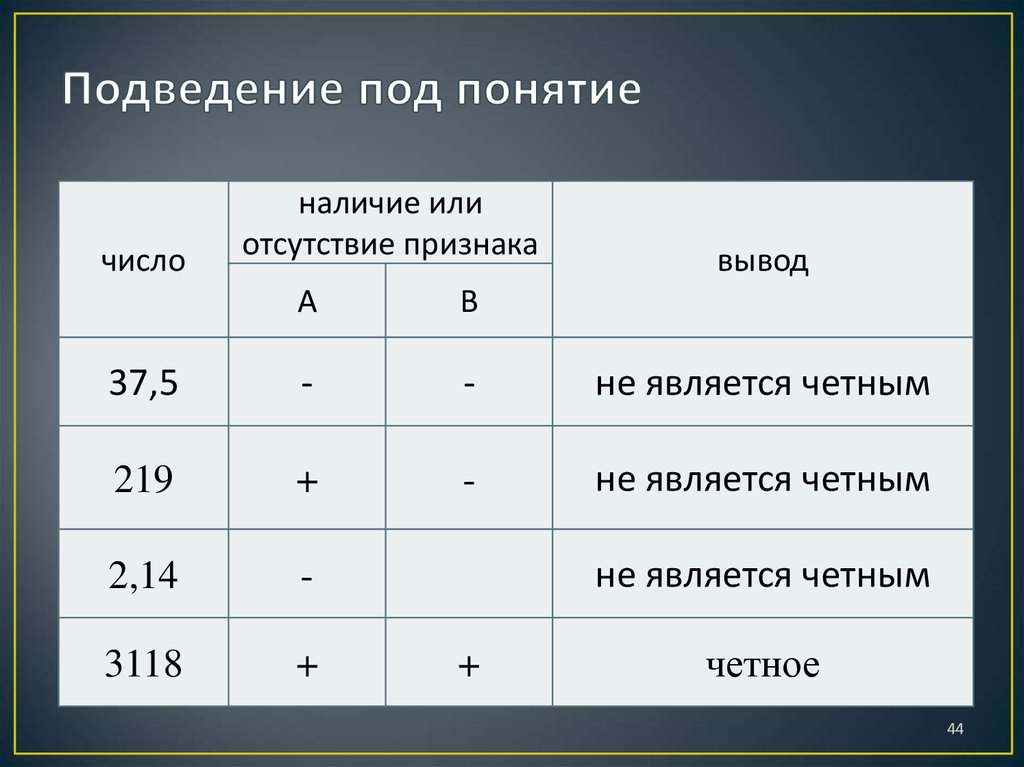
44. Подведение под понятие
числоналичие или
отсутствие признака
вывод
А
В
37,5
-
-
не является четным
219
+
-
не является четным
2,14
-
3118
+
не является четным
+
четное
44
45. Следствия
1. Натуральное число не может быть одновременно четным инечетным. (Каждое натуральное число либо четное, либо
нечетное.)
2. На множестве целых неотрицательных чисел каждое
нечетное число на 1 больше предыдущего четного, то есть
н. = ч. + 1.
3. На множестве натуральных чисел каждое четное число
на 1 больше предыдущего нечетного, то есть ч. = н. + 1.
4. Из двух последовательных натуральных чисел одно
обязательно четное, другое - нечетное.
5. Из трех последовательных натуральных чисел хотя бы одно
число – четное, хотя бы одно – нечетное.
6. Разность последовательных четных (нечетных) чисел равна
45
двум.
46. Проблемный вопрос
Третьеклассница Наташа долго решалапример и, наконец, вычислила ответ.
Вот что у нее получилось:
237512 + 31954 + 80490 + 371238 + 190076 = 911311.
Однако ее сестра пятиклассница Нина,
быстро взглянув на пример, сказала, что
ответ неверный. Как Нина догадалась?
46
47. Свойство 1. Сумма двух четных чисел четна. Доказательство: пусть а и в – два четных числа.
4748. Аксиома
Каждое четное число можетбыть представлено в виде
суммы двух одинаковых
слагаемых .
48
49. Сумма четных чисел четна
№суждение
1 а и в – четные числа
2 а = х + х, в = у + у
3 а + в = (х + х) + (у + у) =
(х + у) + (х + у) =
с + с – четное число
основание (аргумент)
по условию
по аксиоме
переместительное
и
сочетательное свойства
сложения
по аксиоме
Получили, а + в – четное число, что и требовалось
доказать.
49
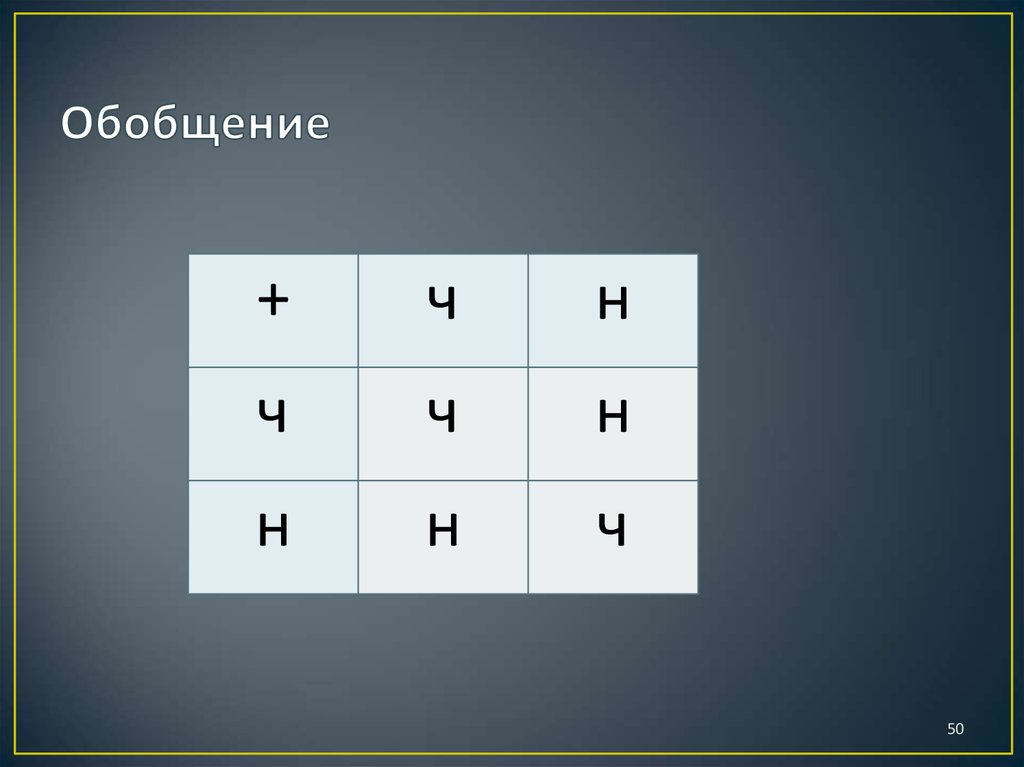
50. Обобщение
+ч
н
ч
ч
н
н
н
ч
50
51. Сумма двух нечетных чисел четна
Дано: два нечетных числаДоказать: н + н = ч (их сумма четна)
Доказательство: представим второе слагаемое как сумму четного числа и
1 (по следствию 2): н + н = н + (ч + 1). Сочетательное свойство сложения
позволяет перегруппировать слагаемые: н + (ч + 1) = (н + ч) + 1. Сумма
нечетного и четного чисел по свойству 3 нечетна. А если к нечетному
числу прибавить 1, то по следствию 3 получим четное число, что и
требовалось доказать.
51
52. Свойства умножения
×ч
н
ч
ч
ч
н
ч
н
52
53. Свойства обратных операций
Свойства вычитанияч–ч=ч
ч–н=н
н–ч=н
н–н=ч
Свойства деления
ч:н=ч
н
ч:ч=
ч
н:н=н
нечетное число не
делится на четное:
н : ч
53
54. 3 этап. Применение теории
5455. Локальная теория на геометрическом материале
5556.
Спасибоза
внимание!
56




































 Педагогика
Педагогика








