Логика как наука

1. Логика как наука

Законы правильного мышления
Гильзер Наталья Владимировна, МБОУ «Лицей № 60», г. Уфа
1

2.

Логика – наука о
законах и формах
мышления
2

3. Мыслить логично – т.е.

• Точно и последовательно
• Не допускать противоречий
• Уметь вскрывать логические
ошибки
3

4. Основатель логики

Философ Аристотель
• Систематизировал формы и правила
мышления.
• Исследовал категории «понятие» и
«суждение».
• Разработал теорию умозаключений и
доказательств.
• Сформулировал основные законы
мышления.
4

5.

Логика – является наукой о способах доказательств и
опровержений.
Начало исследований в области логики
было положено Аристотелем в 4 в. до н.э.
Однако математические подходы к этим
вопросам впервые были указаны
Джорджем Булем.В честь него алгебру
высказываний называют “булевой алгеброй”.
5

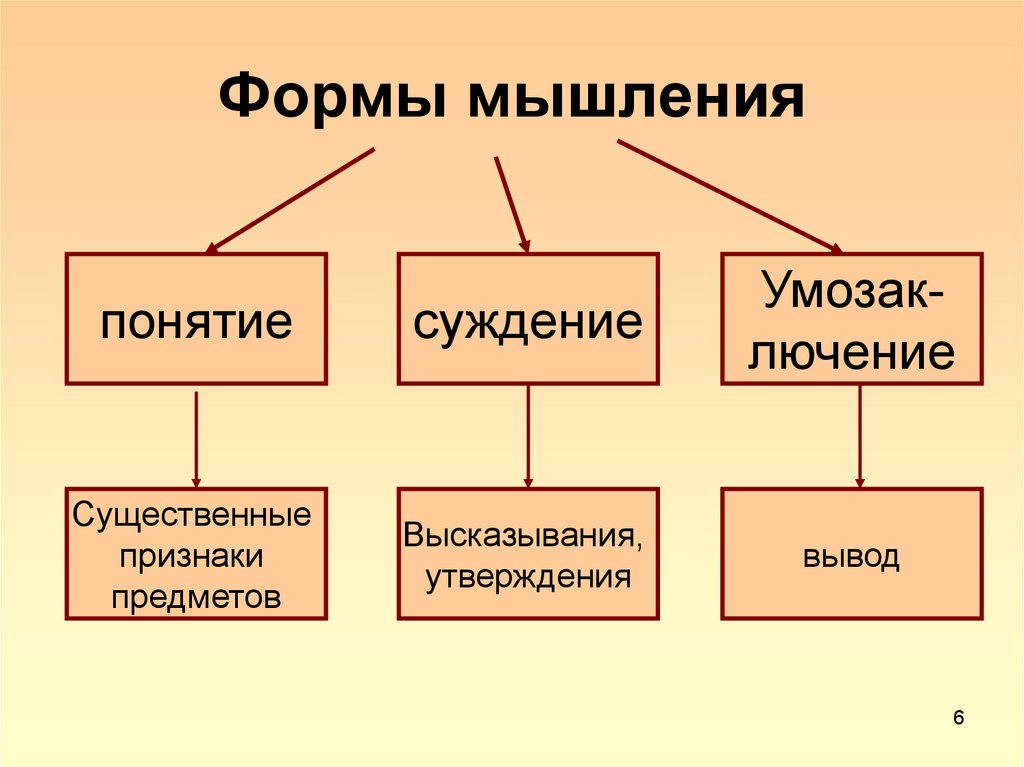
6. Формы мышления

понятие
суждение
Умозаключение
Существенные
признаки
предметов
Высказывания,
утверждения
вывод
6

7. Алгебра логики

• Это алгебра высказываний –
раздел математической логики,
изучающий строение (формулы,
структуру) сложных логических
высказываний и способы
установления их истинности с
помощью алгебраических методов.
7

8. Высказывание

- Повествовательное предложение, о
котором можно сказать истинно оно или
ложно.
Например,
Все ученики – отличники. – ВЛ
Некоторые ученики – отличники. – ВИ
Петя – отличник! – не В
8

9. Высказывания

общие
частные
Единичные
Все, каждый,
всякий…
Некоторые,
многие,…
Оригинальные,
неповторимые
9

10. Термины

Логические величины – это понятия
выражаемые словами И или Л.
Логическая переменная – это
символически выраженная логическая
величина.
Логическое выражение – это простое
или сложное высказывание, о котором
можно сказать И оно или Л.
10

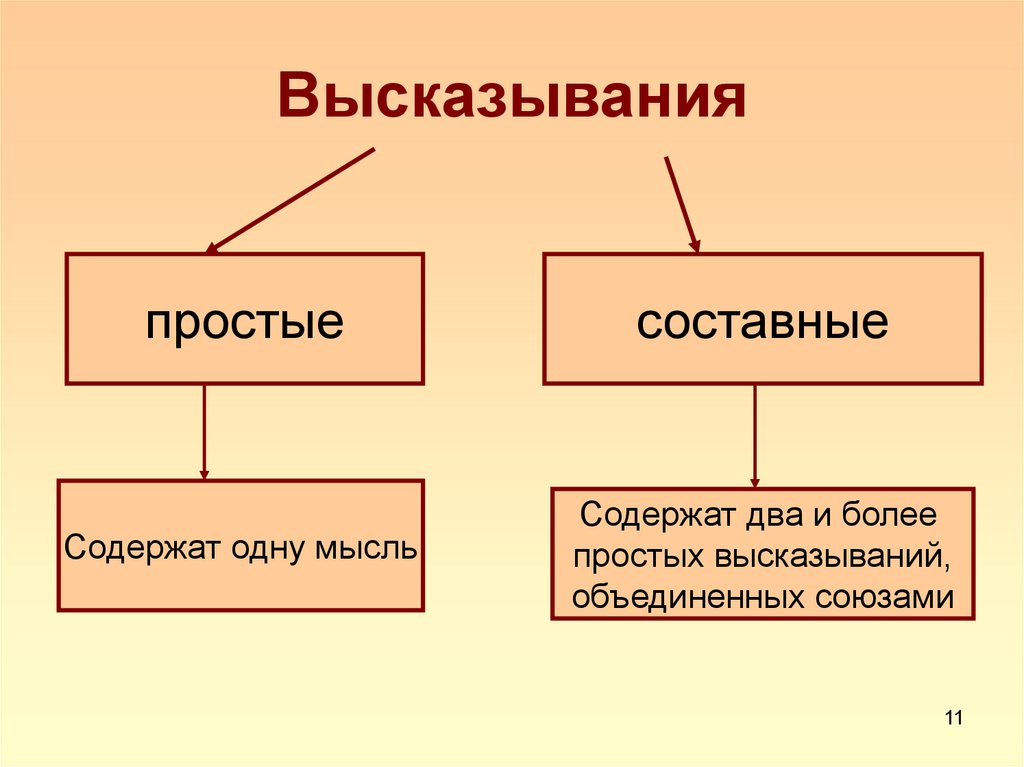
11. Высказывания

простые
составные
Содержат одну мысль
Содержат два и более
простых высказываний,
объединенных союзами
11

12. Логические функции

12

13. Инверсия (отрицание)

не А;
неверно, что А
А,
А, А
А
не А
0
1
1
0
Например,
А – На улице тепло.
не А – Неверно, что на улице тепло.
13

14. Конъюнкция

Логическое
умножение.
F(A,B)=А и В
F(A,B)=А * В
F(A,B)=А & В
F(A,B)=А В
F(A,B)=А and В
А
В
F
0
0
0
0
1
0
1
0
0
1
1
1
Например,
А – У меня есть деньги на покупку машины.
14
В – У меня есть желание на покупку машины.

15. Дизъюнкция

Логическое сложение.
• F(A,B)=А или В
• F(A,B)=А + В
• F(A,B)=А В
• F(A,B)=А or В
• F(A,B)=А | В
А
В
F
0
0
0
0
1
1
1
0
1
1
1
1
Например,
А – Я пойду на дискотеку в школу.
В – Я пойду на дискотеку в Огни Уфы.
15

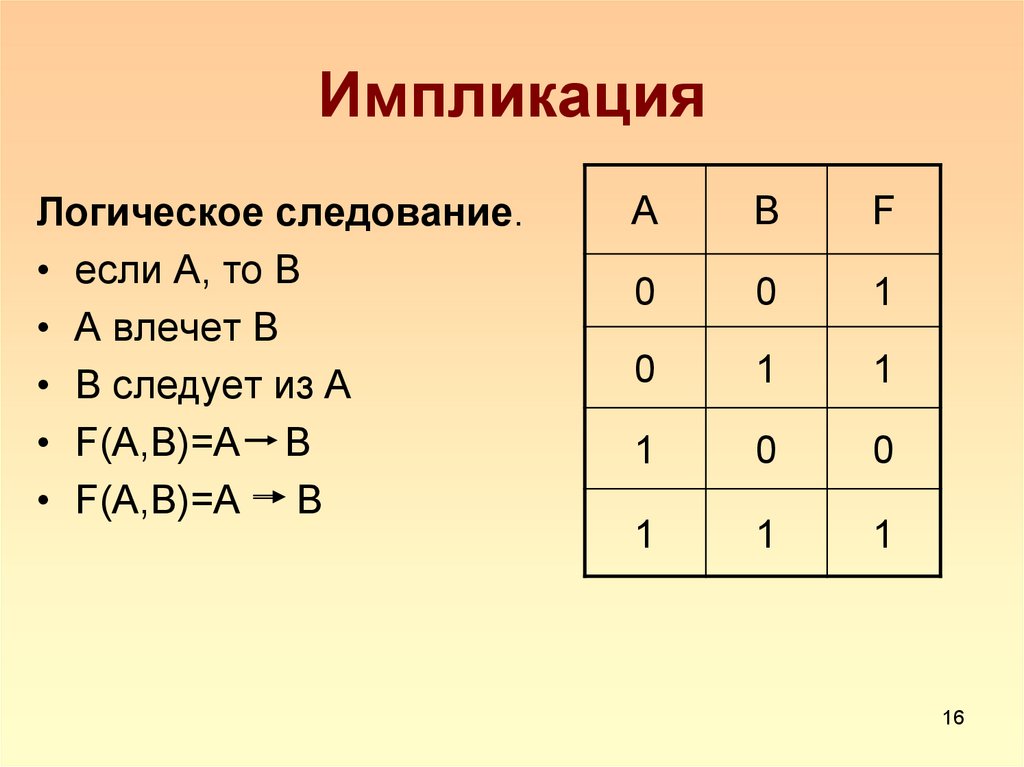
16. Импликация

Логическое следование.
• если А, то В
• А влечет В
• В следует из А
• F(A,B)=А В
• F(A,B)=А В
А
В
F
0
0
1
0
1
1
1
0
0
1
1
1
16

17. Эквивалентность

Логическое равенство,
Тождественность.
А тогда и только тогда,
когда В
F(A,B)=А В
F(A,B)=А В
F(A,B)=А В
А
В
F
0
0
1
0
1
0
1
0
0
1
1
1
17

18. Приоритет действий

1.
2.
3.
4.
5.
6.
Скобки
Отрицание
Конъюнкция
Дизъюнкция
Импликация
Эквивалентность
( )
18