Подходы к моделированию систем

1. Лекция Подходы к моделированию систем

«Моделирование систем управления»
Лекция
Подходы к моделированию систем

2. 1. Классификация систем 2. Подходы к моделированию систем 3. Классификации методов моделирования систем

Вопросы лекции
1. Классификация систем
2. Подходы к моделированию систем
3. Классификации методов моделирования систем

3. 1. Классификация систем.

4. Определение системы:

Система (др.-греч. σύστημα «целое, составленное из частей; соединение») множество элементов, находящихся в отношениях и связях друг с другом,
которое образует определённую целостность, единство.
«Целое больше суммы своих частей». Аристотель. Метафизика
(Открытие синергии)
__________________________________________________________________
_
Потребность в использовании термина «система» возникает в тех случаях,
когда нужно подчеркнуть, что что-то является большим, сложным, не
полностью сразу понятным, при этом целым, единым. В отличие от понятий
«множество», «совокупность» понятие системы подчёркивает
упорядоченность, целостность, наличие закономерностей построения,
функционирования и развития.

5. Попытки классификации систем проводились по следующим признакам:

• виду отображаемого объекта (технические, биологические,
экономические и т.п. системы);
• виду научного направления, используемого для их моделирования
(математические, физические, химические и др.);
• взаимодействию со средой (открытые и закрытые);
величине и сложности;
• уровням сложности (классификация К.Боулдинга).

6.

Кеннет Юарт Бо́ улдинг (англ. Kenneth Ewart Boulding; 18.01.1910 –
18.03.1993) — американский экономист, социолог и поэт англ.
происхождения.
«Мир - очень сложная система. Легко иметь
слишком простой взгляд на это, и легко
причинять вред и делать вещи хуже под
импульсом делать добро и делать вещи
лучше»
«Любой, кто верит, что экспоненциальный
рост может продолжаться вечно в конечном
мире, либо сумасшедший, либо экономист»
«Любая попытка свести сложные свойства
биологических организмов, нервной системы
или человеческого мозга к простым
физическим и химическим системам глупа»

7. Классификация систем по К.Боулдингу (живые системы)

Уровень сложности
Примеры
Трансцендентные системы,
непознанное
Концепции, модель
Интегральные концепции
Социальные системы
Социальные
организации
Социологические концепции,
интегральные концепции
Системы с самосознанием,
мышлением и нетривиальным
поведением
Люди
Физиологические,
психологические концепции
Живые организмы без
самосознания, способные
воспринимать информацию
Животные
Биологические концепции и
модели
Живые организмы с низкой
способностью воспринимать
информацию
Растения
Химические и биологические
концепции
Открытые системы с
самосохраняемой структурой
Клетка
Кибернетические модели

8. Классификация систем по К.Боулдингу (неживые системы)

Уровень сложности
Примеры
Концепции, модель
Кибернетические системы с
управляемыми циклами и
обратной связью
Термостат
Модель обратной связи
Простые динамические
структуры с заданным законом
поведения
Часовой
механизм
Модели специальных
дисциплин, Программное
управление
Статические структуры (остовы) Кристаллы
Физико-математические
концепции и модели

9. Классификации систем по другим признакам:

В первый период развития теории принятия решений и теории
систем широко распространено было выделение классов:
•проблем с достаточной определенностью;
•проблем с неопределенностью;
•проблем с большой неопределенностью.
А.Ньюэлл и Г.Саймон - по принципу «структуризации»:
•хорошо структурированные;
•плохо структурированные;
•неструктурированные.
В.В.Налимов – по степени организованности:
•хорошо организованных систем
•плохо организованных (или диффузных) систем
•самоорганизующихся или развивающихся систем

10. Хорошо организованные системы

1.
2.
Исследователю удается определить все элементы системы и их
взаимосвязи между собой.
Исследователю удается определиться с целями системы в виде
детерминированных (аналитических, графических) зависимостей.
Проблемная ситуация может быть описана в виде выражений, связывающих
цель со средствами, например:
• критерий функционирования
• критерий оптимальности
• критерий эффективности
• целевая функция
3. Может быть предложена формальная математическая модель и
экспериментально доказана ее адекватность реальному объекту.

11. Плохо организованная (диффузная) система

1. Не ставится задача определить все компоненты и их связи с целями системы.
2. Система характеризуется некоторым набором макропараметров и
закономерностями, они выявляются на основе достаточно представительной
выборки компонентов, отображающей исследуемый объект или процесс.
3. На основе такого, выборочного, исследования получают характеристики или
закономерности (статистические, экономические и т.п.) и распространяют эти
закономерности на поведение системы в целом с какой-то вероятностью.
4. Отображение объектов в виде диффузных систем находит широкое применение
при определении пропускной способности систем разного рода, в обслуживающих
учреждениях (методы теории массового обслуживания), для оценки надежности
сложных технических комплексов и т.д.
5. В случае применения статистических закономерностей адекватность моделей
определяется репрезентативностью выборки.
6. Для экономических закономерностей способы доказательства адекватности не
исследованы.

12. Самоорганизующиеся или развивающиеся системы

Характеризуются рядом признаков, особенностей, приближающих их к
реальным развивающимся объектам:
•способность адаптироваться к изменяющимся условиям среды и помехам
•принципиальная неравновестность
•способность противостоять энтропийным (разрушающим систему)
тенденциям
•способность вырабатывать варианты поведения и изменять свою
структуру
•способность и стремление к целеобразованию.
Им неизбежно сопутствуют:
•неоднозначность использования понятий
•нестационарность (изменчивость, нестабильность) параметров
•стохастичность поведения
•уникальность и непредсказуемость поведения системы в конкретных
условиях.

13. 2. Подходы к моделированию систем

14. Традиционный подход:

1) определить элементы (переменные, константы)
2) связать их соответствующим соотношением (формулой, уравнением и
т.п.), отображающим принцип взаимодействия элементов.
Предлагалось обследовать систему, выявить все ее элементы и связи между
ними. Этот подход называли иногда «перечислением» системы.
При обследовании применялись разные способы:
• архивный (изучение документов и архивов предприятия)
• опросный, или анкетный (опрос сотрудников, в том числе с помощью
специально разработанных вопросников – анкет).

15. Другие подходы к моделированию систем:

С самого начала возникновения системных теорий предлагались
подходы, в большей степени ориентированные на прикладные задачи.
Вот некоторые из них:
•бихевиористский подход, основанный на исследовании поведения
(функционирования) систем; весьма трудоемок и не всегда реализуем;
•целенаправленный и терминальный подход (амер. М.Месарович). Терм
– элементарная частица, интересующая исследователя);
•декомпозиция и композиция системы (пол. Р.Куликовски)
•морфологический подход, который помогает искать полезные
объединения элементов путем их комбинаций (швейц. Ф.Цвикки)
•«дерево целей» (амер. Корпорация RAND)
•лингвистический или тезаурусный подход – математическая логика и
математическая лингвистика
•путь поиска связей между элементами / устранения лишних связей.

16. Основные подходы к моделированию систем:

С учетом рассмотренных подходов на основе обобщения
предшествующего опыта сформировалось два основных подхода к
отображению (моделированию) систем:
А) «сверху» или аксиологический - методы структуризации или
декомпозиции , целевой или целенаправленный подход;
Б) «снизу» или каузальный - подход, который называют
морфологическим, лингвистическим, тезаурусным, терминальным
методом «языка» системы. С помощью этого подхода определяется
«пространство состояний» системы и реализуется поиск взаимосвязей
(мер близости) между элементами.

17. В 1970-1980 гг при проектировании организационных структур были предложены три подхода

•Нормативно-функциональный подход направлен на унификацию
организационных форм управления в рамках отрасли.
•Функционально-технологический подход основан на рационализации
потоков информации и технологии ее обработки, на формировании и
анализе организационно-технологических процедур подготовки и
реализации управленческих решений.
•Системно-целевой подход заключается в построении структуры целей,
определении на ее основе функций управления и их организационном
управлении.
В настоящее время широкое применение нашел процессный подход.
Этот подход, который можно считать развитием функциональнотехнологического подхода, основан на структуризации во времени, на
представлении процессов в форме графов.

18. 3. Классификация методов моделирования систем

19. Классы методов моделирования

Методы моделирования систем удобно разделить на два больших
класса:
•методы формального представления систем (МФПС)
•методы направленные на активацию использования интуиции и опыта
специалистов (МАИС).
Разделение методов на МАИС и МФПС находится в соответствии с
основной идеей системного анализа, которая состоит в сочетании в
моделях и методиках формальных и неформальных представлений, что
помогает в разработке методик, выборе методов постепенной
формализации отображения и анализа проблемной ситуации.

20. Вербальное и формальное представление задачи

Постановка любой задачи заключается в том, чтобы перевести ее
словесное, вербальное описание в формальное.
Перевод вербального описания в формальное, осмысление,
интерпретация модели и получаемых результатов - неотъемлемая часть
практически каждого этапа моделирования сложной развивающейся
системы.
Для решения проблемы перевода вербального описания в формальное в
различных областях деятельности стали развиваться специальные
приемы и методы, например методы «мозговой атаки», «сценариев»,
«дерева целей» и т.п.
В свою очередь, развитие математики шло по пути расширения средств
постановки и решения трудноформализуемых задач. Наряду с
детерминированными, аналитическими методами классической
математики возникла теория вероятностей и математическая
статистика (как средство доказательства адекватности модели на
основе представительной выборки и понятия вероятности использования
результатов моделирования).

21. Вербальное и формальное представление задачи

Для задач с большей степенью неопределенности инженеры стали
привлекать
•теорию множеств,
•математическую логику,
•математическую лингвистику,
•теорию графов.
Иными словами, математика стала постепенно накапливать средства
работы с неопределенностью, со смыслом, который классическая
математика исключала из объектов своего рассмотрения.

22. Различные классификации методов моделирования

Одна из первых классификаций, предложенных специально
для целей системных исследований академиком
А.И.Кухтенко по уровням математического абстрагирования
при изучении сложных систем:
•общеалгебраический,
• теоретико-множественный,
• логико-лингвистический,
•информационный,
•эвристический.

23. Классификация обобщенных групп методов Ф.Е.Темникова

• аналитические (методы классической математики, включая интегродифференциальное исчисление, методы поиска экстремумов
функций, вариационное исчисление, методы математического
программирования и т.п.);
• статистические (включающие и теоретические разделы математики
– теорию вероятностей, математическую статистику, и направления
прикладной математики, использующие стохастические
представления – теорию массового обслуживания, методы
статистических испытаний (метод Монте-Карло), методы выдвижения
и проверки статистических гипотез А.Вальда и др.);
• теоретико-множественные;
• логические, лингвистические, семиотические представления
(методы дискретной математики), составляющие теоретическую
основу разработки языков моделирования, автоматизации
проектирования, информационно-поисковых языков;
• графические (включающие теорию графов и разного рода
графических представлений информации типа диаграмм, гистограмм
и других графиков).

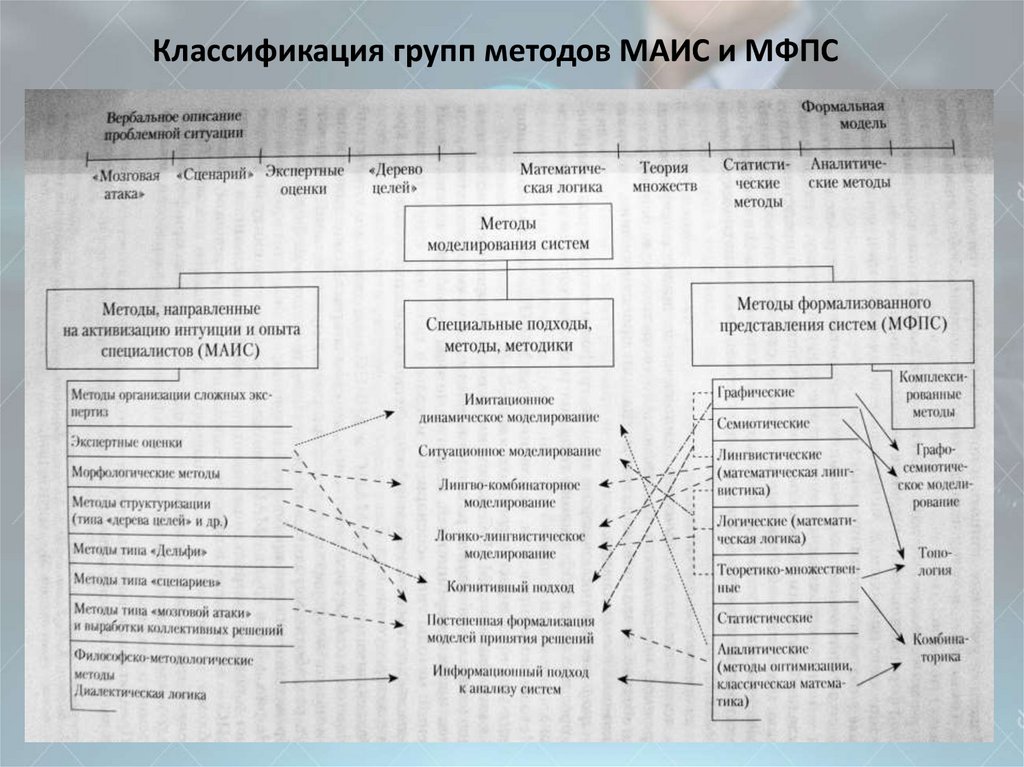
24. Классификация групп методов МАИС и МФПС

25. Теоремы К.Гёделя о неполноте (1931)

Первая теорема утверждает, что если формальная арифметика
непротиворечива, то в ней существует невыводимая и неопровержимая
формула.
Вторая теорема утверждает, что если формальная арифметика
непротиворечива, то в ней невыводима некоторая формула,
содержательно утверждающая непротиворечивость этой арифметики.
Обобщение теорем Гёделя:
В рамках любой формальной системы, сколь бы полной и
непротиворечивой она не казалась, имеются положения (соотношения,
высказывания), истинность или ложность которых нельзя доказать
формальными средствами этой системы, а для преодоления
неразрешимой проблемы нужно расширять формальную систему,
опираясь на содержательный качественный анализ.
Иными словами, строгого разделения на формальные и неформальные
методы не существует.
Можно говорить только о большей или меньшей степени
формализованности или, напротив, большей или меньшей опоре на
интуицию, «здравый смысл».

26. Специальные методы моделирования систем

Имитационное динамическое моделирование (System
Dynamics Symulation Modeling
Предложено Дж.Форрестером (США) в 50-х годах.
Использует удобный для человека структурный язык,
помогающий выражать реальные взаимосвязи, отображающие в
системе замкнутые контуры управления и аналитические
представления (линейные конечно-разностные уравнения),
позволяющие реализовывать формальное исследование
полученных моделей на ЭВМ. – системы управления социальноэкономическими объектами с использованием
специализированного языка «DYNAMO».

27. Специальные методы моделирования систем

Ситуационное моделирование.
Идея предложена Д.А.Поспеловым и реализована
Ю.И.Клыковым.
Это направление базируется на отображении в
памяти ЭВМ и анализе проблемных ситуаций с
применением специализированного языка,
разрабатываемого с помощью:
•выразительных средств теории множеств,
•математической логики,
•теории языков.
19.12.1932 г.
- 30.10.2019 г.
Дмитрий Поспелов — один из наиболее известных советских и российских
специалистов в области изучения и создания методик управления сложными
системами, один из пионеров изучения проблем искусственного интеллекта.

28. Специальные методы моделирования систем

Лингво-комбинаторное моделирование.
Предложено для моделирования плохо формализованных систем
М.Б.Игнатьевым, заключается в том, что
формальная модель строится на основе ключевых слов, характеризующих ту
или иную систему.
На основе ключевых слов строятся лингвистические уравнения,
составленные из суммы произведений ключевых слов на смыслы.
Эти лингвистические уравнения разрешаются путем введения произвольных
коэффициентов, число которых определяется как число сочетаний из n по m,
где n – число переменных, число разных слов, m – число ограничений, число
лингвистических уравнений. Произвольные коэффициенты и их
распределение по матрице эквивалентных уравнений определяет
структурированную неопределенность, эти произвольные коэффициенты
могут быть использованы для адаптации системы к окружающей среде.
Лингво-комбинаторное моделирование – универсальный метод
моделирования, с его помощью получены новые модели атомномолекулярных структур, социально-экономических систем и процессов,
биологических систем и геологических структур.

29. Специальные методы моделирования систем

Логико-лингвистическое моделирование.
Является развитием структурно-лингвистического моделирования,
широко распространенного в 79-е годы в инженерной практике и
основанного на использовании для реализации идей комбинаторики
структурных представлений разного рода, с одной стороны, и средств
математической лингвистики – с другой.
В 2000-е годы логико-лингвистическое моделирование
применительно к анализу и развитию адаптивного управления
социально-экономическими системами развивает Б.Л.Кукор,
используя в качестве языковых (лингвистических) средств и другие
методы дискретной математики (теоретико-множественные
представления, средства математической логики и семиотики).
Логико-рефлексивное моделирование. Термин ввел акад.
А.Г.Ивахненко в 1983 году.

30. Специальные методы моделирования систем

Логико-рефлексивное моделирование. Термин ввел акад.
А.Г.Ивахненко в 1983 году.
Конференция по моделированию СО АН СССР (1987г.) впервые прозвучало это
понятие ЛРМ: необходимость сочетания логических и рефлексивный процедур.
И.Б.Арефьев «Логико-рефлексивное моделирование процессов принятия и
поддержки решений по управлению»
Принцип рефлексии заключается в том, что в процессе мыслительно-языковой
деятельности субъект познаёт и активно изменяет собственные средства
познания. В этом смысле рефлексия соответствует характерному для процессов
управления типу причинности, когда причина и следствие связаны двусторонне
(обратная связь). Такое решение вполне соответствует схеме Н. Винера, когда
состояние объекта оценивается ЛПР через его показатели по информационнотехнической обратной связи.
Именно здесь и наблюдается разрыв в логике принятия решения по
управлению данным объектом: в пределах возможного по обратной связи
можно судить о состоянии объекта, но требуется некоторое обоснованное
заключение о качестве такого состояния. Оно выбирается согласно эталону
(модель, расчёт, матрица и т.п.).

31. Специальные методы моделирования систем

Теория информационного поля и информационных цепей
(информационный подход к моделированию и анализу систем).
Концепция предложена А.А.Денисовым и основана на
использовании для активизации интуиции ЛПР законов
диалектики, а в качестве средства формализованного
отображения – аппарата математической теории поля и теории
цепей.
Этот подход (информационный) – отображение реальных
ситуаций с помощью информационных моделей.

32. Специальные методы моделирования систем

Системно-структурный синтез.
Системно-структурные методы моделирования разрабатывались с
самого начала развития теории систем на основе иерархических и
сетевых структур как средства исследования объектов и процессов
с неопределенностью, когда не могут быть сразу получены
математические модели.
Структурно-функциональный подход основан на порождающем
механизме.
Номинально-структурный подход, основанный на понятиях
номинальной шкалы - одном из элементов теории измерений и
структурности , отражающей целостные свойства системы и
процесса ее проектирования.
Теория системно-структурного синтеза основана на
многоуровневой модели, постепенно сужающей область
допустимых решений.

33. Специальные методы моделирования систем

Когнитивный подход. (cjgnitio – знание, познание)
Базируется на идеях когнитивной психологии.
Существует обилие моделей, предлагаемых для интерпретации
различных аспектов мыслительного процесса.
Направление развивается в РФ применительно к системам
управления муниципальными образованиями и другими
социально-экономическими объектами. В моделях этой школы
графические представления сочетаются с аналитическими
методами исследования импульсных процессов.

34. В качестве заключения

Классификация методов моделирования помогает осознанно
выбирать методы моделирования.
Она может развиваться, дополняться конкретными методами,
т.е. аккумулировать опыт, накапливаемый а процессе
проектирования и управления.

35. Благодарю за внимание