Тематическое консультирование по математике (вариант 1)

1.

© Министерство образования Республики Беларусь
Учреждение образования «Республиканский институт контроля знаний»
РТ–2021/2022 гг. Этап III
Тематическое консультирование по математике
Вариант 1
Раздел программы
вступительных
испытаний. Элемент
содержания
Содержание задания
Комментарий и решение задания
А1. Среди чисел 1,5 102 ; 150 10 1 ; 15 102 ; 15 10 2 ;
укажите
0,15 10
стандартном виде.
1
то,
которое
записано
в
Задание на проверку знания
стандартного вида числа.
Решение:
записи
Учебное издание
Арефьева, И. Г. Алгебра : учеб. пособие для 7-го кл.
учреждений общ. сред. образования с рус. яз. обучения /
И. Г. Арефьева, О. Н. Пирютко. – Минск : Народная
асвета, 2017. – 313 с. : ил. (Гл. 1, § 3, с. 34–43)
1) 1,5 102 ;
Числа и вычисления.
Стандартный вид числа
2) 150 10 1 ;
3) 15 102 ;
4) 15 10 2 ;
5) 0,15 101
А2. Представьте выражение
Выражения и их
преобразования. Степень
с целым показателем и ее
свойства
степени с основанием a.
1) a 8 ;
1
2) a ;
a 7 a 2
3
в виде
В
стандартном
виде
записано
число 1,5 102.
Ответ: 1
Задание на проверку умения применять
свойства степени с целым показателем для
преобразования выражений.
Решение:
a 7 a 2 a 7 a 3 2 a
3
7 6
Арефьева, И. Г. Алгебра : учеб. пособие для 7-го кл.
учреждений общ. сред. образования с рус. яз. обучения /
И. Г. Арефьева, О. Н. Пирютко. – Минск : Народная
асвета, 2017. – 313 с. : ил. (Гл. 1, § 2, с. 22–34)
a 13 .
Ответ: 5
3) a 26 ;
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов.
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by).
РТ–2021/2022 гг. Этап III. Вариант 1
Тематическое консультирование по математике
1

2.

Раздел программы
вступительных
испытаний. Элемент
содержания
Содержание задания
4) a 42 ;
5) a 13
А3. Функция
7; 3
и
y f x
задана
является
на
убывающей
промежутке
на
области
определения. Расположите значения функции
f 5 , f 4 , f 6 в порядке возрастания.
1) f 4 , f 6 , f 5 ;
Координаты и функции.
Возрастание и убывание
функции
2) f 6 , f 4 , f 5 ;
3) f 6 , f 5 , f 4 ;
Комментарий и решение задания
Учебное издание
Задание на проверку знания свойств
функции.
Решение:
Функция
убывает
на
некотором
промежутке, если для любых значений
аргумента
из
этого
промежутка
большему
значению
аргумента
соответствует
меньшее
значение
функции.
Числа
принадлежат
4,
5,
6
Арефьева, И. Г. Алгебра : учеб. пособие для 9-го кл.
учреждений общ. сред. образования с рус. яз. обучения /
И. Г. Арефьева, О. Н. Пирютко. – Минск : Народная
асвета, 2019. – 329 с. : ил. (Гл. 2, § 7, с. 90–103)
функция y
7; 3 . По условию
f x убывает на промежутке
7; 3 ,
значит,
промежутку
4) f 4 , f 5 , f 6 ;
5) f 5 , f 6 , f 4
из
того,
что
4 5 6,
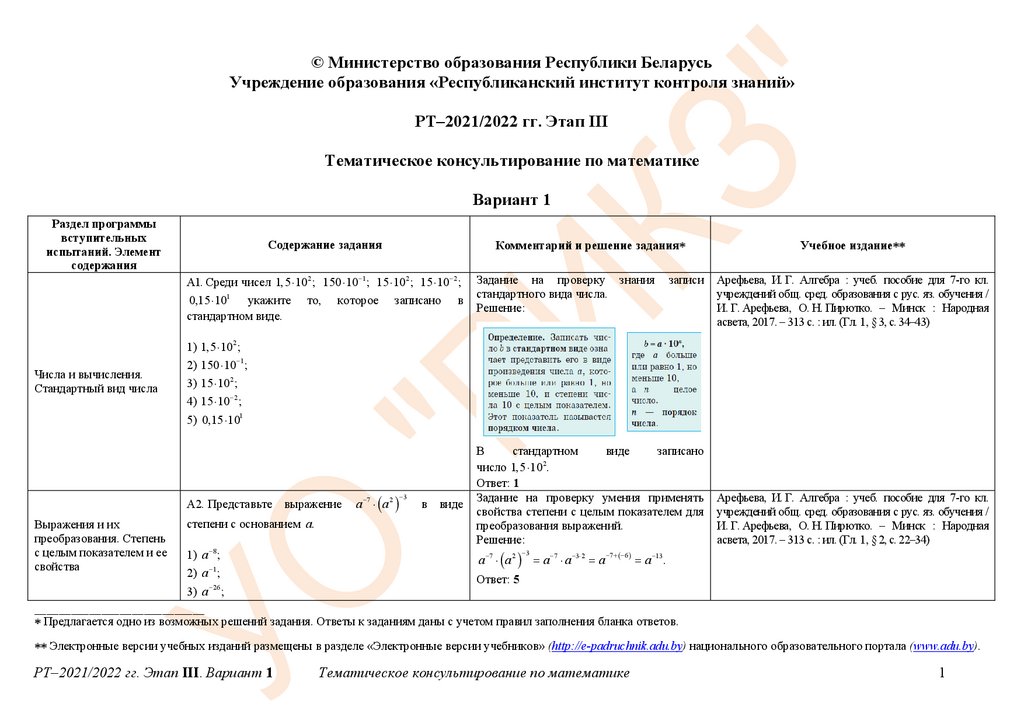
А4. Дана равнобедренная
трапеция
ABCD
Используя
AD
BC
.
Геометрические фигуры
и их свойства. Трапеция
1
данные рисунка, найдите
градусную меру угла 1.
1)
2)
3)
4)
5)
57 ;
89 ;
59 ;
33 ;
58
C
B
57
32
A
следует,
что
f 4 f 5 f 6 .
Ответ: 4
Задание на проверку умения применять
свойства равнобедренной трапеции для
вычислений.
Решение:
Следствие:
в
равнобедренной
трапеции
ABCD
AB DC
D ADB DAC ,
AO DO
и
Казаков, В. В. Геометрия : учеб. пособие для 8-го кл.
учреждений общ. сред. образования с рус. яз. обучения /
В. В. Казаков. – Минск : Народная асвета, 2018. – 199 с. :
ил. (Гл. 1, § 11, с. 60–64)
BO CO
(см. рис. 1).
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов.
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by).
РТ–2021/2022 гг. Этап III. Вариант 1
Тематическое консультирование по математике
2

3.

Раздел программы
вступительных
испытаний. Элемент
содержания
Содержание задания
Комментарий и решение задания
Учебное издание
С
B
O
A
D
Рисунок 1
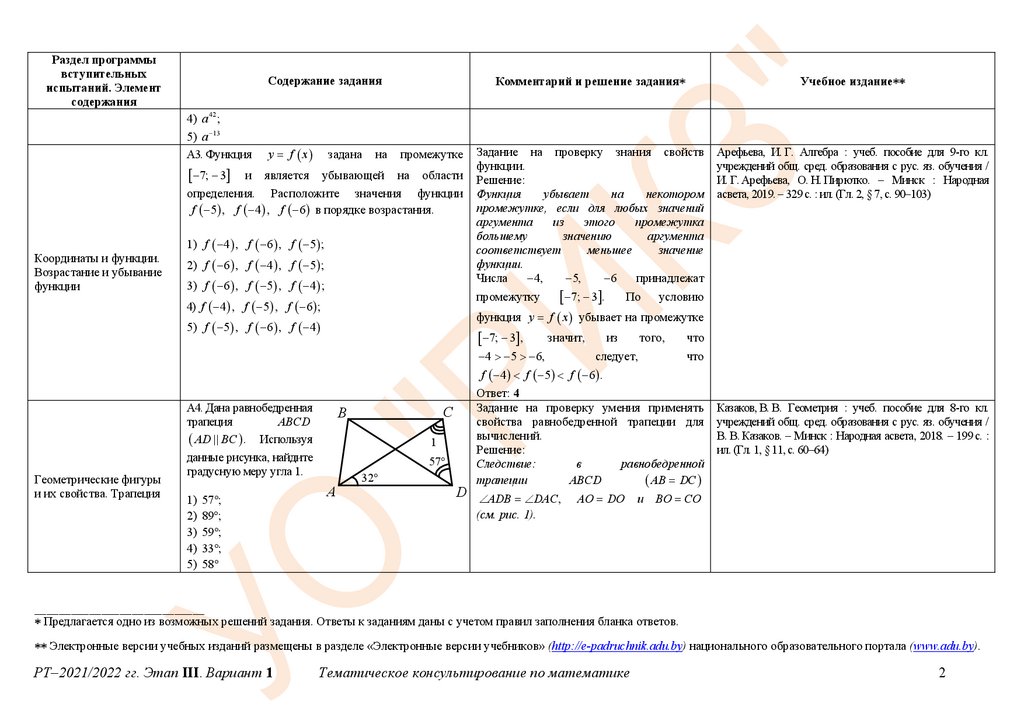
Рассмотрим рисунок 2. Обозначим точку
пересечения диагоналей AС и BD
трапеции ABCD точкой O.
С
B
1
О
32
57
32
D
A
Рисунок 2
Координаты и функции.
Функция y cos x
А5. Среди значений переменной x, равных
7
;
6
По следствию, сформулированному выше,
Внешний
угол
OAD ODA 32 .
СOD треугольника AOD равен сумме
углов OAD и ODA. Значит COD 64 .
Так как сумма градусных мер углов
треугольника COD равна 180 , то
1 180 СOD СDО,
1 180 64 57 , 1 59 .
Ответ: 3
Задание на проверку умения находить
значение функции, используя формулы
приведения.
Решение:
Арефьева, И. Г. Алгебра : учеб. пособие для 10-го кл.
учреждений общ. сред. образования с рус. яз. обучения /
И. Г. Арефьева, О. Н. Пирютко. – Минск : Народная
асвета, 2019. – 285 с. : ил. (Гл. 1, § 5, с. 53–75; § 9,
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов.
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by).
РТ–2021/2022 гг. Этап III. Вариант 1
Тематическое консультирование по математике
3

4.

Раздел программы
вступительных
испытаний. Элемент
содержания
Содержание задания
7
9
3
;
; 4 ;
, укажите то, при котором
4
2
3
значение функции y cos x отрицательное.
1)
2)
3)
4)
5)
Геометрические фигуры
и их свойства. Свойство
медиан треугольника
7
;
6
7
;
3
9
;
4
4 ;
3
2
7
3
cos cos
0.
6
6
6
2
7
1
cos
cos 2 cos 0.
3
3
3 2
Учебное издание
с. 115–128)
cos
9
2
cos 2 cos
0.
4
4
4
2
cos 4 1.
3
cos
0.
2
Ответ: 1.
Примечание. Функция y cos x принимает
отрицательные значения на промежутках
3
2 n , n Z
2 n;
2
2
Задание на проверку умения применять
свойство медиан треугольника.
Решение:
cos
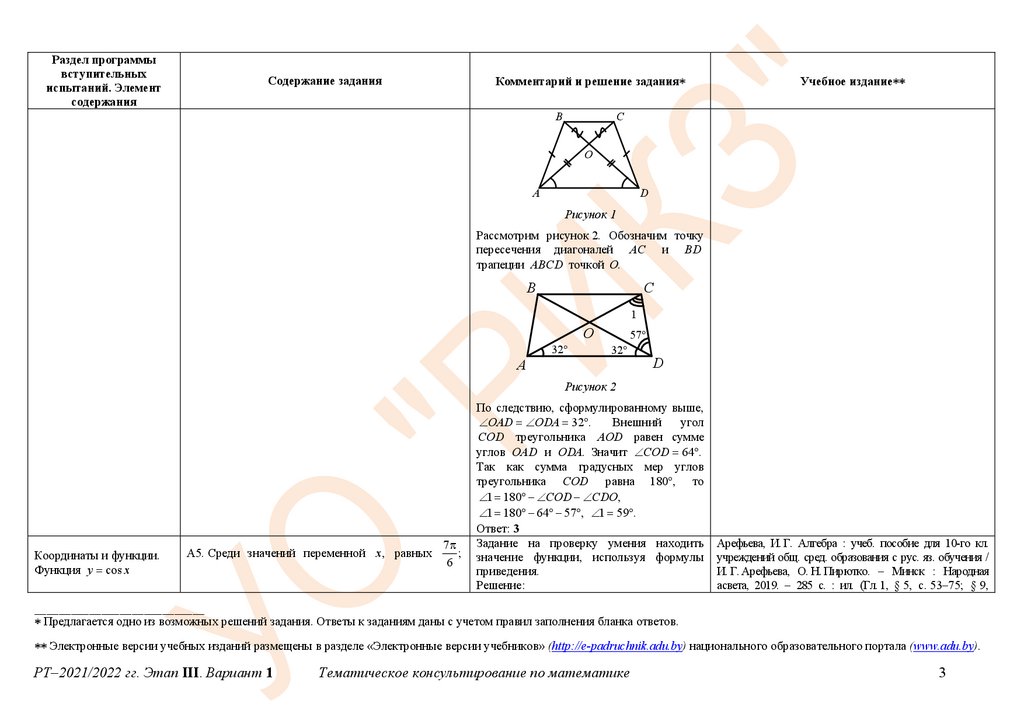
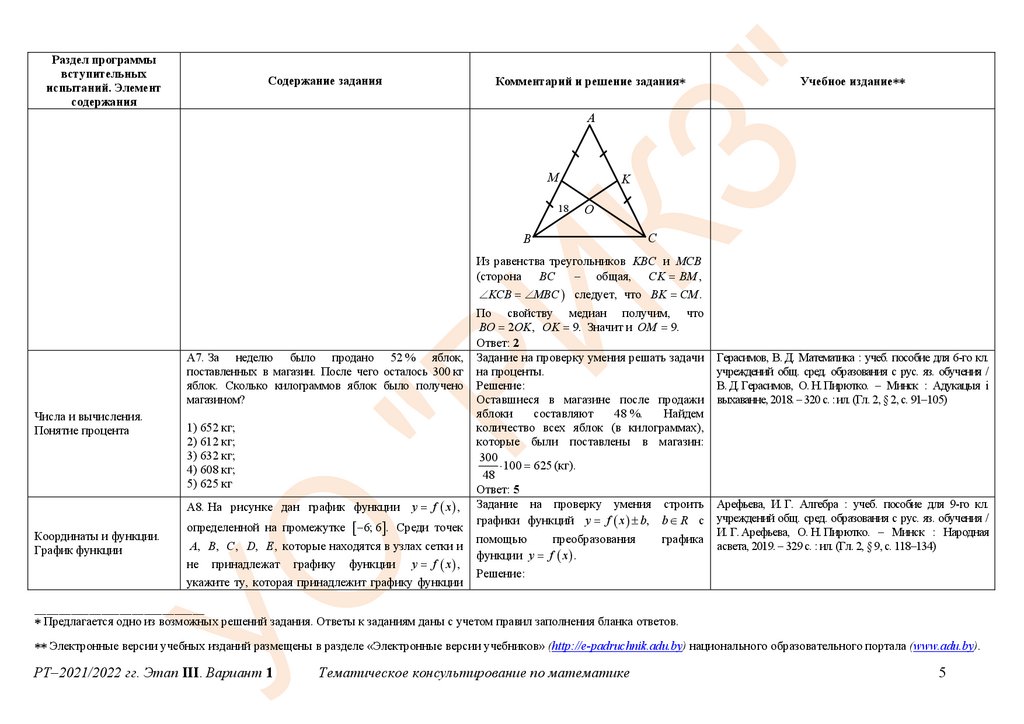
А6. В равнобедренном треугольнике ABC медианы
CM и BK , проведенные к его боковым сторонам AB
и AC соответственно, пересекаются в точке O.
Найдите длину отрезка OM , если BO 18.
1) 6;
2) 9;
3) 27;
4) 12;
5) 15
Комментарий и решение задания
Казаков, В. В. Геометрия : учеб. пособие для 8-го кл.
учреждений общ. сред. образования с рус. яз. обучения /
В. В. Казаков. – Минск : Народная асвета, 2018. – 199 с. :
ил. (Гл. 1, § 9, с. 52–55)
Рассмотрим рисунок.
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов.
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by).
РТ–2021/2022 гг. Этап III. Вариант 1
Тематическое консультирование по математике
4

5.

Раздел программы
вступительных
испытаний. Элемент
содержания
Содержание задания
Комментарий и решение задания
Учебное издание
A
M
K
18
O
B
С
Из равенства треугольников KBC и MCB
(сторона BC
– общая, CK BM ,
А7. За неделю было продано 52 % яблок,
поставленных в магазин. После чего осталось 300 кг
яблок. Сколько килограммов яблок было получено
магазином?
Числа и вычисления.
Понятие процента
1) 652 кг;
2) 612 кг;
3) 632 кг;
4) 608 кг;
5) 625 кг
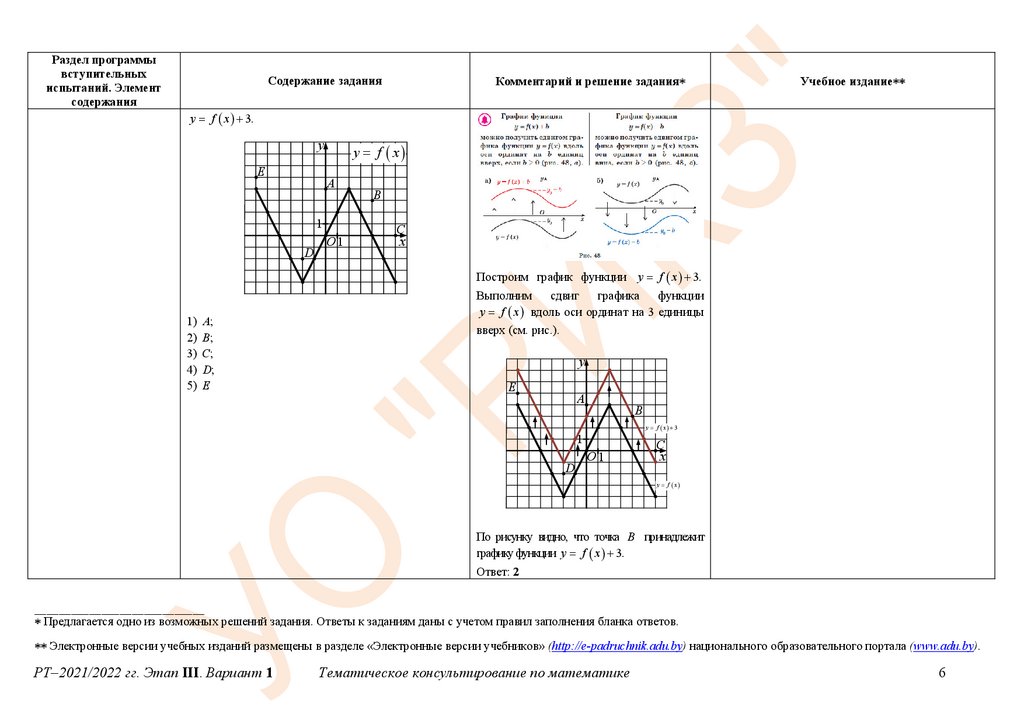
А8. На рисунке дан график функции
Координаты и функции.
График функции
y f x ,
определенной на промежутке 6; 6 . Среди точек
A, B, C , D, E , которые находятся в узлах сетки и
не принадлежат графику функции y f x ,
укажите ту, которая принадлежит графику функции
KCB MBC следует, что BK CM .
По свойству медиан получим, что
BO 2OK , OK 9. Значит и OM 9.
Ответ: 2
Задание на проверку умения решать задачи
на проценты.
Решение:
Оставшиеся в магазине после продажи
яблоки
составляют
48 %.
Найдем
количество всех яблок (в килограммах),
которые были поставлены в магазин:
300
100 625 (кг).
48
Ответ: 5
Задание на проверку умения строить
графики функций y f x b, b R с
помощью
преобразования
графика
функции y f x .
Решение:
Герасимов, В. Д. Математика : учеб. пособие для 6-го кл.
учреждений общ. сред. образования с рус. яз. обучения /
В. Д. Герасимов, О. Н. Пирютко. – Минск : Адукацыя і
выхаванне, 2018. – 320 с. : ил. (Гл. 2, § 2, с. 91–105)
Арефьева, И. Г. Алгебра : учеб. пособие для 9-го кл.
учреждений общ. сред. образования с рус. яз. обучения /
И. Г. Арефьева, О. Н. Пирютко. – Минск : Народная
асвета, 2019. – 329 с. : ил. (Гл. 2, § 9, с. 118–134)
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов.
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by).
РТ–2021/2022 гг. Этап III. Вариант 1
Тематическое консультирование по математике
5

6.

Раздел программы
вступительных
испытаний. Элемент
содержания
Содержание задания
Комментарий и решение задания
Учебное издание
y f x 3.
y
E
y f x
A
1
D
B
C
O1
x
Построим график функции y f x 3.
1)
2)
3)
4)
5)
A;
B;
C;
D;
E
Выполним
сдвиг
графика
функции
y f x вдоль оси ординат на 3 единицы
вверх (см. рис.).
y
E
A
B
y f x 3
1
D
C
O1
x
y f x
По рисунку видно, что точка B принадлежит
графику функции y f x 3.
Ответ: 2
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов.
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by).
РТ–2021/2022 гг. Этап III. Вариант 1
Тематическое консультирование по математике
6

7.

Раздел программы
вступительных
испытаний. Элемент
содержания
Содержание задания
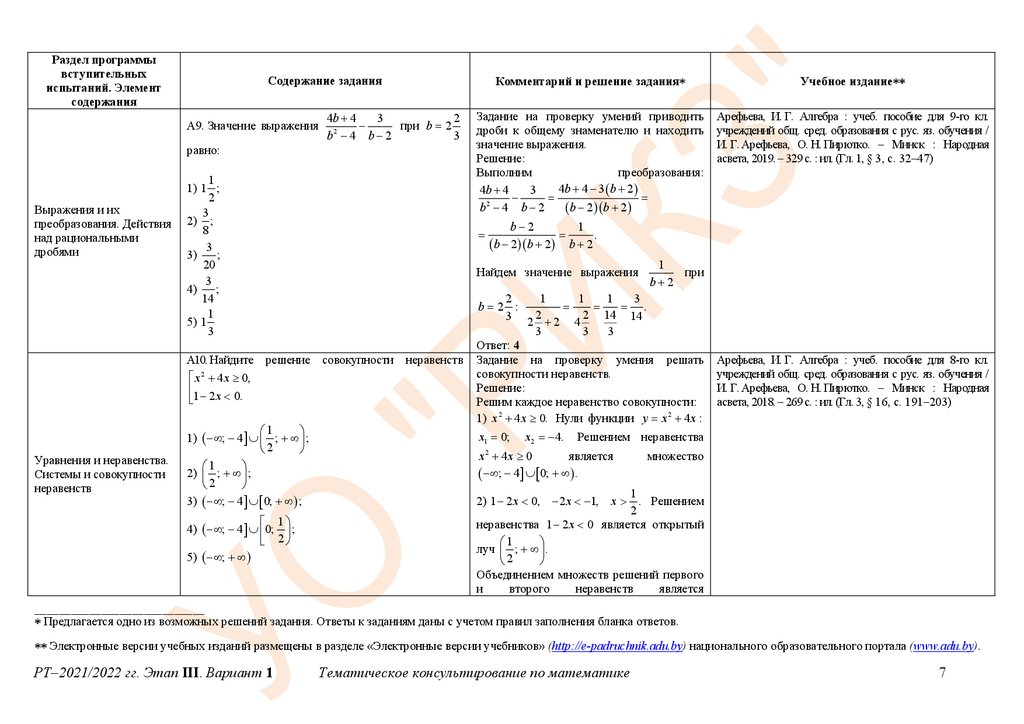
А9. Значение выражения
4b 4
3
2
при b 2
b2 4 b 2
3
равно:
Выражения и их
преобразования. Действия
над рациональными
дробями
1
1) 1 ;
2
3
2) ;
8
3
3)
;
20
3
4)
;
14
1
5) 1
3
Уравнения и неравенства.
Системы и совокупности
неравенств
1
4) ; 4 0; ;
2
5) ;
Учебное издание
Задание на проверку умений приводить
дроби к общему знаменателю и находить
значение выражения.
Решение:
Выполним
преобразования:
4b 4 3 b 2
4b 4
3
b2 4 b 2
b 2 b 2
Арефьева, И. Г. Алгебра : учеб. пособие для 9-го кл.
учреждений общ. сред. образования с рус. яз. обучения /
И. Г. Арефьева, О. Н. Пирютко. – Минск : Народная
асвета, 2019. – 329 с. : ил. (Гл. 1, § 3, с. 32–47)
b 2
1
.
2
2
2
b
b
b
Найдем значение выражения
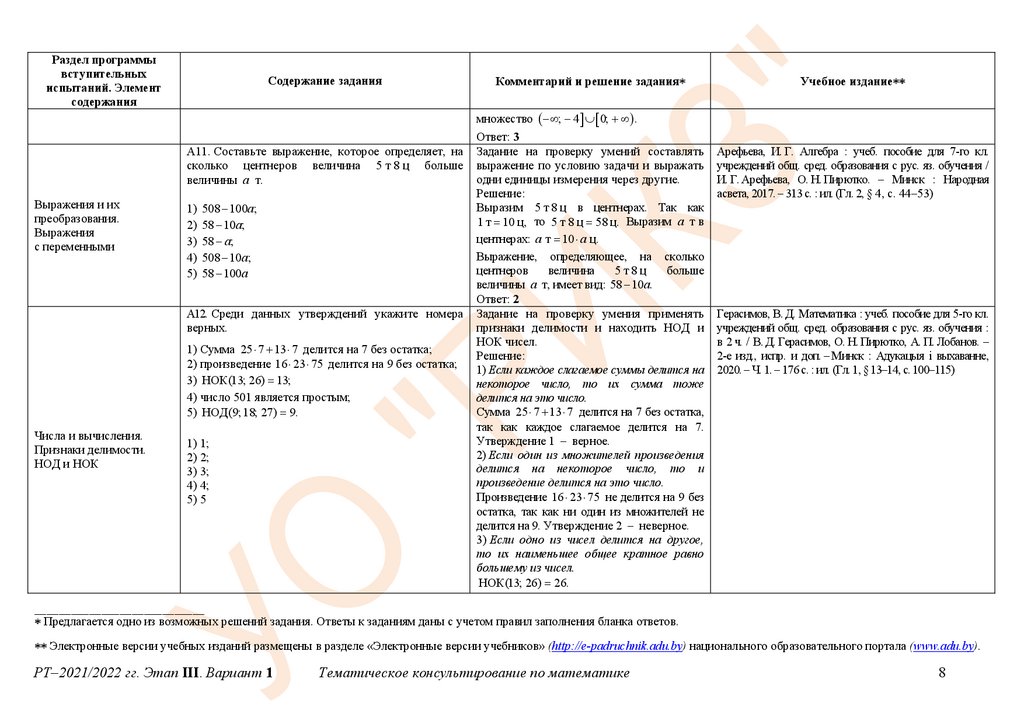
А10. Найдите решение совокупности неравенств
x 2 4 x 0,
1 2 x 0.
1
1) ; 4 ; ;
2
1
2) ; ;
2
3) ; 4 0; ;
Комментарий и решение задания
1
при
b 2
2
1
1
1
3
b 2 :
.
3 2 2 2 4 2 14 14
3
3
3
Ответ: 4
Задание на проверку умения решать
совокупности неравенств.
Решение:
Решим каждое неравенство совокупности:
1) x 2 4 x 0. Нули функции y x 2 4 x :
x1 0;
x2 4.
Арефьева, И. Г. Алгебра : учеб. пособие для 8-го кл.
учреждений общ. сред. образования с рус. яз. обучения /
И. Г. Арефьева, О. Н. Пирютко. – Минск : Народная
асвета, 2018. – 269 с. : ил. (Гл. 3, § 16, с. 191–203)
Решением неравенства
x 4x 0
является
; 4 0; .
2
множество
1
x . Решением
2
неравенства 1 2 x 0 является открытый
1
луч ; .
2
Объединением множеств решений первого
и
второго
неравенств
является
2) 1 2 x 0,
2 x 1,
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов.
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by).
РТ–2021/2022 гг. Этап III. Вариант 1
Тематическое консультирование по математике
7

8.

Раздел программы
вступительных
испытаний. Элемент
содержания
Содержание задания
1)
2)
3)
4)
5)
508 100a;
58 10a;
58 a;
508 10a;
58 100a
А12. Среди данных утверждений укажите номера
верных.
1) Сумма 25 7 13 7 делится на 7 без остатка;
2) произведение 16 23 75 делится на 9 без остатка;
3) НОК(13; 26) 13;
4) число 501 является простым;
5) НОД(9; 18; 27) 9.
Числа и вычисления.
Признаки делимости.
НОД и НОК
Учебное издание
множество ; 4 0; .
А11. Составьте выражение, которое определяет, на
сколько центнеров величина 5 т 8 ц больше
величины a т.
Выражения и их
преобразования.
Выражения
с переменными
Комментарий и решение задания
1) 1;
2) 2;
3) 3;
4) 4;
5) 5
Ответ: 3
Задание на проверку умений составлять
выражение по условию задачи и выражать
одни единицы измерения через другие.
Решение:
Выразим 5 т 8 ц в центнерах. Так как
1 т 10 ц, то 5 т 8 ц 58 ц. Выразим a т в
центнерах: а т 10 а ц.
Выражение, определяющее, на сколько
центнеров
величина
5т8ц
больше
величины a т, имеет вид: 58 10а.
Ответ: 2
Задание на проверку умения применять
признаки делимости и находить НОД и
НОК чисел.
Решение:
1) Если каждое слагаемое суммы делится на
некоторое число, то их сумма тоже
делится на это число.
Сумма 25 7 13 7 делится на 7 без остатка,
так как каждое слагаемое делится на 7.
Утверждение 1 верное.
2) Если один из множителей произведения
делится на некоторое число, то и
произведение делится на это число.
Произведение 16 23 75 не делится на 9 без
остатка, так как ни один из множителей не
делится на 9. Утверждение 2 неверное.
3) Если одно из чисел делится на другое,
то их наименьшее общее кратное равно
большему из чисел.
НОК(13; 26) 26.
Арефьева, И. Г. Алгебра : учеб. пособие для 7-го кл.
учреждений общ. сред. образования с рус. яз. обучения /
И. Г. Арефьева, О. Н. Пирютко. – Минск : Народная
асвета, 2017. – 313 с. : ил. (Гл. 2, § 4, с. 44–53)
Герасимов, В. Д. Математика : учеб. пособие для 5-го кл.
учреждений общ. сред. образования с рус. яз. обучения :
в 2 ч. / В. Д. Герасимов, О. Н. Пирютко, А. П. Лобанов. –
2-е изд., испр. и доп. – Минск : Адукацыя і выхаванне,
2020. – Ч. 1. – 176 с. : ил. (Гл. 1, § 13–14, с. 100–115)
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов.
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by).
РТ–2021/2022 гг. Этап III. Вариант 1
Тематическое консультирование по математике
8

9.

Раздел программы
вступительных
испытаний. Элемент
содержания
Содержание задания
Комментарий и решение задания
Учебное издание
Утверждение 3 неверное.
4) Простым числом называется число,
которое имеет только два различных
делителя.
Утверждение 4 неверное, так как
число 501 имеет больше двух делителей.
Заметим, что сумма цифр числа 501
равна 6, а число 6 делится на 3, значит и
число 501 делится на 3.
5) 9 3 3; 18 2 3 3; 27 3 3 3.
НОД 9; 18; 27 3 3 9.
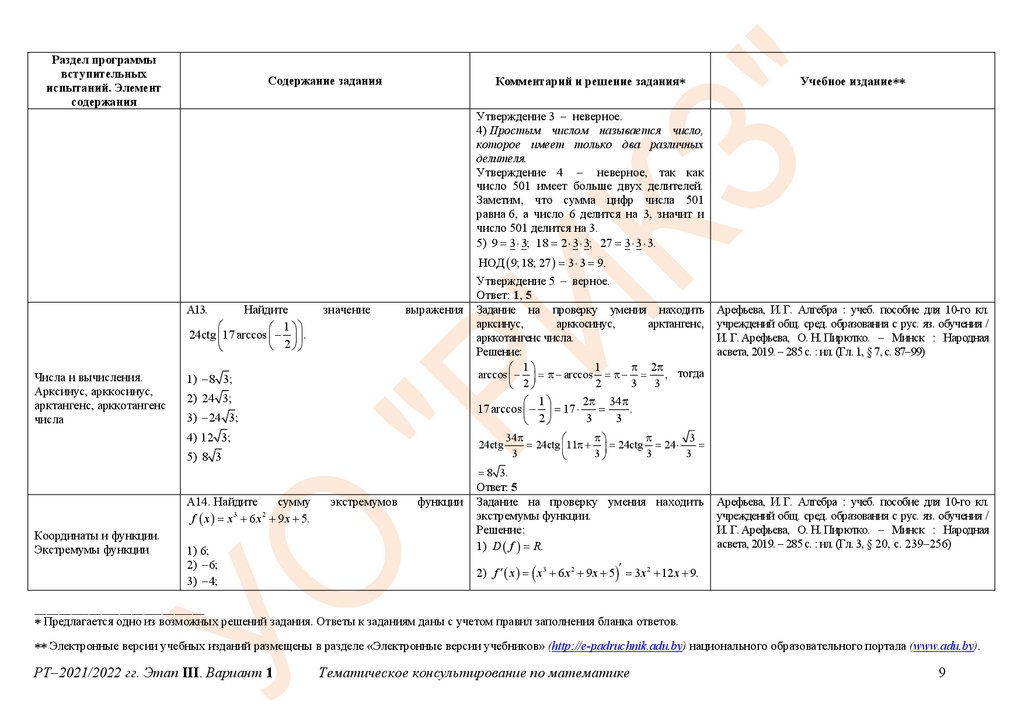
А13.
Найдите
1
24ctg 17 arccos .
2
Числа и вычисления.
Арксинус, арккосинус,
арктангенс, арккотангенс
числа
значение
выражения
1) 8 3;
2) 24 3;
3) 24 3;
4) 12 3;
Утверждение 5 верное.
Ответ: 1, 5
Задание на проверку умения находить
арксинус,
арккосинус,
арктангенс,
арккотангенс числа.
Решение:
1
2
1
arccos arccos
, тогда
2
3 3
2
2 34
1
17 arccos 17
.
2
3
3
24ctg
5) 8 3
Арефьева, И. Г. Алгебра : учеб. пособие для 10-го кл.
учреждений общ. сред. образования с рус. яз. обучения /
И. Г. Арефьева, О. Н. Пирютко. – Минск : Народная
асвета, 2019. – 285 с. : ил. (Гл. 1, § 7, с. 87–99)
34
3
24ctg 11 24ctg 24
3
3
3
3
8 3.
А14. Найдите
сумму
3
2
f x x 6 x 9 x 5.
Координаты и функции.
Экстремумы функции
1) 6;
2) 6;
3) 4;
экстремумов
функции
Ответ: 5
Задание на проверку умения находить
экстремумы функции.
Решение:
1) D f R.
Арефьева, И. Г. Алгебра : учеб. пособие для 10-го кл.
учреждений общ. сред. образования с рус. яз. обучения /
И. Г. Арефьева, О. Н. Пирютко. – Минск : Народная
асвета, 2019. – 285 с. : ил. (Гл. 3, § 20, с. 239–256)
2) f x x3 6 x 2 9 x 5 3x 2 12 x 9.
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов.
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by).
РТ–2021/2022 гг. Этап III. Вариант 1
Тематическое консультирование по математике
9

10.

Раздел программы
вступительных
испытаний. Элемент
содержания
Содержание задания
Комментарий и решение задания
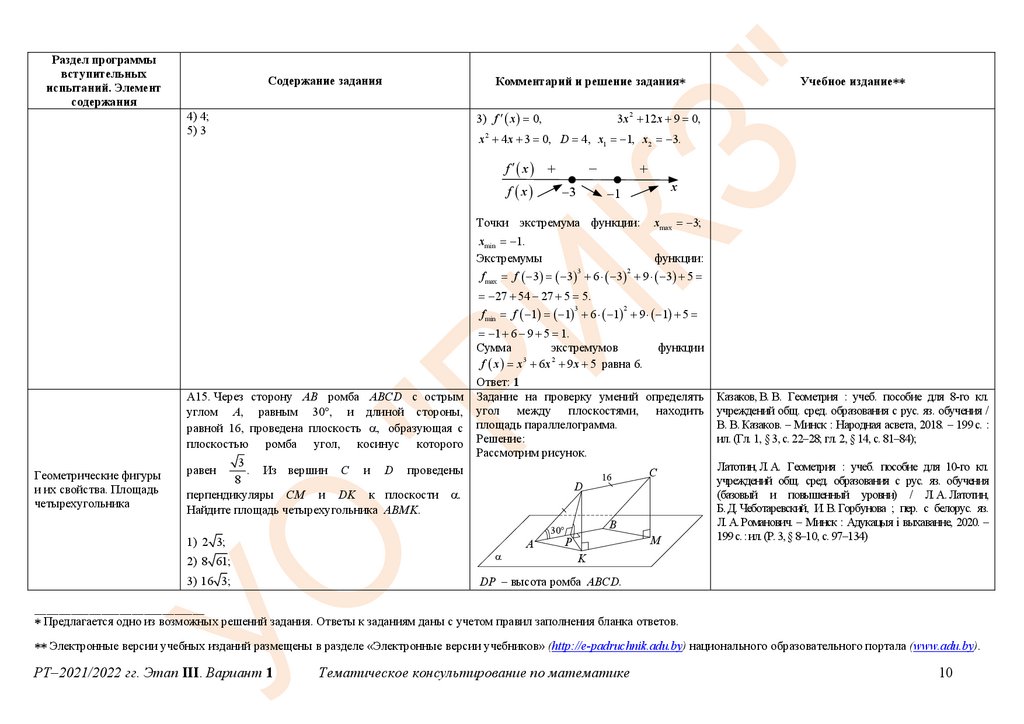
3) f x 0,
4) 4;
5) 3
Учебное издание
3x 2 12 x 9 0,
x 2 4 x 3 0, D 4, x1 1, x2 3.
f x
f x
3
x
1
Точки экстремума функции:
xmax 3;
xmin 1.
Экстремумы
функции:
f max f 3 3 6 3 9 3 5
3
2
27 54 27 5 5.
3
2
f min f 1 1 6 1 9 1 5
1 6 9 5 1.
Сумма
экстремумов
f x x3 6 x 2 9 x 5 равна 6.
А15. Через сторону AB ромба ABCD с острым
углом A, равным 30 , и длиной стороны,
равной 16, проведена плоскость , образующая с
плоскостью ромба угол, косинус которого
Геометрические фигуры
и их свойства. Площадь
четырехугольника
3
. Из вершин C и D проведены
8
перпендикуляры CM и DK к плоскости .
Найдите площадь четырехугольника ABMK .
Ответ: 1
Задание на проверку умений определять
угол между плоскостями, находить
площадь параллелограмма.
Решение:
Рассмотрим рисунок.
равен
D
1) 2 3;
3) 16 3;
A
16
C
B
30
2) 8 61;
функции
M
P
Казаков, В. В. Геометрия : учеб. пособие для 8-го кл.
учреждений общ. сред. образования с рус. яз. обучения /
В. В. Казаков. – Минск : Народная асвета, 2018. – 199 с. :
ил. (Гл. 1, § 3, с. 22–28; гл. 2, § 14, с. 81–84);
Латотин, Л. А. Геометрия : учеб. пособие для 10-го кл.
учреждений общ. сред. образования с рус. яз. обучения
(базовый и повышенный уровни) / Л. А. Латотин,
Б. Д. Чеботаревский, И. В. Горбунова ; пер. с белорус. яз.
Л. А. Романович. – Минск : Адукацыя і выхаванне, 2020. –
199 с. : ил. (Р. 3, § 8–10, с. 97–134)
K
DP – высота ромба ABCD.
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов.
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by).
РТ–2021/2022 гг. Этап III. Вариант 1
Тематическое консультирование по математике
10

11.

Раздел программы
вступительных
испытаний. Элемент
содержания
Содержание задания
4) 8 3;
5) 16 61
Комментарий и решение задания
Учебное издание
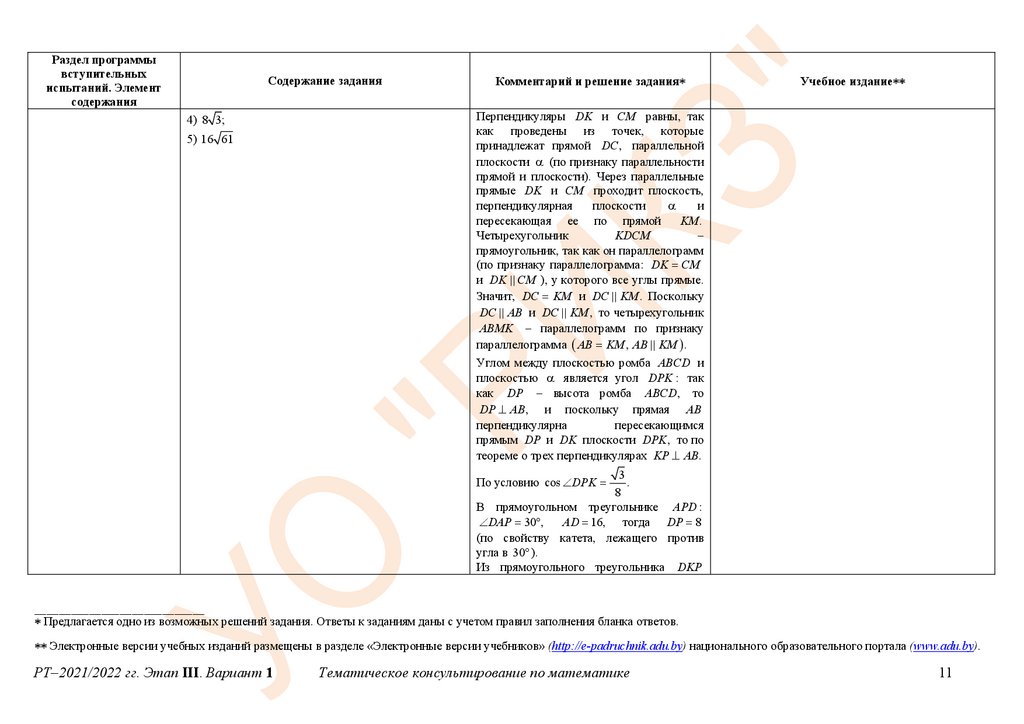
Перпендикуляры DK и CM равны, так
как проведены из точек, которые
принадлежат прямой DC , параллельной
плоскости (по признаку параллельности
прямой и плоскости). Через параллельные
прямые DK и CM проходит плоскость,
перпендикулярная
плоскости
и
пересекающая ее по прямой
KM .
Четырехугольник
–
KDCM
прямоугольник, так как он параллелограмм
(по признаку параллелограмма: DK CM
и DK CM ), у которого все углы прямые.
Значит, DC KM и DC KM . Поскольку
DC AB и DC KM , то четырехугольник
ABMK – параллелограмм по признаку
параллелограмма AB KM , AB KM .
Углом между плоскостью ромба ABCD и
плоскостью является угол DPK : так
как DP – высота ромба ABCD, то
DP AB, и поскольку прямая AB
перпендикулярна
пересекающимся
прямым DP и DK плоскости DPK , то по
теореме о трех перпендикулярах KP AB.
3
.
8
В прямоугольном треугольнике APD :
AD 16, тогда DP 8
DAP 30 ,
(по свойству катета, лежащего против
угла в 30 ).
Из прямоугольного треугольника DKP
По условию cos DPK
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов.
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by).
РТ–2021/2022 гг. Этап III. Вариант 1
Тематическое консультирование по математике
11

12.

Раздел программы
вступительных
испытаний. Элемент
содержания
Содержание задания
Комментарий и решение задания
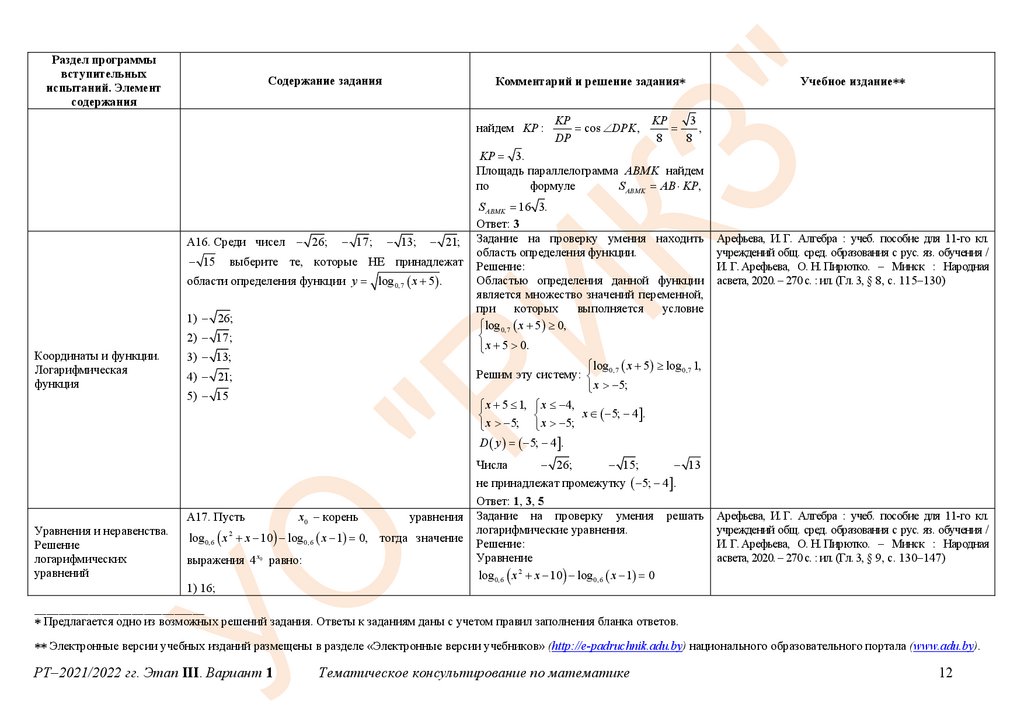
найдем KP :
Учебное издание
KP
KP
3
cos DPK ,
,
DP
8
8
KP 3.
Площадь параллелограмма ABMK найдем
по
формуле
S ABMK AB KP,
А16. Среди чисел 26;
15
17;
13;
21;
выберите те, которые НЕ принадлежат
области определения функции y log 0,7 x 5 .
1) 26;
2) 17;
Координаты и функции.
Логарифмическая
функция
3) 13;
4) 21;
5) 15
S ABMK 16 3.
Ответ: 3
Задание на проверку умения находить
область определения функции.
Решение:
Областью определения данной функции
является множество значений переменной,
при
которых
выполняется
условие
log 0,7 x 5 0,
x 5 0.
log x 5 log 0,7 1,
Решим эту систему: 0,7
x 5;
x 5 1, x 4,
x 5; 4 .
x 5; x 5;
Арефьева, И. Г. Алгебра : учеб. пособие для 11-го кл.
учреждений общ. сред. образования с рус. яз. обучения /
И. Г. Арефьева, О. Н. Пирютко. – Минск : Народная
асвета, 2020. – 270 с. : ил. (Гл. 3, § 8, с. 115–130)
D y 5; 4 .
26;
15;
13
не принадлежат промежутку 5; 4 .
Ответ: 1, 3, 5
Задание на проверку умения решать
логарифмические уравнения.
Решение:
Уравнение
log 0,6 x 2 x 10 log 0,6 x 1 0
Числа
А17. Пусть
Уравнения и неравенства.
Решение
логарифмических
уравнений
x0 – корень
уравнения
log 0,6 x 2 x 10 log 0,6 x 1 0, тогда значение
выражения 4 x0 равно:
1) 16;
Арефьева, И. Г. Алгебра : учеб. пособие для 11-го кл.
учреждений общ. сред. образования с рус. яз. обучения /
И. Г. Арефьева, О. Н. Пирютко. – Минск : Народная
асвета, 2020. – 270 с. : ил. (Гл. 3, § 9, с. 130–147)
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов.
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by).
РТ–2021/2022 гг. Этап III. Вариант 1
Тематическое консультирование по математике
12

13.

Раздел программы
вступительных
испытаний. Элемент
содержания
Содержание задания
2) 40;
3) 12;
4) 64;
5) 72
Комментарий и решение задания
Учебное издание
равносильно
уравнению
2
которое
log 0,6 x x 10 log 0,6 x 1 ,
x 2 x 10 x 1,
равносильно системе:
x 1 0;
x 2 9 0,
x 1;
x 3.
Значит
x 3,
x 3,
x 1;
x 3 x 3 0,
x 1;
x0 3,
тогда
значение
x0
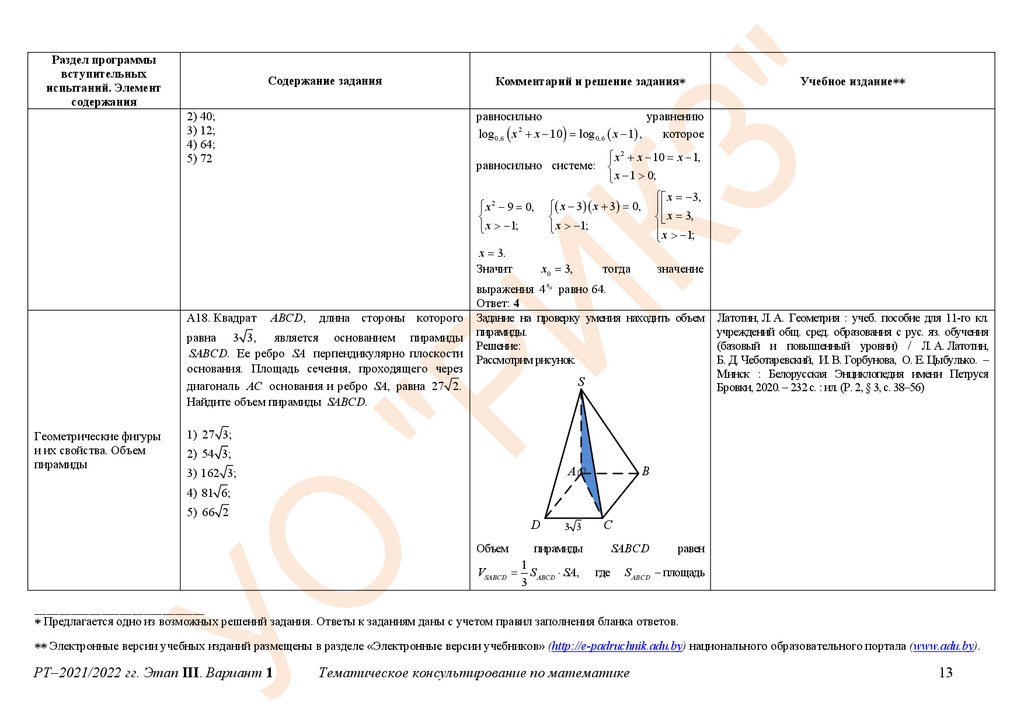
А18. Квадрат
ABCD,
длина стороны которого
равна 3 3, является основанием пирамиды
SABCD. Ее ребро SA перпендикулярно плоскости
основания. Площадь сечения, проходящего через
диагональ AC основания и ребро SA, равна 27 2.
Найдите объем пирамиды SABCD.
Геометрические фигуры
и их свойства. Объем
пирамиды
выражения 4 равно 64.
Ответ: 4
Задание на проверку умения находить объем
пирамиды.
Решение:
Рассмотрим рисунок.
S
Латотин, Л. А. Геометрия : учеб. пособие для 11-го кл.
учреждений общ. сред. образования с рус. яз. обучения
(базовый и повышенный уровни) / Л. А. Латотин,
Б. Д. Чеботаревский, И. В. Горбунова, О. Е. Цыбулько. –
Минск : Белорусская Энциклопедия имени Петруся
Бровки, 2020. – 232 с. : ил. (Р. 2, § 3, с. 38–56)
1) 27 3;
2) 54 3;
B
A
3) 162 3;
4) 81 6;
5) 66 2
D
Объем
VSABCD
3 3
C
пирамиды
равен
SABCD
1
S ABCD SA, где S ABCD – площадь
3
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов.
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by).
РТ–2021/2022 гг. Этап III. Вариант 1
Тематическое консультирование по математике
13

14.

Раздел программы
вступительных
испытаний. Элемент
содержания
Содержание задания
Комментарий и решение задания
Учебное издание
основания пирамиды, SA – высота пирамиды.
является
сечением
Треугольник
SAC
пирамиды плоскостью, проходящей через
диагональ AC и ребро SA.
По условию длина стороны основания
пирамиды равна 3 3, тогда AC 3 6.
По формуле площади прямоугольного
треугольника SAC найдем высоту SA
1
пирамиды:
SSAC SA AC ,
2
1
27 2 SA 3 6, SA 6 3.
2
Площадь основания пирамиды найдем по
формуле: S ABCD AB 2 , S ABCD 27.
1
VSABCD S ABCD SA,
3
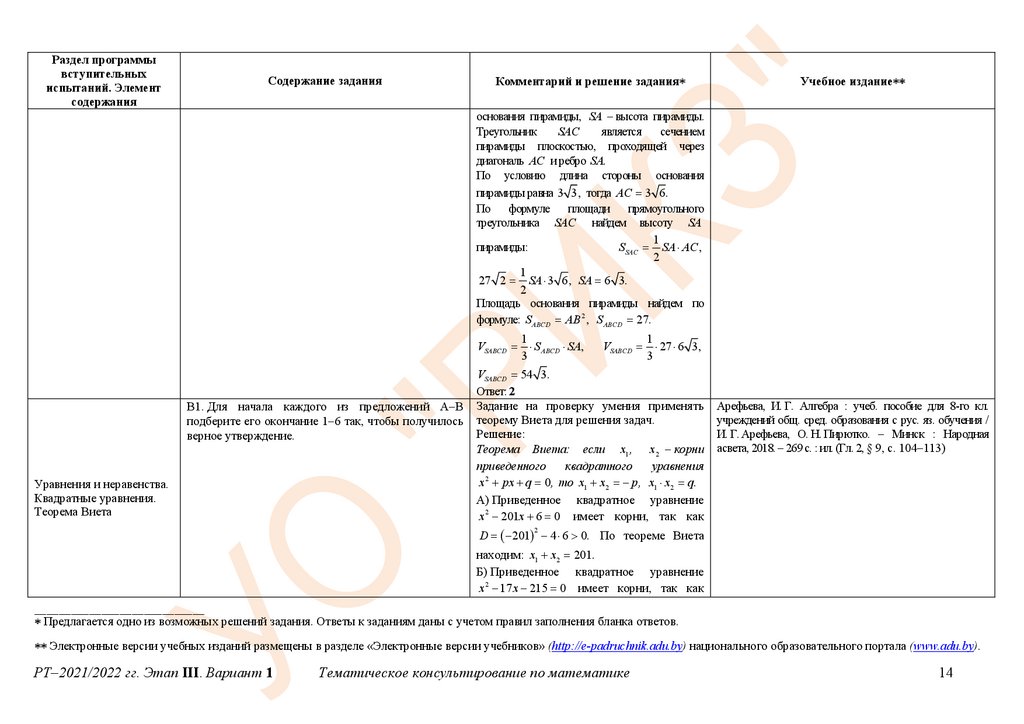
В1. Для начала каждого из предложений А–В
подберите его окончание 1–6 так, чтобы получилось
верное утверждение.
Уравнения и неравенства.
Квадратные уравнения.
Теорема Виета
1
VSABCD 27 6 3,
3
VSABCD 54 3.
Ответ: 2
Задание на проверку умения применять
теорему Виета для решения задач.
Решение:
Теорема Виета: если x1 , x2 – корни
приведенного
квадратного
уравнения
x 2 px q 0, то x1 x2 p, x1 x2 q.
А) Приведенное квадратное уравнение
x 2 201x 6 0 имеет корни, так как
Арефьева, И. Г. Алгебра : учеб. пособие для 8-го кл.
учреждений общ. сред. образования с рус. яз. обучения /
И. Г. Арефьева, О. Н. Пирютко. – Минск : Народная
асвета, 2018. – 269 с. : ил. (Гл. 2, § 9, с. 104–113)
D 201 4 6 0. По теореме Виета
2
находим: x1 x2 201.
Б) Приведенное квадратное уравнение
x 2 17 x 215 0 имеет корни, так как
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов.
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by).
РТ–2021/2022 гг. Этап III. Вариант 1
Тематическое консультирование по математике
14

15.

Раздел программы
вступительных
испытаний. Элемент
содержания
Содержание задания
Комментарий и решение задания
D 17 4 215 0.
2
Начало предложения
А) Сумма корней уравнения
x 2 201x 6 0 равна …
Б) Произведение
корней
уравнения
x 2 17 x 215 0
равно …
В) Сумма
уравнения
равна …
квадратов корней
2 x 2 34 x 15 0
Окончание
предложения
1) 215.
2) 274.
3) 201.
4) 215.
5) 304.
6) 201.
По
Учебное издание
теореме
Виета находим: x1 x2 215.
В) Уравнение
2 x 2 34 x 15 0
имеет
корни, так как D 34 4 2 15 0, и
2
равносильно приведенному квадратному
уравнению x 2 17 x 7,5 0. По теореме
Виета находим: x1 x2 17, x1 x2 7,5.
x12 x2 2 x1 x2 2 x1 x2 17 2 2 7,5
2
289 15 274.
Ответ: А6Б4В2
Ответ запишите в виде сочетания букв и цифр, соблюдая
алфавитную последовательность букв левого столбца.
Помните, что некоторые данные правого столбца могут
использоваться несколько раз или не использоваться
вообще. Например: А1Б1В4
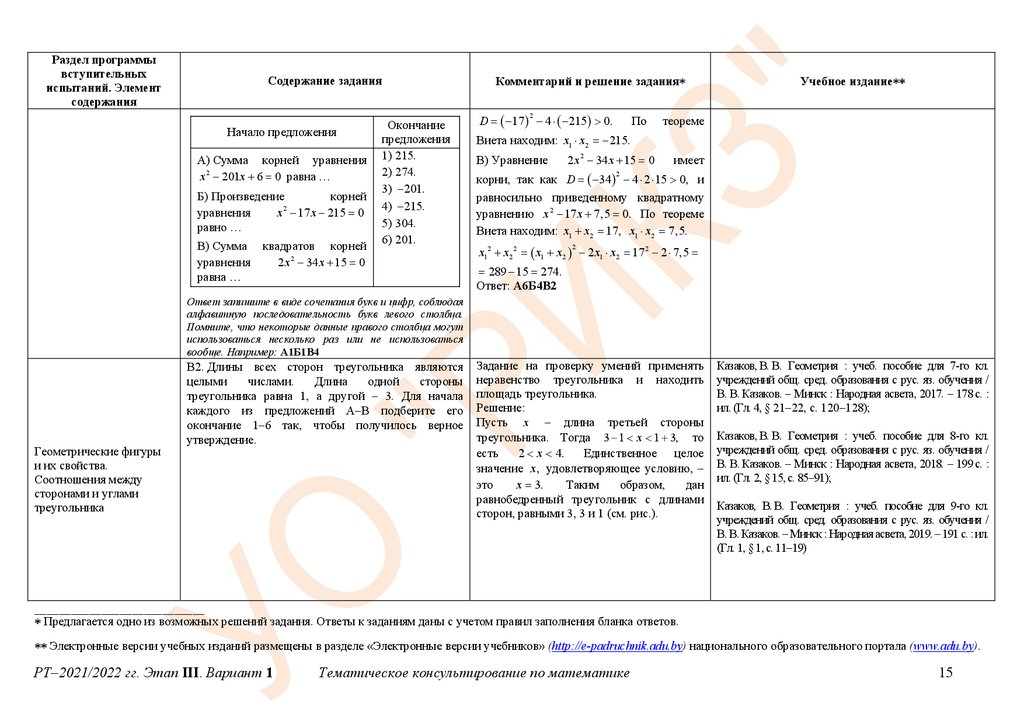
В2. Длины всех сторон треугольника являются
целыми
числами.
Длина
одной
стороны
треугольника равна 1, а другой – 3. Для начала
каждого из предложений А–В подберите его
окончание 1–6 так, чтобы получилось верное
утверждение.
Геометрические фигуры
и их свойства.
Соотношения между
сторонами и углами
треугольника
Задание на проверку умений применять
неравенство треугольника и находить
площадь треугольника.
Решение:
Пусть x – длина третьей стороны
треугольника. Тогда 3 1 x 1 3, то
есть
Единственное целое
2 x 4.
значение x, удовлетворяющее условию, –
это
x 3.
Таким
образом,
дан
равнобедренный треугольник с длинами
сторон, равными 3, 3 и 1 (см. рис.).
Казаков, В. В. Геометрия : учеб. пособие для 7-го кл.
учреждений общ. сред. образования с рус. яз. обучения /
В. В. Казаков. – Минск : Народная асвета, 2017. – 178 с. :
ил. (Гл. 4, § 21–22, с. 120–128);
Казаков, В. В. Геометрия : учеб. пособие для 8-го кл.
учреждений общ. сред. образования с рус. яз. обучения /
В. В. Казаков. – Минск : Народная асвета, 2018. – 199 с. :
ил. (Гл. 2, § 15, с. 85–91);
Казаков, В. В. Геометрия : учеб. пособие для 9-го кл.
учреждений общ. сред. образования с рус. яз. обучения /
В. В. Казаков. – Минск : Народная асвета, 2019. – 191 с. : ил.
(Гл. 1, § 1, с. 11–19)
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов.
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by).
РТ–2021/2022 гг. Этап III. Вариант 1
Тематическое консультирование по математике
15

16.

Раздел программы
вступительных
испытаний. Элемент
содержания
Содержание задания
Начало предложения
А) Периметр
равен …
треугольника
Б) Площадь
равна …
треугольника
Комментарий и решение задания
Окончание
предложения
1) 6.
2)
A
35
.
8
3) 7.
В) Косинус большего
треугольника равен …
угла
Учебное издание
3
3
17
.
18
1
5) .
6
35
6)
.
4
4)
Ответ запишите в виде сочетания букв и цифр, соблюдая
алфавитную последовательность букв левого столбца.
Помните, что некоторые данные правого столбца могут
использоваться несколько раз или не использоваться
вообще. Например: А1Б1В4
B
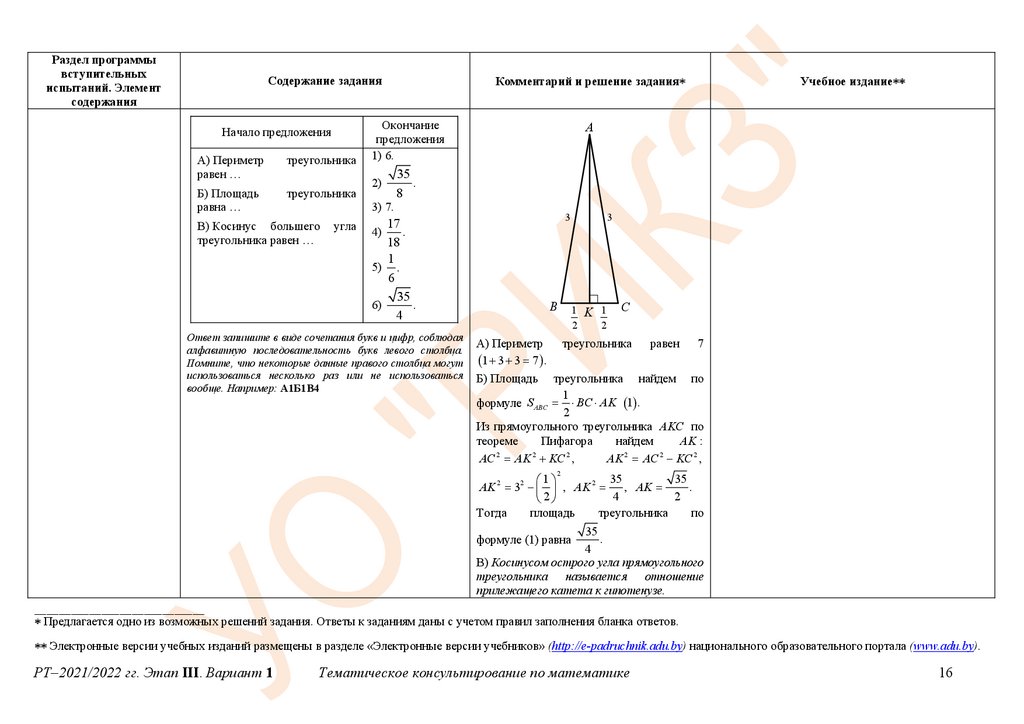
А) Периметр
1 3 3 7 .
1
2
K 1
C
2
треугольника
равен
7
Б) Площадь
треугольника найдем по
1
формуле S ABC BC AK 1 .
2
Из прямоугольного треугольника AKC по
теореме
Пифагора
найдем
AK :
2
2
2
2
2
AC AK KC ,
AK AC KC 2 ,
2
35
35
1
.
AK 2 32 , AK 2 , AK
2
4
2
Тогда
площадь
треугольника
по
35
.
4
В) Косинусом острого угла прямоугольного
треугольника называется отношение
прилежащего катета к гипотенузе.
формуле (1) равна
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов.
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by).
РТ–2021/2022 гг. Этап III. Вариант 1
Тематическое консультирование по математике
16

17.

Раздел программы
вступительных
испытаний. Элемент
содержания
Содержание задания
В3. Выберите три верных утверждения.
Геометрические фигуры
и их свойства. Фигуры,
симметричные
относительно прямой
Комментарий и решение задания
Учебное издание
В треугольнике против большей стороны
лежит больший угол. В нашем случае
большим углом является угол при
основании.
Тогда
KC
cos ACB cos ACK
,
AC
1
cos ACB .
6
Ответ: А3Б6В5
Задание на проверку знания определения
фигуры,
симметричной
относительно
прямой.
Решение:
Герасимов, В. Д. Математика : учеб. пособие для 6-го кл.
учреждений общ. сред. образования с рус. яз. обучения /
В. Д. Герасимов, О. Н. Пирютко. – Минск : Адукацыя і
выхаванне, 2018. – 320 с. : ил. (Гл. 6, § 5, с. 297–301)
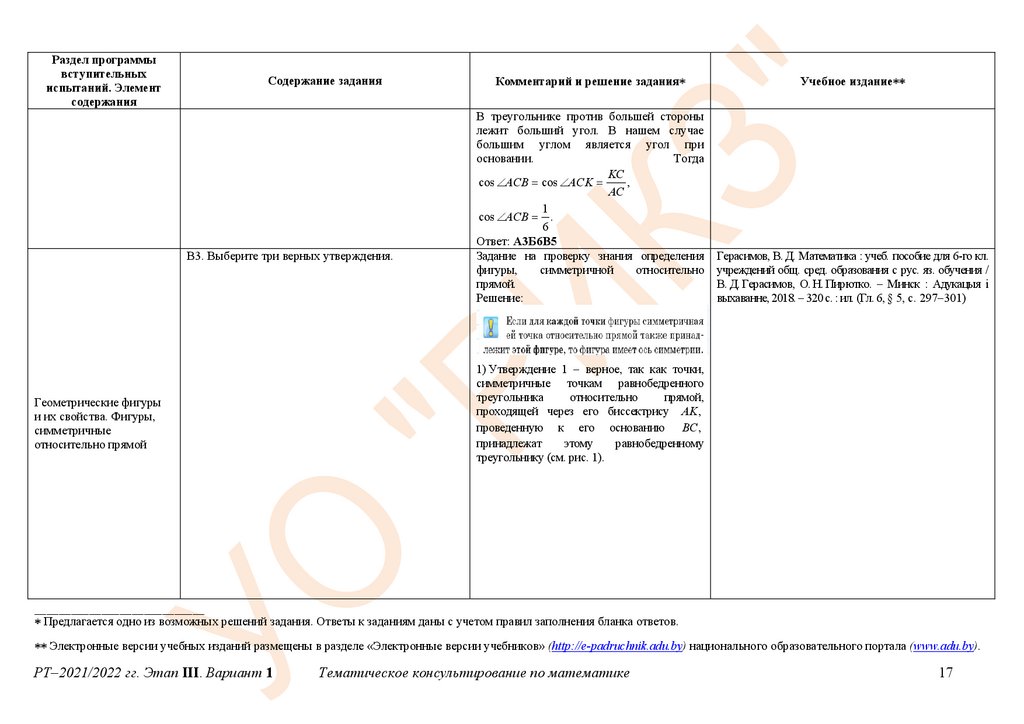
1) Утверждение 1 – верное, так как точки,
симметричные точкам равнобедренного
треугольника
относительно
прямой,
проходящей через его биссектрису AK ,
проведенную к его основанию BC ,
принадлежат
этому
равнобедренному
треугольнику (см. рис. 1).
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов.
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by).
РТ–2021/2022 гг. Этап III. Вариант 1
Тематическое консультирование по математике
17

18.

Раздел программы
вступительных
испытаний. Элемент
содержания
Содержание задания
1
2
3
4
5
6
Комментарий и решение задания
прямая, проходящая через биссектрису
равнобедренного
треугольника,
проведенную к его основанию, является
его осью симметрии
прямая,
проходящая
через
высоту
равнобедренного
треугольника,
проведенную к одной из его боковых
сторон, является его осью симметрии
прямая, проходящая через одну из
диагоналей прямоугольника, в который
нельзя вписать окружность, является его
осью симметрии
прямая, проходящая через одну из
диагоналей ромба, является его осью
симметрии
прямая, проходящая через одну из
диагоналей параллелограмма, в который
нельзя вписать окружность и около которого
нельзя описать окружность, является его
осью симметрии
прямая, проходящая через медиану
прямоугольного
равнобедренного
треугольника,
проведенную
к
его
гипотенузе, является его осью симметрии
Ответ запишите цифрами (порядок
не имеет значения). Например: 123
записи
Учебное издание
A
M1
M
B
C
K
Рисунок 1
2) Утверждение 2 – неверное, так как,
например, точка A1 , симметричная точке A
относительно прямой, которая проходит
через
высоту
равнобедренного
BK
треугольника
ABC
AB AC , не
принадлежит данному равнобедренному
треугольнику (см. рис. 2).
A
цифр
K
C
B
A1
Рисунок 2
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов.
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by).
РТ–2021/2022 гг. Этап III. Вариант 1
Тематическое консультирование по математике
18

19.

Раздел программы
вступительных
испытаний. Элемент
содержания
Содержание задания
Комментарий и решение задания
Учебное издание
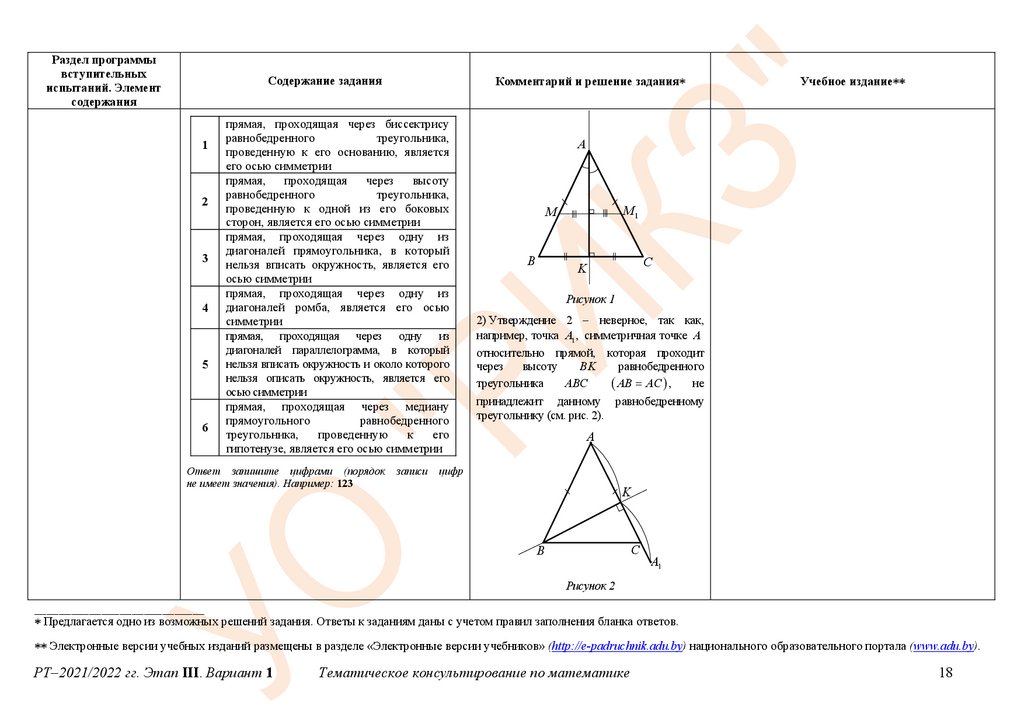
3) Из условия следует, что данный
прямоугольник не является квадратом.
Утверждение 3 – неверное, так как,
например, точка A1 , симметричная точке A
относительно прямой, которая проходит
через диагональ BD
прямоугольника
не
принадлежит
данному
ABCD,
прямоугольнику (см. рис. 3).
B
A
C
D
A1
Рисунок 3
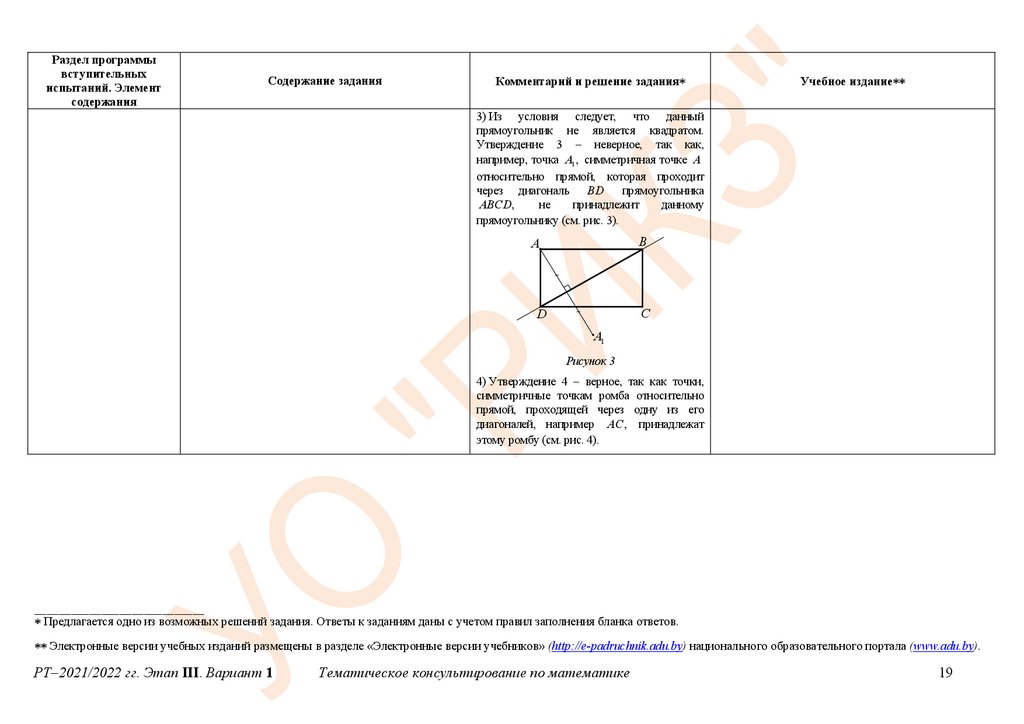
4) Утверждение 4 – верное, так как точки,
симметричные точкам ромба относительно
прямой, проходящей через одну из его
диагоналей, например AC , принадлежат
этому ромбу (см. рис. 4).
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов.
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by).
РТ–2021/2022 гг. Этап III. Вариант 1
Тематическое консультирование по математике
19

20.

Раздел программы
вступительных
испытаний. Элемент
содержания
Содержание задания
Комментарий и решение задания
Учебное издание
B
M
A
C
M1
D
Рисунок 4
5) Из условия следует, что данный
параллелограмм не является квадратом.
Утверждение 5 – неверное, так как,
например, точка A1 , симметричная точке A
относительно прямой, которая проходит
через диагональ BD параллелограмма
не
принадлежит
данному
ABCD,
параллелограмму (см. рис. 5).
B
A
C
D
A1
Рисунок 5
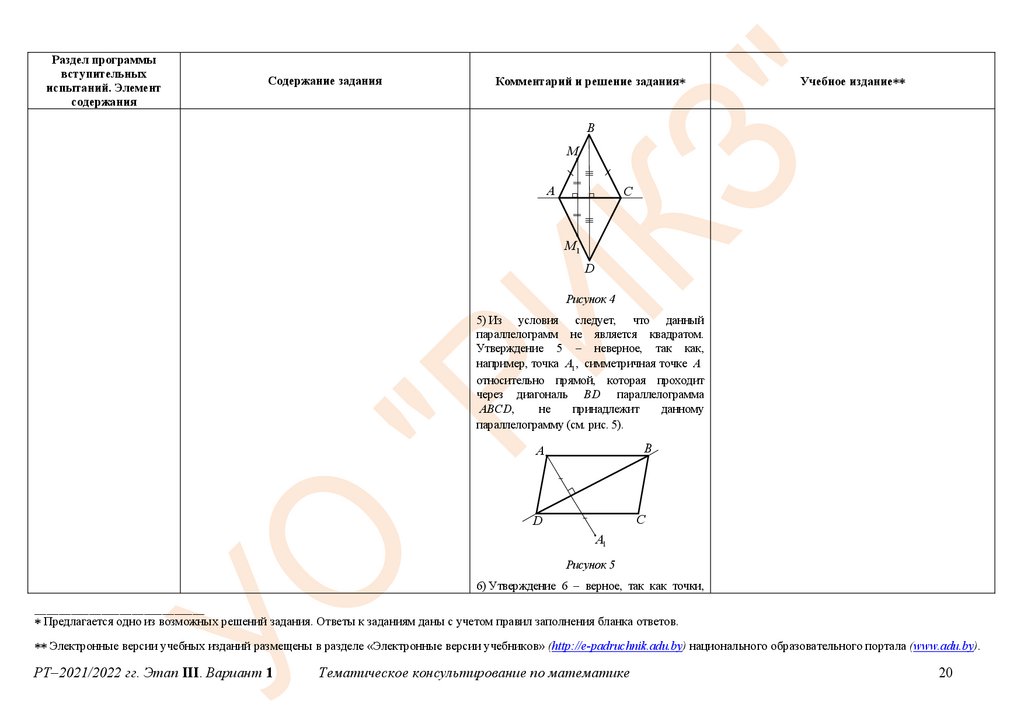
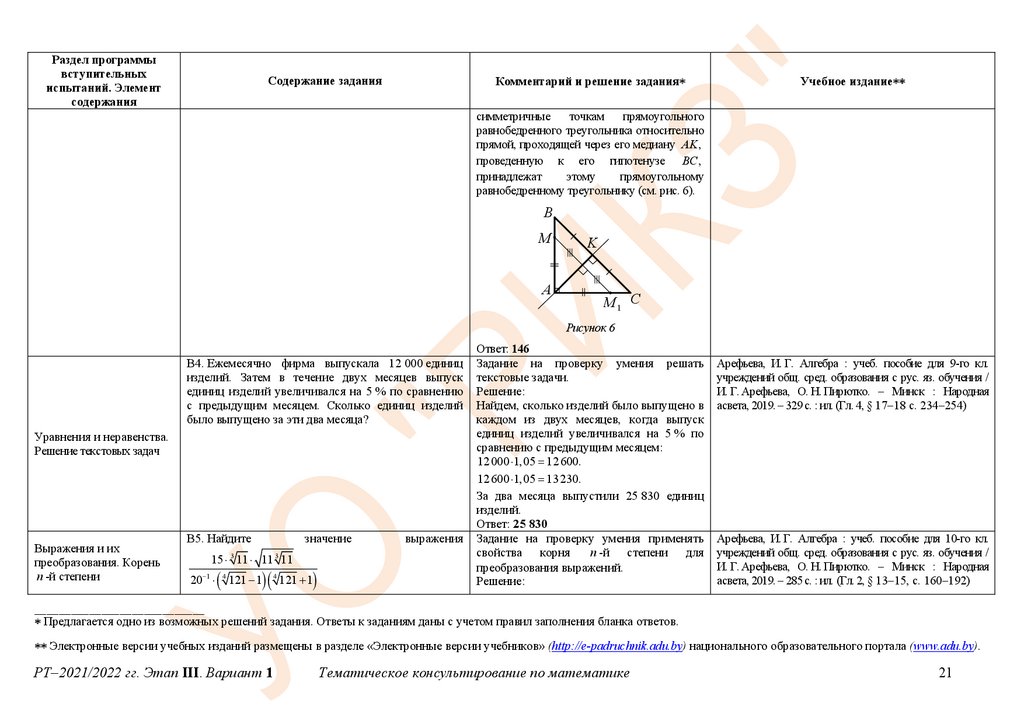
6) Утверждение 6 – верное, так как точки,
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов.
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by).
РТ–2021/2022 гг. Этап III. Вариант 1
Тематическое консультирование по математике
20

21.

Раздел программы
вступительных
испытаний. Элемент
содержания
Содержание задания
Комментарий и решение задания
Учебное издание
симметричные
точкам
прямоугольного
равнобедренного треугольника относительно
прямой, проходящей через его медиану AK ,
проведенную к его гипотенузе BC ,
принадлежат
этому
прямоугольному
равнобедренному треугольнику (см. рис. 6).
B
M
A
K
M1 C
Рисунок 6
В4. Ежемесячно фирма выпускала 12 000 единиц
изделий. Затем в течение двух месяцев выпуск
единиц изделий увеличивался на 5 % по сравнению
с предыдущим месяцем. Сколько единиц изделий
было выпущено за эти два месяца?
Уравнения и неравенства.
Решение текстовых задач
Выражения и их
преобразования. Корень
n -й степени
В5. Найдите
значение
15 11 11 11
3
1
20
4
3
121 1
4
121 1
выражения
Ответ: 146
Задание на проверку умения решать
текстовые задачи.
Решение:
Найдем, сколько изделий было выпущено в
каждом из двух месяцев, когда выпуск
единиц изделий увеличивался на 5 % по
сравнению с предыдущим месяцем:
12 000 1, 05 12 600.
12 600 1, 05 13230.
За два месяца выпустили 25 830 единиц
изделий.
Ответ: 25 830
Задание на проверку умения применять
свойства корня
n -й степени для
преобразования выражений.
Решение:
Арефьева, И. Г. Алгебра : учеб. пособие для 9-го кл.
учреждений общ. сред. образования с рус. яз. обучения /
И. Г. Арефьева, О. Н. Пирютко. – Минск : Народная
асвета, 2019. – 329 с. : ил. (Гл. 4, § 17–18 с. 234–254)
Арефьева, И. Г. Алгебра : учеб. пособие для 10-го кл.
учреждений общ. сред. образования с рус. яз. обучения /
И. Г. Арефьева, О. Н. Пирютко. – Минск : Народная
асвета, 2019. – 285 с. : ил. (Гл. 2, § 13–15, с. 160–192)
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов.
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by).
РТ–2021/2022 гг. Этап III. Вариант 1
Тематическое консультирование по математике
21

22.

Раздел программы
вступительных
испытаний. Элемент
содержания
Содержание задания
Комментарий и решение задания
15 3 11 11 3 11
20 1
4
121 1
20 15 3 11
4
2
4
3
121 12
121 1
114
Учебное издание
300 3 11 3 112
11 1
300 11
330.
10
Ответ: 330
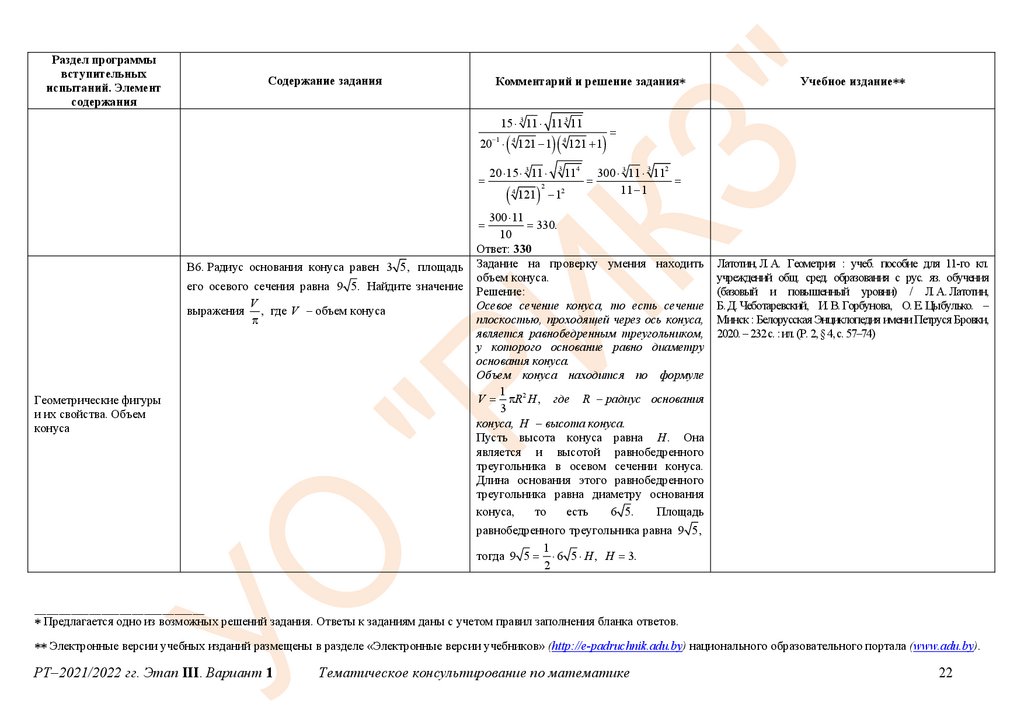
Задание на проверку умения находить
объем конуса.
Решение:
Осевое сечение конуса, то есть сечение
плоскостью, проходящей через ось конуса,
является равнобедренным треугольником,
у которого основание равно диаметру
основания конуса.
Объем конуса находится по формуле
1
V R 2 H , где R – радиус основания
3
конуса, H – высота конуса.
Пусть высота конуса равна H . Она
является и высотой равнобедренного
треугольника в осевом сечении конуса.
Длина основания этого равнобедренного
треугольника равна диаметру основания
конуса,
то
есть
Площадь
6 5.
В6. Радиус основания конуса равен 3 5, площадь
его осевого сечения равна 9 5. Найдите значение
V
выражения , где V – объем конуса
Геометрические фигуры
и их свойства. Объем
конуса
Латотин, Л. А. Геометрия : учеб. пособие для 11-го кл.
учреждений общ. сред. образования с рус. яз. обучения
(базовый и повышенный уровни) / Л. А. Латотин,
Б. Д. Чеботаревский, И. В. Горбунова, О. Е. Цыбулько. –
Минск : Белорусская Энциклопедия имени Петруся Бровки,
2020. – 232 с. : ил. (Р. 2, § 4, с. 57–74)
равнобедренного треугольника равна 9 5,
1
тогда 9 5 6 5 H , H 3.
2
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов.
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by).
РТ–2021/2022 гг. Этап III. Вариант 1
Тематическое консультирование по математике
22

23.

Раздел программы
вступительных
испытаний. Элемент
содержания
Содержание задания
Комментарий и решение задания
В7. Найдите (в градусах) сумму различных корней
9
cos 3 x 3sin x 2 2
уравнения
2
на промежутке 520 ; 120
2
1
1
V R 2 H , V 3 5 3, V 45 .
3
3
V
Значение выражения
равно 45.
Ответ: 45
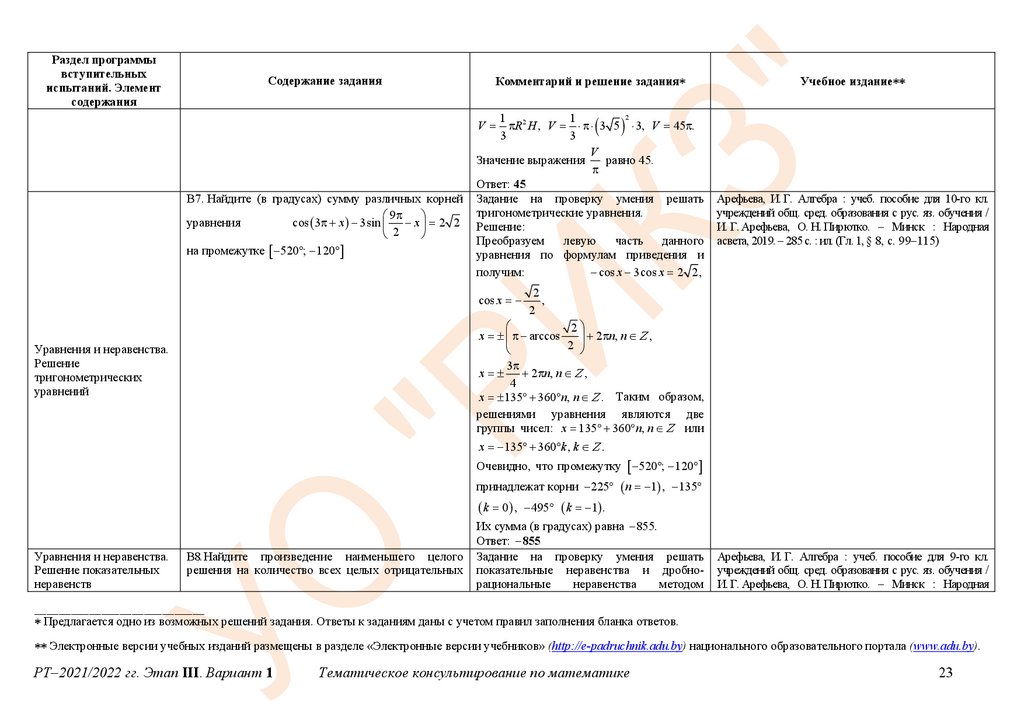
Задание на проверку умения решать
тригонометрические уравнения.
Решение:
Преобразуем
левую
часть
данного
уравнения по формулам приведения и
получим:
cos x 3cos x 2 2,
cos x
Учебное издание
Арефьева, И. Г. Алгебра : учеб. пособие для 10-го кл.
учреждений общ. сред. образования с рус. яз. обучения /
И. Г. Арефьева, О. Н. Пирютко. – Минск : Народная
асвета, 2019. – 285 с. : ил. (Гл. 1, § 8, с. 99–115)
2
,
2
2
x arccos
2 n, n ,
2
3
x 2 n, n ,
4
x 135 360 n, n . Таким образом,
решениями уравнения являются две
группы чисел: x 135 360 n, n или
Уравнения и неравенства.
Решение
тригонометрических
уравнений
x 135 360 k , k .
Очевидно, что промежутку 520 ; 120
принадлежат корни 225 n 1 , 135
k 0 ,
Уравнения и неравенства.
Решение показательных
неравенств
В8. Найдите произведение наименьшего целого
решения на количество всех целых отрицательных
495 k 1 .
Их сумма (в градусах) равна 855.
Ответ: 855
Задание на проверку умения решать
показательные неравенства и дробнорациональные
неравенства
методом
Арефьева, И. Г. Алгебра : учеб. пособие для 9-го кл.
учреждений общ. сред. образования с рус. яз. обучения /
И. Г. Арефьева, О. Н. Пирютко. – Минск : Народная
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов.
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by).
РТ–2021/2022 гг. Этап III. Вариант 1
Тематическое консультирование по математике
23

24.

Раздел программы
вступительных
испытаний. Элемент
содержания
Содержание задания
решений неравенства
3 1
Комментарий и решение задания
x 18 2 x 3
x2 5 x
1
Учебное издание
интервалов.
Решение:
Представим число 1 в виде степени с
основанием
3 1 , тогда неравенство
примет
вид
x 18 2 x 3
3 1
x2 5 x
3 1 1,
то
является
3 1
0
1 .
функция
y
убывающей,
x 18 x 3
Так
асвета, 2019. – 329 с. : ил. (Гл. 3, § 13, с. 182–203);
Арефьева, И. Г. Алгебра : учеб. пособие для 11-го кл.
учреждений общ. сред. образования с рус. яз. обучения /
И. Г. Арефьева, О. Н. Пирютко. – Минск : Народная
асвета, 2020. – 270 с. : ил. (Гл. 2, § 6, с. 80–99)
как
3 1
x
значит,
2
(1)
x2 5x
0,
x 18 x 3
0 2 .
x x 5
2
Решим
неравенство
(2)
интервалов.
Нулями
методом
функции
x 18 x 3
f x
x x 5
2
являются
числа 18 и 3, а при x, равных 5 и 0,
значения
функции
не
существуют.
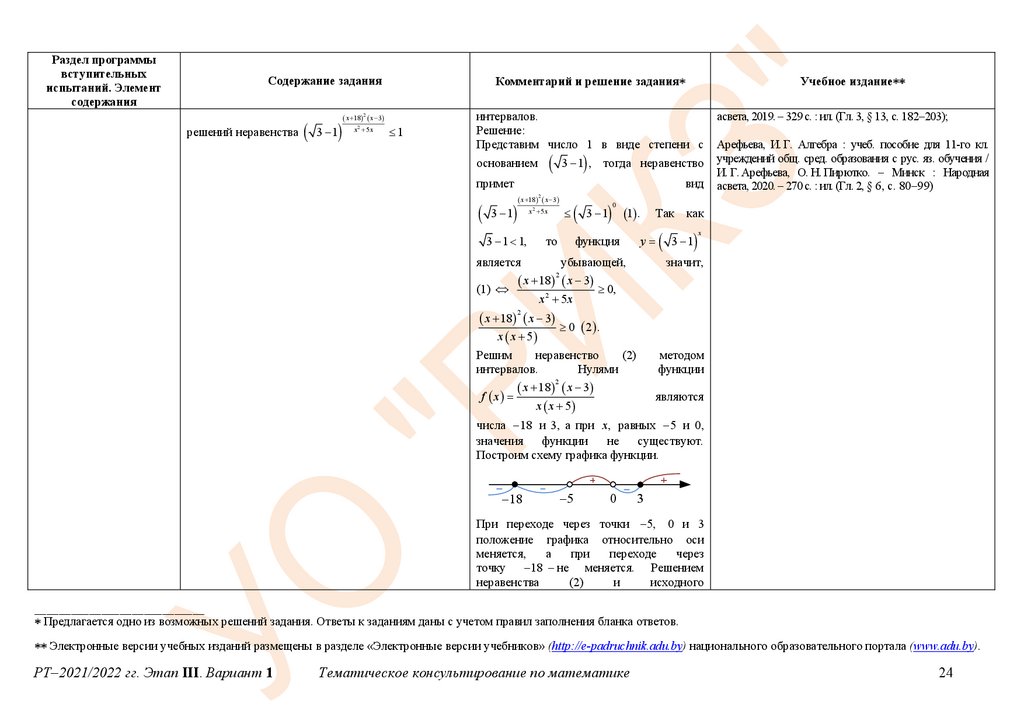
Построим схему графика функции.
18
5
0
3
При переходе через точки 5, 0 и 3
положение графика относительно оси
меняется,
а
при
переходе
через
точку 18 – не меняется. Решением
неравенства
(2)
и
исходного
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов.
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by).
РТ–2021/2022 гг. Этап III. Вариант 1
Тематическое консультирование по математике
24

25.

Раздел программы
вступительных
испытаний. Элемент
содержания
Содержание задания
Комментарий и решение задания
неравенства (1)
является
18 5; 0 3; .
В9. Найдите произведение наибольшего корня на
количество
всех
корней
уравнения
x 2 8 x 26 10 x 4 14 0
Уравнения и неравенства.
Решение иррациональных
уравнений
Учебное издание
множество
Наименьшее
целое решение неравенства равно 18.
Количество целых отрицательных решений
неравенства равно 5. Произведение
наименьшего целого решения неравенства
на количество целых отрицательных
решений неравенства равно 90.
Ответ: 90
Задание на проверку умения решать
иррациональные уравнения и уравнения,
сводящиеся к ним.
Решение:
При решении иррационального уравнения
его заменяют равносильным уравнением
(системой или совокупностью уравнений и
неравенств) либо его следствием (в этом
случае проверка полученных решений
обязательна).
Уравнение
Арефьева, И. Г. Алгебра : учеб. пособие для 8-го кл.
учреждений общ. сред. образования с рус. яз. обучения /
И. Г. Арефьева, О. Н. Пирютко. – Минск : Народная
асвета, 2018. – 269 с. : ил. (Гл. 2, § 12, с. 129–139);
Арефьева, И. Г. Алгебра : учеб. пособие для 10-го кл.
учреждений общ. сред. образования с рус. яз. обучения /
И. Г. Арефьева, О. Н. Пирютко. – Минск : Народная
асвета, 2019. – 285 с. : ил. (Гл. 2, § 17, с. 204–217)
x 2 8 x 26 10 x 4 14 0
равносильно
x 8 x 26 10 x 4 14.
2
уравнению
Обе части
этого уравнения возведем в квадрат и,
выполнив равносильные преобразования,
получим
равносильное
уравнение
x 4
2
10 x 4 24 0.
Обозначим
x 4 y, тогда уравнение примет вид:
y 2 10 y 24 0, его корни – числа 4 и 6.
Возвращаясь к замене, получим два
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов.
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by).
РТ–2021/2022 гг. Этап III. Вариант 1
Тематическое консультирование по математике
25

26.

Раздел программы
вступительных
испытаний. Элемент
содержания
Содержание задания
Комментарий и решение задания
уравнения: x 4 4;
Учебное издание
x 4 6. Корнями
первого уравнения являются числа 0 и 8.
Корнями второго уравнения являются
числа
и
10.
Уравнение
2
x 4
2
10 x 4 24 0
имеет
четыре
корня: 2, 0, 8 и 10. Проверкой
убеждаемся, что эти числа являются
корнями
исходного
уравнения.
Наибольший корень уравнения равен 10.
Произведение наибольшего корня на
количество
корней
уравнения
x 2 8 x 26 10 x 4 14 0 равно 40.
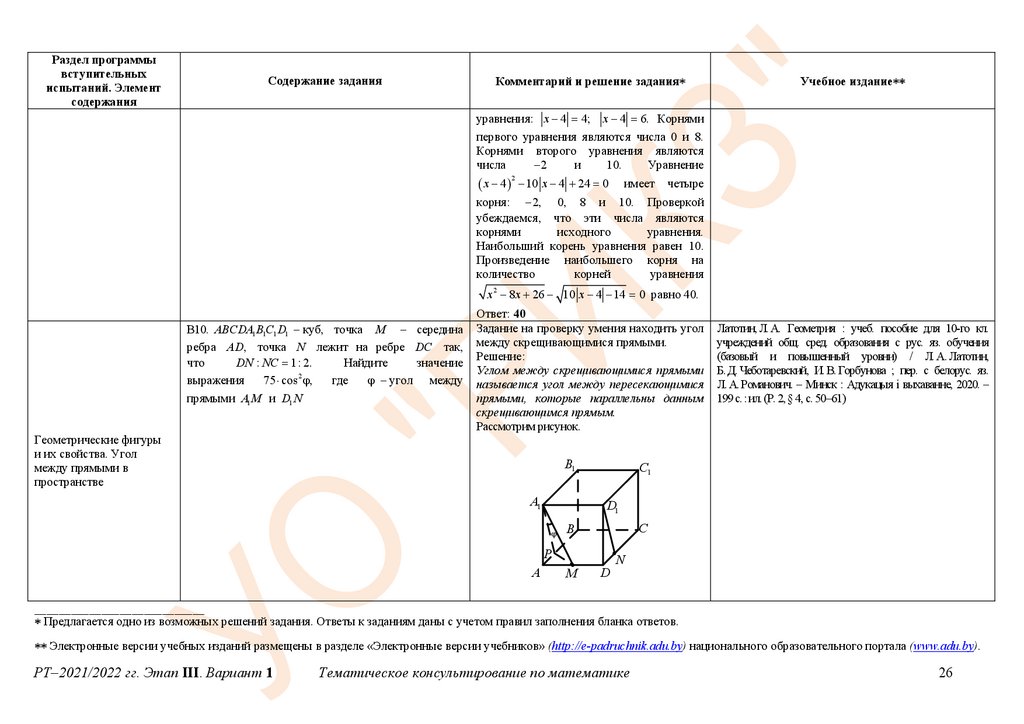
В10. ABCDA1 B1C1 D1 – куб, точка M – середина
ребра AD, точка N лежит на ребре DC так,
что
DN : NC 1: 2.
Найдите
значение
выражения
где
75 cos 2 ,
– угол между
прямыми A1 M и D1 N
Ответ: 40
Задание на проверку умения находить угол
между скрещивающимися прямыми.
Решение:
Углом между скрещивающимися прямыми
называется угол между пересекающимися
прямыми, которые параллельны данным
скрещивающимся прямым.
Рассмотрим рисунок.
Геометрические фигуры
и их свойства. Угол
между прямыми в
пространстве
B1
A1
C1
D1
C
B
P
A
Латотин, Л. А. Геометрия : учеб. пособие для 10-го кл.
учреждений общ. сред. образования с рус. яз. обучения
(базовый и повышенный уровни) / Л. А. Латотин,
Б. Д. Чеботаревский, И. В. Горбунова ; пер. с белорус. яз.
Л. А. Романович. – Минск : Адукацыя і выхаванне, 2020. –
199 с. : ил. (Р. 2, § 4, с. 50–61)
N
M
D
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов.
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by).
РТ–2021/2022 гг. Этап III. Вариант 1
Тематическое консультирование по математике
26

27.

Раздел программы
вступительных
испытаний. Элемент
содержания
Содержание задания
Комментарий и решение задания
Пусть длина ребра куба
Учебное издание
ABCDA1 B1C1 D1
a
.
3
Прямые
и
являются
A1 M
D1 N
скрещивающимися
по
признаку
скрещивающихся прямых A1 M лежит в
равна a. Тогда AM MD
a
,
2
DN
плоскости грани AA1 D1 D, а прямая D1 N
пересекает плоскость этой грани в точке D1 ,
не
лежащей
на
прямой
A1 M .
Для
построения угла между прямыми A1 M
и
D1 N проведем прямую A1 P, A1 P D1 N .
Угол между скрещивающимися прямыми
и
равен углу между
A1 M
D1 N
пересекающимися прямыми A1 P и A1 M ,
тогда PA1 M .
Из прямоугольного треугольника A1 AM по
теореме
Пифагора
найдем
A1 M :
2
A1 M 2 AA12 AM 2 ,
a
A1 M 2 a 2 ,
2
a 5
5a 2
, A1 M
.
4
2
Из прямоугольного треугольника A1 AP по
A1 M 2
теореме
Пифагора
найдем
A1 P :
2
A1 P 2 AA12 AP 2 ,
A1 P 2
a
A1 P 2 a 2 ,
3
10a 2
a 10
, A1 P
.
9
3
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов.
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by).
РТ–2021/2022 гг. Этап III. Вариант 1
Тематическое консультирование по математике
27

28.

Раздел программы
вступительных
испытаний. Элемент
содержания
Содержание задания
Комментарий и решение задания
Учебное издание
Из прямоугольного треугольника MAP по
теореме
Пифагора
найдем
MP :
2
MP 2 AP 2 AM 2 ,
2
a a
MP 2 ,
3 2
13a 2
a 13
, MP
.
36
6
В треугольнике A1 PM по теореме косинусов:
MP 2
MP 2 A1P 2 A1M 2 2 A1P A1M cos ,
13a 2 10a 2 5a 2 5a 2 2
cos ,
36
9
4
3
6
cos
.
5 2
В11. Найдите произведение наименьшего целого
решения на количество всех целых решений
x2
неравенства 15 log 2
log 2 x 0
3 39
2
Уравнения и неравенства.
Решение
логарифмических
неравенств
Значение выражения 75 cos 2 равно 54.
Ответ: 54
Задание на проверку умения решать
логарифмические неравенства методом
замены переменной.
Решение:
Областью
определения
неравенства
2
x
является
15 log 2
log 2 x 0
3 39
2
промежуток 0; . С учетом области
Арефьева, И. Г. Алгебра : учеб. пособие для 11-го кл.
учреждений общ. сред. образования с рус. яз. обучения /
И. Г. Арефьева, О. Н. Пирютко. – Минск : Народная
асвета, 2020. – 270 с. : ил. (Гл. 3, § 10, с. 147–164)
определения преобразуем его к виду
Выполним
2 log 22 x 13log 2 x 15 0 1 .
замену переменной: t log 2 x, тогда
неравенство (1) можно записать в виде
Решим
полученное
2t 2 13t 15 0.
квадратное
неравенство.
Нулями
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов.
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by).
РТ–2021/2022 гг. Этап III. Вариант 1
Тематическое консультирование по математике
28

29.

Раздел программы
вступительных
испытаний. Элемент
содержания
Содержание задания
Комментарий и решение задания
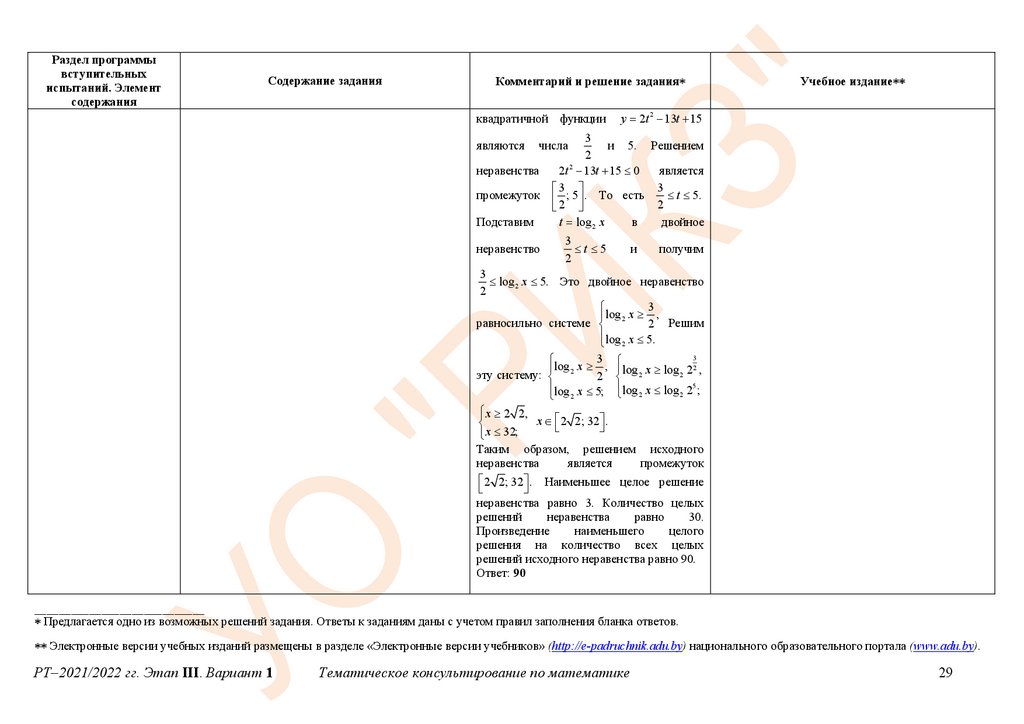
квадратичной функции
являются
Учебное издание
y 2t 2 13t 15
3
и 5. Решением
2
является
2t 2 13t 15 0
3
3
2 ; 5 . То есть 2 t 5.
в
двойное
t log 2 x
числа
неравенства
промежуток
Подставим
неравенство
3
t 5
2
и
получим
3
log 2 x 5. Это двойное неравенство
2
3
log 2 x ,
равносильно системе
2 Решим
log 2 x 5.
3
3
log 2 x , log 2 x log 2 2 2 ,
эту систему:
2
log 2 x 5; log 2 x log 2 25 ;
x 2 2,
x 2 2; 32 .
x 32;
Таким образом, решением исходного
неравенства
является
промежуток
2 2; 32 . Наименьшее целое решение
неравенства равно 3. Количество целых
решений
неравенства
равно
30.
Произведение
наименьшего
целого
решения на количество всех целых
решений исходного неравенства равно 90.
Ответ: 90
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов.
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by).
РТ–2021/2022 гг. Этап III. Вариант 1
Тематическое консультирование по математике
29

30.

Раздел программы
вступительных
испытаний. Элемент
содержания
Содержание задания
Комментарий и решение задания
Учебное издание
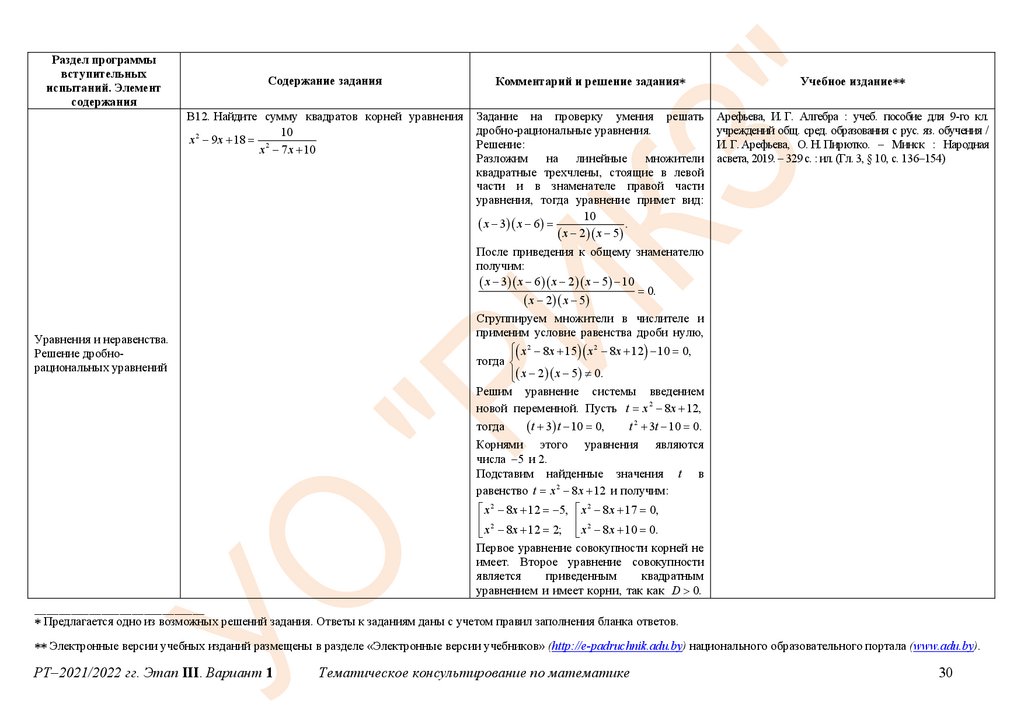
В12. Найдите сумму квадратов корней уравнения
10
x 2 9 x 18 2
x 7 x 10
Задание на проверку умения решать
дробно-рациональные уравнения.
Решение:
Разложим на
линейные множители
квадратные трехчлены, стоящие в левой
части и в знаменателе правой части
уравнения, тогда уравнение примет вид:
10
.
x 3 x 6
x 2 x 5
Арефьева, И. Г. Алгебра : учеб. пособие для 9-го кл.
учреждений общ. сред. образования с рус. яз. обучения /
И. Г. Арефьева, О. Н. Пирютко. – Минск : Народная
асвета, 2019. – 329 с. : ил. (Гл. 3, § 10, с. 136–154)
После приведения к общему знаменателю
получим:
x 3 x 6 x 2 x 5 10
0.
x 2 x 5
Уравнения и неравенства.
Решение дробнорациональных уравнений
Сгруппируем множители в числителе и
применим условие равенства дроби нулю,
x 2 8 x 15 x 2 8 x 12 10 0,
тогда
x 2 x 5 0.
Решим уравнение системы введением
новой переменной. Пусть t x 2 8 x 12,
тогда
t 3 t 10 0,
t 2 3t 10 0.
Корнями этого уравнения являются
числа 5 и 2.
Подставим найденные значения t в
равенство t x 2 8 x 12 и получим:
x 2 8 x 12 5, x 2 8 x 17 0,
2
2
x 8 x 12 2; x 8 x 10 0.
Первое уравнение совокупности корней не
имеет. Второе уравнение совокупности
является
приведенным
квадратным
уравнением и имеет корни, так как D 0.
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов.
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by).
РТ–2021/2022 гг. Этап III. Вариант 1
Тематическое консультирование по математике
30

31.

Раздел программы
вступительных
испытаний. Элемент
содержания
Содержание задания
Комментарий и решение задания
Учебное издание
Очевидно, что эти корни не равны 2 и 5.
По теореме Виета: x1 x2 8, x1 x2 10.
x12 x2 2 x1 x2 2 x1 x2 82 2 10
2
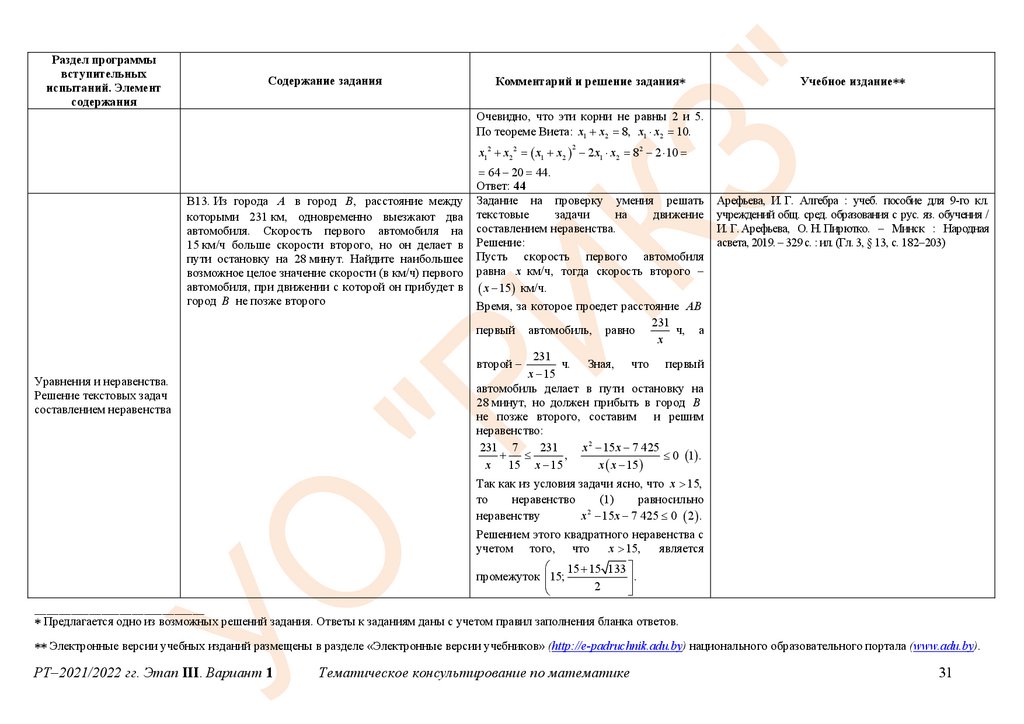
В13. Из города A в город B, расстояние между
которыми 231 км, одновременно выезжают два
автомобиля. Скорость первого автомобиля на
15 км/ч больше скорости второго, но он делает в
пути остановку на 28 минут. Найдите наибольшее
возможное целое значение скорости (в км/ч) первого
автомобиля, при движении с которой он прибудет в
город B не позже второго
Уравнения и неравенства.
Решение текстовых задач
составлением неравенства
64 20 44.
Ответ: 44
Задание на проверку умения решать
текстовые
задачи
на
движение
составлением неравенства.
Решение:
Пусть скорость первого автомобиля
равна x км/ч, тогда скорость второго –
x 15 км/ч.
Арефьева, И. Г. Алгебра : учеб. пособие для 9-го кл.
учреждений общ. сред. образования с рус. яз. обучения /
И. Г. Арефьева, О. Н. Пирютко. – Минск : Народная
асвета, 2019. – 329 с. : ил. (Гл. 3, § 13, с. 182–203)
Время, за которое проедет расстояние AB
231
первый автомобиль, равно
ч, а
x
231
второй –
ч. Зная, что первый
x 15
автомобиль делает в пути остановку на
28 минут, но должен прибыть в город B
не позже второго, составим и решим
неравенство:
231 7
231
x 2 15 x 7 425
,
0 1 .
x 15 x 15
x x 15
Так как из условия задачи ясно, что x 15,
то
неравенство
(1)
равносильно
неравенству
x 2 15 x 7 425 0 2 .
Решением этого квадратного неравенства с
учетом того, что
x 15,
является
15 15 133
промежуток 15;
.
2
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов.
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by).
РТ–2021/2022 гг. Этап III. Вариант 1
Тематическое консультирование по математике
31

32.

Раздел программы
вступительных
испытаний. Элемент
содержания
Содержание задания
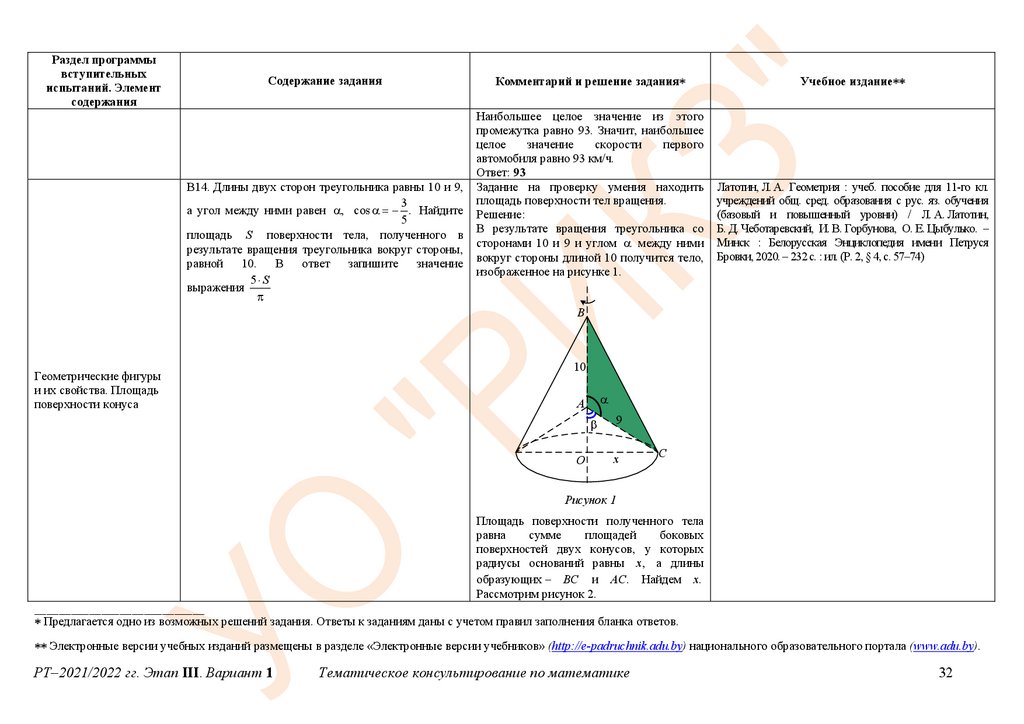
В14. Длины двух сторон треугольника равны 10 и 9,
3
а угол между ними равен , cos . Найдите
5
площадь S поверхности тела, полученного в
результате вращения треугольника вокруг стороны,
равной
10.
В
ответ
запишите
значение
5 S
выражения
Комментарий и решение задания
Наибольшее целое значение из этого
промежутка равно 93. Значит, наибольшее
целое
значение
скорости
первого
автомобиля равно 93 км/ч.
Ответ: 93
Задание на проверку умения находить
площадь поверхности тел вращения.
Решение:
В результате вращения треугольника со
сторонами 10 и 9 и углом между ними
вокруг стороны длиной 10 получится тело,
изображенное на рисунке 1.
Учебное издание
Латотин, Л. А. Геометрия : учеб. пособие для 11-го кл.
учреждений общ. сред. образования с рус. яз. обучения
(базовый и повышенный уровни) / Л. А. Латотин,
Б. Д. Чеботаревский, И. В. Горбунова, О. Е. Цыбулько. –
Минск : Белорусская Энциклопедия имени Петруся
Бровки, 2020. – 232 с. : ил. (Р. 2, § 4, с. 57–74)
B
Геометрические фигуры
и их свойства. Площадь
поверхности конуса
10
A
O
9
х
C
Рисунок 1
Площадь поверхности полученного тела
равна
сумме
площадей
боковых
поверхностей двух конусов, у которых
радиусы оснований равны x, а длины
образующих – BC и AC. Найдем x.
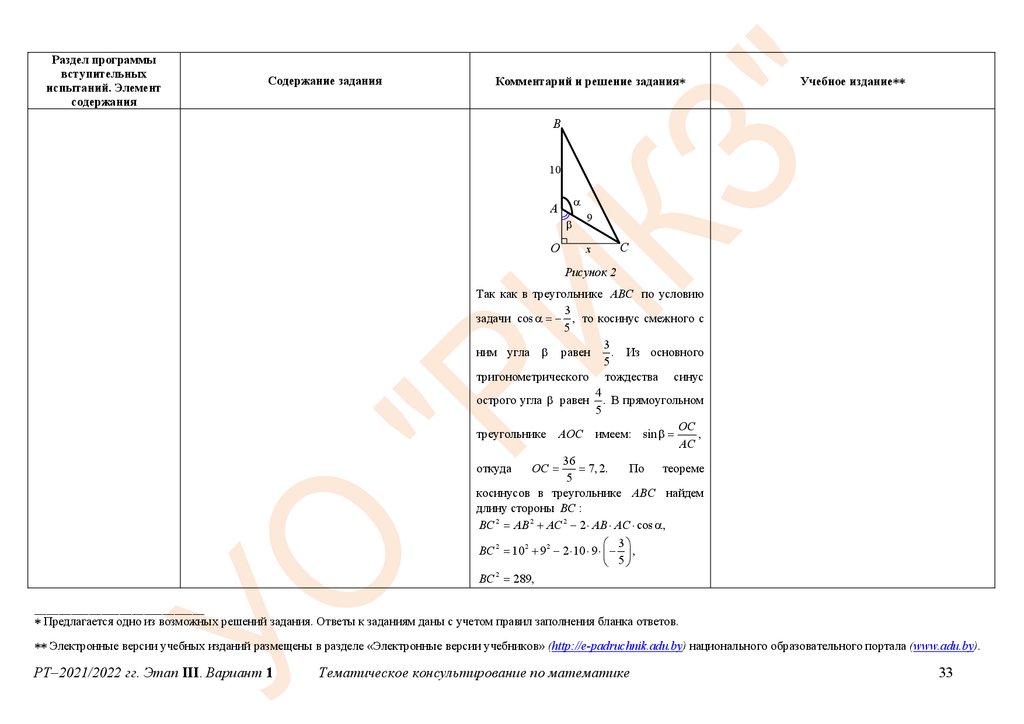
Рассмотрим рисунок 2.
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов.
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by).
РТ–2021/2022 гг. Этап III. Вариант 1
Тематическое консультирование по математике
32

33.

Раздел программы
вступительных
испытаний. Элемент
содержания
Содержание задания
Комментарий и решение задания
Учебное издание
B
10
А
O
9
x
C
Рисунок 2
Так как в треугольнике ABC по условию
3
задачи cos , то косинус смежного с
5
3
ним угла равен
. Из основного
5
тригонометрического тождества синус
4
острого угла равен . В прямоугольном
5
OC
треугольнике AOC имеем: sin
,
AC
36
откуда
OС
7, 2.
По
теореме
5
косинусов в треугольнике ABC найдем
длину стороны BC :
BC 2 AB 2 AC 2 2 AB AC cos ,
3
BC 2 102 92 2 10 9 ,
5
BC 2 289,
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов.
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by).
РТ–2021/2022 гг. Этап III. Вариант 1
Тематическое консультирование по математике
33

34.

Раздел программы
вступительных
испытаний. Элемент
содержания
Содержание задания
Комментарий и решение задания
Учебное издание
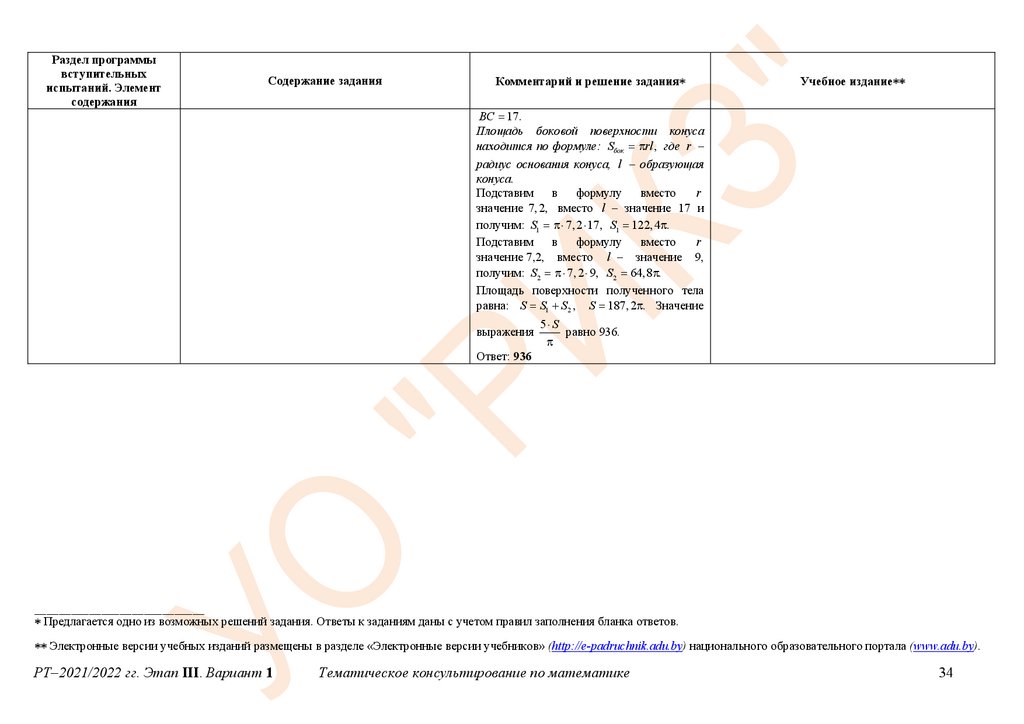
BC 17.
Площадь боковой поверхности конуса
находится по формуле: Sбок rl , где r –
радиус основания конуса, l – образующая
конуса.
Подставим
в
формулу
вместо
r
значение 7, 2, вместо l – значение 17 и
получим: S1 7, 2 17, S1 122, 4 .
Подставим
в
формулу
вместо
r
значение 7,2, вместо l – значение 9,
получим: S2 7, 2 9, S2 64,8 .
Площадь поверхности полученного тела
равна: S S1 S2 , S 187, 2 . Значение
выражения
5 S
равно 936.
Ответ: 936
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов.
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by).
РТ–2021/2022 гг. Этап III. Вариант 1
Тематическое консультирование по математике
34