Методы сортировки. Простые методы (часть 1)

1. Методы сортировки: часть1. Простые методы

Дисциплина : Численные методы и программирование
лектор
Шустрова Марина Леонидовна

2. Что такое массив?

Массив (в некоторых языках программирования также таблица, ряд,
матрица) — структура данных в виде набора компонентов (элементов
массива), расположенных в памяти непосредственно друг за другом.
Массивы могут быть
одномерными и многомерными,
могут содержать числовые, логические и символьные данные.
Характерной
их
особенностью
является принцип, в соответствии с
которым имя присваивается сразу
всех совокупности данных, при
этом обращение к конкретной
ячейке
массива
происходит
посредством
использования
индекса – порядкового номера
записи в общей совокупности
данных.

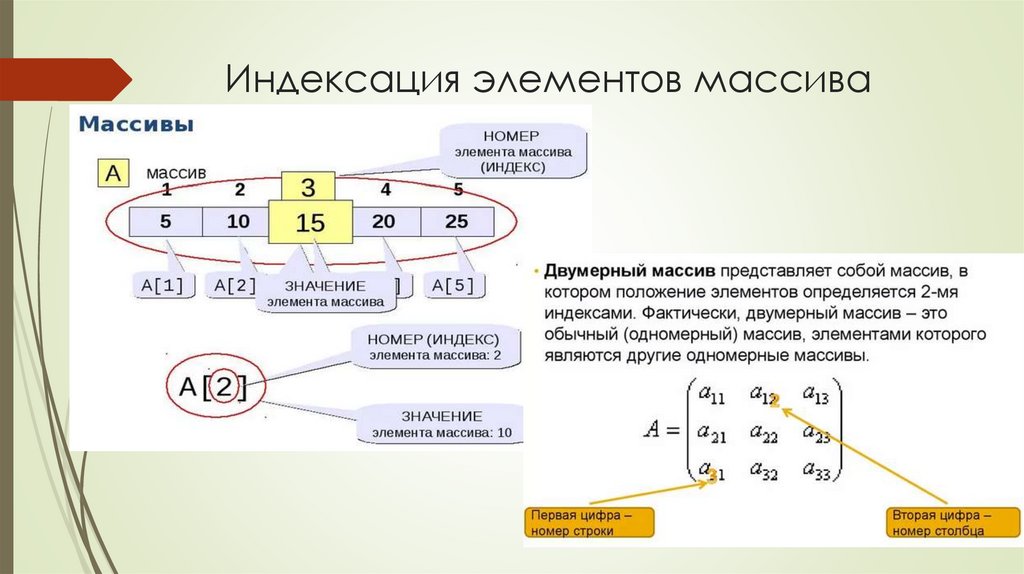
3. Индексация элементов массива

4. Сортировка

Сортировка – расположение информации в
определенном порядке (упорядочивание)
Чаще всего используются следующие виды
сортировки:
по алфавиту
по номеру
в хронологическом порядке

5. Алгоритм сортировки

Алгоритм сортировки — это алгоритм для упорядочивания элементов в
списке.
В случае, когда элемент списка имеет несколько полей, поле, служащее
критерием порядка, называется ключом сортировки.
На практике в качестве ключа часто выступает
число, а в остальных полях хранятся какиелибо данные, никак не влияющие на работу
алгоритма.
Мы будем рассматривать алгоритмы
сортировок на массивах числовых данных

6. Алгоритмы сортировки

В настоящее время разработано великое множество различных алгоритмов
сортировки. В данной лекции мы рассмотрим некоторые из них
Простые методы сортировки
Сортировка пузырьком
Эффективные методы сортировки
Быстрая сортировка
Шейкерная сортировка
Сортировка слиянием
Сортировка расческой
Пирамидальная сортировка
Сортировка чётно-нечётная
Простая сортировка
Сортировка вставками
Сортировка выбором

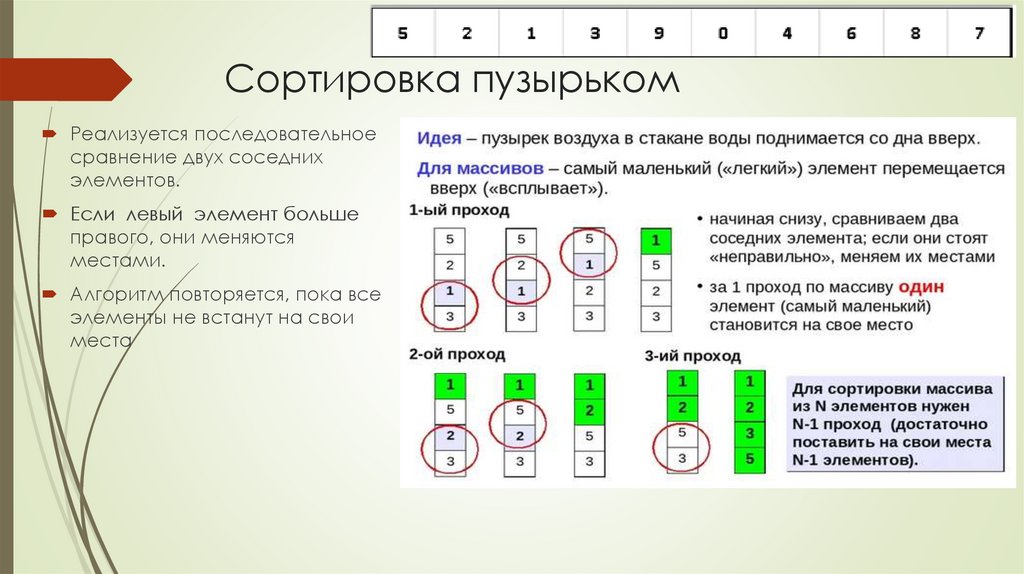
7. Сортировка пузырьком

Реализуется последовательное
сравнение двух соседних
элементов.
Если левый элемент больше
правого, они меняются
местами.
Алгоритм повторяется, пока все
элементы не встанут на свои
места

8. Причем здесь черепашки?

Помните сказку о Кролике и Черепахе? Она нам
сейчас пригодится.
Небольшая предыстория. В 1980 году Влодзимеж
Добосиевич пояснил, почему пузырьковая и
производные от неё сортировки работают так
медленно.
Это всё из-за черепашек. «Черепахи» —
небольшие по значению элементы, которые
находятся в конце списка. Поскольку алгоритм
подразумевает перенос больших элементов в
конец списка, они быстро находят свое место.
Небольшие элементы находят свое место
медленно, меняя свое положение на 1 позицию
в каждой итерации.
Как Вы, возможно, заметили пузырьковые
сортировки ориентированы на «кроликов» –
больших по значению элементов в начале
списка. Они довольно быстро перемещаются к
конце списка. А вот медлительные
пресмыкающиеся на старт ползут неохотно.

9. Шейкерная сортировка

Шейкерная сортировка работает немного быстрее, чем пузырьковая, поскольку
по массиву в нужных направлениях попеременно мигрируют и максимумы и
минимумы.
Шейкерная сортировка- Вариация сортировки пузырьком.
Также ее называют сортировка перемешиванием, она же коктейльная сортировка.
Начинается процесс как в «пузырьке»: максимум перемещается в конец массива.
После этого идём в обратную сторону, при этом уже перенося в начало не максимум, а
минимум.
Отсортировав в массиве первый и последний элементы, снова делаем разворачиваемся,
и т.д.. Заканчиваем процесс, оказавшись в середине списка.

10. Чётно-нечётная сортировка

Тоже вариация «Пузырька»
Идея планомерного обхода слева-направо, но только
сделаем шире шаг.
На первом проходе элементы с нечётным ключом
сравниваем с соседями на чётных местах (1-й сравниваем
со 2-м, затем 3-й с 4-м, 5-й с 6-м и так далее).
Затем наоборот – «чётные по счёту» элементы
сравниваем/меняем с «нечётными». Затем снова «нечёт-чёт»,
потом опять «чёт-нечет».
Процесс останавливается тогда, когда после подряд двух
проходов по массиву («нечётно-чётному» и «чётно-нечётному»)
не произошло ни одного обмена.

11. Сортировка расчёской

Её идея состоит в том, чтобы «устранить» элементы с небольшими
значения в конце массива, которые замедляют работу алгоритма.
В «пузырьке», «шейкере» и «чёт-нечете» при переборе массива
сравниваются соседние элементы.
Основная идея «расчёски» в том, чтобы первоначально брать
достаточно большое расстояние между сравниваемыми
элементами и по мере упорядочивания массива сужать это
расстояние вплоть до минимального. Таким образом, мы как бы
причёсываем массив, постепенно разглаживая на всё более
аккуратные пряди.
Первоначальный разрыв нужно выбирать не случайным образом, а
с учётом специальной величины — фактора уменьшения,
оптимальное значение которого равно 1,247.
Сначала расстояние между элементами будет равняться размеру
массива, поделённому на 1,247; на каждом последующем шаге
расстояние будет снова делиться на фактор уменьшения — и так до
окончания работы алгоритма или пока разность индексов не
достигнет единицы. В этом случае массив досортировывается
обычным пузырьком.

12. Сортировка расчёской: расчет

Допустим, длина массива -10 элементов
Тогда 10: 1,247=
8,0192461908580593424218123496391
Значит, в первом проходе цикла расстояние = 8
Сравниваем 1 и 9 элементы, 2 и 10
2 проход 8:1,247= 6,415396952686447473937
Расстояние возьмем 6
Сравниваем и меняем местами1 и 7, 2 и 8 и тд
3 проход 6:1,247= 4,811547714514
Берем 5
Сравниваем 1 и 6, 2 и 7 и тд
4 проход 5:1,247= 4,0096230
Берем 4
Сравниваем 1 и 5, 2 и 6….
5 проход:
4:1,247=3,2
Берем 3
6 проход 2
7 проход 1
8 - Контрольный проход – все
на местах?

13. Сортировка вставками

При сортировке вставками массив постепенно перебирается слева
направо. При этом каждый последующий элемент размещается так,
чтобы он оказался между ближайшими элементами с минимальным и
максимальным значением.
Элементарный пример:
в магазине вам дали сдачу 550 рублей- одна купюра 500, другая 50.
Заглядываете в кошелек, а там купюры достоинством 10, 100, 1000. Вы
вставляете купюру достоинсвом 50р. между купюрами достоинством
10р и 100р, а купюру в 500 рублей между купюрами 100р и 1000р.
Получается 10, 50, 100, 500, 1000 –
Таким образом с каждым шагом алгоритма, вам необходимо
отсортировать подмассив данных и вставить значение в нужное место.

14. Сортировка выбором: по минимальному значению

Является одним из самых простых алгоритмов сортировки массива. Смысл в том,
чтобы идти по массиву и каждый раз искать минимальный элемент массива,
обменивая его с начальным элементом неотсортированной части массива. На
небольших массивах может оказаться даже эффективнее, чем более сложные
алгоритмы сортировки, но в любом случае проигрывает на больших массивах.
Число обменов элементов по сравнению с "пузырьковым" алгоритмом N/2, где N число элементов массива.
Алгоритм:
1. Находим минимальный элемент в массиве.
2. Меняем местами минимальный и первый элемент местами.
3. Опять ищем минимальный элемент в неотсортированной части массива
4. Меняем местами уже второй элемент массива и минимальный найденный,
потому как первый элемент массива является отсортированной частью.
5. Ищем минимальные значения и меняем местами элементы, пока массив не
будет отсортирован до конца.
https://habr.com/ru/post/422085/

15. Сортировка выбором: по максимальному значению

Аналогично предыдущему методу, но массив сортируется с
конца – с наибольших элементов
Число обменов элементов алгоритмом N/2, где N - число
элементов массива.

16. Модификации сортировки выбором: двухсторонняя сортировка выбором Double selection sort

Проходя по неотсортированной части массива, мы кроме максимума также попутно находим
и минимум.
Минимум ставим на первое место, максимум на последнее. Таким образом,
неотсортированная часть при каждой итерации уменьшается сразу на два элемента.
На первый взгляд кажется, что это ускоряет алгоритм в 2 раза — после каждого прохода
неотсортированный подмассив уменьшается не с одной, а сразу с двух сторон. Но при этом в
2 раза увеличилось количество сравнений, а число свопов осталось неизменным. Двойной
выбор лишь незначительно увеличивает скорость алгоритма, а на некоторых языках даже
почему-то работает медленнее.

17. Модификации сортировка выбором: Бинго - сортировка

В неупорядоченной части запоминается не только максимальный
элемент, но и определяется максимум для следующей итерации.
Это позволяет при повторяющихся максимумах не искать их заново
каждый раз, а ставить на своё место сразу как только этот
максимум в очередной раз встретили в массиве.
Алгоритмическая сложность осталась та же. Но если массив
состоит из повторяющихся чисел, то бинго-сортировка справится в
десятки раз быстрее, чем обычная сортировка выбором.

18. Отличие сортировок выбором от сортировок вставками

Главное отличие: в сортировке вставками мы
извлекаем из неотсортированной части массива
любой элемент и вставляем его на своё место в
отсортированной части.
В сортировке выбором мы целенаправленно ищем
максимальный элемент (или минимальный), которым
дополняем отсортированную часть массива. Во
вставках мы ищем куда вставить очередной элемент,
а в выборе — мы заранее уже знаем в какое место
поставим, но при этом требуется найти элемент,
этому месту соответствующий.

19. Гномья сортировка

Гномья сортировка (англ. Gnome sort) —
алгоритм сортировки, похожий на сортировку
вставками, но в отличие от последней перед
вставкой на нужное место происходит серия
обменов, как в сортировке пузырьком.
Название происходит от предполагаемого
поведения садовых гномов при сортировке
линии садовых горшков.
По существу он смотрит на текущий и
предыдущий садовые горшки: если они в
правильном порядке, он шагает на один горшок
вперёд, иначе он меняет их местами и шагает
на один горшок назад. Граничные условия: если
нет предыдущего горшка, он шагает вперёд;
если нет следующего горшка, он закончил.

20. Гномья сортировка

Алгоритм концептуально простой, не требует
вложенных циклов. Время работы O ( n 2 )
На практике алгоритм может работать так же
быстро, как и сортировка вставками.
Алгоритм находит первое место, где два
соседних элемента стоят в неправильном
порядке и меняет их местами.
Он пользуется тем фактом, что обмен может
породить новую пару, стоящую в неправильном
порядке, только до или после переставленных
элементов. Он не допускает, что элементы
после текущей позиции отсортированы, таким
образом, нужно только проверить позицию до
переставленных элементов.

21. Гномья сортировка

Пример:
Если мы хотим отсортировать массив с элементами [4] [2] [7] [3] от
большего к меньшему, то на итерациях цикла while будет
происходить следующее:
[4] [2] [7] [3] (начальное состояние: i == 1, j == 2);
[4] [2] [7] [3] (ничего не произошло, но сейчас i == 2, j == 3);
[4] [7] [2] [3] (обмен a[2] и a[1], сейчас i == 1, а j == 3 по-прежнему);
[7] [4] [2] [3] (обмен a[1] и a[0], сейчас i == 3, j == 4);
[7] [4] [3] [2] (обмен a[3] и a[2], сейчас i == 2, j == 4);
[7] [4] [3] [2] (ничего не произошло, но сейчас i == 4, j == 5);
цикл закончился, т. к. i не < 4.

22. Так ЧТО ЖЕ БЫСТРЕЕ?

Интересной особенностью сортировки выбором является независимость скорости от
характера сортируемых данных.
Например, если массив почти отсортирован, то, как известно, сортировка вставками его
обработает гораздо быстрее (даже быстрее чем быстрая сортировка). А реверсно
упорядоченный массив для сортировки вставками является вырожденным случаем, она
будет его сортировать максимально долго.
А для сортировки выбором частичная или реверсная упорядоченность массива роли не
играет — она обработает его примерно с той же скоростью что и обычный рандом. Также
для классической сортировки выбором неважно, состоит ли массив из уникальных или
повторяющихся элементов — на скорость это практически не влияет.
А бинго-сортировка учитывает, если массив состоит из повторяющихся элементов. если
массив состоит из повторяющихся чисел, то бинго-сортировка справится в десятки раз
быстрее, чем обычная сортировка выбором.

23. Место для вашего метода или пара слов о дополнительном задании

Что в него входит и как оформлять?
Делаем презентацию, в которой есть обязательно
Титульный лист с указанием автора работы
Описание метода. Прекрасно, если оно дополнено историей его разработки или какими –
то интересными фактами о его применении. Если информации много – разносим на
несколько слайдов
Логика работы метода + gif –иллюстрация его работы
Характеристика быстродействия метода
Список источников, использованных при подготовке материала
Желательно:
Блок-схема
Собственный опыт реализации метода. Если решите сами протестировать – было бы
интересно послушать
Ссылки на видео о методе