Структуры данных. Примеры реализации на С++ для АСУб и ЭВМб. Тема 6-3

1.

Тема 6-3.
Структуры данных
Примеры реализации на С++
для АСУб и ЭВМб

2. Темы лекции

3. Абстрактные типы данных

• Абстрактный тип данных описывает, какие
данные хранятся и какие операции должны
выполняться
• Абстрактный тип данных – это спецификация
или модель для группы значений/данных и
операций с этими значениями
• Какие АТД использовать зависит от задач,
решаемых в разрабатываемом приложении
– Каждый АТД имеет свои плюсы и минусы

4. Абстрактные типы данных: выбор

• Будете ли вы часто искать данные?
• Будут ли данные добавляться часто?
• Будут ли данные изменяться или
удаляться часто?
• Данные будут добавляться небольшими
или большими частями?
• Данные будут иметь однородную или
неоднородную структуру?

5. Абстрактные типы данных: выбор

https://metanit.com/sharp/algoritm/1.1.php
Добавление
https://habr.com/ru/post/444594/
Поиск
Удаление
Изменение, Доступ и т.п.
АТД:
• предметные данные
• служебные данные

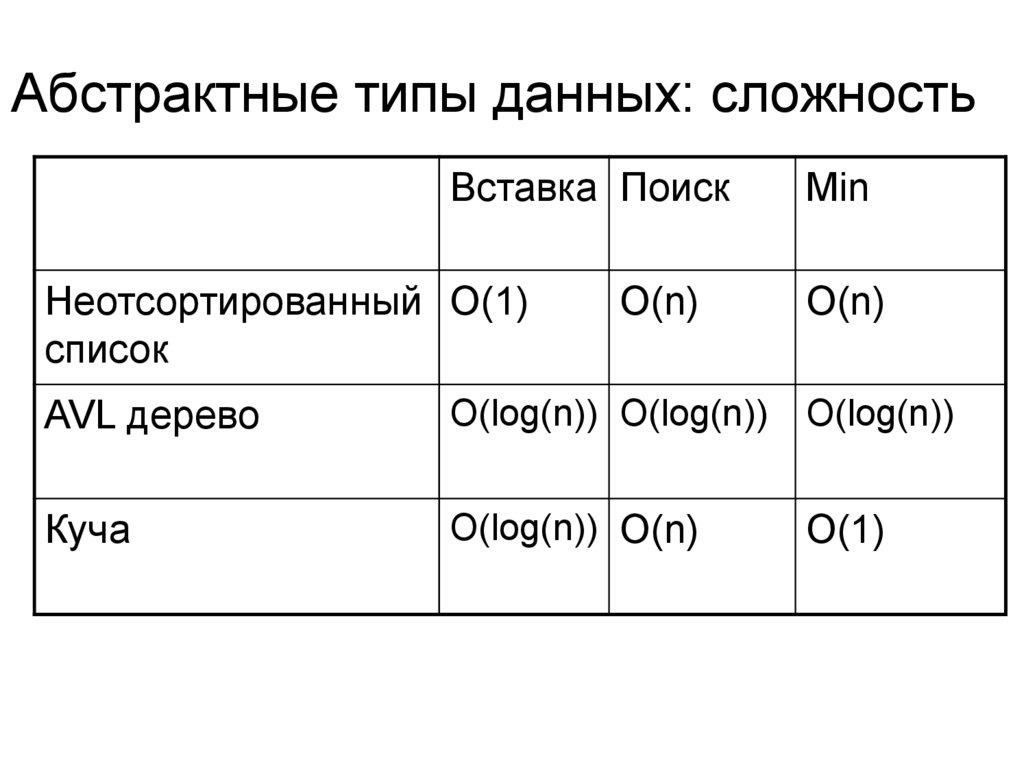
6. Абстрактные типы данных: сложность

Вставка Поиск
Неотсортированный O(1)
список
O(n)
Min
O(n)
AVL дерево
O(log(n)) O(log(n))
O(log(n))
Куча
O(log(n)) O(n)
O(1)

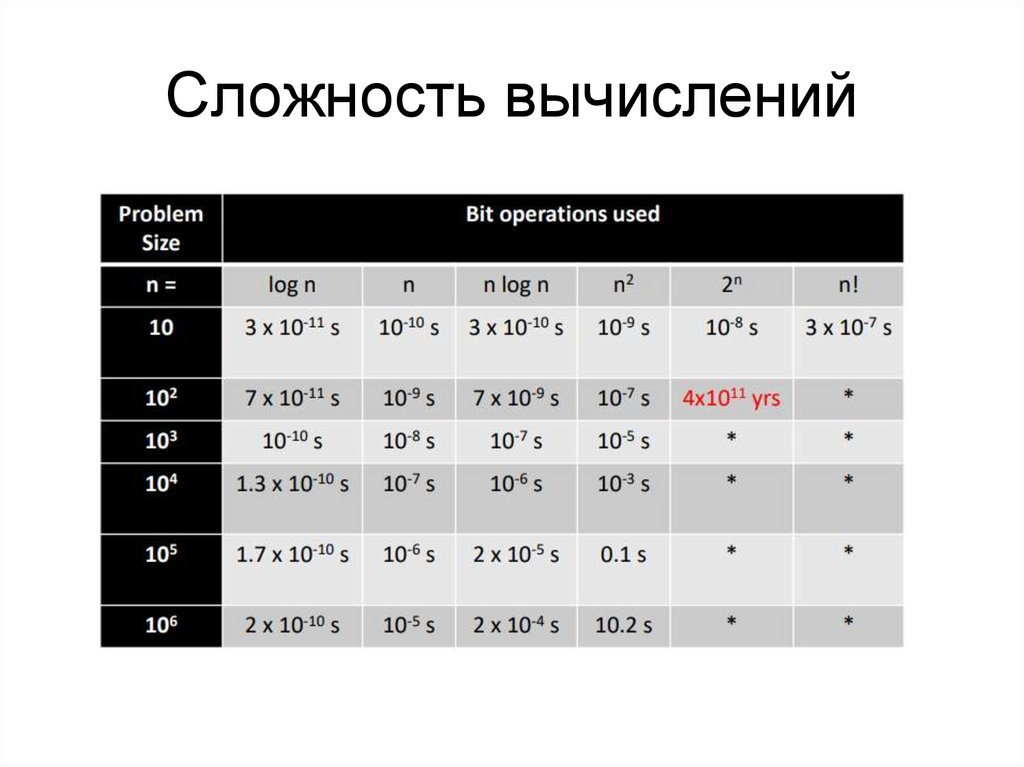
7. Сложность вычислений

8.

9.

Структуры данных
• Основные структуры данных, существующие в
языке Си ++ — это переменные, массивы,
структуры, перечисления. Из них можно
образовывать сложные структуры.
• Переменные, массивы, структуры, перечисления
при объявлении получают имя и тип, для их
хранения выделяется область оперативной
памяти, в которую можно записывать некоторые
значения.
• Данные объекты имеют неизменяемую
(статическую) структуру.

10.

Структуры данных
Существует, достаточно, много задач, в которых
требуются данные с более сложной (динамической)
структурой.
Для такой структуры характерно, что в процессе
вычислений изменяются не только значения
объектов, но и структура хранения информации.
Такие объекты называются динамическими
информационными структурами.
Компоненты, данных структур, на некотором уровне
детализации представляют собой объекты со
статической структурой, то есть они принадлежат к
одному из основных типов данных.

11.

12.

13.

Связные списки
Связный список является простейшим типом данных
динамической структуры, состоящей из элементов (узлов).
Каждый узел включает в себя в классическом варианте два поля:
• данные (в качестве данных может выступать переменная,
объект класса или структуры и т. д.)
• указатель на следующий узел в списке.
Элементы связанного списка можно помещать и исключать
произвольным образом.

14.

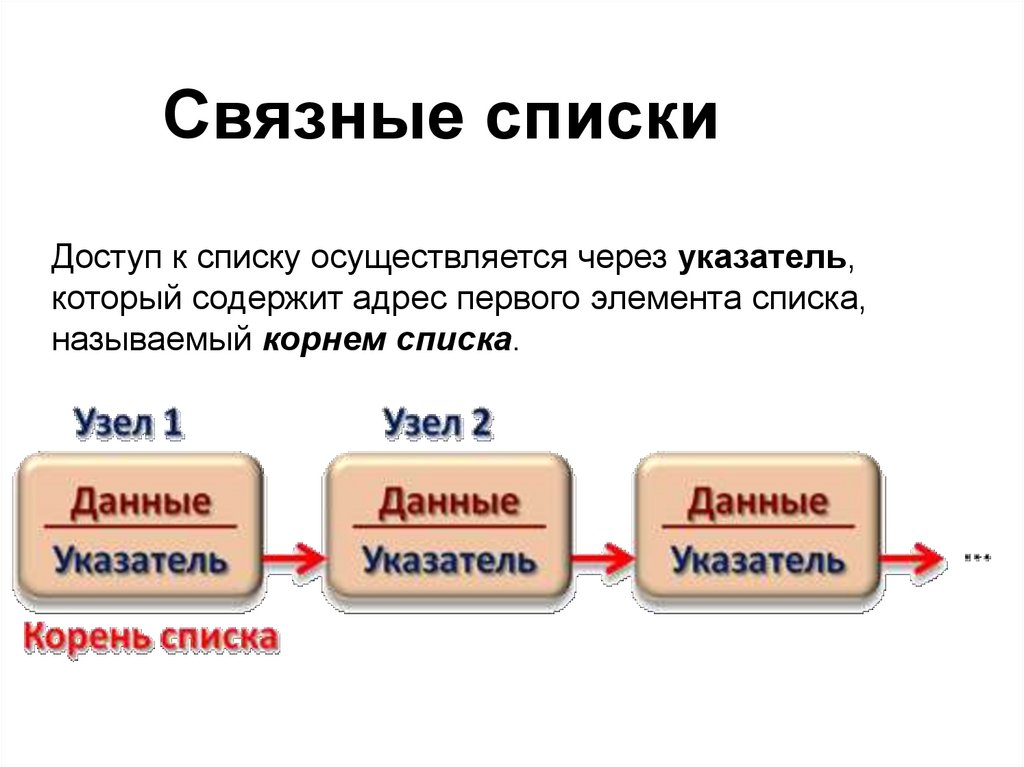
Связные списки
Доступ к списку осуществляется через указатель,
который содержит адрес первого элемента списка,
называемый корнем списка.

15.

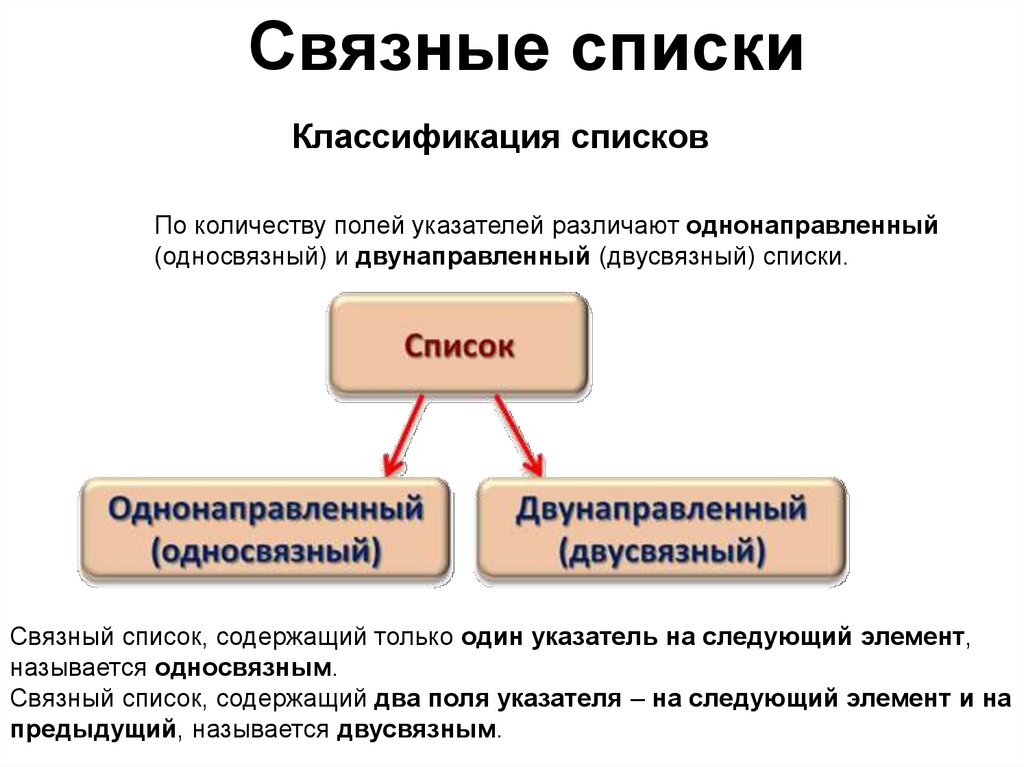
Связные списки
Классификация списков
По количеству полей указателей различают однонаправленный
(односвязный) и двунаправленный (двусвязный) списки.
Связный список, содержащий только один указатель на следующий элемент,
называется односвязным.
Связный список, содержащий два поля указателя – на следующий элемент и на
предыдущий, называется двусвязным.

16.

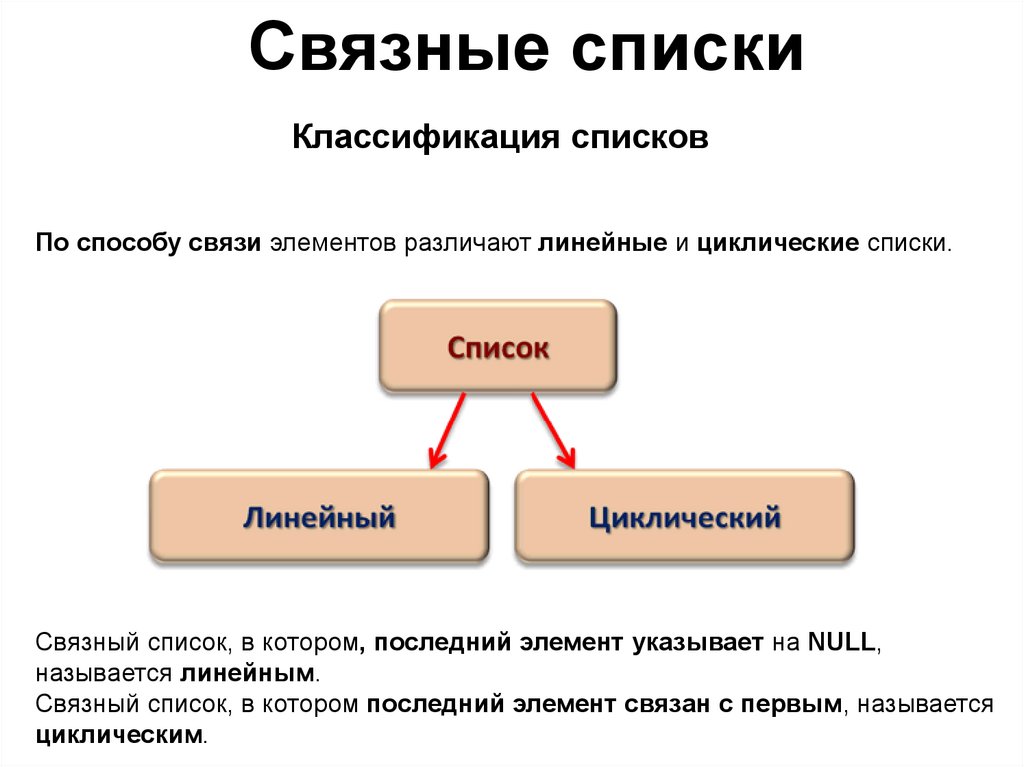
Связные списки
Классификация списков
По способу связи элементов различают линейные и циклические списки.
Связный список, в котором, последний элемент указывает на NULL,
называется линейным.
Связный список, в котором последний элемент связан с первым, называется
циклическим.

17.

Связные списки
Виды списков
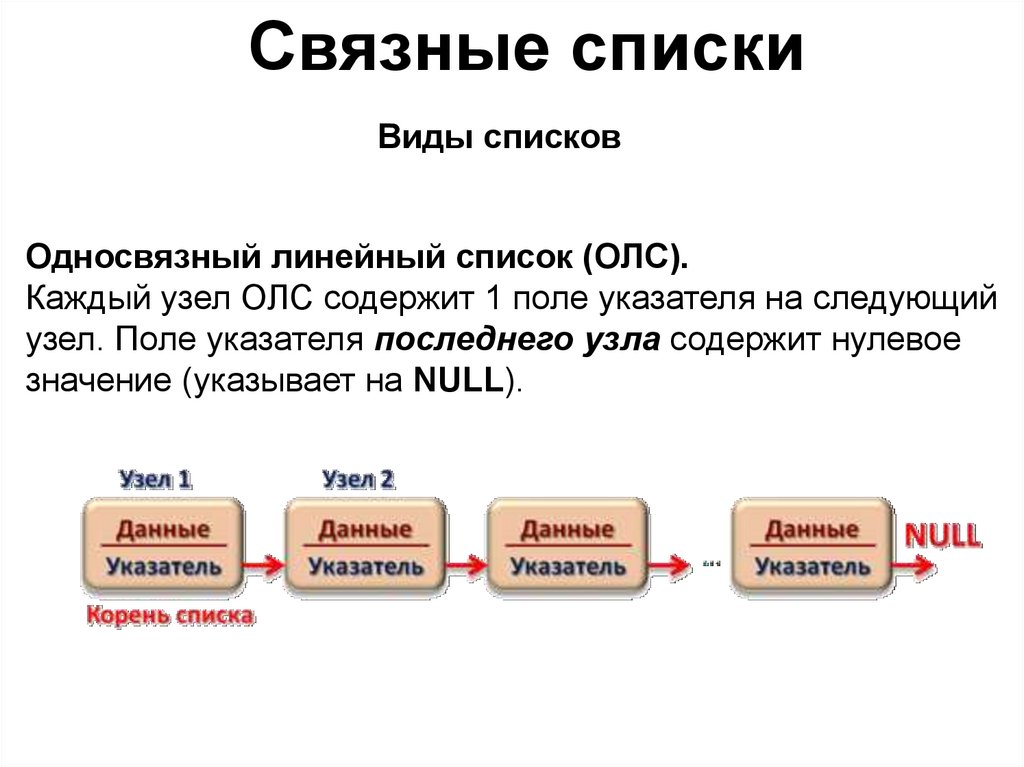
Односвязный линейный список (ОЛС).
Каждый узел ОЛС содержит 1 поле указателя на следующий
узел. Поле указателя последнего узла содержит нулевое
значение (указывает на NULL).

18.

Связные списки
Виды списков
Односвязный циклический список (ОЦС).
Каждый узел ОЦС содержит 1 поле указателя на следующий узел. Поле
указателя последнего узла содержит адрес первого узла (корня списка).

19.

Связные списки
Виды списков
Двусвязный линейный список (ДЛС).
Каждый узел ДЛС содержит два поля указателей: на следующий и на
предыдущий узел. Поле указателя на следующий узел последнего узла
содержит нулевое значение (указывает на NULL). Поле указателя на
предыдущий узел первого узла (корня списка) также содержит нулевое
значение (указывает на NULL).

20.

Связные списки
Виды списков
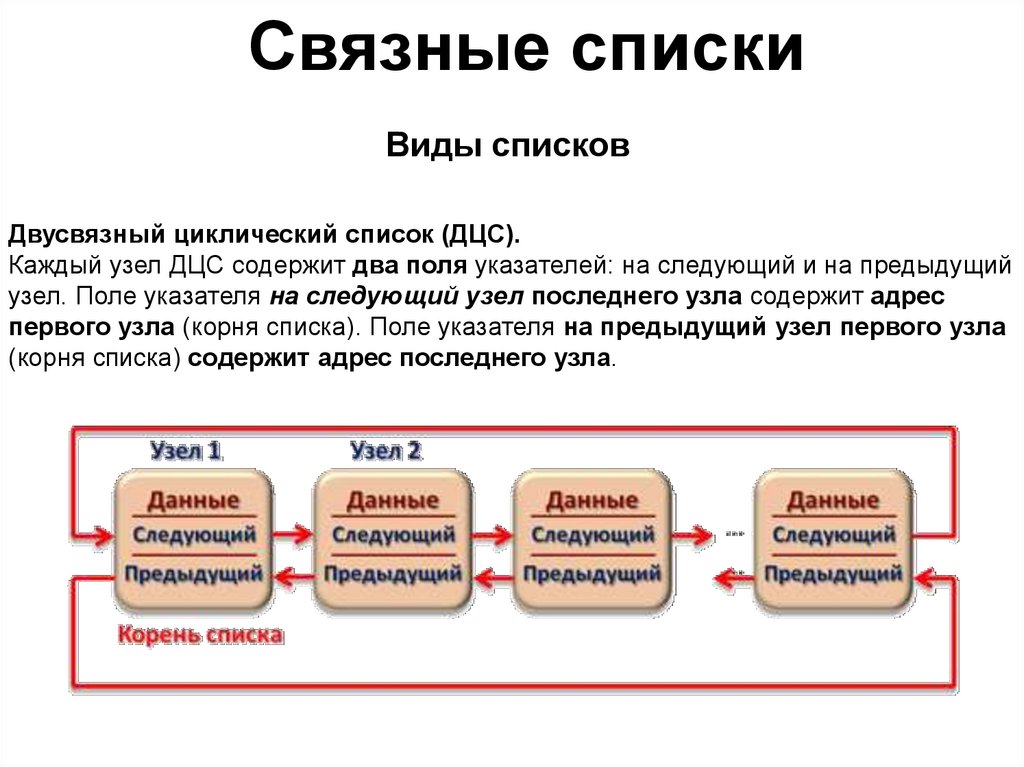
Двусвязный циклический список (ДЦС).
Каждый узел ДЦС содержит два поля указателей: на следующий и на предыдущий
узел. Поле указателя на следующий узел последнего узла содержит адрес
первого узла (корня списка). Поле указателя на предыдущий узел первого узла
(корня списка) содержит адрес последнего узла.

21.

Связные списки
Сравнение массивов и связных списков
Массив
Список
Выделение памяти осуществляется
единовременно под весь массив до
начала его использования
Выделение памяти осуществляется по
мере ввода новых элементов
При удалении/добавлении элемента
требуется копирование всех
последующих элементов для
осуществления их сдвига
Удаление/добавление элемента
осуществляется переустановкой
указателей, при этом сами данные не
копируются
Для хранения элемента требуется объем
Для хранения элемента требуется объем
памяти, достаточный для хранения
памяти, необходимый только для
данных этого элемента и указателей (1
хранения данных этого элемента
или 2) на другие элементы списка
Доступ к элементам может
Возможен только последовательный
осуществляться в произвольном порядке доступ к элементам

22.

Односвязный линейный
список
Каждый узел однонаправленного (односвязного) линейного списка (ОЛС)
содержит одно поле указателя на следующий узел. Поле указателя
последнего узла содержит нулевое значение (указывает на NULL).

23.

Односвязный линейный
список
Узел ОЛС можно представить в виде структуры
struct list
{
int field; // поле данных
struct list *ptr; // указатель на следующий элемент
};

24.

Односвязный линейный
список
Основные действия, производимые над
элементами ОЛС:
Инициализация списка
Добавление узла в список
Удаление узла из списка
Удаление корня списка
Вывод элементов списка
Взаимообмен двух узлов списка

25.

Односвязный линейный
список
Инициализация ОЛС
Инициализация списка предназначена
для создания корневого узла списка,
у которого поле указателя на следующий
элемент содержит нулевое значение.

26.

Односвязный линейный
список
Инициализация ОЛС
list * init(int a) // а- значение первого узла
{
struct list *lst;
// выделение памяти под корень списка
lst = new list;
lst->field = a;
lst->ptr = NULL; // это последний узел списка
return(lst);
}

27.

Односвязный линейный
список
Добавление узла в ОЛС
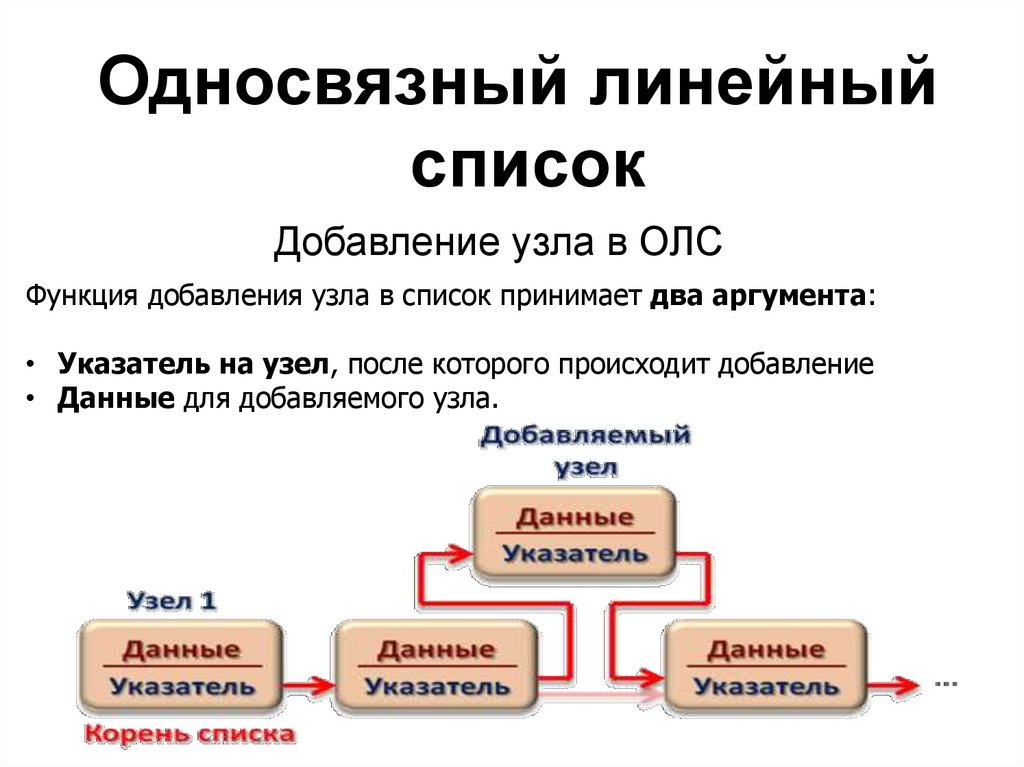
Функция добавления узла в список принимает два аргумента:
• Указатель на узел, после которого происходит добавление
• Данные для добавляемого узла.

28.

Односвязный линейный
список
Добавление узла в ОЛС
Добавление узла в ОЛС включает в себя следующие
этапы:
• создание добавляемого узла и заполнение его
поля данных;
• переустановка указателя узла,
предшествующего добавляемому, на добавляемый
узел;
• установка указателя добавляемого узла на
следующий узел (тот, на который указывал
предшествующий узел).

29.

Односвязный линейный
список
Добавление узла в ОЛС
struct list * addelem(list *lst, int number)
{
struct list *temp, *p;
temp = (struct list*)malloc(sizeof(list));
p = lst->ptr; // сохранение указателя на следующий узел
lst->ptr = temp; // предыдущий узел указывает на
создаваемый
temp->field = number; // сохранение поля данных
добавляемого узла
temp->ptr = p; // созданный узел указывает на следующий
элемент
return(temp);
}

30.

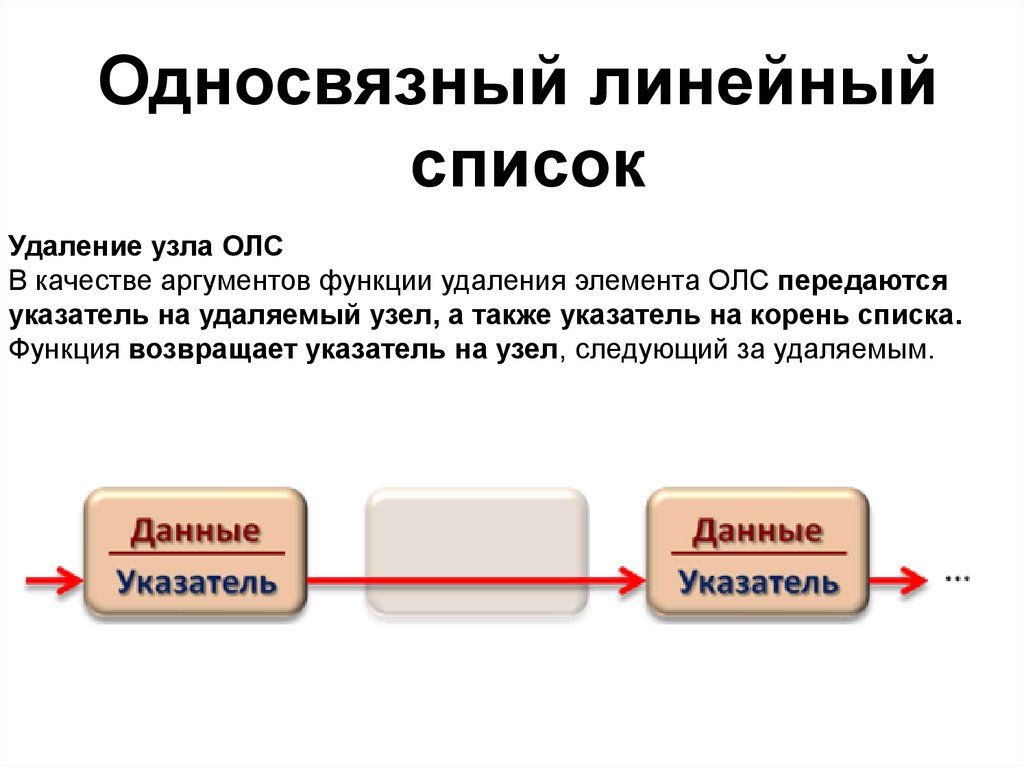
Односвязный линейный
список
Удаление узла ОЛС
В качестве аргументов функции удаления элемента ОЛС передаются
указатель на удаляемый узел, а также указатель на корень списка.
Функция возвращает указатель на узел, следующий за удаляемым.

31.

Односвязный линейный
список
Удаление узла ОЛС
Удаление узла ОЛС включает в себя следующие
этапы:
• установка указателя предыдущего узла на
узел, следующий за удаляемым;
• освобождение памяти удаляемого узла.

32.

Односвязный линейный
список Удаление узла ОЛС
struct list * deletelem(list *lst, list *root)
{
struct list *temp;
temp = root;
while (temp->ptr != lst) // просматриваем список начиная с
корня
{ // пока не найдем узел, предшествующий lst
temp = temp->ptr;
}
temp->ptr = lst->ptr; // переставляем указатель
free(lst); // освобождаем память удаляемого узла
return(temp);
}

33.

Односвязный линейный
список
Удаление корня списка
Функция удаления корня списка в качестве
аргумента получает указатель на текущий корень
списка.
Возвращаемым значением будет новый корень
списка — тот узел, на который указывает
удаляемый корень.

34.

Односвязный линейный
список
Удаление корня списка
struct list * deletehead(list *root)
{
struct list *temp;
temp = root->ptr;
free(root); // освобождение памяти текущего корня
return(temp); // новый корень списка
}

35.

Односвязный линейный
список
Вывод элементов списка
В качестве аргумента в функцию вывода элементов передается указатель на
корень списка.
Функция осуществляет последовательный обход всех узлов с выводом их
значений.
void listprint(list *lst)
{
struct list *p;
p = lst;
do {
printf("%d ", p->field); // вывод значения элемента p
p = p->ptr; // переход к следующему узлу
} while (p != NULL);
}

36.

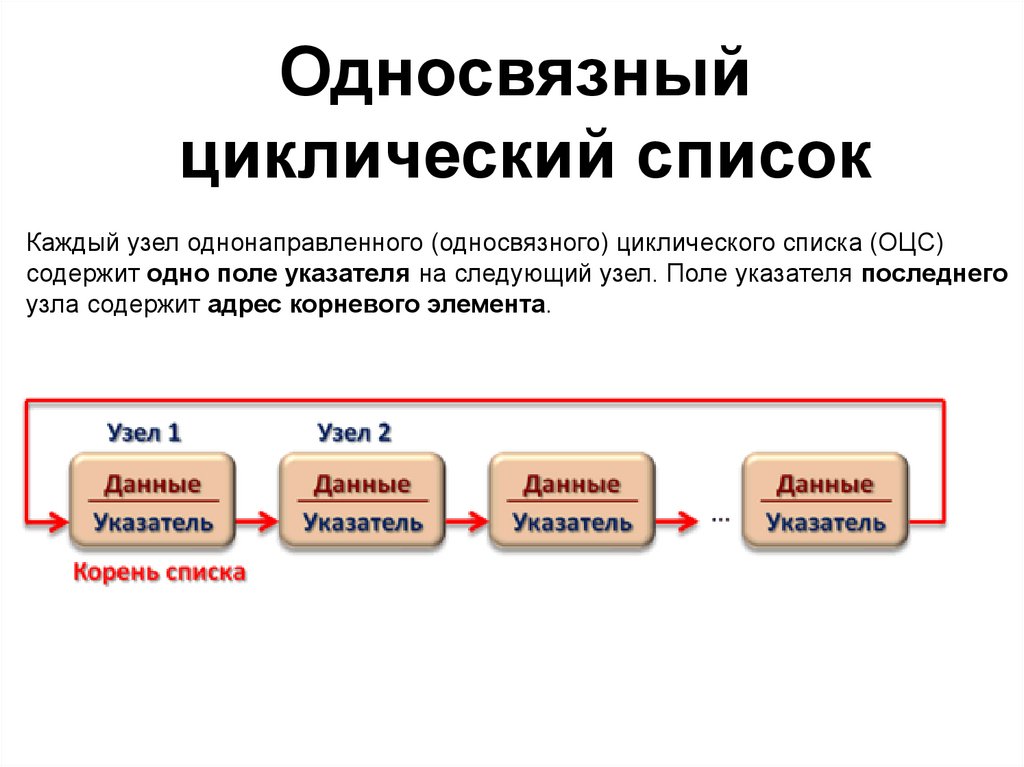
Односвязный
циклический список
Каждый узел однонаправленного (односвязного) циклического списка (ОЦС)
содержит одно поле указателя на следующий узел. Поле указателя последнего
узла содержит адрес корневого элемента.

37.

Односвязный
циклический список
Узел ОЦС можно представить в виде структуры,
аналогичной односвязному линейному списку
struct list
{
int field; // поле данных
struct list *ptr; // указатель на следующий элемент
};

38.

Односвязный
циклический список
Основные действия, производимые над
элементами ОЦС:
• Инициализация списка
• Добавление узла в список
• Удаление узла из списка
• Вывод элементов списка
• Взаимообмен двух узлов списка
Поскольку список является циклическим, реализация
отдельной функции для удаления корня списка не требуется.

39.

Односвязный
циклический список
Инициализация ОЦС
Инициализация списка предназначена для создания
корневого узла списка, у которого поле указателя
на следующий элемент содержит адрес самого
корневого элемента.

40.

Односвязный
циклический список
Инициализация ОЦС
struct list * init(int a) // а- значение первого узла
{
struct list *lst;
// выделение памяти под корень списка
lst = (struct list*)malloc(sizeof(struct list));
lst->field = a;
lst->ptr = lst; // указатель на сам корневой узел
return(lst);
}

41.

Односвязный
циклический список
Добавление узла в ОЦС
Функция добавления узла в список принимает два аргумента:
• Указатель на элемент, после которого происходит добавление
• Данные для добавляемого элемента.

42.

Односвязный
циклический список
Добавление элемента в ОЦС включает в себя
следующие этапы:
• создание добавляемого узла и заполнение его
поля данных;
• переустановка указателя узла,
предшествующего добавляемому, на добавляемый
узел;
• установка указателя добавляемого узла на
следующий узел (тот, на который указывал
предшествующий узел).

43.

Односвязный
циклический список
struct list * addelem(list *lst, int number)
{
struct list *temp, *p;
temp = (struct list*)malloc(sizeof(list));
p = lst->ptr; // сохранение указателя на следующий элемент
lst->ptr = temp; // предыдущий узел указывает на
создаваемый
temp->field = number; // сохранение поля данных
добавляемого узла
temp->ptr = p; // созданный узел указывает на следующий
элемент
return(temp);
}

44.

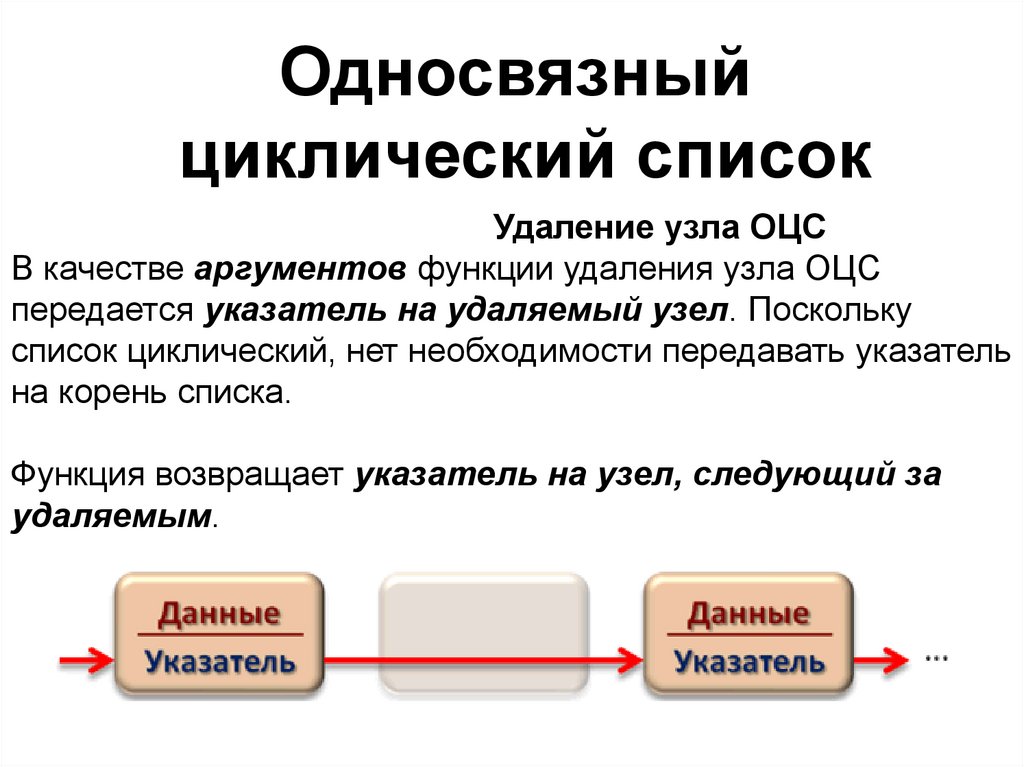
Односвязный
циклический список
Удаление узла ОЦС
В качестве аргументов функции удаления узла ОЦС
передается указатель на удаляемый узел. Поскольку
список циклический, нет необходимости передавать указатель
на корень списка.
Функция возвращает указатель на узел, следующий за
удаляемым.

45.

Односвязный
циклический список
Удаление узла ОЦС включает в себя следующие
этапы:
• установка указателя предыдущего узла на
узел, следующий за удаляемым;
• освобождение памяти удаляемого узла.

46.

Односвязный
циклический список
Удаление узла ОЦС
struct list * deletelem(list *lst)
{
struct list *temp;
temp = lst;
while (temp->ptr != lst) // просматриваем список начиная с
корня
{ // пока не найдем узел, предшествующий lst
temp = temp->ptr;
}
temp->ptr = lst->ptr; // переставляем указатель
free(lst); // освобождаем память удаляемого узла
return(temp);
}

47.

Односвязный
циклический список
Вывод элементов ОЦС
Функция вывода элементов ОЦС аналогична
функции для ОЛС за исключением условия
окончания обхода элементов.
В качестве аргумента в функцию вывода
элементов передается указатель на корень
списка.
Функция осуществляет последовательный обход
всех узлов с выводом их значений.

48.

Односвязный
циклический список
Вывод элементов ОЦС
void listprint(list *lst)
{
struct list *p;
p = lst;
do {
printf("%d ", p->field); // вывод значения узла p
p = p->ptr; // переход к следующему узлу
} while (p != lst); // условие окончания обхода
}

49.

Двусвязный
линейный список
Каждый узел двунаправленного (двусвязного) линейного списка (ДЛС) содержит
два поля указателей — на следующий и на предыдущий узлы. Указатель на
предыдущий узел корня списка содержит нулевое значение. Указатель на
следующий узел последнего узла также содержит нулевое значение.

50.

Двусвязный
линейный список
Узел ДЛС можно представить в виде структуры:
struct list
{
int field; // поле данных
struct list *next; // указатель на следующий элемент
struct list *prev; // указатель на предыдущий
элемент
};

51.

Двусвязный
линейный список
Основные действия, производимые над
узлами ДЛС:
• Инициализация списка
• Добавление узла в список
• Удаление узла из списка
• Удаление корня списка
• Вывод элементов списка
• Вывод элементов списка в обратном порядке
• Взаимообмен двух узлов списка

52.

Двусвязный
линейный список
Инициализация ДЛС
Инициализация списка предназначена для создания
корневого узла списка, у которого поля указателей
на следующий и предыдущий узлы содержат
нулевое значение.

53.

Двусвязный
линейный список
Инициализация ДЛС
struct list * init(int a) // а- значение первого узла
{
struct list *lst;
// выделение памяти под корень списка
lst = (struct list*)malloc(sizeof(struct list));
lst->field = a;
lst->next = NULL; // указатель на следующий узел
lst->prev = NULL; // указатель на предыдущий узел
return(lst);
}

54.

Двусвязный
линейный список
Добавление узла в ДЛС
Функция добавления узла в список принимает два
аргумента:
• Указатель на узел, после которого происходит
добавление
• Данные для добавляемого узла.

55.

Двусвязный
линейный список
Добавление узла в ДЛС включает в себя следующие этапы:
• создание узла добавляемого элемента и заполнение его поля
данных;
• переустановка указателя «следующий» узла,
предшествующего добавляемому, на добавляемый узел;
• переустановка указателя «предыдущий» узла, следующего
за добавляемым, на добавляемый узел;
• установка указателя «следующий» добавляемого узла на
следующий узел (тот, на который указывал предшествующий
узел);
• установка указателя «предыдущий» добавляемого узла на
узел, предшествующий добавляемому (узел, переданный в
функцию).

56.

Двусвязный
линейный список
Добавление узла в ДЛС
struct list * addelem(list *lst, int number)
{
struct list *temp, *p;
temp = (struct list*)malloc(sizeof(list));
p = lst->next; // сохранение указателя на следующий узел
lst->next = temp; // предыдущий узел указывает на создаваемый
temp->field = number; // сохранение поля данных добавляемого узла
temp->next = p; // созданный узел указывает на следующий узел
temp->prev = lst; // созданный узел указывает на предыдущий узел
if (p != NULL)
p->prev = temp;
return(temp);
}

57.

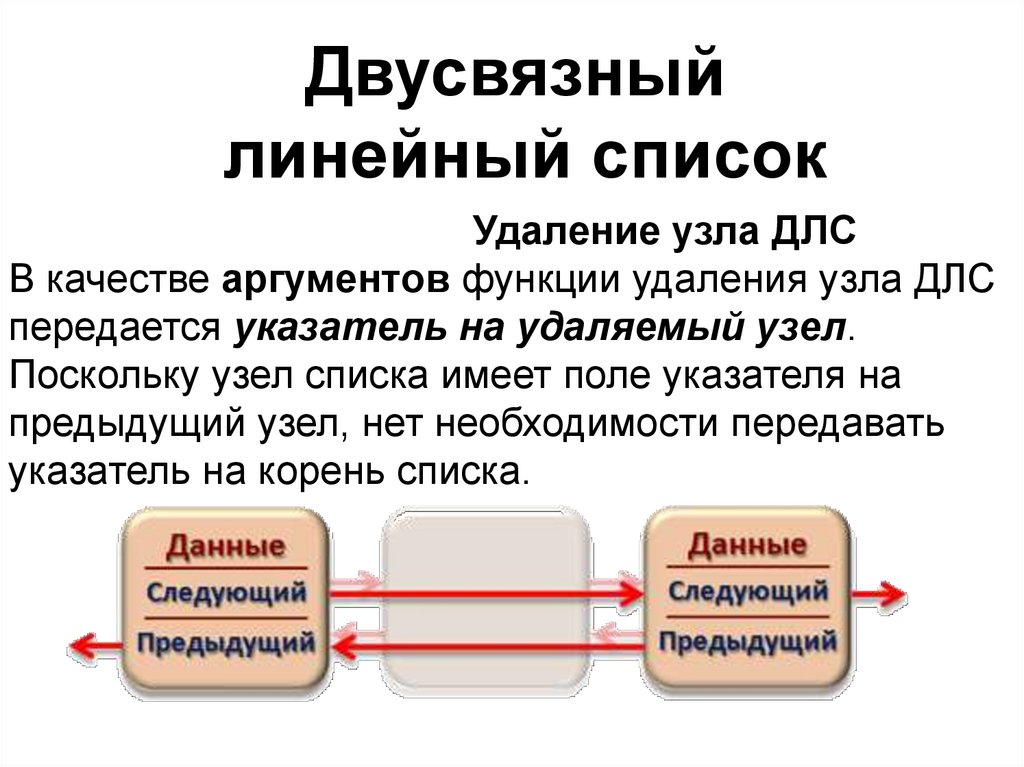
Двусвязный
линейный список
Удаление узла ДЛС
В качестве аргументов функции удаления узла ДЛС
передается указатель на удаляемый узел.
Поскольку узел списка имеет поле указателя на
предыдущий узел, нет необходимости передавать
указатель на корень списка.

58.

Двусвязный
линейный список
Удаление узла ДЛС включает в себя
следующие этапы:
• установка указателя «следующий»
предыдущего узла на узел, следующий за
удаляемым;
• установка указателя «предыдущий»
следующего узла на узел, предшествующий
удаляемому;
• освобождение памяти удаляемого узла.

59.

Двусвязный
линейный список
Удаление узла ДЛС
struct list * deletelem(list *lst)
{
struct list *prev, *next;
prev = lst->prev; // узел, предшествующий lst
next = lst->next; // узел, следующий за lst
if (prev != NULL)
prev->next = lst->next; // переставляем указатель
if (next != NULL)
next->prev = lst->prev; // переставляем указатель
free(lst); // освобождаем память удаляемого элемента
return(prev);
}

60.

Двусвязный
линейный список
Удаление корня ДЛС
Функция удаления корня ДЛС в качестве
аргумента получает указатель на текущий
корень списка.
Возвращаемым значением будет новый
корень списка — тот узел, на который
указывает удаляемый корень.

61.

Двусвязный
линейный список
Удаление корня ДЛС
struct list * deletehead(list *root)
{
struct list *temp;
temp = root->next;
temp->prev = NULL;
free(root); // освобождение памяти текущего корня
return(temp); // новый корень списка
}

62.

Двусвязный
линейный список
Вывод элементов ДЛС
Функция вывода элементов ДЛС аналогична функции для
ОЛС.
В качестве аргумента в функцию вывода элементов
передается указатель на корень списка.
Функция осуществляет последовательный обход
всех узлов с выводом их значений

63.

Двусвязный
линейный список
Вывод элементов ДЛС
void listprint(list *lst)
{
struct list *p;
p = lst;
do {
printf("%d ", p->field); // вывод значения элемента p
p = p->next; // переход к следующему узлу
} while (p != NULL); // условие окончания обхода
}

64.

Двусвязный
линейный список
Вывод элементов ДЛС в обратном порядке
Функция вывода элементов ДЛС в обратном
порядке принимает в качестве аргумента
указатель на корень списка.
Функция перемещает указатель на последний
узел списка и осуществляет последовательный
обход всех узлов с выводом их значений в
обратном порядке.

65.

Двусвязный
линейный список
Вывод элементов ДЛС в
обратном порядке
void listprintr(list *lst)
{
struct list *p;
p = lst;
while (p->next != NULL)
p = p->next; // переход к концу списка
do {
printf("%d ", p->field); // вывод значения элемента p
p = p->prev; // переход к предыдущему узлу
} while (p != NULL); // условие окончания обхода
}

66.

67.

СТРУКТУРА ДАННЫХ СТЕК
Стек (stack) —
абстрактный тип данных, представляющий собой
список элементов, организованных по принципу LIFO ( last in — first out,
«последним пришёл — первым вышел»).
Зачастую стек реализуется в виде однонаправленного списка
(каждый элемент в списке содержит помимо хранимой информации в
стеке указатель на следующий элемент стека).
Но также часто стек располагается в одномерном массиве с
упорядоченными адресами. При этом отпадает необходимость
хранения в элементе стека явного указателя на следующий элемент
стека, что экономит память. При этом указатель стека (Stack Pointer)
обычно является регистром процессора и указывает на адрес головы
стека.
Регистр процессора — блок ячеек памяти, образующий сверхбыструю
оперативную память внутри процессора; используется самим
процессором и большой частью недоступен программисту: например,
при выборке из памяти очередной команды она помещается в регистр
команд, к которому программист обратиться не может.

68.

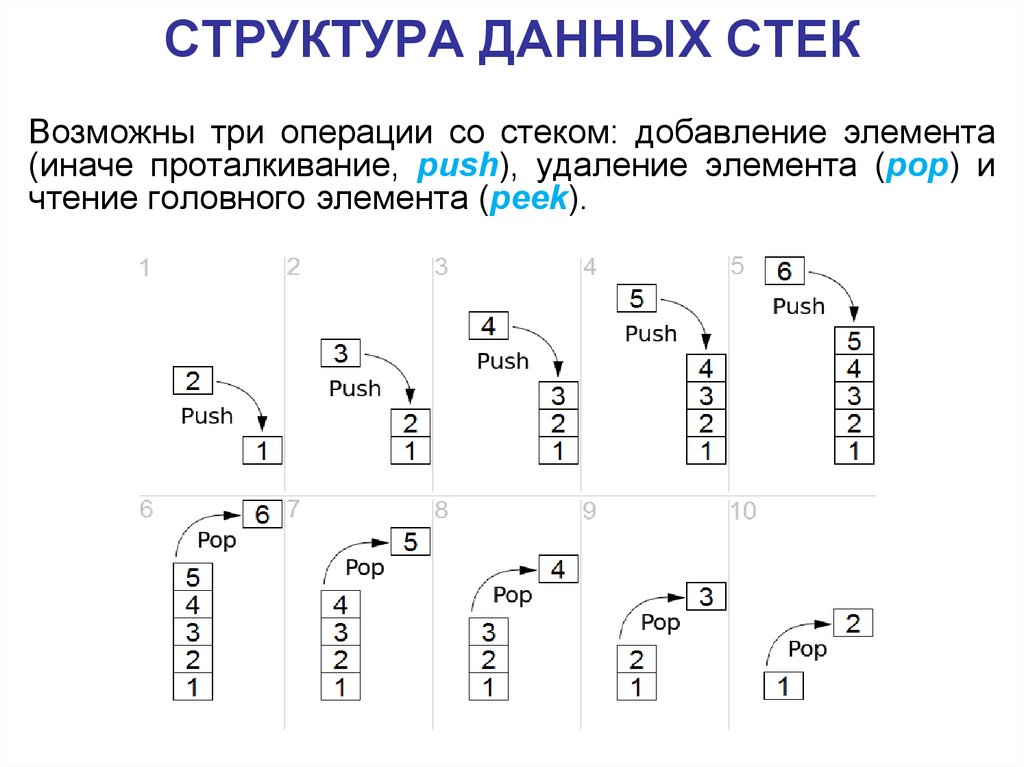
СТРУКТУРА ДАННЫХ СТЕК
Возможны три операции со стеком: добавление элемента
(иначе проталкивание, push), удаление элемента (pop) и
чтение головного элемента (peek).

69.

70. Очередь

• О́чередь — тип данных с принципом
организации «первый пришёл — первый
вышел» (FIFO, First In — First Out).
• Добавление элемента (принято обозначать
словом enqueue — поставить в очередь)
возможно лишь в конец очереди, выборка —
только из начала очереди (что принято
называть словом dequeue — убрать из
очереди), при этом выбранный элемент из
очереди удаляется.

71.

• Деревья

72. Деревья

• Деревья наилучшим образом
приспособлены для решения задач
искусственного интеллекта и
синтаксического анализа текста.
• Примеры применения: программа игры
в шашки или шахматы, докозательство
теоремы, анализ зрительных или
звуковых образов

73. Деревья

• Деревом типа Т называется структура
данных, которая образована данным
типа Т, называемым корнем дерева, и
конечным, возможно пустым
множеством с переменным числом
элементов – деревьев типа Т,
называемых поддеревьями этого
дерева (рекурсивное определение)

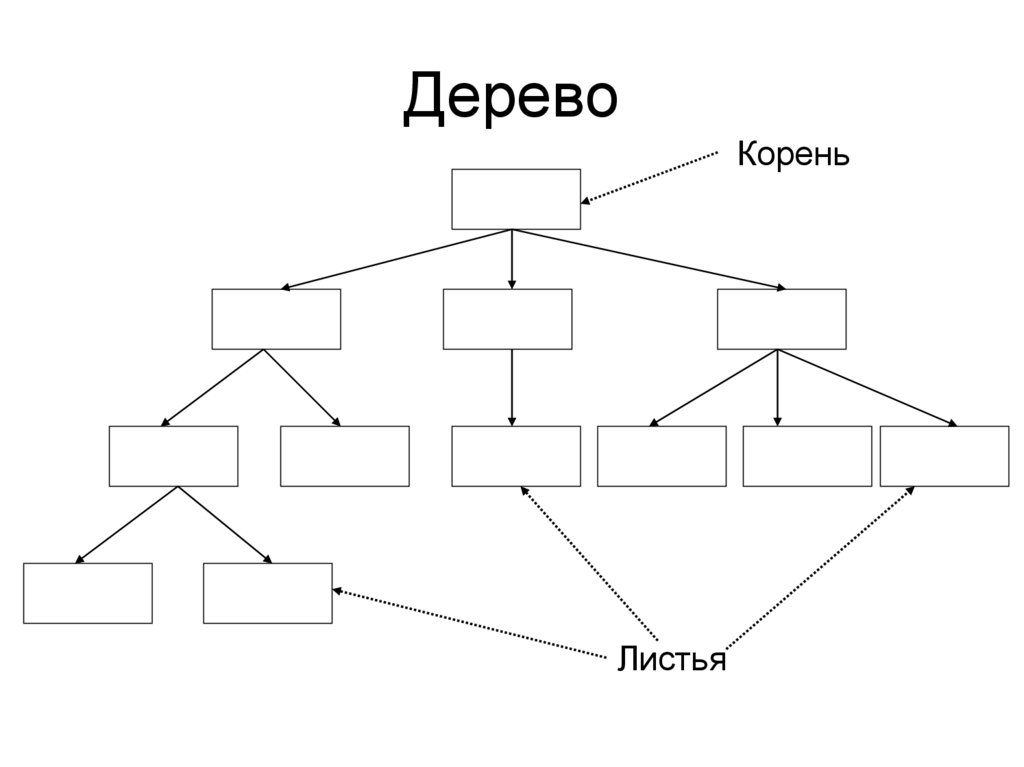
74. Деревья (терминология)

• Лист – это корень поддерева, не
имеющего, в свою очередь,
поддеревьев
• Вершина – это корень подерева. Кореь
и листья дерева являются особыми
вершинами
• Вершина связана с каждым из своих
поддеревьев ветвью

75. Дерево

Корень
Листья

76.

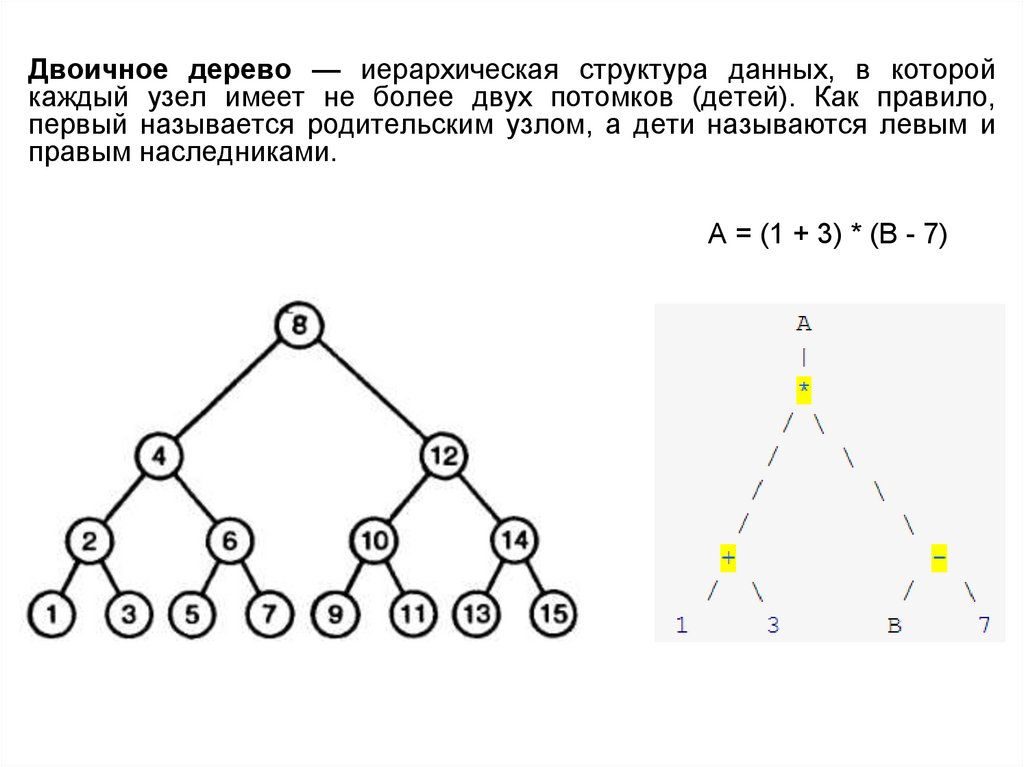
Двоичное дерево — иерархическая структура данных, в которой
каждый узел имеет не более двух потомков (детей). Как правило,
первый называется родительским узлом, а дети называются левым и
правым наследниками.
A = (1 + 3) * (B - 7)

77.

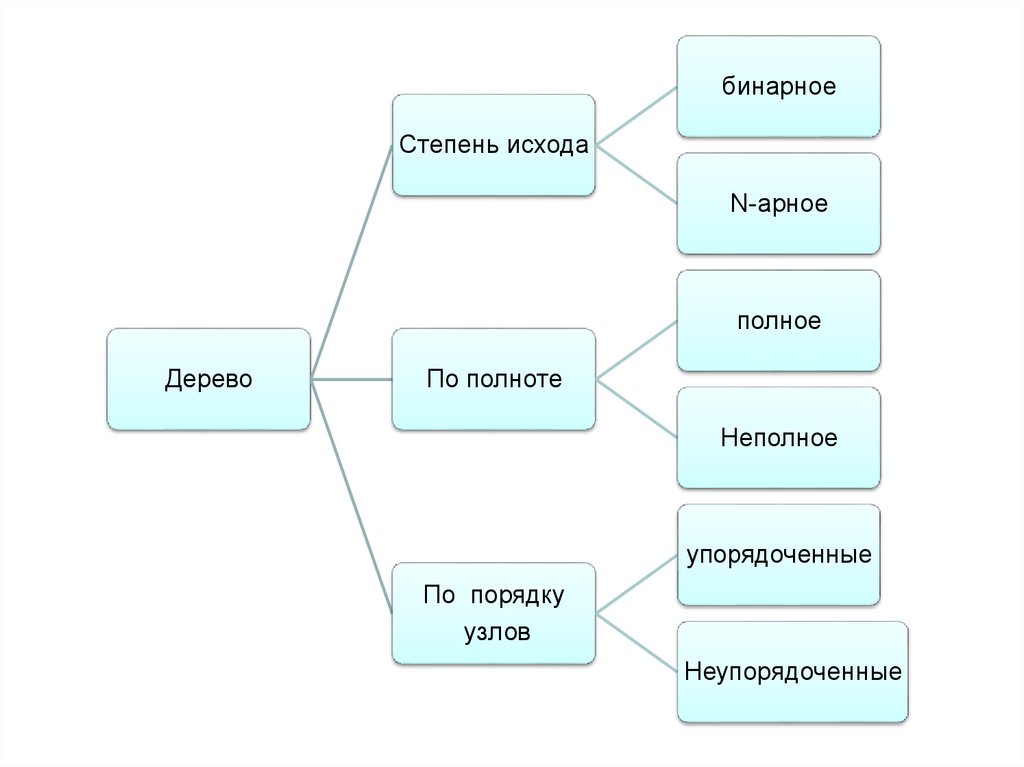
бинарное
Степень исхода
N-арное
полное
Дерево
По полноте
Неполное
упорядоченные
По порядку
узлов
Неупорядоченные

78. Двоичное дерево

• Двоичным деревом типа Т называют
структуру, которая либо пуста либо
образована:
• - данным типа Т, называемым корнем
двоичного дерева
• - двоичным деревом типа Т,
называемым левым поддеревом
двоичного дерева
• - двоичным деревом типа Т,
называемым правым поддеревом
двоичного дерева

79. Двоичное дерево (логическое описание)

• При представлении данных в виде
двоичного дерева будем считать, что
каждое звено (вершина дерева) будет
записью, содержащей четыре поля:
ключ записи, ссылка на левое
поддерево, ссылка на правое
поддерево и информационная часть.

80. Бинарное дерево поиска

• Бинарное дерево называется деревом
поиска, если
– Левый потомок любого элемента и все
элементы поддерева, растущего из левого
потомка, меньше данного элемента
– Правый потомок любого элемента и все
элементы поддерева, растущего из
правого потомка, больше данного
элемента

81. Бинарное дерево поиска

14
8
19
3
1
4
10
9
17
11
16
25
18
23
27

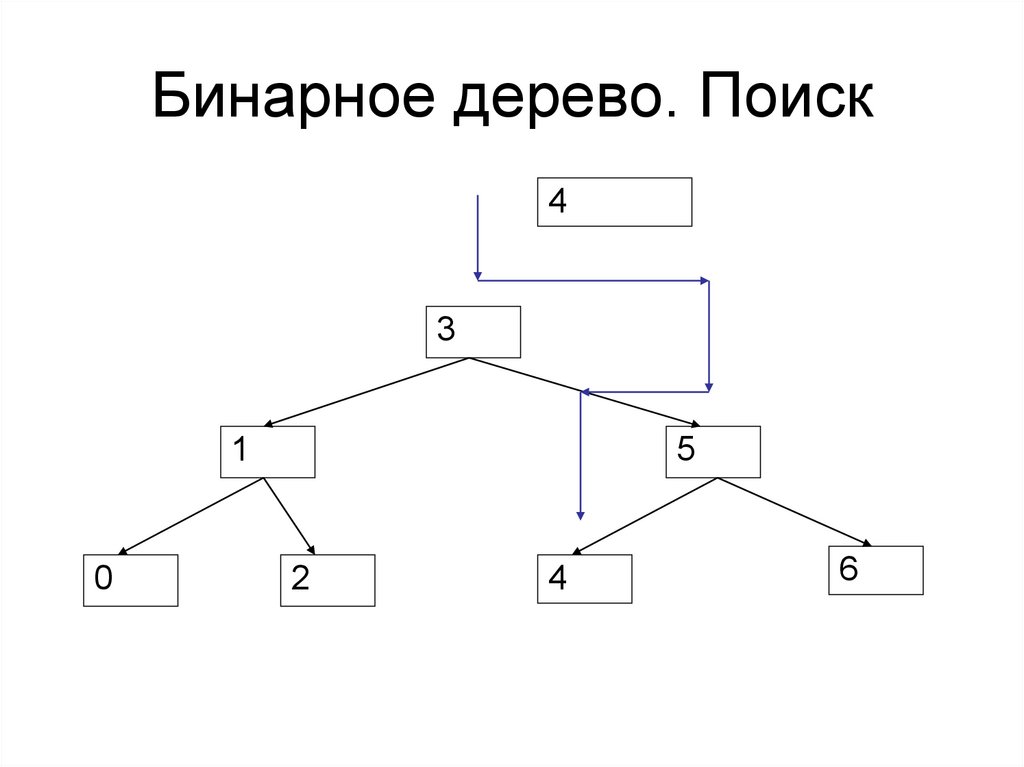
82. Бинарное дерево. Поиск

4
3
1
0
5
2
4
6

83. Бинарное дерево. Добавление элемента

2.5
3
1
0
5
2
4
2.5
6

84. Бинарное дерево поиска

• Как и отсортированный массив,
поддерживает поиск за log(N)
• В отличие от отсортированного
массива, поддерживает добавление
элемента за log(N)

85. Сбалансированное дерево

• Дерево является сбалансированным,
если разница между его максимальной
и минимальной глубиной (количеством
элементов от корня до листа) не
больше 1.

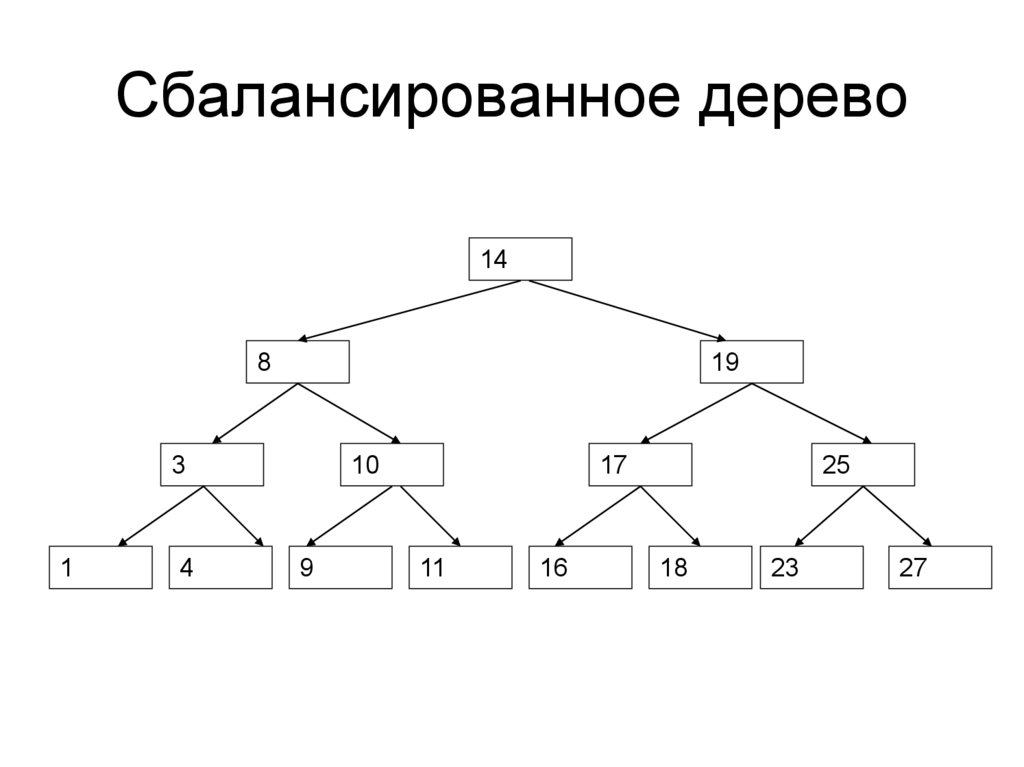
86. Сбалансированное дерево

14
8
19
3
1
4
10
9
17
11
16
25
18
23
27

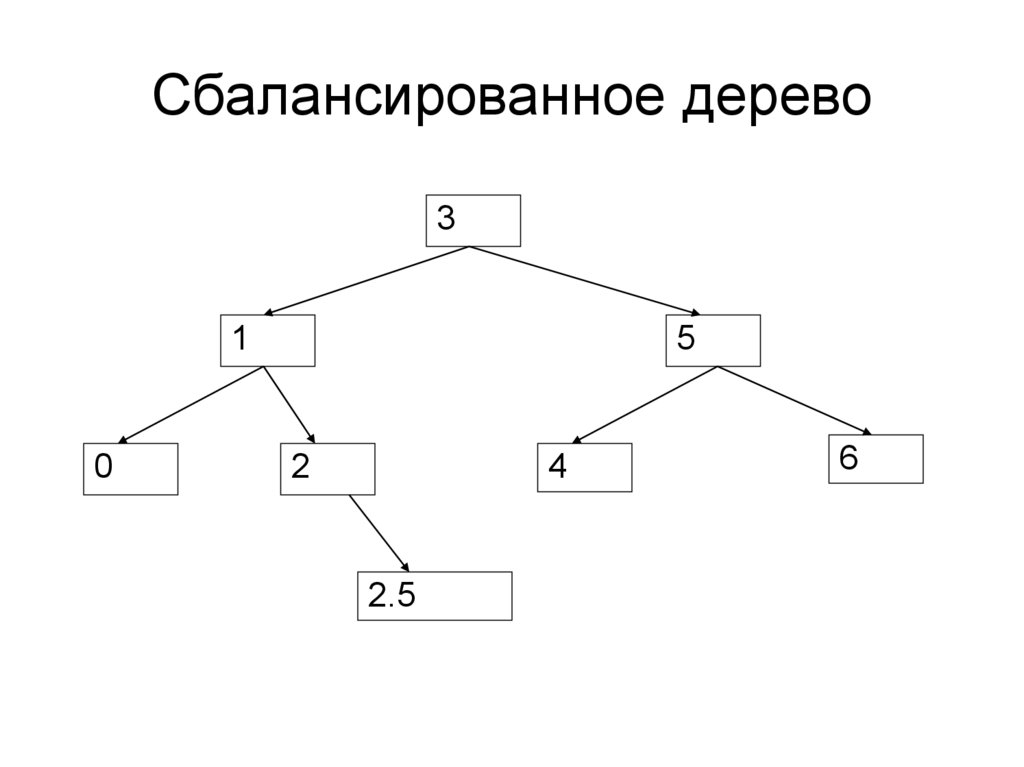
87. Сбалансированное дерево

3
1
0
5
2
4
2.5
6

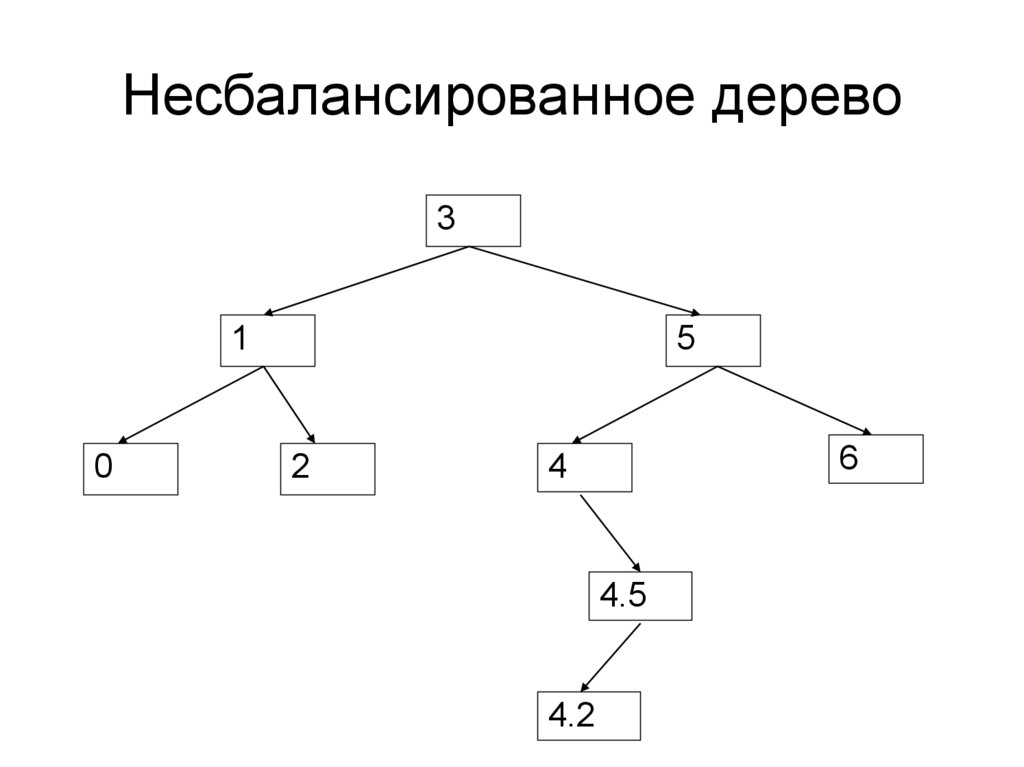
88. Несбалансированное дерево

3
1
0
5
2
6
4
4.5
4.2

89. Сбалансированное дерево

• Дерево должно быть
сбалансированным, чтобы
поддерживать поиск и добавление
элемента за log(N)
• Существуют различные алгоритмы
реализации бинарных деревьев поиска
• Они отличаются способом обеспечения
сбалансированности дерева

90. Сбалансированное дерево

• Варианты:
– Красно-черные деревья
– AVL-деревья