Многогранник

1.

Многогранник - геометрическое тело, ограниченное конечным числом плоских
многоугольников, любые два из которых, имеющие общую сторону, не лежат в одной
плоскости. При этом сами многоугольники называются гранями, их стороны – ребрами
многогранника, а их вершины – вершинами многогранника.

2.

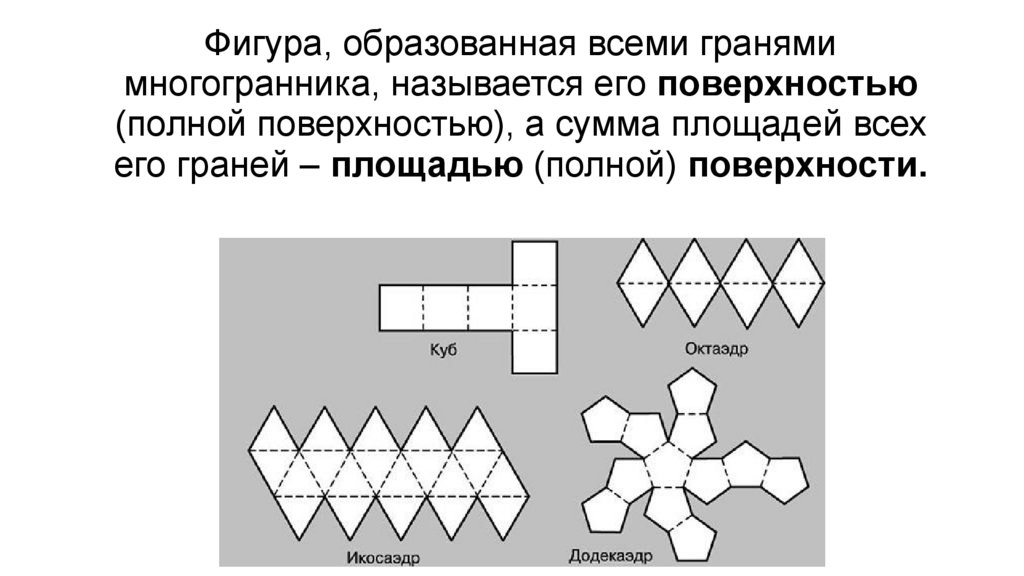
Фигура, образованная всеми гранями
многогранника, называется его поверхностью
(полной поверхностью), а сумма площадей всех
его граней – площадью (полной) поверхности.

3.

Куб – это многогранник, имеющий шесть граней,
которые являются равными квадратами.
Стороны квадратов называются ребрами куба, а
вершины – вершинами куба. Куб – это
многогранник, имеющий шесть граней, которые
являются равными квадратами. Стороны
квадратов называются ребрами куба, а вершины
– вершинами куба.

4.

Параллелепипед – это многогранник, у которого шесть
граней и каждая из них – параллелограмм. Стороны
параллелограммов называются ребрами параллелепипеда, а
их вершины – вершинами параллелепипеда. Две грани
параллелепипеда называются противолежащими, если они
не имеют общего ребра, а имеющие общее ребро
называются смежными. Иногда какие-нибудь две
противолежащие грани параллелепипеда выделяются и
называются основаниями, тогда остальные грани – боковыми
гранями, а их стороны, соединяющие вершины оснований
параллелепипеда, – его боковыми ребрами.

5.

Прямой параллелепипед – это такой параллелепипед, у которого боковые грани –
прямоугольники. Прямоугольный параллелепипед – это параллелепипед, у
которого все грани – прямоугольники. Заметим, что всякий прямоугольный
параллелепипед является прямым параллелепипедом, но не любой прямой
параллелепипед есть прямоугольный.

6.

Призма (n-угольная) – это многогранник, у которого две грани –
равные n-угольники, а остальные n граней – параллелограммы.
Равные n-угольники называются основаниями, а
параллелограммы – боковыми гранями призмы. Прямая призма –
это такая призма, у которой боковые грани – прямоугольники.
Правильная n-угольная призма – это призма, у которой все
боковые грани – прямоугольники, а ее основания – правильные nугольники.

7.

Пирамида (n-угольная) – это многогранник, у
которого одна грань – какой-нибудь n-угольник, а
остальные n граней – треугольники с общей
вершиной; n-угольник называется основанием;
треугольники, имеющие общую вершину,
называются боковыми гранями, а их общая
вершина называется вершиной пирамиды.
Стороны граней пирамиды называются ее
ребрами, а ребра, сходящиеся в вершине,
называются боковыми.

8.

Правильная n-угольная пирамида – это
такая пирамида, основание которой –
правильный n-угольник, а все боковые ребра
равны между собой. У правильной пирамиды
боковые грани – равные друг другу
равнобедренные треугольники.
Треугольная пирамида называется
тетраэдром, если все ее грани – равные
правильные треугольники. Тетраэдр
является частным случаем правильной
треугольной пирамиды (т.е. не каждая
правильная треугольная пирамида будет
тетраэдром).

9.

Линии пересечения двух плоскостей.
Для построения прямой, по которой пересекаются некоторые две
плоскости α и β (например, секущая плоскость и плоскость грани
многогранника), нужно построить две их общие точки, тогда прямая,
проходящая через эти точки, есть линия пересечения плоскостей α и β

10.

Точки пересечения прямой и плоскости.
Для построения точки пересечения прямой l и плоскости α нужно
построить точку пересечения прямой l и прямой l1, по которой
пересекаются плоскость α и любая плоскость, содержащая прямую l.

11.

Взаимное расположение прямых и плоскостей в стереометрии
Теорема 1. Через любую точку пространства, не лежащую на данной прямой,
проходит единственная прямая, параллельная данной прямой.

12.

Теорема 2. Если одна из двух параллельных прямых пересекает
данную плоскость, то и другая прямая пересекает эту плоскость.

13.

Теорема 3 (признак параллельности прямых). Если две прямые параллельны
третьей прямой, то они параллельны между собой.

14.

Возможны три случая взаимного расположения прямой и
плоскости в стереометрии:
Прямая лежит в плоскости (каждая точка прямой лежит в плоскости).

15.

Прямая и плоскость пересекаются (имеют единственную
общую точку).

16.

Прямая и плоскость не имеют ни одной общей точки