Правильные многоугольники

1.

2.

в каж дой еговершине
сх одитсяоднои тож е
числоребер
все егограни - равные
правильные многоу гольники
Замечание
не су ществу ет правильного
многогранника, гранями
которого являютсяправильные
n- у гольники при n≥6.

3.

история
Взначительной мере правильные многогранники
были изу ченыдревними греками. Некоторые
источники приписывают честьих открытия
Пифагору . Дру гие у тверж дают, чтоему были
знакомытолькотетраэдр, ку би додекаэдр, а
честьоткрытияоктаэдраи икосаэдра
принадлеж ит Теэтету Афинскому ,
современнику Платона.Влюбомслучае, Теэтет
дал математическое описание всемпяти
правильныммногогранникам и первоеизвестное
доказательство того, что их ровно пять.
Аристотель
Теэтет Афинский

4.

история
Правильные многогранники характерны для философииПлатона, в честь которого и получили название
«платоновытела». Платонписал оних всвоёмтрактате Тимей (360г до н. э.), где сопоставил каждую из
четырёх стихий (землю,воздух, воду и огонь)определённомуправильному многограннику. Огню
соответствовал тетраэдр, земле — гексаэдр, воздуху — октаэдр, воде — икосаэдр. Данныесопоставления
пояснялисьследующими ассоциациями: жар огня ощущаетсячётко и остро,как пирамидки-тетраэдры;
мельчайшиекомпонентывоздуха октаэдрынастолько гладкие, что их с трудом можно почувствовать; вода
выливается, если её взять в руку, как будто онасделана из множества маленьких шариков, к которым ближе
всего икосаэдры; в противоположность воде,совершеннонепохожие нашаркубики-гексаэдры составляют
землю,которые являютсяпричиной того, что земля рассыпаетсявруках, впротивоположность плавному току
воды.Поповоду пятого элемента,додекаэдра,Платонсделал смутное замечание: «…его богопределил для
Вселенной и прибегнул к нему в качестве образца».

5.

история
Платон

6.

история
Евклид дал полное математическое описание
правильных многогранников в последней, XI I I
книге Начал. Длякаж дого многогранникаЕвклид
нашёл отношение диаметра описанной сферык длине
ребра.В18-мпредложении утверждается, что не
су ществу ет дру гих правильных многогранников.
Евклид

7.

история
ВXVI веке немецкий астрономИоганнКеплерпытался
найти связьмеж ду пятьюизвестными натот момент
планетами Солнечной системы(исключаяЗемлю) и
правильными многогранниками. Позж е от оригинальной
идеи Кеплерапришлосьотказаться, норезультатом его
поисков сталооткрытие двух законов орбитальной
динамики — законов Кеплера, — изменивших ку рс
физики и астрономии,атакже правильных звёздчатых
многогранников (тел Кеплера— Пу ансо).
Кеплер

8.

история

9.

Всего существует 5
правильных
многогранников
Правильный тетраэдр
Замечание
многогранник, составленный из
четырехравносторонних
треугольников. Каждая его вершина
является вершиной трех
треугольников,значитсуммаплоских
углов при каждой вершинеравна 180.

10.

Всего существует 5
правильных
многогранников
Правильный октаэдр
Замечание
многогранник, составленный из
восьми равносторонних
треугольников. Каждая вершина
октаэдра является вершиной четырех
треугольников, значит, сумма
плоскихуглов при каждой вершине
равна 240

11.

Всего существует 5
правильных
многогранников
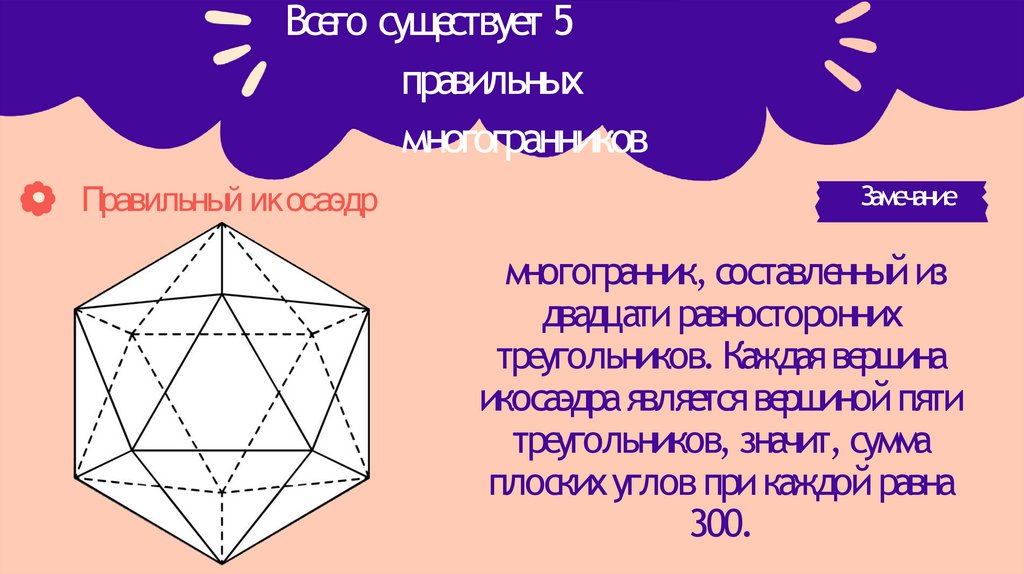
Правильный икосаэдр
Замечание
многогранник, составленный из
двадцати равносторонних
треугольников. Каждая вершина
икосаэдра является вершиной пяти
треугольников, значит, сумма
плоскихуглов при каждой равна
300.

12.

Всего существует 5
правильных
многогранников
Правильный додекаэдр
Замечание
многогранник, составленный из
двенадцати правильных
пятиугольников. Каждая вершина
додекаэдра является вершиной трех
правильныхпятиугольников, значит,
сумма плоскихуглов при каждой
равна 324.

13.

Всего существует 5
правильных
многогранников
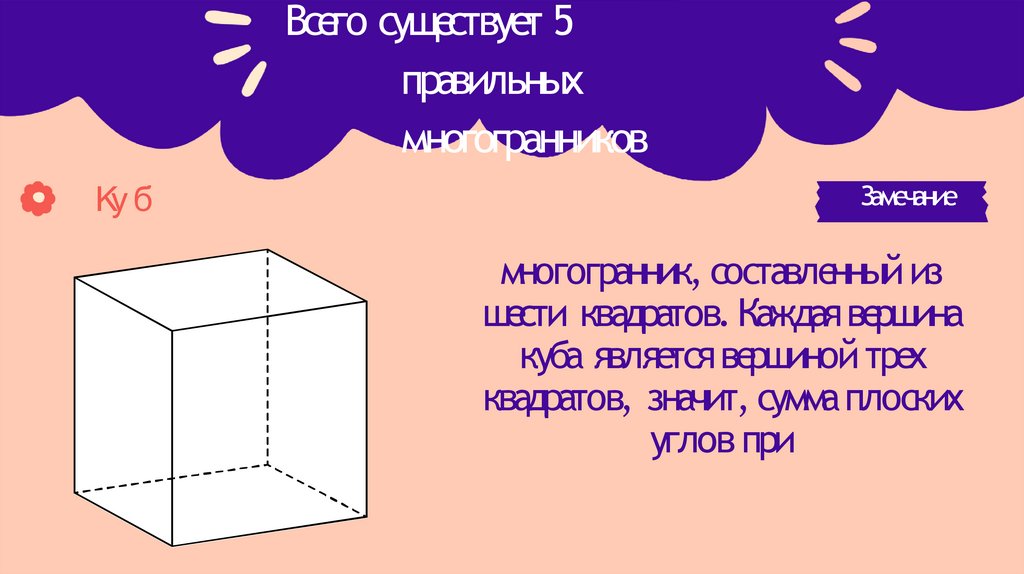
Ку б
Замечание
многогранник, составленный из
шести квадратов. Каждая вершина
куба является вершиной трех
квадратов, значит, сумма плоских
углов при

14.

Всего существует 5
правильных
многогранников
Доказательство. чтоих только 5
Угол правильного n-угольника при n≥6 неменьше120. Сдругой стороны, при
каждой вершинемногогранника должно быть неменеетрех плоских углов.
Поэтому если бы существовал правильный многогранник, у которого грани правильныеn-угольникиприn≥6, то суммаплоских углов при каждой
вершинетакого многогранника была бы неменьше360. Но это невозможно,
таккаксуммавсехплоскихуглов прикаждойвершиневыпуклого
многогранникаменьше360.

15.

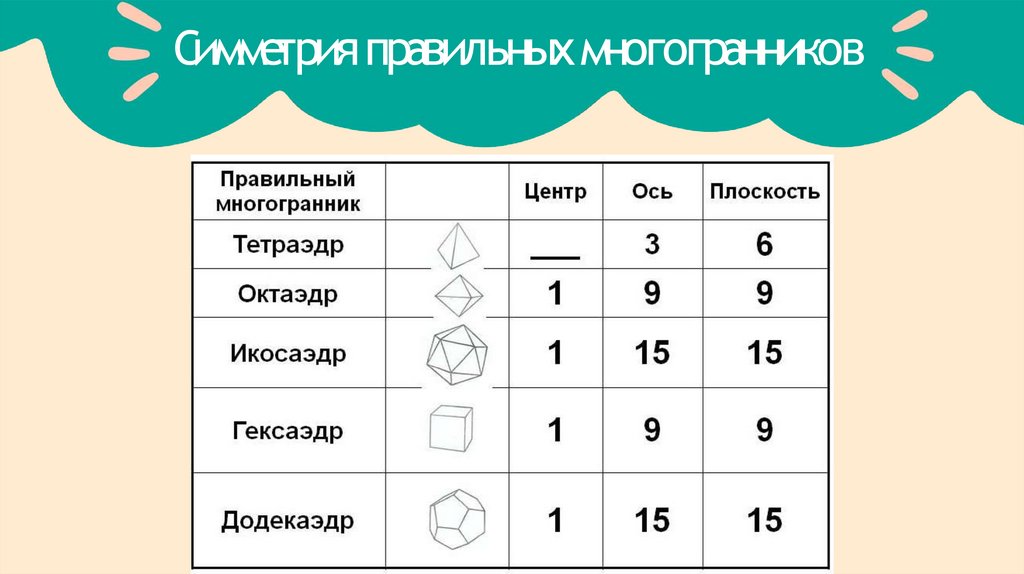
Симметрия правильных
многогранников Элементы
симметрии
1.Осьсимметрии- воображ аемаяось, при повороте вокру г которой нанекоторый
угол, фигура совмещаетсясамас собой в пространстве
2.Центрсимметрии - этоточкавну три многогранника, в которой пересекаютсяи
делятся пополампрямые,соединяющиеодинаковые элементымногогранника
(грани, рёбра,углы)
3.Плоскость симметрии делит многогранник на 2 зеркально равныечасти

16.

Симметрия правильныхмногогранников