Оптика и квантовая физика. Лекция 2

1. Оптика и квантовая физика

для студентов
2 курса ФТФ и ГГФ
Кафедра общей физики

2.

Интерференция света
Часть 2
Интерференция в
тонких пленках
Интерферометры
Временная
когерентность
Условие
пространственной
когерентности
Лекция 2

3.

Методы деления амплитуды
• Тонкие пленки
• Кольца Ньютона
3

4.

Интерференция в тонких пленках
Отражение от более плотной среды
L1 = (AD)·n1 (+λ/2) (“+”, если n > n1)
L2 = (ABC)·n (+λ/2) (“+”, если n2 > n)
∆12 = L2 - L1 = (ABC)·n – (AD)·n1 ± λ/2
∆12 = m λ
AB BC
h
cos
AC 2h tg
- условие максимума
интерференции
2 hn cos m
2
AD AC sin
12 2 hn cos
2
sin n
sin n1
– условие максимума при
интерференции на тонкой пленке
4

5.

Виды интерференционных картин на тонких пленках
1. Цвета тонких пленок
– интерференция при освещении пленки широким пучком
Условия: h = const, пучок лучей широкий и параллельный
Проявление интерференции
При освещении белым светом – окраска области ab в тот цвет, для λ которого
выполняется условие максимума: ∆12 = mλ.
При освещении монохроматическим светом (λ = const) – область ab ярко
освещена, если для λ выполняется условие максимума; область ab черная,
если для λ выполняется условие минимума ∆12 = (m + ½) λ.
5

6.

2. Линии равного наклона
Условия: h = const, λ = const, световой пучок – расходящийся.
12 2 h n cos
2
Свойства полос равного наклона
Полосы локализованы в бесконечности, имеют вид колец.
6

7.

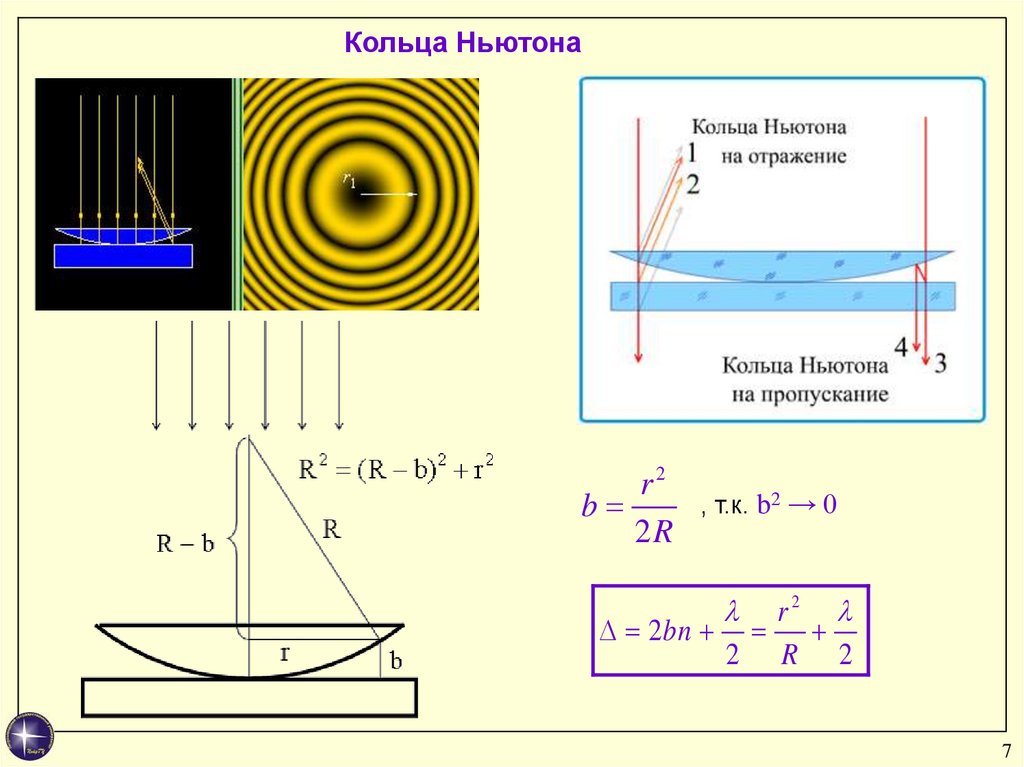
Кольца Ньютона
r2
b
2R
, т.к. b2 → 0
r2
2 bn
2 R 2
7

8.

Условие максимума (светлые кольца) ∆ = m λ, где m – целое число.
rm ( m 1 2) R
- радиус m-го светлого кольца в отраженном свете
(и темного – в прошедшем)
Условие минимума (темные кольца) ∆ = (m + ½) λ.
rm m R
- радиус m-го темного кольца в отраженном свете
(и светлого – в прошедшем)
Кольца Ньютона в зеленом и
красном свете
Пример применения – проверка качества шлифовки линз.
8

9.

3. Линии равной толщины
Условия: толщина пленки плавно изменяется (h ≠ const), представляя
собой клин. Пучок параллельный.
Система полос равной толщины
12 2 h n cos
12 m
1
12 ( m )
2
2
- максимум (светлая полоса)
- минимум (темная полоса)
9

10.

Задание. Определите, какие два зазора из представленных пяти
соответствуют данным системам интерференционных полос равной
толщины:
Пример применения - определение качества обработки поверхностей
10

11.

Примеры применения
1. Просветление оптики
2. Получение диэлектрических зеркал
Схема многослойного диэлектрического
покрытия (n >n , n >n , n l = n l = /4)
1
0
1
2
1 1
2 2
0
С семью слоями R = 0,9 в спектральной области шириной порядка 50 нм. Для
получения коэффициента отражения R = 0,99 (такие зеркала используются в
лазерных резонаторах) надо нанести 11-13 слоев.
11

12.

Интерферометры
Интерферометр Майкельсона
P1 – светоотделитель (полупрозрачная пластинка)
S1′- референтная плоскость (плоскость сравнения)
– совпадает с изображением зеркала S1 в полупрозрачном слое.
Если зеркало S2 совпадает с референтной плоскостью, то ∆ = 2(L1 – L2) = 0
12

13.

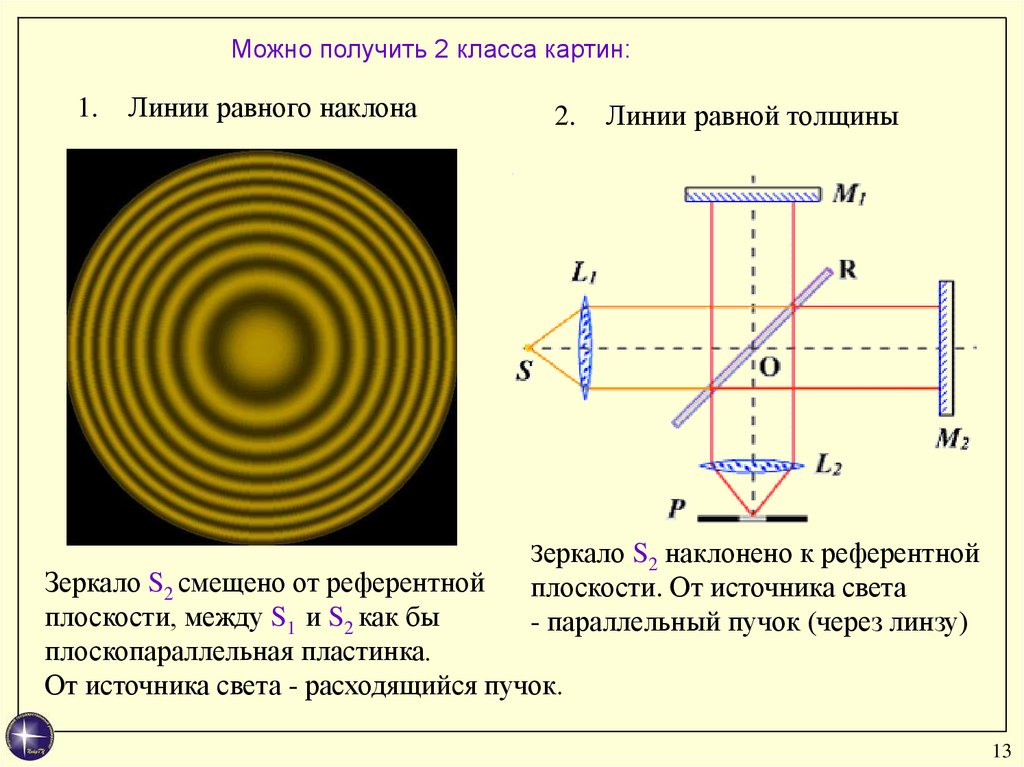
Можно получить 2 класса картин:
1.
Линии равного наклона
2.
Линии равной толщины
Зеркало S2 наклонено к референтной
Зеркало S2 смещено от референтной
плоскости. От источника света
плоскости, между S1 и S2 как бы
- параллельный пучок (через линзу)
плоскопараллельная пластинка.
От источника света - расходящийся пучок.
13

14.

Фурье - спектрометр
Для исследований ИКчасти спектра слабых
источников
14

15.

Многолучевая интерференция
Устройства для наблюдения
Интерферометр Фабри - Перо
стеклянные или кварцевые
пластинки
частично прозрачная
металлическая плёнка
R = 0,95 – 0,98
П1 и П2 - распорные
кольца
Интерференционная картина в виде
колец равного наклона, наблюдаемая в
интерферометре Фабри - Перо в
проходящем свете
d = 1 – 100 мм.
При d = 5 мм – m = 20000
15

16.

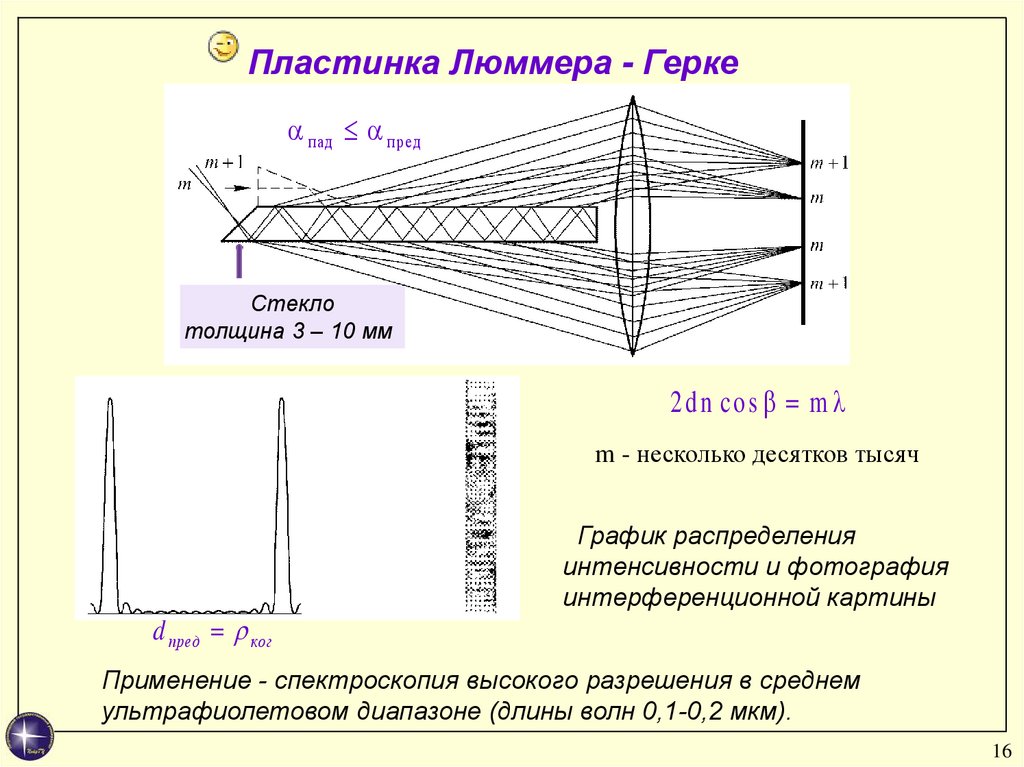
Пластинка Люммера - Герке
пад пред
Стекло
толщина 3 – 10 мм
2 d n co s m
m - несколько десятков тысяч
d пред ког
График распределения
интенсивности и фотография
интерференционной картины
Применение - спектроскопия высокого разрешения в среднем
ультрафиолетовом диапазоне (длины волн 0,1-0,2 мкм).
16

17.

Распределение интенсивности
I max (1 R ) 2
I min (1 R ) 2
R – коэффициент отражения
Кривые распределения интенсивности
в проходящем свете
17

18.

Распределение интенсивности
Анализ картины интерференции
1. Главные максимумы
δ = 2mπ
2. Минимумы
I=0
2
Е = N E0
I = N2 I 0
Δmax = mλ
δ N = k2π, k = 1,2,3,…N-1
2
k
2m
N
1, 2, 3… окружности
min m k
N
m = 0,1,2, …
18

19.

Интерферометр Линника
Предназначен для оценки качества поверхности.
Для этого одно из зеркал нужно заменить поверхностью.
Интерферометр Релея
Предназначен для измерения показателей преломления газов и жидкостей
Внизу свет идет вне кювет. Нижняя система интерференционных полос шкала для отсчета. Добавочная разность хода ∆ = (n2 - n1)l, где n1 и n2 коэффициенты преломления веществ, заполняющих кюветы. Верхняя система
полос сдвинута относительно нижней. По смещению с помощью
компенсатора определяют n2 - n1. Позволяет обнаружить изменение n2 - n1
около 10-7.
19

20.

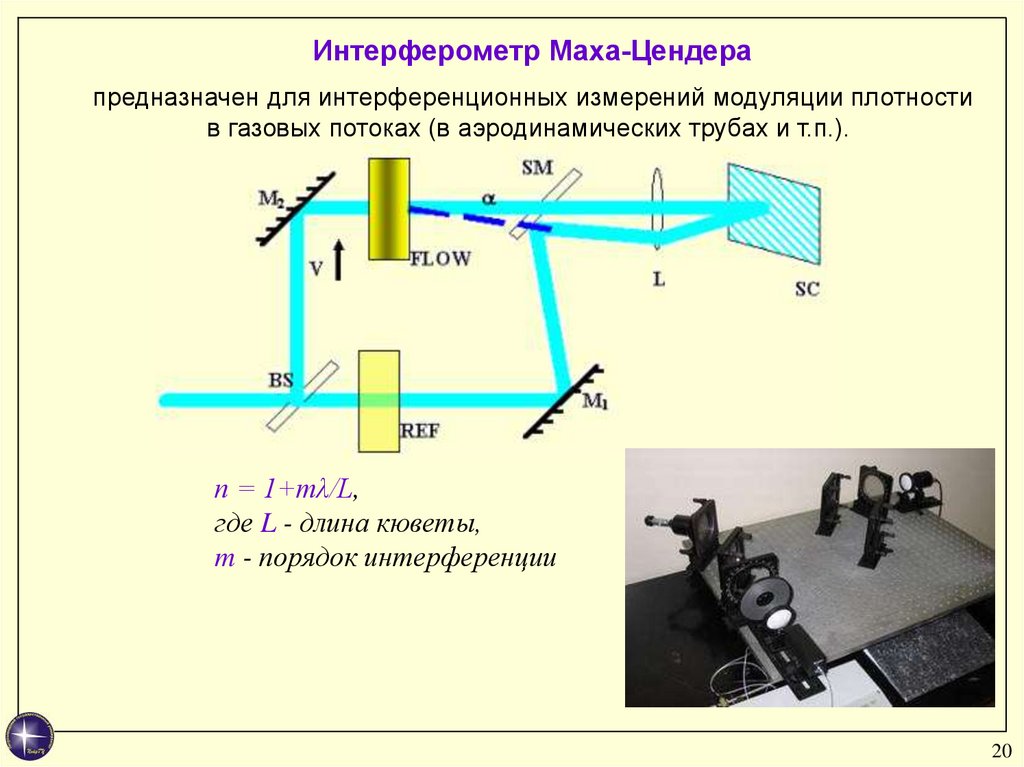
Интерферометр Маха-Цендера
предназначен для интерференционных измерений модуляции плотности
в газовых потоках (в аэродинамических трубах и т.п.).
n = 1+mλ/L,
где L - длина кюветы,
m - порядок интерференции
20

21.

Применение интерференции
Для измерений:
Длины волны λ
Коэффициента преломления n
Длин эталонов
Малых перемещений
Деформаций
Качества обработки поверхностей
21

22.

Когерентность
Условие когерентности: Δφ = const в течение времени наблюдения.
Если Δφ ≠ const → (‹cos Δφ› = 0) → I = I1 + I2 - закон фотометрического
сложения.
Излучение от отдельного источника – набор цугов с хаотически
распределенными фазами и направлениями вектора E → волны,
излучаемые двумя независимыми источниками не когерентны.
Реальные
световые волны
Общая идея получения когерентных волн
Свет от одного и того же источника нужно разделить на два (или несколько)
пучка и затем наложить их друг на друга подходящим способом.
22

23.

Условие временной когерентности:
Δ12 ℓког = ℓцуга
Δt τ ког
Δ12 – разность хода, вносимая схемой
Δt – время запаздывания одного цуга
относительно другого
При Δ12 > ℓког происходит размытие полос
картины интерференции
Оценка ℓког и τ ког
τ Δν ≈ 1 → τ ког ≈ 1/ Δν
ν = с/λ →
ког
2
c
c
2
lког
2
Δ λ – ширина полосы
пропускания фильтра или
ширина спектральной линии
Вывод: временная когерентность
определяется степенью
монохроматичности света
23

24.

Временная когерентность
Временная когерентность – способность световых колебаний к
интерференции в одной точке пространства после разделения исходного
пучка на два и последующего их соединения с некоторой разностью хода.
Временная когерентность - это источник ухудшения картины интерференции,
связанный с разбросом по частотам в данном излучении.
Цуг волн – часть последовательности колебаний, на протяжении
которых сохраняется их регулярность.
τ ког – время испускания цуга или время когерентности – наименьший
интервал времени, в течение которого фаза и амплитуда
монохроматической волны не меняются
ℓ цуга = с·τ ког – длина цуга – расстояние, на которое
распространяется волна за время когерентности
ℓког – длина когерентности – максимальная разность хода, при которой
возможна интерференция: ℓког = ℓ цуга
24

25.

Оценка максимального числа интерференционных полос
lког max m max l ког m max
0
Чем меньше разброс Δλ или Δν тем больше
степень монохроматичности, больше τког и ℓког,
т.е. лучше картина интерференции (больше m)
Примеры
Условия когерентности
1. Белый свет:
|∆λ | ≈ 400 нм, ∆ω ≈ 3·1015 рад/с, ℓког ≈ 8·10-7 м, τ ког ≈ 2,5·10-15 с, mmax ≈ 1;
2. Светофильтр: полоса пропускаемых длин волн
|∆λ | ≈ 10 нм, ∆ω ≈ 6·1013 рад/с, ℓког ≈ 3·10-5 м, τ ког ≈ 1·10-13 с, mmax ≈ 55;
3. Испускаемый атомом цуг волны (идеальный случай):
|∆λ | ≈ 10-4 нм, ∆ω ≈ 6·108 рад/с, ℓког ≈ 3 м, τ ког ≈ 1·10-8 с, mmax ≈ 5,5·106.
25

26.

Условие пространственной когерентности
Пространственная когерентность - это источник ухудшения картины
интерференции, связанный с расходимостью светового пучка и с конечными
размерами источника излучения
Размытие интерференционной картины
26

27.

x
Условие наблюдения картины
интерференции:
x
δх - смещение 0-го max
Из подобия
треугольников
x
x
2
x D 2
b D2
x
b
D1
2 D1
2
b D2 D2
D2
x
→
2 D1
2d
d
b
- угловой размер источника
D1
Оценочное условие пространственной когерентности:
Предельное расстояние между щелями:
d пред
d
d пред ког – радиус когерентности волнового поля, максимальное
расстояние между точками волновой поверхности, на котором вторичные
волны, испускаемые этими точками, еще будут когерентными.
27

28.

Пример
При наблюдении картины интерференции от Солнца
(его угловые размеры φ = 0,1 рад) для λ0 = 550 нм
ког
Условие временной
когерентности:
(повторение)
0 5,5 10 7
d
0, 055 мм
0, 01
ког
2
c
lког
2
Объем когерентности
V ко г ко2 г l ко г
- объединенное условие пространственной и временной когерентности
28

29.

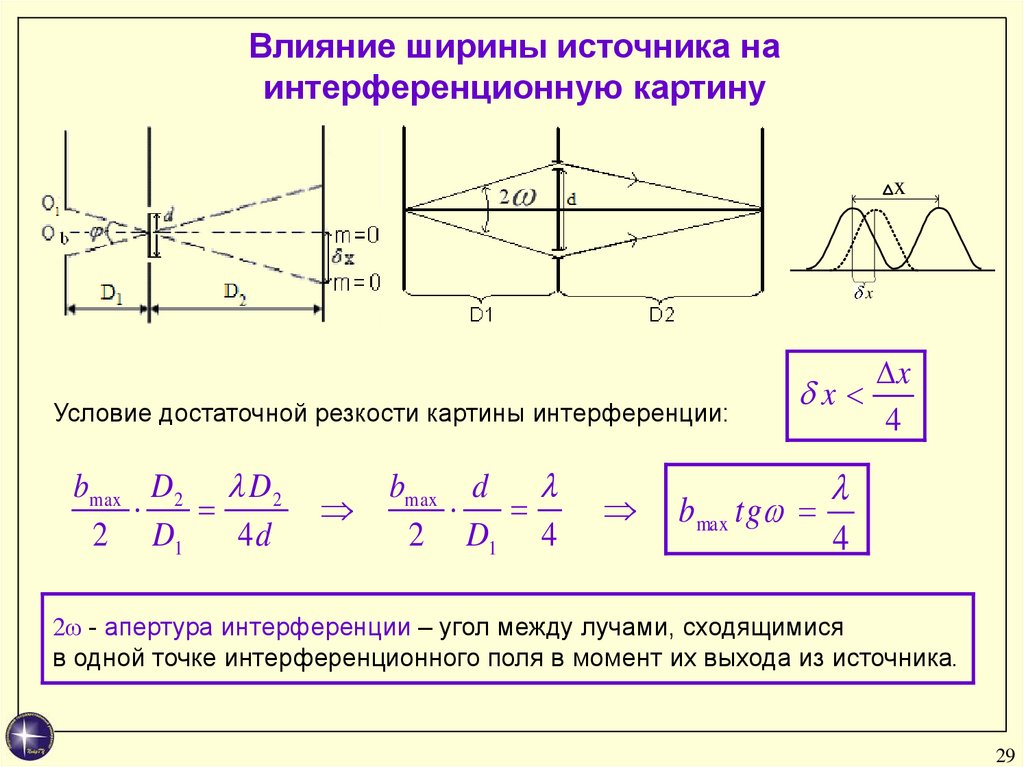
Влияние ширины источника на
интерференционную картину
x
x
Условие достаточной резкости картины интерференции:
bmax D 2 D 2
2 D1
4d
bmax d
2 D1 4
x
x
4
b max tg
4
2ω - апертура интерференции – угол между лучами, сходящимися
в одной точке интерференционного поля в момент их выхода из источника.
29

30.

Дифракционная решетка
50 – 2000 штрихов на миллиметр
30

31.

Распределение интенсивности
I ~ A2
N – число источников одинаковой
интенсивности (N > 2).
δ – сдвиг фаз между соседними 2
источниками
A0 – амплитуда от одного источника (Е0)
A - результирующая амплитуда (Е)
http://www.bollywood.im/videos/многолучевая-интерференция.html
31

32.

Распределение интенсивности
Анализ картины интерференции
3. Побочные максимумы
2
(2k 1)
2m
N
0,5; 1,5; 2,5… окружности
Вывод: многолучевая интерференция характеризуется большой
концентрацией энергии в главных максимумах
32

33.

Продолжение
следует
33