Похожие презентации:
Основные теоремы и формулы планиметрии
1. Основные теоремы и формулы планиметрии
2.
Прямоугольный треугольникА
АВ – гипотенуза
с
АС и СВ – катеты (АС СВ)
b
С
Теорема Пифагора
АВ2=АС2+СВ2
a
В
c2=а2+b2
3.
Прямоугольный треугольникА
с
b
С
a
В
Синус
острого
угла
=
отношению
противолежащего катета к гипотенузе.
AC
sin В
AB
BC
sin A
AB
4.
Прямоугольный треугольникА
с
b
С
a
В
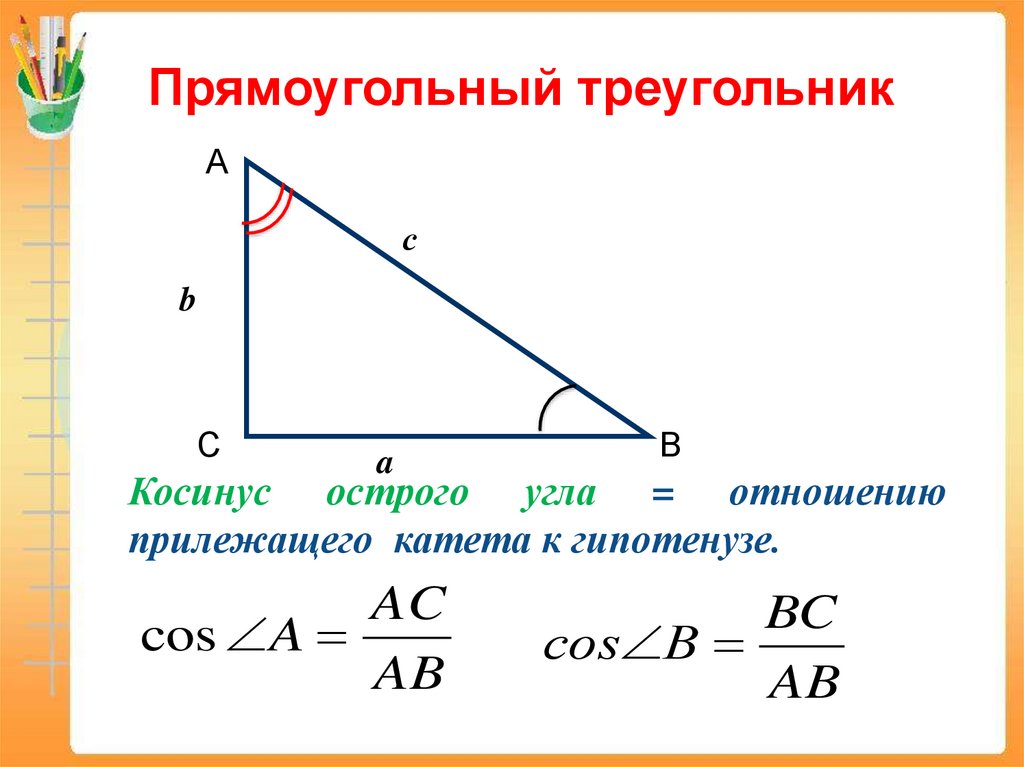
Косинус острого угла = отношению
прилежащего катета к гипотенузе.
AC
cos A
AB
BC
сos В
AB
5.
Прямоугольный треугольникА
с
b
С
a
В
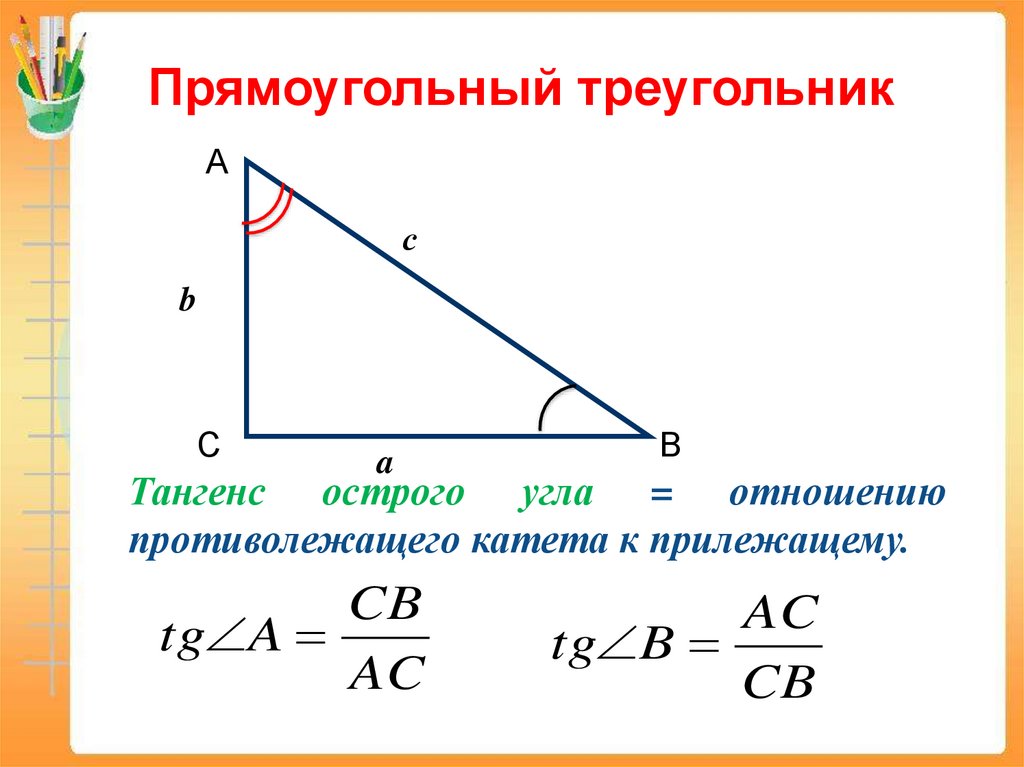
Тангенс острого угла = отношению
противолежащего катета к прилежащему.
CB
tg A
AC
AC
tg B
CB
6.
Прямоугольный треугольникА
30о
С
В
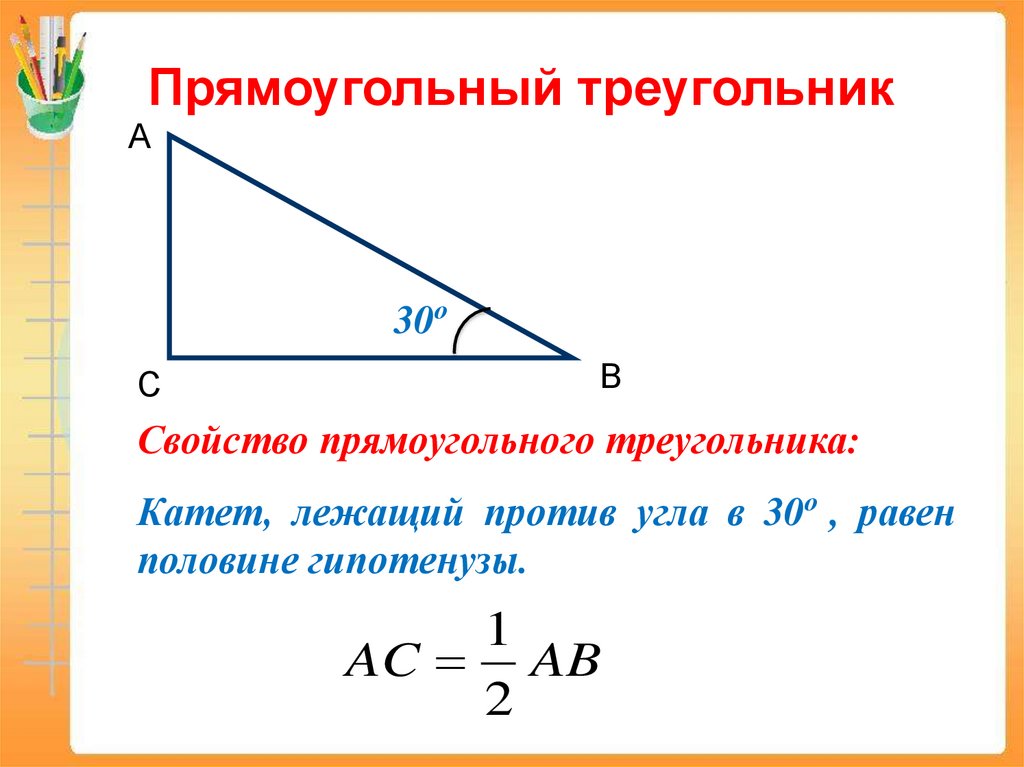
Свойство прямоугольного треугольника:
Катет, лежащий против угла в 30о , равен
половине гипотенузы.
1
AC AB
2
7.
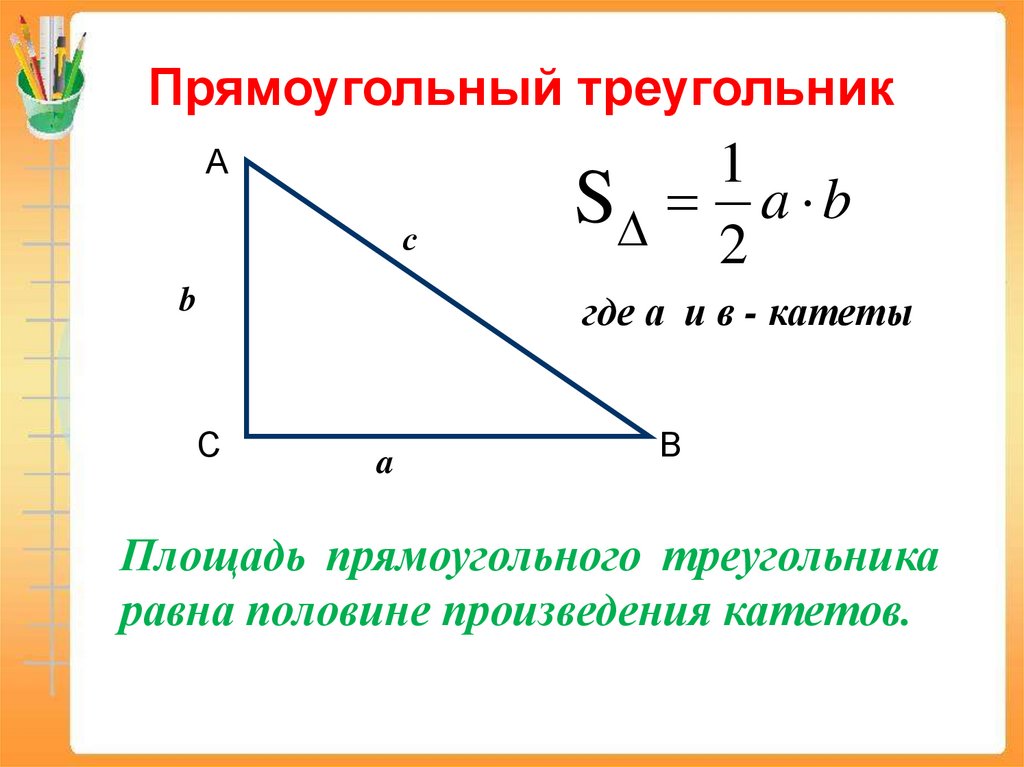
Прямоугольный треугольникА
с
b
1
S a b
2
где а и в - катеты
С
a
В
Площадь прямоугольного треугольника
равна половине произведения катетов.
8.
Теорема косинусовB
C
А
a
b
a b c 2b c cos A
2
2
2
C
9.
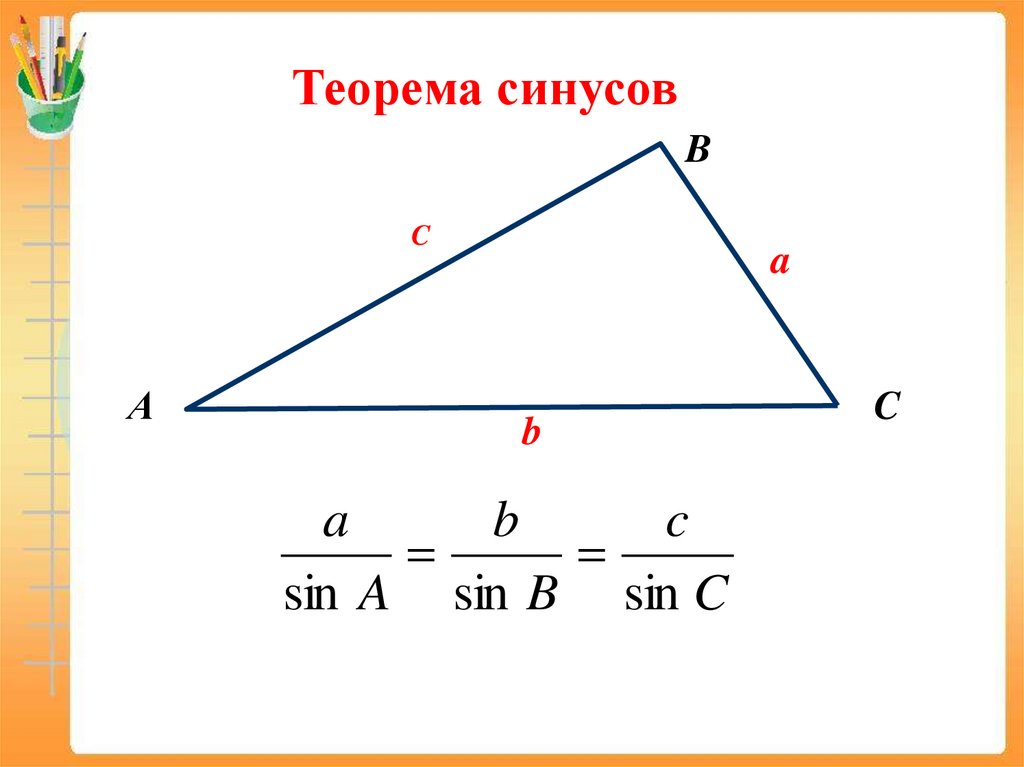
Теорема синусовB
C
А
a
b
a
b
c
sin A sin B sin C
C
10.
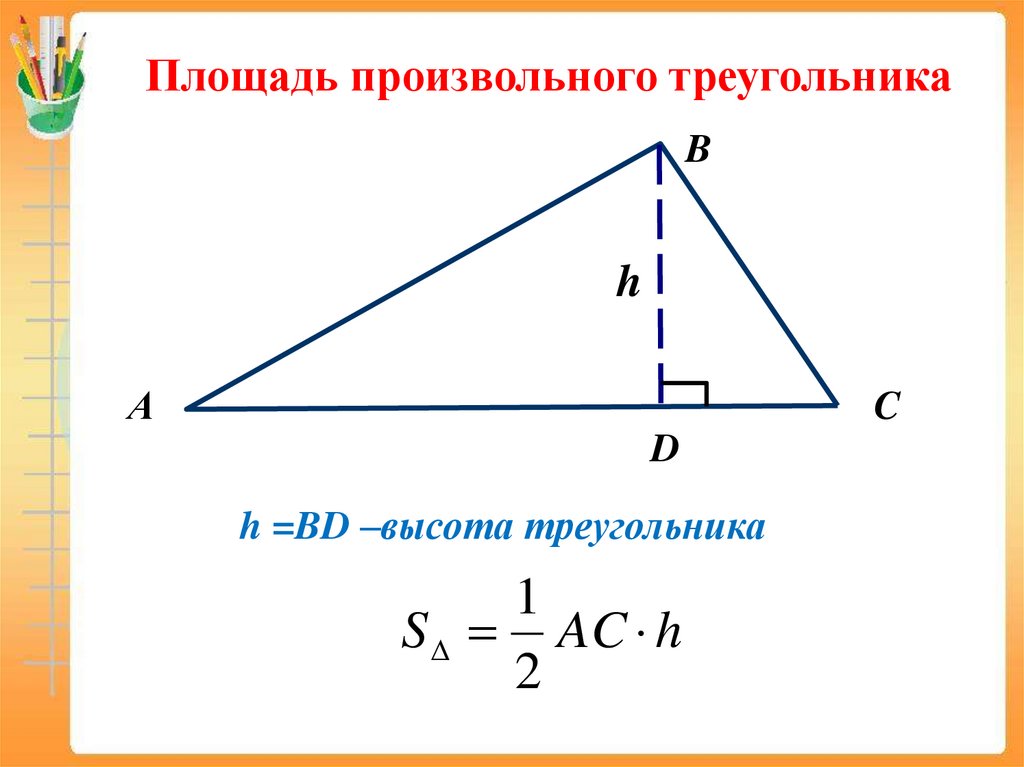
Площадь произвольного треугольникаB
h
А
C
D
h =BD –высота треугольника
1
S AC h
2
11.
Площадь произвольного треугольникаB
C
А
a
b
1
S c b sin A
2
C
12.
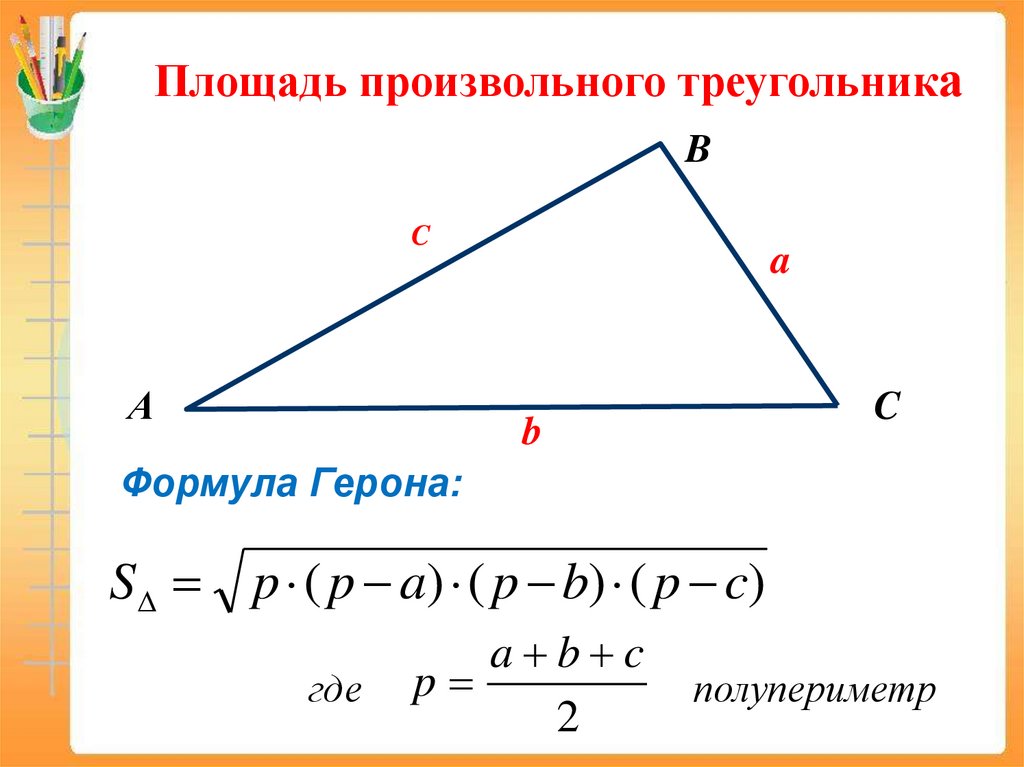
Площадь произвольного треугольникаB
C
А
a
C
b
Формула Герона:
S p ( p a) ( p b) ( p c)
где
a b c
p
2
полупериметр
13.
Произвольный треугольникB
C
a
R
r
А
C
b
R – радиус описанной окружности,
r – радиус вписанной окружности
a b c
R
4S
2S
r
a b c
14.
Равносторонний треугольникB
АВ=ВС=АС=a
à
R
3
R
r
А
a
r
à
2 3
где R – радиус описанной окружности,
r – радиус вписанной окружности
C
Площадь равностороннего треугольника:
3 2
S
a
4
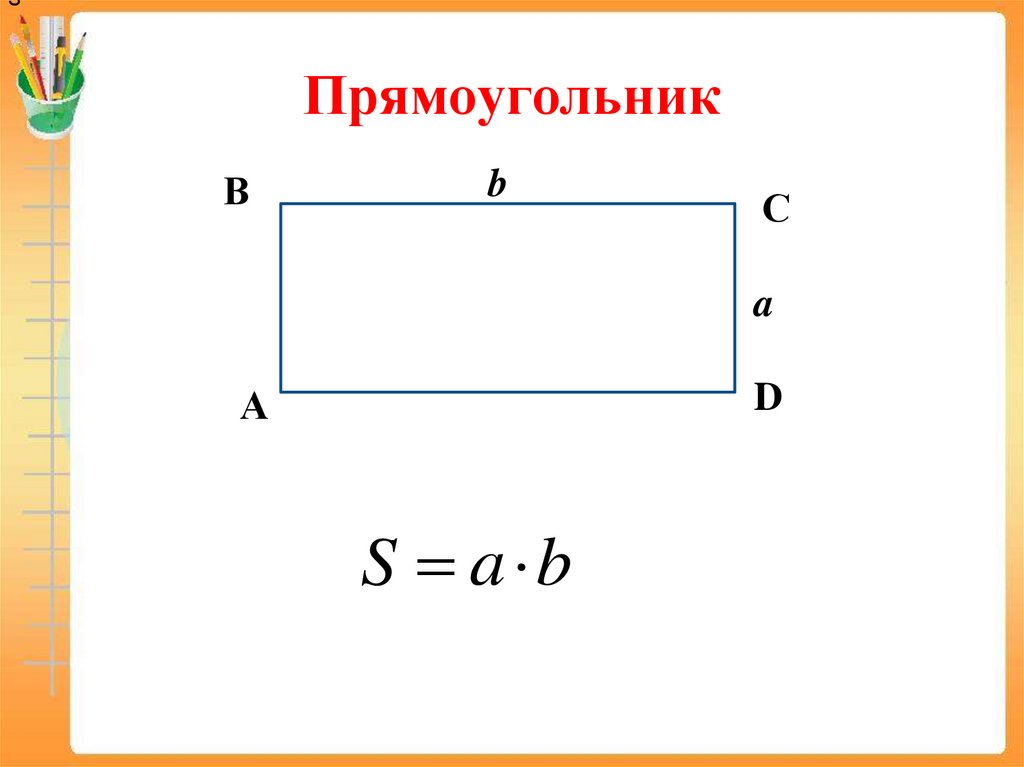
15. Прямоугольник
SПрямоугольник
В
b
С
a
D
А
S a b
16. Параллелограмм
SПараллелограмм
b
В
С
h
А
S b h
a
D
S a b sin A
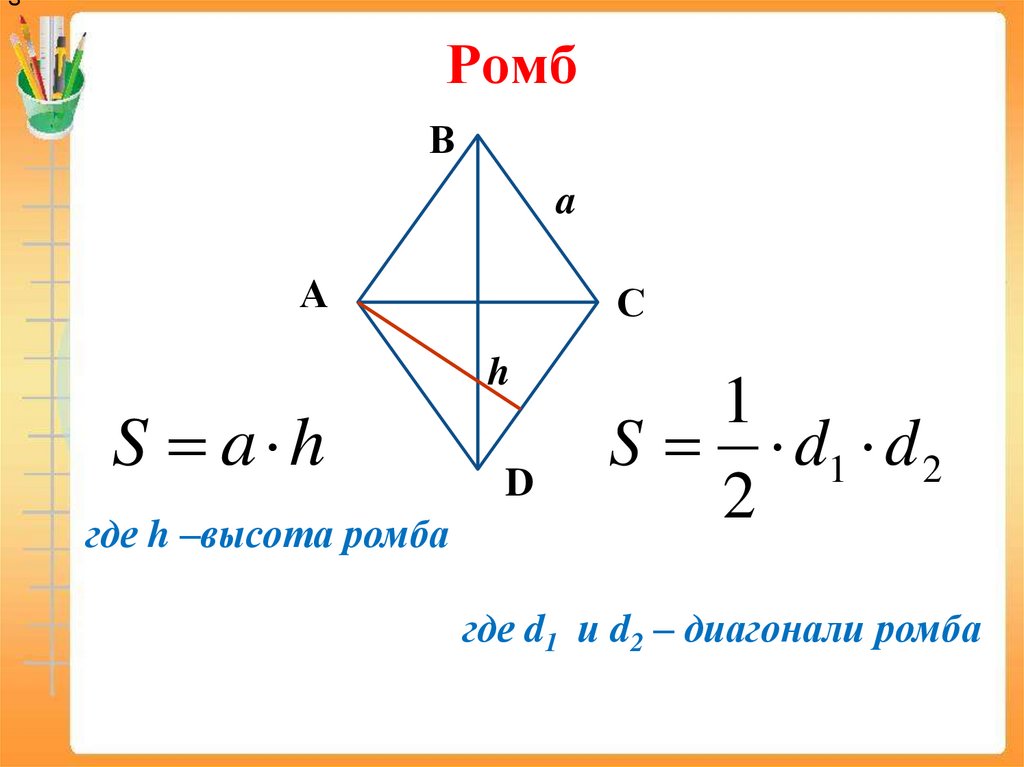
17. Ромб
SРомб
В
a
А
С
h
S a h
где h –высота ромба
D
1
S d1 d 2
2
где d1 и d2 – диагонали ромба
18. Трапеция
SТрапеция
В
С
h
А
D
1
S AD BC h
2
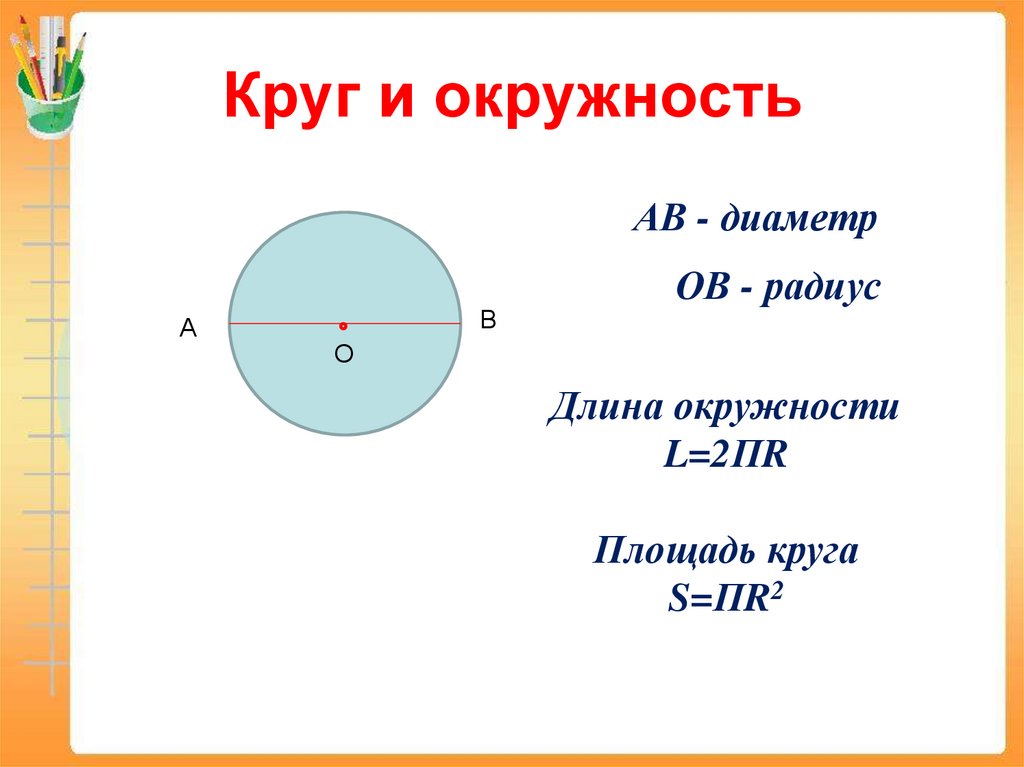
19. Круг и окружность
АВ - диаметрА
В
ОВ - радиус
О
Длина окружности
L=2ПR
Площадь круга
S=ПR2









 Математика
Математика