Треугольник Паскаля

1. Треугольник Паскаля

Цели:
• Познакомиться с
понятием треугольника
Паскаля;
• Изучить свойства
треугольника Паскаля;
• Сформировать умения и
навыки решать задачи на
треугольник Паскаля.

2.

3.

4.

5. Блез Паскаль (1623 – 1662)

• Паскаль умер, когда ему
было 39 лет, но, несмотря
на столь короткую жизнь,
он вошел в историю как
выдающийся математик,
физик, философ и
писатель. Его именем
благодарными потомками
названы единица
давления (паскаль) и
получивший чрезвычайно
широкое распространение
язык программирования.

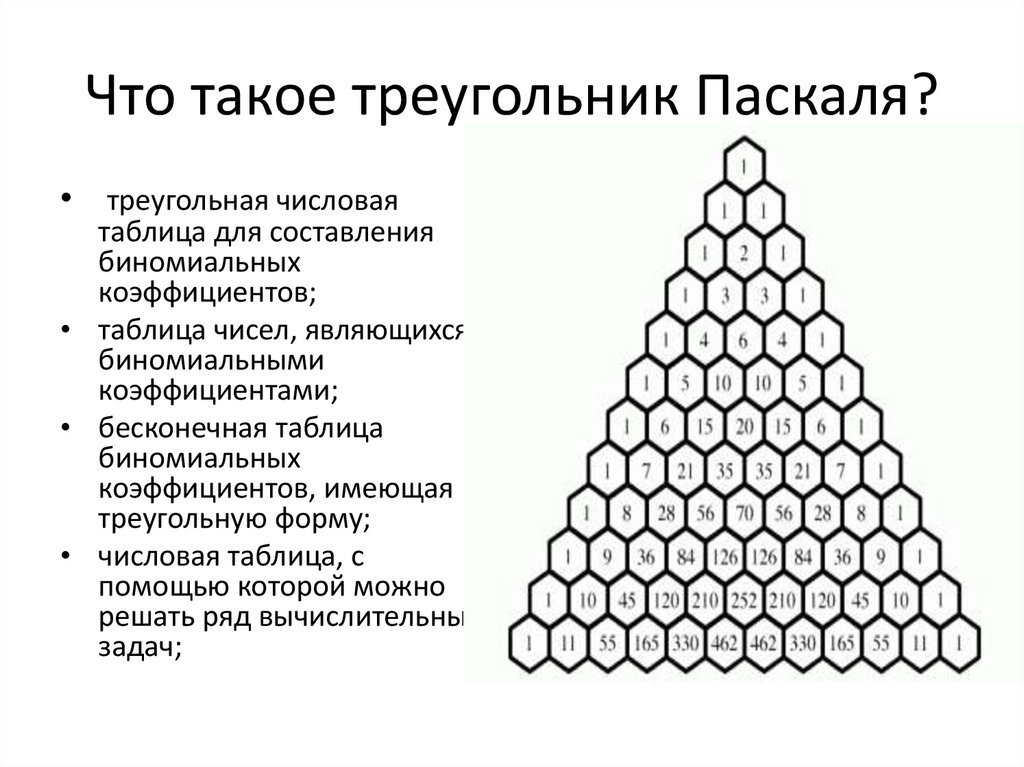
6. Что такое треугольник Паскаля?

• треугольная числовая
таблица для составления
биномиальных
коэффициентов;
• таблица чисел, являющихся
биномиальными
коэффициентами;
• бесконечная таблица
биномиальных
коэффициентов, имеющая
треугольную форму;
• числовая таблица, с
помощью которой можно
решать ряд вычислительных
задач;

7. Мартин Гарднер 21 ОКТЯБРЯ 1914 – 22 МАЯ 2010

Треугольник Паскаля так
прост, что выписать его
сможет даже десятилетний
ребенок. В то же время он
таит в себе неисчерпаемые
сокровища и связывает
воедино различные аспекты
математики, не имеющие на
первый взгляд между собой
ничего общего. Столь
необычные свойства
позволяют считать
треугольник Паскаля одной
из наиболее изящных схем
во всей математике»

8. Принцип построения треугольника Паскаля

• Каждое число равно сумме 2-х чисел, стоящих над ним.

9. Свойства треугольника Паскаля.

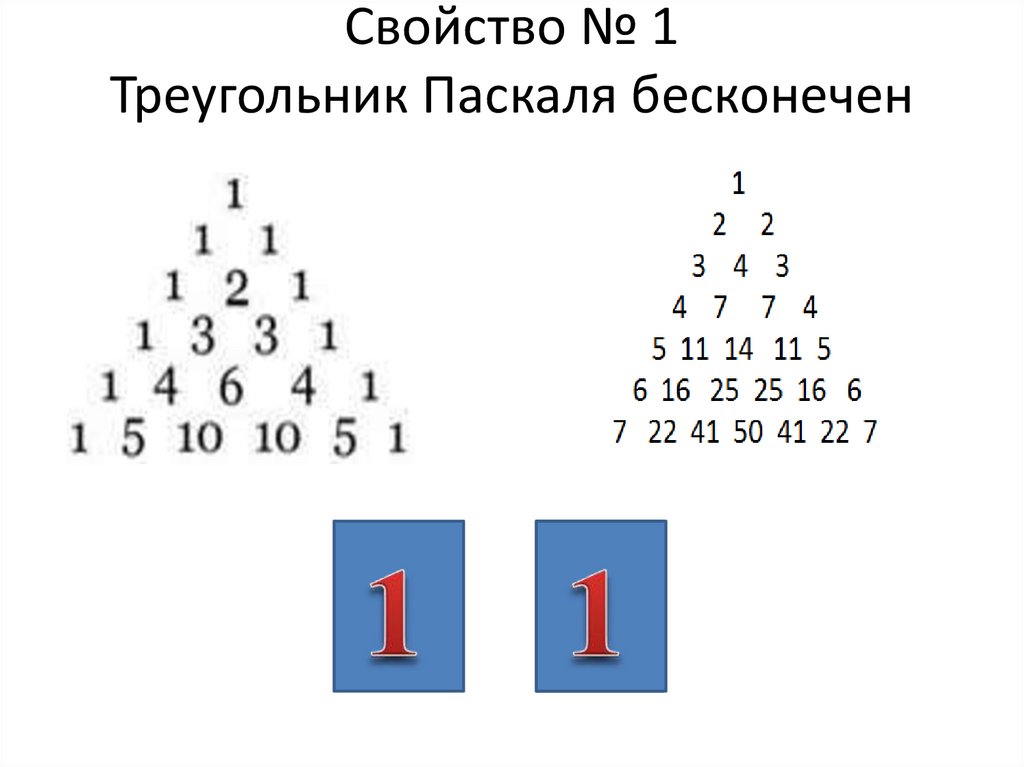
10. Свойство № 1 Треугольник Паскаля бесконечен

11. Свойство № 2 Сумма чисел в строках треугольника Паскаля - 2n, где n - номер строки

1=2°
1+1=2¹
1+2+1=4=2²
1+3+3+1=8=2³
1+4+6+4+1=16= 24
1
2+2=4=2²
3+4+3=10
4+7+7+4=22
5+11+14+11+5=4
6

12. Свойство № 3 Треугольник Паскаля симметричен относительно центрального столбца

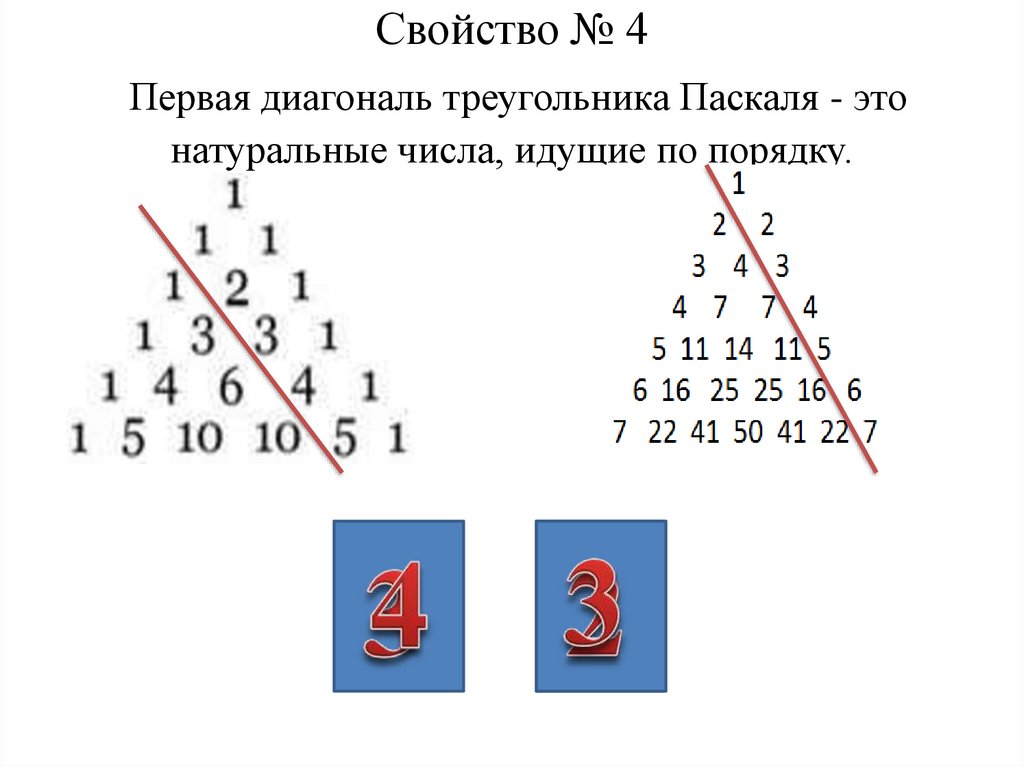
13. Свойство № 4 Первая диагональ треугольника Паскаля - это натуральные числа, идущие по порядку.

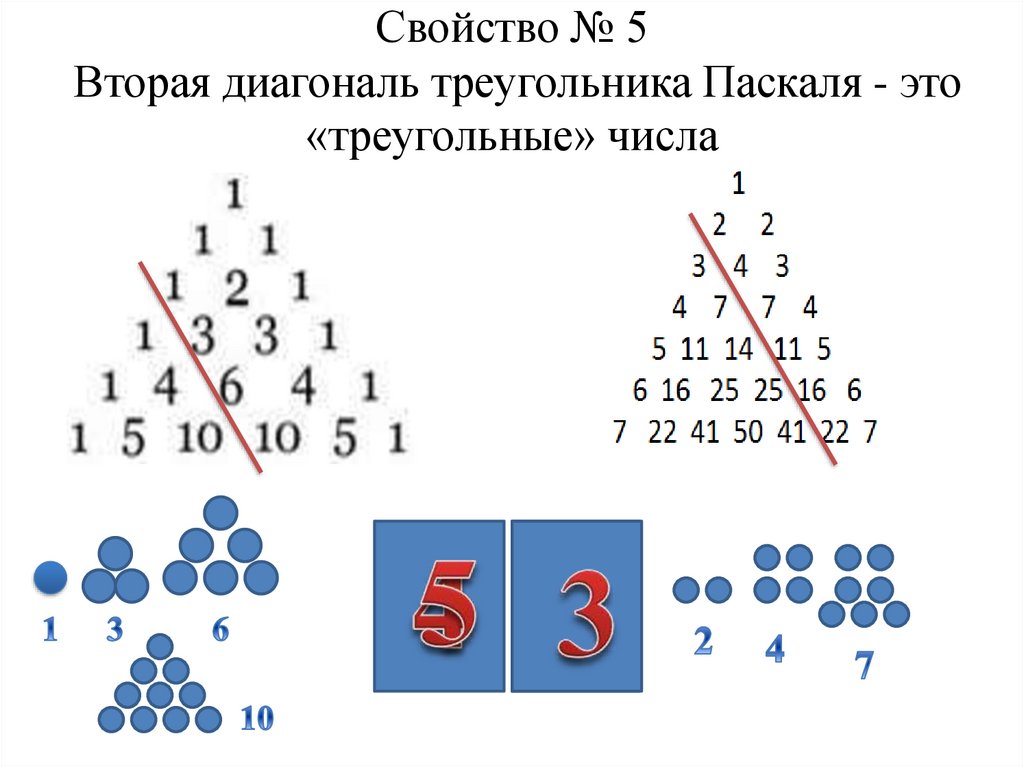
14. Свойство № 5 Вторая диагональ треугольника Паскаля - это «треугольные» числа

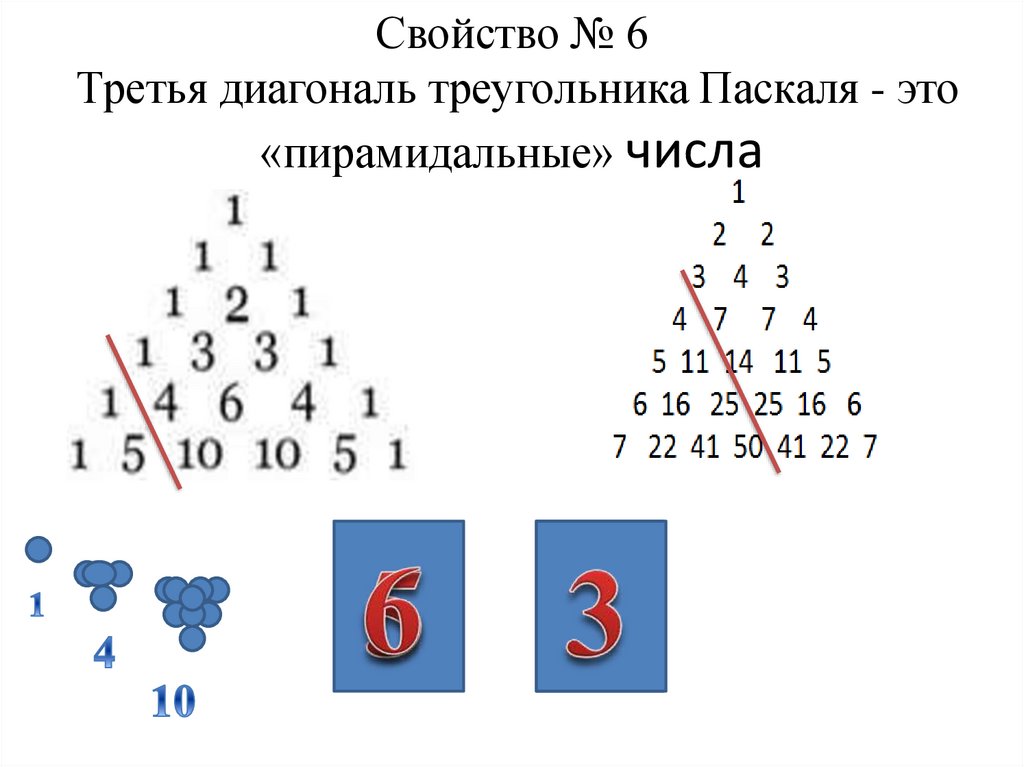
15. Свойство № 6 Третья диагональ треугольника Паскаля - это «пирамидальные» числа

16. Свойство № 7

Четвёртая диагональ треугольника Паскаля это уже
фигурные числа в четырехмерном измерении,
поэтому это можно только представить в
виртуальном мире.

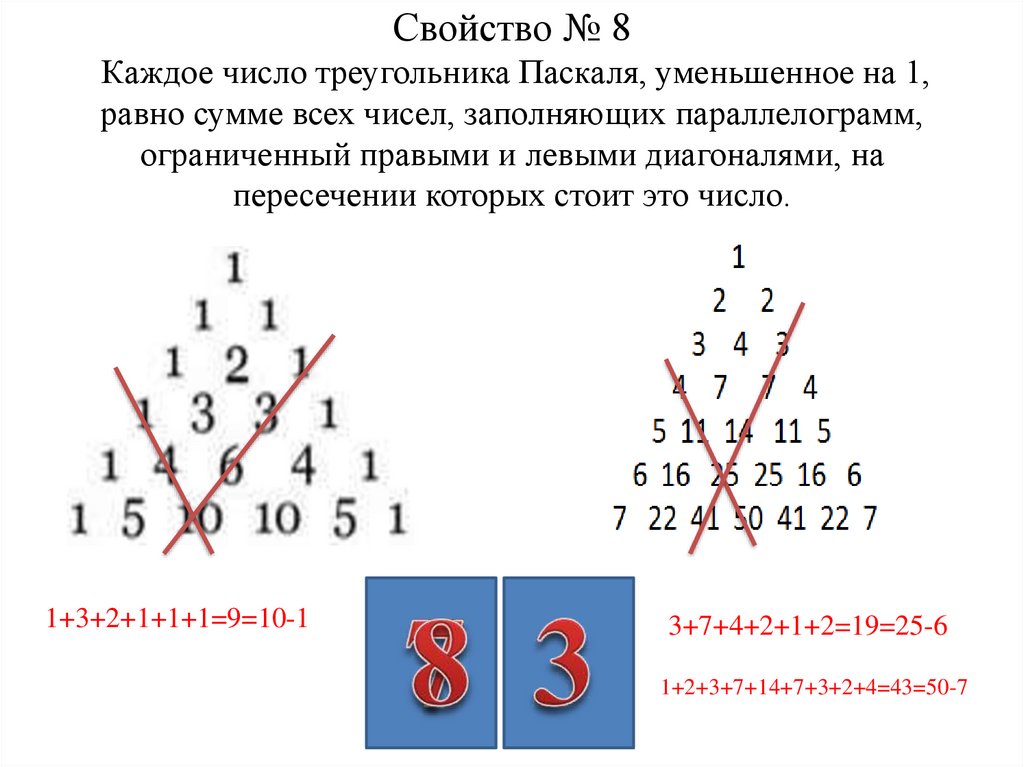
17. Свойство № 8 Каждое число треугольника Паскаля, уменьшенное на 1, равно сумме всех чисел, заполняющих параллелограмм,

ограниченный правыми и левыми диагоналями, на
пересечении которых стоит это число.
1+3+2+1+1+1=9=10-1
3+7+4+2+1+2=19=25-6
1+2+3+7+14+7+3+2+4=43=50-7

18. Свойство № 9 Каждое число треугольника Паскаля равно сумме чисел предыдущей диагонали, стоящей над этим числом.

1+2+3+4=10
2+4+7+11=24=25-1

19. Свойство № 10 В каждой строке треугольника Паскаля сумма чисел на нечётных местах равна сумме чисел на чётных местах.

1+6+1=4+4=8
6+25+16=47=16+25+6
5+14+5= 11+11

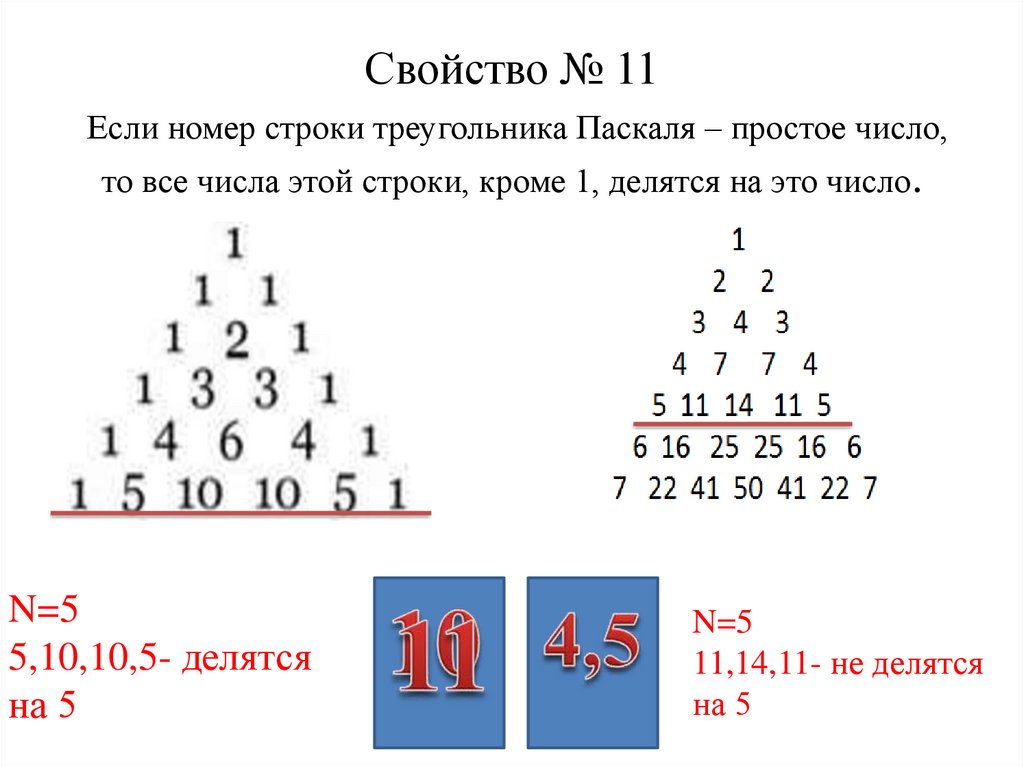
20. Свойство № 11 Если номер строки треугольника Паскаля – простое число, то все числа этой строки, кроме 1, делятся на это число.

N=5
5,10,10,5- делятся
на 5
N=5
11,14,11- не делятся
на 5

21. Свойство № 12 Если нечётное число в треугольнике Паскаля заменить на точки чёрного цвета, а чётные- белого цвета, то

Свойство № 12
Если нечётное число в треугольнике Паскаля
заменить на точки чёрного цвета, а чётныебелого цвета, то треугольник Паскаля
разобьётся на более мелкие треугольники

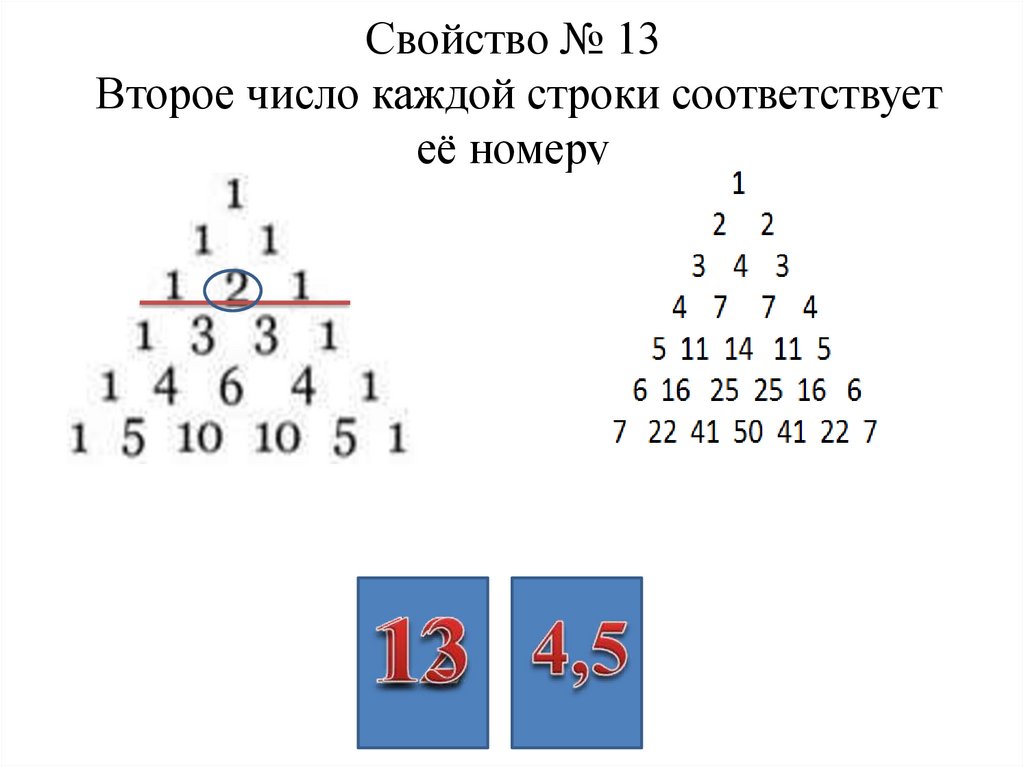
22. Свойство № 13 Второе число каждой строки соответствует её номеру

23. Применение свойств треугольника Паскаля в решении математических задач.

Свойства треугольника Паскаля,
наверное, были бы не столь значимы
если бы на их основе нельзя было
решать математические задачи.
Рассмотрим задачи которые можно
решат с помощью треугольника
Паскаля

24. Задача № 1( олимпиадная)

В город А можно попасть по
единственному входу. На каждом
перекрестке дорога расходится на
две. В город вошли 210 человек.
На каждом перекрестке они
делятся пополам. Сколько
человек окажется на каждом
перекрестке, когда они уже не
смогут разделиться?
Ответ:1,10,45,120,
210,252,210,120,45,
10,1ч.

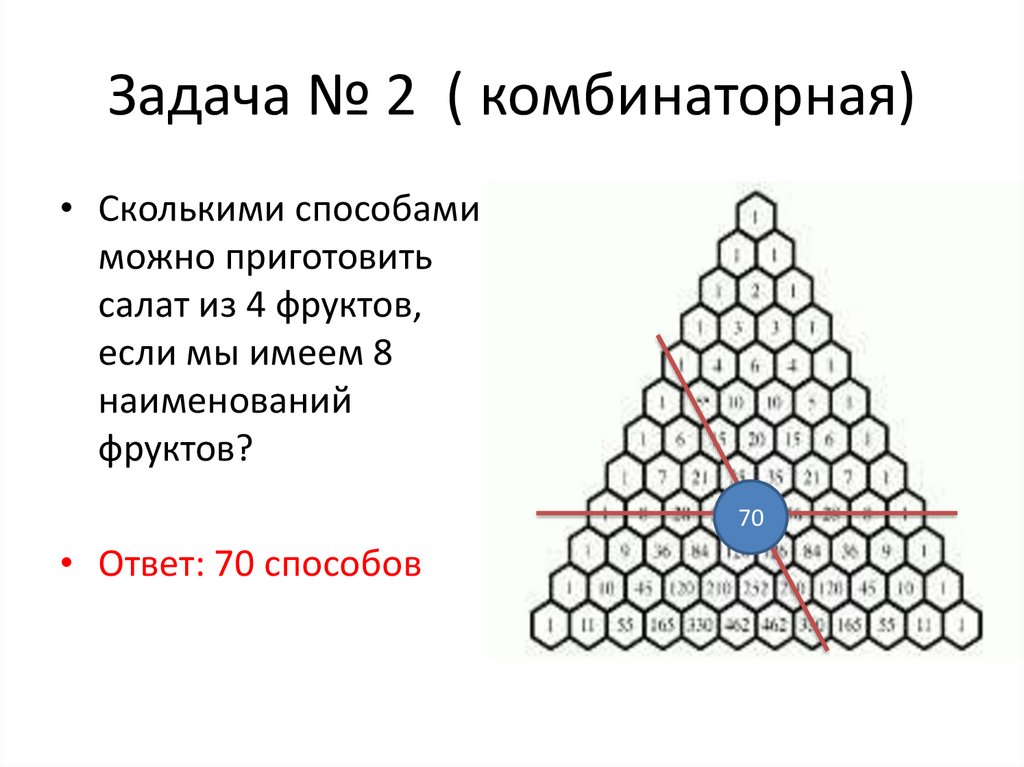
25. Задача № 2 ( комбинаторная)

• Сколькими способами
можно приготовить
салат из 4 фруктов,
если мы имеем 8
наименований
фруктов?
70
• Ответ: 70 способов

26. Задача № 3 ( вероятностная)

• Одновременно вверх
подбросили 7 монет.
Какова вероятность
выпадения 3-х гербов?
35
Ответ: 27%

27. Задача № 4( алгебраическая)

Представить в виде многочлена
выражение (а+в)4
(а+в)0=1
(а+в)1=1а+1в
(а+в)2=1а2+2ав+1в2
……………………………….
(а+в)4=1а4+4а3в+6а2в2+4ав3+1в4

28. Самостоятельная работа

1. Сколькими способами из 9 учебных
предметов можно составить расписание
учебного дня из 6 различных уроков?
2. Сколько различных пятизначных чисел
можно составить из цифр 1, 2, 3, 4, 5?
3. Сколькими способами могут встать в
очередь в билетную кассу 3 человека?
4. Сколькими способами можно выбрать трех
дежурных из группы в 20 человек?

29. Критерии оценки выполнения работы

Критерии оценки выполнения
работы
Оценка
3
4
5
Число заданий,
необходимое для получения
оценки
2
3
4

30. Вывод

• В ходе нашего «путешествия» мы убедились, что
треугольник Паскаля, несмотря на кажущуюся
простоту, действительно обладает рядом
замечательных свойств, знание которых будет
полезно и старшекласснику. Деятельность,
связанную с решением задач с использованием
треугольника Паскаля можно считать по своему
характеру близкой к исследовательской. Решением
таких задач способствует совершенствованию
математической культуры, навыков дедуктивного
мышления и творческих исследовательских
способностей. поэтому этот треугольник и носит
имя одного из выдающихся людей.